An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems

Abstract

Teaching–Learning-Based Optimization (TLBO) algorithms simulate the teaching–learning phenomenon of a classroom to solve multi-dimensional, linear and nonlinear problems with appreciable efficiency. In this paper, the basic TLBO algorithm is improved to enhance its exploration and exploitation capacities by introducing the concept of number of teachers, adaptive teaching factor, tutorial training and self motivated learning. Performance of the improved TLBO algorithm is assessed by implementing it on a range of standard unconstrained benchmark functions having different characteristics. The results of optimization obtained using the improved TLBO algorithm are validated by comparing them with those obtained using the basic TLBO and other optimization algorithms available in the literature.

Keywords

Evolutionary algorithms ; Swarm intelligence based algorithms ; Improved teaching–learning-based optimization ; Unconstrained benchmark functions

1. Introduction

The problem of finding the global optimum of a function with large numbers of local minima arises in many scientific applications. In typical applications, the search space is large and multi-dimensional. Many of these problems cannot be solved analytically, and consequently, they have to be addressed by numerical algorithms. Moreover, in many cases, global optimization problems are non-differentiable. Hence, the gradient-based methods cannot be used for finding the global optimum of such problems. To overcome these problems, several modern heuristic algorithms have been developed for searching near-optimum solutions to the problems. These algorithms can be classified into different groups, depending on the criteria being considered, such as population-based, iterative based, stochastic, deterministic, etc. Depending on the nature of the phenomenon simulated by the algorithms, the population-based heuristic algorithms have two important groups: Evolutionary Algorithms (EA) and swarm intelligence based algorithms.

Some of the recognized evolutionary algorithms are: Genetic Algorithms (GA)  [1] , Differential Evolution (DE)  [2]  and [3] , Evolution Strategy (ES)  [4] , Evolution Programming (EP)  [5] , Artificial Immune Algorithm (AIA)  [6] , and Bacteria Foraging Optimization (BFO)  [7] etc. Some of the well known swarm intelligence based algorithms are: Particle Swarm Optimization (PSO)  [8] , Ant Colony Optimization (ACO)  [9] , Shuffled Frog Leaping (SFL)  [10] , and Artificial Bee Colony (ABC) algorithms  [11] , [12] , [13]  and [14] , etc. Besides the evolutionary and swarm intelligence based algorithms, there are some other algorithms which work on the principles of different natural phenomena. Some of them are: the Harmony Search (HS) algorithm  [15] , the Gravitational Search Algorithm (GSA)  [16] , Biogeography-Based Optimization (BBO)  [17] , the Grenade Explosion Method (GEM)  [18] , the league championship algorithm  [19] and the charged system search  [20]  and [21] .

In order to improve the performance of the above-mentioned algorithms, the exploration and exploitation capacities of different algorithms are combined with each other and hybrid algorithms are produced. Several authors have hybridized different algorithms to improve the performance of individual algorithms  [22] , [23] , [24] , [25] , [26] , [27] , [28] , [29] , [30]  and [31] . Similarly, the performance of existing algorithms is enhanced by modifying their exploration and exploitation capacities  [31] , [32] , [33]  and [34] .

All evolutionary and swarm intelligence based algorithms are probabilistic algorithms and require common controlling parameters, like population size and number of generations. Besides common control parameters, different algorithms require their own algorithm-specific control parameters. For example, GA uses mutation rate and crossover rate. Similarly, PSO uses inertia weight, and social and cognitive parameters. The proper tuning of the algorithm-specific parameters is a very crucial factor affecting the performance of optimization algorithms. The improper tuning of algorithm-specific parameters either increases computational effort or yields the local optimal solution. Considering this fact, recently, Rao et al.  [35]  and [36] and Rao and Patel  [37] introduced the Teaching-Learning-Based Optimization (TLBO) algorithm, which does not require any algorithm-specific parameters. The TLBO requires only common controlling parameters like population size and number of generations for its working. Common control parameters are common in running any population based optimization algorithms; algorithm-specific parameters are specific to that algorithm and different algorithms have different specific parameters to control. However, the TLBO algorithm does not have any algorithm-specific parameters to control and it requires only the control of the common control parameters. Contrary to the opinion expressed by Črepinšek et al.  [38] that TLBO is not a parameter-less algorithm, Rao and Patel  [37] clearly explained that TLBO is an algorithm-specific parameter-less algorithm. In fact, all comments made by Črepinšek et al.  [38] about the TLBO algorithm were already addressed by Rao and Patel  [37] .

In the present work, some improvements in the basic TLBO algorithm are introduced to enhance its exploration and exploitation capacities, and the performance of the Improved Teaching-Learning-Based Optimization (I-TLBO) algorithm is investigated for parameter optimization of unconstrained benchmark functions available in the literature.

The next section describes the basic TLBO algorithm.

2. Teaching-Learning-Based Optimization (TLBO) algorithm

Teaching-learning is an important process where every individual tries to learn something from other individuals to improve themselves. Rao et al.  [35]  and [36] and Rao and Patel  [37] proposed an algorithm, known as Teaching-Learning-Based Optimization (TLBO), which simulates the traditional teaching-learning phenomenon of a classroom. The algorithm simulates two fundamental modes of learning: (i) through the teacher (known as the teacher phase) and (ii) interacting with other learners (known as the learner phase). TLBO is a population-based algorithm, where a group of students (i.e. learner) is considered the population and the different subjects offered to the learners are analogous with the different design variables of the optimization problem. The results of the learner are analogous to the fitness value of the optimization problem. The best solution in the entire population is considered as the teacher. The operation of the TLBO algorithm is explained below with the teacher phase and learner phase  [37] .

2.1. Teacher phase

This phase of the algorithm simulates the learning of the students (i.e. learners) through the teacher. During this phase, a teacher conveys knowledge among the learners and makes an effort to increase the mean result of the class. Suppose there are ‘${\textstyle m}$ ’ number of subjects (i.e. design variables) offered to ‘${\textstyle n}$ ’ number of learners (i.e. population size, ${\textstyle k=1,2,\ldots ,n}$ ). At any sequential teaching-learning cycle, ${\textstyle i,M_{j,i}}$ is the mean result of the learners in a particular subject ‘${\textstyle j}$ ’ (${\textstyle j=1,2,\ldots ,m}$ ). Since a teacher is the most experienced and knowledgeable person on a subject, the best learner in the entire population is considered a teacher in the algorithm. Let ${\textstyle X_{total-kbest,i}}$ be the result of the best learner considering all the subjects who is identified as a teacher for that cycle. The teacher will put maximum effort into increasing the knowledge level of the whole class, but learners will gain knowledge according to the quality of teaching delivered by a teacher and the quality of learners present in the class. Considering this fact, the difference between the result of the teacher and the mean result of the learners in each subject is expressed as:

$Difference\_Mean_{j,i}=r_{i}(X_{j,kbest,i}-T_{F}M_{j,i}){\mbox{,}}$

( 1)

where ${\textstyle X_{j,kbest,i}}$ is the result of the teacher (i.e. best learner) in subject ${\textstyle j}$ . ${\textstyle T_{F}}$ is the teaching factor, which decides the value of mean to be changed, and ${\textstyle r_{i}}$ is the random number in the range ${\textstyle [0,1]}$ . The value of ${\textstyle T_{F}}$ can be either 1 or 2. The value of ${\textstyle T_{F}}$ is decided randomly with equal probability as:

$T_{F}={\mbox{round}}[1+rand(0,1)\lbrace 2-1\rbrace ]{\mbox{,}}$

( 2)

where ${\textstyle rand}$ is the random number in the range [0, 1]. ${\textstyle T_{F}}$ is not a parameter of the TLBO algorithm. The value of ${\textstyle T_{F}}$ is not given as an input to the algorithm and its value is randomly decided by the algorithm using Eq. (2) .

Based on the ${\textstyle Difference\_Mean_{j,i}}$ , the existing solution is updated in the teacher phase according to the following expression:

$X_{j,k,i}^{'}=X_{j,k,i}+Difference\_Mean_{j,i}$

( 3)

where ${\textstyle X_{j,k,i}^{'}}$ is the updated value of ${\textstyle X_{j,k,i}}$ . Accept ${\textstyle X_{j,k,i}^{'}}$ if it gives a better function value. All the accepted function values at the end of the teacher phase are maintained, and these values become the input to the learner phase.

It may be noted that the values of ${\textstyle r_{i}}$ and ${\textstyle T_{F}}$ affect the performance of the TLBO algorithm. ${\textstyle r_{i}}$ is the random number in the range [0, 1] and ${\textstyle T_{F}}$ is the teaching factor. However, the values of ${\textstyle r_{i}}$ and ${\textstyle T_{F}}$ are generated randomly in the algorithm and these parameters are not supplied as input to the algorithm (unlike supplying crossover and mutation probabilities in GA, inertia weight and cognitive and social parameters in PSO, and colony size and limit in ABC, etc.). Thus, tuning of ${\textstyle r_{i}}$ and ${\textstyle T_{F}}$ is not required in the TLBO algorithm (unlike the tuning of crossover and mutation probabilities in GA, inertia weight and cognitive and social parameters in PSO, and colony size and limit in ABC, etc.). TLBO requires tuning of only the common control parameters, like population size and number of generations, for its working, and these common control parameters are required for the working of all population based optimization algorithms. Thus, TLBO can be called an algorithm-specific parameter-less algorithm.

2.2. Learner phase

This phase of the algorithm simulates the learning of the students (i.e. learners) through interaction among themselves. The students can also gain knowledge by discussing and interacting with other students. A learner will learn new information if the other learners have more knowledge than him or her. The learning phenomenon of this phase is expressed below.

Randomly select two learners, ${\textstyle P}$ and ${\textstyle Q}$ , such that ${\textstyle X_{total-P,i}^{'}\not =X_{total-Q,I}^{'}}$ , where, ${\textstyle X_{total-P,i}^{'}}$ and ${\textstyle X_{total-Q,i}^{'}}$ are the updated values of ${\textstyle X_{total-P,i}}$ and ${\textstyle X_{total-Q,i}}$ , respectively, at the end of the teacher phase.

${\begin{array}{l}\displaystyle X_{j,P,i}^{''}=X_{j,P,i}^{'}+r_{i}(X_{j,P,i}^{'}-\\\displaystyle -X_{j,Q,i}^{'}){\mbox{,}}{\mbox{If  }}X_{total-P,i}^{'}>X_{total-Q,i}^{'}{\mbox{,}}\end{array}}$

( 4a)

(The above equations are for maximization problems, the reverse is true for minimization problems.)

Accept ${\textstyle X_{j,P,i}^{''}}$ if it gives a better function value.

3. Improved TLBO (I-TLBO) algorithm

In the basic TLBO algorithm, the result of the learners is improved either by a single teacher (through classroom teaching) or by interacting with other learners. However, in the traditional teaching-learning environment, the students also learn during tutorial hours by discussing with their fellow classmates or even by discussion with the teacher himself/herself. Moreover, sometime students are self motivated and try to learn by themselves. Furthermore, the teaching factor in the basic TLBO algorithm is either 2 or 1, which reflects two extreme circumstances where a learner learns either everything or nothing from the teacher. In this system, a teacher has to expend more effort to improve the results of learners. During the course of optimization, this situation results in a slower convergence rate of the optimization problem. Considering this fact, to enhance the exploration and exploitation capacities, some improvements have been introduced to the basic TLBO algorithm. Rao and Patel  [39]  and [40] made some modifications to the basic TLBO algorithm and applied the same to the optimization of a two stage thermoelectric cooler and heat exchangers. In the present work, the previous modifications are further enhanced and a new modification is introduced to improve the performance of the algorithm.

3.1. Number of teachers

In the basic TLBO algorithm, there is only one teacher who teaches the learners and tries to improve the mean result of the class. In this system of teaching-learning, it might be possible that the efforts of the teacher are distributed and students also pay less attention, which will reduce the intensity of learning. Moreover, if the class contains a higher number of below-average students, then, the teacher has to put more effort into improving their results; even with this effort, there may not be any apparent improvement in the results. In the optimization algorithm, this fact results in a higher number of function evaluations to reach optimum solution and yields a poor convergence rate. In order to overcome this issue, the basic TLBO algorithm is improved by introducing more than one teacher for the learners. By means of this modification, the entire class is split into different groups of learners as per their level (i.e. results), and an individual teacher is assigned to an individual group of learners. Now, each teacher tries to improve the results of his or her assigned group and if the level (i.e. results) of the group reaches up to the level of the assigned teacher, then this group is assigned to a better teacher. This modification is explained in the implementation steps of the algorithm.

The concept of number of teachers is to carry out the population sorting during the course of optimization and, thereby, to avoid the premature convergence of the algorithm.

3.2. Adaptive teaching factor

Another modification is related to the teaching factor (${\textstyle T_{F}}$ ) of the basic TLBO algorithm. The teaching factor decides the value of mean to be changed. In the basic TLBO, the decision of the teaching factor is a heuristic step and it can be either 1 or 2. This practice is corresponding to a situation where learners learn nothing from the teacher or learn all the things from the teacher, respectively. But, in an actual teaching-learning phenomenon, this fraction is not always at its end state for learners but varies in-between also. The learners may learn in any proportion from the teacher. In the optimization algorithm, the lower value of ${\textstyle T_{F}}$ allows the fine search in small steps, but causes slow convergence. A larger value of ${\textstyle T_{F}}$ speeds up the search, but it reduces the exploration capability. Considering this fact, the teaching factor is modified as:

$(T_{F})_{i}=({\frac {X_{total-k}}{X_{total-kbest}}})_{i}k=1,2,\ldots ,n,{\mbox{If  }}X_{total-kbest,i}\not =0{\mbox{,}}$

( 5a)

where ${\textstyle X_{total-k}}$ is the result of any learner, ${\textstyle k}$ , considering all the subjects at iteration, ${\textstyle i}$ , and ${\textstyle X_{total-kbest}}$ is the result of the teacher at the same iteration, ${\textstyle i}$ . Thus, in the I-TLBO algorithm, the teaching factor varies automatically during the search. Automatic tuning of TF improves the performance of the algorithm.

It may be noted that the adaptive teaching factor in TLBO is generated within the algorithm, based on the result of learner and teacher. Thus, the adaptive teaching factor is not supplied as an input parameter to the algorithm.

3.3. Learning through tutorial

This modification is based on the fact that the students can also learn by discussing with their fellow classmates or even with the teacher during the tutorial hours while solving the problems and assignments. Since the students can increase their knowledge by discussion with other students or the teacher, we incorporate this search mechanism into the teacher phase. Mathematical expression of this modification is given in the implementation steps of the algorithm.

3.4. Self-motivated learning

In the basic TLBO algorithm, the results of the students are improved either by learning from the teacher or by interacting with the other students. However, it is also possible that students are self motivated and improve their knowledge by self-learning. Thus, the self-learning aspect to improvise the knowledge is considered in the I-TLBO algorithm.

• Define the optimization problem as Minimize or Maximize ${\textstyle f(X)}$
• where ${\textstyle f(X)}$ is the objective function value and ${\textstyle X}$ is a vector for design variables.
• Initialize the population (i.e. learners, ${\textstyle k=1,2,\ldots ,n}$ ) and design variables of the optimization problem (i.e., number of subjects offered to the learners, ${\textstyle j=1,2,\ldots ,m}$ ), and evaluate them.
• Select the best solution (i.e.  ${\textstyle f(X)_{best}}$ ) who acts as chief teacher for that cycle. Assign him/her to first rank.

$(X_{teacher})_{1}=f(X)_{1}\quad {\mbox{where  }}f(X)_{1}=f(X)_{best}{\mbox{.}}$

• Select the other teachers (${\textstyle T}$ ) based on the chief teacher and rank them,

$f(X)_{s}=f(X)_{1}-rand^{_{\ast }}\quad f(X)_{1}s=2,3,\ldots ,T{\mbox{.}}$

(If the equality is not met, select the ${\textstyle f(X)_{s}}$ closest to the value calculated above)

$(X_{teacher})_{s}=f(X)_{s}{\mbox{,}}\quad {\mbox{where}}s=2,3,\ldots ,T{\mbox{.}}$

• Assign the learners to the teachers according to their fitness value as:
• For ${\textstyle k=1:(n-s)}$
• If ${\textstyle f(X)_{1}\geq f(X)_{k}>f(X)_{2}}$ ,
• assign the learner ${\textstyle f(X)_{k}}$ to teacher ${\textstyle 1}$ (i.e ${\textstyle f(X)_{1}}$ ).
• Else, if ${\textstyle f(X)_{2}\geq f(X)_{k}>f(X)_{3}}$ ,
• assign the learner ${\textstyle f(X)_{k}}$ to teacher ${\textstyle 2}$ (i.e ${\textstyle f(X)_{2}}$ ).
• ${\textstyle \vdots }$
• Else, if ${\textstyle f(X)_{T-1}\geq f(X)_{k}>f(X)_{T}}$ ,
• assign the learner ${\textstyle f(X)_{k}}$ to teacher ‘${\textstyle T-1}$ ’ (i.e ${\textstyle f(X)_{T-1}}$ ).
• Else,
• assign the learner ${\textstyle f(X)_{k}}$ to teacher ‘${\textstyle T}$ ’
• End
• (The above procedure is for a maximization problem; the procedure is reversed for a minimization problem.)
• Keep the elite solutions of each group.
• Calculate the mean result of each group of learners in each subject (i.e.  ${\textstyle (M_{j})_{s}}$ ).
• For each group, evaluate the difference between the current mean and the corresponding result of the teacher of that group for each subject by utilizing the adaptive teaching factor (given by Eqs.  and  ) as:

${\begin{array}{l}\displaystyle (Difference_{M}ean_{j})_{s}=rand(X_{j,teacher}-T_{F}M_{j})_{s}\quad s=1\\\displaystyle 2,\ldots ,T,j=1,2\ldots ,m{\mbox{.}}\end{array}}$

• For each group, update the learners’ knowledge with the help of the teacher’s knowledge, along with the knowledge acquired by the learners during the tutorial hours, according to:

${\begin{array}{l}\displaystyle (X_{j,k}^{'})_{s}=(X_{j,k}+Difference_{M}ean_{j})_{s}+rand(X_{hh}-\\\displaystyle -X_{k})_{s}{\mbox{,}}{\mbox{If}}f(X)_{hh}>f(X)_{k}\end{array}}$

where ${\textstyle hh\not =k}$ and,

• For each group, update the learners’ knowledge by utilizing the knowledge of some other learners, as well as by self learning, according to:

${\begin{array}{l}\displaystyle (X_{j,k}^{''})_{s}=X_{j,k,i}^{'}+rand(X_{j,k}^{'}-X_{j,p}^{'})_{s}+\\\displaystyle +rand(X_{teacher}-E_{F}X_{j,k}^{'})_{s}{\mbox{,}}{\mbox{If  }}f(X_{k}^{'})>f(X_{p}^{'})\end{array}}$

where ${\textstyle E_{F}={\mbox{exploration factor}}={\mbox{round}}(1+{\mbox{rand}})}$ .

• (The above equations are for a maximization problem, the reverse is true for a minimization problem.)
• Replace the worst solution of each group with an elite solution.
• Eliminate the duplicate solutions randomly.
• Combine all the groups.
• Repeat the procedure from step 3 to 13 until the termination criterion is met.

At this point, it is important to clarify that in the TLBO and I-TLBO algorithms, the solution is updated in the teacher phase as well as in the learner phase. Also, in the duplicate elimination step, if duplicate solutions are present, then they are randomly modified. So, the total number of function evaluations in the TLBO algorithm is = {(2 × population size × number of generations) + (function evaluations required for duplicate elimination)}. In the entire experimental work of this paper, the above formula is used to count the number of function evaluations while conducting experiments with TLBO and I-TLBO algorithms.

4. Experiments on unconstrained benchmark functions

In this section, the ability of the I-TLBO algorithm is assessed by implementing it for the parameter optimization of several unconstrained benchmark functions with different dimensions and search space. Results obtained using the I-TLBO algorithm are compared with the results of the basic TLBO algorithm, as well as with other optimization algorithms available in literature. The considered benchmark functions have different characteristics, like unimodality/multimodality, separability/non-separability and regularity/non-regularity.

4.1. Experiment-1

This experiment is conducted to identify the ability of the I-TLBO algorithm to achieve the global optimum value. In this experiment, eight different benchmark functions are tested using the TLBO and I-TLBO algorithms, which were earlier solved using ABC and modified ABC by Akay and Karaboga  [33] . The details of the benchmark functions are given in Table 1 . Previously, Akay and Karaboga  [33] experimented all functions with 30 000 maximum function evaluations. To maintain the consistency in the comparison, TLBO and I-TLBO algorithms are also experimented with the same maximum function evaluations.

Table 1. Benchmark functions considered in experiment 1.

No.	Function	Formulation	${\textstyle D}$	Search range	Initialization range
1	Sphere	${\textstyle F_{min}=\sum _{i=1}^{D}x_{i}^{2}}$	10	${\textstyle [-100,100]}$	${\textstyle [-100,50]}$
2	Rosenbrock	${\textstyle F_{min}=\sum _{i=1}^{D}[100(x_{i}^{2}-x_{i+1})^{2}+(1-x_{i})^{2}]}$	10	${\textstyle [-2.048,2.048]}$	${\textstyle [-2.048,2.048]}$
3	Ackley	${\textstyle F+min=-20exp(-0.2{\sqrt {{\frac {1}{D}}\sum _{i+1}^{D}x_{i}^{2}}})-exp({\frac {1}{D}}\sum _{i=1}^{D}cos2\pi x_{i})+20+e}$	10	${\textstyle [-32.768,32.768]}$	${\textstyle [-32.768,16]}$
4	Griewank	${\textstyle F_{min}={\frac {1}{4000}}\sum _{i=1}^{D}x_{i}^{2}-\prod _{i=1}^{D}cos({\frac {x_{i}}{\sqrt {i}}})+1}$	10	${\textstyle [-600,600]}$	${\textstyle [-600,200]}$
5	Weierstrass	${\textstyle {\begin{array}{l}\displaystyle F_{min}=\sum _{i=1}^{D}(\sum _{k=0}^{k_{m}ax}[a^{k}cos(2\pi b^{k}(x_{i}+0.5))])-\\\displaystyle -D\sum _{k=0}^{k_{m}ax}[a^{k}cos(2\pi b^{k}0.5)],a=0.5,b=3,k_{max}=20\end{array}}}$	10	${\textstyle [-0.5,0.5]}$	${\textstyle [-0.5,0.2]}$
6	Rastrigin	${\textstyle F_{min}=\sum _{i=1}^{D}[x_{i}^{2}-10cos(2\pi x_{i})+10]}$	10	${\textstyle [-5.12,5.12]}$	${\textstyle [-5.12,2]}$
7	NCRastrigin	${\textstyle F_{min}=\sum _{i=1}^{D}[y_{i}^{2}-10cos(2\pi y_{i})+10]y_{i}=\lbrace {\begin{array}{cc}x_{i}{\mbox{,}}&\vert x_{i}\vert <0.5{\mbox{,}}\\{\frac {{\mbox{round}}(2x_{i})}{2}}{\mbox{,}}&\vert x_{i}\vert \geq 0.5\end{array}}}$	10	${\textstyle [-5.12,5.12]}$	${\textstyle [-5.12,2]}$
8	Schwefel	${\textstyle F_{min}=-\sum _{i=1}^{D}(x_{i}sin({\sqrt {\vert x_{i}\vert }}))}$	10	${\textstyle [-500,500]}$	${\textstyle [-500,500]}$

D: Dimension.

Each benchmark function is experimented 30 times with TLBO and I-TLBO algorithms and comparative results, in the form of mean value and standard deviation of objective function obtained after 30 independent runs, are shown in Table 2 . Except TLBO and I-TLBO algorithms, the rest of the results are taken from the previous work of Akay and Karaboga  [33] . Moreover, the I-TLBO algorithm is experimented with different numbers of teachers, and the effect on the obtained objective function value is reported in Table 2 .

Table 2. Comparative results of TLBO and I-TLBO with other evolutionary algorithms over 30 independent runs.

	Mean ± SD	Mean ± SD	Mean ± SD	Mean ± SD
	Sphere	Rosenbrock	Ackley	Griewank
PSO–w	7.96E−051 ± 3.56E−050	3.08E+000 ± 7.69E−001	1.58E−014 ± 1.60E−014	9.69E−002 ± 5.01E−002
PSO–cf	9.84E−105 ± 4.21E−104	6.98E−001 ± 1.46E+000	9.18E−001 ± 1.01E+000	1.19E−001 ± 7.11E−002
PSO–w-local	2.13E−035 ± 6.17E−035	3.92E+000 ± 1.19E+000	6.04E−015 ± 1.67E−015	7.80E−002 ± 3.79E−002
PSO–cf-local	1.37E−079 ± 5.60E−079	8.60E−001 ± 1.56E+000	5.78E−002 ± 2.58E−001	2.80E−002 ± 6.34E−002
UPSO	9.84E−118 ± 3.56E−117	1.40E+000 ± 1.88E+000	1.33E+000 ± 1.48E+000	1.04E−001 ± 7.10E−002
FDR	2.21E−090 ± 9.88E−090	8.67E−001 ± 1.63E+000	3.18E−014 ± 6.40E−014	9.24E−002 ± 5.61E−002
FIPS	3.15E−030 ± 4.56E−030	2.78E+000 ± 2.26E−001	3.75E−015 ± 2.13E−014	1.31E−001 ± 9.32E−002
CPSO-H	4.98E−045 ± 1.00E−044	1.53E+000 ± 1.70E+000	1.49E−014 ± 6.97E−015	4.07E−002 ± 2.80E−002
CLPSO	5.15E−029 ± 2.16E−28	2.46E+000 ± 1.70E+000	4.32E−10 ± 2.55E−014	4.56E−003 ± 4.81E−003
ABC	7.09E−017 ± 4.11E−017	2.08E+000 ± 2.44E+000	4.58E−016 ± 1.76E−016	1.57E−002 ± 9.06E−003
Modified ABC	7.04E−017 ± 4.55E−017	4.42E−001 ± 8.67E−001	3.32E−016 ± 1.84E−016	1.52E−002 ± 1.28E−002
TLBO	0.00 ± 0.00	1.72E+00 ± 6.62E−01	3.55E−15 ± 8.32E−31	0.00 ± 0.00
I-TLBO
${\textstyle (NT=1)}$	0.00 ± 0.00	1.29E+00 ± 3.97E−01	3.11E−15 ± 4.52E−15	0.00 ± 0.00
${\textstyle (NT=2)}$	0.00 ± 0.00	1.13E+00 ± 4.29E−01	2.93E−15 ± 1.74E−15	0.00 ± 0.00
${\textstyle (NT=3)}$	0.00 ± 0.00	6.34E−01 ± 2.53E−01	2.02E−15 ± 1.51E−15	0.00 ± 0.00
${\textstyle (NT=4)}$	0.00 ± 0.00	2.00E−01 ± 1.42E−01	1.42E−15 ± 1.83E−15	0.00 ± 0.00
	Weierstrass	Rastrigin	NCRastrigin	Schwefel
PSO–w	2.28E−003 ± 7.04E−003	5.82E+000 ± 2.96E+000	4.05E+000 ± 2.58E+000	3.20E+002 ± 1.85E+002
PSO–cf	6.69E−001 ± 7.17E−001	1.25E+001 ± 5.17E+000	1.20E+001 ± 4.99E+000	9.87E+002 ± 2.76E+002
PSO–w-local	1.41E−006 ± 6.31E−006	3.88E+000 ± 2.30E+000	4.77E+000 ± 2.84E+000	3.26E+002 ± 1.32E+002
PSO–cf-local	7.85E−002 ± 5.16E−002	9.05E+000 ± 3.48E+000	5.95E+000 ± 2.60E+000	8.78E+002 ± 2.93E+002
UPSO	1.14E+000 ± 1.17E+00	1.17E+001 ± 6.11E+000	5.85E+000 ± 3.15E+000	1.08E+003 ± 2.68E+002
FDR	3.01E−003 ± 7.20E−003	7.51E+000 ± 3.05E+000	3.35E+000 ± 2.01E+000	8.51E+002 ± 2.76E+002
FIPS	2.02E−003 ± 6.40E−003	2.12E+000 ± 1.33E+000	4.35E+000 ± 2.80E+000	7.10E+001 ± 1.50E+002
CPSO-H	1.07E−015 ± 1.67E−015	0 ± 0	2.00E−001 ± 4.10E−001	2.13E+002 ± 1.41E+002
CLPSO	0 ± 0	0 ± 0	0 ± 0	0 ± 0
ABC	9.01E−006 ± 4.61E−005	1.61E−016 ± 5.20E−016	6.64E−017 ± 3.96E−017	7.91E+000 ± 2.95E+001
Modified ABC	0.00E+000 ± 0.00E+000	1.14E−007 ± 6.16E−007	1.58E−011 ± 7.62E−011	3.96E+000 ± 2.13E+001
TLBO	2.42E−05 ± 1.38E−20	6.77E−08 ± 3.68E−07	2.65E−08 ± 1.23E−07	2.94E+02 ± 2.68E+02
I-TLBO
${\textstyle (NT=1)}$	9.51E−06 ± 1.74E−05	3.62E−12 ± 7.82E−11	1.07E−08 ± 6.19E−08	2.73E+02 ± 2.04E+02
${\textstyle (NT=2)}$	3.17E−06 ± 2.66E−06	2.16E−15 ± 9.13E−16	5.16E−09 ± 4.43E−09	2.62E+02 ± 2.13+02
${\textstyle (NT=3)}$	0.00 ± 0.00	0.00 ± 0.00	7.78E−016 ± 4.19E−015	1.49E+02 ± 1.21+02
${\textstyle (NT=4)}$	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	1.10E+02 ± 1.06E+02

Results of algorithms except TLBO and I-TLBO are taken from Ref.  [33] .

It is observed from the results that the I-TLBO algorithm has achieved the global optimum value for Sphere, Griewank, Weierstrass, Rastrtigin and NCrastrigin functions, within the specified number of function evaluations. For the Rosenbrock function, I-TLBO performs better than the rest of the algorithms. The performance of TLBO and I-TLBO algorithms is better than the rest of the considered algorithms for Sphere and Griewank functions. For Weierstrass, Rastrigin and NCrastrigin functions, the performance of I-TLBO and CLPSO are identical and better than the rest of the considered algorithms. For the Ackley function, ABC and I-TLBO algorithms perform equally well. For the Schwefel function, the modified ABC algorithm performs better than the rest of the considered algorithms.

It is observed from the results that the fitness value of the objective function is improved as the number of teachers is increased from 1 to 4 for the I-TLBO algorithm. During the experimentation, it is observed that with a further increase in the number of teachers beyond 4, the improvement in the fitness value of the objective function is insignificant and it involves significant increment in computational effort.

4.2. Experiment-2

To indentify the computational effort and consistency of the I-TLBO algorithm, eight different benchmark functions considered by Ahrari and Atai  [18] are tested in this experiment. The results obtained using the I-TLBO algorithm are compared with the basic TLBO algorithm, along with other well known optimization algorithms. The details of the benchmark functions are given in Table 3 .

Table 3. Benchmark functions considered in experiment 2.

No.	Function	Formulation	${\textstyle D}$	Search range
1	De Jong	${\textstyle F_{min}=3905.93-100(x_{1}^{2}-x_{2})^{2}-(1-x_{1})^{2}}$	2	${\textstyle [-2.048,2.048]}$
2	GoldStein–Price	${\textstyle {\begin{array}{l}\displaystyle F_{m}in=[1+(x_{1}+x_{2}+1)^{2}(19-14x_{1}+3x_{1}^{2}-14x_{2}+6x_{1}x_{2}+\\\displaystyle +3x_{2}^{2})][30+(2x_{1}-3x_{2})^{2}(18-32x_{1}+12x_{1}^{2}+48x_{2}-\\\displaystyle -36x_{1}x_{2}+27x_{2}^{2})]\end{array}}}$	2	${\textstyle [-2,2]}$
3	Branin	${\textstyle F_{min}=(x_{2}-{\frac {5.1}{4\pi ^{2}}}x_{1}^{2}+{\frac {5}{\pi }}x_{1}-6)^{2}+10(1-{\frac {1}{8\pi }})cosx_{1}+10}$	2	${\textstyle [-5,10]}$
4	Martin and Gaddy	${\textstyle F_{min}=(x_{1}-x_{2})^{2}+[(x_{1}+x_{2}-10)/3]^{2}}$	2	${\textstyle [0,10]}$
5	Rosenbrock	${\textstyle F_{min}=100(x_{1}^{2}-x_{2})^{2}+(1-x_{1})^{2}}$	2	${\textstyle [-1.2,1.2]}$
6	Rosenbrock	${\textstyle F_{min}=100(x_{1}^{2}-x_{2})^{2}+(1-x_{1})^{2}}$	2	${\textstyle [-10,10]}$
7	Rosenbrock	${\textstyle F_{min}=\sum _{i=1}^{D}(100(x_{1}^{2}-x_{2})^{2}+(1-x_{1})^{2})}$	3	${\textstyle [-10,10]}$
8	Hyper Sphere	${\textstyle F_{min}=\sum _{i=1}^{D}x_{i}^{2}}$	6	${\textstyle [-5.12,5.12]}$

D: Dimension.

To maintain the consistency in the comparison between all comparative algorithms, the execution of the TLBO and I-TLBO algorithms are stopped when the difference between the fitness obtained by the algorithm and the global optimum value is less than 0.1% (in cases where the optimum value is 0, the solution is accepted if it differs from the optimum value by less than 0.001). While making this complete study, the I-TLBO algorithm is examined for different numbers of teachers and its effect on the performance of the algorithm is included in the results. Each benchmark function is experimented 100 times with the TLBO and I-TLBO algorithms and the comparative results in the form of mean function evaluations and success percentage is shown in Table 4 . The results of the other algorithms are taken from Ahrari and Atai  [18] .

Table 4. Comparison of results of evolutionary algorithms considered in experiment 2.

	MNFE	Succ %	MNFE	Succ %	MNFE	Succ %	MNFE	Succ %
	De Jong		Goldstein and Price		Branin		Martin and Gaddy
SIMPSA	–	–	–	–	–	–	–	–
NE-SIMPSA	–	–	–	–	–	–	–	–
GA	10 160	100	5662	100	7325	100	2488	100
ANTS	6000	100	5330	100	1936	100	1688	100
Bee Colony	868	100	999	100	1657	100	526	100
GEM	746	100	701	100	689	100	258	100
TLBO	1070	100	452	100	443	100	422	100
I-TLBO
${\textstyle (NT=1)}$	836	100	412	100	438	100	350	100
${\textstyle (NT=2)}$	784	100	386	100	421	100	312	100
${\textstyle (NT=3)}$	738	100	302	100	390	100	246	100
${\textstyle (NT=4)}$	722	100	288	100	367	100	233	100
	Rosenbrock (${\textstyle D=2}$ )		Rosenbrock (${\textstyle D=2}$ )		Rosenbrock (${\textstyle D=4}$ )		Hyper sphere (${\textstyle D=6}$ )
SIMPSA	10 780	100	12 500	100	21 177	99	–	–
NE-SIMPSA	4508	100	5007	100	3053	94	–	–
GA	10 212	100	–	–	–	–	15 468	100
ANTS	6842	100	7505	100	8471	100	22 050	100
Bee Colony	631	100	2306	100	28 529	100	7113	100
GEM	572	100	2289	100	82 188	100	423	100
TLBO	669	100	1986	100	21 426	100	417	100
I-TLBO
${\textstyle (NT=1)}$	646	100	1356	100	20 462	100	410	100
${\textstyle (NT=2)}$	602	100	1268	100	20 208	100	396	100
${\textstyle (NT=3)}$	554	100	1024	100	18 490	100	382	100
${\textstyle (NT=4)}$	522	100	964	100	17 696	100	376	100

Results of algorithms except TLBO and I-TLBO are taken from Ref.  [18] .

It is observed from Table 4 that except for function 7 (i.e. Rosenbrock (${\textstyle D=4}$ )), the I-TLBO algorithm requires less number of function evaluations than other algorithms to reach the global optimum value, with a very high success rate of 100%. For the Rosenbrock 4 dimension function, the ant colony system (ANTS) performs better than I-TLBO with 100% success rate. Similar to previous experiments, here, also, the results are improved further as the number of teachers is increased from 1 to 4 at the cost of more computational time.

4.3. Experiment-3

In this experiment, the performance of the I-TLBO algorithm is compared with the recently developed ABC algorithm, along with its improvised versions (I-ABC and GABC) and hybrid version (PS-ABC). In this part of the work, TLBO and I-TLBO are experimented on 23 unconstrained benchmark functions (as shown in Table 5 ), which was earlier attempted by Li et al.  [31] . This experiment is conducted from small scale to large scale by considering the dimensions 20, 30 and 50 of all the benchmark functions.

Table 5. Benchmark functions considered in experiment 3.

No.	Function	Formulation	Search range	C
1	Sphere	${\textstyle F_{min}=\sum _{i=1}^{D}x_{i}^{2}}$	${\textstyle [-100,100]}$	US
2	Schwefel 2.22	${\textstyle F_{min}=\sum _{i=1}^{D}\vert x_{i}\vert +\prod _{i=1}^{D}\vert x_{i}\vert }$	${\textstyle [-10,10]}$	UN
3	Schwefel 1.2	${\textstyle F_{min}=\sum _{i=1}^{D}(\sum _{j=1}^{i}x_{j}^{2})^{2}}$	${\textstyle [-100,100]}$	UN
4	Schwefel 2.21	${\textstyle F_{min}=max(\vert x_{i}\vert )}$	${\textstyle [-100,100]}$	UN
5	Rosenbrock	${\textstyle F_{min}=\sum _{i=1}^{D}[100(x_{i}^{2}-x_{i+1})^{2}+(1-x_{i})^{2}]}$	${\textstyle [-30,30]}$	UN
6	Step	${\textstyle F_{min}=\sum _{i=1}^{D}[\vert x_{i}+0.5\vert ]^{2}}$	${\textstyle [-100,100]}$	US
7	Quartic	${\textstyle F_{min}=\sum _{i=1}^{D}ix_{i}^{4}+{\mbox{rand}}\quad (0,1)}$	${\textstyle [-1.28,1.28]}$	US
8	Schwefel	${\textstyle F_{min}=-\sum _{i=1}^{D}(x_{i}sin({\sqrt {\vert x_{i}\vert }}))}$	${\textstyle [-500,500]}$	MS
9	Rastrigin	${\textstyle F_{min}=\sum _{i=1}^{D}[x_{i}^{2}-10cos(2\pi x_{i})+10]}$	${\textstyle [-5.12,5.12]}$	MS
10	Ackley	${\textstyle F_{min}=-20exp(-0.2{\sqrt {{\frac {1}{D}}\sum _{i=1}^{D}x_{i}^{2}}})-exp({\frac {1}{D}}\sum _{i=1}^{D}cos2\pi x_{i})+20+e}$	${\textstyle [-32,32]}$	MN
11	Griewank	${\textstyle F_{min}={\frac {1}{4000}}\sum _{i=1}^{D}x_{i}^{2}-\prod _{i=1}^{D}cos({\frac {x_{i}}{\sqrt {i}}})+1}$	${\textstyle [-600,600]}$	MN
12	Penalized	${\textstyle F_{min}={\frac {\pi }{D}}[10sin^{2}(\pi y_{1})+\sum _{i=1}^{D-1}(y_{i}-1)^{2}\lbrace 1+10sin^{2}(\pi y_{i+1})\rbrace +(y_{D}-1)^{2}]+\sum _{i=1}^{D}u(x_{i},10,100,4),u(x_{i},a,k,m)=\lbrace {\begin{array}{cc}k(x_{i}-a)^{m}&x_{i}>a{\mbox{,}}\\0{\mbox{,}}&-a\leq x_{i}\leq a{\mbox{,}}\\k(-x_{i}-a)^{m}{\mbox{,}}&x_{i}<-a\end{array}}y_{i}=1+1/4(x_{i}+1)}$	${\textstyle [-50,50]}$	MN
13	Penalized 2	${\textstyle F_{min}=0.1[sin^{2}(\pi x_{1})+\sum _{i=1}^{D-1}(x_{i}-1)^{2}\lbrace 1+sin^{2}(3\pi x_{i+1})\rbrace +(x_{D}-1)^{2}+(1+sin^{2}(2\pi x_{D}))]+\sum _{i=1}^{D}u(x_{i},5,100,4),u(x_{i},a,k,m)=\lbrace {\begin{array}{cc}k(x_{i}-a)^{m}&x_{i}>a{\mbox{,}}\\0{\mbox{,}}&-a\leq x_{i}\leq a{\mbox{,}}\\k(-x_{i}-a)^{m}{\mbox{,}}&x_{i}<-a\end{array}}}$	${\textstyle [-50,50]}$	MN
14	Foxholes	${\textstyle F_{min}=[{\frac {1}{500}}+\sum _{j=1}^{25}{\frac {1}{j+\sum _{i=1}^{2}(x_{i}-a_{ij})^{6}}}]^{-1}}$	${\textstyle [-65.536,65.536]}$	MS
15	Kowalik	${\textstyle F_{min}=\sum _{i=1}^{11}(a_{i}-{\frac {x_{1}(b_{i}^{2}+b_{i}x_{2})}{b_{i}^{2}+b_{i}x_{3}+x_{4}}})^{2}}$	${\textstyle [-5,5]}$	MN
16	6 Hump camel back	${\textstyle F_{min}=4x_{1}^{2}-2.1x_{1}^{4}+{\frac {1}{3}}x_{1}^{6}+x_{1}x_{2}-4x_{2}^{2}+4x_{2}^{4}}$	${\textstyle [-5,5]}$	MN
17	Branin	${\textstyle F_{min}=(x_{2}-{\frac {5.1}{4\pi ^{2}}}x_{1}^{2}+{\frac {5}{\pi }}x_{1}-6)^{2}+10(1-{\frac {1}{8\pi }})cosx_{1}+10}$	${\textstyle [-5,10][0,15]}$	MS
18	GoldStein–Price	${\textstyle {\begin{array}{l}\displaystyle F_{m}in=[1+(x_{1}+x_{2}+1)^{2}(19-14x_{1}+3x_{1}^{2}-14x_{2}+6x_{1}x_{2}+\\\displaystyle +3x_{2}^{2})][30+(2x_{1}-3x_{2})^{2}(18-32x_{1}+12x_{1}^{2}+48x_{2}-\\\displaystyle -36x_{1}x_{2}+27x_{2}^{2})]\end{array}}}$	${\textstyle [-5,5]}$	MN
19	Hartman 3	${\textstyle F_{min}=-\sum _{i=1}^{4}c_{i}exp[-\sum _{j=1}^{3}a_{ij}(x_{j}-p_{ij})^{2}]}$	${\textstyle [0,1]}$	MN
20	Hartman 6	${\textstyle F_{min}=-\sum _{i=1}^{4}c_{i}exp[-\sum _{j=1}^{6}a_{ij}(x_{j}-p_{ij})^{2}]}$	${\textstyle [0,1]}$	MN
21	Shekel 5	${\textstyle F_{min}=-\sum _{i=1}^{5}[(x-a_{i})(x-a_{i})^{T}+c_{i}]^{-1}}$	${\textstyle [0,10]}$	MN
22	Shekel 7	${\textstyle F_{min}=-\sum _{i=1}^{7}[(x-a_{i})(x-a_{i})^{T}+c_{i}]^{-1}}$	${\textstyle [0,10]}$	MN
23	Shekel 10	${\textstyle F_{min}=-\sum _{i=1}^{10}[(x-a_{i})(x-a_{i})^{T}+c_{i}]^{-1}}$	${\textstyle [0,10]}$	MN

C: Characteristic, U: Unimodal, M: Multimodal, S: Separable, N: Non - separable.

Li et al.  [31] attempted all these functions using ABC, I-ABC, GABC and PS-ABC with colony size 40 and number of cycles of 400 (i.e. 40 000 maximum function evaluations). But, it is observed that in the PS-ABC algorithm, three different food positions are generated for each employed bee and the corresponding nectar amount is calculated for each position. Out of these three food positions, the employed bee selected the best food position based on the calculated nectar amount. Similarly, for each onlooker bee, three more food positions are generated and out of these three positions, the onlooker bees select the best position. In that way, the total number of function evaluations in the PS-ABC algorithm is not equal to colony size multiplied by number of cycles. In the PS-ABC algorithm, three fitness evaluations are required for each employed bee for selecting the best food position. Similarly, three fitness evaluations are required for each onlooker bee for selecting the best food position. So, the total number of function evaluations for the PS-ABC algorithm is equal to 3*colony size*number of cycles. Considering this fact, in the present work, TLBO and I-TLBO are implemented with 40 000 function evaluations to compare its performance with ABC, I-ABC and GABC algorithms, and 120 000 function evaluations to compare its performance with the PS-ABC algorithm.

In this experiment, each benchmark function is experimented 30 times with TLBO and I-TLBO algorithms and the results are obtained in the form of mean solution and standard deviation of objective function after 30 independent runs of the algorithms. Table 6 shows the comparative results of ABC, I-ABC, GABC, TLBO and I-TLBO algorithms for the first 13 functions with 40 000 maximum function evaluations. Except for TLBO and I-TLBO algorithms, the rest of the results are taken from the previous work of Li et al.  [31] .

Table 6.

Comparative results of TLBO and I-TLBO algorithms with different variants of ABC algorithm over 30 independent runs (for functions 1–13 of Table 5 with 40 000 maximum function evaluations).

	${\textstyle D}$	ABC  [31]		I-ABC  [31]		GABC  [31]		TLBO		I-TLBO
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Sphere	20	6.18E−16	2.11E−16	0.00	0.00	3.19E−16	7.39E−17	0.00	0.00	0.00	0.00
	30	3.62E−09	5.85E−09	0.00	0.00	6.26E−16	1.08E−16	0.00	0.00	0.00	0.00
	50	1.11E−05	1.25E−05	0.00	0.00	1.25E−05	6.05E−09	0.00	0.00	0.00	0.00
Schwefel 2.22	20	1.35E−10	7.15E−11	0.00	0.00	9.36E−16	1.33E−16	0.00	0.00	0.00	0.00
	30	5.11E−06	2.23E−06	0.00	0.00	1.31E−10	4.69E−11	0.00	0.00	0.00	0.00
	50	2.92E−03	9.05E−04	0.00	0.00	2.37E−05	6.19E−06	0.00	0.00	0.00	0.00
Schwefel 1.2	20	3.13E+03	1.19E+03	4.54E+03	2.69E+03	2.69E+03	1.46E+03	3.29E−38	1.20E−37	0.00	0.00
	30	1.24E+04	3.01E+03	1.43E+04	2.73E+03	1.09E+04	2.57E+03	3.25E−27	8.21E−27	0.00	0.00
	50	4.57E+04	6.46E+03	4.69E+04	7.36E+03	4.12E+04	5.83E+03	1.38E−21	4.00E−21	0.00	0.00
Schwefel 2.21	20	3.9602	1.37E+00	0.00	0.00	0.3325	1.08E+00	7.19E−278	6.90E−278	0.00	0.00
	30	24.5694	5.66E+00	1.21E−197	0.00	12.6211	2.66E+00	3.96E−253	4.24E−253	4.7E−324	0.00
	50	56.3380	4.84E+00	25.5055	5.67E+00	45.3075	4.32E+00	4.77E−234	5.11E−234	4.9E−324	0.00
Rosenbrock	20	1.1114	1.80E+00	15.7165	1.40E+00	1.6769	2.90E+00	16.0706	3.68E−01	11.0955	8.71E−01
	30	4.5509	4.88E+00	26.4282	1.40E+00	7.4796	1.91E+01	26.6567	2.94E−01	22.7934	5.82E−01
	50	48.03	4.67E+01	47.0280	8.60E−01	25.7164	3.18E+01	47.0162	3.56E−01	43.9786	4.55E−01
Step	20	5.55E−16	1.69E−16	6.31E−16	2.13E−16	3.34E−16	1.02E−16	1.99E−20	5.03E−20	6.16E−33	4.11E−33
	30	2.49E−09	3.68E−09	3.84E−10	2.32E−10	6.45E−16	1.11E−16	2.74E−09	5.36E−09	1.17E−26	3.55E−26
	50	1.36E−05	1.75E−05	1.84E−05	1.74E−05	5.65E−09	3.69E−09	6.26E−04	6.33E−04	1.39E−11	1.61E−11
1.01E−02	6.31E−03	6.45E−03	Quartic	20	6.51E−02	2.03E−02	8.71E−03	3.24E−03	3.31E−02	7.93E−03	1.71E−02
30	1.56E−01	4.65E−02		1.96E−02	9.34E−03	8.48E−02	2.79E−02	1.71E−02	8.95E−03	8.29E−03	4.30E−03
50	4.88E−01	1.07E−01		8.83E−02	2.55E−02	2.46E−01	4.72E−02	1.59E−02	8.11E−03	9.68E−03	3.88E−03
Schwefel	20	−8327.49	6.63E+01	−8323.770	7.40E+01	−8355.92	7.23E+01	−8105.47	1.74E+02	−8202.98	1.27E+02
	30	−12 130.31	1.59E+02	−12 251.030	1.67E+02	−12 407.29	1.06E+02	−12 311.72	2.21E+02	−12 351.4	1.35E+02
	50	−19 326.50	2.66E+02	−19 313.490	2.77E+02	−19 975.29	2.31E+02	−20 437.84	1.48E+02	−20 533.71	2.46E+02
Rastrigin	20	1.41E−11	4.05E−11	0.00	0.00	0.00	0.00	1.95E−13	2.32E−13	0.00	0.00
	30	0.4531	5.15E−01	0.00	0.00	0.0331	1.81E−01	1.87E−12	6.66E−12	0.00	0.00
	50	8.4433	2.70E+00	0.00	0.00	2.1733	1.07E+00	2.03E−12	5.46E−12	0.00	0.00
Ackley	20	2.83E−09	2.58E−09	8.88E−16	0.00	2.75E−14	3.58E−15	3.55E−15	8.32E−31	7.11E−16	1.50E−15
	30	2.75E−05	2.13E−05	8.88E−16	0.00	7.78E−10	2.98E−10	3.55E−15	8.32E−31	1.42E−15	1.83E−15
	50	4.71E−02	3.40E−02	8.88E−16	0.00	1.11E−04	3.88E−05	3.55E−15	8.32E−31	1.42E−15	1.83E−15
Griewank	20	3.71E−03	6.61E−03	0.00	0.00	6.02E−04	2.23E−03	0.00	0.00	0.00	0.00
	30	3.81E−03	8.45E−03	0.00	0.00	6.96E−04	2.26E−03	0.00	0.00	0.00	0.00
	50	1.19E−02	1.97E−02	0.00	0.00	1.04E−03	2.74E−03	0.00	0.00	0.00	0.00
Penalized	20	4.06E−16	9.42E−17	4.17E−16	1.09E−16	3.26E−16	6.67E−17	1.13E−06	1.15E−06	4.00E−08	9.72E−15
	30	1.18E−10	2.56E−10	7.10E−12	5.25E−12	5.86E−16	1.13E−16	6.16E−03	2.34E−02	2.67E−08	1.15E−13
	50	8.95E−06	3.21E−05	5.42E−07	2.98E−07	9.30E−11	7.96E−11	6.01E−02	6.71E−02	5.72E−08	2.81E−08
Penalized 2	20	6.93E−08	2.92E−07	1.75E−16	4.54E−16	6.55E−08	2.44E−07	1.13E−06	1.15E−06	2.54E−08	3.77E−11
	30	2.27E−07	4.12E−07	4.78E−08	2.04E−07	2.17E−07	5.66E−07	6.16E−03	2.34E−02	2.55E−08	4.89E−11
	50	1.35E−05	2.78E−05	2.41E−05	4.35E−05	8.87E−07	1.53E−06	6.01E−02	6.71E−02	1.82E−06	1.08E−06

It is observed from the results that the I-TLBO algorithm outperforms the rest of the considered algorithms for Schwefel1.2, Step and Quartic functions for all the dimensions. For the Schwefel 2.21 function, the I-TLBO outperforms the other algorithms for dimensions 30 and 50, while the performances of I-TLBO and I-ABC are identical for dimension 10. For the Schwefel function, the performance of the I-TLBO is better than rest of the algorithms for dimension 50, while performances of GABC and ABC, I-ABC and GABC are better than the I-TLBO for dimensions 30 and 20, respectively. GABC outperforms the other algorithms for the penalized 1 function. For the penalized 2 function, performances of I-ABC, I-TLBO and GABC are better than other algorithms for dimensions 20, 30 and 50, respectively. For the Rosenbrock function, the performance of basic ABC and GABC is better than the other algorithms for dimensions 20 and 30, while GABC is better than the other algorithms for dimension 50. For Sphere, Schwefel 2.22 and Griewank functions, TLBO, I-TLBO and I-ABC perform equally well for all the dimensions. Similarly, for the Rastrigin function, performances of I-ABC and I-TLBO are identical and better than the other considered algorithms. For the Ackley function, performances of I-ABC, GABC, TLBO and I-TLBO algorithms are more or less identical.

Table 7 shows the comparative results of PS-ABC, TLBO and I-TLBO algorithms for the first 13 functions with 120 000 maximum function evaluations. It is observed from the results that I-TLBO outperforms the basic TLBO and PS-ABC algorithms for Step and Quartic functions (for all the dimensions) and the Schwefel 2.21 function (for dimensions 30 and 50). The PS-ABC outperforms the TLBO and I-TLBO for Rosenbrock and Schwefel functions. For the Schwefel 1.2 function, the performance of TLBO and I-TLBO is identical and better than the PS-ABC algorithm. Performance of PS-ABC and I-TLBO is identical for the Rastrigin function, while performance of all three algorithms is identical for Sphere, Schwefel 2.22 and Griewank functions. For Ackley, penalized 1 and penalized 2 functions, performances of PS-ABC and I-TLBO are more or less similar.

Table 7. Comparative results of TLBO and I-TLBO algorithms with PS-ABC algorithm over 30 independent runs (for functions 1–13 of Table 5 with 120 000 maximum function evaluations).

		PS-ABC  [31]		TLBO		I-TLBO
		Mean	SD	Mean	SD	Mean	SD
Sphere	20	0.00	0.00	0.00	0.00	0.00	0.00
	30	0.00	0.00	0.00	0.00	0.00	0.00
	50	0.00	0.00	0.00	0.00	0.00	0.00
Schwefel 2.22	20	0.00	0.00	0.00	0.00	0.00	0.00
	30	0.00	0.00	0.00	0.00	0.00	0.00
	50	0.00	0.00	0.00	0.00	0.00	0.00
Schwefel 1.2	20	1.04E+03	6.11E+02	0.00	0.00	0.00	0.00
	30	6.11E+03	1.69E+03	0.00	0.00	0.00	0.00
	50	3.01E+04	4.11E+03	0.00	0.00	0.00	0.00
Schwefel 2.21	20	0.00	0.00	0.00	0.00	0.00	0.00
	30	8.59E−115	4.71E−114	4.9E−324	0.00	0.00	0.00
	50	19.6683	6.31E+00	9.9E−324	0.00	0.00	0.00
Rosenbrock	20	0.5190	1.08E+00	15.0536	2.28E−01	1.3785	8.49E−01
	30	1.5922	4.41E+00	25.4036	3.50E−01	15.032	1.2E+00
	50	34.4913	3.03E+01	45.8955	2.89E−01	38.7294	7.57E−01
Step	20	2.61E−16	3.86E−17	9.24E−33	4.36E−33	0.00	0.00
	30	5.71E−16	8.25E−17	1.94E−29	1.88E−29	0.00	0.00
	50	1.16E−15	1.41E−16	3.26E−13	5.11E−13	1.51E−32	8.89E−33
Quartic	20	6.52E−03	2.25E−03	1.07E−02	5.16E−03	5.16E−03	4.64E−03
	30	2.15E−02	6.88E−03	1.15E−02	3.71E−03	5.36E−03	3.72E−03
	50	6.53E−02	1.77E−02	1.17E−02	5.00E−03	5.60E−03	3.40E−03
Schwefel	20	−8379.66	4.72E−12	−8210.23	1.66E+02	−8263.84	1.16E+02
	30	−12 564.23	2.55E+01	−12 428.60	1.53E+02	−12 519.92	1.16E+02
	50	−20 887.98	8.04E+01	−20 620.72	1.89E+02	−20 700.70	1.64E+02
Rastrigin	20	0.00	0.00	6.41E−14	6.16E−14	0.00	0.00
	30	0.00	0.00	6.95E−13	1.64E−12	0.00	0.00
	50	0.00	0.00	7.90E−13	1.89E−12	0.00	0.00
Ackley	20	8.88E−16	0.00	3.55E−15	8.32E−31	7.11E−16	0.00
	30	8.88E−16	0.00	3.55E−15	8.32E−31	7.11E−16	0.00
	50	8.88E−16	0.00	3.55E−15	8.32E−31	7.11E−16	0.00
Griewank	20	0.00	0.00	0.00	0.00	0.00	0.00
	30	0.00	0.00	0.00	0.00	0.00	0.00
	50	0.00	0.00	0.00	0.00	0.00	0.00
Penalized	20	2.55E−16	4.97E−17	4.00E−08	6.85E−24	2.42E−16	1.09E−16
	30	5.53E−16	8.68E−17	2.67E−08	6.79E−12	4.98E−16	2.14E−16
	50	1.02E−15	1.58E−16	5.18E−05	1.92E−04	9.19E−16	5.38E−16
Penalized 2	20	2.34E−18	2.20E−18	2.34E−08	6.85E−24	1.93E−18	1.12E−18
	30	6.06E−18	5.60E−18	2.37E−08	4.91E−10	5.92E−18	4.74E−18
	50	5.05E−17	1.53E−16	1.52E−03	5.29E−03	4.87E−17	4.26E−17

Table 8 shows the comparative results of the considered algorithms for 14 to 23 functions. Here, the results of ABC, I-ABC, GABC, TLBO and I-TLBO algorithms are obtained with 40 000 maximum function evaluations, while the result of the PS-ABC algorithm is obtained with 120 000 maximum function evaluations. It is observed from the results that all the algorithms perform identically for functions 14, 16, 18, 19 and 21–23. The performance of the I-TLBO is better than rest of the algorithms for the Kowalik function, while performances of different variants of ABC are better than the TLBO for the Hartman 6 function.

Table 8. Comparative results of TLBO and I-TLBO algorithms with different variants of ABC algorithm over 30 independent runs (for functions 14–23 of Table 5 ).

	ABC	I-ABC	GABC	PS-ABC	TLBO	I-TLBO
Foxholes	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980
Kowalik	6.74E−04	3.76E−04	5.54E−04	4.14E−04	3.08E−04	3.08E−04
6 Hump camel back	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
Branin	0.7012	0.3978	0.6212	0.6300	0.3978	0.3978
Goldstein-Price	3.0010	3.0000	3.0000	3.0000	3.0000	3.0000
Hartman 3	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628
Hartman 6	−3.3220	−3.3220	−3.3220	−3.3220	−3.2866	−3.2948
Shekel 5	−10.1532	−10.1532	−10.1532	−10.1532	−10.1532	−10.1532
Shekel 7	−10.4029	−10.4029	−10.4029	−10.4029	−10.4029	−10.4029
Shekel 10	−10.5364	−10.5364	−10.5364	−10.5364	−10.5364	−10.5364

Results of algorithms except TLBO and I-TLBO are taken from Ref.  [31] .

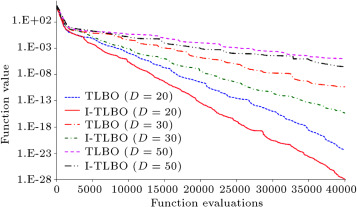
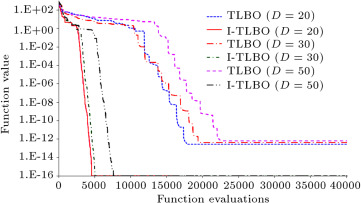
In order to identify the convergence of TLBO and I-TLBO, a unimodal (Step) and a multimodal (Rastrigin) function are considered for the experiment with dimensions 20, 30 and 50. Maximum function evaluations are set as 40 000 and a graph is plotted between the function value (on logarithmic scale) and function evaluations. The function value is taken as the average of the function value for 10 different independent runs. Figure 1  and Figure 2 show the convergence graphs of unimodal and multimodal functions, respectively. It is observed from the graphs that the convergence rate of the I-TLBO is faster than the basic TLBO algorithm for both unimodal and multimodal functions for all the dimensions. Similarly, Table 9 shows the computational effort of TLBO and I-TLBO algorithms for the lower dimension problem (functions 14–23) in the form of the mean number of function evaluations required to achieve a global optimum value with a gap of 10⁻³ . Here, the mean number of function evaluations is obtained through 30 independent runs on each function. Here, also, the I-TLBO algorithm requires less number of function evaluations than the basic TLBO algorithm to achieve the global optimum value. Moreover, as the number of teachers is increased from 1 to 4, the convergence rate of the I-TLBO algorithm is also improved.

Figure 1. Convergence of TLBO and I-TLBO algorithms for a unimodal function (step).

Figure 2. Convergence of TLBO and I-TLBO algorithms for a multimodal function (Rastrigin).

Table 9. Mean number of function evaluations required for TLBO and I-TLBO algorithms for functions 14–23 of Table 5 .

	TLBO	I-TLBO
		${\textstyle NT=1}$	${\textstyle NT=2}$	${\textstyle NT=3}$	${\textstyle NT=4}$
Foxholes	524	472	431	344	278
Kowalik	2488	2464	2412	2344	2252
6 Hump camel back	447	426	408	339	276
Branin	443	438	421	390	367
Goldstein-Price	582	570	553	511	473
Hartman 3	547	524	492	378	310
Hartman 6	24 847	18 998	18 542	17 326	16 696
Shekel 5	1245	1218	1212	1124	1046
Shekel 7	1272	1246	1228	1136	1053
Shekel 10	1270	1251	1233	1150	1062

5. Conclusion

An improved TLBO algorithm has been proposed for unconstrained optimization problems. Two new search mechanisms are introduced in the proposed approach in the form of tutorial training and self motivated learning. Moreover, the teaching factor of the basic TLBO algorithm is modified and an adaptive teaching factor is introduced. Furthermore, more than one teacher is introduced for the learners. The presented modifications enhance the exploration and exploitation capacities of the basic TLBO algorithm. The performance of the I-TLBO algorithm is evaluated by conducting small scale to large scale experiments on various unconstrained benchmark functions and the performance is compared with that of the other state-of-the-art algorithms available in the literature. Furthermore, the comparison between the basic TLBO and I-TLBO is also reported. The experimental results have shown the satisfactory performance of the I-TLBO algorithm for unconstrained optimization problems. The proposed algorithm can be easily customized to suit the optimization of any system involving large numbers of variables and objectives.

A possible direction for future research work is extending the I-TLBO algorithm to handle single objective and multi-objective constrained optimization problems and explore its effectiveness. Analyzing the effect of the number of teachers on the fitness value of the objective function and experimentation on very large dimension problems (i.e. 100 and 500) are also possible future research directions.

References

1. [1] J.H. Holland; Adaptation in Natural and Artificial Systems; University of Michigan Press, Ann Arbor, USA (1975)
2. [2] R. Storn, K. Price; Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces; J. Global Optim., 11 (1997), pp. 341–359
3. [3] K. Price, R. Storn, A. Lampinen; Differential Evolution—A Practical Approach to Global Optimization; Springer-Verlag, Berlin, Germany (2005)
4. [4] T.P. Runarsson, X. Yao; Stochastic ranking for constrained evolutionary optimization; IEEE Trans. Evol. Comput., 4 (3) (2000), pp. 284–294
5. [5] L.J. Fogel, A.J. Owens, M.J. Walsh; Artificial Intelligence Through Simulated Evolution; John Wiley, New York, USA (1966)
6. [6] J.D. Farmer, N. Packard, A. Perelson; The immune system, adaptation and machine learning; Physica D, 22 (1986), pp. 187–204
7. [7] K.M. Passino; Biomimicry of bacterial foraging for distributed optimization and control; IEEE Control Syst. Mag., 22 (2002), pp. 52–67
8. [8] Kennedy, J. and Eberhart, R.C. “Particle swarm optimization”, IEEE Int. Conf. on Neural Networks , 4, Washington DC, USA, pp. 1942–1948 (1995).
9. [9] Dorigo, M., Maniezzo, V. and Colorni, A. “Positive feedback as a search strategy”, Tech. Report 91-016 , Politecnico di Milano, Italy (1991).
10. [10] M. Eusuff, E. Lansey; Optimization of water distribution network design using the shuffled frog leaping algorithm; J. Water. Res. Pl.-ASCE, 129 (2003), pp. 210–225
11. [11] Karaboga, D. “An idea based on honey bee swarm for numerical optimization”, Tech. Report-TR06 , Computer Engineering Department, Erciyes University, Turkey (2005).
12. [12] D. Karaboga, B. Basturk; A powerful and efficient algorithm for numerical function optimization: Artificial Bee Colony (ABC) algorithm; J. Global Optim., 39 (3) (2007), pp. 459–471
13. [13] D. Karaboga, B. Basturk; On the performance of Artificial Bee Colony (ABC) algorithm; Appl. Soft Comput., 8 (1) (2008), pp. 687–697
14. [14] D. Karaboga, B. Akay; A comparative study of Artificial Bee Colony algorithm; Appl. Math. Comput., 214 (2009), pp. 108–132
15. [15] Z.W. Geem, J.H. Kim, G.V. Loganathan; A new heuristic optimization algorithm: harmony search; Simulation, 76 (2001), pp. 60–70
16. [16] E. Rashedi, H. Nezamabadi-pour, S. Saryazdi; GSA: a gravitational search algorithm; Inform. Sci., 179 (2009), pp. 2232–2248
17. [17] D. Simon; Biogeography-based optimization; IEEE Trans. Evol. Comput., 12 (2008), pp. 702–713
18. [18] A. Ahrari, A.A. Atai; Grenade explosion method—a novel tool for optimization of multimodal functions; Appl. Soft Comput., 10 (2010), pp. 1132–1140
19. [19] A.H. Kashan; An efficient algorithm for constrained global optimization and application to mechanical engineering design: league championship algorithm (LCA); Comput. Aided Des., 43 (2011), pp. 1769–1792
20. [20] A. Kaveh, S. Talatahari; A novel heuristic optimization method: charged system search; Acta Mech., 213 (2010), pp. 267–286
21. [21] A. Kaveh, S. Talatahari; An enhanced charged system search for configuration optimization using the concept of fields of forces; Struct. Multidiscip. Optim., 43 (2011), pp. 339–351
22. [22] J. Gao, J. Wang; A hybrid quantum-inspired immune algorithm for multi-objective optimization; Appl. Math. Comput., 217 (2011), pp. 4754–4770
23. [23] S.E. Moumen, R. Ellaia, R. Aboulaich; A new hybrid method for solving global optimization problem; Appl. Math. Comput., 218 (2011), pp. 3265–3276
24. [24] S.S. Fan, E. Zahara; A hybrid simplex search and particle swarm optimization for unconstrained optimization; European J. Oper. Res., 181 (2007), pp. 527–548
25. [25] J. Olenŝek, T. Tuma, J. Puhan, Ă. Bürmen; A new asynchronous parallel global optimization method based on simulated annealing and differential evolution; Appl. Soft Comput., 11 (2011), pp. 1481–1489
26. [26] G. Liu, Y. Li, X. Nie, H. Zheng; A novel clustering-based differential evolution with 2 multi-parent crossovers for global optimization; Appl. Soft Comput., 12 (2012), pp. 663–681
27. [27] Z. Cai, W. Gong, C.X. Ling, H. Zhang; A clustering-based differential evolution for global optimization; Appl. Soft Comput., 11 (2011), pp. 1363–1379
28. [28] M.H. Mashinchi, M.A. Orgun, W. Pedrycz; Hybrid optimization with improved tabu search; Appl. Soft Comput., 11 (2011), pp. 1993–2006
29. [29] M.M. Noel; A new gradient based particle swarm optimization algorithm for accurate computation of global minimum; Appl. Soft Comput., 12 (2012), pp. 353–359
30. [30] S.J. Sadjadi, R. Soltani; An efficient heuristic versus a robust hybrid meta-heuristic for general framework of serial–parallel redundancy problem; Reliab. Eng. Syst. Saf., 94 (11) (2009), pp. 1703–1710
31. [31] G. Li, P. Niu, X. Xiao; Development and investigation of efficient Artificial Bee Colony algorithm for numerical function optimization; Appl. Soft Comput., 12 (2012), pp. 320–332
32. [32] G. Zhu, S. Kwong; Gbest-guided Artificial Bee Colony algorithm for numerical function optimization; Appl. Math. Comput., 217 (2010), pp. 3166–3173
33. [33] B. Akay, D. Karaboga; A modified Artificial Bee Colony algorithm for real-parameter optimization; Inform. Sci., 192 (1) (2012), pp. 120–142
34. [34] M. Mahdavi, M. Fesanghary, E. Damangir; An improved harmony search algorithm for solving optimization problems; Appl. Math. Comput., 188 (2007), pp. 1767–1779
35. [35] R.V. Rao, V.J. Savsani, D.P. Vakharia; Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems; Comput. Aided Des., 43 (3) (2011), pp. 303–315
36. [36] R.V. Rao, V.J. Savsani, D.P. Vakharia; Teaching–learning-based optimization: a novel optimization method for continuous non-linear large scale problems; Inform. Sci., 183 (1) (2011), pp. 1–15
37. [37] R.V. Rao, V. Patel; An elitist teaching–learning-based optimization algorithm for solving complex constrained optimization problems; Int. J. Ind. Eng. Comput., 3 (4) (2012), pp. 535–560
38. [38] M. C˘repinšek, S.H. Liu, L. Mernik; A note on teaching–learning-based optimization algorithm; Inform. Sci., 212 (2012), pp. 79–93
39. [39] R.V. Rao, V. Patel; Multi-objective optimization of two stage thermoelectric cooler using a modified teaching–learning-based optimization algorithm; Eng. Appl. Artif. Intell., 26 (1) (2013), pp. 430–445
40. [40] R.V. Rao, V. Patel; Multi-objective optimization of heat exchangers using a modified teaching–learning-based optimization algorithm; Appl. Math. Model., 37 (3) (2013), pp. 1147–1162