Probabilistic pounding-induced damage assessment using PEERs methodology. Application to a seismically isolated overpass.

Resumen

En países de sismicidad moderada es habitual el uso de puentes cuyo tablero está unido mediante apoyos elastoméricos y/o deslizantes, tanto a las pilas como a los estribos. La principal vulnerabilidad sísmica de estos puentes está asociada a los choques. Dicha vulnerabilidad puede valorarse estimando la probabilidad de que se produzca un determinado daño en un periodo de tiempo. En este artículo se plantean las líneas actuales para estudiar este problema, y se aplican al estudio de la vulnerabilidad de un paso superior situado en la provincia de Granada, que puede considerarse como sísmicamente aislado.

El marco del estudio es la metodología del Pacific Earthquake Engineering Research Center , cuya aplicación se ha adaptado al caso estudiado. En el artículo se describen cada una de las etapas de que consta, aunque se presta especial atención a la identificación y caracterización de los daños susceptibles de producirse. El modelo de la estructura, que debe permitir una adecuada caracterización de los choques, también será presentado en detalle.

Dado que el puente es representativo de una gran cantidad de estructuras del inventario construido en España, los resultados son doblemente importantes. Por una parte, sirven de guía para la aplicación de esta metodología a estructuras similares. Y por otra, proporcionan valores de probabilidades que pueden servir de referencia.

Abstract

Bridges with deck supported either on sliding or elastomeric bearings are common in mid-seismicity regions. Pounding between deck and abutments is linked with their main seismic vulnerabilities, which can be assessed by estimating the probability of a given state of damage being reached in a given time period. This paper presents a state of the art methodology used to solve that problem, as well as its application to the assessment of the vulnerability of an overpass placed in Granada area (South-east of Spain), belonging to the previously mentioned typology.

The Pacific Earthquake Engineering Research Center methodology will be adapted and applied. Their main steps will be briefly presented, although the identification and characterization of damage likely to occur will be described in more detail. The model of the structure, and specially pounding modeling, will also be detailed.

Results are interesting since this bridge can be considered as a representative of a widespread class. The adapted methodology may be applied to similar structures. Also, probability values obtained may serve as benchmarks.

Palabras clave

Metodología PEER ; Puente ; Choque ; Sísmica

Keywords

PEER methodology ; Bridge ; Pounding ; Seismic

1. Introducción

La excitación sísmica puede producir choques entre estructuras adyacentes o partes de una misma estructura. Este fenómeno se explica por la existencia de una separación insuficiente y por movimientos desfasados debidos a las distintas características dinámicas de los elementos involucrados.

Está bien documentada la importancia de este fenómeno en los daños detectados tras numerosos terremotos (por ejemplo, el de Ciudad de México en 1985, el de Loma Prieta en 1989, o del de Kobe en 1995 [1] ). Habitualmente el daño asociado a los choques se circunscribe a elementos no estructurales. Aun siendo así, debido a su extensión, los costes asociados a su reparación pueden resultar importantes dentro del total.

En las últimas décadas, el aumento en la capacidad de cálculo ha permitido el desarrollo de modelos más sofisticados que han contribuido a una mejor comprensión del fenómeno. En un primer momento, el esfuerzo se dirigió a los edificios, buscando por ejemplo la estimación de la distancia de separación entre ellos que evita los choques [2] , o las probabilidades de que se produzcan choques [3] .

En el caso de los puentes, en la literatura se encuentran numerosos estudios que prentenden arrojar algo de luz sobre la importancia de algunos parámetros de los modelos ([4]  and [5] ). Recientemente los autores han estudiado la forma de caracterizar las fuerzas de reacción que se producen durante los choques [6] , elemento clave para el estudio de prestaciones.

La tendencia actual que sigue la ingeniería sísmica es la del desarrollo de Performace Based Design (PBD, ‘proyectos basados en prestaciones’). Bajo esta filosofía, el objetivo del proyecto es conseguir estructuras que proporcionen unas prestaciones fijadas por sus propietarios, y que se cuantifican mediante variables llamadas de decisión. Ejemplos de estas últimas son el coste anual medio de mantenimiento, o las pérdidas probables por la acción de sismos durante su vida útil.

Entre las distintas alternativas metodológicas para la evaluación de prestaciones, es decir, para la cuantificación de las variables de decisión, en la comunidad sísmica goza de gran aceptación la propuesta del Pacific Earthquake Engineering Research Center (PEER) [7] .

Este trabajo pretende reflejar la sistemática de la aplicación de la metodología PEER mediante su aplicación a un paso superior situado en la provincia de Granada, para estimar las probabilidades anuales de que se produzcan distintos tipos de daños producidos por un terremoto. La presentación de las principales etapas de la misma, así como una primera discusión sobre su aplicación al problema considerado, ocuparán la primera parte del mismo. A continuación se presentará la estructura y se detallarán los aspectos más importantes de su modelado para el estudio de los choques.

En la literatura existen otros ejemplos de aplicación de la metodología a puentes [8] , pero sus resultados no son aplicables a un puente del tipo del estudiado, donde la vulnerabilidad principal está asociada a choques entre tablero y estribos. La identificación de los daños susceptibles de producirse y su caracterización ocuparán la tercera parte del trabajo.

En la cuarta y última parte se presentarán los valores resultantes de probabilidad de alcanzar los estados de daño considerados. Además se presentarán algunos resultados intermedios de interés.

2. Metodología del estudio

2.1. La metodología del PEER

El desarrollo del proyecto basado en prestaciones consiste en analizar, proyectar y construir estructuras que cumplan unos determinados objetivos de desempeño fijados por la propiedad. En el campo de la ingeniería sísmica goza de gran popularidad la metodología desarrollada por el PEER, que se basa en la desagregación de probabilidades y la integración numérica de distribuciones de probabilidad condicionadas.

El objetivo es estimar un vector de variables de decision (DV, por sus siglas en inglés), que se supone deben permitir valorar la bondad del proyecto. Un ejemplo es el valor promedio de los costes de reparación debido a daños sísmicos. La desagregación de probabilidades conduce a dividir el problema en otros cuatro distintos y separados.

El primero es el estudio de peligrosidad, en el que se determina la probabilidad anual de que se supere un determinado valor de una medida de intensidad sísmica (IM, del inglés intensity measure ). Esta puede ser bien escalar bien vectorial. Un ejemplo es la aceleración pico. El siguiente, es el estudio de la respuesta, y consiste en evaluar la respuesta condicionada a la intensidad, en general apoyándose en simulaciones. La respuesta se caracteriza por una o más variables denomindas engineering demand parameters (EDP). En tercer lugar, se tiene el análisis de daños, en el que se caracteriza un vector de variables de daño (DM, del inglés damage measure ) condicionadas a la respuesta. El material de partida para esta etapa puede ser bien datos experimentales, bien opinión de expertos. Por último, se tiene el análisis de costes, donde se caracteriza la variable de decisión condicionada al nivel de daño.

La llamada fórmula del PEER se construye por aplicación reiterada del teorema de la probabilidad total, y expresa que la variabilidad de la variable de decisión DV, depende del producto de las probabilidades condicionadas de las variables intermedias IM, EDP y DM:

$\lambda (dv)=\int \int \int G(dv\vert dm)dG(dm\vert edp)dG(edp\vert im)\vert d\lambda (im)\vert$

( 1)

donde λ (x ) representa la frecuencia anual de eventos tales que x  ≤ X por año, y G (x |y ) representa la complementaria de la función de distribución de probabilidad de la variable X condicionada a la variable Y .

2.2. Aplicación al estudio del paso superior

2.2.1. Alcance del estudio

Este estudio se limitará a las tres primeras etapas de la metodología. Además no se considerará el daño como una variable continua, sino como una variable binaria cuyo valor depende de que este se haya producido o no. Se tratará, por tanto, de evaluar la probabilidad de que se produzca un determinado daño en un periodo de tiempo dado.

Cada tipo de daño dará lugar a un cálculo separado. Así la función G (dm |edp ) indicará la probabilidad de que se produzca el daño condicionada al nivel de respuesta edp , y la ecuación 1 podrá escribirse:

$P(da{\tilde {n}}o)=\int \int P(da{\tilde {n}}o\vert edp)dG(edp\vert im)\vert d\lambda (im)\vert$

( 2)

La primera dificultad de la aplicación de la fórmula es la selección de las variables intermedias EDP e IM adecuadas. Estas deben seleccionarse de forma que sirva para caracterizar adecuadamente el daño. En la frase anterior adecuadamente quiere decir que la dependencia entre ellas y el daño sea markoviana [9] de acuerdo con la expresión 2 , y que se requiera poco esfuerzo para una estimación de la dependencia [10] .

En este estudio se considerarán daños directamente relacionados con las fuerzas que se producen durante los choques. Por tanto, la variable de respuesta más adecuada es el valor máximo de las fuerzas de reacción que se producen durante el periodo de actuación de la acción sísmica. A esta variable se la denominará en adelante R_max . Su caracterización así como la selección de la variable de intensidad adecuada se presentan a continuación.

Los tipos de daño y su caracterización se discutirán en el apartado 4 , una vez presentado el puente.

2.2.2. Estudio de peligrosidad y de la respuesta

La selección de una variable de intensidad adecuada, y la caracterización de las fuerzas de reacción en función de la intensidad, fue estudiada por los autores para puentes de la tipología de la estructura objeto de estudio [6] . Los resultados indican que es necesario utilizar una medida vectorial de intensidad compuesta por la acelaración pico (en adelante PGA , del inglés peak ground acceleration ) y el valor de la pseudo aceleración espectral para el periodo de vibración libre de la estructura Sa (T_s ). Se dedujo también que la forma de la dependencia entre R_max e IM  = (PGA , Sa (T_s )) es del tipo:

$R_{max}={\overset {\mbox{ˆ}}{R}}_{max}\cdot \eta$

( 3)

${\overset {\mbox{ˆ}}{R}}_{max}={\beta }_{0}\cdot Sa(T_{s})^{{\beta }_{1}}\cdot {\left({\frac {PGA}{Sa(T_{s})}}\right)}^{{\beta }_{2}}$

( 4)

Además, se tiene la siguiente estructura de los residuos:

$log\eta =log(R_{max})-log({\overset {\mbox{ˆ}}{R}}_{max})=$$\epsilon \sim N(0,{\sigma }_{\epsilon })$

( 5)

Con estos elementos se tiene la caracterización completa de G (edp |im ) en función de cuatro parámetros, que deben obtenerse a partir de resultados de simulaciones, mediante un ajuste de mínimos cuadrados: β₀ , β₁ , β₂ y σ_ϵ .

El último ingrediente necesario para obtener la probabilidad de daño utilizando la fórmula 2 es la caracterización de la función de densidad de probabilidad conjunta de IM  = [PGA , Sa (T_s )]. Esta información, dependiente del emplazamiento, se obtiene de los estudios de peligrosidad. Aunque la metodología existe [11] , los estudios que proporcionan directamente la distribución conjunta no son lo habitual. Los estudios de peligrosidad estándar [12] proporcionan información sobre las distribuciones marginales de Sa (T_s ) para un conjunto reducido de T_s . Falta por tanto una hipótesis adicional.

Baker y Cornell [13] han estudiado este problema y han propuesto que, dados dos periodos de vibración T₁ y T₂ , la distribución conjuntamente normal puede ajustarse a la distribución conjunta de los logaritmos de S_a (T₁ ) y S_a (T₂ ). Además, a partir de bases de datos de registros, han llegado a la expreseión siguiente para el coeficiente de correlación.

$\rho =1-cos\left[{\frac {\pi }{2}}-\left(0{\mbox{,}}359+\right.\right.$$\left.\left.0{\mbox{,}}163\quad I_{0{\mbox{,}}189}ln{\frac {T_{min}}{0{\mbox{,}}189}}\right)ln{\frac {T_{max}}{T_{min}}}\right]$

( 6)

El parámetro I_0,189 vale 1 si T_min es menor de 0,189 y 0 en el caso contrario. El rango de validez de estas correlaciones está entre 0,05 y 5 s.

Con esta información se completa la caracterización de λ (im ), último elemento necesario para utilizar la fórmula 2 .

3. Presentación de la estructura y modelo de EF

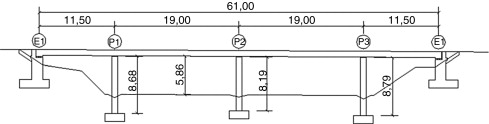
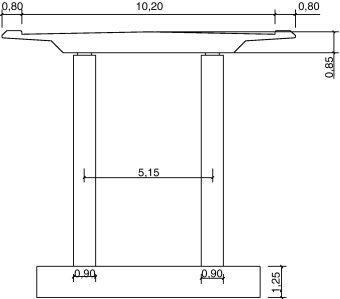
El paso superior seleccionado se encuentra en la provincia de Granada, cerca de la localidad de Dúrcal. Se trata de un puente de 61 m de longitud total, con cuatro vanos (fig. 1 ). El tablero es continuo, de hormigón pretensado, y descansa sobre tres grupos de dos pilas circulares de hormigón armado (fig. 2 ). La cimentación de cada grupo de dos pilas está constituida por una zapata rectangular.

Figura 1. Alzado lateral del paso superior.

Figura 2. Sección transversal del paso superior sobre un grupo de pilas.

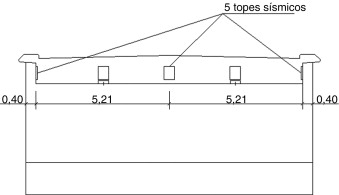
Ambos estribos son del tipo flotante, con aletas en vuelta (fig. 3 ). Entre el tablero y las pilas se han dispuesto apoyos elastoméricos circulares. En los estribos, dos apoyos rectangulares horizontales aseguran la transmisión de cargas verticales entre tablero y estribos. En los paramentos verticales, se han dispuesto 5 topes sísmicos en cada estribo, tres actuando según la dirección longitudinal, y dos según la transversal.

Figura 3. Alzado frontal del estribo.

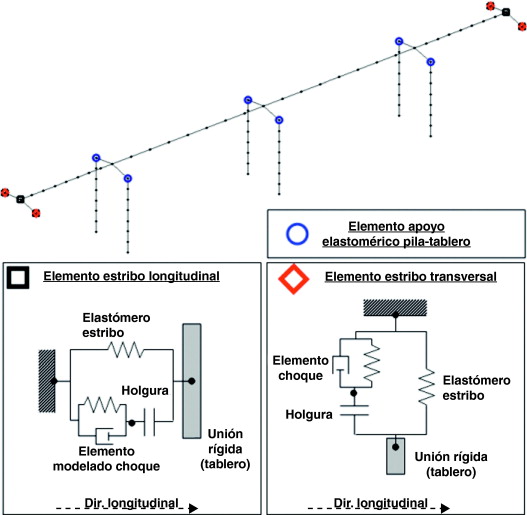
Para los cálculos dinámicos se ha construido un modelo de elementos finitos tridimensional (fig. 4 ) utilizando OpenSees [14] . Tanto los pilares como el tablero se han modelado utilizando elementos viga de Bernoulli con comportamiento elástico ya que en el rango de intensidades del estudio en estos elementos no se sobrepasarán los límites de plastificación. Cada vano del tablero se ha dividido en 8 elementos, y cada pila en 7. El centro de gravedad del tablero se encuentra situado a 0, 451 m de su base. Puesto que los elementos del tablero se han dispuesto a lo largo de su baricentro, se han colocado elementos rígidos entre él y los elementos que modelan los elastómeros sobre las pilas. Lo mismo ocurre en las secciones extremas. Los elastómeros se han modelado mediante elementos muelle-amortiguador viscoelástico concentrados.

Figura 4. Modelo de elementos finitos de la estructura.

En cada estribo se han dispuesto distintos conjuntos de elementos para modelar los topes sísmicos: tres en la dirección longitudinal, y dos en la transversal. Cada uno consta de tres elementos y tres nudos (c.f. fig. 4 ).

Para desplazamientos del nudo inferiores al valor de la holgura, la rigidez del apoyo viene dada por la de los apoyos elastoméricos horizontales en los que apoya el tablero. Si se supera este valor, a la rigidez del apoyo horizontal hay que añadir la del conjunto tope elastomérico-estribo (incluyendo la contribución del relleno) en el dirección longitudinal, o la del tope elastomérico-tope transversal en la otra dirección. Además el amortiguador sirve para modelar la disipación de energía. Este tipo de elemento ha sido empleado en estudios de puentes similares ([4]  and [15] ).

Durante los choques en dirección longitudinal, la rigidez resultante es la de un sistema en serie formado por el tope sísmico, el murete y el terreno. Sus valores respectivos se han estimado modelos de elementos finitos y fórmulas basadas en ensayos [17] llegándose a la conclusión de que es la última la que domina puesto que es bastante menor que las otras. La rigidez del tope elastoméricose ha determinado mediante las fórmulas habituales.

En la dirección transversal, la rigidez viene dominada por el tope elastomérico, que es mucho menor que la del tope transversal de hormigón que lo sostiene. Esta última se ha estimado a partir de un modelo de elementos finitos del tope transversal. El valor de los amortiguadores que modelan la disipación de energía durante el choque se ha determinado considerando un valor del coeficiente de amortiguamiento del 15% ([6]  and [18] ). A partir de él, se deduce el valor del coeficiente global de disipación viscosa que se distribuye uniformemente entre los elementos que actúen cuando se produzca un choque (tres en dirección longitudinal y dos en la transversal).

Se ha considerado que cada una de las 6 pilas está empotrada en su base. Estudios estáticos demuestran que, tanto en dirección longitudinal como transversal, antes del choque, la rigidez del paso superior viene dada por la rigidez de los apoyos elastoméricos que unen el tablero a las pilas y los estribos. Por ello, la rigidez del empotramiento bajo las pilas es poco importante a la hora de estimar la respuesta en el tablero.

Se ha realizado un cálculo modal después de aplicar la acción de la gravedad. Los resultados muestran que la estructura, en el plano horizontal, se comporta fundamentalmente según dos modos en los que el tablero se mueve como un sólido rígido, y los apoyos elastoméricos horizontales se deforman tanto en dirección longitudinal como transversal. Sus periodos característicos valen 1, 41 s.

4. Tipos de daño y selección de variables intermedias

En la literatura se encuentran disponibles algunos modelos de daño asociados a pérdida de recubrimiento y pandeo de armaduras longitudinales en pilas [20] . En un puente como el estudiado, este tipo de daño solo se producirá una vez se haya llegado a otros como la plastificación del relleno de los estribos o el fallo de los topes transversales. Estos últimos tipos se han considerado en la literatura [15] atendiendo a los desplazamientos residuales a que dan lugar. Esto requiere modelar el comportamiento trás la plastificación de estos elementos, cosa que en este estudio se ha evitado por las enormes incertidumbres asociadas. Se ha preferido considerar como daño el punto en que los choques producen modificaciones significativas en los elementos que colisionan, y así evitar modelar el comportamiento más allá del mismo. El punto en que comienza el daño se definirá a partir de las fuerzas.

Se consideran dos tipos de daño. El primero consiste en la plastificación del terreno en el trasdós, y está asociado al movimiento longitudinal. El segundo consiste en el fallo de los topes transversales, y lógicamente, está asociado al movimiento en esta dirección.

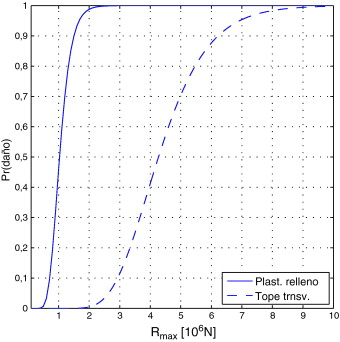
Se supone que las dos funciones de daño, que definen la probabilidad de que se alcance dicho estado condicionada al valor de la fuerza de R_max , tienen la forma de una función de distribución logarítmico-normales (fig. 5 ). Esta hipótesis es habitual [16] . Los valores característicos se listan en la tabla 1 y se justifican a continuación.

Figura 5. Funciones de daño.

Tabla 1. Parámetros característicos de las funciones de daño

Tipo daño	mediana [1016 N]	Coef. de var.
Plastif. relleno	1,03	0,3
Tope transv.	4,23	0,3

4.1. Plastificación del relleno en el trasdós

El valor de la fuerza que hace que plastifique el relleno del estribo se ha calculado con las reglas de CALTRANS, establecidas a partir de ensayos en modelos a escala [17] . Este valor es similar al que se obtiene al determinar el valor del empuje pasivo para un relleno con densidad γ  = 1,800 kg /m³ , y un ángulo de rozamiento ϕ  = 30, empleando la fórmulas de Rankine.

$E_{p}={\frac {1}{2}}\gamma H^{2}\left({\frac {1+sen\phi }{1-sen\phi }}\right)L^{est}$

( 7)

donde H es la altura del muro del estribo y L la longitud transversal.

Se ha considerado un valor alto del coeficiente de variación ya que existe una gran incertidumbre asociada a la predicción.

4.2. Fallo topes transversales

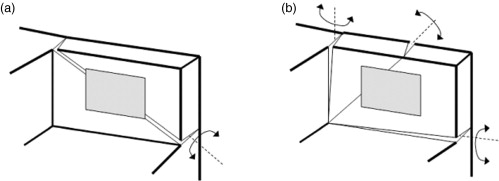
Se estima a continuación el valor de la fuerza que produce el fallo de tope transversal considerando la formación de varias rótulas plásticas en el murete transversal. Se parte de una placa biempotrada, con una fuerza uniformemente repartida a lo largo de la superficie del tope elastomérico. Se plantean los dos mecanismos de fallo que se presentan en la figura 6 . El primero consiste en la plastificación a lo largo de la línea que une los dos vértices extremos de los empotramientos. En el segundo, se producen plastificaciones a lo largo de los dos lados empotrados, además de a lo largo de una línea que pasa por la intersección de ambos.

Figura 6. Hipótesis consideradas para determinar el mecanismo de fallo en el tope transversal: (a) una rótula, (b) tres rótulas.

El dato de partida lo constituyen los valores del momento plástico por unidad de longitud de las secciones vertical y transversal del tope (410 y 510 kN , respectivamente). Para cada mecanismo de fallo, la aplicación del principio de los trabajos virtuales permite deducir el valor de la fuerza que activa el mecanismo. En el primer caso (c.f. fig. 6 [a]) la determinación es sencilla y su valor es f_{lim ,1}  = 1, 15 · 10⁷  N . En el segundo (c.f. fig. 6 [b]), el valor de la fuerza depende del ángulo que forma la rótula diagonal, teniendo sentido físico solo el ángulo correspondiente al valor mínimo. Su valor es f_{lim ,2}  = 4, 27 · 10⁶  N . Por tanto, el mecanismo que se produce es el segundo de ellos.

La UCSD ha propuesto un modelo de bielas y tirantes [19] que permite obtener los valores de las fuerzas que marcan el inicio de la fisuración y el fallo en los topes de cortante. Estas fórmulas son aplicables a topes unidos por una única de sus aristas. En el caso del paso superior aquí estudiado, dos de las mismas están unidas al estribo, por lo que estas no son aplicables. Sin embargo, sirven para estimar el orden de magnitud. En la tabla 2 se presentan los resultados parciales correspondientes a los casos en los que se considera que la unión se realiza mediante el plano vertical u horizontal.

Tabla 2. Determinación de la rigidez y las fuerzas que producen daños en el tope de transversal considerando un único plano de apoyo

Plano	K [N/m]	Vlim
Vertical	2,71 · 108	1,69 · 106
Horizontal	2,28 · 108	1,55 · 106

Los valores son del mismo orden de magnitud pero inferiores a los obtenidos considerando la formación de rótulas. Este sesgo va en la dirección adecuada puesto que las fórmulas suponen una única arista de contacto.

El valor del coeficiente de variación se toma de Mackie et al. [20] .

5. Resultados

5.1. Estudio de peligrosidad

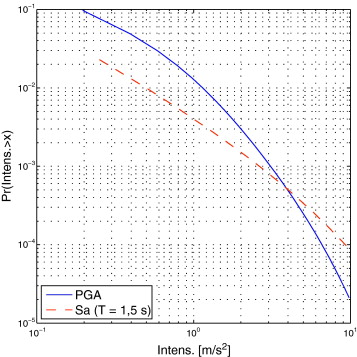
Se parte de un estudio de peligrosidad, realizado según la metodología probabilista zonificada, realizado para el emplazamiento que proporciona las curvas de peligrosidad para la pseudo-aceleración espectral en distintos valores del periodo de vibración (fig. 7 ). Concretamente se toman las curvas para la PGA y para Sa (T  = 1, 5 s). Este ultimo se toma por ser el valor más cercano T  = 1, 41 s disponible en el estudio.

Figura 7. Curvas de peligrosidad para el emplazamiento.

La función de densidad de probabilidad conjunta de PGA y Sa se determina a partir de las funciones marginales de densidad de probabilidad, que se deducen de las curvas de peligrosidad. Se supone un coeficiente de correlación ρ  = 0, 56 obtenido mediante la fórmula 6 .

5.2. Análisis de la respuesta

La caracterización de la demanda se realiza a partir de los resultados de simulaciones, considerando como entrada parejas de registros de terremotos convenientemente modulados para conseguir la intensidad deseada.

Se han tomado una colección de 12 parejas de registros horizontales, correspondiente a un amplio rango de intensidades y distancias. La selección se ha realizado partiendo de un conjunto más grande, eliminando aquellos que no cumplían con las tres condiciones siguientes. Primero, que no hubiese sido filtrada la energía en bandas cercanas al periodo de vibración de la estructura. Segundo, que no tengan un periodo predominante, puesto que estos inducen sesgo [6] . Tercero, que sus componentes no tuviesen intensidades muy diferentes. Si fuese el caso, se tendría una pérdida de correlación entre la intensidad que provoca el choque en teoría y en la práctica. Este punto se discute en detalle a continuación.

A la hora de atribuir un valor espectral a la pareja, se ha optado por utilizar la media geométrica de los valores individuales.

$Sa(T_{s})={\sqrt {{Sa}_{x}(T_{s})\cdot {Sa}_{y}(T_{s})}}$

( 8)

Puesto que los valores de Sa (T_s ) para cada componente de un mismo registro son en general distintos, y como se modulan con respecto a la media geométrica en una dirección, el choque se producirá antes de lo previsto (cuando la holgura es igual al desplazamiento espectral), mientras que en la otra se producirá después. Si las diferencias entre los valores son importantes, existirá una gran diferencia entre la intensidad relativa teórica (considerando la Sa promedio geométrico) y la real (considerando la Sa de cada dirección). Con objeto de evitar esta distorsión se han eliminado los registros en los que la diferencia entre los valores individuales y el valor de la media geométrica es mayor del 20%.

Este último es un valor de compromiso, que limita las diferencias manteniendo un número relativamente grande de registros. Pese a que sería posible recurrir a un mayor número de registros para poder reducir el valor límite, se prefiere mantenerlo para poder por una parte exponer las consecuencias que tiene considerar valores relativamente altos del mismo, y por otra plantear una forma de resolver el problema.

5.3. Caracterización incondicional de la demanda

La caracterización de la demanda se realiza mediante ajuste por mínimos cuadrados de los coeficientes de la ecuación 4 a partir de las muestras obtenidas (los valores de R_{m áx} para las distintas simulaciones). Además se caracteriza la variablilidad alrededor de las predicciones.

Con esta información es posible caracterizar incondicionalmente R_{m áx} , es decir, se puede determinar la probabilidad de que se supere un determinado valor de la misma en un periodo de tiempo teniendo en cuenta que:

$\lambda (x)=\int \int Pr(R_{m{\acute {a}}x}>x\vert PGA,Sa)f_{PGA,Sa}\cdot dPGA\cdot dSa$

( 9)

$Pr(R_{m{\acute {a}}x}>x\vert PGA,Sa)=1-\Phi \left({\frac {log(x)-log{\overset {\mbox{ˆ}}{R_{m{\acute {a}}x}}}}{\epsilon }}\right)$

( 10)

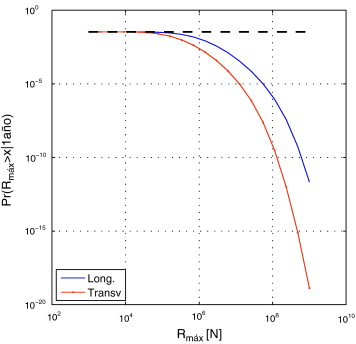
El resultado del cálculo se presenta en la figura 8 . La curva relativa a la dirección longitudinal asocia valores mayores de fuerza de reacción máxima para las mismas probabilidades de superación. El valor máximo de la probabilidad de fallo coincide con el valor de la curva de peligrosidad para el valor en el que ${\textstyle Sa(T=}$$1{\mbox{,}}5\quad s)={\omega }_{s}^{2}\cdot gap=0{\mbox{,}}02\quad g$ (la intensidad para la que se desencadenan los choques). Este valor es Pr (Sa (T  = 1, 5 s ) ≤ 0, 02 g ) = 0, 034.

Figura 8. Probabilidad (anual) incondicional de la variable respuesta Rm áx en ambas direcciones.

5.4. Determinación de la probabilidad de daño

La deducción de los valores de probabilidades de daño se realiza por convolución de la caracterización incondicional de R_{m áx} con las curvas de daño definidas en el apartado 4 :

$P(da{\tilde {n}}o)={\int }_{0}^{\infty }P(da{\tilde {n}}o\vert r)f_{R_{m{\acute {a}}x}}(r)dr$

( 11)

donde ${\textstyle f_{R_{m{\acute {a}}x}}}$ es la diferencial de la curva de respuesta incondicional asociada al daño deducida mediante la expresión 10 .

Los resultados de las probabilidades anuales de alcanzar cada uno de los estados de daño estudiados se presentan en la tabla 3 .

Tabla 3. Probabilidades anuales de alcanzar distintos estados de daño

Daño	Plast.relleno	Tope transv.
Pr(%)	1,14	0,021

De los resultados se deduce que el daño asociado a los choques en dirección longitudinal es mucho más probable que el asociado al movimiento transversal. Esto es lógico puesto que, por una parte las fuerzas son mayores en dirección longitudinal, y por otra el nivel de fuerzas que conduce al daño es menor en esa dirección.

6. Conclusiones

Este artículo presenta todos los elementos necesarios para evaluar las probabilidades de que se produzcan daños asociados a choques en una tipología muy habitual, a través de un ejemplo construido en el sur de España. Se ha detallado la modelización de la estructura compatible con el estudio y la caracterización de los daños susceptibles de producirse.

Dada su modularidad y flexibilidad, ha sido posible adaptar la metodología del PEER a este problema. El resultado del estudio son dos valores de probabilidad anual de que se produzcan estos daños. Estos no deben considerarse de manera absoluta. Su valor es el de servir de elemento de comparación.

En direción longitudinal (plastificación del relleno del estribo), el valor obtenido es relativamente alto comparado con los valores de probabilidad de que se produzca un choque, lo que indica una gran vulnerabilidad. La razón es que tras desencadenarse los choques, las fuerzas que se producen son rápidamente lo suficientemente grandes como para que se produzcan daños.

En sentido transversal (fallo de los topes transversales), la vulnerabilidad es mucho menor. Esto se debe a que las fuerzas que se producen durante los choques son relativamente menores, y a la mayor resistencia de los topes transversales.

Agradecimientos

Este trabajo ha sido financiado por el Ministerio de Fomento, Proyecto 80007/A04. Los autores quieren expresar su agradecimiento a la Prof. Belén Benito, de la Universidad Politécnica de Madrid, por proporcionarles los resultados del estudio de peligrosidad del emplazamiento.

References

1. [1] R. Jankowski; Non-Linear viscoelastic modelling of earthquake-induced structural pounding; Earthquake Eng. Struct. Dyn., 34 (2005), pp. 595–611
2. [2] S.A. Anagnostopoulos; Pounding of buildings in series during earthquakes; Earthquake Eng. Struct. Dyn., 16 (1998), pp. 443–456
3. [3] J.H. Lin, C.C. Weng; Probability analysis of seismic pounding of adjacent buildings; Earthquake Eng. Struct. Dyn., 30 (2001), pp. 1539–1557
4. [4] X. Ma, C.P. Pantelides; Nonlinear pounding of bridges in earthquakes; En Structures Congress ASCE, Chicago (17-19 April 1996), pp. 1180–1187
5. [5] R. Jankowski, K. Wilde, Y. Fujino; Pounding of superstructure segments in bridge during earthquakes; Earthquake Eng. Struct. Dyn., 27 (1998), pp. 487–502
6. [6] J. Vega, I. del Rey, E. Alarcón; Pounding forcce assessment in performance-based design of bridges; Earthquake Eng. Struct. Dyn., 38 (2009), pp. 1525–1544
7. [7] C.A. Cornell, H. Krawinkler, Progress and Challenges in Seismic Performance Assessment [consultado 16/11/2010] (2000). Disponible en: http://peer.berkeley.edu/news/2000spring/performance.html .
8. [8] S.K. Kunnath, L. Larson, E. Miranda; Modelling considerations in probabilistic performance-based seismic evaluation: Case study of the I-880 viaduct; Earthquake Eng. Struct. Dyn., 35 (2006), pp. 57–75
9. [9] A. Der Kiureghian; Non-ergodicity and PEERs framework formula; Earthquake Eng. Struct. Dyn., 34 (2005), pp. 1643–1652
10. [10] N. Luco, C.A. Cornell; Structure-Specific Scalar Intensity Measures for Near-Source and Ordinary Earthquake Ground Motions; Earthquake Spectra, 23 (2) (2007), pp. 357–392
11. [11] P. Bazzurro, C.A. Cornell; Vector-valued probabilistic seismic hazard.; En 7th U.S. National conference on Earhquake Engineering, Boston, Massachusetts (2002 21-25 julio), p. 10
12. [12] C.A. Cornell; Engineering Seismic Risk Analysis; Bull. Seism. Soc. Am., 58 (1968), pp. 1583–1606
13. [13] J.W. Baker, C.A. Cornell; Correlation of Response Spectral Values for Multicomponent Ground Motions; Bull Seism. Soc. Am., 96 (1) (2006), pp. 215–227
14. [14] F. McKeena, Object-Oriented Finite Element Programming: Frameworks for Analysis, Algorithms, and Parallel Computing. PhD thesis. University of California, Berkeley, CA (1997).
15. [15] B.G. Nielson, R. DesRoches; Analytical seismic sragility curves for typical bridges in central and southeastern United States; Earthquake Spectra, 23 (3) (2007), pp. 615–633
16. [16] P.E. Pinto, R. Giannini, P. Franchin; Seismic Reliability Analysis of Structures, IUSS Press, Pavia, Italia (2004)
17. [17] Caltrans, Seismic Design Criteria V.1.3 (2004).
18. [18] J. Azevedo, R. Bento; Design criteria for buildins subjected to pounding.; En 11th World Conf. Earthquake Engineering, Acapulco, México (1996 23-28 junio), p. 1063
19. [19] A. Bozorgzadeh, S.H. Megally, S. Ashford, J.I. Restrepo, Seismic response of sacrificial exterior shear keys in bridge abutments. Dept. Structural Engineering. University of California San Diego. Report No.SSRP-04/14 (2007).
20. [20] K.R. Mackie, J.M. Wong, B. Stajadinovic, Integrated probabilistic performance-based evaluation of benchmark reinforced concrete brigdes. PEER Report 2007/09. University of California, Berkeley (2008).