Abstract
Nowadays, fluid-structure interaction problems are a great challenge of different fields in engineering and applied sciences. In civil engineering applications, wind flow and structural motion may lead to aeroelastic instabilities on constructions such as long-span bridges, high-rise buildings and light-weight roof structures. On the other hand, biomechanical applications are interested in the study of hemodynamics, i.e. blood flow through large arteries, where large structural membrane deformations interact with incompressible fluids.
In the structural part of this work, a new methodology for the analysis of geometrically nonlinear orthotropic membrane and rotation-free shell elements is developed based on the principal fiber orientation of the material. A direct consequence of the fiber orientation strategy is the possibility to analyze initially out-of-plane prestressed membrane and shell structures. Additionally, since conventional membrane theory allows compression stresses, a wrinkling algorithm based on modifying the constitutive equation is presented. The structure is modeled with finite elements emerging from the governing equations of elastodynamics.
The fluid portion of this work is governed by the incompressible Navier-Stokes equations, which are modeled by stabilized equal-order interpolation finite elements. Since the monolithic solution for these equations has the disadvantage that take great computer effort to solve large algebraic system of equations, the fractional step methodology is used to take advantage of the computational efficiency given by the uncoupling of the pressure from the velocity field. In addition, the generalized- time integration scheme for fluids is adapted to be used with the fractional step technique.
The fluid-structure interaction problem is formulated as a three-field system: the structure, the fluid and the moving fluid mesh solver. Motion of the fluid domain is accounted for with the arbitrary Lagrangian-Eulerian formulation with two different mesh update strategies. The coupling between the fluid and the structure is performed with the strong coupling block Gauss-Seidel partitioned technique. Since the fluid-structure interaction problem is highly nonlinear, a relaxation technique based on Aitken's method is implemented in the strong coupling formulation to accelerate the convergence.
Finally several example problems are presented in each field to verify the robustness and efficiency of the overall algorithm, many of them validated with reference solutions.
1 Introduction
1.1 Motivation
Modeling of structural elements, such as membranes and thin shells, is widely used in many engineering fields. In civil engineering applications, their elegance, effectiveness and optimal material usage make these light weight structures an ideal construction element.
The introduction of new fiber materials, such as glass, carbon or aramide fibers with orthotropic material behavior have motivated a deep study of such elements which are used to build membrane and thin shell structures.

|
| Figure 1: Membrane long span structure |
Moreover membrane and thin shell structures are characterized by their low flexural stiffness. Consequently these elements should not resist any compression at all. Therefore the usage of such construction materials is performed by introducing a prestressed force to the structure. Figs. 1 and 2 show different applications of membranes in civil engineering structures.

|
| Figure 2: Prestressed membrane structure |
Other examples where light weight structures can be found include aircraft and spacecraft applications, parachutes, automobile airbags, sails, windmills and human tissues.
Since this kind of structures are highly flexible systems, they are susceptible to wind loads applied to them. Wind flow and structural motion may lead to aeroelastic instabilities which may cause important damage or even collapse of the structure.
Maybe one of the most important examples of aeroelastic instabilities is the disaster of the Tacoma Narrows suspension bridge that took place in the U.S.A. on November 7, 1940. The collapse of the bridge was due to wind-induced vibrations that at the beginning produced large transverse and rotational oscillations, as can be seen in Fig. 3.

|
| Figure 3: Aeroelastic instabilities of the Tacoma Narrows suspension bridge, U.S.A. |
In general many physical problems of different fields belong to multiphysic problems. In particular, numerical simulation of fluid-structure interaction problems have gained great interest from the industry community in order to reduce development time and cost in coupled systems. This kind of problems are complex because they consist of structural nonlinear boundary conditions imposed on fluid moving domains where the position is part of the solution.
Recently biomechanical applications are interested in the numerical simulation of hemodynamics, which study the blood flow through veins and arteries. In this problem, large structural deformations of the arteries interact with viscous blood flow as a consequence of each heart beat. Another field where fluid-structure interaction plays an important role is the aerospace engineering which study wind flow around flexible wings of aircrafts.
1.2 Background
In this work, membrane and shell structures with large deformations are studied. A numerical solution for membranes may be constructed using the finite element method, which solution for small deformations can be found in [1], [2] or [3].
Theory for large deformations can proceed following the presentations of [4], [5], [6] or [7]. In particular a large displacement formulation of membrane elements composed by three-node triangular finite elements based on rectangular Cartesian coordinates is proposed by [8].
This last formulation together with the study of [9] form the basis for the development of the membrane formulation given in this work, which includes orthotropic material behavior and prestressed forces.
Several studies have been carried out to study the geometrically nonlinear behavior of shells, for example the works of [4], [5], [10], among many others. Since shell analysis requires a lot of memory and cpu-time to compute, several authors have tried to derive plate and shell elements with displacements as the only nodal variables.
In this area, [11] proposed a general procedure based on finite volume concepts for deriving linear thin plate elements of triangular and quadrilateral shapes with the nodal deflections as the only degree of freedom. [12] proposed a different approach to compute the constant curvature field within each triangle in terms of the six-node displacement of a macro-element. This triangular element was successfully applied to nonlinear shell analysis using an explicit dynamic approach. [13] continue with the study of rotation free elements of [11] developing new triangular elements. This formulation applied to large deformations with an explicit dynamic procedure was presented by [14]. [15] proposed the same element that [14] but applied to metal forming processes.
As an alternative formulation for large strain plasticity, the BST shell element was introduced by [16]. This formulation constitutes the starting point for the development of the rotation-free shell formulation developed in this work, which includes orthotropic material behavior and prestressed forces.
Besides the structural developments, to perform a fluid-structure interaction study the fluid flow for incompressible problems has to be implemented. Finite element analysis of fluids present potential numerical instabilities that emerge for incompressible flow problems. To circumvent these problems, different stabilization techniques have been proposed. One of the stabilization techniques that has been extensively used is the streamline-upwind/Petrov-Galerkin SUPG method. Here numerical oscillations could be avoided by introducing numerical diffusion only along the streamlines as explained in the work of [17] for advection-diffusion equation. The use of the streamline diffusion in the context of weighted residual methods is given in [18]. Another kind of stabilization is the pressure-stabilizing/Petrov-Galerkin PSPG method. In [19], the SUPG and PSPG stabilization methods are used together with equal-order interpolations.
With the idea to better understand the origins of stabilized methods, which can be derived from a firm theoretical foundation and a precise definition of the intrinsic time scale parameter, [20] developed the subgrid scale method. In the context of these methods, the orthogonal sub-scales OSS method was introduced by [21]. The stabilization methods described require the addition of some artificial diffusion terms. However another technique where the stabilization terms emerge from the governing equations of the problem is the finite calculus FIC method given by [22]. An application of the FIC for incompressible viscous flow problems can be found in [23].
The monolithic coupled equations for incompressible fluid problems have the disadvantage that take great computer effort to solve the algebraic system for each time step in a transient analysis. Since the original works of [24] and [25], fractional step methods for the incompressible Navier-Stokes equations have earned widespread popularity because of the computational efficiency given by the uncoupling of the pressure from the velocity field. A detailed stability analysis of fractional step methods for incompressible flows is given in [26]. In this work, the FIC and OSS stabilization techniques are implemented to study the coupled problem of large structural deformations and incompressible fluids flow using pressure segregation methods.
With the structural and fluid problem introduced, the remaining task to study is the coupled problem between both of them. The implementation of a coupled problem can be done using two different global strategies, which are the monolithic methods and the partitioned methods. In partitioned methods application of existing appropriate and sophisticated solvers for either structural or fluid subsystems will be used. Partitioned methods were introduced by [27]. The key idea for these methods is clearly described in [28]. Partitioned solutions with staggered coupling algorithms are developed by [29] to be used in aeroelastic wing problems.
Applications of strongly partitioned algorithms to large displacements structural problems coupled to viscous incompressible fluids are given by [30] and [31]. Other large displacements structural problems interacting with incompressible fluids are detailed in [32], [33] and [34]. More sophisticated developments on strong partitioned method for FSI problems can be found in [35], [36] and [37]. A study on strong coupling partitioned methods for fluid-structure interaction problems applied to hemodynamic can be found in [38], [39], and [40]. In this work, strong coupling partitioned methods are used for fluid-structure interaction problems.
1.3 Objectives
Two general objectives in this work are pursued. The first of them is the improvement of prior developments made at CIMNE related to nonlinear membrane and shell analysis. The second general objective is the study of fluid-structure interaction problems using fluid flow pressure segregation methods and stabilization techniques developed at CIMNE.
The two general objectives must be implemented in one efficient, robust and accurate computational tool that use finite element technology to solve the problem in study, which also must have possibilities to analyze each subproblem, i.e. the solid or fluid part, independently as a highly developed software that exchange data for the solution of the coupled problem with other separate solvers.
The following particular objectives belong to the structural part:
- To review the state of the art for geometrically nonlinear membrane and shell finite elements.
- To improve the membrane and rotation-free shell finite elements developed at CIMNE in prior studies.
- To develop a new methodology to analyze orthotropic material behavior of membrane and shell finite elements, including the wrinkling phenomena to avoid compression stresses in membranes.
- To propose a new strategy to study prestressed membrane elements.
- To explore existing time integration schemes for structural dynamic problems and to work with the best choice for long time analysis periods.
- To implement the membrane and rotation-free shell finite elements together with their new developments in the COMET program, which is a software for coupled contact, mechanical and thermal analysis built at CIMNE.
The particular objectives belonging to the fluid-structure interaction problem part are:
- To implement in the COMET program the finite element fluid problem based on the incompressible Navier-Stokes equations and to use the stabilization techniques developed at CIMNE.
- To implement the mesh update strategy developed at CIMNE for the motion of the fluid domain.
- To explore existing time integration schemes for fluid dynamic problems and to work with the best choice for long time analysis periods.
- To review the state of the art for fluid-structure interaction problems.
- To implement a general and simple methodology to perform the study of coupled problems using the COMET program.
All these objectives are oriented to improve and to combine the developments made in-the-house in the solid mechanics field, i.e. membrane and thin shell finite elements, and the fluid dynamics field, i.e. stabilization techniques and mesh moving algorithms, to perform fluid-structure interaction of problems involving large structural displacements and incompressible fluid flows.
1.4 Outline
Since this work deals with different topics, a detailed review of the state-of-the-art is provided at the beginning of each theme to be developed. The work presented is organized as follows:
Chapter 2. Since the computational models emerged in this work are developed from the mechanics of a continuous medium, in this chapter the kinematics, stress and strain measures for solids and fluids, conservation equations, and the constitutive and Navier-Stokes equations used in this work are given. The remainder of this work is referred to these equations.
Chapter 3. In this chapter a review of the total Lagrangian formulation for geometrically nonlinear solid mechanics is made. From the continuum mechanics theory, the general formulation of each subject is presented which later is discretized with finite elements. Here the concept of principal fiber orientation is introduced. Next a new formulation for membrane elements is developed based on the fiber orientation, including orthotropic material behavior and initially out-of-plane prestressed conditions. Also a basic wrinkling algorithm to avoid compression stresses is studied. Then the rotation-free shell elements are derived, using the fiber orientation to yield a new formulation to study prestressed and orthotropic material behavior of shells. Later a review of some time integration schemes for solids are addressed. The solution strategy used in this work and linearization of the semi-discrete equations of motion is explained. Finally some example problems are presented to validate the finite element implementations in the COMET code.
Chapter 4. This chapter deals with the fluid dynamic equations that solve the incompressible flow problem. Next the governing equations which yield the weak form and the finite element discretization for fluids are explained. Later a review of some time integration schemes for fluids are studied. Two different pressure segregation methods to solve the incompressible fluid equations problem are presented. Then three stabilization techniques for the incompressible fluid problem are introduced. The solution strategy used in this work to solve the nonlinear algebraic equations is shown. Finally some benchmark problems are solved and compared to validate the finite element implementation in the COMET program.
Chapter 5. In this chapter the coupling strategies for fluid-structure interaction problems are explained. The finite element formulation described in chapter 4 dealing with the incompressible flow problem is extended to account for moving fluid domains by means of the arbitrary Lagrangian-Eulerian formulation. Next the governing equations which yield the weak form of the coupled problem are obtained. Then different partitioned methods to solve the fluid-structure interaction problem are studied. Later two different mesh update techniques are presented. A detailed algorithm for the strong coupling with relaxation used in this work is given. Finally some example problems are presented to validate the finite element implementations in the COMET code.
Chapter 6. Here the conclusions and achievements of this work are presented. This monograph concludes with some suggestions for future research lines to be developed as a direct consequence of this work.
2 Continuum Mechanics
This work deals with the study of structures with large deformations interacting with incompressible fluids. As mentioned in [41], the distinction between solids and fluids is not a sharp one. While a solid has a definite shape which changes are small when there is a small change in the external conditions, a fluid does not have a preferred shape and the relative positions of their elements change by an amount which is not small even tough the applied forces are small.
The macroscopic behavior of fluids, solids and structures is given by models emerged from the mechanics of a continuous medium. In this chapter a summary of the continuum mechanics used in this work for fluid-structure interaction problems is presented. A general and more detailed description of continuum mechanics can be found in [42], [43], [44], [41], [45], and [46] among many other well known books.
This chapter begins with the kinematics that involved motion of a body. Next the concepts of stress and strain related to nonlinear solid mechanics and fluids are described. Then the conservation equations, also known as balance equations, are presented. Finally the constitutive and Navier-Stokes equations are given.
2.1 Kinematics
Kinematics is the study of motion and deformation of a body without regard to the forces responsible for such action. A body can be imagined as a composition of a set of particles which are called material points. This body is in an initial state when time as shown in Fig. 4. The domain of the body in this state is denoted by which occupies a region in space and is known as the initial configuration. To describe the kinematics of a body another configuration is needed where equations are referred to and is called the reference configuration. Most of the times the initial configuration is used as the referenced configuration, unless we specify otherwise.
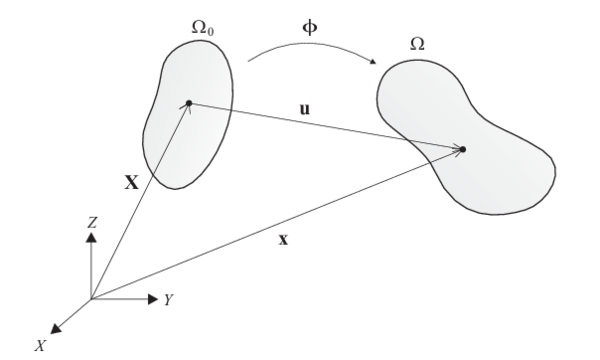
|
| Figure 4: Configurations of a body |
Now we assume that the domain moves to a new region which is occupied by the body for any subsecuent time . At this time the configuration of the body is called the current configuration, also known as the deformed configuration. The boundary of the domain, in this case for the current configuration, is denoted by . The dimension of any model is denoted by denoting the number of space dimensions of the body .
The position vector of a material point in the reference configuration is defined by X, where
|
|
(1) |
where are the components of X in the reference configuration and are the unit base vectors for a rectangular Cartesian coordinate system. The variable vectors X are called material coordinates or Lagrangian coordinates. The motion of the body is given by
|
|
(2) |
where
|
|
(3) |
is the position of the material point X in the current configuration. The variable vectors x are called spatial coordinates or Eulerian coordinates, and the function is a mapping of the reference configuration onto the current configuration.
When describing the kinematics of a continuum two approaches can be used. First, if we take material coordinates and time as the independent variables, the description is called material description or Lagrangian description. On the other hand, if the independent variables are the spatial coordinates and time , we are taking about a spatial description or Eulerian description. In general solid mechanics use Lagrangian descriptions while fluid mechanics use Eulerian descriptions.
The difference for a material point between its current and reference configuration gives the displacement which in material description is
|
|
(4) |
Using Eq. (1) and Eq. (2) into Eq. (4) yields
|
|
(5) |
since for , which means that at reference configuration . Given as the independent variables, the inverse mapping of the motion is defined as
|
|
(6) |
meaning that the material point X is associated with the place x at time t. For a material point the velocity is the rate of change, or derivative, of the position vector. When X is held constant then the derivative is called material time derivative or total time derivative. Using Eq. (2) and Eq. (5) the material velocity is given by
|
|
(7) |
The material acceleration is the rate of change of the velocity, or the material time derivative of the velocity expressed by
|
|
(8) |
For expressions given in spatial description, i.e. the velocity where we use Eq. (2), its material time derivative can be found using
|
|
(9) |
where is the spatial time derivative and the second term in the right hand side is the convective term, where is the right gradient of the velocity vector field with respect to the spatial coordinates, which in indicial form is or in tensor notation is . Using the inverse mapping of the motion, Eq. (6) to express the velocity in spatial description, Eq. (9) can be written as
|
|
(10) |
where is the left gradient of the velocity vector field with respect to the spatial coordinates, which in indicial form is . It is important to see that
|
|
(11) |
In general the material time derivative of any function, vector or tensor given in spatial variables x and time t can be obtained with
|
|
(12) |
When a continuum body moves from the reference configuration to the current configuration , it changes its size and shape giving a deformation. A primary measure of deformation in nonlinear mechanics is the material deformation gradient tensor given by
|
|
(13) |
which relates a quantity in the reference configuration to its corresponding quantity in the current configuration. For example consider an infinitesimal line segment d X in the reference configuration, then using Eq. (13) the resulting line segment d x in the current configuration is
|
|
(14) |
The deformation gradient F is also known as the Jacobian matrix. Another important quantity related to F is the Jacobian determinant given by
|
|
(15) |
The Jacobian determinant is useful to relate integrals in the reference configuration to its counterpart in the current configuration.
Using x from Eq. (4) in Eq. (13), the deformation gradient tensor can be expressed by
|
|
(16) |
where / is the material displacement gradient tensor and is the Kronecker delta which values are
|
|
(17) |
2.2 Strain Measures
In the behavior of materials, the strain measures the geometrical deformation caused by the forces applied on a continuum body . The strain is computed as the change between the undeformed initial configuration of the body and its final deformed configuration. Therefore, the strain expresses itself the motion and deformation of a body.
There are many kinematic measures of strain in continuum mechanics. For Lagrangian descriptions the most essential strain is the Green-Lagrange strain tensor defined by
|
|
(18) |
which also can be expressed as a function of the displacement gradient tensor yielding
|
|
(19) |
For linear strain problems, the infinitesimal strain tensor can be found from Eq. (19) by neglecting the nonlinear terms giving
|
|
(20) |
Now we define the spatial velocity gradient tensor by
|
|
(21) |
which can be decomposed into its symmetric and skew-symmetric parts using
|
|
(22) |
where the spatial rate of deformation tensor d, also known as the velocity strain tensor or strain rate tensor is given by the symmetric part of the velocity gradient according to
|
|
(23) |
The spatial rate of rotation tensor w, also known as the spin tensor is given by the skew-symmetric part of l yielding
|
|
(24) |
Taking the material time derivative of the deformation gradient tensor, Eq. (13), gives
|
|
(25) |
and now Eq. (21) can be written as
|
|
(26) |
where we use the spatial deformation gradient tensor
|
|
(27) |
If we take the material time derivative of the Green-Lagrange strain tensor, Eq. (18), we get
|
|
(28) |
2.3 Stress Measures
The motion and deformation of a continuum body gives rise to forces emerging from interactions between interior parts of the body or between the body and its environment. Physically, the stress measures a force per unit area within a body. Let P be a point on the boundary of the body, n the outward normal unit vector for P and d the part of the surface on the body where P is contained. Then is the surface force acting at P that depends of n and d. Henceforth the surface traction t at point P on the surface with normal n is defined by
|
|
(29) |
where t does not necessarily coincide in direction with n. It is important to see that the surface traction has units of force per unit area. There exists a spatial tensor field }\sigma\mbox{ called the Cauchy stress tensor such that for each unit vector n
|
|
(30) |
which is also known as the Cauchy's theorem. Since the Cauchy stress tensor involves the normal to the current surface and the traction on the current surface too, this tensor is also known as the true physical stress tensor and has the property that is symmetric, see section 2.4.2. In the reference configuration the counterpart of Eq. (30) is
|
|
(31) |
where P is the nominal stress tensor and and is the traction force and unit normal respectively in the reference configuration. Unlike the Cauchy stress tensor, the nominal stress tensor is not symmetric and is important to see that the normal is to the left. The transpose of the nominal stress tensor is the first Piola-Kirchhoff stress tensor. The second Piola-Kirchhoff stress tensor S is defined by
|
|
(32) |
where the transformation of the forces by makes it a symmetric tensor. The transformation between these stresses is given by
|
|
(33) |
|
|
(34) |
|
|
(35) |
2.4 Conservation Equations
The conservation equations reflect some physical quantity for a continuum medium which always must be satisfied and that are not restricted in their application to any material. Applying the conservation equations to the domain of a body leads to an integral relation. Since the integral relation must hold for any subdomain of the body, then the conservation equations can be expressed as partial differential equations.
Before continuing with the conservation equations, the material time derivative of an integral relation for any spatial property is defined by
|
|
(36) |
which is the Reynold's transport theorem. The divergence taken respect to current coordinates can also be expressed as or in indicial form .
2.4.1 Mass Conservation
Consider the domain of a body bounded by the surface which is filled with a constant material density . Then the mass of the body is given by
|
|
(37) |
where we use Eq. (15) to relate integrals in the reference and current configurations. Mass conservation requires that the mass of any material domain be constant. Consequently the material time derivative of the mass must be zero, giving
|
|
(38) |
which leads to the following integral relation using Eq. (36)
|
|
(39) |
where the quantities used are expressed in spatial coordinates. Since the above holds for any subdomain , the mass conservation yields the following first-order partial differential equation
|
|
(40) |
The above equation is also known as the continuity equation. Using the definition of material time derivative Eq. (12) in first term of Eq. (40), the continuity equation can be written as
|
|
(41) |
which is known as the conservative form of the mass conservation equation. When a material is said to be incompressible, the density keeps constant in time so that its material time derivative vanishes and the continuity equation becomes
|
|
(42) |
This is the continuity equation used in this work for fluid problems which always are considered as incompressible.
For Lagrangian descriptions, the mass conservation equation Eq. (38) can be integrated in time to obtain an algebraic equation for the density in the form of Eq. (37) yielding
|
|
(43) |
which is the Lagrangian description for the mass conservation equation.
2.4.2 Conservation of Linear and Angular Momentum
The conservation of linear momentum states that the rate of change of its linear momentum is equal to the total force applied to it. The conservation of linear momentum is also known as the balance of momentum principle or simply the momentum conservation principle. If we consider an arbitrary domain with boundary in the current configuration subjected to body forces and surface tractions t, where b is a force per unit mass, then the total force f is given by
|
|
(44) |
The linear momentum is given by the product of the density and the velocity v over the domain in the form
|
|
(45) |
Hence the conservation of linear momentum is expressed by
|
|
(46) |
Using Eq. (36) and Eq. (40) in Eq. (46), the rate of change of the linear momentum is found to be
|
|
(47) |
The boundary integral in Eq. (46) can be transformed to a domain integral using Eq. (30) and Gauss' divergence theorem yielding
|
|
(48) |
Substituting Eq. (47) and (48) into (46) gives
|
|
(49) |
and since it holds for any arbitrary domain we find
|
|
(50) |
This is called the momentum equation. In an Eulerian description for the momentum equation, the material time derivative of the velocity in Eq. (50) is developed using Eq. (12) yielding
|
|
(51) |
where all the quantities are given is spatial coordinates. In this work, Eq. (51) is the one to be used in the fluid mechanics problem. For fluid finite elements this equation is called Eulerian formulation.
The momentum equation Eq. (50) can also be written in a Lagrangian description where all the quantities are expressed in material coordinates, giving
|
|
(52) |
Since Eq. (50) is in the current configuration, the divergence term is taken respect to spatial coordinates and therefore is expressed by so that the spatial gradient of the stress field can be evaluated. For nonlinear solid finite elements, Eq. (52) is called updated Lagrangian formulation.
The conservation of angular momentum is obtained by taking the cross product of the current vector position x by each term of the linear momentum equation Eq. (46), yielding
|
|
(53) |
where it can be shown that leads to the following result
|
|
(54) |
The acceleration term in Eq. (50) can be neglected when the loads are applied slowly so that the inertial forces become insignificant. Then we can write
|
|
(55) |
which is known as the equilibrium equation. Problems that use Eq. (55) are called static problems.
The conservation of linear momentum can also be expressed in the reference configuration. Consider an arbitrary domain with boundary in the reference configuration subjected to body forces and surface tractions , then the total force f is given by
|
|
(56) |
The linear momentum is given by
|
|
(57) |
Hence the conservation of linear momentum is expressed by
|
|
(58) |
The boundary integral in Eq. (58) can be transformed to a domain integral using Eq. (31) and Gauss' divergence theorem yielding
|
|
(59) |
where is the divergence taken respect to material coordinates. Leaving the derivation of the conditions which follow from Eq. (58), the conservation of linear momentum in reference configuration for Lagrangian coordinates is
|
|
(60) |
This is called the Lagrangian form of the momentum equation. For nonlinear solid finite elements, Eq. (60) is called total Lagrangian formulation. The corresponding equilibrium equation for this description is
|
|
(61) |
As a consequence of the conservation of angular momentum Eq. (53) and Eq. (54) the nominal stress tensor yields
|
|
(62) |
which is in general not symmetric. The number of conditions imposed by angular momentum conservation are usually imposed directly on the constitutive equation. Using Eq. (34) in Eq. (62) we obtain that for the second Piola-Kirchhoff stress
|
|
(63) |
is a symmetric tensor.
2.4.3 Conservation of Energy
The kinetic energy of a material is given by
|
|
(64) |
which for a continuum body is only part of the total energy. The remainder energy is called the internal energy that is expressed by per unit mass. The internal energy per unit volume is denoted by
|
|
(65) |
The total energy is then expressed by . Then the conservation of energy requires that the power of the total energy equals the power of the applied forces plus the power at which other energy enters in the domain. The other energy may take different forms, but the most important is the energy due to heat sources and heat flux across . Other energy sources arise from radiation, chemical changes, electromagnetic fields, etc. We consider thermomechanical processes only.
The power of the total energy is given by
|
|
(66) |
while the power of the applied forces is expressed by
|
|
(67) |
The power supplied by heat sources s and the heat flux q is
|
|
(68) |
The conservation of energy states that
|
|
(69) |
which is known as the first law of thermodynamics. Replacing Eqs. (66)-(68) into Eq. (69) yields the equation of conservation of energy
|
|
(70) |
The equation which emerges from the above integral form leads to the following Eulerian partial differential equation of energy conservation
|
|
(71) |
For a purely mechanical process, the above equation becomes
|
|
(72) |
which is no longer a partial differential equation. As a consequence of Eq. (72) we can say that the Cauchy stress tensor and the rate of deformation tensor d are conjugate in power.
The conservation of energy can also be expressed in Lagrangian coordinates and in the reference configuration, where the counterpart of Eq. (70) gives
|
|
(73) |
which gives the Lagrangian partial differential equation of energy conservation
|
|
(74) |
For a purely mechanical process, the Lagrangian energy conservation is
|
|
(75) |
showing that the nominal stress tensor is conjugate in power to the material time derivative of the deformation gradient tensor. Using Eq. (34) in Eq. (75) we obtain the energy conservation equation in terms of the second Piola-Kirchhoff stress tensor
|
|
(76) |
which shows that the second Piola-Kirchhoff stress tensor is conjugate in power to the rate of the Green-Lagrange strain tensor.
2.5 Constitutive Equations
The equations given so far are still insufficient to describe the mechanical behavior of any material. Therefore we need additional equations called constitutive equations which complete the set of equations specifying the mechanical properties of a material. For a purely mechanical process, the constitutive equation of a material specifies the dependence of the stress tensor in terms of kinematic variables such as the strain tensor.
2.5.1 Linear Elasticity
Engineering materials such as metals or concrete usually undergo very small changes of shape when they are subjected to the forces which they are exposed. They also have an initial shape to which they will return if the forces applied are removed. Since the changes of shape are very small, there is no difference between the reference and current configuration.
The linear elasticity theory gives an excellent model for the behavior of such materials. The infinitesimal strain tensor is used to measure strains while the Cauchy stress tensor measures the stresses. For the linear elasticity theory the energy conservation equation takes the form
|
|
(77) |
where and are conjugate in power.
It is conventional to denote the internal energy per unit volume by which is called the strain energy function. For a linear elastic material the strain energy function depends only of the components and is a quadratic function of the form
|
|
(78) |
where are called elastic constants. Since the elastic constants possess symmetry of the form
|
|
(79) |
then for an isotropic material, its properties are the same in all directions.
Since depends only on , the material time derivative of Eq. (78) gives
|
|
(80) |
where the symmetry of the material has been used. Substituting Eq. (80) into Eq. (77) gives
|
|
(81) |
However from Eq. (78) and Eq. (79)
|
|
(82) |
Substituting Eq. (82) into Eq. (81) yields
|
|
(83) |
which is the constitutive equation that relates stresses and strains. The constitutive equation complete the equations to describe the mechanical behavior of linear elastic materials. For an isotropic material takes the form
|
|
(84) |
where only two constants and of the original 81 of the fourth-order tensor survived after the restrictions of material isotropy and stress symmetry. The two independent material constants and are called the Lamé constants, I is the second-order identity tensor and is the fourth-order symmetric identity tensor given by . The constitutive equation Eq. (83) becomes
|
|
(85) |
where is the trace of .
2.5.2 Nonlinear Elasticity
Engineering applications also involved small strains and large deformations, where these effects arise from large displacements and large rotations of the structure. The response of such materials may be modeled with a Saint Venant-Kirchhoff material which is a generalization of the linear theory to large deformations giving the nonlinear elasticity theory.
The strain energy function for a nonlinear elastic material is a generalization of Eq. (78) and is given by
|
|
(86) |
where the stress is
|
|
(87) |
The counterpart of Eq. (83) in the nonlinear theory yields
|
|
(88) |
where is given by Eq. (84). Finally, the constitutive equation for nonlinear elastic materials is
|
|
(89) |
The Lamé constants and can be expressed in terms of other physical measurements given by
|
|
(90) |
|
|
(91) |
|
|
(92) |
where is the Young's modulus, is the Poisson's ratio and is the bulk modulus.
2.5.3 Newtonian Fluid
An equation that linearly relates the stress tensor to the rate of strain tensor in a fluid medium is called the constitutive equation for Newtonian fluids.
In a static fluid there are only normal components of the stress tensor on a boundary, so the stress tensor for a fluid at rest is isotropic and takes the form
|
|
(93) |
where p is the thermodynamic pressure related to the density and the temperature T. A moving fluid develops additional components of stress due to viscosity yielding
|
|
(94) |
where the deviatoric stress tensor is linearly related to the strain rate tensor by
|
|
(95) |
Substituting Eq. (23) and Eq. (84) into Eq. (95) and this new equation in Eq. (94), the resulting equation is
|
|
(96) |
where is the volumetric strain rate. If the Stokes assumption, , is used in Eq. (96) to relate and the new equation is
|
|
(97) |
which is the constitutive equation for Newtonian fluids. For incompressible fluids the continuity equation Eq.(42) is substituted into Eq. (97) and the constitutive equation for incompressible fluids takes the simple form
|
|
(98) |
where p is the pressure. For incompressible fluids, p is called mechanical pressure.
The equation of motion for a Newtonian fluid is obtained by substituting the constitutive equation for Newtonian fluids Eq. (97) into the momentum equation in Eulerian description Eq. (51) to obtain
|
|
(99) |
Equation (99) is the general form of the Navier-Stokes equation. If is taken as a constant, the derivative in the right hand side term can be written as
|
|
(100) |
where is the Laplacian1 of . For incompressible fluids the continuity equation Eq.(42) is substituted into Eq. (100) and the Navier-Stokes equation reduces to
|
|
(101) |
If viscous effects are negligible, which may occur far from boundaries of the flow field,
|
|
(102) |
and the Euler equation is obtained. Now consider given a characteristic velocity scale and a characteristic length scale , then the Reynolds number is defined as . When the Reynolds number for the flow is very low, the convective term can be neglected yielding
|
|
(103) |
which is known as the Stokes flow. In the literature, it is common to express Eq. (103) without the inertial term.
References
[1] O. C. Zienkiewicz and Robert L. Taylor. The Finite Element Method, Volume 1 and 2. McGraw-Hill, 4th Edition, 1989
[2] Robert D. Cook and David S. Malkus and Michael E. Plesha. Concepts and Applications of Finite Element Analysis. Wiley, 3rd Edition, 1989
[3] Eugenio Oñate. El Metodo de los Elementos Finitos. CIMNE, 1992
[4] Juan Carlos Simo and D. D. Fox. On a stress resultant geometrically exact shell model. Part I: Formulation and optimal parametrization, Volume 72. Computer Methods in Applied Mechanics and Engineering 267-304, 1989
[5] Juan Carlos Simo and D. D. Fox and M. S. Rifai. On a stress resultant geometrically exact shell model. Part III: Computational aspects of the nonlinear theory, Volume 79. Computer Methods in Applied Mechanics and Engineering 21-70, 1990
[6] N. Bütchter and E. Ramm and D. Roehl. Three-dimensional extension of non-linear shell formulations based on the enhanced assumed strain concept, Volume 37. International Journal for Numerical Methods in Engineering 2551-2568, 1992
[7] M. Braun and M. Bischoff and E. Ramm. Nonlinear shell formulations for complete three-dimensional constitutive laws include composites and laminates, Volume 15. Computational Mechanics 1-18, 1994
[8] Robert L. Taylor. Finite Element Analysis of Membrane Structures. Internal CIMNE report, 2001
[9] K. Lu and M. Accorsi and J. Leonard. Finite element analysis of membrane wrinkling, Volume 50. International Journal for Numerical Methods in Engineering 1017-1038, 2001
[10] Juan Carlos Simo and J. G. Kennedy. On a stress resultant geometrically exact shell model. Part V: Nonlinear plasticity: Formulation and integration algorithms, Volume 96. Computer Methods in Applied Mechanics and Engineering 133-171, 1992
[11] Eugenio Oñate and Miguel Cervera. Derivation of thin plate elements with one degree of freedom per node, Volume 10. Engineering Computations 543-561, 1993
[12] M. Brunet and F. Sabourin. Prediction of necking and wrinkles with a simplified shell element in sheet forming. 27-48, 1994
[13] Francisco Zárate. Nuevos Elementos Finitos para Placas y Láminas, 1996
[14] Patricio Cendoya. Nuevos elementos finitos para el análisis dinámico elasto-plástico no lineal de estructuras laminares, 1996
[15] J. Rojek and E. Oñate and E. Postek. Application of explicit codes to simulation of sheet and bulk metal forming processes, Volume 80-81. Journal of Materials Processing Technology 620-627, 1998
[16] Fernando G. Flores and Eugenio Oñate. A basic thin shell triangle with only translational dofs for large strain plasticity, Volume 51. International Journal for Numerical Methods in Engineering 57-83, 2001
[17] T. J. R. Hughes and A. N. Brooks. A multi-dimensional upwind scheme with no crosswind diffusion. ASME , 1979
[18] T. J. R. Hughes and A. N. Brooks. A theoretical framework for Petrov-Galerkin methods with discontinuous weighting functions: applications to the streamline upwind procedure, Volume IV. Wiley 46-65, 1982
[19] T. E. Tezduyar and R. Shih and S. Mittal. Time-accurate incompressible flow computations with quadrilateral velocity-pressure elements, Volume August. University of Minnesota. Supercomputer Institute Research Report UMSI 90/143 , 1990
[20] T. J. R. Hughes. Multiscale phnomena: Green's functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods, Volume 127. Computer Methods in Applied Mechanics and Engineering 387-401, 1995
[21] Ramón Codina. Stabilization of incompressibility and convection through orthogonal sub-scales in finite element methods, Volume 190. Computer Methods in Applied Mechanics and Engineering 1579-1599, 2000
[22] Eugenio Oñate. Derivation of stabilized equations for numerical solution of advective-diffusive transport and fluid flow problems, Volume 151. Computer Methods in Applied Mechanics and Engineering 233-265, 1998
[23] Eugenio Oñate. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation, Volume 182. Computer Methods in Applied Mechanics and Engineering 355-370, 2000
[24] A. J. Chorin. A numerical method for solving incompressible viscous problems, Volume 2. Journal of Computational Physics 12-26, 1967
[25] R. Temam. Sur l'approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionaires (I), Volume 32. Archives for Rational Mechanics and Analysis 135-153, 1969
[26] Ramón Codina. Pressure stability in fractional step finite element methods for incompressible flows, Volume 170. Journal of Computational Physics 112-140, 2001
[27] K. C. Park and Carlos A. Felippa. Partitioned analysis of coupled systems. Elsevier Science Publishers 157-219, 1983
[28] Carlos A. Felippa and K. C. Park and C. Farhat. Partitioned Analysis of Coupled Systems. CIMNE , 1998
[29] C. Farhat and M. Lesoinne and P. Stern and S. Lantéri. High Performance Solution of Three-Dimensional Nonlinear Aeroelastic Problems via Parallel Partitioned Algorithms, Volume 28. Advances in Engineering Software 43-61, 1997
[30] Wolfgang A. Wall and Ekkerhard Ramm. Fluid-Structure Interaction based upon a stabilized (ALE) finite element method. CIMNE , 1998
[31] Wolfgang A. Wall. Fluid-Struktur-Interaktion mit stabilisierten Finiten Elementen, 1999
[32] Daniel Pinyen Mok. Partitionierte Lösungsansätze in der Strukturdynamik und der Fluid-Struktur-Interaktion, 2001
[33] D. P. Mok and W. A. Wall. Partitioned analysis schemes for the transient interaction of incompressible flows and nonlinear flexible structures. CIMNE 689-698, 2001
[34] P. Le Tallec and J. Mouro. Fluid structure interaction with large structural displacements, Volume 190. Computer Methods in Applied Mechanics and Engineering 3039-3067, 2001
[35] Jan Steindorf. Partitionerte Verfahren für Probleme der Fluid-Struktur Wechselwirkung, 2002
[36] Hermann G. Matthies and Jan Steindorf. Partitioned Strong Coupling Algorithms for Fluid-Structure-Interaction. Institute of Scientific Computing, Technical University Braunschweig, 2004
[37] T. E. Tezduyar and Sunil Sathe and Keith Stein. Solution techniques for the fully discretized equations in computation of fluid-structure interactions with space-time formulations, Volume 195. Computer Methods in Applied Mechanics and Engineering 5743-5753, 2006
[38] Fabio Nobile. Numerical Approximation of Fluid-Structure Interaction Problems with Application to Haemo-dynamics, 2001
[39] P. Causin and J. F. Gerbeau and F. Nobile. Added-mass effect in the design of partitioned algorithms for fluid-structure problems, Volume 194. Computer Methods in Applied Mechanics and Engineering 4506-4527, 2005
[40] Miguel Angel Fernández and Marwan Moubachir. A Newton method using exact jacobians for solving fluid-structure coupling, Volume 83. Computers and Structures 127-142, 2005
[41] G. K. Batchelor. An introduction to fluid dynamics. Cambridge University Press, 1st Cambridge Mathematical Library Edition, 2000
[42] Lawrence E. Malvern. Introduction to the Mechanics of a Continuous Medium. Prentice-Hall, 1969
[43] Morton E. Gurtin. An Introduction to Continuum Mechanics. Academic Press, 1981
[44] Gerhard A. Holzapfel. Nonlinear Solid Mechanics. Wiley, 2000
[45] Pijush K. Kundu and Ira M. Cohen. Fluid Mechanics. Academis Press, 2002
[46] A. J. M. Spencer. Continuum Mechanics. Longman mathematical texts, 1980
Document information
Published on 01/01/2007
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?