Resumen
Se presenta una nueva alternativa para la estimación de la masa modal, con el objeto de escalar los modos de vibración obtenidos a partir de ensayos de análisis modal operacional, utilizando técnicas de optimización, en la situación de amortiguamiento proporcional independiente de la frecuencia (estructural o histerético), alcanzando resultados óptimos incluso con la presencia de un alto nivel de ruido en la señal.
Tras una breve exposición de los fundamentos teóricos y de las limitaciones en el estado del arte actual, se analiza la determinación de parámetros modales mediante un sistema dinámico acoplado, utilizando técnicas de optimización.
Para ilustrar el procedimiento, se presentan dos ejemplos de aplicación, en primer lugar, a un modelo de viga elemental de dimensiones reducidas, y a continuación, para confirmar la capacidad del método propuesto para ser aplicado a estructuras civiles reales, se ilustra aquella, mediante una simulación numérica sobre un puente muy esbelto actualmente en servicio, y con una geometría interna de su viga principal muy compleja.
Palabras clave: Dinámica estructural, análisis modal, identificación, masa modal, optimización
Abstract
A new alternative is presented for the estimation of modal mass, in order to scale the vibration modes obtained from operational modal analysis tests, using optimization techniques, in the frequency-independent proportional damping situation (structural or hysteretic), achieving optimal results even with the presence of a high level of noise in the signal.
After a brief exposition of the theoretical foundations, and the limitations in the current state of the art, the determination of modal parameters is analyzed in a coupled dynamic system, using optimization techniques.
To illustrate the procedure, two examples of application are presented: first, for the case of an elementary beam model of small dimensions; and then, to confirm the capacity of the proposed method to be applied to real civil structures, said capacity is illustrated by a numerical simulation, on a very slender bridge currently in service, and with a very complex internal geometry of its main beam.
Keywords: Structural dynamics, modal analysis, identification, modal mass, optimization
1. Introducción
La elección del análisis modal experimental clásico (en adelante AME) puede no ser la mejor opción en el caso de grandes estructuras civiles, por la dificultad de conseguir excitarlas artificialmente en su totalidad. Además, el coste de los equipos necesarios es muy notable. Sin embargo, esos métodos permiten determinar la totalidad del modelo modal de la estructura, incluidos modos de vibración normalizados respecto de la matriz de masa, así como el amortiguamiento con una gran exactitud [1,2].
El método que se propone representa una alternativa al problema del escalado de los modos de vibración, obtenidos por ensayos de análisis modal operacional (en adelante AMO), siendo útil para determinar la masa modal (o por ende el factor de escala) correspondiente a un modo de vibración obtenido a partir de AMO [3,4].
Entre los métodos de escalado de los vectores modales, se encuentran procedimientos involucrados en la determinación de la matriz de masa de la estructura [5], de la misma forma que el conocimiento de las propiedades inerciales o de masa de una estructura son determinadas o estimadas para realizar un cálculo estático de la misma. Este conocimiento de aquella puede ser utilizado para el análisis dinámico. Sin embargo, esta no tiene nada que ver con la masa modal generalizada, la cual es una propiedad dinámica que mide la proporción o cadencia en que la masa total de la estructura colabora en la oscilación de cada modo de vibración.
En el método que se desarrolla en los siguientes apartados, se utiliza, por una parte, la respuesta de la estructura, y, por otra, la respuesta de la estructura conjuntamente con un sistema dinámico acoplado en una ubicación de la misma de interés, cuyo modelo espacial es totalmente conocido: propiedades inerciales m, de rigidez k, y de amortiguamiento , para el sistema dinámico. Todo el procedimiento se ha implementado para amortiguamiento proporcional, estructural o histerético, también conocido como amortiguamiento independiente de la frecuencia, y este es el tipo de amortiguamiento que se considera, tanto en el sistema dinámico acoplado, como en la estructura analizada.
Entre las ventajas asociadas a este procedimiento se encuentran:
- a) Es suficiente con conocer la frecuencia natural y su modo de vibración asociado (vector modal).
- b) El montaje e infraestructura necesarios, que envuelve a la estructura bajo análisis, es mucho más elemental de lo requerido para otros métodos alternativos ya citados, que precisan un conocimiento de la señal de excitación (AME).
- c) La masa del sistema dinámico acoplado puede ser muy pequeña con respecto a la masa modal de la estructura (sobre un 1%); se sintoniza su vibración en las proximidades de la frecuencia de resonancia asociada al modo bajo estudio.
- d) Además, el valor exacto de esta frecuencia natural (sintonizada), del sistema dinámico no es crítica, en el sentido de que es suficiente con que sea un valor próximo a la frecuencia natural del modo de interés perteneciente a la estructura.
En Porras et al. [6], se presentó un método en el dominio de la frecuencia, muy ingenioso y sencillo, pero que lamentablemente, no tenía en cuenta el efecto del amortiguamiento (viscoso en ese caso). Está basado en la relación entre masas y frecuencias naturales que existe en un sistema de 2 grados de libertad (en adelante g.d.l.); asignándose una frecuencia natural a la correspondiente del modo de vibración de interés en la estructura original, y la otra, a la propia del sistema dinámico acoplado.
Por otra parte, en Acunzo et al. [7], se presentó recientemente otra posibilidad para la determinación de masas modales desde ensayos de análisis modal operacional, pero en este caso, su aplicación se encuentra limitada a una única tipología estructural, la correspondiente a estructuras de edificación. Este método tiene una cierta similitud con el modelado estructural como modelo de edificio simple, considerando el forjado de cada planta, como un diafragma rígido (3 g.d.l. por planta: 2 de desplazamiento horizontal, contenidos en el plano del forjado, ortogonales entre si, y un tercero correspondiente al giro según un eje vertical).
Finalmente, en el campo de la ingeniería de estructuras, en general, y del análisis dinámico de las mismas, en particular, el uso de programas comerciales de elementos finitos no se ha extendido tanto como en otros campos de la ingeniería. Entre los motivos se encontrarían, por una parte, la dificultad para modelizar de forma realista estructuras de geometría compleja, y por otra, la existencia en numerosos reglamentos, guías de diseño y normativas, de métodos o procedimientos simplificativos que permiten realizar comprobaciones con un cierto margen de seguridad. A pesar de todo, la información que se puede extraer de este tipo de modelos es muy útil, de cara al diseño inicial, y a las posibles modificaciones de este, al objeto de evitar afrontar modificaciones futuras más costosas, cuando la estructura se encuentra en un nivel de ejecución alto, o incluso ya finalizada. Y es aquí donde el conocimiento de la masa modal se hace necesario, para el escalado de los modos de vibración, con el fin de un posterior ajuste más riguroso de estos modelos de elementos finitos [8].
2. Relación entre la masa modal y el factor de escala asociados a un modo de vibración
A continuación, se ilustra la equivalencia entre el factor de escala y la masa modal, asociados a un modo de vibración . Aplicando un cambio de masa a la estructura, tal y como se describe en [9,10], se propone que el factor de escala que relaciona los modos de vibración escalados respecto de la matriz de masa, y los que carecen de esta normalización , se relacionan de la siguiente forma, para un modo dado
|
|
(1) |
por otra parte, en Mendes y Montalvão [1] la relación entre ambas parejas de modos de vibración es
|
|
(2) |
Combinando ambas ecuaciones (1) y (2), resulta
|
|
(3) |
Con lo que también se puede determinar la magnitud de la masa modal generalizada, a partir del conocimiento del factor de escala asociado a un modo de vibración de la estructura.
3. Análisis de estructuras acopladas
En ocasiones, es útil realizar un análisis dinámico de una estructura, aislando algunas de sus partes o componentes estructurales (subestructuras). Su ventaja es la facilidad para describir las propiedades dinámicas de estas subestructuras mucho más elementales, y obtener, posteriormente, la respuesta acoplada de todo el conjunto estructural.
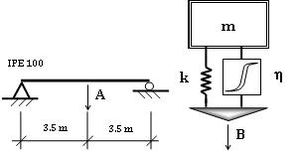
En la Figura 1, se presentan dos subestructuras, las cuales se van a utilizar en el primer ejemplo del presente trabajo. Efectivamente, este análisis se aplica a un caso concreto, en donde el acoplamiento tiene lugar en un único g.d.l. de interés
| Figura 1. Izquierda: modelo viga de laboratorio. Derecha: sistema dinámico oscilante de 1 g.d.l. |
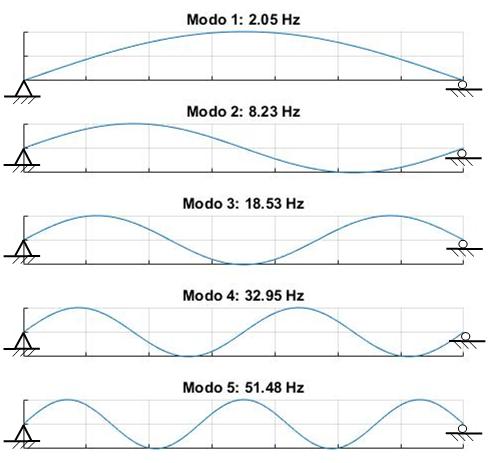
Las dos componentes, 1) viga biapoyada (A), y 2) sistema dinámico oscilante (B), tienen un g.d.l. en común, en el cual se va a realizar el acoplamiento. En este proceso, no existe ninguna restricción en los g.d.l. de cada subestructura. De esta forma, para definir adecuadamente la forma de los diferentes modos de vibración de la viga biapoyada (Figura 2), han sido necesarios varios g.d.l. uniformemente espaciados en toda su longitud, pero solo uno de ellos, en el punto medio de la luz, es utilizado para materializar el acoplamiento entre estas dos subestructuras.
| Figura 2. Modelo viga de laboratorio: primeros cinco modos de vibración vertical |
Por su parte, el sistema dinámico oscilante acoplado se ha definido mediante un único g.d.l., y se conocen todas las propiedades de su modelo espacial: masa , rigidez y amortiguamiento .
La tipología del amortiguamiento tenida en cuenta se corresponde con el estructural (o independiente de la frecuencia) proporcional, tanto en la estructura como en el sistema dinámico oscilante.
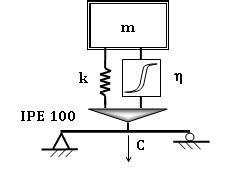
El sistema dinámico acoplado consiste en una masa conectada a la estructura, mediante un elemento elástico (resorte) y con un cierto grado de amortiguamiento, cuya frecuencia de oscilación es próxima al modo de interés (Figuras 2 y 3). En este punto, es necesario destacar que algunas estructuras, especialmente las más esbeltas y con el objeto de reducir sus vibraciones, tienen instalado un amortiguador de masa sintonizado, el cual puede ser útil para el fin propuesto, sin necesidad de realizar en la estructura ningún montaje especial y temporal [6].
| Figura 3. Modelo viga de laboratorio con el sistema dinámico oscilante ensamblado en el g.d.l. central |
A ambas subestructuras, les corresponde una función de respuesta en frecuencia (en adelante FRF): y como relación (cociente) entre su respuesta y la excitación aplicada en el dominio de la frecuencia [1] (nótese que en el caso de sería de un único g.d.l.). En el punto (g.d.l.) de conexión (C) (Figura 3), al aplicar las condiciones de compatibilidad de deformaciones y equilibrio de fuerzas, se tiene
|
|
(4) |
de donde fácilmente se obtiene
|
|
(5) |
y por tanto
|
|
(6) |
De esta manera se relacionan las FRF (y todas las propiedades dinámicas que de ellas se deducen), entre ambas subestructuras independientes, y la estructura total combinada en el g.d.l. central.
4. Determinación de parámetros modales mediante un sistema dinámico acoplado aplicando técnicas de optimización
En la dinámica estructural de varios g.d.l., cada modo de vibración individual contribuye a la respuesta total de la estructura, como una suma de todos ellos. Las FRF, con su parte real y compleja en el dominio de la frecuencia, contienen el modelo de respuesta del sistema estructural. De ellas se pueden extraer los parámetros modales que constituyen el modelo modal de la estructura: frecuencias naturales, razones de amortiguamiento y modos de vibración escalados respecto de la masa del sistema estructural.
Así, para la estructura de partida (caso A), y en el caso general de amortiguamiento independiente de la frecuencia o estructural, se demuestra que para la receptancia (analíticamente es habitual trabajar con ella) [1]:
|
|
(7) |
El modelo modal está constituido por autovalores complejos , razones de amortiguamiento y autovectores también complejos en el caso de normalización, de estos últimos, respecto de la matriz de masa, y en el caso de que carezcan de esta normalización. Siendo [1]
|
|
(8) |
En el segundo quebrado de la ecuación (7), si solo se dispone de autovectores no normalizados, se conoce únicamente la proporción de la respuesta entre cada g.d.l., es decir, relativa entre ellos y no absoluta, por lo que el resultado queda entonces en función de la masa modal generalizada. Esta es la situación de partida desde los resultados extraídos de ensayos de AMO.
Igualmente, representa el residuo y la frecuencia natural, ambas para el modo , siendo la unidad imaginaria o compleja
|
|
(9) |
Se sabe además que , debido a que por la simetría respecto de la diagonal principal (principio de reciprocidad) de todas las matrices FRF del modelo de respuesta, independientemente de su naturaleza.
Asimismo, entre la masa de la estructura que interviene en la oscilación de un modo de vibración (masa modal generalizada correspondiente a ese modo), y su frecuencia natural coligada , se verifica
|
|
(10) |
Siendo, a su vez, la rigidez generalizada correspondiente. Por otra parte, el coeficiente surge como una fracción de la rigidez del sistema, siendo una constante, dependiente del material y con dimensiones de rigidez, denominado coeficiente de amortiguamiento histerético
|
|
(11) |
En la representación gráfica de las FRF de un sistema estructural, se pueden identificar manualmente cada uno de los picos de las curvas (intervalos de frecuencias), que representan, cada uno de ellos, a los modos de vibración de la estructura, en los que se pretende estimar la masa modal.
Nótese que las receptancias tienen parte real y compleja, al igual que los residuos. Sin embargo, su descomposición no es tan inmediata como en el caso de estos.
Volviendo, entonces, al punto en donde se había dejado el desarrollo del procedimiento en el anterior apartado (ecuación (6)) y dado que la expresión analítica de cualquier receptancia de las involucradas en este proceso, , , o tienen componente real e imaginaria, es necesario proceder previamente a separar las mismas, con el objeto de realizar las estimaciones de ellas por separado, ya que los programas comerciales de cálculo numérico para optimización, no trabajan con magnitudes complejas, solo reales [11].
Según lo dicho, si cada FRF (receptancia) posee una parte real y compleja como función de la frecuencia , entonces, la referida ecuación (6) quedaría
|
|
(12) |
Después de efectuar el producto del numerador, agrupar términos, y multiplicar por el conjugado del denominador ambas partes del quebrado, tras unas cuantas operaciones, se llega a
|
|
(13) |
|
|
(14) |
lo que representa la partición buscada. Por otra parte, estas expresiones van a ser necesarias en el segundo ejemplo del trabajo (Apartados 6 y 7), en la simulación numérica, ya que no se dispone de mediciones experimentales de la estructura del puente, con el sistema dinámico oscilante dispuesto sobre el.
Llegados a este punto, es necesario destacar, que de aquí hasta el final del presente apartado, en cuanto a expresiones analíticas se refiere, el proceso para realizar el análisis de regresión es bastante común. De todas formas, se indica, seguidamente, para no dejar el desarrollo incompleto. Por consiguiente, se utiliza a continuación un análisis de regresión, para ajustar las parejas de abscisas y ordenadas (puntos) que definen el pico de la curva (intervalo de frecuencias). El procedimiento más idóneo es el método de estimación del mínimo valor absoluto [12]
|
|
(15) |
Mediante la resolución del siguiente problema de programación no lineal, se estiman los parámetros modales
|
|
(16) |
El conjunto de restricciones no lineales del problema, definen el conjunto de soluciones admisibles
|
|
(17) |
donde es el número de puntos en los que se ha medido la respuesta a lo largo del eje de frecuencias, y representan la magnitud de la misma (se trata de los datos: las ordenadas de la FRF), y , constituyen la estimación, respectivamente, de la parte real y compleja en el intervalo de la receptancia () considerada (ecuaciones (6), y por ende las ecuaciones (13) y (14)).
Debido a la experiencia del autor con el lenguaje de programación para optimización GAMS, se ha utilizado el mismo para la codificación. Sin embargo, en el mercado hay otros paquetes comerciales de características similares, como por ejemplo el AMPL y el AIMS; en principio, para la codificación del problema, todos ellos serían válidos.
En todo el proceso de optimización, únicamente se utiliza una FRF, evidentemente vinculada al g.d.l. de interés; y dentro de ella, se escoge una porción de la misma, que contiene esa frecuencia natural (un único pico de aquella en toda la curva).
Una vez finalizada la exposición del procedimiento analítico de estimación y para ilustrar el mismo, se presentan seguidamente dos ejemplos de aplicación. Por una parte, una viga elemental de dimensiones reducidas, y por otra, se realiza una simulación numérica, utilizando para ello, conjuntamente, el programa Matlab a un puente actualmente en servicio.
5. Modelo de viga elemental
Se demuestra que la suma de las masas modales generalizadas, correspondientes a los infinitos modos de vibración de una estructura, es igual a la masa total de la misma. En general, a medida que se incrementa el número de orden del modo de vibración de una estructura, la masa generalizada asociada a aquél se va reduciendo progresivamente, aunque esto no siempre es así, como sucede en el caso presente (Figura 1), correspondiente a una estructura elemental: viga biapoyada y de canto constante, constituida por un perfil laminado IPE-100; en este caso, la masa modal se mantiene uniforme para todos los modos de vibración (véase, por ejemplo, [13]), adoptando la magnitud de
|
|
(18) |
siendo la masa modal generalizada (teórica), la masa por unidad de longitud 8.1 kg/m, el vector modal asociado a esa masa generalizada y la longitud de la viga entre apoyos, de 7 m de luz. Otros datos, para esta viga elemental, son los siguientes: densidad del acero kg/m, módulo de elasticidad Pa, área A de la sección transversal 10.32 cm, y momento de inercia de la sección transversal respecto del eje débil 15.92 cm. Con todo ello, resulta una masa teórica generalizada de 28.35 kg, para todos y cada uno de los modos de vibración de la viga biapoyada; este es el valor de referencia que se indica en la tabla 1, y se utilizará posteriormente.
En una primera etapa, para este modelo de viga biapoyada se pueden determinar las frecuencias naturales y los modos de vibración en flexión vertical mediante AMO. Adicionalmente, y sin que sea necesario para el procedimiento expuesto en el Apartado 4, sino solo con el objeto de corroborar resultados al tratarse de una estructura elemental que por sus dimensiones se puede manejar y medir en laboratorio, se puede complementar el registro con un AME, empleando un martillo modal, en el que además se pueden obtener las razones de amortiguamiento y los modos de vibración escalados respecto de la matriz de masa.
En una segunda etapa, se suspende una masa en el punto medio de la luz, dotada de una cierta rigidez en su vinculación, con el objeto de repetir la medición, es decir un sistema dinámico oscilante elemental de un único g.d.l. La masa para este sistema dinámico oscilante se ha escogido en 3 kg (aproximadamente un 1% de la masa modal), estimando la rigidez del soporte en 483.87 N/m, y resultando una frecuencia natural de 12.70 rad/s. Para la razón de amortiguamiento , correspondiente a un resorte de acero, se ha estimado en un valor de 0.003. A este respecto, en Montalvão y Silva [14], se describe un procedimiento para la determinación experimental del mismo. De esta forma, se consigue sintonizar la vibración del sistema dinámico oscilante en las proximidades del modo de vibración de la viga IPE-100 de acero.
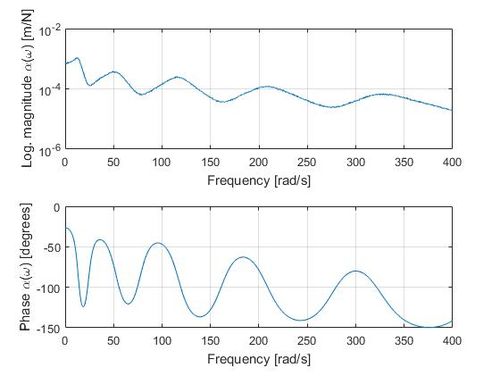
En la Figura 4, se representa una FRF para la viga biapoyada y en la Tabla 1 se muestran los resultados obtenidos en el proceso de optimización realizado sobre el conjunto indicado en la Figura 3, frente a las magnitudes de referencia (análisis modal), para los modos de vibración 1, 3 y 5. Nótese que en el punto medio de la luz, la contribución de los modos 2 y 4 a la respuesta es prácticamente nula (Figura 2), por lo que no es posible estimar la masa generalizada correspondiente a estos modos para la ubicación actual del sistema dinámico oscilante (g.d.l. vertical en el punto medio de la separación entre apoyos).
| Figura 4. Modelo viga de laboratorio: función de respuesta en frecuencia. Arriba: magnitud en escala logarítmica. Abajo: fase en grados |
| Modelo de laboratorio | |||||||
|---|---|---|---|---|---|---|---|
| Modo de vibración nº | Análisis modal | Acoplamiento de sistema dinámico | |||||
| [rad/s] | [kg] | [rad/s] | [kg] | Intervalo frec. [rad/s] en FRF | |||
| 1 | 12.94 | 0.59 | 28.35 | 12.94 | 0.58 | 28.20 | 0.50 32.50 |
| 3 | 116.46 | 0.21 | 28.35 | 116.08 | 0.23 | 27.66 | 84.00 162.0 |
| 5 | 323.50 | 0.16 | 28.35 | 323.77 | 0.16 | 29.37 | 265.00 395.00 |
Por otra parte, en la Tabla 1, en el subapartado de resultados correspondientes al acoplamiento del sistema dinámico, aparte de la estimación de la masa generalizada frente a la teórica , se indican también las estimaciones de las frecuencias naturales , y las razones de amortiguamiento , obtenidas en el proceso conjunto de optimización. El indicar las frecuencias naturales entre los resultados viene dado por el hecho de que, en el algoritmo de optimización, se definen como variables, con valores comprendidos en un intervalo, en ocasiones muy reducido, según lo afilado que se encuentre en la representación gráfica el pico correspondiente a ese modo en la FRF [11].
6. Características del puente analizado
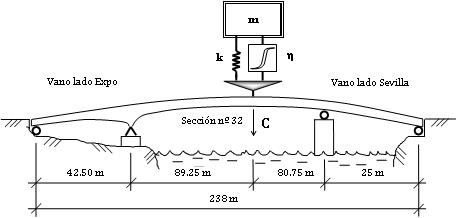
El puente de La Cartuja está ubicado en el Meandro de San Jerónimo, en Sevilla (España), sobre el río Guadalquivir [15,16]. Se trata de un puente de tipo viga cajón continua de sección variable, con tablero ortótropo, totalmente metálico, que respeta la visibilidad del entorno, mediante una estructura discreta y elegante.
Consta de 3 vanos, con una longitud total de 238 m: 42.5 m en el vano lado Expo, 170 m en el vano central, y 25.5m en el vano lado Sevilla. La viga cajón o viga principal del puente está rigidizada mediante marcos de rigidización transversal cada 4.25 m, los cuales dividen el puente en 56 módulos. El peso acabado del puente es de 1869 t, equivalente a 714 kp/m2 (Figuras 5 y 6).
| Figura 5. Alzado general del Puente de La Cartuja |
| Figura 6. Puente de La Cartuja: vista sobre el Río Guadalquivir del vano principal (central) y parte del vano lado Sevilla |
El ancho del tablero es de 11 m y el canto de la viga variable, desde los 1.92m del estribo lado Expo que aumenta progresivamente hasta llegar a los 6 m en la pila del mismo margen, para disminuir hasta alcanzar los 3 m manteniéndose prácticamente constante en buena parte del vano central y vano lateral lado Sevilla, lo cual representa una relación luz/canto de 56.6. Este valor, en su día, fue el menor registrado en un puente, por lo que se convirtió en el puente más esbelto del mundo, haciendo gala de una elegancia inédita hasta entonces. Figura desde el año 2007 en el Libro Guinnes de los records.
La continuidad de la viga del puente en los tres vanos permite alcanzar esta esbeltez, gracias a los vanos laterales relativamente cortos y a las ménsulas ubicadas en el tablero y en los estribos, a través de los cuales se trasmiten reacciones negativas (Figura 5).
7. Análisis de resultados
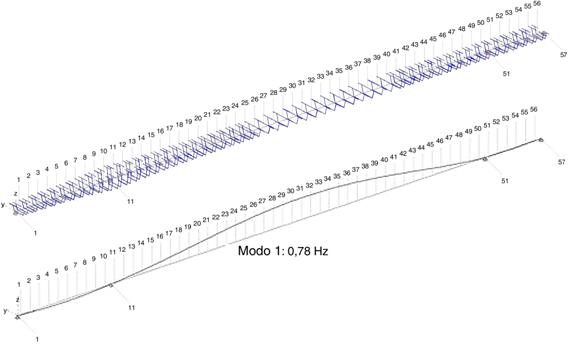
El método propuesto ha sido usado para estimar la masa modal del primer modo de vibración en flexión vertical del puente (Figura 7), cuyos parámetros modales (frecuencia natural Hz, razón de amortiguamiento y vector modal , de este primer modo de flexión vertical) han sido determinados en un trabajo anterior [10].
| Figura 7. Arriba: modelización del Puente de la Cartuja, viga cajón continua de sección variable, con tablero ortótropo. Abajo: flexión vertical, primer modo de vibración |
A pesar de un desarrollo analítico extenso y de su correspondiente trabajo de campo, inherentes al procedimiento, el esfuerzo computacional correspondiente al mismo es reducido. Nótese que en el cálculo se está utilizando una única FRF asociada a ese g.d.l. de interés y, dentro de la misma, una única frecuencia natural (una porción de la curva FRF correspondiente a un único pico de la misma en toda la curva), por lo que el tiempo de cálculo es muy bajo.
Por otra parte, dentro del AMO se considera que la excitación de entrada es un ruido blanco, o sea, independiente de la frecuencia y con una magnitud media constante de su espectro. Asimismo, se ha verificado que el procedimiento propuesto es muy poco sensible a la presencia de ruido en la señal.
En el modelo de respuesta, la matriz FRF [] contiene los parámetros modales objeto de la identificación; en ella el ruido se simula numéricamente, añadiendo un ruido blanco a la FRF de la siguiente forma
|
|
(19) |
siendo la FRF de interés, el nivel de ruido (del 20%) y una distribución normal estándar, con un valor medio de 0 y una desviación típica de 1, o sea, una N(0,1). Las magnitudes de la curva FRF se ven afectadas tanto para la parte real como para la parte imaginaria.
La masa, para el sistema dinámico oscilante del puente (Figura 8), se ha escogido en 500 kg (aproximadamente un 1% de la masa modal), estimando la rigidez k del soporte en 11.7 kN/m y resultando una frecuencia natural de 4.8373 rad/s (0.7698 Hz). Para la razón de amortiguamiento , se utiliza el mismo valor empleado en el caso del Apartado 5.
| Figura 8. Puente de la Cartuja: ubicación del sistema dinámico oscilante sobre un marco de rigidización transversal correspondiente a la sección nº 32 de la viga principal, en las proximidades de la clave del mismo |
Con respecto a la ubicación del sistema dinámico oscilante, se ha elegido una sección transversal coincidente con uno de los marcos de rigidización transversal en la viga principal del puente; de esta manera se evita la influencia de las oscilaciones de elementos locales del tablero en la respuesta total (por ejemplo otras pequeñas vigas del tablero transversales y/o longitudinales -entre marcos- u otros elementos de rigidización). De esta forma, se ha escogido el marco de rigidización transversal correspondiente a la sección nº 32 de la viga principal del puente, en las proximidades de la clave del mismo.
En la Tabla 2, se presenta un resumen de resultados para la masa modal, correspondiente al primer modo de vibración en flexión vertical del Puente de La Cartuja, calculada por diversos procedimientos:
- A partir del ajuste de una FRF, realizado en un trabajo anterior [10]:
- A través de una estimación, mediante el método de cambio de masa (propuesta del Prof. Brincker y Andersen) [10,17]:
- Y finalmente, realizando una simulación numérica, mediante el método propuesto, vinculando un sistema dinámico oscilante a la estructura:
En los dos primeros casos, se utiliza la ecuación (3), que muestra la relación entre el factor de escala y la masa modal generalizada, de esta forma, esta última se determina a partir de aquel. Asimismo, en la Tabla 2, también se indican los resultados del algoritmo de optimización para la frecuencia natural , y la razón de amortiguamiento , así como el intervalo de frecuencias empleado en la curva, a ambos lados del pico de la frecuencia natural.
| Modo de vibración flexión vcal. nº | Análisis modal. Ajuste de FRF [10] | Método cambio de masa. Estimación [10,17] | Acoplamiento de sistema dinámico. Simulación numérica | |||||
|---|---|---|---|---|---|---|---|---|
| [Hz] | [t] | [t] | [t] | Intervalo frec. [rad/s] en FRF | ||||
| 1 | 0.78 | 0.0173 | 4.778 | 4.784 | 4.588 | 0.78 | 0.0180 | 2.0 7.5 |
Finalmente, indicar que el sistema dinámico oscilante se puede realizar mediante sacos de arena dispuestos sobre una chapa de acero de espesor suficiente, y apoyada a su vez en su cara inferior sobre un cierto número de resortes de acero, los cuales se dispondrían a su vez sobre el pavimento del puente. De esta forma, quedarían dispuestos en paralelo y su rigidez equivalente sería el producto de su número por la rigidez de uno de ellos. A este respecto, una opción interesante para los resortes sería la elección de cojines metálicos, consistentes en un hilo de acero inoxidable tricotado, corrugado y prensado con la forma geométrica deseada; la forma cilíndrica simple para los mismos puede resultar bastante cómoda para este caso.
8. Conclusiones
El procedimiento expuesto se ha comprobado útil para determinar, con una buena exactitud, la masa modal generalizada de los modos de vibración en estructuras civiles, lo cual permite escalar los autovectores modales identificados mediante ensayos de AMO, en la situación de amortiguamiento proporcional independiente de la frecuencia (estructural o histerético). Asimismo, es bastante insensible a la presencia de ruido en la señal.
Además, la alternativa expuesta, puede ser muy competitiva en el caso de que la estructura civil ya tenga instalado un amortiguador de masa sintonizado para reducir las vibraciones, ya que se puede utilizar este para que haga la función de sistema dinámico oscilante.
Referencias
[1] Mendes N.M., Montalvão J.M. Theoretical and experimental modal analysis. Research Studies Press Ltd., John Wiley Sons Inc., New York, 1997.
[2] Cacho-Pérez M., Frechilla N., Lorenzana A. Estimación de parámetros modales de estructuras civiles a partir de la Función de Respuesta en Frecuencia. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 33(3-4):197-203, 2017. http://dx.doi.org/10.1016/j.rimni.2016.02.001
[3] Lardiès J. Modal parameter identification by an iterative approach and by the state space model. Mechanical Systems and Signal Processing, 95:239–251, 2017. http://dx.doi.org/10.1016/j.ymssp.2017.03.010
[4] Sitarz P., Powałka B. Modal parameters estimation using ant colony optimisation algorithm. Mechanical Systems and Signal Processing, 76-77:531–554, 2016. http://dx.doi.org/10.1016/j.ymssp.2016.01.013 En Proceedings of the International Modal Analysis Conference (IMAC) XX, Los Angeles, California, 2002.
[6] Porras J., Sebastián J. de, Casado C., Lorenzana A. Modal mass estimation from output-only data using oscillator assembly. Mechanical Systems and Signal Processing, 26:15–23, 2012. 10.1016/j.ymssp.2011.06.015
[7] Acunzo G., Fiorini N., Mori F., Spina D. Modal mass estimation from ambient vibrations measurement: A method for civil buildings. Mechanical Systems and Signal Processing, 98:580–593, 2018. http://dx.doi.org/10.1016/j.ymssp.2017.05.014
[8] Frechilla N., Cacho-Pérez M., Lorenzana A. Análisis modal y dinámico de una pasarela peatonal en servicio. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 34(1):18, 2018. [http://dx.doi.org/10.23967/j.rimni.2017.8.004]
[9] Parloo E., Verboven P., Guillaume P., Van Overmeire M. Sensitivity-based operational mode shape normalization. Mechanical Systems and Signal Processing, 16(5):757-767, 2002.
[10] Villa L.M. Comparison of the estimated modal parameters of structures from classical and operational modal analysis with mass changes. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 33(3-4):188–196, 2017. http://dx.doi.org/10.1016/j.rimni.2016.04.003
[11] Villa L.M. Application of optimization techniques for determining modal parameters by means of frequency response functions. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 23-4:395-414, 2007.
[12] Castillo E., Hadi A.S., Lacruz B. Regresion diagnostic for the least absolute value and the minimax methods. Communications in Statistics, Theory and Methods, 30:381-395, 2001.
[13] Paz M. Dinámica estructural. Reverté, Barcelona, 1992.
[14] Montalvão D., Silva J.M.M. An alternative method to the identification of the modal damping factor based on the dissipated energy. Mechanical Systems and Signal Processing, 54-55:108–123, 2015. http://dx.doi.org/10.1016/j.ymssp.2014.08.025
[15] Asensio Cerver F. Bridges. Atrium, Barcelona, 1992.
[16] Sevilla: Puentes del 92, Colegio de Ingenieros de Caminos, Canales y Puertos de Andalucía (Sección de Publicaciones), 1992.
[17] Brincker R., Andersen P. A way of getting scaled mode shapes in output only modal analysis. In Proc. Of the International Modal Analysis Conference (IMAC) XXI, paper 141, 1-5, February 2003.
Document information
Published on 09/09/20
Accepted on 05/09/20
Submitted on 26/04/20
Volume 36, Issue 3, 2020
DOI: 10.23967/j.rimni.2020.09.002
Licence: CC BY-NC-SA license