A stabilized meshless method for the solution of the lagrangian equations of newtonian fluids

M. Urrecha^a, , I. Romero^{a, b,}

• ^aETS Ingenieros Industriales, Universidad Politécnica de Madrid, José Gutiérrez Abascal, 2, 28006 Madrid, España
• ^bIMDEA Materiales, Eric Kandel 2, Tecnogetafe, Madrid 28906, España

Under a Creative Commons license

Resumen

En este artículo, presentamos métodos numéricos para resolver problemas de fluidos incompresibles. Tres son los problemas que se abordan: el flujo de Stokes estacionario, el flujo de Stokes transitorio y el problema general del movimiento de los fluidos newtonianos. En los tres casos, se emplea una discretización que no requiere una malla del dominio, sino que se utilizan funciones de aproximación de la máxima entropía. Además, para garantizar la robustez de la solución, se emplea una técnica de estabilización. El problema más general, el del movimiento de fluidos newtonianos, se formula de forma lagrangiana y, con los resultados presentados, se comprueba que el uso de métodos sin malla estabilizados puede ser una alternativa competitiva a otras técnicas que se emplean en la actualidad.

Abstract

In this article we present numerical methods for the approximation of incompressible flows. We have addressed three problems: the stationary Stokes’ problem, the transient Stokes’ problem, and the general motion of newtonian fluids. In the three cases a discretization is employed that does not require a mesh of the domain but uses maximum entropy approximation functions. To guarantee the robustness of the solution a stabilization technique is employed. The most general problem, that of the motion of newtonian fluids, is formulated in lagrangian form. The results presented verify that stabilized meshless methods can be a competitive alternative to other approached currently in use.

Palabras clave

Métodos sin malla ; Estabilización ; Fluidos lagrangianos

Keywords

Meshless methods ; Stabilization ; Lagrangian fluids

1. Introducción

En la actualidad, existe un interés creciente en la descripción lagrangiana de fluidos y su posterior aproximación numérica. Los motivos primordiales de este renovado interés se deben a la inherente facilidad de este tipo de formulaciones para describir superficies libres de fluidos y su interacción con sólidos y estructuras, ya sean rígidos o deformables [1] , [2]  and [3] .

Aunque las ecuaciones lagrangianas de la mecánica de fluidos son las mismas que las de la mecánica de sólidos (con las modificaciones constitutivas correspondientes) y, por tanto, bien conocidas, sin duda es más sencillo resolver los flujos a partir de su descripción euleriana. La razón última de esta complejidad es que las partículas fluidas experimentan desplazamientos muy grandes, en la mayoría de los problemas de interés, que son difíciles de estimar con cualquier método numérico que emplee una malla fija a las partículas del cuerpo. Una dificultad añadida de los métodos lagrangianos es la imposición de ciertas condiciones de contorno, como la de los flujos entrantes o salientes de material en un volumen de control.

Al referirnos al método de los elementos finitos, acaso la técnica de aproximación numérica más versátil de las empleadas en ingeniería mecánica, las ecuaciones lagrangianas de los fluidos se pueden aproximar sin dificultad aparente [4] , pero como ya se ha indicado, su resolución requiere una actualización periódica de la conectividad en la malla, o incluso la modificación del conjunto nodal. La única dificultad añadida que puede aparecer es el tratamiento numérico de la condición de incompresibilidad, cuando se desee imponer esta condición.

Dado que la distorsión de la malla es un aspecto que limita las formulaciones basadas en elementos finitos, una posible alternativa es utilizar métodos sin malla. Existe una gran variedad de métodos de este tipo [5] , algunos de ellos basados directamente en la resolución del movimiento de las partículas (por ejemplo, el método SPH) y otros basados en las formulaciones de Galerkin con espacios de interpolación que no necesitan una malla.

En este trabajo, presentamos una formulación de Galerkin con funciones de interpolación del tipo LME (Local-Max-Entropy) [6] , que no requieren la definición de una malla. Con ellas, la resolución numérica de las ecuaciones de los fluidos viscosos es posible, aun dentro de un marco lagrangiano, si se tratan adecuadamente los problemas asociados a la incompresibilidad. Para evitar los problemas derivados de esta restricción, empleemos una formulación estabilizada, en concreto la propuesta por Douglas y Wang [7] para el problema de Stokes. Este tipo de estabilización garantiza, incluso para aproximaciones no polinómicas, la coercividad del operador de Stokes y permite formular algoritmos de integración temporal incondicionalmente estables cuando son aplicados al problema de Stokes transitorio. Este problema es de interés en sí mismo, pero en este artículo lo estudiamos porque sus ecuaciones son exactamente las mismas que las de los fluidos lagrangianos, si el dominio de integración se actualiza con la deformación. A partir de la formulación estable del problema lineal transitorio de Stokes, propondremos una formulación para el problema no lineal y demostraremos su estabilidad.

El artículo se estructura del modo siguiente. En el apartado 2 , se resumen las ecuaciones de la mecánica de fluidos en forma lagrangiana. Después, en los apartados 3  and 4 y 5 se presenta un marco general para abordar, respectivamente, el problema de Stokes, el problema de Stokes transitorio y las ecuaciones de los fluidos newtonianos. En el apartado 6 se describen las funciones de aproximación utilizadas y en el apartado 7 los resultados de la validación y los ejemplos. El artículo concluye con un resumen de los resultados principales en el apartado 8 .

2. Las ecuaciones de la mecánica de fluidos newtonianos

Como cualquier otro medio continuo, el movimiento de un cuerpo fluido se describe mediante una deformación ${\textstyle \varphi :B_{o}\times [0,T]\rightarrow \mathbb {R} ^{3}}$ , siendo ${\textstyle B_{o}}$ la configuración de referencia del mismo y [0, T ] el intervalo en que se quiere estudiar el movimiento. Si la densidad del fluido en esta configuración es ρ   y ${\textstyle V={\dot {\varphi }}}$ es la velocidad material (donde la notación ${\textstyle {\dot {()}}}$ indica la derivada temporal material), y el cuerpo es incompresible, entonces las ecuaciones que gobiernan este problema son:

${\begin{array}{cc}2\mu {\mbox{   }}\nabla \cdot (\nabla ^{s}v)-\nabla p+f&=\rho {\mbox{   }}a\quad \\\nabla \cdot v&=0\quad \\&\end{array}}$

( 1)

que deben cumplir en todo punto ${\textstyle x\in B_{t}=\varphi _{t}(B_{o})}$ . El símbolo μ indica la viscosidad dinámica del fluido; p representa el campo de presiones; f es el vector de fuerzas por unidad de volumen; ${\textstyle v=V\circ \varphi ^{-1}}$ es la velocidad espacial; ${\textstyle a={\dot {V}}\circ \varphi ^{-1}}$ es la aceleración espacial, y ∇, ∇· son los operadores gradiente y divergencia espacial, respectivamente, y (·)^s indica la parte simétrica del operador. La primera de estas ecuaciones expresa el equilibrio de fuerzas y la segunda, la condición de incompresibilidad. Para finalizar la definición del problema han de añadirse condiciones iniciales y de contorno, como por ejemplo:

${\begin{array}{cc}v(x,0)=v_{o}(x)&x\in B_{t},\\v(x,t)=0&x\in \partial B_{t}.\\\end{array}}$

( 2)

Las ecuaciones diferenciales (1) están planteadas con campos y operadores que son funciones de los puntos en la configuración deformada ${\textstyle B_{t}}$ y, por tanto, se dice que es un planteamiento espacial o euleriano del problema. La formulación material o lagrangiana , en que los campos y los operadores diferenciales están expresados en función de las partículas de la configuración de referencia, se emplea muy poco para describir fluidos, pero es completamente equivalente. La transformación entre ambas formulaciones se obtiene, de forma estándar, empujando hacia delante o tirando hacia atrás los campos y los operadores diferenciales de las ecuaciones (por ejemplo, [8] para una descripción detallada de estas operaciones y [2] para su aplicación a las ecuaciones de los fluidos).¹

En este trabajo, estamos interesados en formular métodos numéricos que resuelvan las ecuaciones lagrangianas de la mecánica de fluidos newtonianos pues, una vez resueltas, obtendremos por definición, la posición, la velocidad y la presión de cada partícula, identificadas todas ellas por su posición en la configuración de referencia. Antes de formular un método numérico para este problema, en las secciones 3 y 4 estudiamos aproximaciones numéricas para la formulación euleriana de dos problemas más sencillos, a saber, el flujo estacionario y transitorio de Stokes.

3. Un método numérico para el problema de Stokes

El movimiento de los fluidos newtonianos muy viscosos (o con número de Reynolds muy pequeño) se describe habitualmente mediante las ecuaciones de Stokes. En ellas, y dado un dominio ${\textstyle \Omega \subset \mathbb {R} ^{N}}$ (con N  = 2 o 3), el objeto es encontrar un campo de velocidades ${\textstyle v\in V=(H_{o}^{1}(\Omega ))^{N}}$ y un campo de presiones ${\textstyle p\in Q=L^{2}(\Omega )/\mathbb {R} }$ tales que:

${\begin{array}{c}-2\mu \nabla \cdot \nabla ^{s}v+\nabla p=f,\\\nabla \cdot v=0,\end{array}}$

( 3)

en todo punto de Ω, con ${\textstyle v=0}$ en ∂Ω. Existen otras posibles condiciones de contorno pero, por simplicidad, solo mencionamos las anteriores. Con relación a la discusión al final de la sección 2 , las ecuaciones (3) del flujo de Stokes son eulerianas.

A continuación, describimos la forma débil de este problema de contorno a partir de una forma bilineal ${\textstyle a:V\times V\rightarrow \mathbb {R} }$ y una segunda forma bilineal ${\textstyle b:V\times Q\rightarrow \mathbb {R} }$ definidas, respectivamente

$a(v,w)=\int _{\Omega }2\mu \nabla ^{s}v\cdot \nabla ^{s}w\quad d\Omega ,\quad b(v,q)=-\int _{\Omega }\nabla \cdot v{\mbox{   }}q\quad d\Omega .$

( 4)

La solución ${\textstyle (v,p)\in V\times Q}$ del problema de Stokes ha de satisfacer

${\begin{array}{cc}a(v,w)+b(w,p)=(f,w)&\\b(v,q)=0,&\end{array}}$

( 5)

siendo (· , ·) el producto escalar en L² (Ω).

En este trabajo, nos centramos en métodos numéricos de tipo Galerkin. Su uso para resolver el problema de Stokes no es trivial porque, como es bien sabido, la aproximación de las ecuaciones (5) requiere espacios de interpolación distintos para el campo de las velocidades y para el de las presiones, de tal manera que se cumpla la condición inf-sup[9] .

Supongamos que construimos un espacio de funciones de dimensión finita ${\textstyle M^{h}\subset H_{o}^{1}(\Omega )\cap L^{2}(\Omega )/\mathbb {R} }$ . Este espacio puede construirse a partir de una triangulación de Ω, como en el caso del método de los elementos finitos, pero estamos más interesados en espacios generados sin necesidad de construir una malla, como veremos más adelante. A partir de ${\textstyle M^{h}}$ podemos definir los espacios de velocidades y de presiones como ${\textstyle V^{h}=(M^{h})^{N}}$ y ${\textstyle Q^{h}=M^{h}}$ .

Para garantizar un método estable que permita resolver el problema de Stokes de forma robusta, se puede emplear un método de Galerkin estabilizado [10]  and [11] . De entre los métodos de este tipo que existen en la literatura, el de Douglas y Wang [7] propone encontrar ${\textstyle (v^{h},p^{h})\in V^{h}\times Q^{h}}$ que satisfagan

${\begin{array}{l}\displaystyle a(v^{h},w^{h})+b(w^{h},p^{h})+(\tau (-2\mu \nabla \cdot \nabla ^{s}v^{h}+\nabla p^{h}-f)\\\displaystyle -2\mu \nabla \cdot \nabla ^{s}w^{h})=(f,w^{h})-b(v^{h},q^{h})+(\tau (-2\mu \nabla \cdot \nabla ^{s}v^{h}+\nabla p^{h}-f)\\\displaystyle \nabla q^{h})=0,\end{array}}$

( 6)

para todo ${\textstyle (w^{h},q^{h})\in V^{h}\times Q^{h}}$ , ${\textstyle \tau ={\frac {\alpha }{\mu }}h^{2}}$ , siendo h una cierta medida local del tamaño de la discretización. En estas expresiones, los productos escalares añadidos a la forma estándar de Galerkin en cada una de las ecuaciones se anulan cuando se evalúan para la solución exacta, de modo que no modifican la consistencia del método. En las formulaciones de elementos finitos, los espacios de solución no tienen suficiente diferenciabilidad para permitir la evaluación en todo punto de los operadores laplacianos, pero en este caso puede demostrarse que basta con evaluar estos productos escalares en el interior de los elementos.

La formulación (6) tiene la propiedad de ser incondicionalmente estable para todo valor del parámetro adimensional α  > 0, que suponemos, a partir de ahora, igual a 1. Esto no ocurre así con otros métodos estabilizados cuya estabilización depende esencialmente del valor de este parámetro, valor que se puede estimar para la aproximación de elementos finitos, pero no para otras más generales como las que estudiamos en este trabajo (véase, por ejemplo, el análisis que se presenta en [11] ).

4. Integración temporal del problema transitorio de Stokes

A continuación, consideramos el problema transitorio de Stokes en un intervalo de tiempo t  ∈ [0, T ]. Para ello, indicamos la densidad del fluido incompresible con el símbolo ρ   . Dado un campo de velocidad inicial ${\textstyle v_{o}}$ , que ha de ser solenoidal, la velocidad y la presión del problema transitorio son ${\textstyle v(t)\times p(t)\in V\times Q}$ , que satisfacen

${\begin{array}{cc}\rho \quad \partial _{t}v-2\mu \nabla \cdot \nabla ^{s}v+\nabla p&=f,\\\nabla \cdot v&=0,\end{array}}$

( 7)

en todo el dominio Ω, donde la notación ${\textstyle \partial _{t}v}$ indica la derivada parcial con respecto al tiempo de la velocidad ${\textstyle v}$ , es decir, la derivada temporal espacial. El problema inicial se completa con las condiciones iniciales y de contorno

$v(x,0)=v_{o}(x),\quad x\in \Omega \quad \quad v(x,t)=0,\quad x\in \partial \Omega .$

( 8)

Asociado a este problema, podemos definir la formulación variacional: hallar ${\textstyle v(\cdot ,t)\times p(\cdot ,t)\in V\times Q}$ tal que:

${\begin{array}{cc}(\rho \quad \partial _{t}v,w)+a(v,w)+b(w,p)&=(f,w)\\b(v,q)&=0\quad \end{array}}$

( 9)

para todo ${\textstyle (w,q)\in V\times Q}$ . Como en el caso del problema de Stokes estacionario, las ecuaciones (7) tienen una formulación euleriana y los métodos numéricos que presentamos a continuación son también eulerianos.

Para aproximar la solución del problema (9) , este se debe discretizar en el espacio y en el tiempo. La aproximación descrita en la sección 3 se puede utilizar para la proyección espacial, mientras que para la temporal se propone el uso de una integración de Euler hacia atrás (Backward Euler ). Para ello, suponemos que el intervalo de integración [0, T ] se puede subdividir en intervalos [t_n , t_{n +1} ] y se define Δt_n  = t_{n +1}  − t_n . Si la solución en el instante t_n se indica como ${\textstyle (v_{n}^{h},p_{n}^{h})}$ , entonces la solución en el instante t_{n +1}  = t_n  + Δt_n se ha de obtener resolviendo

${\begin{array}{l}\displaystyle (\rho {\frac {v_{n+1}^{h}-v_{n}^{h}}{\Delta t_{n}}},w^{h})+a(v_{n+1}^{h},w^{h})+b(w^{h}\\\displaystyle p_{n+1}^{h})+(\tau (-2\mu \nabla \cdot \nabla ^{s}v_{n+1}^{h}+\nabla p_{n+1}^{h}-f_{n+1})\\\displaystyle -2\mu \nabla \cdot \nabla ^{s}w^{h})=(f_{n+1},w^{h})-b(v_{n+1}^{h}\\\displaystyle q^{h})+(\tau (-2\mu \nabla \cdot \nabla ^{s}v_{n+1}^{h}+\nabla p_{n+1}^{h}-f_{n+1}),\nabla q^{h})=0,\end{array}}$

( 10)

para todo ${\textstyle (w^{h},q^{h})\in V^{h}\times Q}$ . El parámetro de estabilización se define, para el problema transitorio,

$\tau =\left(\left({\frac {2}{\Delta t_{n}}}\right)^{2}+\left({\frac {\mu }{\rho h^{2}}}\right)^{2}\right)^{-1/2}$

( 11)

siguiendo, por ejemplo, el análisis de [12] .

Aunque el método de integración (10) es únicamente de primer orden, tiene la ventaja de que, como se puede comprobar fácilmente, la energía cinética de la solución discreta es monótona decreciente cuando f  = 0 , lo cual implica la estabilidad de la velocidad en todo instante. Para demostrar esta afirmación, basta con seleccionar ${\textstyle w^{h}=v_{n+1}^{h}}$ y ${\textstyle q^{h}=p_{n+1}^{h}}$ en la ecuación (10) , que resulta, una vez simplificada,

${\begin{array}{l}\displaystyle (\rho {\frac {v_{n+1}^{h}-v_{n}^{h}}{\Delta t_{n}}},v_{n+1}^{h})+a(v_{n+1}^{h}\\\displaystyle v_{n+1}^{h})+\parallel \tau ^{1/2}(-2\mu \nabla \cdot \nabla ^{s}v_{n+1}^{h}+\nabla p_{n+1}^{h})\parallel ^{2}=0\end{array}}$

( 12)

Como el primer término se puede reescribir de la siguiente manera,

${\begin{array}{l}\displaystyle (\rho {\frac {v_{n+1}^{h}-v_{n}^{h}}{\Delta t_{n}}}\\\displaystyle v_{n+1}^{h})={\frac {\rho }{2}}\parallel v_{n+1}^{h}\parallel ^{2}-{\frac {\rho }{2}}\parallel v_{n}^{h}\parallel ^{2}+{\frac {\rho }{2}}\parallel v_{n+1}^{h}-v_{n}^{h}\parallel ^{2},\end{array}}$

( 13)

la ecuación (12) es equivalente a

${\begin{array}{l}\displaystyle {\frac {\rho }{2}}\parallel v_{n+1}^{h}\parallel ^{2}-{\frac {\rho }{2}}\parallel v_{n}^{h}\parallel ^{2}=-a(v_{n+1}^{h}\\\displaystyle v_{n+1}^{h})-\parallel \tau ^{1/2}(-2\mu \nabla \cdot \nabla ^{s}v_{n+1}^{h}+\nabla p_{n+1}^{h})\parallel ^{2}-{\frac {\rho }{2}}\parallel v_{n+1}^{h}-\\\displaystyle -v_{n}^{h}\parallel .\end{array}}$

( 14)

Como todos los términos del lado derecho de la igualdad son no positivos, queda demostrado que la norma de la velocidad ha de ser decreciente.

5. El problema transitorio de Stokes en la configuración actualizada

Supongamos un fluido incompresible cuyo movimiento está gobernado por las ecs.(9) y cuyo campo de velocidades se emplea para actualizar el dominio de integración. El problema completo consiste en encontrar φ_t tal que:

${\begin{array}{cc}v&={\dot {\varphi _{t}}}\circ \varphi _{t}^{-1}\\\rho \quad \partial _{t}v-2\mu \nabla \cdot \nabla ^{s}v+\nabla p&=f,\end{array}}$

( 15)

en todos los puntos de ${\textstyle B_{t}=\varphi _{t}(B_{o})}$ . La forma débil de este problema consiste en hallar φ_t y p tales que:

${\begin{array}{cc}(\rho \quad \partial _{t}v,w)_{t}+a_{t}(v,w)+b_{t}(w,p)&=(f,w)\\b_{t}(v,q)&=0,\end{array}}$

( 16)

con las formas bilineales

${\begin{array}{cc}a_{t}(v,w)&=\int _{B_{t}}2\mu \nabla ^{s}v\cdot \nabla ^{s}w\quad dV\\b_{t}(v,p)&=-\int _{B_{t}}\nabla \cdot v{\mbox{   }}p\quad dV\\(f,w)_{t}&=\int _{B_{t}}f\cdot w\quad dV.\end{array}}$

( 17)

Comparando la ecs.(16) con las del problema de los fluidos lagrangianos (ecs.(1) ) se comprueba que son idénticas. Además, formalmente son iguales a las del problema transitorio de Stokes (ecs.(9) ), y solo se diferencian de estas últimas en que los dominios de integración cambian en la formulación general y son fijos en el problema de Stokes.

La diferencia en los dominios de integración de las ecuaciones (9) y (16) hace que estas últimas sean no lineales con lo cual su resolución es más compleja. A tal efecto, se puede volver a emplear un método de Galerkin estabilizado que discretice las ecuaciones en el espacio y una integración de Euler en el tiempo. Puesto que el objeto es formular un método lagrangiano, la velocidad espacial ${\textstyle v}$ ha de obtenerse a partir de la relación ${\textstyle v=V\circ \varphi _{t}^{-1}}$ , siendo ${\textstyle V={\dot {\varphi }}_{t}}$ la velocidad material. Del mismo modo, el campo de presiones que aparece en las ecuaciones ha de calcularse a partir del campo de presiones materiales P   de tal manera que ${\textstyle p=P\circ \varphi _{t}^{-1}}$ .

Definiendo subespacios de funciones con dimensión finita ${\textstyle V^{h}}$ y ${\textstyle Q^{h}}$ , como en la sección 4 , el método numérico que se propone consiste en encontrar ${\textstyle (\varphi _{n}^{h},P_{n}^{h})\in V^{h}\times Q^{h}}$ , aproximaciones a la deformación y a la presión en el instante t_n tales que:

${\begin{array}{cc}{\frac {\varphi _{n+1}^{h}-\varphi _{n}^{h}}{\Delta t_{n}}}&=V_{n+1}^{h}\\\left(\rho {\frac {v_{n+1}-v_{n}}{\Delta t_{n}}},w\right)_{t}+a_{t}(v_{n+1},w)+b_{t}(w,p_{n+1})+(\tau (-2\mu \nabla \cdot \nabla ^{s}v_{n+1}+\nabla p_{n+1}-f_{n+1}),-2\mu \nabla \cdot \nabla ^{s}w)_{t}&=(f_{n+1},w)_{t}\\-b_{t}(v_{n+1},q)+(\tau (-2\mu \nabla \cdot \nabla ^{s}v_{n+1}+\nabla p_{n+1}-f_{n+1}),\nabla q)_{t}&=0,\end{array}}$

( 18)

para todo ${\textstyle (w^{h},q^{h})\in V^{h}\times Q^{h}}$ , siendo

${\begin{array}{ccc}v_{n+1}&=V_{n+1}^{h}\circ (\varphi _{n+1}^{h})^{-1}\quad \quad w&=W^{h}\circ (\varphi _{n+1}^{h})^{-1},\\p_{n+1}&=P_{n+1}^{h}\circ (\varphi _{n+1}^{h})^{-1}\quad \quad q&=Q^{h}\circ (\varphi _{n+1}^{h})^{-1},\end{array}}$

( 19)

y con las correspondientes condiciones iniciales y de contorno. Nótese que, en lugar de las ecs.(18) y (19) , se podría haber reformulado todo el problema en función de las cantidades materiales ${\textstyle \varphi _{n}^{h}}$ y ${\textstyle P_{n}^{h}}$ , con sus consiguientes variaciones. Esta alternativa da lugar a un sistema de ecuaciones completamente equivalente al descrito anteriormente, aunque es difícil reconocer en este la relación con el problema de Stokes, relación que resulta evidente cuando se escribe como en la ec.(16) .

Cabe destacar que, una vez resuelto el problema para cada partícula X e instante t_n , se conoce su deformación φ_n (X ), su velocidad V_n (X ) y su presión P_n (X ). A partir de la primera, por ejemplo, se pueden describir las trayectorias en el fluido sin realizar ninguna integración adicional.

La formulación propuesta hereda de la formulación lineal la estabilidad de la velocidad, en el sentido de que la energía cinética de la solución decrece monótonamente cuando no existen fuerzas externas sobre el fluido.

6. Aproximación con un método sin malla

Los resultados de las secciones anteriores son generales, puesto que no se especifican los espacios de Galerkin que se emplean para la proyección espacial de las incógnitas en los diferentes problemas planteados. En particular, una opción sería emplear espacios de elementos finitos. Sin embargo, en los problemas de fluidos lagrangianos, la deformación es tan grande que la malla tendría que actualizarse muy a menudo.

En este trabajo, hemos decidido emplear métodos de Galerkin con aproximaciones que no requieren definir una malla. Aunque lo que presentamos a continuación podría definirse con otros métodos de aproximación, hemos optado por los espacios definidos con funciones de máxima entropía locales, o de max-ent[6]  and [13] . Estas funciones aproximan la información de los nodos de una discretización a los puntos de cuadratura, donde se evalúan todas las integrales de la forma débil del problema. Esta aproximación se realiza de la forma más imparcial posible, es decir, maximizando la entropía de la información y concentrando las funciones alrededor de los nodos.

Para resumir el cálculo de las funciones de max-ent   , supongamos que en un dominio ${\textstyle \Omega \subset \mathbb {R} ^{N}}$ se definen M puntos distintos de coordenadas x_a , a  = 1, …, M cuyo cierre convexo C   aproxima Ω. Asociada a cada uno de esos puntos, se define una función de aproximación ${\textstyle N^{a}:C\rightarrow \mathbb {R} }$ , de tal manera que, en un punto cualquiera q  ∈ C , el valor de esta se obtiene resolviendo el siguiente problema de optimización: dado β  > 0, minimizar

${\begin{array}{c}\beta \sum _{a}N^{a}(q)\vert q-x_{a}\vert ^{2}+\sum _{a}N^{a}(q)logN^{a}(q)\\tal{\mbox{   }}que\quad N^{a}(q)\geq 0,\quad \sum _{a}N^{a}(q)=1,\quad \sum _{a}N^{a}(q)\quad x_{a}=q.\end{array}}$

( 20)

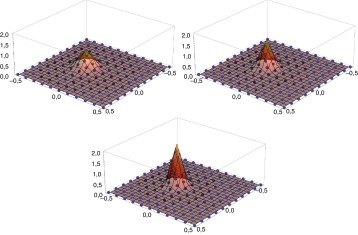
Estas funciones tienen algunas propiedades que las hacen muy interesantes para aproximar la solución en problemas numéricos: son infinitamente diferenciables, positivas, y satisfacen débilmente la propiedad de la delta de Kronecker, es decir, el valor en puntos del contorno de C solo depende de los puntos x_a  ∈ ∂C . La primera propiedad facilita la formulación de métodos estabilizados, pues las derivadas de alto orden que se emplean véase, por ejemplo, (6) – se pueden calcular globalmente. La última de las propiedades facilita la imposición de condiciones de contorno, una cuestión que suele ser complicada para otros métodos sin malla. En la figura 1 , se pueden observar tres funciones del tipo descrito en un dominio cuadrado.

Figura 1. Tres funciones locales de máxima entropía para una distribución regular de puntos en el dominio [− 5, 5]2 y con β  = 100, 150 y 200.

Una vez definidas las funciones de aproximación, todas las integrales que aparecen en la definición de las formas débiles en los tres problemas descritos en las secciones 2 a 4 se aproximan mediante una cuadratura numérica. Para ello, es necesario definir K   puntos de cuadratura ${\textstyle \lbrace q_{k}\rbrace _{k=1}^{K}}$ , con sus correspondientes pesos ${\textstyle \lbrace W_{k}\rbrace _{k=1}^{K}}$ , de tal manera que toda integral se calcula numéricamente como:

$\int _{\Omega }f(x)\quad dV\approx \sum _{k=1}^{K}f(q_{k})W_{k}.$

( 21)

Para el problema estacionario de Stokes de la sección 3 y el problema transitorio de la sección 4 , el método numérico propuesto necesita que, como paso inicial, se definan los nodos x_a  ∈ Ω y los puntos de cuadratura q_k  ∈ C . Después, todas las integrales de la forma variacional se pueden evaluar una vez conocido el valor de las funciones de aproximación en cada uno de los puntos de cuadratura. La selección óptima de puntos de cuadratura y sus pesos asociados son un problema que no está resuelto todavía [6] . En las simulaciones presentadas en el apartado 7 estos puntos se han escogido realizando una teselación sobre la configuración de referencia y utilizando reglas de cuadratura estándar para mallas de elementos finitos. Es importante indicar que el único propósito de estas mallas es la definición inicial de los puntos de cuadratura; una vez generados, la malla es eliminada.

En el problema no lineal de la sección 5 , el paso inicial es igual al de los otros dos métodos, y es necesario definir tanto los nodos como los puntos de cuadratura y sus pesos. A diferencia de los otros dos problemas, en que el dominio de integración era fijo, en este problema no lineal la posición de los nodos cambia con la deformación y los puntos de integración se ven arrastrados por el movimiento de los primeros.

7. Validación y simulaciones numéricas

En esta sección, se muestra cómo los métodos de los apartados 2 y 4 , cuando se emplean funciones de aproximación de max-ent , resultan métodos numéricos con las propiedades identificadas, y se presentan algunos ejemplos de simulación complejos que revelan la capacidad de estos métodos para aproximar la solución de problemas con superficies libres.

7.1. El problema de Stokes

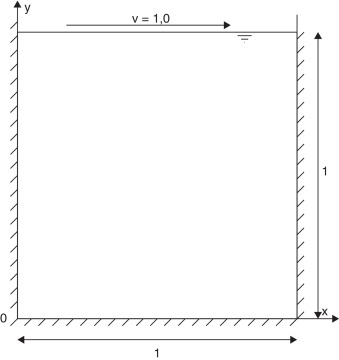
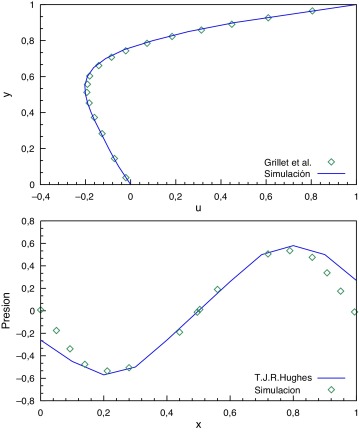
En primer lugar, se muestran resultados numéricos para el problema estacionario de Stokes. La mayor dificultad de este problema, como es bien sabido, es debido a la restricción de incompresibilidad del fluido, que puede manifestarse en forma de pérdida de estabilidad, especialmente cuando los espacios de aproximación de la velocidad y la presión son iguales. La estabilización empleada permite definir un método estable cuyos resultados comparamos, en primer lugar, con el problema plano de una cavidad cuadrada con la velocidad impuesta en todos sus bordes [14] . La geometría del mismo se ilustra en la figura 2 . En la figura 3 se muestran los resultados de la velocidad y la presión en dos cortes del dominio de solución, y estas se comparan con los resultados de la literatura [15] , lo cual permite apreciar que la aproximación con el método propuesto es buena. La discrepancia en el valor de las presiones puede deberse a la técnica de suavizado aplicada en la solución referencia.

Figura 2. Cavidad con flujo incompresible de Stokes.

Figura 3. Velocidad en el plano medio y presión en el plano a y  = 0.35 sobre la base del ejemplo de validación.

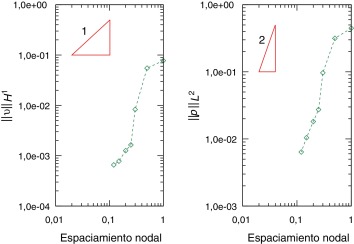
Para confirmar que el método propuesto es convergente, estudiamos a continuación el flujo de Stokes en el mismo dominio cuadrado con una solución conocida. La solución analítica [16] se empleará para medir la norma del error, tanto en las velocidades como en las presiones. Para ello, se impone velocidad nula en las cuatro paredes del recinto y se aplica sobre el cuerpo la fuerza de volumen b ,

$\left\{{\begin{array}{cc}b_{x}&=0,\\b_{y}&=120(2x-1)y^{2}(1-y)^{2}\\&+80x(1-x)(1-2x)(6y^{2}-6y+1)\\&+8(6x^{5}-15x^{4}+10x^{3}).\end{array}}\right.$

( 22)

La solución conocida tiene la expresión polinómica siguiente:

$\left\{{\begin{array}{cc}v_{x}&=20x^{2}(1-x)^{2}y(1-y)(1-2y),\\v_{y}&=-20x(1-x)(1-2x)\quad y^{2}(1-y)^{2}\\p&=40x(1-x)(1-2x)\quad y(1-y)(1-2y)\\&+4(6x^{5}-15x^{4}+10x^{3})(2y-1).\end{array}}\right.$

( 23)

La convergencia en el error se observa en la fig. 4 donde la seminorma H¹ de la velocidad se compara con una pendiente lineal y la norma L² de la presión se compara con una pendiente cuadrática.

Figura 4. Convergencia del error en función del espaciado.

7.2. El problema de Stokes transitorio

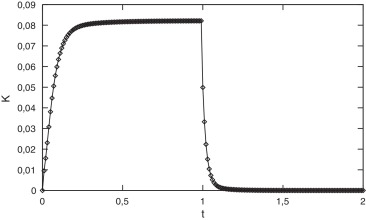
A continuación, se estudia el problema de Stokes transitorio propuesto en (10) . Para ello, la cavidad mostrada en la fig. 2 se considera de nuevo llena de un fluido incompresible con propiedades μ  = 1.0e⁻⁶  Pa ·s y ρ  = 1.0 kg/m³ . Las paredes laterales e inferior tienen condiciones de contorno de velocidad nula, y la presión es fijada a 0 en la esquina inferior izquierda. La tapa superior tiene la velocidad impuesta ${\textstyle v_{x}=1.0}$  m/s desde el instante inicial hasta el instante t  = 1.0 s, momento en que se libera esta condición. El fluido, al ser liberado, ha de tender a la posición de reposo en su evolución con el tiempo. En la figura 5 , se muestra efectivamente cómo decae la energía cinética total del sistema desde el momento en que se retira la imposición de velocidad en la tapa superior y tiende asintóticamente al reposo.

Figura 5. Energía cinética del sistema.

7.3. Los fluidos lagrangianos

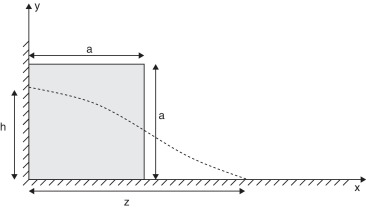
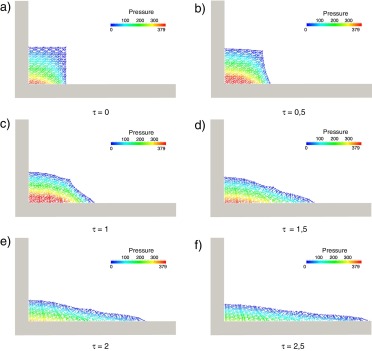
La tercera validación que presentamos es la de la simulación de fluidos newtonianos mediante la formulación lagrangiana descrita en la sección 5 . Para ello, se utiliza un ejemplo con soluciones conocidas en la literatura, tanto numéricas [17] como experimentales [18] . El problema simula la rotura repentina de una presa, donde el agua inicialmente está en reposo, tal como se muestra en la figura 6 . En el instante t  = 0 s, la pared vertical de la derecha se elimina y se deja que el fluido libre se derrame.

Figura 6. Rotura repentina de una presa.

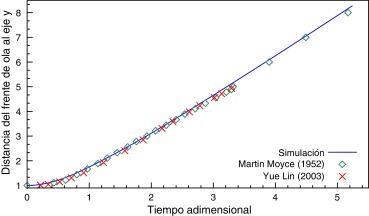
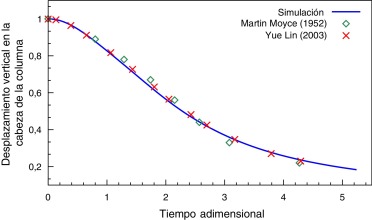
Con objeto de validar los resultados, se toma la dimensión a  = 5.72 · 10⁻³  m. La fuerza de la gravedad g  = 9.81 m/s² actúa en la dirección negativa del eje y , y las propiedades del fluido se asumen como ρ  = 10³  kg/m³ y μ  = 1 Pa·s. La distancia del frente de ola (z ) con respecto al eje vertical y la altura remanente de la columna de agua (h ) se han medido en función del tiempo, y los resultados adimensionalizados se muestran en las figuras 7 y 8 , donde se aprecia una buena concordancia con respecto a las soluciones conocidas. Todas las dimensiones han sido adimensionalizadas como sigue:

$z=Z/a,\quad h=H/a,\quad t=T{\sqrt {g/a}}.$

( 24)

Figura 7. Distancia del frente de ola al eje vertical.

Figura 8. Altura de la columna de agua remanente.

Por último, en la fig. 9 se muestra la evolución de la columna de agua para seis instantes diferentes de tiempo, donde se ha reproducido el campo de presiones.

Figura 9. Evolución del perfil del fluido tras la rotura de la presa en seis instantes diferentes. De arriba abajo, izquierda a derecha: instantes t  = 0,0; 0,5; 1,0; 1,5; 2,0; 2,5 s.

7.4. Llegada y retirada de una ola a la costa

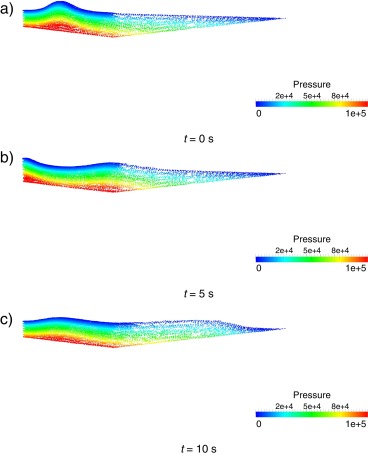
Finalmente, presentamos los resultados numéricos de una simulación tridimensional que muestra la llegada de una ola a la orilla y su posterior retirada. Para este ejemplo final, no disponemos de resultados analíticos para la validación de las simulaciones y lo presentamos únicamente para poder apreciar cómo el método lagrangiano planteado se puede aplicar directamente a problemas tridimensionales.

El cuerpo definido en la figura 10 está compuesto por un fluido con las propiedades siguientes: viscosidad dinámica μ  = 10 Pa·s y ρ  = 10³  kg/m³ . El cuerpo está contenido entre cinco planos: tres planos verticales (x  = −50, z  = 0 y z  = 2.5), 1 horizontal (y  = 0) y uno oblicuo (−0.12x  + 0.99y  + 6 =0). La superficie libre del cuerpo ha sido inicialmente perturbada sobre la base de la ecuación siguiente

Figura 10. Configuración inicial.

$\eta =h+a\quad sech^{2}\left({\sqrt {\frac {3a}{4h^{3}}}}x\right)$

( 25)

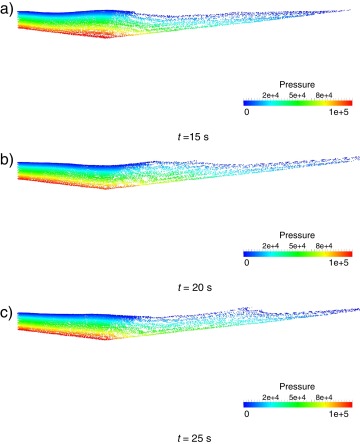
donde η es la altura de la superficie libre desde la base; h  = 10 m, la altura de la superficie no perturbada; a  = 5 m, la amplitud máxima de la perturbación y x el valor del punto en el eje horizontal. Las longitudes definidas en la figura 10 tienen los valores L₁  = 100 m y L₂  = 132 m. El comportamiento general de la ola se detalla en los seis instantes capturados en las figuras 11 y 12 . Se puede observar cómo la presión se mantiene estable en toda la simulación y cómo, tras liberar en el instante inicial la superficie libre con la joroba de agua a mayor altura, esta cae y genera ondas en las dos direcciones (11 )b. Mientras la onda que impacta sobre el plano vertical produce un efecto de rebote (11 )c, el frente de avance hacia el plano oblicuo que simula la costa provoca un desplazamiento del fluido sobre el plano (12 )a. Finalmente, se producen movimientos acoplados debidos al retroceso del agua que ha llegado a la costa con la onda que proviene del rebote con el otro extremo (12 b y 12 c).

Figura 11. Evolución del problema del avance y el retroceso de la ola. De arriba abajo, instantes t  = 0, 5 y 10 s.

Figura 12. Evolución del problema del avance y el retroceso de la ola. De arriba abajo, instantes t  = 15, 20 y 25 s.

7.5. Impacto de una columna de agua

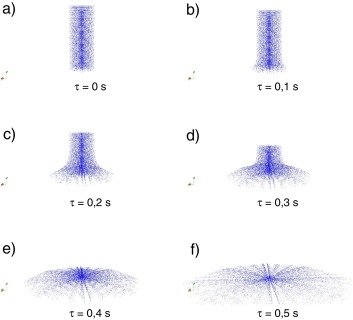
Por último, mostramos los resultados de una simulación tridimensional sin solución analítica o experimental con que compararla, para ilustrar la capacidad de la formulación presentada para resolver problemas complejos. En este ejemplo, una columna cilíndrica de fluido, con un eje orientado según el eje coordenado x₃ , cae sobre un plano rígido x₃  = 0, impulsada por su propio peso. La columna tiene una altura de 1 m y un diámetro de 0,2 m. El fluido tiene una viscosidad dinámica μ  = 10 Pa·s, una densidad ρ  = 1.000 kg/m³ y está sometido a la gravedad. Inicialmente, todos los puntos de la columna están en reposo y los de su base están en contacto con el plano rígido.

En la figura 13 se puede observar la forma de la columna en seis instantes del impacto. Inicialmente es cilíndrica, impacta, se deshace y se esparce sobre el plano rígido. Aunque el problema tiene simetría de revolución, la solución que se muestra se ha obtenido con una discretización tridimensional, resolviendo el método lagrangiano descrito en la sección 5 .

Figura 13. Impacto de una columna de fluido sobre un plano rígido.

El contacto entre el fluido y el plano se calcula mediante un método de penalización sencillo. En este método, si un punto material tiene por coordenadas x  = (x₁ , x₂ , x₃ ), recibe en cada instante una fuerza

$f=K\left\langle -x_{3}\right\rangle {\mbox{   }}e_{3}\quad$

( 26)

siendo 〈 · 〉 el corchete de Macaulay, K una constante de penalización y e₃ el vector unitario en dirección positiva de x₃ .

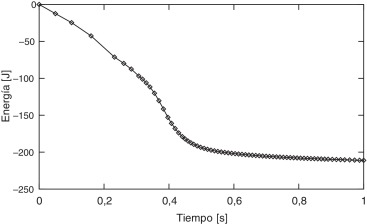
En la figura 14 , se muestra la evolución de la energía total del fluido durante la simulación. En ella se aprecia que la energía decrece monotónicamente, a pesar de que esta propiedad solo está garantizada en los problemas lineales.

Figura 14. Energía de la columna de fluido durante el impacto sobre un plano rígido.

8. Conclusiones

La simulación de fluidos mediante formulaciones lagrangianas se presenta como una oportunidad para afrontar problemas con fluidos, en que el seguimiento de las superficies libres y sus fronteras es clave para realizar una aproximación correcta. Si bien es difícil resolver este tipo de fenómenos mediante aproximaciones eulerianas, su tratamiento lagrangiano es trivial. Por contra, las formulaciones de este último tipo tienen sus propios problemas, casi siempre asociados a la distorsión del dominio de aproximación.

En este trabajo, hemos presentado un método de Galerkin sin malla que permite resolver las ecuaciones de los fluidos newtonianos incompresibles en un marco lagrangiano. El método emplea funciones de aproximación de máxima entropía y necesita una estabilización para ser capaz de acomodar la restricción de incompresibilidad del fluido. El resultado es un método incondicionalmente estable para los problemas lineales de Stokes y su contrapartida transitoria. Su extensión a problemas no lineales, en que el dominio fluido se ve arrastrado por su propia velocidad, es relativamente sencilla y hereda una cierta noción de estabilidad.

El método propuesto ha sido validado con problemas expuestos en la literatura. Su robustez lo hace especialmente idóneo para la resolución de problemas con fluidos incompresibles y superficies libres. En un futuro, estudiaremos su aplicación para la resolución de problemas de interacción entre fluidos y sólidos deformables.

Agradecimientos

Los autores agradecen la financiación recibida del Ministerio de Economía y Competitividad del Gobierno de España, a través del proyecto DPI2012-36429.

References

1. [1] S.R. Idelsohn, E. Oñate, F. Del Pin; The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves; Int. J. Numer. Meth. Engng., 61 (7) (2004 September), pp. 964–989
2. [2] M. Cremonesi, A. Frangi, U. Perego; A Lagrangian finite element approach for the analysis of fluid-structure interaction problems; Int. J. Numer. Meth. Engng., 84 (2010), pp. 610–630
3. [3] P.B. Ryzhakov, R. Rossi, S.R. Idelsohn, E. Oñate; A monolithic Lagrangian approach for fluid-structure interaction problems; Comput. Mech., 46 (6) (2010), pp. 883–899
4. [4] R. Radovitzky, M. Ortiz; Lagrangian finite element analysis of newtonian fluid flows; Int. J. Numer. Meth. Engng., 43 (1998), pp. 607–619
5. [5] S. Li, W.K. Liu; Meshfree particle methods; Springer-Verlag, Berlin, Heidelberg (2004)
6. [6] M. Arroyo, M. Ortiz; Local maximum-entropy approximation schemes: a seamless bridge between finite elements and meshfree methods; Int. J. Numer. Meth. Engng., 65 (2006), pp. 2167–2202
7. [7] J. Douglas, J. Wang; An Absolutely Stabilized Finite-Element Method for the Stokes Problem; Math. Comp., 52 (186) (1989), pp. 495–508
8. [8] J.E. Marsden, T.J.R. Hughes; Mathematical foundations of elasticity; Prentice-Hall Englewood Cliffs (1983)
9. [9] D. Boffi, F. Brezzi, and M. Fortin. Mixed Finite Element Methods and Applications, volume 44 of Springer Series in Computational Mathematics. Springer Science and Business Media, Berlin, Heidelberg, July 2013.
10. [10] TJ.R. Hughes, L.P. Franca, M. Balestra; A new finite element formulation for computational fluid dynamics: V. Circumventing the Babuška-Brezzi condition: A stable Petrov-Galerkin formulation of the Stokes problem accommodating equal-order interpolations; Comput. Methods Appl. Mech. Engrg., 59 (1) (1986), pp. 85–99
11. [11] T. Barth, P. Bochev, M. Gunzburguer, J.N. Shadid; A Taxonomy of Consistently Stabilized Finite Element Methods for the Stokes Problem; SIAM J. Sci. Comput., 25 (5) (2004 January), pp. 1585–1607
12. [12] F. Shakib, T.J.R. Hughes; A new finite element formulation for computational fluid dynamics: IX. Fourier analysis of space-time Galerkin/least-squares algorithms; Comput. Methods Appl. Mech. Engrg., 87 (1) (1991), pp. 35–58
13. [13] N. Sukumar; Construction of polygonal interpolants: a maximum entropy approach; Int. J. Numer. Meth. Engng., 61 (12) (2004), pp. 2159–2181
14. [14] J.R. Koseff, R.L. Street; The Lid-Driven Cavity Flow: A Synthesis of Qualitative andQuantitative Observations; J. Fluids Eng., 106 (1984), pp. 1–9
15. [15] T.J.R. Hughes; The finite element method; Prentice-Hall Inc., Englewood Cliffs, New Jersey (1987)
16. [16] T. Kashiwabara; On a finite element approximation of the Stokes equations under a slip boundary condition of the friction type; Japan J. Indust. Appl. Math., 30 (2013), pp. 227–261
17. [17] W. Yue, C.L. Lin, V.C. Patel; Numerical simulation of unsteady multidimensional free surface motions by level set method; Int. J. Numer. Meth. Fluids, 42 (2003), pp. 853–884
18. [18] J.C. Martin, W.J. Moyce; Part IV. An Experimental Study of the Collapse of Liquid Columns on a Rigid Horizontal Plane; Philos. Trans. Roy. Soc. London Ser. A, 244 (882) (1952), pp. 312–324

Notes

1. Estas operaciones son denominadas push-forward y pull-back en la literatura anglosajona.