Resumen
Este artículo muestra la resolución del problema de propagación de ondas sísmicas en 2-D, mediante la utilización de esquemas explícitos en diferencias finitas generalizadas (GFD), lo que permite la utilización de mallas regulares e irregulares.
Puesto que se utiliza un método explícito, es necesario obtener la condicióń de estabilidad, lo que se ha realizado mediante un análisis de von Neumann. También se obtienen las relaciones de dispersión en la estrella de las velocidades de fase para las ondas P y S, así como las de las velocidades de grupo.
Dada la importancia que en la aplicación del método tiene el control sobre la irregularidad de la malla, se han definido unos índices de irregularidad para la estrella (IIS) y la malla (IIC), analizándose su relación con la dispersión y el paso de tiempo utilizado en los cálculos.
Abstract
This paper shows the solution to the problem of seismic wave propagation in 2-D using generalized finite difference (GFD) explicit schemes. Regular and irregular meshes can be used with this method.
As we are using an explicit method, it is necessary to obtain the stability condition by using the von Neumann analysis. We also obtained the star dispersion formulas for the phase velocities for the P and S waves, as well as the ones for the group velocities.
As the control over the irregularity in the mesh is very important in the application of this method, we have defined an index of irregularity for the star (IIS) and another for the cloud (IIC), analyzing its relationship with the dispersion and time step used in the calculations.
Palabras clave
Métodos sin malla ; Diferencias finitas generalizadas ; Ondas ; Estabilidad ; Dispersión ; Mallas irregulares ; Método explícito
Keywords
Meshless methods ; Generalized finite difference ; Waves ; Stability ; Dispersion ; Irregular meshes ; Explicit method
1. Introducción
Son muchos los trabajos publicados sobre propagación de ondas sísmicas, incluso centrándonos en los relativos a la utilización del método de Diferencias Finitas (FD) y dentro de ellos los que tratan aspectos relativos al tipo de malla, la estabilidad y dispersión, que son los aspectos en que fundamentalmente se centra el presente trabajo. Así, durante más de diez a os se utilizarón mallas convencionales en FD, pudiéndose destacar los trabajos de Altermann y Karal [1] y Kelly et al. [2] .
Los esquemas Staggered-grid (S-G) en FD fueron introducidos por Madariaga [3] , popularizándose su uso en problemas de propagación de ondas con los trabajos de de Virieux [4] , [5] en los que se usa un esquema de segundo orden para la formulación en velocidad-tensión con ondas SH y P-SV respectivamente.
Otros esquemas han sido presentados por Levander [6] para una formulación en cuarto orden para ondas P-SV, Graves [7] , Graves et al. [8] , Ohnimato and Chovet [9] que lo aplican en un esquema de segundo orden en la formulación desplazamiento-tensión. También pueden destacarse los trabajos de Kristek et al. [10] , [11] .
A pesar de los trabajos citados de Virieux y Levander sobre dispersión y Crase et al. [12] que obtienen condiciones de estabilidad para ondas P-SV para un orden arbitrario de aproximación, Moczo, Kristek y Halada [13] se dan cuenta de que la dispersión de los esquemas S-G en 3-D no están suficientemente investigados y lo estudian para esquemas de cuarto orden en el espacio y segundo orden en el tiempo con validez para formulaciones en desplazamiento-tensión, velocidad-tensión y desplazamiento-velocidad-tensión. También Graves et al. [8] han estudiado la estabilidad y Mozco et al. [14] presentan trabajos recopilatorios de gran interés.
Las mallas parcialmente Staggered(P-S-G) fueron utilizadas por primera vez por Andrews [15] para medios anisótropos y Zhang [16] las utiliza para la formulación velocidad-tensión en 2-D. Cruz-Atienza y Virieux [17] las utilizan para la simulación de una rotura de falla en 2-D.
El primero en utilizar una malla con espaciado variable fue Boore [18] para un caso veritcal 1-D, Mikuano y Miyatarke [19] usan un espaciado variable en un medio elástico en 2-D para analizar el proceso de rotura de falla. Pitarka [20] presenta un esquema de cuarto orden para la formulación en velocidad-tensión sobre una malla rectangular con espaciado variable y Wang et al. [21] combinan mallas con diferentes espaciados.
Los métodos que en general se pueden denominar métodos sin malla, surgieron hace aproximadamente treinta a os, aunque el interés y el esfuerzo investigador ha sido mínimo hasta hace poco tiempo. Así pues, la referencia más alejada en el tiempo y que puede condiderarse como punto de partida es el método de partículas (SPHM) que fue desarrollado por en 1977 por Lucy [22] . En 1982 y 1988 Monaghan ([23] y [24] ) desarrolla una explicación más rigurosa del método.
Una camino paralelo al indicado en el desarrollo de aproximaciones sin malla se basa en la idea de realizar una aproximación local mediante el método de mínimos cuadrados móviles de Lancaster y Salkauskas (1981) ([25] ). Nayroles, Touzot y Villon (1992) ([26] ) fueron los primeros en utilizar una aproximación de este tipo en un método de Galerkin, denominado método de los elementos difusos (DEM).
Belytschko, Lu y Gu (1994) ([27] ) refinaron y desarrollaron una implementación alternativa del método de los elementos difusos, que mejoró la precisión al utilizar multiplicadores de Lagrange para imponer las condiciones de contorno esenciales y un orden de cuadratura mayor en la integración. Ellos denominaron al método Galerkin libre de elementos (EFG).
Un salto importante en el desarrollo de estos métodos se ha producido a partir de los trabajos de Duarte y Oden (1995) ([28] ) y de Babuska y Melenk (1995) ([29] ) que realizan una generalización muy interesante de la aproximación por mínimos cuadrados móviles usando el concepto de partición de la unidad, que los primeros denominaron nubes hp (hp clouds) y de partición de la unidad (PUFEM) los segundos.
Otro camino en la evolución de los métodos sin malla se ha constituido mediante el desarrollo del método de diferencias finitas generalizadas (GFDM) que surge como consecuencia de la evolución del método de diferencias finitas clásicas. Los trabajos de Jensen (1972) ([30] ) y Perrone y Kao (1975) ([31] ) pusieron las bases del método. Liszka y Orkisz (1980) ([32] ) y Orkisz (1998) ([33] ) han realizado importantes contribuciones a la mejora y desarrollo del método.
El método de diferencias finitas generalizadas (GFDM) se basa en la utilización de mínimos cuadrados móviles, lo que permite aplicar esquemas en diferencias finitas en dominios irregulares. Al desarrollo de este método han contribuido los trabajos de los autores. Así, se han obtenido fórmulas explícitas en diferencias para el caso de estrellas irregulares, analizandose la influencia de los parámetros fundamentales que aperecen en la formulación [34] , se ha obtenido un método adaptativo para la mejora de la solución aproximada utilizando GFDM [35] , en [36] se muestra la aplicación del método adaptativo en GFDM a la resolución de ecuaciones diferenciales en derivadas parciales de segundo orden y [37] es un resumen global de GFDM que incluye las aportaciones realizadas por los autores y su aplicación a problemas elásticos.
Los artículos [38] y [39] muestran la aplicación del método de diferencias finitas generalizadas a la resolución de ecuaciones en derivadas parciales dependientes del tiempo.
Los métodos numéricos constituyen una herramienta irremplazable en la investigacíón de los movimientos sísmicos y entre ellos el actualmente dominante es el DF, es más Moczo et al. [40] opinan que está por llegar el mejor momento de la aplicación del método Df en sismología. Tras estas consideraciones parece oportuno presentar las aplicación del GFDM a este tipo de problemas.
Con el presente artículo se pretende establecer una base sólida para la aplicación de un método que ofrece grandes posibilidades entre las que inicialmente hay que destacar la capacidad de utilizar mallas irregulares directamente, evitando artificios en la realización de algunos modelos híbridos. Se desea hacer hincapié en la solidez metodológica puesto que no solo se presenta la formulación en GFD para la aplicación indicada, sino que se estudia de forma rigurosa su estabilidad y se analiza detalladamente la dispersión.
2. Esquema en diferencias finitas generalizadas para el problema de propagación de ondas sísmicas en dominios homogéneos
2.1. Planteamiento del problema
El problema de propagación de ondas sísmicas en 2-D viene caracterizado por el sistema de ecuaciones diferenciales en derivadas parciales
|
|
( 1) |
con las condiciones iniciales
|
|
( 2) |
y la condición de contorno
|
|
( 3) |
siendo f1 (x , y ), f2 (x , y ), f3 (x , y ), f4 (x , y ), g1 (t ) y g2 (t ) funciones conocidas,
|
|
ρ es la densidad, λ cortante de Lamé y μ el módulo de rigidez. Las funciones U (x , y , t ), V (x , y , t ) son al menos dos veces diferenciables con continuidad en el dominio Ω con frontera Γ.
2.2. Esquema en diferencias finitas generalizadas
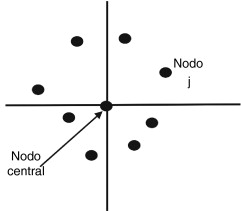
Para la obtención de las fórmulas explícitas en diferencias finitas de las derivadas espaciales, una vez discretizado el dominio Ω ∪ Γ, a cada nodo del mismo se le asigna un conjunto de nodos a su alrededor que se denomina estrella. En la figura 1 se muestra una estrella irregular con ocho nodos seleccionados con el criterio de los cuatro cuadrantes (dos nodos por cuadrante, que son los más próximos al nodo central, considerando este como origen).
|
|
|
Figura 1. Estrella irregular de 9 nodos. |
La derivada segunda respecto del tiempo en el nodo central de la estrella se aproxima por:
|
|
( 4) |
donde , , y son los valores aproximados de las funciones U (x , y , t ), V (x , y , t ) en el nodo central de coordenadas espaciales (x0 , y0 ) para los tiempos n ▵ t y (n + 1) ▵ t respectivamente.
Las derivadas espaciales se aproximan por las expresiones explícitas en diferencias finitas generalizadas, obtenidas en [36] y [38] :
|
|
( 5) |
donde N es el número de nodos de la estrella cuyo nodo central tiene de coordenadas (x0 , y0 ) (en este trabajo N = 8 y son seleccionados mediante el criterio de los cuatro cuadrantes), m0 , η0 y ζ0 son los coeficientes que multiplican a los valores aproximados de las funciones U y V en el nodo central para el tiempo n ▵ t ( y respectivamente) de las expresiones explícitas en diferencias finitas generalizadas para las derivadas espaciales , y respectivamente, mj , ηj y ζj son los coeficientes que multiplican a los valores aproximados de las funciones U y V en el resto de los nodos de la estrella para el tiempo n ▵ t ( y respectivamente) de las expresiones explícitas en diferencias finitas generalizadas para las derivadas espaciales , y respectivamente ([32] , [33] , [34] , [37] ).
Si en el sistema de ecuaciones 1 se sustituyen las derivadas parciales por las expresiones 4 y 5 se obtiene:
|
|
( 6) |
que constituyen el esquema en diferencias finitas generalizadas para el pro-blema planteado.
3. Criterio de estabilidad
Para estudiar la estabilidad se utiliza el análisis de von Neumann. Para lo cual se realiza una descomposición armónica de la solución aproximada de la forma
|
|
( 7) |
donde x0 es vector de posición del nodo central de la estrella, xj , j = 1, …, N son los vectores de posición del resto de los nodos de la estrella y hj son los vectores de las posiciones relativas de los nodos de la estrella con respecto al nodo central cuyas coordenadas son hjx = xj − x0 , hjy = yj − y0 .
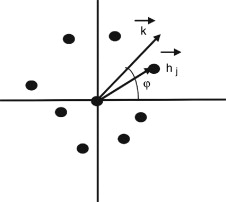
ξ = e−iw ▵t es el llamado factor de amplificación, cuyo valor determinará la condición de estabilidad, es la frecuencia angular y k es el vector del número de onda (ver figura 2 )
|
|
|
Figura 2. Número de onda . |
|
|
Al sustituir las expresiones 7 en la ecuación 6 , y simplificar, se obtiene.
|
|
( 8) |
Teniendo en cuenta que los coeficientes mj , ηj , ζj , son particiones de la unidad, se tiene
|
|
( 9) |
al sustituir las expresiones 9 en la ecuación 8 , se obtiene el sistema de dos ecuaciones con dos incógnitas, A y B , siguiente
|
|
( 10) |
en el que al despejar B de la segunda ecuación del sistema 10 , y sustituir en la primera ecuación, y tras operar, se obtiene
|
|
( 11) |
Tras operar, se obtienen las siguientes condiciones:
Parte real
|
|
( 12) |
Parte imaginaria
|
|
( 13) |
Al operar con estas ecuaciones, simplificando mediante el uso de criterios conservadores y eligiendo entre ambas la condición más restrictiva, se obtiene
|
|
( 14) |
que es la condición de estabilidad de la estrella. Por tanto, el paso de tiempo (▵t ) deberá ser el mínimo de los obtenidos para cada una de las estrellas de la malla.
4. Dispersión en la estrella
4.1. Dispersión de las ondas P
De la ecuación 12 se tiene
|
|
( 15) |
donde
|
|
( 16) |
donde
|
|
( 17) |
y
|
|
Se sabe que
|
|
( 18) |
donde cgrid y λgrid son la velocidad de fase (αgrid o βgrid ) y la longitud de onda ( y ) en la estrella respectivamente ([4] , [5] , [6] , [7] , [12] , [13] , [14] ).
Si se definen las relaciones:
|
|
( 19) |
|
|
( 20) |
|
|
( 21) |
La razón de velocidades es
|
|
( 22) |
y por tanto
|
|
( 23) |
Si se sutituyen las ecuaciones (15) and (20) , 21 y 23 en la ecuación 18 particularizada para las ondas P, tras operar, se obtiene la relación de dispersión para las ondas P
|
|
( 24) |
4.2. Dispersión de las ondas S
Se sabe que
|
|
( 25) |
Si se sustituyen las ecuaciones (15) and (19) y 21 en la ecuación 25 , tras operar, se obtiene
|
|
( 26) |
4.3. Dispersión de la velocidad de grupo ondas P
Por definición la velocidad de grupo para las ondas P , se obtiene al derivar , dada por la expresión 15 , respecto de k , por tanto
|
|
( 27) |
donde
|
|
( 28) |
designando
|
|
( 29) |
Teniendo en cuenta las ecuación 29 y 21 , se tiene
|
|
( 30) |
4.4. Dispersión de la velocidad de grupo ondas S
|
|
( 31) |
4.5. Irregularidad de la estrella y dispersión
Los coeficientes, m0 , η0 , ζ0 , que aparecen en el criterio de estabilidad dependen del número de nodos en la estrella, de las coordenadas de cada nodo respecto del nodo central de la estrella y de la función de ponderación elegida ([34] ).
Fijados el número de nodos por estrella, en nuestro caso 9 (N = 8), y la función de ponderación, , la expresión
|
|
( 32) |
depende de la razón de velocidades y de las coordenadas relativas de cada nodo de la estrella respecto del nodo central de la misma.
Al disminuir las coordenadas relativas de los nodos de la estrella, aumentan los coeficientes m0 , η0 , ζ0 , lo cual ocurre al aumentar el número de nodos en la malla. Para un mismo número de nodos en la malla el mínimo valor de los coeficientes mencionados se obtiene para la malla regular ([36] ).
Sea τl la media de las distancias de los nodos de la estrella l a su nodo central. Sea τ la media de todas las τl de las estrellas de la malla, una vez discretizado nuestro dominio. Se tiene que:
|
|
( 33) |
|
|
( 34) |
en las que la barra superior indica valores medios.
La condición de estabilidad puede reescribirse
|
|
( 35) |
En el caso de malla regular de ocho nodos la expresión 35 resulta ser
|
|
( 36) |
Si se multiplica el segundo miembro de la expresión 36 por el factor
|
|
( 37) |
se obtiene la expresión 35 .
El factor obtenido en 37 , que para una estrella regular (esquema de ocho nodos más el nodo central) es la unidad, resulta ser un indicador de la irregularidad de la estrella, IIS0 , cuyo nodo central tiene de coordenadas (x0 , y0 ). Se adopta como indicador de irregularidad de la malla (IIC) el valor mínimo de los indicadores de irregularidad obtenidos para cada una de las estrellas de la malla.
El control sobre la irregularidad de la malla es importante, ya que al disminuir el IIC , disminuye el paso del tiempo. Sin embargo, mediante un proceso adaptativo de la malla (a adiendo nodos de forma selectiva [35] ) se pueden conseguir índices de irregularidad más próximos a la unidad y, por tanto, pasos de tiempo mayores y menores relaciones de dispersión.
5. Resultados numéricos
5.1. Irregularidad y estabilidad
En esta subsection se muestran los resultados obtenidos al resolver el problema definido en 2.1 en Ω = [0, 1] × [0, 1] ⊂ R2 , con las condiciones de contorno Dirichlet y las condiciones iniciales
|
|
( 38) |
utilizando irregulares (ver figuras 4 y 5 ) de 121 nodos. La solución analítica
|
|
( 39) |
La función de ponderación utilizada ha sido
|
|
( 40) |
y el criterio de selección de los nodos es el del cuadrante. El error global ha sido calculado para cada paso de tiempo utilizando la siguiente norma
|
|
( 41) |
donde sol (j ) es el valor de la solución aproximada en el nodo j , exac (j ) es el valor de la solución exacta en el nodo j , exacmax es el máximo valor de la solución exacta en los nodos interiores de de la malla considerada y NT es el número de nodos del interior.
|
|
|
Figura 4. Malla irregular (IIC = 0, 65). |
|
|
|
Figura 5. Malla irregular (IIC = 0, 89). |
Los valores de los errores globales, para n = 500, al variar ▵t , utilizando la malla irregular de 121 nodos de la figura 4 , con IIC = 0, 6524, se muestran en la tabla 1 .
Tabla 1.
Influencia del ▵t en el error global con α = 1 ; β = 0, 5 ; IIC = 0, 6524 ; n = 500
| Error Global V | ▵t | Error Global U |
|---|---|---|
| 0,0316 | 2, 078 × 10−3 | 9, 875 × 10−4 |
| 0,0223 | 7, 423 × 10−4 | 3, 123 × 10−4 |
| 0,01 | 2, 514 × 10−4 | 1, 217 × 10−4 |
| 0,007 | 1, 423 × 10−4 | 1, 012 × 10−4 |
Los valores de los errores globales, para n = 500, al variar ▵t , utilizando la malla irregular de 121 nodos de la figura 5 , con IIC = 0, 8944, se muestran en la tabla 2 .
| ▵t | Error Global U | Error Global V |
|---|---|---|
| 0,0316 | 7, 331 × 10−4 | 5, 167 × 10−4 |
| 0,0223 | 2, 685 × 10−4 | 1, 950 × 10−4 |
| 0,01 | 1, 102 × 10−4 | 8, 428 × 10−5 |
| 0,007 | 9, 575 × 10−5 | 7, 340 × 10−5 |
5.2. Resultados para distintas longitudes de onda
La tabla 3 muestra los resultados de los errores globales de U y V , para n = 500 y ▵t = 0, 01, al resolver el problema definido en 2.1, utilizando una malla regular de 121 nodos (figura 3 ), para funciones cuyas soluciones analíticas son: 39 y
| Ecuación (sol. anal.) | Error global U | Error global V |
|---|---|---|
| 42 | 1, 646 × 10−6 | 1, 778 × 10−6 |
| 39 | 1, 232 × 10−5 | 2, 443 × 10−5 |
| 43 | 4, 081 × 10−4 | 2, 001 × 10−4 |
| 44 | 9, 188 × 10−2 | 8, 647 × 10−2 |
| 45 | 3, 035 × 10−1 | 3, 275 × 10−1 |
| 46 | 4, 942 × 10−1 | 4, 999 × 10−1 |
|
|
|
Figura 3. Malla regular. |
|
|
( 42) |
|
|
( 43) |
|
|
( 44) |
|
|
( 45) |
|
|
( 46) |
y las correspondientes condiciones de contorno Dirichlet e iniciales
5.3. Resultados de la dispersión
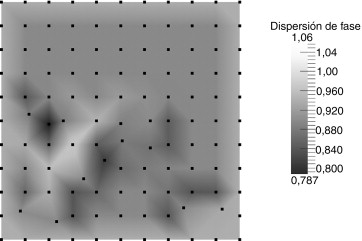
Los valores obtenidos de la dispersión en cada una de las estrellas de la malla irregular con IIC = 0, 8944 de las ondas P , para tres valores distintos de del ángulo φ = 0, 45, 90, se han representado sobre los nodos en la figura 6 . Puesto que los valores en los tres casos únicamente difieren a partir de la tercera cifra decimal la figura 6 solo muestra el resultado para el caso φ = 45
|
|
|
Figura 6. Dispersión de las ondas P (IIC = 0, 89). |
6. Conclusiones
En este artículo se muestran las expresiones explíctas, en diferencias finitas generalizadas, para la propogación de ondas sísmicas en 2-D. Se estudia la estabilidad, obteniéndose un criterio en función de la razón de velocidades y los coeficientes de las fórmulas explícitas.
Se analiza la dispersión y se relaciona con la irregularidad de la estrella utilizando el índice de irregularidad de la malla. La utilización de mallas irregulares, según la geometría del problema, puede suponer dispersiones elevadas en algunas estrellas, lo cual va asociado con valores peque os del IIC y un menor paso de tiempo. En este caso se puede aumentar el IIC , y por tanto, el paso del tiempo y disminuir las dispersiones, realizando una redefinición de la malla, para lo que se puede utilizar un proceso adaptativo como el presentado por los autores en [35] .
Por último es fácil ver como el error aumenta al disminuir el número de puntos de la discretización por longitud de onda, apreciándose que hasta el orden de diez puntos por longitud de onda se obtienen errores generalmente admisibles inferiores al 10%.
Agradecimientos
Los autores agradecen la ayuda recibida del Ministerio de Ciencia e Innovación de Espa a en el proyecto TISMANCA, Ref.: CGL2008-01757/CLI.
References
- [1] Z. Alterman, F.C. Karal; Propagation of elastic waves in layered media by finite-difference methods, Bulll; Seism. Society American, 58 (1968), pp. 367–398
- [2] L.R. Kelly, R.W. Ward, S. Freitel, R.M. Alford; Synthetic seismograms: a finite-difference approach; Geophysics, 41 (1976), pp. 2–27
- [3] R. Madariaga; Dynamics of an expanding circular fault, Bull; Seism. Soc. Am., 67 (1976), pp. 163–182
- [4] J. Virieux; SH-wave propagation in heterogeneus media: velocity-stress finite difference method; Geophysics, 49 (1984), pp. 1933–1957
- [5] J. Virieux; P-SV wave propagation in heterogeneus media: velocity-stress finite difference method; Geophysics, 51 (1986), pp. 889–901
- [6] A.R. Levander; Fourth-order finite-difference P-SV seismograms; Geophysics, 53 (1988), pp. 1425–1436
- [7] R.W. Graves; Simulating seimisc wave propagation in 3-D elastic media using staggered-grid finite differences, Bull; Seism. Soc. Am., 93 (1996), pp. 283–300
- [8] R.W. Graves, S.M. Day; Stability and accuracy analysis of course-grain viscoelastic simulations, Bull; Seism. Soc. Am., 87 (2003), pp. 494–515
- [9] T. Ohnimato, B.A. Chovet; A free-surface boundary condition for including 3-D topography in finite difference method, Bull; Seism. Soc. Am., 87 (1997), pp. 494–515
- [10] J. Kristek, P. Moczo, P.J. Archuleta; Efficient method to simulate planar free surface in the 3-D 4th order staggered-grid finite difference schemes, Studia Geophys ; Geod., 46 (2002), pp. 355–381
- [11] J. Kristek, P. Moczo; Seismic wavw propagation in viscoelastic media with material discontinuities- a 3-D 4th order staggered grid finite-difference modeling, Bull ; Seism. Soc. Am., 93 (2003), pp. 2273–2280
- [12] E. Crase, Ch. Wideman, N. Noble, A. Tarantula; Non linear elastic waveform inversion of land seismic reflection data; J. Geophys. Rev., 97 (1992), pp. 4685–4703
- [13] P. Moczo, J. Kristek, L. Halada; 3-D 4th order staggered-grid finite-difference schemes: stability and grid dispersion, Bull ; Seism. Soc. Am., 90 (2000), pp. 587–603
- [14] P. Moczo, J. Kristek and L. Halada, The finite-difference method for siemologists. An introduction, Comenius University, Bratislava.
- [15] D.J. Andrews; A numerical study of tectonic stress relase by underground explosions, Bulll; Seism. Society American, 63 (1973), pp. 1375–1391
- [16] J. Zhang; Quadruple-grid velocity-stress finite-difference method for elastic wave-propagation simulation; Geophysics J. Int., 131 (1997), pp. 127–134
- [17] V.M. Cruz-Atienza, J. Virieux; Dynamic rupture simulation of non-planar faultnwith finite-difference aproach, Geophys; J. Int., 158 (2004), pp. 939–954
- [18] D.M. Boore; Love waves in non uniform waveguides: finite-difference calculations; J. Geophys. Rev, 75 (1970), pp. 1512–1527
- [19] T. Mikumo, Miyatake; B.A. Bott (Ed.), Numerical modeling of realistic fault rupture process. Seismic motion synthetics, Academic Press (1987), pp. 91–151
- [20] A. Pitarka; 3-D elastic finite-difference modeling of seismic motion using staggered grids with non uniform spacing, Bull; Seism. Soc. Am., 89 (1999), pp. 54–68
- [21] Y. Wang, J. Xu and G.T. Schuster, Viscoelastic wave simulation in basins by a variable-grid finite-difference method, Bull. Seism. Soc. Am. 91, 1641-1749 (2001Bull. Seism. Soc. Am. 90, 587-603 (2000).).
- [22] L. Lucy; A numerical approach to testing the fission hypotesis; App. Jour., 82 (1977), pp. 1013–1024
- [23] J.J. Monaghan; Why particle methods work?, SIAM Scientific; Journal of stat. Comp., 3 (1982), pp. 422–433
- [24] J.J. Monaghan; And introduction to SPH; Comput. Phys. Comun., 48 (1988), pp. 89–96
- [25] P. Lancaster y, K. Salkauskas; Surfaces generated by moving least square methods; Mathematics of computation, 37 (1981), pp. 141–158
- [26] B. Nayroles, G. Touzpt y, P. Villon; Generalizing the finite element method: Diffuse approximation and diffuse elements; Computational mechanics, Springer-Verlag, 30 (1992), pp. 7–318
- [27] T. Belytschko, Y.Y. Lu y, L. Gu; Element-free Galerkin methods; International journal for numerical methods in engineering, 37 (1994), pp. 229–256
- [28] C.A. Duarte y, J.T. Oden; A meshless method to solve boundary-value problems; TICAM report, 9 (1995), pp. 5–105
- [29] I. Babuska and J.M. Melenk, The partition of unity method, International journal for numerical methods in engineering, vol 40, 727-758. Jhon Wiley & Sons, 1995.
- [30] P.S. Jensen; Finite difference techniques for variable grids; Computers & Structures, 2 (1972), pp. 17–29
- [31] N. Perrone, R. Kao; A general finite difference method for arbitrary meshes; Computers & Structures, 5 (1975), pp. 45–58
- [32] T. Liszka y J. Orkisz, The finite difference method at arbitrary irregular grids and its application in applied mechanics, Computers & Structures 11, 83-95. Pergamon Press 1980.
- [33] J. Orkisz, Meshless finite difference method II. Adaptative approach, Computation Mechanics, CIMNE, 1998.
- [34] J.J. Benito, F. Ureñy, L. Gavete; Influence several factors in the generalized finite difference method; Applied Mathematical Modeling pp., 25 (2001), pp. 1039–1053
- [35] J.J. Benito, F. Ureñ, L. Gavete y, R. Alvarez; An h-adaptive method in the generalized finite difference; Comput. Methods Appl. Mech. Eng., 192 (2003), pp. 735–759
- [36] J.J. Benito, F. Ureñ, L. Gavete y, B. Alonso; Application of the Generalized Finite Difference Method to improve the approximated solution of pdes; Computer Modelling in Engineering & Sciences, 38 (2009), pp. 39–58
- [37] J.J. Benito, F. Ureñy, L. Gavete; Leading-Edge Applied Mathematical Modelling Research (chapter 7); Nova Science Publishers, New York (2008)
- [38] J.J. Benito, F. Ureñ, L. Gavete y, B. Alonso; Solving parabolic and hyperbolic equations by Generalized Finite Difference Method; Journal of Computational and Applied Mathematics, 209 (2) (2007), pp. 208–233
- [39] F. Ureñ, J.J. Benito, L. Gavete, R. Alvarez, Resolución de ecuaciones diferenciales en derivadas parciales dependientes del tiempo de segundo orden utilizando Diferencias Finitas Generalizadas. Revista Internacional de Métodos Numéricos para Cálculo y Diseñen Ingeniería. Vol. 19, 3, 331-340 (2003).
- [40] P. Moczo, J. Kristek, M. Galis, P. Pazak, M. Balazokjech; The finite difference and finite element modelling of seismic wave propagation and earthquake moltion; Acta physica slovaca, 57 (2) (2007), pp. 177–406
Document information
Published on 01/12/11
Accepted on 31/03/11
Submitted on 16/03/11
Volume 27, Issue 4, 2011
DOI: 10.1016/j.rimni.2011.08.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?