1 Introducción
Uno de los grandes desafíos en muchas ramas de la ciencia, es la obtención de simulaciones numéricas precisas, de mayor alcance, rápidas y de forma accesible. En particular, la complejidad de los problemas en dinámica de fluidos es tal, que las simulaciones numéricas requieren mucho tiempo de ejecución, cuyos resultados pueden durar varios días, incluso hasta meses. En la mayoría de estos problemas, la solución de la ecuación de Poisson representa el mayor costo computacional, inclusive más del 90% de la simulación total del problema [1,2,3,4]. Parte del problema, es que su discretización proporciona un sistema de ecuaciones lineales donde el número de variables puede alcanzar los miles de millones.
Existen diferentes métodos para la solución de la ecuación de Poisson en dos dimensiones (2D). Aunque cada método tiene sus propias fortalezas y limitaciones. Debido a sus características y al éxito que ha tenido al ser implementado en numerosos fenómenos físicos, el método de diferencias finitas [5,6,7] es el método numérico implementado en este trabajo.
La discretización de la ecuación de Poisson usando diferencias finitas proporciona un sistema de ecuaciones lineales donde el número de incógnitas es proporcional al número de puntos usados en el mallado. Tradicionalmente los sistemas lineales son resueltos usando métodos iterativos, los cuales aproximan la solución mediante un número de iteraciones hasta que cierta tolerancia se satisface. Métodos como el Gradiente Conjugado [8,9] y el Generalized Minimal Residual (GMRES) [10,11] pueden ser considerados. Sin embargo, estos últimos tienen una mayor dificultad en el momento de implementar y especialmente al tratar de obtener un programa más eficiente en paralelo. Por otro lado, métodos clásicos como Jacobi, Gauss-Seidel y Succesive-Over Relaxation (SOR) pueden ser usados con cierto grado de dificultad de implementación y convergencia razonable [12,13,14]. Como primera aproximación, este trabajo se concentrará en el método de Jacobi, el cual es el más sencillo de implementar pero es base para solución de otros algoritmos más complejos.
Varios algoritmos en paralelo han sido desarrollados para resolver grandes sistemas lineales en distintos campos de la ciencia, incluyendo diversas plataformas como los son MPI(Message Passing Interface), GPU Graphics Processing Unit), OpenMP(Open Multi-Processing), entre otros. Por ejemplo, se han utilizado para algoritmos involucrados con imágenes médicas [15], Finanzas Computacionales [16], Bioinformática [17] y Dinámica de Fluidos [18], por citar algunos.
Cada metodología en paralelo tiene sus diferentes grados de dificultad y eficiencia, sin embargo, algunas de las ventajas de usar MPI [20,19,21] es su grado de universalidad. El modelo de paso de mensajes se adapta bien a la mayoría de las actuales super-computadoras debido a su arquitectura de procesadores separados pero conectados por una red de comunicación. En cuanto a su desempeño y rendimiento, con el modelo de paso de mensajes uno puede asociar explícitamente un espacio de memoria a un proceso lo cual otorga un mejor uso de las caches y jerarquías de memoria, lo cual se ve reflejado directamente en el rendimiento. Aún más, en sistemas de memoria compartida se puede mejorar el rendimiento al tener más control sobre la localidad de los datos en la memoria.
El objetivo de este trabajo es diseñar e implementar un algoritmo en paralelo para obtener la solución de manera más rápida de sistemas de ecuaciones lineales obtenidas del método de diferencias finitas y el método de descomposición de dominios. Más aún en este trabajo se propone mejorar los algoritmos en paralelo usando diferentes técnicas de cómputo como el manejo de la forma de acceso a la memoria. Las siguientes secciones están organizadas como se explica a continuación. En la segunda sección se introduce la discretización de la ecuación de Poisson usando diferencias finitas. En la tercera sección se presenta el algoritmo en paralelo. La cuarta sección presenta los resultados numéricos. Finalmente, en la última sección se dan las conclusiones finales de este trabajo.
2 Discretización de la ecuación de Poisson en 2D usando diferencias finitas
En esta sección se describirá brevemente el método de diferencias finitas usado para discretizar la ecuación de Poisson en dos dimensiones. Además, una vez obtenido el sistema de ecuaciones lineales resultantes, se presentará el método iterativo para su correspondiente solución.
Considérese la siguiente ecuación de Poisson en dos dimensiones:
|
|
(1) |
sobre un dominio . Además, se considera condiciones de frontera de Dirichlet en la frontera , es decir, la solución es conocida de manera exacta en todas las fronteras del dominio.
2.1 El método de diferencias finitas
La forma discreta del dominio viene dada por una malla estructurada rectangular. Se considera los índices y , donde y son el número de puntos en la dirección y , respectivamente. Los tamaños de paso están definidos como y . Finalmente los puntos donde la solución es aproximada están dados por . Para mayor detalles véase la Figura 1.
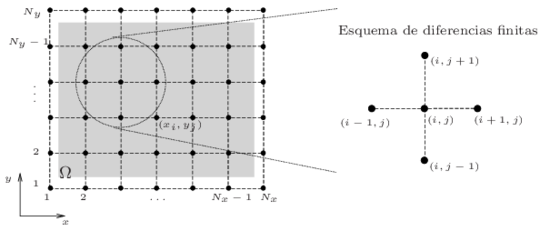
|
| Figura 1: Dominio y esquema de diferencias finitas empleados. La zona sombreada es donde los valores son aproximados. |
Como se tiene un dominio rectangular y una malla regular, la ecuación diferencial puede ser discretizada usando diferencias finitas centradas para la segunda derivada parcial. Ésta es obtenida usando desarrollos de series de Taylor. Así, las aproximaciones están dadas por
|
donde . Sustituyendo (2)-(3) en la ecuación (1), se obtiene
|
|
donde . Finalmente la discretización en diferencias finitas de la ecuación de Poisson (1) está dada por
|
|
(4) |
donde . Se puede observar que el esquema resultante relaciona un valor con sus cuatro vecinos más cercanos, como es ilustrado en la Figura 1.
2.2 El sistema lineal resultante
Todos los valores de la frontera son conocidos, es decir, ya no es necesario calcular , , y . Así, sólo se aproximan los valores donde y . Se establece un indexado natural para resolver el sistema. Este consiste en ordenar todas las variables en un vector, enumerando las variables por columna, así, el vector de incógnitas a resolver es
|
|
(5) |
donde cada elemento () es un vector columna dada por
|
|
Así, se tiene el sistema lineal
|
|
(6) |
donde
|
|
Notar que la matriz es una matriz tridiagonal a bloques, donde los bloques son a su vez unas matrices tridiagonales dadas por
|
|
y las matrices corresponden a la matriz identidad. Los valores del lado derecho están dados por los valores correspondientes mas los valores conocidos de la frontera.
2.3 Solución del sistema por el método de Jacobi
Es bien conocido que el método de Jacobi converge lentamente a la solución del problema. Sin embargo, este tiene la notoria característica que para calcular una nueva iteración sólo se requieren de todos los elementos en el paso anterior. Esta propiedad es raramente compartida por otros solucionadores de sistemas lineales. Por ejemplo, en los métodos de Gauss-Seidel y SOR, la actualización de un elemento depende de otros elementos ya calculados en la misma iteración. Eso implica que el método se realice de a uno por uno en un orden estricto, imposibilitando la paralelización por bloques de dicho método. Existen técnicas en las cuales se puede realizar la paralelización; sin embargo, en este trabajo únicamente se propone un algoritmo en paralelo para el método iterativo de Jacobi, dejando las otras técnicas para trabajos futuros.
Para obtener el método iterativo de Jacobi se considera la descomposición de la matriz en donde , y son las matrices diagonal, tridiagonal inferior y triangular superior de , respectivamente. Con esta descomposición podemos sustituir en (6) para obtener de la cual se obtiene la iteración para el método de Jacobi
|
|
(7) |
en donde y son las aproximaciones obtenidas mediante y iteraciones, respectivamente. Finalmente, el método iterativo de Jacobi resulta de iterar repetidamente
|
|
(8) |
hasta que el residuo del método sea menor o igual a una tolerancia dada. Notar que los índices se han cambiado por y para recalcar que estos no son los mismos de los índices , correspondientes a la malla, sino que estos representan la posición de los elementos en la matriz global. En otras palabras, un elemento para cierto indice y .
El método iterativo de Jacobi (8) puede ser fácilmente aplicable al problema, dado que cada fila de la matriz tiene a lo más 5 componentes, así fácilmente se puede ver que
|
|
(9) |
Notar que los índices en (9) han sido cambiados a su notación original para mayor facilidad de identificación del esquema.
Para poder calcular el criterio de paro del método iterativo es necesario obtener el residuo, éste viene definido por . En este artículo usaremos la norma . Finalmente, para el cálculo más eficiente del residuo y de la solución, el método iterativo (9) se modifica levemente como:
|
|
(10) |
3 Algoritmo en paralelo en entornos multicore
En esta sección se describe el método de descomposición de dominios para la programación en paralelo del sistema lineal resultante usando el método iterativo de Jacobi en un entorno multicore, incluyendo las técnicas de comunicación entre procesos.
Aunque existen diversos modelos de computación paralela, en este trabajo se emplea el paso de mensajes. Éste modelo se caracteriza principalmente en que cada proceso tiene su propia memoria local, pero son capaces de comunicarse entre sí enviando y recibiendo mensajes. MPI (Message Passing Interface) es una especificación de dicho modelo. Este no es un lenguaje de programación, MPI es una librería que especifíca los nombres y las llamadas de funciones o subrutinas. Dichos programas pueden ser compilados con los compiladores ordinarios de cada lenguaje y únicamente necesitan ser vinculados con la librería MPI [21].
3.1 Método de descomposición del dominio
La estrategia del algoritmo en paralelo planteada en este artículo requiere que el dominio sea dividido en varios sub-dominios. Cada sub-dominio será asignado a un proceso, y por medio del método iterativo de Jacobi cada proceso resolverá su propio sistema en su sub-dominio asignado. En la Figura 2 se ejemplifica la descomposición de un dominio estructurado en tres sub-dominios. Se puede observar que a cada sub-dominio se le han incorporado los elementos adicionales de los sub-dominios vecinos.
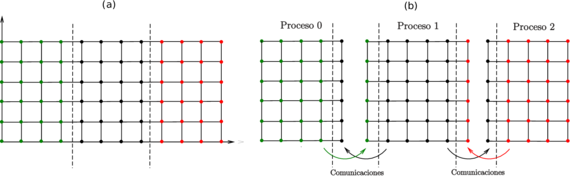
|
| Figura 2: División del dominio con un mallado rectangular en sub-dominios y sus comunicaciones. |
El esquema numérico de cinco puntos en cruz proporcionado por el método de Jacobi (10), ver Figura 1, combinado con el método de descomposición de dominio requiere que cada elemento del sub-dominio recopile información de sus elementos vecinos por cada iteración. Esto da como resultado que los elementos del borde (o de frontera artificial) de cada sub-dominio requieran información de elementos que pertenecen al sub-dominio vecino. Lo anterior representa la primera dificultad técnica del algoritmo en paralelo dado que los procesos no tienen acceso directo a la memoria de los demás procesos. Para solucionar este problema, en este artículo, los sub-dominios son creados de tal manera que estén sobrepuestos. Así los sub-dominios incluyen los elementos vecinos colindantes entre ellos.
Como hemos mencionado anteriormente, el método de Jacobi (10) sólo requiere de los elementos de la iteración anterior para actualizar todos los elementos del siguiente paso. Sin embargo, al inicio de la nueva iteración, los elementos adicionales en los bordes no han sido actualizados. Así, los procesos deben comunicarse enviando y recibiendo los resultados de sus elementos frontera después de cada iteración. De este modo, cada proceso tendrá la información actualizada que requiere para generar los nuevos resultados. En la siguiente sección profundizaremos un poco más en el tema de la comunicación entre procesadores.
3.2 Comunicación entre procesos
Una de las partes más importantes a considerar a la hora de realizar un algoritmo en paralelo en MPI es la comunicación entre los procesos, ya que en la mayoría de los casos, varios procesos estarán haciendo una misma operación u operaciones parecidas sobre una sección del problema global. Así, será necesario que los procesos comuniquen sus resultados a otros procesos antes de continuar o empezar de nuevo un ciclo de operaciones.
Un solo algoritmo debe ser programado para diferentes números de procesos. Así la comunicación debe hacerse de forma dinámica. Es decir, las órdenes de envío y recepción de mensajes se deben ajustar automáticamente al número de procesos. No es recomendable escribir un código para cada caso particular ya que las instrucciones condicionales para elegir el caso correspondiente también consumen un tiempo valioso de ejecución.
Para poder enviar simultáneamente múltiples mensajes y que se envíen al destinatario correcto sin tener que especificar para cada proceso un caso particular, basta con que se conozca desde un principio quiénes son los vecinos de cada sub-dominio. Por la forma en que se organizó la malla, esa información es conocida desde el inicio del programa. A cada sub-dominio se le asignó un proceso, dicho proceso identificado con el rank obtenido de la sub-rutina MPI_Comm_rank. Si pensamos que la división de dominios es únicamente unidimensional, entones a su vecino derecho le corresponde el identificador rank+1. De la misma manera, a su vecino izquierdo le corresponde rank-1. De tal modo que al usar como parámetro los identificadores correspondientes a sus vecinos, dicho parámetro se vuelve un parámetro “dinámico”. Para cada proceso que ejecute la sub-rutina de envío de mensaje, el parámetro tendrá un valor distinto que será correspondiente al proceso vecino de a quién se enviará.
A pesar de que la técnica anterior de programación simplifica mucho la programación del código, aún hay que considerar ciertos casos que pueden hacer que el programa no funcione correctamente. Para esto se implementan otros índices que ayudan a localizar en dónde se encuentra el proceso asignado a un sub-dominio con respecto al dominio global. Dado que el dominio es de forma rectangular, la malla aplicada es estructurada con rectángulos del mismo tamaño, la asignación de los procesos es de orden ascendente, primero a lo ancho y luego a lo largo. Mas aún, se conoce el número de sub-dominios a lo ancho (numx) y el número de sub-dominios a lo largo (numy). Así
- Se puede conocer en que columna de sub-dominios se encuentra el proceso (idx) al obtener el valor del identificador del proceso módulo 2 (idx = modulo(rank,numx)).
- Igualmente se puede obtener en qué fila de sub-dominios se encuentra el proceso (idy) al aproximar al entero inferior más cercano el resultado de dividir el valor de su identificador entre el número de sub-dominios a lo ancho (idy = rank/numx).
En Fortran 90 dado que los operadores están definidos como INTEGER, automáticamente el valor toma sólo la parte entera, lo que resulta equivalente a obtener el entero inferior más cercano. En el código de la Figura 3 se presenta la implementación de la comunicación a un programa con un dominio regular rectangular y mallado estructurado.
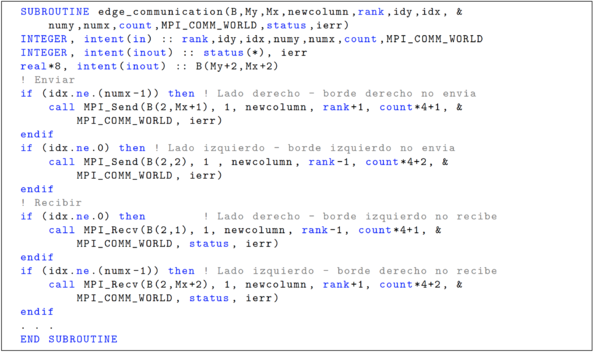
|
| Figura 3: Código correspondiente a la subrutina de comunicación entre sub-dominios. |
4 Simulaciones Numéricas
En esta sección se presentan las simulaciones numéricas usando el algoritmo propuesto en paralelo. Inicialmente se propone un ejemplo donde se analiza el desempeño de la subdivisión de dominios, la comunicación y el manejo de memoria. Posteriormente se analiza la solución de la ecuación de Poisson en 2D y su correspondiente desempeño en paralelo. Los resultados son reportados usando una máquina estándar de 20 cores 3.0 GHz Intel Xeon. Todos los códigos fueron implementados en el lenguaje Fortran 90.
4.1 Ejemplo 1: Pruebas de desempeño
Con el objetivo de medir el desempeño del algoritmo en paralelo propuesto, se desarrolló este ejemplo que consiste en aplicar un esquema en el que cada elemento es sustituido por el promedio de sí mismo y sus cuatro vecinos (superior, inferior, derecho e izquierdo). Dicho proceso es repetido 10 veces. La matriz global es de dimensiones . Con este número (equivalente a ) el dominio es divisible exactamente por todos los enteros del 1 al 20. La suma del número 2 es porque al dividir el dominio no se consideran los elementos del borde.
4.1.1 Prueba 1. División en sub-dominios
En esta prueba el dominio únicamente es dividido a lo ancho, es decir, que los sub-dominios están únicamente uno a lado del otro, sin tener sub-dominios vecinos superiores e inferiores. De esta manera, cada procesador únicamente tiene que comunicar sus bordes a sus vecinos derecho e izquierdo, evitando así el tener que crear comunicaciones entre vecinos superiores e inferiores.
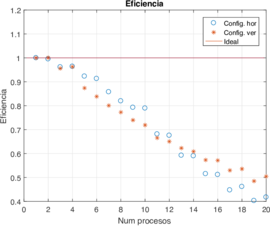
El tiempo de acceso a la memoria en Fortran depende mucho del orden de acceso de los índices de una matriz. Así, puede haber diferencias de tiempo si se accede a elementos contiguos horizontales y que a elementos contiguos verticales y . Dado lo anterior, se realizó una segunda prueba invirtiendo las dimensiones de la matriz y dividiendo el dominio a lo vertical en lugar de a lo horizontal. La Figura 4 muestra las medianas de los tiempos de cómputo y de la eficiencia usando ambas configuraciones.
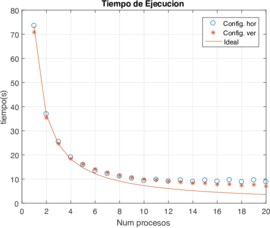
|
|
| Figura 4: Tiempo de ejecución (en segundos) y eficiencia comparando la configuración horizontal contra configuración vertical usando diferente número de procesos. | |
Se puede observar que la eficiencia tiende a alejarse del ideal mientras aumenta el número de procesos en paralelo. Los tiempos de ejecución de la configuración vertical fueron reducidos en comparación a los datos obtenidos en la horizontal. Sin embargo, la mejora en la eficiencia no es consistente para todos los números de procesos. Más aún, la caída de rendimiento en el algoritmo en ambos casos es más de lo que se espera. Aunque los resultados no son mostrados aquí, los tiempos de comunicación no varían se mantienen estables con el cambio del número de procesos. Por lo tanto, la comunicación de los bordes no está contribuyendo a reducir de manera significativa el rendimiento del algoritmo.
4.1.2 Prueba 2. Mejoras en el acceso a memoria
Como mencionamos anteriormente, el orden de acceder a la memoria por medio de los índices de las matrices en Fortran puede variar la velocidad de dicho acceso. Así en esta segunda prueba se presentan los resultados de cambiar el orden en cómo se ejecuta el esquema numérico, invirtiendo el orden de los índices de los ciclos do, como se muestra en el extracto de los códigos en las Figuras 5 y 6.

|
| Figura 5: Código de la configuración del stencil original. |

|
| Figura 6: Código de la configuración del stencil con acceso invertido. |
En el código 5, siguiendo el orden de los ciclos do de la configuración original, la matriz se recorre haciendo barridos horizontales a través del índice mientras avanza a lo vertical con el índice después de cada barrido horizontal. Dicha configuración fue cambiada de tal manera que se invirtiera el orden del acceso, como se ve en el código 6. En dicho código se recorre la matriz haciendo barridos verticales a través del índice mientras avanza a lo horizontal con el índice después de cada barrido vertical.
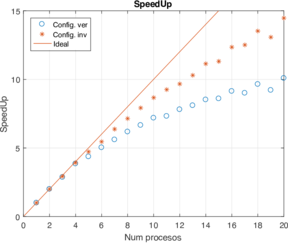
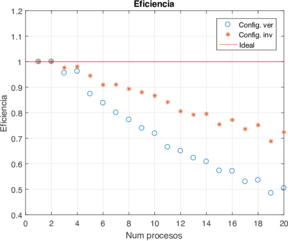
Los resultados con estos cambios se presentan en la Figura 7. Se puede observar que el cambiar el orden de acceso a la matriz al momento de aplicar el esquema numérico mejora significativamente el tiempo de ejecución y consecuentemente el speed-up y la eficiencia. También se puede observar que la configuración vertical obtiene mejores resultados consiguiendo hasta un 72% de eficiencia para 20 procesos en paralelo, comparado con el primer código que se usó en el que sólo se obtuvo un 41%, ver Figura 4.
|
|
| Figura 7: Speed-up y eficiencia de la configuración vertical usando diferente número de procesos y cambiando el orden de acceso a la memoria (versión invertida). | |
4.1.3 Prueba 3. Implementación de punteros
Aunque se logró mejorar, aún existe una caída significativa del rendimiento del algoritmo. Notar que en los Códigos 5 y 6, después de aplicar el esquema numérico a la matriz , es necesario actualizar dicha matriz. Una matriz almacena temporalmente los nuevos resultados y posteriormente es copiada a . Este proceso de actualización de la matriz local consume relativamente mucho tiempo, ya que los procesos de lectura y escritura son procesos computacionales que se consideran “costosos”, ya que son lentos si los comparamos con los procesos lógico-aritméticos.
Para solucionar el problema planteado, se consideró hacer uso de punteros como medio alternativo para actualizar las matrices locales luego de aplicar el esquema numérico. En Fortran, el uso de punteros no supone mucha complicación, ya que basta con editar y agregar unas cuantas líneas para hacer uso de ellos. Como se observa en el código de la Figura 8, una vez declarados los punteros y las matrices locales y , sólo es necesario apuntar con el puntero pB a la matriz local y con el puntero pC a la matriz .

|
| Figura 8: Código de la implementación de punteros para actualizar matriz local. |
En la sección del código en el que se aplica el esquema, es necesario remplazar el uso de las matrices locales y por sus respectivos punteros. De esta manera, la actualización de las matrices locales consistirá en hacer que los punteros pB y pC intercambien sus direcciones a las que apuntan. Para ello es necesario hacer que el puntero pB apunte a lo que apuntaba pC y que el puntero pC apunte a lo que apuntaba pB, para este proceso es necesario utilizar un puntero auxiliar, pSwap.
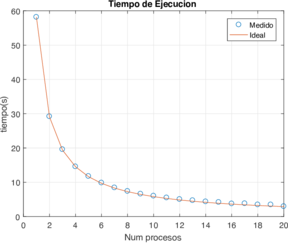
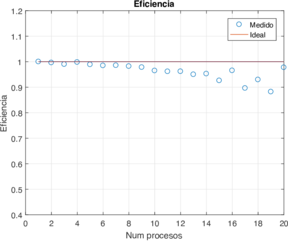
En la Tabla 1 se encuentran los mejores resultados obtenidos, los cuales se lograron con la configuración vertical y acceso a matriz con barridos horizontales. En la Figura 9 se observan los tiempos de ejecución y la eficiencia, en las que se aprecia el nivel de rendimiento obtenido de la configuración vertical con acceso a la matriz por barridos horizontales e implementando punteros. Notar que inclusive con 20 procesadores podemos obtener una eficiencia de $97%$.
| Procesos | Tiempo (s) | Speed-up | Eficiencia |
| 1 | 58.173 | 1.000 | 1.000 |
| 2 | 29.199 | 1.992 | 0.996 |
| 3 | 19.590 | 2.969 | 0.989 |
| 4 | 14.572 | 3.991 | 0.997 |
| 5 | 11.766 | 4.943 | 0.988 |
| 6 | 9.846 | 5.908 | 0.984 |
| 7 | 8.433 | 6.897 | 0.985 |
| 8 | 7.404 | 7.856 | 0.982 |
| 9 | 6.608 | 8.802 | 0.978 |
| 10 | 6.030 | 9.647 | 0.964 |
| 11 | 5.499 | 10.577 | 0.961 |
| 12 | 5.040 | 11.542 | 0.961 |
| 13 | 4.710 | 12.349 | 0.949 |
| 14 | 4.362 | 13.336 | 0.952 |
| 15 | 4.188 | 13.890 | 0.926 |
| 16 | 3.766 | 15.445 | 0.965 |
| 17 | 3.818 | 15.235 | 0.896 |
| 18 | 3.476 | 16.731 | 0.929 |
| 19 | 3.471 | 16.759 | 0.882 |
| 20 | 2.975 | 19.547 | 0.977 |
|
|
| Figura 9: Tiempo de ejecución (en segundos) y eficiencia usando la configuración horizontal e implementando punteros con diferente número de procesos. | |
4.2 Ejemplo 2: Solución de la ecuación de Poisson en paralelo
En este ejemplo se muestran los resultados obtenidos con el programa desarrollado para resolver sistemas lineales por el método de Jacobi provenientes de la ecuación de Poisson y el método de diferencias finitas aplicado a un dominio rectangular con mallado estructurado. Considérese la ecuación de Poisson en 2D dada por (1) donde la solución analítica y la función del lado derecho están dadas por
|
|
(11) |
respectivamente. Con estas funciones se aplican condiciones de frontera Dirichlet nulas sobre el dominio dado por .
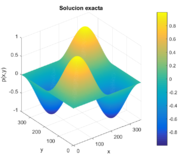
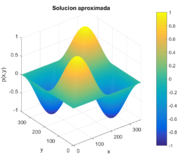
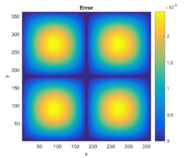
Para esta prueba se eligió un mallado de dimensiones . Dicho tamaño se escogió pensando en generar un tiempo considerable de ejecución y una malla que tenga una gran cantidad de divisores de manera que, sin contar sus fronteras, es exactamente divisible entre la cantidad de procesos que se ejecuten en paralelo. Por último se escogió una tolerancia de para determinar la condición de paro del método iterativo. En la Figura 10 se puede observar la solución exacta y numérica, así como los errores absolutos de este ejemplo. El algoritmo propuesto resuelve de manera correcta el problema y otorga una solución precisa a la solución exacta.
|
|
|
| Figura 10: Solución exacta, solución numérica y error absoluto de la ecuación de Poisson en 2D. | ||
A continuación se presentan los resultados obtenidos de los tiempos de ejecución logrados en las configuraciones con distintos número de procesos. Hay que recordar que la máxima eficiencia del programa se logra si la dimensión de la malla (sin fronteras) es divisible exacto entre el número de procesos en paralelo ejecutándose. El mallado de es divisible entre 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18 y 20. La Tabla 2 muestra la mediana de los tiempos de ejecución después de ejecutar varias veces el programa. Los resultados de speed-up y eficiencia también pueden ser observados en sus representaciones gráficas en la Figura 12.
| Procesos | Tiempo (s) | Speed-up | Eficiencia |
| 1 | 198.256 | 1.000 | 1.000 |
| 2 | 102.978 | 1.925 | 0.962 |
| 3 | 68.377 | 2.899 | 0.966 |
| 4 | 50.172 | 3.951 | 0.987 |
| 5 | 41.049 | 4.829 | 0.965 |
| 6 | 33.978 | 5.834 | 0.972 |
| 8 | 25.112 | 7.894 | 0.986 |
| 9 | 22.041 | 8.994 | 0.999 |
| 10 | 20.177 | 9.825 | 0.982 |
| 12 | 17.763 | 11.160 | 0.930 |
| 15 | 13.689 | 14.482 | 0.965 |
| 18 | 11.323 | 17.508 | 0.972 |
| 20 | 10.289 | 19.268 | 0.963 |
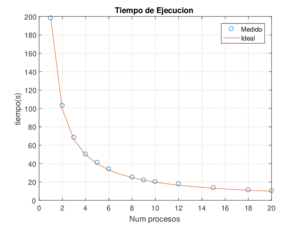
|
| Figura 11: Tiempos de ejecución usando diferente número de procesos. |
Como se puede observar, los resultados muestran altos niveles de eficiencia. Por ejemplo, la menor eficiencia del programa se obtiene usando 12 procesadores con un . Más aún, todas las configuraciones mantienen un nivel parecido de eficiencia, es decir, que no se logra apreciar una pérdida de rendimiento conforme más procesos se ejecuten. Lo anterior da como consecuencia que se logre hasta un speed-up de 19.2 con 20 procesos, muy cercano a lo ideal que sería 20. En tiempos de cómputo reales, una simulación en serie que duraba más de tres minutos, puede ser ahora obtenida en tan sólo 10 segundos con la misma precisión.
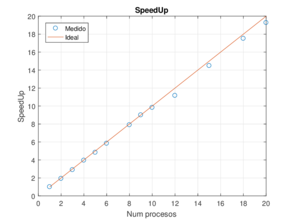
|
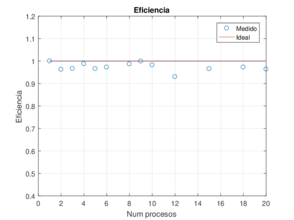
|
| Figura 12: Rendimiento de la aproximación de la ecuación de Poisson en 2D empleando una malla de . | |
5 Conclusiones
En este trabajo se presentó el método iterativo de Jacobi en paralelo para resolver el sistema de ecuaciones lineales resultante de discretizar la ecuación de Poisson en 2D usando el método de diferencias finitas. Aunque este método tiene la desventaja de una lenta convergencia en comparación con otros métodos iterativos más avanzados, el tiempo de ejecución se compensa con la fácil implementación del algoritmo en paralelo. Se plantearon varias alternativas para implementar el algoritmo incluyendo diferentes opciones de acceso a la memoria. La configuración con pivotes mostró los resultados con mayor rendimiento. Se tuvo una eficiencia por arriba del 90% y un speed-up de hasta 19.2 con 20 procesos en paralelo. En trabajos futuros se implementarán el mismo análisis para aproximaciones de la ecuación de Poisson en 2D usando volúmenes finitos y mallados triangulares no estructurados. También se implementará métodos iterativos con mayor velocidad de convergencia, lo cual ayudará a reducir aún más el tiempo de ejecución de las simulaciones numéricas.
Agradecimientos
Se agradece al Consejo Nacional de Ciencia y Tecnología (CONACYT) por el apoyo para la realización de este trabajo con el proyecto de Investigadoras e Investigadores por México.
BIBLIOGRAFÍA
[1] Notay, Y., & Napov, A. (2015). A massively parallel solver for discrete Poisson-like problems. Journal of computational physics, 281, 237-250. [2] Bolis, A., Cantwell, C. D., Moxey, D., Serson, D., & Sherwin, S. J. (2016). An adaptable parallel algorithm for the direct numerical simulation of incompressible turbulent flows using a Fourier spectral/hp element method and MPI virtual topologies. Computer physics communications, 206, 17-25. [3] Uh Zapata, M., Zhang, W., Van Bang, D. P., & Nguyen, K. D. (2019). A parallel second-order unstructured finite volume method for 3D free-surface flows using a coordinate. Computers & Fluids, 190, 15-29. [4] Zhang, W., Uh Zapata, M., Bai, X., Pham-Van-Bang, D., & Nguyen, K. D. (2020). Three-dimensional simulation of horseshoe vortex and local scour around a vertical cylinder using an unstructured finite-volume technique. International Journal of Sediment Research, 35(3), 295-306. [5] Nicholls, A., & Honig, B. (1991). A rapid finite difference algorithm, utilizing successive over?relaxation to solve the Poisson?Boltzmann equation. Journal of computational chemistry, 12(4), 435-445. [6] Gupta, M. M., & Kouatchou, J. (1998). Symbolic derivation of finite difference approximations for the three?dimensional Poisson equation. Numerical Methods for Partial Differential Equations: An International Journal, 14(5), 593-606. [7] Balls, G. T., & Colella, P. (2002). A finite difference domain decomposition method using local corrections for the solution of Poisson's equation. Journal of Computational Physics, 180(1), 25-53. [8] Basermann, A., Reichel, B., & Schelthoff, C. (1997). Preconditioned CG methods for sparse matrices on massively parallel machines. Parallel computing, 23(3), 381-398. [9] Gordon, D., & Gordon, R. (2010). CARP-CG: A robust and efficient parallel solver for linear systems, applied to strongly convection dominated PDEs. Parallel Computing, 36(9), 495-515. [10] De Sturler, E., & van der Vorst, H. A. (1995). Reducing the effect of global communication in GMRES (m) and CG on parallel distributed memory computers. Applied Numerical Mathematics, 18(4), 441-459. [11] Ghysels, P., Ashby, T. J., Meerbergen, K., & Vanroose, W. (2013). Hiding global communication latency in the GMRES algorithm on massively parallel machines. SIAM journal on scientific computing, 35(1), C48-C71. [12] Evans, D. J. (1984). Parallel SOR iterative methods. Parallel computing, 1(1), 3-18. [13] Tang, T., Liu, W., & McDonough, J. M. (2013). Parallelization of linear iterative methods for solving the 3-D pressure Poisson equation using various programming languages. Procedia Engineering, 61, 136-143. [14] Uh Zapata, M., Van Bang, D. P., & Nguyen, K. D. (2018). Parallel simulations for a 2D x/z two-phase flow fluid-solid particle model. Computers & Fluids, 173, 103-110. [15] Smelyanskiy, M., et al. (2009). Mapping high-fidelity volume rendering for medical imaging to CPU, GPU and many-core architectures. IEEE transactions on visualization and computer graphics, 15(6), 1563-1570. [16] Abbas?Turki, L. A., Vialle, S., Lapeyre, B., & Mercier, P. (2014). Pricing derivatives on graphics processing units using Monte Carlo simulation. Concurrency and Computation: Practice and Experience, 26(9), 1679-1697. [17] Liu, Y., Schmidt, B., & Maskell, D. L. (2011). DecGPU: distributed error correction on massively parallel graphics processing units using CUDA and MPI. BMC bioinformatics, 12(1), 1-13. [18] Lehmkuhl, O., Perez-Segarra, C. D., Borrell, R., Soria, M., & Oliva, A. (2009). TERMOFLUIDS: A new Parallel unstructured CFD code for the simulation of turbulent industrial problems on low cost PC Cluster. In Parallel computational fluid dynamics 2007 (275-282). Springer, Berlin, Heidelberg. [19] Becker, D. J., Sterling, T., Savarese, D., Dorband, J. E., Ranawak, U. A., & Packer, C. V. (1995, August). BEOWULF: A parallel workstation for scientific computation. In Proceedings, International Conference on Parallel Processing (Vol. 95, pp. 11-14). [20] Schikuta, E. (1994). Message-passing-interface-forum: Mpi: A message-passing interface standard. Techn. Ber., University of Tennessee, Knoxville, Tennesee, 30.[21] Gropp, W., Gropp, W. D., Lusk, E., Skjellum, A., & Lusk, A. D. F. E. E. (1999). Using MPI: portable parallel programming with the message-passing interface (Vol. 1). MIT press.
Document information
Published on 14/12/21
Submitted on 13/11/21
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?