Failure load prediction of single lap adhesive joints using artificial neural networks

Abstract

The objective of this paper was to predict the failure load in single lap adhesive joints subjected to tensile loading by using artificial neural networks. Experimental data obtained from the literature cover the single lap adhesive joints with various geometric models under the tensile loading. The data are arranged in a format such that two input parameters cover the length and width of bond area in single lap adhesive joints and the corresponding output is the ultimate failure load. An artificial neural network model was developed to estimate relationship between failure loads by using geometric dimensions of bond area as input data. A three-layer feedforward artificial neural network that utilized Levenberg–Marquardt learning algorithm model was used in order to train network. It was observed that artificial neural network model can estimate failure load of single lap adhesive joints with acceptable error. Mean absolute percentage error and Nash–Sutcliffe coefficient of efficiency values of both training and testing data were 3.523 and 3.524 and 0.997 and 0.992, respectively. The results showed that the artificial neural network is an efficient alternative method to predict the failure load of single lap adhesive joints. Also estimated results are in very good agreement with the experimental data.

Keywords

Adhesive joints; Artificial neural networks; Failure load; Single lap joints

1. Introduction

As an alternative method to welding, riveting and other conventional fasteners, applications of adhesive joints have been increased in structures and industries such as aircraft and automobile [1]. In an assembly of composite structures, usage of mechanical fasteners causes high stress concentration that results in structurally inefficient joints. On the other hand, adhesive joints are capable of redistributing the loads so that stress concentrations can be lowered [2]. Adhesive joints provide good strength–weight and cost-effectiveness ratios. These requirements cannot be met by mechanical joints [3].

Recently, interest in using artificial neural networks (ANNs) for forecasting has led to huge increase in research areas [4]. Experimental studies are typically time consuming and costly processes and sometimes even complex to perform. To be able to overcome these problems, various modeling techniques are used. ANNs are one of the most popular techniques which get inspired from biological neural networks. The basic units of ANNs are the neurons which are connected to each other with weights. They can be trained to perform a particular function by adjusting the values of these weights [5]. As an effective prediction tool, ANN was frequently used by researchers.

Bardak et al. [6] used ANN to estimate bonding strength of wood joints pressed under different conditions. Their study showed that model predicted bonding strength with acceptable accuracy. Tiryaki and Hamzaçebi [7] predicted modulus of rupture (MOR) and modulus of elasticity (MOE) of heat treated woods by using ANN. They compared the actual values of MOR and MOE with the outputs of ANN model and concluded that ANN is successful in estimation of them. Ayatollahi and Akhavan-Safar [8] proposed a new failure criterion in order to predict the static strength of single lap adhesive joints under tensile loading. Their predictions based on the proposed criterion have good agreements with the experimental data. Tiryaki and Aydın [9] modeled an ANN structure to estimate compression strength parallel to grain of heat treated woods. With this model, there will be no need to comprehensive experiments. They suggested that, with the usage of ANN, satisfactory results can be obtained which reduces the testing time and cost.

Zgoul [10] used ANN modeling for the rate dependent response of adhesive materials with the purpose of expanding the established method for modeling the response of adhesively bonded structures, and in particular single lap joints. Tiryaki et al. [11] investigated the bonding strength of beech wood based on the amount of adhesive, pressing pressure, and pressing time. They used ANN modeling approach and concluded that this approach was useful tool in characterizing the effects of amount of adhesive, pressing pressure, and pressing time on the bonding strength of wood. Sekercioglu and Kovan [12] developed a prediction method to estimate a static shear force and fatigue life by using ANN. The results showed that developed model was convenient and powerful tool for static shear force and fatigue life prediction of adhesively bonded cylindrical joints. Apalak and Ekici [13] studied the three-dimensional stress state of an adhesively bonded double containment cantilever joint in tension. Furthermore, the effects of the joint dimensions and the compositional gradient exponent were determined by using an ANN model, and the design rules were presented for an optimal joint design. Balcıoğlu et al. [14] investigated the effects of bonding angle, patching type (single side and double side) and patching structure on the failure load in the adhesively bonded pultruded composites by using ANN. Domińczuka and Kuczmaszewski [15] investigated the suitability of artificial intelligence for processing of experimental information related to strength of adhesive joints. They compared the efficiency of ANN with the efficiency of typical methods of statistical analysis such as linear and polynomial regression. Tiryaki et al. [16] investigated multiple linear regression and ANN model to predict optimum bonding strength of heat treated woods. An ANN based explicit formulation for predicting the edge breakout shear capacity of single adhesive anchors post-installed into concrete member was proposed by Güneyisi et al. [17]. Gunes et al. [18] conducted the 3-D free vibration analysis of an adhesively bonded functionally graded tubular single lap joint by using the finite element (FE) analysis. The optimal design parameters of the adhesive joint were searched using both the ANNs and the genetic algorithms (GAs). Akpinar et al. [19] investigated the application of protrusion in single lap joints subjected to tension and bending loads using FE method experimental. They observed that the protrusion reduces the strength in the joint under tension, while the protrusion increases the strength in the joint under bending. Alia et al. [20] investigated the mechanical behavior of adhesive joints when subjected to long-term tests, adverse environmental conditions (i.e., immersion in seawater and different temperature) and stress in different mixed modes between peel and shear experimentally.

In this study, the failure load in single lap adhesive joints subjected to tensile loading was estimated by using ANN technique. The results showed that ANN model has reliable prediction capability and ANN results are in a very good agreement with the experimental data.

2. Materials and method

2.1. Experimental detail

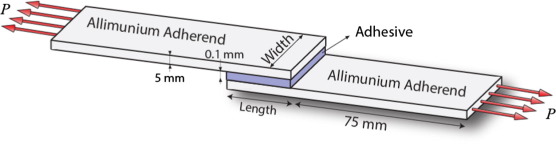
The experimental data values in Table 1, width (W) and length of bond area (L) in single lap adhesive joints and failure load under tensile loading are the values used for the training of the ANN. These values were taken from an experimental work of Gültekin et al. [21]. In the experimental study, as adhesive was chosen a two-part epoxy DP460 produced by 3M (St. Paul, MN, USA). AA2024-T3 aluminum alloy was used as adherend. Thickness of adherend and bond is 5 and 0.1 mm, respectively. The geometry of the model is shown in Fig. 1.

Table 1. Average maximum failure loads and displacement values.

Data no	W	L	Failure load	Data no	W	L	Failure load
1	25	25	9094	21	25	15	5177
2	20	25	5381	22	20	15	4692
3	15	25	4311	23	15	15	3565
4	10	25	3980	24	10	15	2160
5	5	25	1827	25	5	15	1015
6	25	25	9094	26	15	25	4311
7	25	20	6390	27	15	20	4048
8	25	15	5177	28	15	15	3565
9	25	10	5039	29	15	10	2695
10	25	5	2507	30	15	5	1679
11	25	20	6390	31	25	10	5039
12	20	20	5006	32	20	10	3709
13	15	20	4048	33	15	10	2695
14	10	20	2903	34	10	10	1601
15	5	20	1371	35	5	10	596
16	20	25	5381	36	10	25	3980
17	20	20	5006	37	10	20	2903
18	20	15	4692	38	10	15	2160
19	20	10	3709	39	10	10	1601
20	20	5	2055	40	10	5	1102

Figure 1. Dimensions of a single lap joint.

The experiments of specimen were performed using Shimadzu AG-IS 100 (Shimadzu Corporation, Tokyo, Japan) (100 kN) machine at room temperature and relative humidity 30. During tensile tests, the crosshead speeds were maintained at 1 mm/min [21].

2.2. Artificial neural network

Inspiration of artificial neural network comes from biological neural networks. Basic unit of a biological network is called as neuron and it has four basic components: dendrites, soma, axon, and synapses which receive input signals from the outside and combines them to perform generally nonlinear operation on the result [22]. A typical biological neuron was shown in Fig. 2.

Figure 2. A typical biological neuron.

ANN that consists of interconnected processing unit can be considered as highly simplified model of the structure of biological neural network [23]. ANN is very powerful tool for solving complicated engineering problems [24]. Instead of complex rules and mathematical formulations, ANNs are capable of learning key information patterns within a multi-information domain [25]. A simple ANN consists of three layers: input, hidden and output layer. Connection between layers is achieved by weights and they indicate the strength of the connection [26].

Haykin stated mathematically that, we can describe a neuron k by the following equations [27]:

$u_{k}=\sum _{j=1}^{m}w_{kj}x_{j}$

(1)

$y_{k}=\varphi (u_{k}+b_{k})$

(2)

Bias, denoted by b_k, has the effect of increasing or lowering the net input of the activation function. x₁, x₂, … , x_m are the inputs; w_k1, w_k2, … , w_km are the weights of the neuron k; u_k   is the linear combiner output due to input signals; ${\textstyle \varphi (.)}$ is the activation function; y_k is the output signal of the neuron.

A typical block diagram of model of a neuron is shown in Fig. 3.

Figure 3. Block diagram of model of a neuron [27].

3. Results and discussions

3.1. ANN results

In this study, input layer with two neuron, hidden layer with five neurons and output layer with one neuron ANN architecture were used (2-5-1). Data were divided into two parts: training and testing. 88% of data were used to train the network and remaining 12% was used to test the performance of network. Test data were written with bold fonts in Table 1.

Weight and bias values between input and hidden layer was shown in Table 2.

Table 2. Weight and bias values between input and hidden layer for failure load prediction.

i	W1i	W2i	i	bi
1	54.98314	−2.41357	1	−41.7572
2	−6.94778	−2.37484	2	14.60742
3	−2.04793	−5.50244	3	3.344352
4	−95.247	46.92676	4	−36.351
5	2.070685	5.488765	5	−3.34514

A three-layer feedforward ANN model was constructed and a backpropagation algorithm was used in order to train network. Levenberg–Marquardt (LM) algorithm was selected as learning algorithm in the present study. Several combinations of transfer functions for hidden and output layer were tried and it was concluded that logistic sigmoid transfer function (logsig) and linear transfer function (purelin) gave best results in the hidden layer and output layer of the network as an activation function, respectively. Since there is no certain rule to decide number of hidden layer neurons, various combinations were tried. After trial and error procedure, best results with minimum errors were obtained with 2-5-1 neuron structure for input, hidden and output layer, respectively.

Since normalizing of the training inputs generally improves the quality of the training [26], numerical values were normalized by the following formula:

$x_{i}={\frac {x-x_{min}}{x_{max}-x_{min}}}$

(3)

where ${\textstyle x}$, ${\textstyle x_{i}}$, ${\textstyle x_{min}}$ and ${\textstyle x_{max}}$ are original, normalized, minimum and maximum values, respectively.

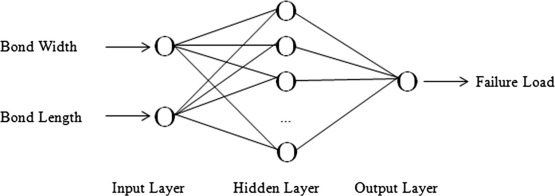
Illustration of ANN can be seen in the following Fig. 4.

Figure 4. Simple model of ANN.

Bond width (W) and bond length (L) were used as input neuron to predict failure load in the network. Prediction equation of failure load was given below:

${\mbox{Failure load}}=-0.2202{_{\ast }}F_{1}-152.3947{_{\ast }}F_{2}+$$76.2188{_{\ast }}F_{3}-0.1559{_{\ast }}F_{4}+76.66{_{\ast }}F_{5}+$$76.184$

(4)

Sigmoid function was used to calculate each F values.

$F_{i}={\frac {1}{1+e^{-E_{i}}}}$

(5)

$E_{i}=W_{1i}{_{\ast }}W+W_{2i}{_{\ast }}L+b_{1i}$

(6)

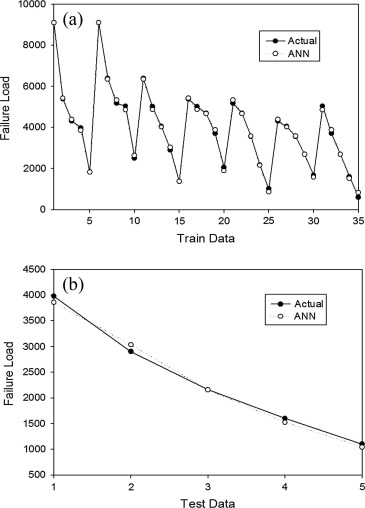
Fig. 5 shows results obtained for training (a) and testing (b) period from the ANN model. As seen from the figures, predicted values were compared with experimental values and they are in good agreement and correlation.

Figure 5. (a) Training and (b) testing period of ANN.

3.2. Performance of ANN

Various performance parameters can be used to evaluate the convergency of experimental values to predict values. Mean absolute error (MAE), mean absolute percentage error (MAPE), root mean-square error (RMSE) and correlation coefficient (R) were used to study the convergence between the target values and the output values [28].

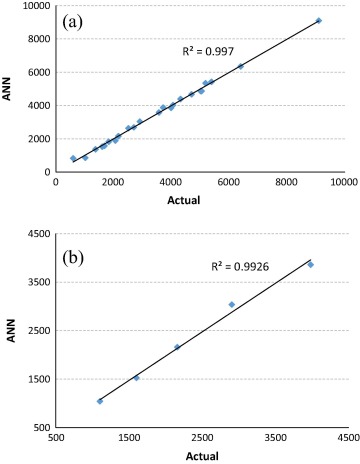
In this study, MAPE, Nash–Sutcliffe coefficient of efficiency (NS) and R² were used as performance parameters. R² values can clearly be seen from Fig. 6.

${\mbox{MAPE}}={\frac {1}{n}}\sum _{i=1}^{n}{\frac {\vert o_{i}-t_{i}\vert }{t_{i}}}\cdot 100$

(7)

${\mbox{NS}}=1-{\frac {\sum {\left(t_{i}-o_{i}\right)}^{2}}{\sum {\left(t_{i}-{\overline {t_{i}}}\right)}^{2}}}$

(8)

where ${\textstyle t}$ is target value, ${\textstyle {\overline {t_{i}}}}$ is mean of target, ${\textstyle o}$ is output value and ${\textstyle n}$ is total number of data.

Figure 6. Correlation between actual (experimental) and ANN results for (a) training and (b) testing period.

NS can get negative or positive values with a maximum absolute value of 1. A positive value indicates that the predicted values describe the trend of the measured data better than the mean of the actual values, whereas a negative value indicates that the corresponding model output is dissimilar to the behavior of the studied system [29].

MAPE values (%) and NS values of both training and testing data are 3.523 and 3.524 and 0.997 and 0.992, respectively. As seen from the results that, ANN showed good prediction performance for both training and testing periods.

4. Conclusion

In the present study, an ANN model was developed in order to predict failure load of single lap adhesive joints. In training period, LM learning algorithm was used. The best results were obtained in the ANN structure of 2-5-1. In model, R² values were 0.997 and 0.9926 for training and testing periods, respectively. On the other hand, MAPE (%) values of both training and testing data were 3.523 and 3. 524, respectively. NS values were 0.997 for training period and 0.992 for testing period. Estimated results were within acceptable error limits. All these show that the learning ability of ANN for estimation is very good and using of this method can strongly be suggested to eliminate complicated and time consuming experimental laboratory works.

References

1. [1] M.R. Ayatollahi, A. Akhavan-Safar; Failure load prediction of single lap adhesive joints based on a new linear elastic criterion; Theor. Appl. Fract. Mech., 80 (2015), pp. 210–217 http://dx.doi.org/10.1016/j.tafmec.2015.07.013
2. [2] C. Sarrado, A. Turon, J. Costa, J. Renart; On the validity of linear elastic fracture mechanics methods to measure the fracture toughness of adhesive joints; Int. J. Solids Struct., 81 (2016), pp. 110–116 http://dx.doi.org/10.1016/j.ijsolstr.2015.11.016
3. [3] A. Çalik, S. Yildirim; An investigation on the effect of parallel slot in bi-adhesive single lap joints with spew fillet; J. Eng. Res., 3 (4) (2015), pp. 95–110
4. [4] G. Zhang, B.Y. Eddy Patuwo, M. Hu; Forecasting with artificial neural networks; Int. J. Forecast., 14 (1) (1998), pp. 35–62 http://dx.doi.org/10.1016/s0169-2070(97)00044-7
5. [5] M. Amirjan, H. Khorsand, M.H. Siadati, R. Eslami Farsani; Artificial neural network prediction of Cu–Al₂O₃ composite properties prepared by powder metallurgy method; J. Mater. Res. Technol., 2 (4) (2013), pp. 351–355 http://dx.doi.org/10.1016/j.jmrt.2013.08.001
6. [6] S. Bardak, S. Tiryaki, G. Nemli, A. Aydın; Investigation and neural network prediction of wood bonding quality based on pressing conditions; Int. J. Adhes. Adhes., 68 (2016), pp. 115–123 http://dx.doi.org/10.1016/j.ijadhadh.2016.02.010
7. [7] S. Tiryaki, C. Hamzaçebi; Predicting modulus of rupture (MOR) and modulus of elasticity (MOE) of heat treated woods by artificial neural networks; Measurement, 49 (2014), pp. 266–274 http://dx.doi.org/10.1016/j.measurement.2013.12.004
8. [8] M.R. Ayatollahi, A. Akhavan-Safar; Failure load prediction of single lap adhesive joints based on a new linear elastic criterion; Theoret. Appl. Fract. Mech., 80 (2015), pp. 210–217 http://dx.doi.org/10.1016/j.tafmec.2015.07.013
9. [9] S. Tiryaki, A. Aydın; An artificial neural network model for predicting compression strength of heat treated woods and comparison with a multiple linear regression model; Constr. Build. Mater., 62 (2014), pp. 102–108 http://dx.doi.org/10.1016/j.conbuildmat.2014.03.041
10. [10] M.H. Zgoul; Use of artificial neural networks for modelling rate dependent behaviour of adhesive materials; Int. J. Adhes. Adhes., 36 (2012), pp. 1–7 http://dx.doi.org/10.1016/j.ijadhadh.2012.03.003
11. [11] S. Tiryaki, S. Bardak, T. Bardak; Experimental investigation and prediction of bonding strength of oriental beech (Fagus orientalis Lipsky) bonded with polyvinyl acetate adhesive; J. Adhes. Sci. Technol., 29 (23) (2015), pp. 2521–2536 http://dx.doi.org/10.1080/01694243.2015.1072989
12. [12] T. Sekercioglu, V. Kovan; Prediction of static shear force and fatigue life of adhesive joints by artificial neural network; Metallic Mater., 46 (1) (2008), p. 51
13. [13] Z. Gul Apalak, R. Ekici; Elastic stresses in an adhesively bonded functionally graded double containment cantilever joint in tension; J. Reinf. Plast. Compos., 26 (13) (2007), pp. 1291–1318 http://dx.doi.org/10.1177/0731684407079370
14. [14] H.E. Balcıoğlu, A.C. Seckin, M. Aktas; Failure load prediction of adhesively bonded pultruded composites using artificial neural network; J. Compos. Mater. (2015) http://dx.doi.org/10.1177/0021998315617998
15. [15] J. Domińczuk, J. Kuczmaszewski; Modelling of adhesive joints and predicting their strength with the use of neural networks; Comput. Mater. Sci., 43 (1) (2008), pp. 165–170 http://dx.doi.org/10.1016/j.commatsci.2007.07.052
16. [16] S. Tiryaki, Ş. Özşahin, İ. Yıldırım; Comparison of artificial neural network and multiple linear regression models to predict optimum bonding strength of heat treated woods; Int. J. Adhes. Adhes., 55 (2014), pp. 29–36 http://dx.doi.org/10.1016/j.ijadhadh.2014.07.005
17. [17] E.M. Güneyisi, M. Gesoğlu, E. Güneyisi, K. Mermerdaş; Assessment of shear capacity of adhesive anchors for structures using neural network based model; Mater. Struct., 49 (3) (2015), pp. 1065–1077 http://dx.doi.org/10.1617/s11527-015-0558-x
18. [18] R. Gunes, M.K. Apalak, M. Yildirim; Free vibration analysis of an adhesively bonded functionally graded tubular single lap joint; J. Adhes., 87 (9) (2011), pp. 902–925 http://dx.doi.org/10.1080/00218464.2011.600672
19. [19] S. Akpinar, Ş. Temiz, M.D. Aydin, A. Özel; Effect of protrusion at the ends of bondline in single lap joints under tension and bending; J. Adhes. Sci. Technol., 26 (23) (2012), pp. 2591–2602 http://dx.doi.org/10.1080/01694243.2012.691002
20. [20] C. Alia, J.M. Arenas, J.C. Suárez, P. Pinilla; Mechanical behavior of polyurethane adhesive joints used in laminated materials for marine structures; Ocean Eng., 113 (2016), pp. 64–74 http://dx.doi.org/10.1016/j.oceaneng.2015.12.044
21. [21] K. Gültekin, S. Akpinar, A. Özel; The effect of the adherend width on the strength of adhesively bonded single-lap joint: experimental and numerical analysis; Compos. B Eng., 60 (2014), pp. 736–745 http://dx.doi.org/10.1016/j.compositesb.2014.01.022
22. [22] L. Amayreh, M. Saka; Failure load prediction of castellated beams using artificial neural networks; ASIAN J. Civ. Eng. (Build. Hous.), 6 (1–2) (2005), pp. 35–54
23. [23] B. Yegnanarayana; Artificial Neural Networks; PHI Learning Pvt. Ltd., New Delhi (2005)
24. [24] S.J.S. Hakim, H. Abdul Razak, S.A. Ravanfar; Fault diagnosis on beam-like structures from modal parameters using artificial neural networks; Measurement, 76 (2015), pp. 45–61 http://dx.doi.org/10.1016/j.measurement.2015.08.021
25. [25] İ. Uçkan, T. Yılmaz, E. Hürdoğan, O. Büyükalaca; Development of an artificial neural network model for the prediction of the performance of a silica-gel desiccant wheel; Int. J. Green Energy, 12 (11) (2014), pp. 1159–1168 http://dx.doi.org/10.1080/15435075.2014.895733
26. [26] G. Krauss, J.I. Kindangen, P. Depecker; Using artificial neural networks to predict interior velocity coefficients; Build. Environ., 32 (4) (1997), pp. 295–303 http://dx.doi.org/10.1016/s0360-1323(96)00059-5
27. [27] S.S. Haykin; Neural Networks: A Comprehensive Foundation; Prentice Hall (1999)
28. [28] M. Bilgili, B. Sahin; Comparative analysis of regression and artificial neural network models for wind speed prediction; Meteorol. Atmos. Phys., 109 (1–2) (2010), pp. 61–72 http://dx.doi.org/10.1007/s00703-010-0093-9
29. [29] M. Zounemat-Kermani; Hydrometeorological parameters in prediction of soil temperature by means of artificial neural network: case study in Wyoming; J. Hydrol. Eng., 18 (6) (2013), pp. 707–718 http://dx.doi.org/10.1061/(asce)he.1943-5584.0000666