Changes in wave propagation in a guitar top plate due to the fan bracing and the bridge

Resumen

Se exploró la propagación de ondas en una tapa de guitarra mediante análisis transitorios, es decir, a través de su evolución en el tiempo. La finalidad de usar el dominio del tiempo, en vez del dominio de la frecuencia como se suele reportar típicamente, fue lograr un análisis más visual de la influencia del abanico y el puente. Para ello, se midieron las propiedades elásticas de una tapa real mediante experimentos simples, para usarlas en un modelo con elementos finitos. El modelo mostró buena concordancia con comportamientos experimentales reportados en la literatura. En la misma tapa, se simuló la propagación de dos tipos de onda; se hizo un análisis usando una onda con contenido espectral bajo, y otro aplicando una onda con contenido espectral alto. Los resultados mostraron, a simple vista, que la velocidad de propagación sobre la tapa cambió notablemente debido a las estructuras adheridas. El cambio fue particularmente notorio para perturbaciones de longitud de onda corta, es decir, para frecuencias altas. En consecuencia, está claro que el diseño del abanico y del puente de una guitarra es crucial, principalmente, en los sonidos más agudos emitidos por el instrumento.

Abstract

Wave propagation on a guitar top plate was explored using transient analysis. The goal of using time domain, instead of frequency domain as it is commonly reported, was to achieve a more simple approach about the influence of the fan bracing and the bridge. For this purpose, the elastic properties of a real top plate were measured through simple experiments, in order to build the respective finite element model. The model exhibited good agreement with experimental behaviors of the literature. In the same top plate, the propagation of two kinds of waves was simulated; one analysis was done using one wave of high harmonic content, and another applying a wave with low harmonic content. Results showed, to naked eye, that the velocity of propagation over the top plate clearly changed due to their interactions with the attached structures. Such change was particularly noticeable for waves of short wavelength, in other words, for high frequencies. Then, it is evident that for guitars, designs of fan bracing and bridge are crucial, mainly, in treble sounds radiated by the instruments.

Palabras clave

Guitarra ; Transitorio ; DispersiÓn ; Abanico ; Deflexiones

Keywords

Guitar ; Transient ; Dispersive ; Bracing ; Deflections

1. Introducción

Las investigaciones sobre acústica de la guitarra se suelen reportar usando el dominio de la frecuencia [1] , [2] , [3] , [4]  and [5] . Esto se debe a que suele ser conveniente analizar el comportamiento dinámico de una estructura encontrando patrones vibratorios primarios, llamados modos de vibración, que ocurren a frecuencias determinadas. Los modos de vibración se obtienen mediante una técnica conocida como análisis modal, la cual arroja resultados en el dominio de la frecuencia.

Ciertamente, cualquier vibración de una estructura puede obtenerse como una combinación de sus modos de vibración; sin embargo, combinarlos requiere un soporte teórico considerable. En consecuencia, en algunas ocasiones puede ser más conveniente analizar la vibración de la estructura en el dominio del tiempo, mientras esta es forzada con señales arbitrarias. Este tipo de análisis se conoce como transitorio y podría resultar muy útil para analizar guitarras, pero esta aplicación se ha explorado poco en el instrumento.

Por ejemplo, los lauderos suelen tener mucho cuidado con el diseño del abanico de las guitarras que construyen: las barras adheridas refuerzan la tapa para soportar la tensión de las cuerdas, pero también influyen en las vibraciones de la tapa [4] y, en consecuencia, en su sonido. Sin embargo, usar el dominio de la frecuencia para analizar ondas que no son estacionarias en tapas de guitarra es una labor complicada [6] . Para estudiar propagación de ondas de una manera más natural, resultaría mucho más apropiado un análisis transitorio. Por ejemplo, el análisis transitorio podrá ser útil para detectar si las barras cambian radicalmente la velocidad de propagación de ondas a través de la guitarra o para estudiar el desarrollo inicial de una perturbación, de donde puede extraerse información relevante sobre el comportamiento de instrumentos musicales [7]  and [8] .

Si bien están disponibles algunos estudios del violín que se centran en analizar ondas en el dominio del tiempo [7] , [8]  and [9] , es difícil encontrar investigaciones sobre vibraciones transitorias de una guitarra. En el pasado, Boullosa [3] encontró algunas dificultades en procedimientos experimentales transitorios en guitarras. Por ejemplo, comentó que el rango de frecuencia de excitación por un impacto de martillo en el puente solo alcanzó 300 Hz. Un contenido espectral limitado a 300 Hz resulta insuficiente al analizar el instrumento esperando condiciones similares a las reales. Se sabe que la vibración de una cuerda pulsada puede contener armónicos de frecuencia mucho más alta, alrededor de 5 kHz [10] .

Es factible analizar la guitarra en el dominio del tiempo mediante simulaciones numéricas, como algunos autores han mostrado. Bécache et al. [11] simularon ondas transitorias en una guitarra completa mediante métodos numéricos exhaustivos; sin embargo, para simplificar su modelo, la tapa no incluyó una de las partes cruciales en el diseño de la guitarra: el abanico. De forma similar, en una simulación donde se exploraron las propiedades más importantes para caracterizar una tapa de guitarra [12] , no se consideró el abanico.

Recientemente, el método del elemento finito (MEF) se ha aplicado eficazmente para simular tapas con abanico en el dominio de la frecuencia [1] ; e inclusive otro modelo además incluyó el puente [5] . Sin embargo, simulaciones MEF en el dominio de la frecuencia no proveen información directa para deducir el comportamiento de una onda propagándose mientras atraviesa el abanico y el puente.

El objetivo de la presente investigación es conocer cómo influye un abanico típico de guitarra en una onda vibratoria que se propaga por la tapa. Con esta finalidad, se modeló tridimensionalmente una tapa real de guitarra usando el MEF. La onda en propagación se generó mediante una fuerza transitoria que perturbó el sistema brevemente, y después lo dejó vibrar libremente. De esta manera, se obtuvieron y analizaron varios instantes de la propagación de la onda en la tapa.

2. Teoría

La propagación de ondas en placas es fundamentalmente diferente de la propagación en columnas de aire, cuerdas y membranas. Las ondas transversales en placas, las ondas de flexión, son dispersivas. Los componentes de frecuencia alta se propagan más rápidamente que los componentes de frecuencia baja, y entonces la propagación de un pulso cambia su forma con el tiempo. En materiales anisotrópicos, como la tapa de una guitarra, la velocidad de fase (para amplitudes iguales) será diferente en diferentes direcciones [9] . No obstante, la velocidad de fase no puede exceder la velocidad de una onda cortante ${\textstyle v}$ en una placa sin estructuras adheridas , la cual viene dada por

$v={\sqrt {G/\rho }},$

( 1)

donde G es el módulo cortante y ρ es la densidad de la placa. Claramente, para estudiar sobre dichos tópicos, el estudio de ondas estacionarias no es práctico y es más conveniente usar el análisis transitorio.

A diferencia del análisis modal [3] o armónico [5]  and [13] , el análisis transitorio es una técnica utilizada para determinar la respuesta dinámica de una estructura bajo la acción de cualquier carga dependiente del tiempo, incorporando el comportamiento de la inercia. La ecuación general de movimiento

$M{\ddot {u}}+C{\dot {u}}+Ku=F(t),$

( 2)

donde M representa la matriz de masa del sistema, C la matriz de amortiguamiento, K la matriz de rigidez, u el vector de desplazamientos y F el vector de fuerza aplicada al sistema, debe ser resuelta ya sea para F (t ) = 0 (análisis modal), F (t ) = F₀cosωt (análisis armónico), o F (t ) siendo una entrada arbitraria (análisis transitorio) [14] . En la sección 3 se detalla el modelo de la tapa de guitarra sometida a análisis transitorios.

3. Simulaciones

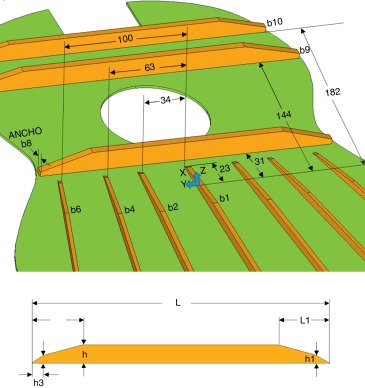
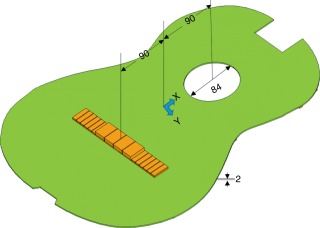
Para el presente trabajo se adaptó el modelo de MEF de una tapa de guitarra, cuyo comportamiento vibratorio ha sido previamente calibrado mediante procedimientos experimentales [5]  and [13] . El diseño de las barras adheridas a la tapa está basado en el abanico tradicional de Antonio de Torres. Los detalles de las barras se incluyen en la tabla 1 y en la figura 1 . El origen del sistema cartesiano de referencia se impuso a la mitad del eje de simetría de la tapa (fig. 1 ), con sentido positivo hacia la boca (considerado X), hacia la derecha viendo el puente (considerado Y), y de la placa hacia el abanico (considerado Z). El puente fue modelado mediante una placa de 80×26,5×5 mm centrada sobre otra placa de 185×26,5×4 mm (fig. 2 ). Para esta simulación se preservaron las ranuras del puente usadas en los experimentos previos [5]  and [13] .

Tabla 1. Medidas en milímetros de las barras del abanico y las transversales. La última fila en cursiva es el ángulo agudo en el plano de la tapa, que forma la barra con respecto al eje de simetría de la tapa (eje X)

	b1	b2	b4	b6	b8	b9	b10
h	7	6	6	5	17	16,5	15
h1	2	1,5	1,5	1	4,4	4,4	4,4
h2	2	1,5	1,5	1	4	4	4
L	239	245	233	204	237	272	249
L1	59,5	61	58,5	50	41	46	39
L2	59,5	61	55	53	41	46	39
L3	4	4	4	4	0	0	0
Ancho	4	4	3	3	6	6	5
∠ejeXbarra	0o	5o	10o	15o	90o	90o	90o

Figura 1. Planos de la tapa (mm).

Figura 2. Ubicación del puente con respecto al origen del sistema de referencia.

3.1. Condiciones de frontera

El funcionamiento correcto de la simulación de una estructura vibrante depende considerablemente de imponer las condiciones de frontera exactas en el modelo. Si bien el montaje de la tapa en una guitarra real parece estar entre una condición empotrada y de bisagra, ambos casos parecen funcionar al simular tapas de guitarra en elemento finito. En la referencia [2] se implementó una simulación usando la condición empotrada, restringiendo a cero tanto los desplazamientos como las rotaciones del contorno, y los resultados mostraron una concordancia suficientemente buena con pruebas experimentales. En otro trabajo [1] , los resultados de otra simulación similar pero con condición de bisagra en las fronteras (restringiendo a cero únicamente los desplazamientos del borde pero permitiendo una rotación libre) mostró variaciones de poca consideración en los modos de vibración calculados; aunque, ciertamente, no reportaron una validación experimental. Debido a la falta de validación experimental en [1] , en la simulación del presente trabajo la tapa fue empotrada como en [2] , imponiendo u  = 0, al igual que ${\textstyle {\frac {\partial u}{\partial x}}=}$${\frac {\partial u}{\partial y}}={\frac {\partial u}{\partial z}}=$$0$ , en su contorno.

3.2. Propiedades de las maderas

Los análisis del MEF aplicado en guitarras suelen mostrar una buena concordancia con resultados experimentales a frecuencias relativamente bajas [1] , [5]  and [13] si la madera se caracteriza como un material ortotrópico. A medida que aumenta la frecuencia, calibrar un modelo de MEF de una guitarra es más complicado, aunque totalmente viable. Sin embargo, esta dificultad no es debida a los conocidos errores de un método numérico, a saber, errores de discretización (a causa de una pobre representación geométrica), de formulación (referido a un planteamiento físico incorrecto) o de truncamiento (originado desde una mala programación de la plataforma), ni tampoco al incremento de la frecuencia como tal (de hecho, el segundo autor ha calibrado simulaciones de MEF rigurosamente, para estructuras a escala micrométricas vibrando a frecuencias mayores de 1000 kHz [15] ).

Las complicaciones de simular una guitarra a frecuencias relativamente altas radica en la anisotropía de un trozo de madera específico. La longitud de onda estructural va disminuyendo conforme aumenta la frecuencia, y en consecuencia, una onda en la placa de madera podría encontrar diversas propiedades elásticas a medida que se propaga por toda la placa. Una caracterización detallada de los materiales sería necesaria para modelar algún instrumento musical específico ; sin embargo, para los fines del presente estudio es suficiente una caracterización ortotrópica de la madera para obtener un panorama general del comportamiento transitorio de una perturbación en una tapa de guitarra.

A todas las maderas usadas para la tapa real se les midió la densidad ρ y, además, para la madera de la tapa se midió el módulo de Young longitudinal E_L (paralelo a las vetas de la madera) y transversal E_T (perpendicular a las vetas de la madera), así como el cortante G_LT . Para la madera del puente se midió E_L y G_LT , y E_L para las barras del abanico y las transversales. Para el puente y el resto de las barras, se obtuvo cada módulo de Young identificando el primer modo libre típico de una viga. Una vez identificada la frecuencia de resonancia correspondiente f , su módulo de Young se calculó aplicando

$E={\frac {\rho l^{4}f^{2}}{1.0446h^{2}}}$

( 3)

donde l es la longitud de la barra y h es su altura. La ec. 3 se obtuvo a partir de una simplificación del análisis publicado por Caldersmith [16] , considerando el caso particular de 2 líneas nodales para los modos de vibración libre de una viga. Para el caso de la placa de la tapa, se cortaron 2 barras para usarlas de probetas y aplicar la ec. 3 ; la longitud de una de las barras fue paralela a las vetas de la madera (para obtener E_L ), mientras que la longitud de la otra barra fue perpendicular (para obtener E_T ).

El valor de G_LT se estimó combinando datos experimentales con simulaciones en MEF, como se explica a continuación. Se simuló el análisis modal en condiciones libres de 2 placas rectangulares ortotrópicas; una placa se modeló con las dimensiones de la placa de madera usada para construir la tapa de guitarra experimental, y otra se modeló según las dimensiones de la placa para el puente. El modo libre (1,1) de las placas ortotrópicas reales, correspondiente a su primera frecuencia de resonancia, se obtuvo usando el método de Chladni (fig. 3 arriba). Esta frecuencia resulta ser proporcional al valor buscado G_LT , presumiblemente debido al carácter torsional que presenta el modo [16] . A continuación, el dato de G_LT en el modelo numérico se ajustó hasta que la frecuencia del modo simulado (fig. 3 , abajo) coincidió con la experimental.

Figura 3. Modo (1,1) experimental (parte superior) y simulado (parte inferior), utilizados para estimar GLT de una placa de madera. Una vez que se obtuvieron EL y ET usando la ec. 3 , GLT se ajustó en la simulación hasta que la frecuencia de resonancia de este modo de vibración coincidió con la frecuencia experimental.

Las relaciones de Poisson ν y el resto de las propiedades elásticas de las maderas no se pudieron medir. Esto se debió a que la geometría de las piezas de madera no permitió la detección de modos de vibración proporcionales a las propiedades elásticas correspondientes. Tal fue el caso de la dimensión transversal tanto de las vigas para el abanico como la de la madera del puente. Las propiedades faltantes simplemente se estimaron a partir de valores encontrados en tablas de propiedades de madera [17] , lo cual se justifica porque dichas propiedades no serían relevantes para caracterizar una placa ortotrópica [18] . Por ejemplo, E_R no sería útil para caracterizar deflexiones ni a lo largo ni a lo ancho de la placa, sino deflexiones en su espesor, siendo un comportamiento completamente despreciable tanto en bajas como en altas frecuencias de la tapa. Los valores medidos y estimados se muestran en la tabla 2 .

Tabla 2. Propiedades de las maderas para la tapa

MADERA	b3, b4	b8	b10	b1, b2	b5, b6	b9	puente	tapa
ρ (kg/m3)	447,4	455,3	435,9	445,29	484,69	431,2	1153,6	330
EL (GPa)	12,1	0,7	0,7	10,9	12,3	0,7	0,7	6,6
ET (GPa)		12,5	11,1			11	13,6	0,66
ER (GPa)		0,3	0,3			0,3	0,3	0,41
GTR (GPa)		0,3	0,3			0,3	2,91	0,11
GLT (GPa)	0.3	0,05	0,1	0,3	0,3	0,1	0,1	0,77
GLR (GPa)		0,01	0,1			0,1	0,1	0,6
νLT	0,3	0,6	0,6	0,3	0,3	0,6	0,3	0,03
νLR		0,013	0,013			0,013	0,013	0,019
νTR		0,025	0,025			0,025	0,025	0,33

3.3. Discretización

Un detalle inherente de un modelo en elementos finitos radica en que la precisión de los resultados depende de la densidad de elementos utilizada y por ende de su tamaño [19] . Por lo tanto, en los análisis que se llevaron a cabo en el presente trabajo, el tamaño de los elementos de la estructura se disminuyó iterativamente hasta determinar que no se tuvieran variaciones considerables en los resultados al aumentar la densidad de elementos. De esta manera, el tamaño máximo permitido para cualquier elemento en el proceso de mallado resultó de 1 cm, y la figura 4 muestra el modelo discretizado obtenido.

Figura 4. Mallado en elemento finito de la tapa de guitarra.

3.4. Análisis transitorio

Se calcularon por separado 2 análisis transitorios para la misma tapa, con duración de 10 ms cada uno. Para determinar la resolución temporal en cada análisis (tiempo de integración) se consideró que la magnitud de cada incremento de tiempo fuera lo suficientemente pequeña para discretizar el movimiento de la estructura hasta 5 kHz. Se escogió esta frecuencia de corte debido a que se espera que el contenido espectral de una cuerda vibrante incluya frecuencias de hasta 5 kHz [10] .

Aunque con un tiempo de integración de la mitad del periodo de la frecuencia máxima de interés T_5kHz  = 200 μs sería suficiente para que el análisis incluya dicha frecuencia, se requiere un tiempo de integración mucho menor para conocer adecuadamente su forma de onda. Por lo tanto, un tiempo de integración de 10 μ s fue impuesto. De esta manera, se garantizaron al menos 20 instantes distintos durante un periodo de la deformación en la estructura para un rango de frecuencias que alcanza hasta los 5 kHz.

Al inicio de cada simulación, se aplicó una fuerza perpendicular a la superficie de la tapa para causar una perturbación, en un nodo localizado justo detrás del puente en x = –9 cm, y = –6 cm. La señal de la carga aplicada tuvo la forma de media onda sinusoidal, con el objetivo de simular el golpe de un martillo [14] . De esta manera, los resultados se pueden comparar a experimentos transitorios en una guitarra como el de la referencia [3] .

Además, es sabido que el tiempo de aplicación de una carga está directamente relacionado con el contenido espectral de dicha señal [14] . En el presente trabajo, la única diferencia entre las 2 simulaciones de 10 ms de duración fue el tiempo de aplicación de la fuerza. En una de las simulaciones, la duración de la fuerza de media onda sinusoidal fue de 1,64 ms, mientras que para la otra simulación fue de 0,1 ms. En ambos casos, la amplitud máxima de la fuerza fue 1 N. De aquí en adelante, ambas simulaciones se etiquetarán de acuerdo al tipo de fuerza aplicada: con fuerza de duración larga o con fuerza de duración corta, respectivamente.

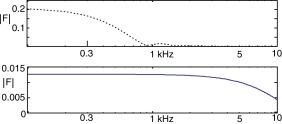
El objetivo de la aplicación de una fuerza de duración larga fue excitar un rango de frecuencias bajas, por debajo de 300 Hz, semejante a los experimentos reportados en la referencia [3] . El contenido espectral de la fuerza de duración larga se muestra en la figura 5 (parte superior), a través de la señal en el dominio de la frecuencia. En cuanto a la fuerza de duración corta, se buscó un contenido espectral más amplio, con frecuencia de corte por encima de los 5 kHz; el espectro correspondiente se muestra en la figura 5 (parte inferior). Una vez se eliminó por completo cada fuerza aplicada, la variación de los desplazamientos respecto al tiempo continuó calculándose sin cargas externas durante el resto de la simulación.

Figura 5. Espectros de los impulsos de 1 N aplicados en cada análisis transitorio: uno con duración de 1,64 ms (parte superior) y otro de 0,1 ms (parte inferior). El tipo de línea correspondiente se preserva en la figura 6 .

4. Resultados y discusiones

Antes de discutir detalladamente las simulaciones obtenidas en el presente trabajo es conveniente mostrar, mediante comparaciones con resultados reportados por otros autores [1] , [7] , [9] , [8] , [3]  and [11] , que su funcionamiento es adecuado. Ciertamente las comparaciones son cualitativas; sin embargo, esto suele considerarse suficiente analizando guitarras debido a la multidimensionalidad del problema, ya que se involucran 3 dimensiones espaciales, otras 3 para las deformaciones, y para este análisis en particular una dimensión más para el tiempo. Por ejemplo, en [1] los modos simulados en ese trabajo se comparan cualitativamente con datos de análisis modal experimental; o incluso en [11] la calibración de su modelo numérico consiste en comparaciones con interferometrías obtenidas por otros autores.

Primeramente, las frecuencias excitadas para la simulación de la fuerza de duración larga sí exhibieron un contenido espectral bajo, análogo al espectro experimental correspondiente obtenido por Boullosa [3] (compárese el espectro de la fuerza de larga duración en la figura 5 con el espectro de la fuerza en la figura 3 b de la referencia). Además, las flexiones graficadas en la figura 8 comienzan con un patrón en la parte baja de la tapa semejante al típico dipolo del segundo modo de vibración de una tapa de guitarra [3] , [1] , [11]  and [5] y a los desplazamientos transitorios de la guitarra analizada en la referencia [11] (véase su figura 11).

Además, se ha estudiado que las estructuras adheridas a una placa, como los abanicos y las barras incluidos en los modelos del presente trabajo, modifican la velocidad de propagación [7] . En consecuencia, el hecho de que las deflexiones presentadas en las figuras 7 y 8 no se propaguen siguiendo un patrón elíptico simple (como los reportados en experimentos análogos en placas de madera sin estructuras adheridas [9] ) es un buen indicio del funcionamiento adecuado de estas simulaciones. Una prueba más contundente es que las perturbaciones simuladas son distorsionadas desde una elipse nominal, cuando la propagación encuentra barras del abanico (fig. 7 , parte inferior) y el puente (fig. 7 , parte superior), tal como sucedió en un análisis experimental similar en un violín [8] .

Finalmente, nótese que en el primer instante capturado por interferometría en la propagación de onda en un violín [8] aún no se interfieren las 2 ondas perturbadas en su experimento (t = 0,1 ms) ni tampoco han alcanzado alguna frontera donde pueda rebotar. Dado que el radio de curvatura del centro de la tapa del violín en la dirección paralela al grano de la madera es suficientemente grande (de más de 1 m), es factible comparar dicha imagen de [8] con las primeras deflexiones en una placa plana, particularmente en la figura 7 del presente trabajo, pues en ambos reportes el instante de captura fue a t = 0,1 ms. Un análisis a simple vista exhibe buena concordancia entre las simulaciones del presente trabajo y el experimento en [8] . Nótese que la distancia recorrida por las ondas perturbadas en ambos trabajos es de unos 2 o 3 cm en la dirección paralela al grano de la madera. Adicionalmente, la presencia del puente en la tapa de guitarra claramente incrementó la velocidad de propagación en la dirección transversal, en comparación con la onda que se propagó en el violín (que en esa zona de la tapa no tiene una estructura adherida en la dirección transversal).

En las siguientes subsecciones se presentan 2 tipos de resultados. Por un lado, se analizan las fuerzas aplicadas durante todo el tiempo que dura cada simulación, así como los correspondientes desplazamientos en el punto de excitación. Por otro lado, se analiza la evolución temporal de ondas propagándose por la superficie de la tapa también.

4.1. Curvas temporales

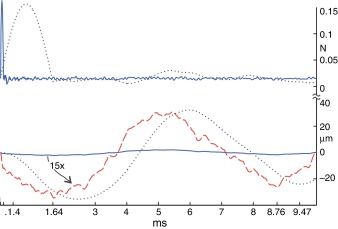
En la figura 6 (parte superior) se muestra el comportamiento, en el dominio del tiempo, de la fuerza total ejercida sobre la tapa de la guitarra en cada análisis. La línea punteada corresponde a la fuerza de duración larga, mientras que la línea continua a la fuerza de duración corta. Estas gráficas se calcularon mediante la suma de las fuerzas de reacción. Los desplazamientos correspondientes en el punto de excitación también se muestran en la figura 6 (parte inferior); los desplazamientos causados por la fuerza de duración larga se graficaron con una línea punteada, mientras que los generados por la fuerza de duración corta, mediante una línea continua. Además, los desplazamientos causados por la fuerza de duración corta se amplificaron quince veces para que la gráfica ajustara mejor en el tamaño de la figura 6 (línea discontinua).

Figura 6. Fuerza total ejercida en la tapa (parte superior) y desplazamiento en el punto de excitación (parte inferior). Se muestran 2 análisis transitorios con cargas diferentes: utilizando una fuerza de duración larga (línea punteada) y usando una fuerza de duración corta (línea continua), donde los desplazamientos generados están amplificados –quince veces– (línea discontinua) con el fin de ajustar mejor en el tamaño de la figura.

Obviamente, la amplitud de los desplazamientos está en proporción a la fuerza total. La respuesta de desplazamiento es dominada claramente por un modo de periodo largo, y la duración de las fuerzas de excitación es suficientemente pequeña comparada a dicho periodo. Por tanto, los desplazamientos máximos se pueden interpretar como análogos a los que produciría un impulso ideal de magnitud igual al área bajo las curvas fuerza-tiempo. Paralelamente, será fácil encontrar que una velocidad inicial distinta de cero está implicada para t = 0, simplemente si se deriva la señal de desplazamiento con respecto al tiempo.

El efecto de la inercia, considerado en la simulación, se detecta en los resultados. Nótese que la fase de la onda sinusoidal de desplazamiento está vinculada al instante de máxima amplitud de la fuerza aplicada. Específicamente, las amplitudes máximas para las cargas aplicadas fueron a t = 0,05 ms y t = 0,82 ms, mientras que las magnitudes máximas de los desplazamientos fueron a t = 1,69 ms y t = 2,44 ms, respectivamente. Tales resultados muestran la respuesta inercial de la tapa, pues los desplazamientos de mayor magnitud se causan después de eliminar la carga aplicada.

Respecto al contenido espectral que se observa en la figura 5 , la diferencia entre ambas simulaciones se puede detectar a través del dominio del tiempo. Para tal finalidad, compárese la forma de onda de los desplazamientos normales obtenidos por ambos análisis en la figura 6 (parte inferior). Nótese cómo la fuerza de duración corta generó desplazamientos de periodos cortos (línea discontinua), teniendo como límite el ancho temporal del impulso. De igual manera, con la fuerza de duración larga los desplazamientos tuvieron como resultado una curva más suave (línea punteada) debido a que solo se pueden generar vibraciones de periodo igual o más largo que el ancho temporal de su respectivo impulso.

4.2. Deformaciones instantáneas en toda la tapa

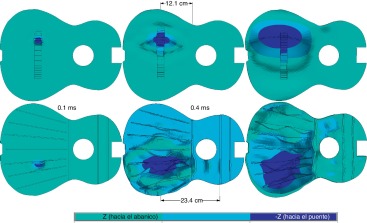
Las deflexiones instantáneas en toda la superficie exhiben detalles particularmente interesantes. La figura 7 muestra las deformaciones normales de la tapa en 3 instantes diferentes de cada análisis. En la parte superior se graficaron las deflexiones calculadas al aplicar la fuerza de duración larga, y en la parte inferior las obtenidas mediante la fuerza de duración corta. Con el objetivo de visualizar las estructuras del abanico y puente, las deflexiones causadas por la fuerza de duración larga muestran la cara del puente, mientras que las deflexiones causadas por la fuerza de duración corta muestran la cara del abanico de la misma tapa.

Figura 7. Deflexiones normales (véase la barra de escala adjunta) para 3 instantes mientras se aplica la fuerza de duración larga (parte superior de la gráfica). Se muestran las deflexiones para los mismos instantes, causados por la fuerza de duración corta (parte inferior de la gráfica). Se incluyen la cara de la tapa que muestra el puente y la que muestra el abanico, con el fin de analizar la influencia de ambas estructuras pegadas en la propagación de la onda.

Para evitar las confusiones comentadas en la referencia [8] acerca de diferenciar picos y valles en datos obtenidos por interferometría, se tomaron en cuenta varias acciones en el presente trabajo. Primeramente, las deflexiones se amplificaron exageradamente. Además, se sombreó la estructura de manera conveniente, mientras que se impusieron 3 contornos para diferenciar la magnitud relativa de las deflexiones. Se incluyó una barra de contornos con sus correspondientes direcciones de desplazamiento respetando el eje de referencia mostrado en la figura 1 .

En la gráfica mostrada en la parte inferior de la figura 7 , correspondiente al instante t = 0,1 ms, la fuerza de duración corta está terminando su aplicación en la tapa (véase fuerza vs. tiempo, fig. 6 ). En comparación con las deflexiones causadas por la fuerza de duración larga, en el mismo instante t = 0,1 ms (véase la parte superior de la fig. 7 ), pocas diferencias se pueden encontrar adicionales a la magnitud de deformación. Obviamente, la fuerza causó que la tapa se flexionara en la misma dirección de la fuerza –hacia el puente– aplicada en el punto de excitación. Sin embargo, también es notoria una deflexión hacia el abanico alrededor del punto de excitación, lo cual no se había podido detectar en trabajos previos.

Las perturbaciones perpendiculares forzadas en la tapa causaron ondas de flexión, tal y como se espera. Sin embargo, una inspección detallada de las figuras 7 y 8 (particularmente del comportamiento de las barras adheridas) revela que además existen ondas transversales (o cortantes). Este comportamiento concuerda con algunas características de las ondas transversales que Fahy [20] detalla: aunque es difícil generar ondas trasversales en una placa plana mediante fuerzas aplicadas; estas ondas juegan un papel importante en el proceso de transmisión y reflexión de vibración a través de discontinuidades lineales, que resulta ser justamente el caso que se presenta en el presente análisis debido a las estructuras adheridas a la placa y a las fronteras empotradas. Al parecer, los abanicos, barras y bordes de la tapa de guitarra distorsionan la onda de flexión que nominalmente perturba la fuerza impulsiva aplicada y entonces se generan ondas cortantes.

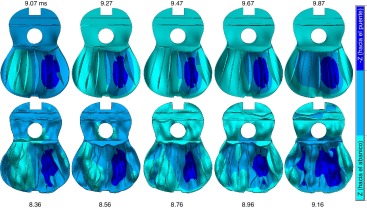
Figura 8. Deflexión normal de la tapa durante el segundo valle de la gráfica de desplazamiento mostrado en la Figura 6 , causada por la fuerza de duración larga (parte superior). También se incluyen los datos correspondientes causados por la fuerza de duración corta (parte inferior).

4.2.1. Velocidad de propagación

En la parte superior de la figura 7 para t = 0,4 ms se puede ver que las ondas de flexión causadas por la fuerza de larga duración apenas han alcanzado la barra b8, a 12,1 cm del punto de excitación. Esto implica una velocidad de propagación de ≈302 m/s. Si bien la velocidad máxima de propagación de la placa sin barras adheridas (560 m/s según la ec. 1 , usada con el valor de G_LT y ρ correspondiente en la tabla 2 ) no es rebasada hasta ese instante de la simulación, la situación cambia al generar la onda perturbada por la fuerza de duración corta.

Al analizar las deflexiones causadas por la fuerza de duración corta, en la parte inferior de la figura 7 , para t = 0,4 ms se detecta un incremento considerable en la velocidad de propagación de la onda a través de la estructura: las perturbaciones con longitudes de onda corta (es decir, los componentes de frecuencia alta) se alejan más rápidamente del punto de excitación. Esto pone en evidencia cómo dichas perturbaciones logran alcanzar la barra b9 localizada a 23,4 cm del punto de excitación. Para este caso, se calcula una velocidad de propagación de ≈585 m/s e incluso resulta ser mayor que la velocidad de propagación máxima obtenida para la placa sin barras adheridas. Este incremento en la velocidad de propagación en la tapa se debe a barras adheridas, y resulta congruente con los comportamientos experimentales de [7]  and [8] , donde explican mediante interferogramas que las ondas en el violín viajan más rápidamente del lado donde la tapa tiene una barra.

4.2.2. Evolución temporal de las ondas sobre la tapa

Al analizar los resultados que se muestran en la figura 7 en t = 1,64 ms (cuando la fuerza de duración larga se ha eliminado por completo) se puede inferir que no es posible realizar una comparación directa del comportamiento de la tapa entre los resultados aplicando la fuerza de duración larga y los de duración corta. Lo anterior se debe a las fases diferentes entre las deflexiones de ambas simulaciones. Es evidente que las gráficas de desplazamiento muestran un desfase (véase desplazamiento vs. tiempo en la fig. 6 ). No obstante, es factible encontrar una comparación análoga en la propagación de ondas para ambos análisis. El procedimiento propuesto consistió en inspeccionar las secuencias de deflexiones, definiendo como punto de referencia al último valle de cada gráfica de desplazamiento en la figura 6 . De esta manera, en vez de comparar la propagación de onda de cada análisis en el mismo instante correspondiente, la comparación se hizo durante el mismo valle de la onda de periodo largo detectada en cada análisis.

Por lo tanto, el último valle en la gráfica de desplazamiento causado por la fuerza de duración corta (fig. 6 , línea discontinua) fue aproximadamente a t = 8,76 ms, y las correspondientes secuencias de deflexión de la tapa fueron alrededor de dicho instante, tal y como se observa en la parte inferior de la figura 8 . El mismo procedimiento se llevó a cabo en el análisis de las deflexiones generadas al aplicar la fuerza de duración larga (fig. 6 , línea punteada), pero el valor de tiempo correspondiente fue diferente, de 9,47 ms (véase la fig. 8 , parte superior). Las secuencias de ambas deflexiones se espaciaron por 0,2 ms, exhibiendo una mejor resolución comparada con el análisis temporal mostrado en la referencia [11] , cuyas capturas se espaciaron cada 0,36 ms.

La parte inferior de la tapa fue la parte predominantemente deformada en las deflexiones graficadas en la figura 8 . Sin embargo, algunas deflexiones de longitud de onda corta aparecen en este caso, es decir, componentes de frecuencia alta para la fuerza de duración corta (parte inferior de la fig. 8 ). Nótese la relación entre la forma de las deflexiones de longitud de onda corta y el diseño del abanico (por ejemplo, en la parte inferior de la fig. 8 algunas ondas se encuentran entre las barras).

Además, las ondas alrededor de la roseta (fig. 8 , parte inferior) implican que hay involucrados modos de vibración multipolares de frecuencia alta, pues en modos de frecuencia inferior a 600 Hz prácticamente solo se mueve la parte inferior de la tapa. Las vibraciones de la parte inferior de la tapa de una guitarra están bien documentadas, pero pocos han reportado análisis acerca de las vibraciones de una tapa cerca de la roseta, quizás debido a la dificultad para manejar las frecuencias altas en procedimientos experimentales [3] . Aun así, las vibraciones en la parte superior de la tapa no se deben despreciar, teniendo en cuenta el alto contenido de armónicos en las vibraciones de las cuerdas de la guitarra.

Las discusiones aquí presentadas mostraron claramente que las ondas propagándose por una tapa de guitarra se dispersarán de maneras inevitablemente diferentes dependiendo de cada diseño. Tal y como implica la ec. 2 , dichas diferencias vendrán dadas por la geometría, masa, amortiguamiento y rigidez de cada instrumento. Las variaciones en la dispersión de las ondas implican que carece de sentido intentar buscar una sola velocidad de propagación para caracterizar una tapa de guitarra.

Ciertamente, la importancia del abanico en cada guitarra para definir su comportamiento vibratorio –y consecuentemente su calidad– es ampliamente aceptada. Sin embargo, explicaciones como las que aquí se reportan (es decir, involucrando el dominio en el tiempo) son poco frecuentes en investigaciones enfocadas en la guitarra, y podrían resultar útiles para lauderos sin necesidad de una preparación científica sólida.

Paralelamente, estas observaciones podrían resultar útiles al elegir geometrías simples para modelar la radiación de tapas con diseños específicos, dado que escribir modelos analíticos para la radiación de superficies de geometría complicada no es sencillo y sigue en estudio [21] .

5. Conclusiones

La simulación de análisis transitorios en una tapa de guitarra completa exhibió la influencia del abanico y del puente, en ondas vibratorias propagándose por su superficie. Claramente, la madera adherida a la placa incrementa la velocidad de propagación en la estructura. Esto implica que la propagación de una onda en una tapa de guitarra debe ser completamente distinta dependiendo de cada diseño de abanico usado. Sin embargo, para notarlo, fue necesario simular la propagación de una onda con contenido espectral alto (incluyendo frecuencias de hasta 5 kHz). Los cambios producidos por diferentes abanicos parecen ser despreciables para ondas de contenido espectral bajo. Estos resultados ponen en evidencia que las diferencias en el funcionamiento de distintas guitarras tiende a suceder en frecuencias altas, al menos arriba de 600 Hz.

Adicionalmente, la evolución de las deflexiones simuladas en el dominio del tiempo permitió ver el comportamiento de la tapa de una forma extraordinariamente simple, y ciertamente algo llamativa por poder realizarse a simple vista. De esta manera, el presente trabajo ofrece una alternativa para estudiar la influencia del abanico y del puente de una guitarra, incluso sin tener conocimientos sólidos en acústica.

Agradecimientos

Los autores agradecen al Dr. Pablo L. Rendón de CCADET UNAM, al Dr. Javier Naranjo de la UAC, y a Goretti Paredes por su apoyo durante la redacción del presente trabajo.

References

1. [1] M.J. Elejabarrieta, A. Ezcurra, C. Santamaría; Vibrational behaviour of the guitar soundboard analysed by the finite element method; Acta Acustica united with Acustica, 87 (2001), pp. 128–136
2. [2] B. Richardson, G. Roberts; The adjustment of mode frequencies in guitars: A study by means of holographic interferometry and finite element analysis; Proc. SMAC 83. Royal Swedish Academy of Music, Stockholm (1983), pp. 285–302
3. [3] R.R. Boullosa; The use of transient excitation for guitar frequency response testing; CAS Newsletter (1981), pp. 17–20
4. [4] E. Skrodzka, A. Lapa, B. Linde, E. Rosenfeld; Modal parameters of two incomplete and complete guitars differing in the bracing pattern of the soundboard; J. Acoust. Soc. Am., 130 (4) (2011), pp. 2186–2194
5. [5] J.A. Torres, R.R. Boullosa; Influence of the bridge on the vibrations of the top plate of a classical guitar; App. Acoust., 70 (2009), pp. 1371–1377
6. [6] J.A. Torres, P.L. Rendon, R.R. Boullosa; Complex mode shapes due to small-scale samping in a guitar top-plate; J. App. Res. Tech., 8 (2010), pp. 144–152
7. [7] N.-E. Molin, A.O. Wahlin, E.V. Jansson; Transient wave response of the violin body; J. Acoust. Soc. Am., 88 (1990), pp. 2479–2481
8. [8] N.-E. Molin, A.O. Wahlin, E.V. Jansson; Transient wave response of the violin body revisited; J. Acoust. Soc. Am., 90 (1991), pp. 2192–2195
9. [9] N. Molin, E.V. Jansson; Transient wave propagation in wooden plates for musical instruments; J. Acoust. Soc. Am., 85 (1989), pp. 2179–2184
10. [10] J. Woodhouse; On the synthesis of guitar plucks; Acta Acustica united with Acustica, 90 (5) (2004), pp. 928–944
11. [11] E. Bécache, A. Chaigne, G. Derveaux, P. Joly; Numerical simulation of a guitar; Computers & Structures, 83 (2005), pp. 107–126
12. [12] A. Ezcurra; Influence of the material constants on the low frequency modes of a free guitar plate; J. Sound Vib., 194 (4) (1996), pp. 311–322
13. [13] J.A. Torres, R.R. Boullosa; Radiation efficiency of a guitar top plate linked with edge or corner modes and intercell cancellation; J. Acoust. Soc. Am., 130 (1) (2011), pp. 546–556
14. [14] D.I. Inman; Engineering Vibration; (1st edition)Prentice Hall, New Jersey (1994)
15. [15] F.E. Beltrán, J. Muñoz Saldaña, D. Torres-Torres, R. Torres-Martínez, G. Schneider; Atomic force microscopy cantilever simulation by finite element methods for quantitative atomic force acoustic microscopy measurements; J. Mat. Res., 21 (2006), pp. 3072–3079
16. [16] G. Caldersmith; Vibration theory and wood properties; JCAS, 42 (1984), pp. 4–11
17. [17] V. Bucur; Acoustics of Wood; CRC Press, New York (1995)
18. [18] M. McIntyre, J. Woodhouse; On measuring the elastic and damping constants of orthotropic sheet materials; Acta Metall., 36 (6) (1988), pp. 1397–1416
19. [19] E. Dufeu, J. Gómez, F. Cugnon, P. Beckers; Control del error en la optimización de forma de estructuras bidimensionales; Rev. int. métodos numér. cálc. diseño ing., 13 (2) (1997), pp. 165–183
20. [20] F. Fahy; Sound radiation by vibrating structures; Sound and structural vibration, Springer-Verlag, London (1983), pp. 81–86
21. [21] J. Alba, J. Arenas, R. del Rey; Descomposición en pistones circulares para la obtención de la radiación acústica de un pistón rectangular; Rev. int. métodos numér. cálc. diseñoing., 28 (1) (2012), pp. 12–17