Abstract
For some applications that use pseudorandom numbers it is essential to keep the record of numbers generated so far. Such a representative example is cryptanalytic TMTO approach. In order to save the space, instead of straightforward recording of individual numbers generated, an ordered tree-like data structure which tracks the intervals of generated numbers is proposed. For estimating the memory requirements of this structure as a function of pseudorandom numbers range size, an analytical probabilistic model is established and used. This model determines the maximum number of intervals during recording which corresponds to the tree size. The result obtained from analytical model is fully validated experimentally by means of simulation for a wide spectrum of range sizes.
Keywords: Pseudorandom numbers, interval trees, simulation analysis
1. Introduction
Random events are immanent to numerous natural phenomena. Being fully unpredictable they can be modelled by random number sequences which do not follow any specific rules. Computer simulation of random processes requires computer-based generation of random numbers [1]. However, in practice such computer generated number sequences are not entirely random since detereministic algorithms are employed for this purpose. It means that for the same initial state these algorithms always produce the same sequences of numbers. This is the reason why the computer generated numbers are regarded as pseudorandom. Although true randomness can not be expected to achieve in a computer environment, quite often a sequence of pseudorandom numbers satisfies the most of the statistical testes of randomness [2-6]. Without a precise definition of relevant tests which would guarantee the reliability of obtained results, the implementation of pseudorandom generators is usually based on detailed mathematical analysis of their characteristics.
Pseudorandom numbers have a widespread application in various fields. The examples of their intensive use are the areas of statistics, gambling, probability and chance games, computer simulations, cryptography, etc. In some aplications, it is quite essential to constantly keep the record of already generated pseudorandom numbers.
An example that represents an immediate motivation for the analysis conducted in this paper is found in the area of cryptanalysis. This is a well-known Hellman TMTO algorithm which solves the main cryptanalytical problem of inverting one-way function in order to find the secret key [7]. This method, as well as its follow-up improvements [8,9], tries to achive a trade-off between time and memory requirements in this very computationally demanding task. An off-line, precomputation phase of the algorithm generates the fixed-length chains of keys (which can be regarded as pseudorandom), so that an on-line, attack phase can perform more efficient search. However, the main problem is that no record is kept during generation of chains about keys already included, so the multiple occurence of some keys in chains is inevitable. This leads to some irregular situations like looping and merging of chains. On the other hand, since the total number of keys in chains is equal to the size of the key space, multiple occurence of some keys prevents some other keys to be included into chains which incures a lower coverage of the key space. The consequence is that such keys can not be found at all, while the repeated key values are responsible for erroneous situations (false alarms). Therefore, the success of the attack is impaired, making the method probabilistic. The problems can be avoided by keeping the record of the randomly chosen keys which are already included into chains during off-line phase. In this way, resulted perfect chains avoid key repetion and attain full key space coverage, making the method deterministic. The relevant characteristics of perfect chains are examined in [10] by using probabilitic analytical and simulation model.
Pseudorandom number generator produces the numbers by a random choice from a given set, usually a range of numbers. If the range of possible numbers is quite large, which is an often case, the tracking of already generated numbers can be practically infeasible because of the extreme space demands. In order to decrease the memory required for tracking, instead of keeping each individual generated number, only the record of intervals of generated numbers can be kept. Consequently, an ordered dynamic tree-like structure is proposed where each node represents an interval of generated numbers with its lower and upper bounds. As the new numbers are generated and the tree updated accordingly, it is expected that number of nodes increases from one to some maximum number. Then, as new numbers are generated, the nodes are expeted to coalesce and the number of nodes decreases until all numbers are generated and the tree colapses to one node. The main goal of this paper is to determine the maximum number of nodes as a function of size of the generated numbers range.
A precise formal procedure of keeping the record during random number generation and the problem statement are given in Section 2. Then, problem is theoretically solved by an analytical approach which is described in Section 3. The result of this analysis is validated by means of simulation evaluation presented in Section 4. Finally, the conclusion is drawn in Section 5.
2. Problem statement
Let the random number generator (RNG) generates integers from the given range (denoted as set ) long enough to guarantee that each number from appears at least once. After RNG generates a number, the check is made if this number is already generated before. If not, it is used in application and some record of numbers generated so far is updated; otherwise, RNG generates a new number. The process is carried on until all numbers from are generated and included into the record.
For the sake of clarity of the following presentation and analysis, during the process of random generation we will maintain two sets. The record of numbers generated so far is kept as a set of integers (denoted as ). In order to save the space, it is implemented in an appropriate form of intervals of consecutive integers. These intervals of already used numbers will be referred as –intervals. The remaining numbers from are kept in a set of unused integers (denoted as ), also implemented in the form of intervals (–intervals). In both set implementations, only lower and upper bound for each interval are recorded in memory. The interval can have only one element, referred to as single element interval (e.g., ), or more than one element, referred to as multiple element interval (e.g., [, ], ). Since and sets are complements in respect to set (i.e., ), in practical implementation it is sufficient to maintain only one of these sets for memory efficiency. Figure 1 illustrates alternating layout of –intervals and –intervals within the set . Used numbers are denoted as circles and –intervals are represented as shaded boxes, while unused numbers are denoted with squares and –intervals are represented as white boxes.
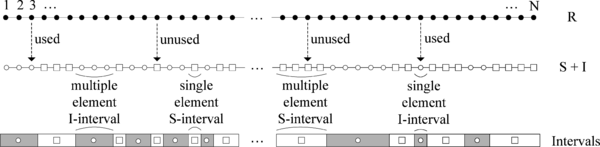
|
| Figure 1. Layout of I–intervals and S–intervals |
Let we start with set of integers (i.e., ) and an empty set . In each step, we randomly choose an element from and move it to ; i.e., and . Consequently, after steps we will have and . In each step, the record of numbers already chosen and included into is updated in the following way:
- A. In step , an element is randomly chosen and included into . Now, there is only one -interval, [, ].
- B. In step , currently randomly chosen element is checked for adjacency to existing –intervals with three possible outcomes:
- 1. if it is not adjacent to any of existing –intervals, a new –interval is created,
- 2. if it is adjacent to only one interval [, this –interval is extended with (e.g., if , interval is extended to or if , interval is extended to ),
- 3. if it is adjacent to two –intervals and in a way that and , these two intervals are merged into interval ( previously corresponded to a single element –interval).
Obviously, after an element is included into , three outcomes are possible in a step:
- number of –intervals is increased by 1 (cases A and B.1),
- number of –intervals stays the same (case B.2),
- number of –intervals is decreased by 1 (case B.3).
In step , the number of –intervals is 1. Then, it increases until some maximum is reached as new –intervals are created. After reaching maximum, it is expected that –intervals are progessively coalescing, and their number will fall until only one interval, [1, ], remains in step (all elements from are now moved to , and ).
For practical viability of this procedure, one of the crucial things is the memory needed for keeping the record of generated elements in set (and also of unused elements in ). Memory requirements are directly proportional to since can be implemented as a dynamic structure in which only upper and lower bound of each interval are recorded, as it will be explained in Section 4. In the following sections, the maximum number of –intervals is determined by both analytical and simulation means.
3. Analytical solution
Let us assume that in step , , an element is chosen from and moved to . After that, the number of elements in is . Let the number of –intervals after adding to be denoted as . In the next step , , an element is chosen from . As previosly elaborated, its inclusion into can lead to:
- decreased number of –intervals - (merging of two intervals),
- increased number of –intervals - (creating a new interval),
- the same number of –intervals - (extending an existing interval).
Let the symbols , and stand for probabilities that the number of –intervals will increase, decrease or stay the same, respectively. Also, the following equation must hold
In a given step, these probabilities depend on current positions of –intervals of used numbers within range . Three possible layouts of range are shown in Figure 2. –intervals are sequenced from 1 to and again represented by shaded boxes, while intervening –intervals of unused numbers are represented by white boxes.
Let , and denote the probabilities of layouts , and after step , respectively, and is the number of -combinations from set of elements. Then, these probabilities can be calculated as:
We will now derive the expressions for probabilities , and in case of each particular layout. To this end, we define an important parameter denoted as . It represents an average number of single element –intervals after step . This type of interval is important since its only element which belongs to separates two consecutive –intervals and its selection from and inclusion into in some later step makes that these two –intervals are merged into one.
Let us assume that in step one of elements from is chosen.
Layout A
In case of this layout, the number of –intervals () is equal to the number of –intervals (Figure 2a). The number of –intervals can be decreased only if the chosen number belongs to some single element –interval other than [1, 1] and . The probability that single element –interval lies at 1 or is , while the probability of the opposite case is 1 – . Therefore, the probability of merging two consecutive –intervals is
|
|
(1) |
The number of –intervals can be increased only if the chosen number does not belong to some single element –interval and also if it is not adjacent to some bound of any –interval. The probability of such a case is
|
|
(2) |
The number of –intervals stays the same if the chosen number is adjacent to a bound of some I–interval. It can belong to some multiple element –interval or to single element –interval [1, 1] or . The probability for such a case is
|
|
(3) |
Using expressions (1)–(3), assuming layout after step an average number of –intervals after step can be calculated as
|
|
(4) |
Layout B
For this layout, the number of –intervals is while the number of –intervals is – 1 (Figure 2b). The number of –intervals will be decreased only if the chosen number corresponds to some single element –interval. The probability for such an event when two –intervals are merged is
|
|
(5) |
The number of –intervals will be increased if the chosen number neither corresponds to any single element –interval nor is adjacent to a bound of any –interval. Then, a new –interval is created with probability
|
|
(6) |
The number of –intervals does not change if chosen number corresponds to a bound of some multiple element –interval. It can happen with probability
|
|
(7) |
Based on expressions (5)–(7), assuming layout after step an average number of I–intervals after step can be calculated as
|
|
(8) |
Layout C
For this layout, the number of –intervals is while the number of –intervals is (Figure 2c). The number of –intervals will be decreased if the chosen number corresponds to some single element –interval other than [1, 1] and .
The probability that no one single element –interval lies on range bounds 1 and is
The probability that one single element –interval lies on a range bound (1 or ) is
The probability that two single element –intervals lie on range bounds 1 and is
Then, the probability that number of –intervals will be decreased is
|
|
(9) |
The number of –intervals will be increased if the chosen number neither corresponds to any single element –interval nor is adjacent to a bound of any –interval. The probability of such a case is:
|
|
(10) |
The number of –intervals stays the same if the chosen number corresponds to a bound of some multiple element –interval or to a single element –interval at any bound of range (1 or ). It can happen with probability
|
|
(11) |
Since it can be calculated from above that
and it holds that
the expressions (9)–(11) become:
|
|
(12) |
|
|
(13) |
|
|
(14) |
From expressions (12)–(14), assuming layout after step , the average number of I–intervals after step can be derived as:
|
|
(15) |
Expressions (4), (8) and (15) shows that an average number of –intervals () does not depend on the number of single element –intervals () for all three possible layouts , and .
Finally, an average number of intervals after step can be calculated as:
|
|
(16) |
Solving the recurrence from (16), we obtain:
|
|
(17) |
Let . The average number of –intervals as a function of current number of steps is shown in Figure 3. First and second derivation of this function are
respectively. Since , has a local maximum for (). The value of this local maximum is
For it gives which represents the solution of the stated problem.
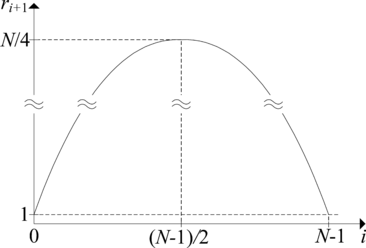
|
| Figure 3. An average number of –intervals |
4. Simulation results
Theoretical finding of the analytical approach conducted in the previuos section is also verified by means of software simulation. An appropriate program that simulates the procedure of random number generation elaborated in Section 2 is implemented. Random number generator from [11] is exploited in this simulation. For keeping the record of randomly numbers generated so far (implementation of set ) a structure called interval tree is used. It is a modification of standard binary search tree [12], whose nodes correspond to –intervals instead of single values. An example of such a tree is given in Figure 4.
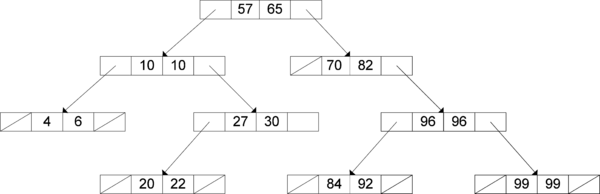
|
| Figure 4. An example of an interval tree |
Each node has two integer fields for lower and upper bounds of the corresponding interval and two pointer fields to its left and right subtrees, so memory consumed is () where is the maximum number of nodes ( –intervals). All intervals in the left subtree are lower, while the intervals in the right subtree are higher, so an efficient binary search is possible with average time complexity of (log ) [12].
The experimental results are presented in Table 1. The size of random number range ( – first column) is varied from 100 to 10000000. For each value of , the results are averaged over 10 experiments. Theoretically expected number of – intervals is calculated from analytical model as and given in the second column. The statistics about the maximum number of nodes ( – intervals) in the interval tree is collected ( – third column). Fourth column shows a relative difference between the results of analytical and simulation models calculated as . As this difference decreases with and become negligible, it is evident that the results of analytical model perfectly match the experimental results. Also, the number of generated values included into tree when the number of nodes reaches the maximum is also kept ( – fifth column). Then, an average size of an – interval is calculated as (sixth column).
| (%) | |||||
| 100 | 25.5025 | 27 | 0.058720 | 47 | 1.74 |
| 1000 | 250.50025 | 253 | 0.009979 | 482 | 1.90 |
| 10000 | 2500.500025 | 2509 | 0.003399 | 4945 | 1.97 |
| 100000 | 25000.5000025 | 25020 | 0.000780 | 50060 | 2.00 |
| 1000000 | 250000.50000025 | 250015 | 0.000058 | 500278 | 2.00 |
| 10000000 | 2500000.500000025 | 2494898 | 0.000041 | 5005260 | 2.00 |
5. Conclusion
Random number generation is widely exploited in many applications. Not rarely it is required that each number from the given range should be chosen and used in application only once. In that case it is necessary to keep the record of already generated numbers. For very large range sizes the recording procedure can be extremely space demanding. The goal of this paper is to estimate the memory needed for this purpose.
Instead of straightforward recording of each individual number, an advanced data structure in form of an interval tree is employed. It allows for an efficient binary search, and each node represents an interval of already generated numbers keeping only upper and lower bound for each interval. Memory demands are directly proportional to maximum number of nodes in this tree. These demands are first estimated using an analytical probabilistic model. It was obtained that for a range size N the maximum number of intervals (or nodes in the interval tree) is N/4 approximately. This finding is proved by simulation means since the experimental results entirely verified the theoretical one. The fact that the memory savings are within a constant factor of linear memory complexity implies that such a recording is still practically infeasible for very large range sizes.
Acknowledgement
This work has been partially supported by the Serbian Ministry of Education and Science (the projects III 44006 and III 44009).
References
[1] Knuth, D. The Art of computer programming. 3rd ed. Vol. 2: Seminumerical Algorithms, Addison Wesley, 1997.
[2] Zaman S.U., Ghosh R. Review on fifteen statistical tests proposed by NIST. J. of Theor. Phys. and Cryptogr., 1:18-31, 2012.
[3] Senn S.J., Rothman K.J., Carlin J.B., Poole C., Goodman S.N., Altman D.G. Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur. J. of Epidemiol., 31:337-350, 2016.
[4] Doganaksoy A., Sulak F., Uguz M., Seker O., Akcengiz Y. New statistical ramdomness tests based on length of runs. Math. Probl. in Eng., 2015:14 pages, 2015.
[5] Mohammad O.J., Abbas S., Horbaty E., Salem A. A new trend of pseudo random number generation using QKD. Int. J. of Comput. Appl., 96:13-17, 2014.
[6] Liu C., Lai X. Evaluation of statistical tests for randomness using conditional entropy. Int. Conf. on Cyber-enabled Distrib. Comput. and Knowl. Discov., 504-509, 2013.
[7] Hellman M. A cryptanalytic time-memory trade-off. IEEE Trans. on Inf. Theory, 4:401-406, 1980.
[8] Standaert F., Rouvroy G., Quisquater J., Legat J. A time memory tradeoff using distinguished points; new analysis & FPGA results. Lect. Notes in Comput. Sci., 2523:593-609, 2003.
[9] Oechslin P. Making a faster cryptanalytic time-memory trade-off. Lect. Notes in Comput. Sci., 2729:617-630, 2003.
[10] Tomašević V., Tomašević M. An analysis of chain characteristics in the cryptanalytic TMTO method. Theor. Comput. Sci., 501:52-61, 2013.
[11] Matsumoto M., Nishimura T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. on Model. and Comput. Simul. 8:3-30, 1998.
[12] Cormen, T., Leiserson, C., Rivest, R., Stein, C. Introduction to algorithms. Third ed. MIT Press, 2009.
Document information
Published on 24/06/19
Accepted on 10/06/19
Submitted on 06/06/19
Volume 35, Issue 2, 2019
DOI: 10.23967/j.rimni.2019.06.003
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?
