Numerical study of efficiencies for box type solar cooker with internal reflectors

Resumen

En este trabajo se muestran los resultados del estudio de las eficiencias termodinámicas de 1.^a y 2.^a ley aplicadas a 4 arreglos diferentes de estufas solares de tipo caja con reflectores internos. La estufa solar tiene 2 vidrios en su cubierta para disminuir la pérdida de calor por radiación y convección, y crear así el efecto invernadero. El interior de la estufa tiene espejos colocados a diferentes ángulos para dirigir la radiación solar hacia un recipiente con agua que se encuentra también dentro de la estufa. Los resultados obtenidos están basados en las temperaturas de calentamiento del agua, las cuales fueron obtenidas por medio de una simulación numérica que permite comparar los 4 arreglos de estufas solares bajo condiciones idénticas. El tratamiento de los resultados revela que la cantidad de energía que impacta en las estufas solares no es aprovechada de manera adecuada para los fines de calentamiento de agua. La mayor parte de la energía aprovechable se almacena en los vidrios de la tapa, lo que evidencia la necesidad de trabajar en el desarrollo de mejores materiales para mejorar tal situación.

Abstract

In this work, results of efficiencies for first and second law of thermodynamics applied to four box-type solar cookers with internal reflectors are shown. The solar cooker has two glasses on its cover to diminish the losses of heat for radiation and convection, besides creating the effect hothouse inside the cooker. The interior of the cooker has flat mirrors placed at different angles to reflect the solar radiation toward a recipient with water inside the cooker. The obtained results are based on heating water temperatures which were obtained by means of numeric simulation, allowing comparison under identical conditions of four solar cookers. The treatment of the results revealed that the quantity of energy that impacts on the solar cookers is not used in right way for the heating water ends. Most of the profitable energy is stored in the glasses of the cover, what evidences the necessity to work in the development of better materials to diminish such situation.

Palabras clave

Estufa solar ; Reflector interno ; Eficiencia ; Exergía ; Radiación solar

Keywords

Solar cooker ; Inner reflector ; Efficiency ; Exergy ; Solar radiation

Nomenclatura

Variables

c_p- Calor específico a presión constante, kJ /kg K

c_v- Calor específico a volumen constante, kJ /kg K

m- Masa, kg

t- Tiempo, s

Δt- Intervalo de tiempo, s

ψ_sistema- Exergía del sistema, kJ

Q- Tasa de transferencia de calor, W

U- Energía interna, J

U₀- Energía interna en el punto muerto, J

u- Energía interna específica, J /kg

V- Volumen geométrico, m³

V₀- Volumen geométrico en el punto muerto, m³

P- Presión, Pa

P₀- Presión en el punto muerto, Pa

T- Temperatura, K

T₀- Temperatura en el punto muerto, K

S- Entropía, J /kgK

S₀- Entropía en el punto muerto, J /kgK

σ- Constante de Stefan-Boltzmann 5,67 × 10⁻⁸W /m²K⁴

α- Absortancia, adimensional

ρ- Reflectancia, adimensional

ε- Emitancia, adimensional

τ- Transmitancia, adimensional

η- Eficiencia, adimensional

G- Radiación solar incidente, W /m²

${\textstyle A_{v_{i}}}$- Área del vidrio i (i  = 1, 2), m²

A_m- Área mojada, m²

A_{ref  n}- Área de reflexión, m²

θ_{ref ,n}- Ángulo de reflexión del reflector n , grados

${\textstyle h_{v_{1}\rightarrow {int}_{1}}}$- Coeficiente de convección entre la temperatura del vidrio 1 (exterior) y la temperatura del vidrio 2 (interior), W /m²K

${\textstyle h_{v_{1}\rightarrow amb}}$- Coeficiente de convección entre la temperatura del vidrio 1 y la temperatura ambiente exterior, W /m²K

${\textstyle h_{v_{2}\rightarrow {int}_{1}}}$- Coeficiente de convección entre la temperatura del vidrio 2 y la temperatura del vidrio 1, W /m²K

${\textstyle h_{v_{2}\rightarrow {int}_{2}}}$- Coeficiente de convección entre la temperatura del vidrio 2 y la temperatura interior de la estufa, W /m²K

${\textstyle h_{{\boldsymbol {\mbox{t}}}\rightarrow {int}_{2}}}$- Coeficiente de convección entre la temperatura de la tapa del recipiente y la temperatura del medio interior de la estufa, W /m²K

${\textstyle h_{{\boldsymbol {\mbox{t}}}\rightarrow {int}_{3}}}$- Coeficiente de convección entre la temperatura de la tapa del recipiente y la temperatura del medio definido por la interfaz de la superficie del fluido y la tapa del recipiente, W /m²K

${\textstyle h_{r\rightarrow {int}_{2}}}$- Coeficiente de convección entre la temperatura del recipiente y la temperatura interior de la estufa, W /m²K

${\textstyle h_{r\rightarrow {int}_{3}}}$- Coeficiente de convección entre la temperatura de la tapa del recipiente y la temperatura del aire en el interior del recipiente, W /m²K

h_{r →fl}- Coeficiente de convección entre la temperatura del recipiente y la temperatura del fluido, W /m²K

Subíndices

_amb- Ambiente

₀- Referencia al punto muerto

${\textstyle {}_{v_{i}}}$- Vidrio i , i  = 1, 2

_t- Tapa

_r- Recipiente

_f- Fluido

_fl- Lateral del fluido

1. Introducción

Existen varios tipos de estufas solares con concentradores, calentadas por colectores de placa plana y de tipo caja. Las estufas solares con reflectores internos han sido estudiadas desde varios enfoques usando modelos matemáticos tal como lo indican en su trabajo El-Sebaii y Domanski [1] , que muestran que la distribución de temperaturas obtenidas de manera experimental es muy cercana a los resultados numéricos del modelo construido. En Tanta (Egipto), Thulasi et al. [2] obtuvieron un modelo matemático para una estufa solar de tipo caja con reflectores internos, el cual muestra los problemas presentados por la gran cantidad de parámetros involucrados en la operación de esta estufa. Sus resultados permiten establecer el comportamiento térmico de este tipo de estufas para condiciones de operación establecidas. Funk y Larson [3] presentaron un modelo paramétrico para la operación de una estufa solar con la finalidad de predecir su poder de cocción basado en 3 parámetros controlados (el área de intercepción solar, el coeficiente de pérdida de calor y la conductividad térmica de absorción de la base de la placa) y 3 variables no controladas (la insolación, la diferencia de temperatura y la distribución de carga). Reddy y Rao [4] obtuvieron un modelo matemático para una estufa solar con una cubierta de doble vidrio que operaba con 2 tipos diferentes de vasija. La intención de su modelo es mejorar los diseños de este tipo de estufa. Amer [5] estableció un estudio orientado a describir la influencia de los componentes de una estufa solar en su operación térmica. Sus resultados permiten describir, a través de los valores logrados, dónde y cómo los valores de temperatura son más importantes en el dispositivo.

En general, el trabajo experimental con los dispositivos solares tiene muchas dificultades debido a la simplificación de las hipótesis necesarias para el diseño de los dispositivos o las variaciones climáticas y sus consiguientes efectos en los procesos de transferencia de calor, por ejemplo. Estas situaciones justifican el trabajo basado en la simulación numérica, como complemento en el desarrollo experimental.

El objetivo de este trabajo es aplicar un modelo matemático para obtener las eficiencias en una estufa solar de tipo caja con reflectores internos que tienen variaciones geométricas en sus ángulos. El modelo matemático definido es representado por un sistema de ecuaciones diferenciales que se obtiene por medio de balances energéticos para puntos de interés particular en la estufa. La estufa considerada en este trabajo está fabricada en madera y tiene una tapa que la cierra, compuesta de 2 vidrios. En su interior tiene un arreglo de reflectores fabricados con papel aluminio que están colocados en diferentes ángulos respecto a la horizontal y un recipiente que permite calentar líquidos, en este caso, agua.

Es importante señalar que el estudio realizado mediante la aplicación de métodos numéricos a una estufa solar de tipo caja con reflectores internos para evaluar sus eficiencias de 1.^a y 2.^a ley no ha sido tratado en la literatura especializada.

2. Modelo matemático

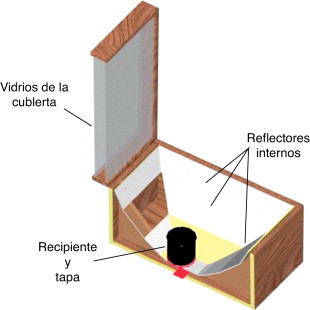
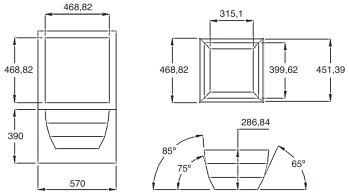
La estufa solar con reflectores internos que se considera en este trabajo se muestra en la figura 1 .

Figura 1. Estufa solar con reflectores internos.

La tapa de esta estufa solar, conformada por dos vidrios, busca reducir las pérdidas de calor por convección hacia el exterior y generar un efecto invernadero en su interior. El interior de la estufa tiene reflectores colocados en diferentes ángulos para dirigir la radiación solar hacia el recipiente que contiene el fluido que hay que calentar. El modelo matemático considerado para obtener las soluciones numéricas de interés en este trabajo está constituido por 5 ecuaciones diferenciales no lineales. Los elementos considerados en el modelo comprenden: los vidrios de la tapa, la tapa del recipiente, el recipiente y el fluido (agua). Un detalle de estos elementos puede verse en la figura 2 .

Figura 2. Partes de la estufa solar con reflectores internos.

El desarrollo completo del modelo matemático de la estufa puede consultarse en el trabajo de Terres [6] . Para el desarrollo del modelo se realizan las siguientes consideraciones y suposiciones:

• No se considera el gradiente de temperaturas en el espesor de los vidrios 1 y 2, en el recipiente, ni en la tapa. Esto provocaría un aumento de la cantidad de incógnitas que se deben determinar en el modelo matemático.
• La radiación solar es normal a los cuerpos receptores y no se toman en consideración los cambios por efecto de nubosidades, ya que se considera que la radiación normal a un cuerpo tiene una mayor concentración de energía que la que se provee de manera inclinada.
• Las propiedades radiativas como la absortancia (α ), la reflectancia (ρ ) y la transmitancia (τ ) se consideran constantes, puesto que los rangos de temperatura de la estufa solar (0 a 99 °C) no modifican las propiedades radiativas de los diferentes materiales que la componen. Además, el calor específico también es constante, es decir, c_v  = c_p  = c , en el caso de fluidos incompresibles.
• La tapa y el cuerpo del recipiente son del mismo material, por tanto, también son iguales sus propiedades radiativas.
• Los coeficientes de convección son constantes. Se hace esto para facilitar la solución numérica del modelo, sin embargo, esta suposición se encuentra debidamente justificada por el trabajo experimental realizado por Thulasi et al. [2] . Ya que el sistema es transitorio, el tiempo es una variable muy importante del modelo matemático. Esto se debe a que la temperatura ambiente y la radiación solar varían en el tiempo y son muy importantes para el funcionamiento de la estufa. Por tanto, cuanto mayor sea la cantidad de datos utilizados para la temperatura ambiente y la radiación solar, con más detalle se podrá estudiar el comportamiento de la estufa solar. El modelo obtenido se muestra en las ecuaciones (1) , (2) , (3) , (4)  and (5) , cuyas variables se definen en la nomenclatura, al comienzo del artículo.

Para el vidrio 1 (${\textstyle v_{1}}$ ):

$m_{v_{1}}c_{v_{1}}{\frac {{dT}_{v_{1}}}{dt}}=A_{v_{1}}G{\alpha }_{v_{1}}+A_{v_{1}}\sigma {\epsilon }_{v_{1}}\left(T_{v_{2}}^{4}-T_{v_{1}}^{4}\right)$ $-A_{v_{1}}h_{v_{1}\rightarrow {int}_{1}}\left(T_{v_{2}}-T_{v_{1}}\right)$ $-A_{v_{1}}\sigma {\epsilon }_{v_{1}}\left(T_{v_{1}}^{4}-{\left(0,0552T_{amb}^{1.5}\right)}^{4}\right)$ $-A_{v_{1}}h_{v_{1}\rightarrow amb}\left(T_{v_{1}}-T_{amb}\right)$

( 1)

Para el vidrio 2 (${\textstyle v_{2}}$ ):

$m_{v_{2}}c_{v_{2}}{\frac {{dT}_{v_{2}}}{dt}}={\tau }_{v_{2}}A_{v_{2}}G{\alpha }_{v_{2}}-A_{v_{2}}\sigma {\epsilon }_{v_{2}}\left(T_{v_{2}}^{4}-T_{v_{1}}^{4}\right)$ $-A_{v_{2}}h_{v_{2}\rightarrow {int}_{1}}\left(T_{v_{2}}-T_{v_{1}}\right)$ $+A_{\boldsymbol {\mbox{t}}}\sigma {\epsilon }_{\boldsymbol {\mbox{t}}}\left(T_{\boldsymbol {\mbox{t}}}^{4}-T_{v_{2}}^{4}\right)$ $-A_{v_{2}}h_{v_{2}\rightarrow {int}_{2}}\left({\frac {T_{v_{2}}+T_{\boldsymbol {\mbox{t}}}+T_{r}}{3}}-T_{v_{2}}\right)$ $-A_{r}\sigma {\epsilon }_{r}\left(T_{r}^{4}-T_{v_{2}}^{4}\right)$

( 2)

Para la tapa (t ):

$m_{\boldsymbol {\mbox{t}}}c_{\boldsymbol {\mbox{t}}}{\frac {{dT}_{\boldsymbol {\mbox{t}}}}{dt}}=-A_{\boldsymbol {\mbox{t}}}\sigma {\epsilon }_{\boldsymbol {\mbox{t}}}\left(T_{\boldsymbol {\mbox{t}}}^{4}-T_{v_{2}}^{4}\right)$ $+A_{\boldsymbol {\mbox{t}}}h_{{\boldsymbol {\mbox{t}}}\rightarrow {int}_{2}}\left(T_{\boldsymbol {\mbox{t}}}-T_{{int}_{2}}\right)$ $+A_{\boldsymbol {\mbox{t}}}G{\tau }_{v_{2}}^{2}{\alpha }_{\boldsymbol {\mbox{t}}}-A_{\boldsymbol {\mbox{t}}}h_{{\boldsymbol {\mbox{t}}}\rightarrow {int}_{3}}\left(T_{\boldsymbol {\mbox{t}}}-T_{f}\right)$ $-A_{\boldsymbol {\mbox{t}}}\sigma {\epsilon }_{\boldsymbol {\mbox{t}}}\left(T_{\boldsymbol {\mbox{t}}}^{4}-T_{f}^{4}\right)$

( 3)

Para el recipiente (r ):

$m_{r}c_{r}{\frac {{dT}_{r}}{dt}}=-A_{r}h_{r\rightarrow {int}_{2}}\left({\frac {T_{v_{2}}+T_{\boldsymbol {\mbox{t}}}+T_{r}}{3}}-T_{r}\right)$ $+4\sum _{i=1}^{n}\rho A_{ref,n}G{\tau }_{v_{2}}^{2}cos\left(90-{\theta }_{ref,n}\right)$ $-A_{r}\sigma {\epsilon }_{r}\left(T_{r}^{4}-T_{v_{2}}^{4}\right)-A_{r}\sigma {\epsilon }_{r}\left(T_{r}^{4}-T_{f}^{4}\right)$ $-A_{m}h_{r\rightarrow fl}\left(T_{r}-T_{f}\right)$

( 4)

Para el fluido (f ):

$m_{f}c_{f}{\frac {{dT}_{f}}{dt}}=A_{\boldsymbol {\mbox{t}}}h_{r\rightarrow {int}_{3}}\left(T_{\boldsymbol {\mbox{t}}}-T_{f}\right)+A_{\boldsymbol {\mbox{t}}}\sigma {\epsilon }_{\boldsymbol {\mbox{t}}}\left(T_{\boldsymbol {\mbox{t}}}^{4}-T_{f}^{4}\right)$ $A_{r}\sigma {\epsilon }_{r}\left(T_{r}^{4}-T_{f}^{4}\right)+A_{m}h_{r\rightarrow fl}\left(T_{r}-T_{f}\right)$

( 5)

La solución del modelo matemático representado por las ecuaciones diferenciales no lineales (1) , (2) , (3) , (4)  and (5) se obtuvo por el método de Runge-Kutta de cuarto orden, que permite estimar la evolución en el tiempo de las temperaturas en las diferentes partes de la estufa, utilizando como condiciones iniciales datos de la temperatura ambiente y de la radiación solar. La solución numérica del modelo se realizó mediante un programa de cómputo desarrollado en C++, el cual permite el estudio de diferentes casos de aplicación de estufas solares de tipo caja con reflectores internos. La validación del programa que da solución al modelo matemático obtenido en este trabajo muestra una diferencia máxima del 10% entre los valores experimentales considerados para las temperaturas en el modelo matemático y la solución numérica obtenida. En un trabajo previo presentado por Terres-Peña y Quinto-Diez [7] se muestran tanto la validación del programa de cómputo como algunas características relevantes de la solución numérica del modelo matemático.

3. Análisis de eficiencias en estufas solares con reflectores interiores

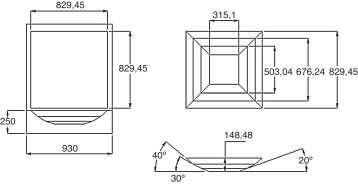
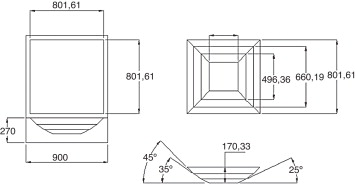
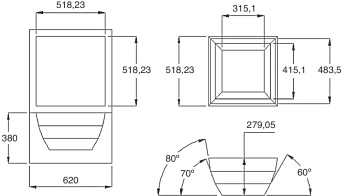
Para estudiar el comportamiento de las eficiencias en varias estufas se consideran los arreglos de estufas mostrados en las figuras Figura 3 , Figura 4 , Figura 5  and Figura 6 . Estos arreglos se establecieron teniendo en cuenta la afinidad y las características geométricas del recipiente. Además, se buscó que las modificaciones dieran una profundidad a la estufa para poder ponderar el efecto de los reflectores en el proceso de calentamiento del fluido. Los datos dimensionales de las estufas se pueden consultar en la tabla 1 .

Figura 3. Estufa solar 1 (ES-1). Acotación: mm.

Figura 4. Estufa solar 2 (ES-2). Acotación: mm.

Figura 5. Estufa solar 3 (ES-3). Acotación: mm.

Figura 6. Estufa solar 4 (ES-4). Acotación: mm.

Tabla 1. Dimensiones geométricas de estufas solares

Estufa solar(ES)	Reflector	Ángulo del reflector [grados]	Área del reflector [m2 ]	Área de los vidrios 1-2 [m2 ]	Espesor de los vidrios 1-2 [m ]	Área tapa del recipiente [m2 ]	Área superficial del recipiente [m2 ]	Fluido (agua) [kg ]
	1	20	0,0409
1	2	30	0,0589	0,6879	0,005	0,0314	0,0942	2
	3	40	0,0752
	1	25	0,0405
2	2	35	0,0578	0,6425	0,005	0,0314	0,0942	2
	3	45	0,0730
	1	60	0,0350
3	2	70	0,0449	0,2685	0,005	0,0314	0,0942	2
	3	80	0,0500
	1	65	0,0357
4	2	75	0,0425	0,2197	0,005	0,0314	0,0942	2
	3	85	0,0460

Para el análisis de eficiencias se han hecho las siguientes consideraciones:

• El recipiente en el interior de la estufa solar es un sistema cerrado.
• La pérdida de calor hacia el medio ambiente a los lados de la estufa solar es insignificante.
• El calor específico es constante, es decir c_v  = c_p  = c .
• La distribución de temperatura en las diferentes partes de la estufa es uniforme.

De acuerdo con Russell y Adebiyi [8] , las eficiencias termodinámicas para el recipiente dentro de la estufa solar son definidas como:

Eficiencia de 1.^a ley, definida en la ecuación (6) .

${\eta }_{I}={\frac {Q_{sale}}{Q_{entra}}}$

( 6)

donde:

$Q_{sale}=m(u_{final}-u_{inicial})$

( 7)

$Q_{entra}={\frac {A_{v_{1}}G\Delta t}{1.000}}$

( 8)

Eficiencia de 2.^a ley mediante exergía, definida en la ecuación (9) .

${\eta }_{II}={\frac {{\psi }_{sistema}}{Q_{entra}}}$

( 9)

Donde se establece:

${\psi }_{sistema}=(U-U_{0})+P_{0}(V-V_{0})-T(S-S_{0})$

( 10)

Considerando un fluido incompresible en un recipiente rígido, se tiene:

$(U-U_{0})\approx mc(T-T_{0})$

( 11)

$V\approx V_{0}$

( 12)

$S-S_{0}=mcln\left({\frac {T}{T_{0}}}\right)$

( 13)

Sustituyendo las ecuaciones (11) -(13) en (10) y simplificando, se tiene:

${\psi }_{sistema}=mcT_{0}\left[{\frac {T}{T_{0}}}-1-ln\left({\frac {T}{T_{0}}}\right)\right]$

( 14)

Es importante mencionar que las ecuaciones (11) y (13) son definidas en Russell y Adebiyi [8] , y corresponden al cambio de la energía interna y entropía respectivamente.

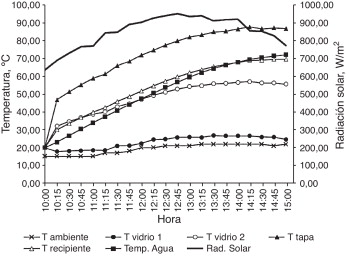
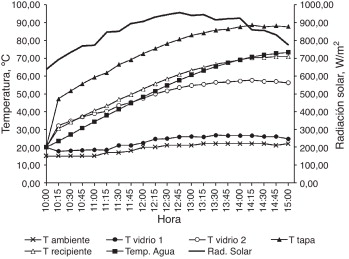
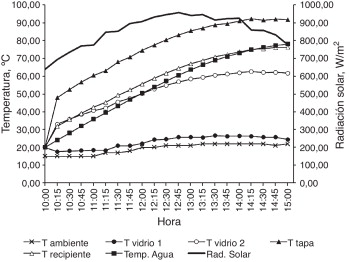
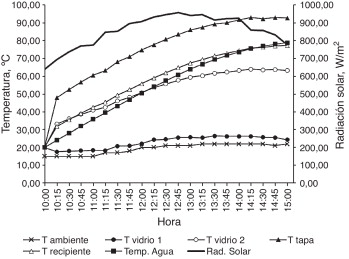
Para generar los resultados que deben ser utilizados en las ecuaciones (6) y (9) , se consideró la simulación de las estufas solares en un intervalo de 10:00 a 15:00 horas para un día promedio del mes de febrero en la Ciudad de México. En la evaluación se utilizaron 2 kg de agua como fluido. Los resultados obtenidos se muestran de manera gráfica en las figuras Figura 7 , Figura 8 , Figura 9  and Figura 10 .

Figura 7. Resultados numéricos para la estufa solar 1.

Figura 8. Resultados numéricos para la estufa solar 2.

Figura 9. Resultados numéricos para la estufa solar 3.

Figura 10. Resultados numéricos para la estufa solar 4.

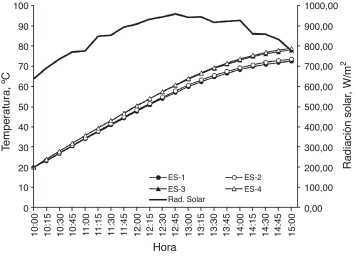
Los arreglos considerados fueron establecidos en términos de la operatividad que puede darse en la manipulación del recipiente contenedor del fluido, el cual se complica con una abertura menor. Los valores de temperatura del agua logrados son los que se utilizan para el cálculo de las eficiencias en las estufas consideradas. Una comparativa de las temperaturas del agua se muestra en la figura 11 .

Figura 11. Temperaturas del agua en las estufas solares.

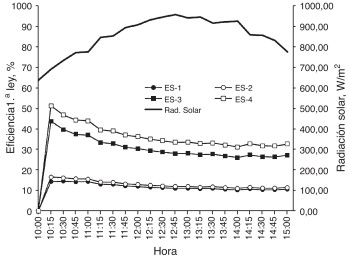
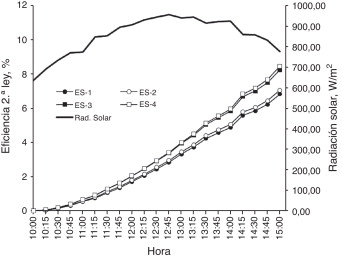
Aplicando las ecuaciones (6) y (9) a los resultados numéricos obtenidos se establecen las eficiencias de 1.^a y 2.^a ley para el desempeño de las estufas solares. En las figuras 12 y 13 se muestran los resultados obtenidos.

Figura 12. Eficiencias de 1.a ley para estufas solares.

Figura 13. Eficiencias de 2.a ley para estufas solares.

4. Discusión

Los valores presentados en las figuras Figura 7 , Figura 8 , Figura 9  and Figura 10 muestran el comportamiento térmico de las variables de la estufa que fueron consideradas para establecer el estudio, y permiten visualizar su evolución en el tiempo, por lo que se obtiene así una identificación general del comportamiento de la temperatura. Los valores de las temperaturas indican que el comportamiento es ${\textstyle T_{\boldsymbol {\mbox{t}}}>T_{r}>T_{f}>T_{v_{2}}>T_{v_{1}}}$ , el cual es consistente con el proceso de calentamiento en un recinto cerrado y expuesto a un medio de energía solar, como el caso de la estufa. La figura 11 muestra cómo el caso 4 para la estufa es el que permite lograr la mayor temperatura. Esto ocurre porque el área de reflexión provista por los reflectores es significativamente mayor respecto de los otros casos y particularmente de los casos 1 y 2. Las figuras 12 y 13 ilustran el comportamiento de las estufas bajo el concepto de eficiencias térmicas de 1.^a y 2.^a ley de la termodinámica. Por un lado, la figura 12 no contempla los efectos asociados a irreversibilidades, que ocurren principalmente por pérdidas en la estufa. En cambio, la figura 13 sí toma en consideración estos efectos y otros asociados a las consideraciones que dan sustento al modelo matemático de la estufa solar.

La máxima eficiencia de 2.^a ley obtenida es de 8,4 %, que corresponde a la ES-4 a las 15:00 horas. Para este mismo tiempo, la eficiencia de 1.^a ley para esta misma estufa es de 32,7 %. Aunque el valor de la eficiencia de 1.^a ley es importante, no representa el comportamiento real de la estufa. En cambio, la eficiencia de 2.^a ley sí lo representa porque considera el efecto del cambio de entropía que caracteriza la irreversibilidad del sistema, y con esto, las contribuciones de pérdidas que ocurren en el proceso de calentamiento.

Identificar el orden de magnitud de la eficiencia real en una estufa solar permite visualizar cuánto podría mejorarse si su eficiencia aumentara. Cabe destacar que Petela [9] determinó que, para una estufa cilíndrico-parabólica, la eficiencia de 1.^a ley (energía) es superior al 18%, y la eficiencia de 2.^a ley (exergía) es apenas superior al 1,6%. Por otro lado, Hüseyin [10] encontró que, para una estufa solar parabólica, la eficiencia de energía y exergía se encuentra en el rango de 2,8-15,7% y 0,4-1,25% respectivamente. Los datos antes referidos dan congruencia a los valores de las eficiencias térmicas establecidas en este trabajo. La razón principal por la que la eficiencia de 2.^a ley es baja se relaciona con el hecho de que la radiación solar que incide en la estufa no es usada completamente, dado que una parte significativa es absorbida por los vidrios, sobre todo por el vidrio 2. Esta situación puede apreciarse en los valores de las temperaturas de los vidrios de la tapa en la estufa solar, especialmente del vidrio 2. El valor máximo de las eficiencias de 1.^a y 2.^a ley corresponden a la ES-4, en virtud de que su configuración refleja en mayor medida la radiación solar hacia el recipiente.

El aumento de temperatura del fluido durante el proceso de calentamiento es debido a la combinación de la radiación solar y la temperatura ambiente. Cuando esta combinación se incrementa, también lo hace el rendimiento. Aunque los resultados muestran satisfactoriamente tanto el comportamiento térmico de la estufa como su eficiencia en condiciones variantes de sus ángulos reflectores, es importante señalar que esta información puede ser la referencia en el estudio de otros mecanismos relevantes en el proceso de calentamiento del fluido, tal como el efecto de la convección entre vidrios y la distribución de temperatura en el interior de la estufa, que puede realizarse, por ejemplo, mediante el método de los elementos finitos [11] , usando como condiciones iniciales los valores obtenidos en este trabajo.

5. Conclusiones

El análisis mostrado en este trabajo permite obtener información del comportamiento térmico de las estufas solares, que es muy útil y necesario en su definición y diseño. El trabajo expuesto en este artículo es de gran utilidad, dado que genera una dirección bien definida en la mejora del funcionamiento de las estufas solares que, según los resultados reportados, se centra en la cubierta de la estufa.

Es importante señalar que no hay referencias sobre trabajos previos que permitan cuantificar una comparativa de eficiencias para el tipo de estufa solar considerado en este estudio. De esta manera, se puede afirmar que los resultados logrados son los primeros de su tipo en el campo de aplicación orientado al diseño de estufas solares de tipo caja con reflectores internos.

El modelo matemático y la solución numérica empleados en este trabajo son de gran ayuda para generar resultados simulados en el caso aplicado a estufas solares del tipo estudiado, lo que permite comparar diseños distintos de una misma estufa solar bajo condiciones de operación idéntica. El análisis de 1.^a y 2.^a ley de la termodinámica muestra en qué medida se aprovecha la radiación solar en las estufas solares.

References

1. [1] A.A. El-Sebaii, R. Domanski; Experimental and Theoretical Investigation of a Box Type Solar Cooker with Multi-Step Inner Reflectors; Energy, 19 (10) (1994), pp. 1011–1021
2. [2] T.C. Thulasi Das, S. Karmakar, D.P. Rao; Solar Box Cooker: part I-modeling and part II-analysis and simulation; Solar Energy, 52 (3) (1994), pp. 274–295
3. [3] P.A. Funk, D.L. Larson; Parametric model of solar cooker performance; Solar Energy, 62 (1) (1998), pp. 63–68
4. [4] A.R. Reddy, A.V.N. Rao; Prediction and experimental verification of performance of box type solar cooker - Part I. Cooking vessel with central cylindrical cavity; Energy Conversion and Management, 48 (2007), pp. 2034–2043
5. [5] E.H. Amer; Theoretical and experimental assessment of a double exposure solar cooker; Energy Conversion and Management, 44 (2003), pp. 2651–2663
6. [6] H. Terres-Peña (2002), Diseño y evaluación numérica del funcionamiento de estufas solares tipo caja con reflectores interiores, Tesis de Maestría, SEPI-ESIME, IPN, México.
7. [7] H. Terres-Peña, P. Quinto-Diez; Applications of numerical simulation of solar cooker type box with multi-step inner reflector; Proceedings of ISEC 2003, International Solar Energy Conference, Hawaii, USA (2003) 44060
8. [8] L.D. Russell, G.A. Adebiyi; Classical Thermodynamics; Saunders College Publishing, Orlando, Florida, EUA (1993)
9. [9] R. Petela; Exergy analysis of the solar cylindrical-parabolic cooker; Solar Energy, 79 (3) (September 2005), pp. 221–233
10. [10] H. Hüseyin Öztürk; Experimental determination of energy and exergy efficiency of the solar parabolic-cooker; Solar Energy, 77 (1) (2004), pp. 67–71
11. [11] O.C. Zienkiewicz, R.L. Taylor, J.Z. Zhu, (1989, 1991), The finite element method. McGraw Hill, Vol. I, (1989), Vol. II (1991).