Robust adaptive fault tolerant control for nonlinear systems with actuator failure and mismatched disturbance

Abstract

In this paper, a class of nonlinear systems with mismatched disturbance and actuator failure is investigated. A disturbance observer is proposed to estimate the disturbance first and the error of the estimation converges to zero exponentially. By introducing an integral sliding mode surface, the disturbance observer-based integral sliding mode fault tolerant control scheme is proposed to attenuate the disturbance and guarantee the stability of the system. In particular, the control law is designed for decoupling the partial disturbance and attenuating the disturbance that cannot be decoupled. Finally, two examples are given to illustrate the effectiveness of the proposed method.

Keywords: Actuator fault, fault tolerant control (FTC), disturbance observer, adaptive integral sliding mode control, nonlinear system

1. Introduction

Faults frequently occur in the engineering system because of the increasing complexity and scalability of industrial applications. Unexpected deviations of performance or system parameters can induce serious damage and even break down the system in the presence of a fault. With the growing demand for higher reliability, safety, and maintainability, it is desired that the fault can be detected at the early stage, determine the location and magnitude of the fault, identify the severity of the fault, and then accommodate the effects on the system and provide an acceptable performance. Abundant of results have been reported on the theme and many achievements have been applied to industrial systems such as aircraft systems [1], electric systems [2], and motor systems [3-4], etc. Many excellent methods were exploited such as robust control [5], sliding mode control [6-7], observer-based control [8], intelligent learning control [9], and adaptive control [10-11].

As aforementioned, the fault is vulnerable to occur in the practical system, which certainly reduces the nominal performance, results in vibration, destroys the stability of the system, and even causes catastrophic accidents. Actuator fault as the most common fault has caused wide attention. In Ye and Yang [12], the flight tracking control system with actuator fault was investigated; an adaptive controller was designed. In Zuo et al. [13], a class of singular systems with actuator saturation was developed; an adaptive controller was designed to compensate for the fault effects through the linear matrix inequality (LMI) technique. A class of nonlinear large-scale systems with actuator fault was considered and an observer-based fuzzy adaptive control was developed in Tong et al. [14]. The problem of part loss of effectiveness of the actuator was addressed in Li and Yang [15]. In Van et al. [16], a class of nonlinear systems with partial loss of actuator was considered; a third-order sliding model control was developed to compensate for the actuator faults. These results have considered linear or nonlinear systems, however, the nonlinear function either satisfies the matched condition [16], i.e., the nonlinear function is in the control channel.

It is worth pointing out that disturbance exists widely in many industrial processes, which affects the stability of the system seriously. The basic characteristics of disturbance are its uncertainty, nonlinearity, and complexity. In some cases, the fault is considered as an additional uncertainty, disturbance, or nonlinear function in the system [16,17]. The common method is to make a compensator, i.e. construct an anti-disturbance mechanism to compensate for the disturbance. As the characteristics of the disturbance, observer design is necessary and popular in the existing literature, i.e., disturbance observer (DO). In Kempf and Kobayashi [18], a precision positioning table system was studied and a discrete time-tracking controller was designed based on the DO. In Chen et al. [19], the ball mill grinding circuits system was investigated and a DO was designed to estimate the strong disturbance, the controller was designed based on the observer to compensate for the disturbance. In Chen [20], a class of nonlinear systems was investigated, by introducing a disturbance generator; the DO-based control law was established. Yao and Guo [21] addressed a class of Markovian jump systems with multiple disturbances; the control law was designed by integrating the DO output information and state feedback control. Wu et al. [22] take an insight into a generic hypersonic vehicle system with modeled and unmodeled disturbances. In these results, the disturbance matrix $B_{d}$ and the control matrix $B$ are assumed to satisfy the match condition, i.e., $rank\left(B\right)=rank\left(\left[{\begin{array}{cc}B&B_{d}\end{array}}\right]\right)$, this limitation may not be applicable in some control processes.

It should be pointed out that the mismatched disturbance, that is, the disturbance enters the system in different channels, is more practical in industrial dynamic systems. In Zhang et al. [23], a class of nonlinear systems with actuator fault, sensor fault, and mismatched disturbance was considered. In Wei and Guo [24], the disturbance was considered as two parts, the matched disturbance was compensated by the DO while the mismatched disturbance was attenuated by variable structure control. In Yang et al. [25], by constructing a nonlinear disturbance observer (NDO), the sliding mode control scheme was developed to counteract the mismatched disturbance.

Based on the aforementioned analysis, this paper attempts to solve the FTC problem for a class of nonlinear systems with actuator fault and mismatched disturbance. The main works can be summarized as follows. First of all, an improved nonlinear disturbance observer is designed to estimate the mismatched disturbance. Then, the integral sliding mode controller is presented based on the observer, where the reachability of sliding motion is proved. Furthermore, the mismatched disturbance is divided into two parts, in which the matched part is compensated by the disturbance information while the remaining part is attenuated by the adaptive controller. Finally, the adaptive control law is proposed, which can adaptively adjust controller parameters to compensate for the fault and disturbance. The effectiveness of the method is verified through two examples.

The remaining part of this paper is organized as follows. In section 2, the system description and some assumptions are presented. In section 3, the construction of the observer and the design of the controller are presented. In section 4, two simulation examples are used to illustrate the effectiveness of the method, and some conclusions are obtained in section 5.

2. Problem formulation

Consider the following nonlinear system with actuator fault and mismatched disturbance as

$\left\{{\begin{array}{c}{\dot {x}}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+B_{d}d\left(t\right)+\Delta f\left(x,t\right)+\xi \left(x,t\right)\\y=Cx\left(t\right)\end{array}}\right.$

(1)

where $x\left(t\right)\in R^{n}$ is the state vector, $y\left(t\right)\in R^{q}$ is the output of the system, $u\left(t\right)\in R^{p}$ is the control input, $\Delta f\left(x,t\right)$ is a nonlinear function, which can be regarded as the un-modeled uncertainty, $d\left(t\right)\in R^{v}$ is the unmatched external disturbance, $\xi \left(x,t\right)$ is the mismatched nonlinearity, $A$, $B$, $B_{d}$, and $C$ are known constant coefficient matrices with appropriate dimensions.

In this paper, the actuator failure problem is concerned. The actuators can be divided into two parts $u_{H}$ and $u_{F}$, where $u_{H}$ stands for the health actuator and $u_{F}$ represent the actuator in a fault condition. Then system (1) becomes (2)

$\left\{{\begin{array}{c}{\dot {x}}\left(t\right)=Ax\left(t\right)+B_{H}u_{H}\left(t\right){\mbox{ }}+B_{F}u_{F}\left(t\right)+B_{d}d\left(t\right)+\Delta f\left(x,t\right)+\xi \left(x,t\right)\\y=Cx\left(t\right)\end{array}}\right.$

(2)

where ${\textstyle B_{H}}$ and ${\textstyle B_{F}}$ denote the healthy and fault matrices.

One can see that proposer designing of $u_{H}$ can guarantee the stability of the system despite the existence of external disturbance.

Assumption 1 [17]. The actuators in fault condition work abnormally, and the remaining actuators work normally.

With assumption 1, one can use ${\overline {u}}_{F}$ and $u_{F}$ represent the actual control and designed control respectively for the actuators in fault condition. Then system (2) becomes (3)

$\left\{{\begin{array}{c}{\dot {x}}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+B_{F}\Delta u_{F}\left(t\right)+B_{d}d\left(t\right)+\Delta f\left(x,t\right)+\xi \left(x,t\right)\\y=Cx\left(t\right)\end{array}}\right.$

(3)

where $\Delta u_{F}={\overline {u}}_{F}-u_{F}$.

Assumption 2 [15]. There exists a known function ${\overline {f}}\left(x\right)$ and two unknown constants ${\theta }_{0}$ and ${\upsilon }_{0}$ , such that the following inequality holds,

$\Delta f\left(x,t\right)\leq {\theta }_{0}{\overline {f}}\left(x\right)+{\upsilon }_{0}$.

(4)

Assumption 3. The disturbance and the derivative of the disturbance are bounded, i.e., $\Vert d\left(t\right)\Vert \leq {\epsilon }_{1}$, $\Vert {\dot {d}}\left(t\right)\Vert \leq {\epsilon }_{d}$, where ${\epsilon }_{1}$ and ${\epsilon }_{d}$ are two positive constants.

Assumption 4. The nonlinearity function $\xi \left(x,t\right)$ is bounded and satisfies the following condition

${\tilde {\xi }}{\left(x,t\right)}^{T}R\Delta {\tilde {\xi }}\left(x,t\right)\leq {\tilde {x}}{\left(x,t\right)}^{T}Q{\tilde {x}}\left(x,t\right)$

(5)

where $R$ and $Q$ are two positive symmetry matrices, ${\tilde {\xi }}\left(x,t\right)=\xi \left(x_{1},t\right)-$$\xi \left(x_{2},t\right)$, ${\tilde {x}}\left(x,t\right)=x_{1}\left(x,t\right)-x_{2}\left(x,t\right)$.

Remark 1. The assumption 1 is general for the actuator failure condition [16,17], in which the actuator fault can be treated as an additional uncertainty or disturbance. Compared with the results in [26], the assumption 2 in this study has been much more relaxed. Assumption 3 is common in FTC control results [15]. Assumption 4 is more general compared with the traditional Lipschitz condition [16], it should be noted that if $R{\mbox{=}}I$, and $Q=l_{f}{}^{2}I$, then assumption 4 degenerates to the normal Lipschitz condition, where $l_{f}$ is the Lipschitz constant.

With assumptions 1 and 2, the object of the paper is to design a control law to compensate for the effects of the disturbance and fault so that the stability and convergence of the system can be guaranteed in normal and fault conditions.

3. Main results

In this part, an observer will be applied to estimate the external disturbance, and an observer-based integral sliding mode fault colorant control scheme will be designed.

3.1 Observer design

For the feasibility of the observer, the following assumption is necessary.

Assumption 5 [16]. The additional fault term $\varphi \left(t\right)=B_{F}\Delta u_{F}\left(t\right)$ satisfies the following condition, $\Vert B_{F}\Delta u_{F}\left(t\right)\Vert \leq {\overline {\omega }}_{b}$, where ${\overline {\omega }}_{b}$ is a positive scalar.

For system (3), the following observer is proposed in the form of

$\left\{{\begin{array}{l}\quad {\dot {p}}\left(t\right)=-g\left(x\right)B_{d}p\left(t\right)-g\left(x\right)[B_{d}p\left(t\right)+Ax\left(t\right)\\\qquad \qquad +Bu\left(t\right){\mbox{ }}+{\overline {\omega }}_{b}+B_{d}d\left(t\right){\mbox{ }}+\Delta f\left(x,t\right)+\xi \left(x,t\right)]+T_{n}{\delta }_{n}\left(t\right)\\\quad {\overset {\mbox{ˆ}}{d}}\left(t\right)=p\left(t\right)+q\left(x\right)\end{array}}\right.$

(6)

where $p\left(t\right)$ is the internal state of the observer, ${\overset {\mbox{ˆ}}{d}}\left(t\right)$ is the estimation of the disturbance $d\left(t\right)$, $q\left(x\right)$ is a nonlinear function to be designed, $T_{n}$ is a parameter matrix with proper dimensions, and $g\left(x\right)$ is the observer gain and satisfies the following condition

$g\left(x\right)={\frac {\partial q\left(x\right)}{\partial x}}$

(7)

${\delta }_{n}$ is the error compensator and is defined by

${\delta }_{n}=-{\frac {T_{n}{}^{T}}{{\Vert T_{n}\Vert }^{2}}}{\delta }_{d}$

(8)

where ${\delta }_{d}={\overline {\omega }}_{b}-\Vert B_{F}\Delta u_{F}\left(t\right)\Vert$.

Lemma 1. With the assumption 4 and the observer (6), the error of the observer converges to zero exponentially.

Proof. Define $e_{d}\left(t\right)=d\left(t\right)-{\overset {\mbox{ˆ}}{d}}\left(t\right)$. From the observer (6), it is easy to obtain that

${\begin{array}{c}{\dot {\overset {\mbox{ˆ}}{d}}}\left(t\right)=-g\left(x\right)B_{d}p\left(t\right)-g\left(x\right)[B_{d}p\left(t\right)+Ax\left(t\right)+Bu\left(t\right)+{\overline {\omega }}_{b}\\+B_{d}d\left(t\right)+\Delta f\left(x,t\right)+\xi \left(x,t\right)]+{\frac {\partial q\left(x\right)}{\partial x}}{\dot {x}}\left(t\right)\\\quad =g\left(x\right)B_{d}e_{d}\left(t\right)+g\left(x\right)\left(B_{F}\Delta u_{F}\left(t\right)-{\overline {\omega }}_{b}\right)+T_{n}{\delta }_{n}\left(t\right)\end{array}}$

(9)

It can be derivate that

${\dot {e}}_{d}\left(t\right)=-g\left(x\right)B_{d}e_{d}\left(t\right)+$$g\left(x\right)\left(B_{F}\Delta u_{F}\left(t\right)-{\overline {\omega }}_{b}\right)+$${\dot {d}}\left(t\right)-T_{n}{\delta }_{n}\left(t\right)$

(10)

The solution of (9) is given by

$e_{d}{\mbox{=}}e^{-g\left(x\right)B_{d}t}e_{d}\left(0\right)+$${\int }_{0}^{t}e^{-g\left(x\right)B_{d}\left(t-s\right)}{\dot {d}}\left(s\right)ds-$${\int }_{0}^{t}e^{-g\left(x\right)B_{d}\left(t-s\right)}g\left(x\right)\left(B_{F}\Delta u_{F}\left(s\right)-\right.$$\left.{\overline {\omega }}_{b}-T_{n}{\delta }_{n}\left(t\right)\right)ds$

(11)

From Eq.(10), one can deduce that

${\begin{array}{c}e_{d}\leq \Vert e^{-g\left(x\right)B_{d}t}e_{d}\left(0\right)\Vert +{\int }_{0}^{t}\Vert e^{-g\left(x\right)B_{d}\left(t-s\right)}{\dot {d}}\left(s\right)\Vert ds\\+{\int }_{0}^{t}\Vert e^{-g\left(x\right)B_{d}\left(t-s\right)}g\left(x\right)\left(\Vert B_{F}\Delta u_{F}\left(s\right)\Vert -{\overline {\omega }}_{b}-T_{n}{\delta }_{n}\left(t\right)\right)\Vert ds\\\leq \Vert e^{-g\left(x\right)B_{d}t}e_{d}\left(0\right)\Vert +{\int }_{0}^{t}\Vert e^{-g\left(x\right)B_{d}\left(t-s\right)}{\epsilon }_{d}\Vert ds{\mbox{ }}\end{array}}$

(12)

According to the inequality $\Vert e^{At}\Vert \leq ce^{-\rho t}$ [3], where $c$ and $\rho$ are two positive constants. The one can obtain that

${\begin{array}{c}e_{d}\leq \Vert e^{-g\left(x\right)B_{d}t}e_{d}\left(0\right)\Vert +{\int }_{0}^{t}\Vert e^{-g\left(x\right)B_{d}\left(t-s\right)}{\epsilon }_{d}\Vert {\mbox{ }}ds\\=ce^{-\rho t}h_{0}+c{\int }_{0}^{t}{\epsilon }_{d}e^{-\rho \left(t-s\right)}ds\\=ce^{-\rho t}h_{0}+{\frac {c{\epsilon }_{d}}{\rho }}\left(1-e^{-\rho t}\right)\end{array}}$

(13)

where $h_{0}$ is a constant bound satisfy $\Vert e_{d}\left(0\right)\Vert \leq h_{0}$ . Define ${\overline {\kappa }}=ce^{-\rho t}h_{0}+{\frac {c{\epsilon }_{d}}{\rho }}\left(1-\right.$$\left.e^{-\rho t}\right)$ , then (13) can be written as $e_{d}\leq {\overline {\kappa }}$ . This completes the proof.

3.2 Adaptive FTC design

In this section, the observer-based integral sliding mode fault tolerant control will be designed. ${\overline {\kappa }}$ and ${\upsilon }_{0}$ are supposed to be unknown, the adaptive controller is designed as follows:

$u\left(t\right)=u_{m}\left(t\right)+u_{n}\left(t\right)$

(14)

where

$u_{m}\left(t\right)=\left(K_{1}\left(t\right)+K_{2}\left(t\right)+\right.$$\left.K_{3}\left(t\right)\right)x\left(t\right)-\left(K_{d1}+\right.$$\left.K_{d2}\right){\overset {\mbox{ˆ}}{d}}\left(t\right)$

(15)

$u_{n}\left(t\right)=u_{1}\left(t\right)+u_{2}\left(t\right)+$$u_{3}\left(t\right)$

(16)

where $K_{1}\left(t\right)$, $K_{2}\left(t\right)$, $K_{3}\left(t\right)$ $K_{d1}\left(t\right)$ and $K_{d2}\left(t\right)$ are the parameter functions to be designed

$u_{1}\left(t\right)=-{\frac {{\left(DB\right)}^{-1}DB_{d}B_{d}{}^{T}D^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)DB_{d}\Vert }}\left({\overset {\mbox{ˆ}}{\overline {\kappa }}}+\right.$$\left.{\lambda }_{1}\right)$

(17)

$u_{2}\left(t\right)=-{\frac {{\left(DB\right)}^{-1}DD^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)D\Vert }}\left({\overset {\mbox{ˆ}}{\delta }}_{m}+\right.$$\left.{\overset {\mbox{ˆ}}{\upsilon }}_{0}+{\lambda }_{2}\right)$

(18)

$u_{3}\left(t\right)=-{\frac {{\left(DB\right)}^{-1}D{\overline {f}}\left(x\right){\overline {f}}{\left(x\right)}^{T}D^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)D{\overline {f}}\left(x\right)\Vert }}{\gamma }_{1}^{_{\ast }}$

(19)

where ${\lambda }_{1}$ and ${\lambda }_{2}$ are two positive scalars, ${\upsilon }_{1}\geq {\upsilon }_{0}$ , ${\gamma }_{1}^{_{\ast }}\geq {\gamma }_{1}$ and ${\gamma }_{1}$ is defined in Eq.(23), ${\delta }_{m}$ is the bound of the nonlinear function $\xi \left(x,t\right)$, ${\overset {\mbox{ˆ}}{\overline {\kappa }}}$, ${\overset {\mbox{ˆ}}{\upsilon }}_{0}$ and ${\overset {\mbox{ˆ}}{\delta }}_{m}$ are the estimate of ${\overline {\kappa }}$, ${\upsilon }_{0}$ and ${\delta }_{m}$ , and the adaptive control laws are designed in the form of

${\dot {\overset {\mbox{ˆ}}{\overline {\kappa }}}}={\chi }_{q}\left(\Vert s^{T}\left(t\right)DB_{d}\Vert +\right.$$\left.{\beta }_{q}\right)$

(20)

${\dot {\overset {\mbox{ˆ}}{\upsilon }}}_{0}={\chi }_{p}\left(\Vert s^{T}\left(t\right)D\Vert +\right.$$\left.{\beta }_{p}\right)$

(21)

${\dot {\overset {\mbox{ˆ}}{\delta }}}_{m}={\chi }_{r}\left(\Vert s^{T}\left(t\right)D\Vert +\right.$$\left.{\beta }_{r}\right)$

(22)

where ${\chi }_{p}$ ${\chi }_{q}$, ${\chi }_{r}$, ${\beta }_{p}$, ${\beta }_{q}$ and ${\beta }_{r}$ are positive parameters.

The control law will be used in the integral sliding mode control, $u_{m}$ is used to make the system asymptotically stable, $u_{n}$ is used to compensate for the effects of the actuator fault, disturbance estimation error, and nonlinear factors. In this paper, the sliding mode switching function is designed as follows

$s\left(t\right)=Dx\left(t\right)-Dx\left(0\right)-$$D{\int }_{0}^{t}\left(Ax\left(\tau \right)+Bu_{m}\left(\tau \right)+\right.$$\left.B_{d}{\overset {\mbox{ˆ}}{d}}\left(\tau \right)\right)d\tau$

(23)

where $D\in R^{p\times n}$ is a designed matrix that $DB$ is invertible. In the next section, the reaching ability will be verified.

Theorem 1. With the controller in Eq.(14), the state strategies of the system will drive onto the sliding surface $s\left(t\right)$ in finite time.

Proof. Denote ${\tilde {\overline {\kappa }}}={\overline {\kappa }}-{\overset {\mbox{ˆ}}{\overline {\kappa }}}$, ${\tilde {\upsilon }}_{0}={\upsilon }_{0}-{\overset {\mbox{ˆ}}{\upsilon }}_{0}$, ${\tilde {\delta }}_{m}={\delta }_{m}-{\overset {\mbox{ˆ}}{\delta }}_{m}$ . Consider the following Lyapunov function candidate

$V\left(t\right)={\frac {1}{2}}s{\left(t\right)}^{T}s\left(t\right)+$${\frac {1}{2{\chi }_{q}}}{\tilde {\overline {\kappa }}}^{2}+$${\frac {1}{2{\chi }_{p}}}{\tilde {\upsilon }}_{0}{}^{2}$

(24)

From the expression (20), the time derivative of $s\left(t\right)$ is

${\begin{array}{c}{\dot {s}}\left(t\right)=D\left(Ax\left(t\right)+Bu\left(t\right){\mbox{ }}+B_{F}\Delta u_{F}\left(t\right){\mbox{ }}+B_{d}d\left(t\right){\mbox{ }}\right)-DAx\left(t\right)\\-DBu_{m}\left(t\right)-DB_{d}{\overset {\mbox{ˆ}}{d}}\left(t\right)+D\left(\Delta f\left(x,t\right)+\xi \left(x,t\right)\right)\\=DBu_{n}\left(t\right)+DB_{F}\Delta u_{F}\left(t\right)+DB_{d}d\left(t\right)\\-DB_{d}{\overset {\mbox{ˆ}}{d}}\left(t\right)+D\Delta f\left(x,t\right)+D\xi \left(x,t\right)\end{array}}$

(25)

From assumption 2, one has

${\theta }_{0}\leq {\gamma }_{1}$

(26)

From Eq.(23), one has

${\begin{array}{c}{\dot {s}}\left(t\right)=DBu_{n}\left(t\right)+DB_{F}\Delta u_{F}\left(t\right)+DB_{d}d\left(t\right)-DB_{d}{\overset {\mbox{ˆ}}{d}}\left(t\right)+D\Delta f\left(x,t\right)+D\xi \left(x,t\right)\\\leq -{\frac {DB_{d}B_{d}{}^{T}D^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)DB_{d}\Vert }}\left({\overline {\kappa }}+{\lambda }_{1}\right)-{\frac {DD^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)D\Vert }}\left({\delta }_{m}+{\upsilon }_{0}+{\lambda }_{2}\right)-{\frac {D{\overline {f}}\left(x\right){\overline {f}}{\left(x\right)}^{T}D^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)D{\overline {f}}\left(x\right)\Vert }}{\gamma }_{1}\\+DB_{d}e_{d}\left(t\right)+D\left({\gamma }_{1}{\overline {f}}\left(x\right)+\xi \left(x,t\right)+B_{F}\Delta u_{F}\left(t\right)+{\nu }_{0}\right)\end{array}}$

(27)

The time derivative of Eq.(35) can be determined as

${\dot {V}}\left(t\right)=s{\left(t\right)}^{T}{\dot {s}}\left(t\right)+$${\frac {1}{{\chi }_{q}}}{\tilde {\overline {\kappa }}}{\dot {\overset {\mbox{ˆ}}{\overline {\kappa }}}}+$${\frac {1}{{\chi }_{p}}}{\tilde {\upsilon }}_{0}{\dot {\overset {\mbox{ˆ}}{\upsilon }}}_{0}+$${\frac {1}{{\chi }_{r}}}{\tilde {\delta }}_{m}{\dot {\overset {\mbox{ˆ}}{\delta }}}_{m}$

(28)

By introducing Eqs.(17)-(27), Eq.(28) can be rewritten as

${\begin{array}{c}{\dot {V}}\left(t\right)\leq -{\frac {s{\left(t\right)}^{T}DB_{d}B_{d}{}^{T}D^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)DB_{d}\Vert }}\left({\overset {\mbox{ˆ}}{\overline {\kappa }}}+{\lambda }_{1}\right)+\Vert s{\left(t\right)}^{T}DB_{d}\Vert {\overline {\kappa }}-{\frac {s{\left(t\right)}^{T}DD^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)D\Vert }}\\\left({\overset {\mbox{ˆ}}{\delta }}_{m}+{\overset {\mbox{ˆ}}{\upsilon }}_{0}+{\lambda }_{2}\right)+\Vert s{\left(t\right)}^{T}D\Vert \left({\delta }_{m}+{\upsilon }_{0}\right)\\-{\frac {s{\left(t\right)}^{T}D{\overline {f}}\left(x\right){\overline {f}}{\left(x\right)}^{T}D^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)D{\overline {f}}\left(x\right)\Vert }}{\gamma }_{1}^{_{\ast }}+{\gamma }_{1}\Vert s{\left(t\right)}^{T}D{\overline {f}}\left(x\right)\Vert -{\tilde {\overline {\kappa }}}\\\left(\Vert s^{T}\left(t\right)DB_{d}\Vert +{\beta }_{q}\right)-{\tilde {\upsilon }}_{0}\left(\Vert s^{T}\left(t\right)D\Vert +{\beta }_{p}\right)\\-{\tilde {\delta }}_{m}\left(\Vert s^{T}\left(t\right)D\Vert +{\beta }_{r}\right)<-{\lambda }_{1}\Vert s^{T}\left(t\right)DB_{d}\Vert -{\lambda }_{2}\Vert s^{T}\left(t\right)D\Vert <0\end{array}}$

(29)

Thus, the reaching ability is satisfied, this completes the proof.

Remark 2. The controller proposed in (14) is discontinuous, to reduce chattering in the practical implementation, the discontinuous function can be replaced, for example, $u_{1}\left(t\right)$ can be replaced by $-{\frac {{\left(DB\right)}^{-1}DB_{d}B_{d}{}^{T}D^{T}s\left(t\right)}{\Vert s^{T}\left(t\right)DB_{d}\Vert +\alpha }}\left({\overset {\mbox{ˆ}}{\overline {\kappa }}}+\right.$$\left.{\lambda }_{1}\right)$, where $\alpha$ is a small positive constant.

3.3 Stability analysis

In this section, the stability of the closed-loop system will be analyzed. By solving the equation ${\dot {s}}\left(t\right)=0$ in Eq.(25), the equivalent control law can be obtained as

$u_{eq}\left(t\right)=-{\left(DB\right)}^{-1}DB_{F}\Delta u_{F}\left(t\right)-$${\left(DB\right)}^{-1}DB_{d}e_{d}\left(t\right)-{\left(DB\right)}^{-1}D\Delta f\left(x,t\right)-$${\left(DB\right)}^{-1}D\xi \left(x,t\right)$

(30)

Substituting Eqs.(26) and (30) into the system (3) yields

${\dot {x}}\left(t\right)=\left(A+B\left(K_{1}\left(t\right)+\right.\right.$$\left.\left.K_{2}\left(t\right)+K_{3}\left(t\right)\right)\right)x\left(t\right)-$$BK_{d}{\overset {\mbox{ˆ}}{d}}\left(t\right)+B_{F}\Delta u_{F}\left(t\right){\mbox{ }}+$$\Delta f\left(x,t\right)+\xi \left(x,t\right)+B_{d}d\left(t\right){\mbox{ }}-$$B{\left(DB\right)}^{-1}DB_{F}\Delta u_{F}\left(t\right)-$$B{\left(DB\right)}^{-1}DB_{d}e_{d}\left(t\right)-B{\left(DB\right)}^{-1}D\left(\Delta f\left(x,t\right)+\right.$$\left.\xi \left(x,t\right)\right)$

(31)

By defining $K_{d}{}_{1}={\left(DB\right)}^{-1}DB_{d}$, ${\overline {B}}_{d}=B_{d}-B{\left(DB\right)}^{-1}DB_{d}$, ${\overline {M}}=I-B{\left(DB\right)}^{-1}D$, Eq.(31) can be rewritten as

${\dot {x}}\left(t\right)=\left(A+B\left(K_{1}\left(t\right)+\right.\right.$$\left.\left.K_{2}\left(t\right)+K_{3}\left(t\right)\right)\right)x\left(t\right)+$${\overline {B}}_{d}d\left(t\right)-BK_{d2}{\overset {\mbox{ˆ}}{d}}\left(t\right)+$${\overline {M}}B_{F}\Delta u_{F}\left(t\right){\mbox{ }}+$${\overline {M}}\left(\Delta f\left(x,t\right)+\xi \left(x,t\right)\right)$

(32)

As before mentioned, the disturbance-matched condition is not satisfied, i.e. $rank\left(B\right)<rank\left(B,B_{d}\right)$. From the definition of ${\overline {B}}_{d}$, we can easily check that $rank\left(B\right)<rank\left(B,{\overline {B}}_{d}\right)$. In this paper, the disturbance is divided into two parts, i.e.,

${\overline {B}}_{d}=\left[{\begin{array}{cc}{\overline {B}}_{d_{1}}&{\overline {B}}_{d_{2}}\end{array}}\right]$, $d={\left[{\begin{array}{cc}d_{1}&d_{2}\end{array}}\right]}^{T}$,

then ${\overline {B}}_{d}d\left(t\right)$ can be written as

${\overline {B}}_{d}d\left(t\right)={\overline {B}}_{d1}d_{1}\left(t\right)+$${\overline {B}}_{d2}d_{2}\left(t\right)$,

where

${\begin{array}{l}{\overline {B}}_{d_{1}}=\left[{\begin{array}{cccc}{\overline {B}}_{d_{\kappa 1}}&{\overline {B}}_{d_{\kappa 2}}&...&{\overline {B}}_{d_{\kappa m1}}\end{array}}\right]\in R^{n\times m_{1}},\\{\overline {B}}_{d_{2}}=\left[{\begin{array}{cccc}{\overline {B}}_{d_{\theta 1}}&{\overline {B}}_{d_{\theta 2}}&...&{\overline {B}}_{d_{\theta m2}}\end{array}}\right]\in R^{n\times m_{2}},\\d_{1}={\left[{\begin{array}{cccc}d_{\kappa 1}&d_{\kappa 2}&...&d_{\kappa m_{1}}\end{array}}\right]}^{T}\in R^{m_{1}\times 1},\\d_{2}={\left[{\begin{array}{cccc}d_{\theta 1}&d_{\theta 2}&...&d_{\theta m_{1}}\end{array}}\right]}^{T}\in R^{m_{2}\times 1},\\m_{1}+m_{2}=\nu \end{array}}$

Let $rank\left(B\right)=rank\left(B,{\overline {B}}_{d{\mbox{1}}}\right)$, $rank\left(B\right)<rank\left(B,{\overline {B}}_{d2}\right)$ and the parameter $K_{d2}$ in Eq.(15) can be chosen as $K_{d2}=\left[{\begin{array}{cccc}K_{s1}&K_{s1}&...&K_{s\upsilon }\end{array}}\right]\in R^{p\times \upsilon }$, where $BK_{si}={\overline {B}}_{d\kappa i}$ for $i\leq m_{1}$ and $K_{si}=0$ for $i>m_{1}$. Then the equation $BK_{d2}={\overline {B}}_{d{\mbox{1}}}$ is solvable. Note that ${\overline {M}}=B{\tilde {M}}$ and ${\tilde {M}}=\left(B^{\dagger }-{\left(DB\right)}^{-1}D\right)$, where $B^{\dagger }=B^{T}{\left(BB^{T}\right)}^{-1}$. Then (32) can be rewritten as

${\dot {x}}\left(t\right)=\left(A+B\left(K_{1}\left(t\right)+\right.\right.$$\left.\left.K_{2}\left(t\right)+K_{3}\left(t\right)\right)\right)x\left(t\right)+$${\overline {B}}_{d2}d_{2}\left(t\right)+{\overline {B}}_{d1}e_{d1}\left(t\right)+$$B{\tilde {M}}B_{F}\Delta u_{F}\left(t\right){\mbox{ }}+B{\tilde {M}}\left(\Delta f\left(x,t\right)+\right.$$\left.\xi \left(x,t\right)\right)$

(33)

Remark 3. We can see that if ${\overline {B}}_{d2}=0$, then $rank\left(B\right)=rank\left(B,{\overline {B}}_{d}\right)$, so the matched condition is a special case, i.e., this paper considers a more general case. In addition, we can also obtain that one of the solutions of $K_{d2}$ is $K_{si}=B^{\dagger }{\overline {B}}_{d\kappa i}$ and $B^{\dagger }$ is the general inverse of $B$.

The object of the next part is to design $K_{1}\left(t\right)$, $K_{2}\left(t\right)$ and $K_{3}\left(t\right)$ such that the stability of the system can be guaranteed. The control laws are designed as follows

$K_{1}\left(t\right)=-{\frac {{\overset {\mbox{ˆ}}{\varpi }}B^{T}P\Vert x^{T}P\Vert }{{\Vert x^{T}PB\Vert }^{2}}}$

(34)

$K_{2}\left(t\right)=-{\frac {K_{d2}{\overset {\mbox{ˆ}}{w}}_{1}{\overline {B}}_{d1}{}^{T}P}{\Vert x^{T}P{\overline {B}}_{d1}\Vert }}$

(35)

$K_{3}\left(t\right)=-{\frac {{\tilde {M}}{\overset {\mbox{ˆ}}{\gamma }}^{2}{}_{1}{\overline {f}}^{2}\left(x\right){\tilde {M}}^{T}B^{T}P}{\Vert x^{T}PB{\tilde {M}}\Vert {\overline {f}}\left(x\right){\overset {\mbox{ˆ}}{\gamma }}_{1}+\sigma \left(t\right)}}$

(36)

where ${\overset {\mbox{ˆ}}{w}}_{1}$, ${\overset {\mbox{ˆ}}{\varpi }}$ and ${\overset {\mbox{ˆ}}{\gamma }}_{1}$ are estimations of $w_{1}$, $\varpi$ and ${\gamma }_{1}$, respectively, $w_{1}$ and $\varpi$ are designed in Eqs.(59) and (60), $P$ is a positive symmetry matrix, and $\sigma \left(t\right)$ is a continuous function, and satisfies

${\int }_{0}^{\infty }\sigma \left(t\right)dt\leq {\sigma }^{_{\ast }}<\infty$ .

(37)

where ${\sigma }^{_{\ast }}$ is a positive scalar.

The adaptive updating control laws are given by

${\dot {\overset {\mbox{ˆ}}{\varpi }}}=-{\beta }_{1}{\overset {\mbox{ˆ}}{\varpi }}\sigma \left(t\right)+$$2{\beta }_{1}\Vert x^{T}P\Vert$

(38)

${\dot {\overset {\mbox{ˆ}}{w}}}_{1}=-{\beta }_{2}{\overset {\mbox{ˆ}}{w}}_{1}\sigma \left(t\right)+$$2{\beta }_{2}\Vert x^{T}PB_{d1}\Vert$

(39)

${\dot {\overset {\mbox{ˆ}}{\gamma }}}_{1}=-{\beta }_{3}{\overset {\mbox{ˆ}}{\gamma }}_{1}\sigma \left(t\right)+$$2{\beta }_{3}\Vert x^{T}PB{\tilde {M}}\Vert {\overline {f}}\left(x\right)$

(40)

where ${\beta }_{1}$, ${\beta }_{2}$ and ${\beta }_{3}$ are three positive constants.

Denote ${\tilde {\varpi }}=\varpi -{\overset {\mbox{ˆ}}{\varpi }}$, ${\tilde {w}}_{1}=w_{1}-{\overset {\mbox{ˆ}}{w}}_{1}$, ${\tilde {\gamma }}_{1}={\gamma }_{1}-{\overset {\mbox{ˆ}}{\gamma }}_{1}$, we can obtain the following dynamics

${\dot {\tilde {\varpi }}}=-{\beta }_{1}{\tilde {\varpi }}\sigma \left(t\right)+$${\beta }_{1}\varpi \sigma \left(t\right)-2{\beta }_{1}\Vert x^{T}P\Vert$

(41)

${\dot {\tilde {w}}}_{1}={\beta }_{2}w_{1}\sigma \left(t\right)-$${\beta }_{2}{\tilde {w}}_{1}\sigma \left(t\right)-2{\beta }_{2}\Vert x^{T}PB_{d1}\Vert$

(42)

${\tilde {\gamma }}_{1}={\beta }_{3}{\gamma }_{1}\sigma \left(t\right)-$${\beta }_{3}{\tilde {\gamma }}_{1}\sigma \left(t\right)-$$2{\beta }_{3}\Vert x^{T}PB{\overline {M}}\Vert {\overline {f}}\left(x\right)$

(43)

Theorem 2. With the controller (34)-(36) and the adaptive control laws (38)-(40), the closed-loop system is stable if there exist two positive symmetry matrices $P$ and $Q$ , such that the following condition holds

$\left[{\begin{array}{cc}PA+A^{T}P+Q&P_{1}\\{_{\ast }}&-I\end{array}}\right]<0$

(44)

where $P_{1}=PB{\tilde {M}}$, ${\textstyle Q}$ is defined in Eq.(5).

Proof. Design the Lyapunov function candidate as

$V\left(t\right)=x{\left(t\right)}^{T}Px\left(t\right)+$${\frac {1}{2{\beta }_{1}}}{\tilde {\varpi }}^{2}+{\frac {1}{2{\beta }_{2}}}{\tilde {w}}_{1}{}^{2}+$${\frac {1}{2{\beta }_{3}}}{\tilde {\gamma }}_{1}{}^{2}$

(45)

Then the time derivative of Eq.(51) can be obtained as

${\begin{array}{c}{\dot {V}}\left(t\right)=2x{\left(t\right)}^{T}P{\dot {x}}\left(t\right)+{\frac {1}{{\beta }_{1}}}{\tilde {\varpi }}{\dot {\tilde {\varpi }}}+{\frac {1}{{\beta }_{2}}}{\tilde {w}}_{1}{\dot {\tilde {w}}}_{1}+{\frac {1}{{\beta }_{3}}}{\tilde {\gamma }}_{1}{\dot {\tilde {\gamma }}}_{1}\\=2x{\left(t\right)}^{T}P\left(\left(A+B\left(K_{1}\left(t\right)+K_{2}\left(t\right)+K_{3}\left(t\right)\right)\right)x\left(t\right)+{\overline {B}}_{d1}e_{d1}\right)+2x{\left(t\right)}^{T}P\left(B{\tilde {M}}B_{F}\Delta u_{F}\left(t\right){\mbox{ }}+{\overline {B}}_{d2}d_{2}\left(t\right)\right)\\+2x{\left(t\right)}^{T}PB{\tilde {M}}\Delta f\left(x,t\right)+2x{\left(t\right)}^{T}PB{\tilde {M}}\xi \left(x,t\right)+{\frac {1}{{\beta }_{1}}}{\tilde {\varpi }}{\dot {\tilde {\varpi }}}+{\frac {1}{{\beta }_{2}}}{\tilde {w}}_{1}{\dot {\tilde {w}}}_{1}+{\frac {1}{{\beta }_{3}}}{\tilde {\gamma }}_{1}{\dot {\tilde {\gamma }}}_{1}\end{array}}$

(46)

From Eqs.(41)-(46), it can be derivative that

$2x^{T}\left(t\right)PBK_{1}\left(t\right)x\left(t\right)=$$-2x^{T}\left(t\right)PB{\frac {{\overset {\mbox{ˆ}}{\varpi }}B^{T}P\Vert x^{T}P\Vert }{{\Vert x^{T}PB\Vert }^{2}}}=$$-2{\overset {\mbox{ˆ}}{\varpi }}\Vert x^{T}P\Vert$

(47)

$2x^{T}\left(t\right)PBK_{2}\left(t\right)x\left(t\right)=$$-2x^{T}\left(t\right)PB{\frac {K_{d2}{\overset {\mbox{ˆ}}{w}}_{1}{\overline {B}}_{d1}{}^{T}P}{\Vert x^{T}P{\overline {B}}_{d1}\Vert }}=$$-2\Vert x^{T}P{\overline {B}}_{d1}\Vert {\overset {\mbox{ˆ}}{w}}_{1}$

(48)

$2x^{T}\left(t\right)PBK_{3}\left(t\right)x\left(t\right)=$$-2{\frac {{\overset {\mbox{ˆ}}{\gamma }}^{2}{}_{1}{\overline {f}}^{2}\left(x\right){\Vert x^{T}PB{\tilde {M}}\Vert }^{2}}{\Vert x^{T}PB{\tilde {M}}\Vert {\overline {f}}\left(x\right){\overset {\mbox{ˆ}}{\gamma }}_{1}+\sigma \left(t\right)}}$

(49)

${\begin{array}{c}{\frac {1}{{\beta }_{1}}}{\tilde {\varpi }}{\dot {\tilde {\varpi }}}={\frac {1}{{\beta }_{1}}}{\tilde {\varpi }}\left(-{\beta }_{1}{\tilde {\varpi }}\sigma \left(t\right)+{\beta }_{1}\varpi \sigma \left(t\right)-2{\beta }_{1}\Vert x^{T}P\Vert \right)\\=-{\tilde {\varpi }}^{2}\sigma \left(t\right)+{\tilde {\varpi }}\varpi \sigma \left(t\right)-2{\tilde {\varpi }}\Vert x^{T}P\Vert \end{array}}$

(50)

${\begin{array}{c}{\frac {1}{{\beta }_{2}}}{\tilde {w}}_{1}{\dot {\tilde {w}}}_{1}={\frac {1}{{\beta }_{2}}}{\tilde {w}}_{1}\left({\beta }_{2}w_{1}\sigma \left(t\right)-{\beta }_{2}{\tilde {w}}_{1}\sigma \left(t\right)-2{\beta }_{2}\Vert x^{T}PB_{d1}\Vert \right)\\={\tilde {w}}_{1}w_{1}\sigma \left(t\right)-{\tilde {w}}^{2}{}_{1}\sigma \left(t\right)-2{\tilde {w}}_{1}\Vert x^{T}PB_{d1}\Vert \end{array}}$

(51)

${\begin{array}{c}{\frac {1}{{\beta }_{3}}}{\tilde {\gamma }}_{1}{\dot {\tilde {\gamma }}}_{1}={\frac {1}{{\beta }_{3}}}{\tilde {\gamma }}_{1}\left({\beta }_{3}{\gamma }_{1}\sigma \left(t\right)-{\beta }_{3}{\tilde {\gamma }}_{1}\sigma \left(t\right)-2{\beta }_{3}\Vert x^{T}PB{\tilde {M}}\Vert \right)\\={\tilde {\gamma }}_{1}{\gamma }_{1}\sigma \left(t\right)-{\tilde {\gamma }}^{2}{}_{1}\sigma \left(t\right)-2{\tilde {\gamma }}_{1}\Vert x^{T}PB{\tilde {M}}\Vert \end{array}}$

(52)

By assumptions 2, 4, 5, and lemma 1, we can derivative that the following inequalities hold

$\Vert B{\tilde {M}}B_{F}\Delta u_{F}\left(t\right)\Vert +$$\Vert {\overline {B}}_{d2}\Vert \Vert d_{2}\left(t\right)\Vert +$$\Vert B{\tilde {M}}{\upsilon }_{0}\Vert \leq \varpi$

(53)

$e_{d1}\leq w_{1}$

(54)

${\begin{array}{c}2x{\left(t\right)}^{T}PB{\tilde {M}}\xi \left(x,t\right)\leq 2\Vert x{\left(t\right)}^{T}PB{\tilde {M}}\Vert \Vert \xi \left(x,t\right)\Vert \\\leq {\Vert x{\left(t\right)}^{T}PB{\tilde {M}}\Vert }^{2}+{\Vert \xi \left(x,t\right)\Vert }^{2}=x{\left(t\right)}^{T}\left(P_{1}{}^{T}P_{1}+Q\right)x\left(t\right)\end{array}}$

(55)

where $\varpi$ and $w_{1}$ are positive scalars.

Substituting Eqs.(47)-(55), Eq.(46) can be rewritten as

${\dot {V}}\left(t\right)\leq x{\left(t\right)}^{T}\left(PA+\right.$$\left.A^{T}P+P_{1}{}^{T}P_{1}+Q\right)x\left(t\right)-2{\overset {\mbox{ˆ}}{\varpi }}\Vert x^{T}P\Vert +$$\Vert 2x{\left(t\right)}^{T}P{\overline {B}}_{d1}\Vert w_{1}$ $-2{\frac {{\overset {\mbox{ˆ}}{\gamma }}^{2}{}_{1}{\overline {f}}^{2}\left(x\right){\Vert x^{T}PB{\tilde {M}}\Vert }^{2}}{\Vert x^{T}PB{\tilde {M}}\Vert {\overline {f}}\left(x\right){\overset {\mbox{ˆ}}{\gamma }}_{1}+\sigma \left(t\right)}}$$-2{\tilde {\gamma }}_{1}\Vert x^{T}PB{\tilde {M}}\Vert +2{\gamma }_{1}\Vert x^{T}P{\tilde {M}}\Vert {\overline {f}}\left(x\right)$ $-2\Vert x^{T}P{\overline {B}}_{d1}\Vert {\overset {\mbox{ˆ}}{w}}_{1}+\Vert 2x{\left(t\right)}^{T}P\Vert \varpi -2{\tilde {\varpi }}\Vert x^{T}P\Vert -2{\tilde {w}}_{1}\Vert x^{T}PB_{d1}\Vert$

(56)

Note that the following equalities

$\Vert 2x{\left(t\right)}^{T}P\Vert w_{1}-2\Vert x^{T}P{\overline {B}}_{d1}\Vert {\overset {\mbox{ˆ}}{w}}_{1}+$$2{\tilde {w}}_{1}\Vert x^{T}PB_{d1}\Vert =0$

(57)

$\Vert 2x{\left(t\right)}^{T}P\Vert \varpi -2{\overset {\mbox{ˆ}}{\varpi }}\Vert x^{T}P\Vert -$$2{\tilde {\varpi }}\Vert x^{T}P\Vert =0$

(58)

$2{\gamma }_{1}\Vert x^{T}P{\tilde {M}}\Vert {\overline {f}}\left(x\right)-$$2{\tilde {\gamma }}_{1}\Vert x^{T}PB{\tilde {M}}\Vert {\overline {f}}\left(x\right)-$$2{\frac {{\overset {\mbox{ˆ}}{\gamma }}^{2}{}_{1}{\overline {f}}^{2}\left(x\right){\Vert x^{T}PB{\tilde {M}}\Vert }^{2}}{\Vert x^{T}PB{\tilde {M}}\Vert {\overline {f}}\left(x\right){\overset {\mbox{ˆ}}{\gamma }}_{1}+\sigma \left(t\right)}}=$${\frac {2{\overset {\mbox{ˆ}}{\gamma }}_{1}\Vert x^{T}P{\tilde {M}}\Vert {\overline {f}}\left(x\right)\sigma \left(t\right)}{\Vert x^{T}P{\tilde {M}}\Vert {\overline {f}}\left(x\right){\overset {\mbox{ˆ}}{\gamma }}_{1}+\sigma \left(t\right)}}$

(59)

Substituting Eqs.(57)-(59) into (56) yields

${\dot {V}}\left(t\right)\leq x{\left(t\right)}^{T}\left(PA+\right.$$\left.A^{T}P+P_{1}{}^{T}P_{1}+Q\right)x\left(t\right)-\sigma \left(t\right)\left({\tilde {\varpi }}^{2}-\right.$$\left.{\tilde {\varpi }}\varpi \right)-\sigma \left(t\right)\left({\tilde {w}}^{2}{}_{1}-\right.$$\left.{\tilde {w}}_{1}w_{1}+{\tilde {\gamma }}^{2}{}_{1}-{\tilde {\gamma }}_{1}{\gamma }_{1}\right)+$${\frac {2{\overset {\mbox{ˆ}}{\gamma }}_{1}\Vert x^{T}P{\tilde {M}}\Vert {\overline {f}}\left(x\right)\sigma \left(t\right)}{\Vert x^{T}P{\tilde {M}}\Vert {\overline {f}}\left(x\right){\overset {\mbox{ˆ}}{\gamma }}_{1}+\sigma \left(t\right)}}$

(60)

For any positive scalar ${\lambda }_{m}$ and ${\lambda }_{n}$ , the following equality holds $0\leq {\frac {{\lambda }_{m}{\lambda }_{n}}{{\lambda }_{m}+{\lambda }_{n}}}\leq {\lambda }_{n}$. Then we can obtain that

${\dot {V}}\left(t\right)\leq x{\left(t\right)}^{T}\left(PA+\right.$$\left.A^{T}P+P_{1}{}^{T}P_{1}+Q\right)x\left(t\right)+{\zeta }_{\kappa }\sigma \left(t\right)$

(61)

where ${\zeta }_{\kappa }=2+{\frac {1}{4}}\left({\varpi }^{2}+w^{2}{}_{1}+{\gamma }^{2}{}_{1}\right)$.

According to Eq.(45), by integrating Eq.(61) yields

${\begin{array}{c}V\left(t\right)\leq V\left(t_{0}\right)-{\int }_{t_{0}}^{t}{\lambda }_{\min }\left(Q_{1}\right){\Vert x\left(s\right)\Vert }^{2}ds+{\int }_{t_{0}}^{t}{\zeta }_{\kappa }\sigma \left(s\right)ds\\\leq V\left(t_{0}\right)-{\int }_{t_{0}}^{t}{\lambda }_{\min }\left(Q_{1}\right){\Vert x\left(s\right)\Vert }^{2}ds+{\zeta }_{\kappa }{\sigma }^{_{\ast }}\end{array}}$

(62)

which means the system described in Eq.(33) is bounded. ${\lambda }_{\min }\left(Q{}_{}^{1}\right)$ denotes the minimum eigenvalue of $Q_{1}$, and $-Q_{1}=A^{T}P+PA+P_{1}{}^{T}P_{1}+Q$. Eq.(68) also implies

${\int }_{t_{0}}^{t}{\lambda }_{\min }\left(Q_{1}\right){\Vert x\left(s\right)\Vert }^{2}ds\leq V\left(t_{0}\right)+$${\zeta }_{\kappa }{\sigma }^{_{\ast }}$

(63)

According to Barbalat Lemma, we have ${\underset {t\rightarrow \infty }{\lim }}{\Vert x\left(t\right)\Vert }^{2}=$$0$. This completes the proof.

Remark 4. Compared with the results in [15], where the nonlinear function is matched, i.e., $\Delta f\left(x,t\right)$ is in the control channel. In this paper, $\Delta f\left(x,t\right)$ exists in the different channel from the control input, i.e., which means that $\Delta f\left(x,t\right)$ is more general.

4. Numerical examples

In this section, two examples are simulated to illustrate the effectiveness of the proposed method.

Example 1. In this example, the linearized longitudinal dynamic of the VTOL aircraft which is borrowed from [23] is considered. It is assumed that the system is subjected to unmodeled dynamics, actuator fault, and external disturbance. Then, the system can be described as system (1), where $x\left(t\right)={\left[{\begin{array}{cccc}x_{1}\left(t\right)&x_{2}\left(t\right)&x_{3}\left(t\right)&x_{4}\left(t\right)\end{array}}\right]}^{T}$, $x_{1}\left(t\right)$ is the horizontal velocity ($knot$), $x_{2}\left(t\right)$ represents the vertical velocity ($knot$), $x_{3}\left(t\right)$ is the pitch rate ($degree/s$), and $x_{4}\left(t\right)$ expresses the pitch angle ($degree$). The parameters of the system are given as follows

$A=\left[{\begin{array}{cccc}-9.9477&-0.7476&0.2632&5.0337\\52.1659&2.7452&5.5532&-24.4221\\26.0922&2.6361&-4.1975&-19.2774\\0&0&1&0\end{array}}\right]$ , $B=\left[{\begin{array}{cc}0.4422&0.1761\\3.5446&-7.5922\\-5.5200&4.4900\\0&0\end{array}}\right]$, $C=\left[{\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&1&1&1\end{array}}\right]$ , $B_{d}=\left[{\begin{array}{cc}0.4422&0.116\\3.5446&-0.102\\-5.5200&0\\0&0\end{array}}\right]$ , $B_{F}=\left[0.1767.5924.4900\right]$.

The nonlinear unmodeled uncertainty and mismatched nonlinearity are assumed to be: $\Delta f\left(x,t\right)=\sin \left(x_{4}\right)$, $\xi \left(x,t\right)=\sin \left(x_{1}\right)$. The actuator fault and external are supposed to be as follows

$f\left(t\right)=\left\{{\begin{array}{c}0\left(0\leq t<8\right)\\0.5\sin \left(2t+1\right)\left(8\leq t<10\right)\\0\left(10\leq t<15\right)\end{array}}\right.$ , $\left\{{\begin{array}{c}d_{1}\left(t\right)=2\sin \left(2t+1\right)\left(0\leq t<15\right)\\d_{2}\left(t\right)=0.5\sin \left(2t-3\right){\mbox{ }}\left(0\leq t<15\right)\end{array}}\right.$.

Note that the mismatched disturbance and the condition $rank\left(B\right)\not =rank\left(B,{\overline {B}}_{d}\right)$ hold, hence that the traditional method will be failed in this example. Choosing the matrix $D=\left[{\begin{array}{cccc}1&0&1&0\\-1&1&0&1\end{array}}\right]$ , we can check that $DB$ is invertible. By solving (50), we can obtain that

$P=\left[{\begin{array}{cccc}14843&161.7&226.9&-745.0\\161.7&25.50&12.80&-101.8\\226.9&12.80&74.80&-47.40\\745.0&-101.8&-47.40&896.5\end{array}}\right]$ .

Choose $\sigma \left(t\right)=2e^{-t}$, the results of the simulation are as follows.

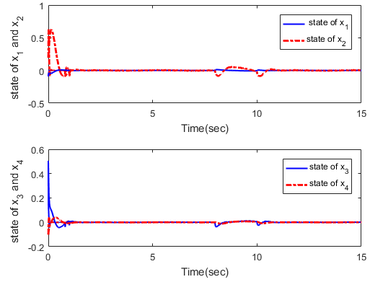
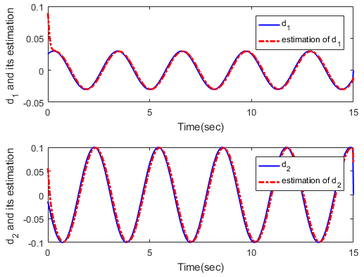
Figure 1 shows the trajectory of the system. Figure 2 illustrates the estimation of the disturbance signals, the solid line is the original signal and the dashed line is the estimated value. From Figure 1, we can know that the states of the system have a fast response with the proposed method. In addition, the controller can ensure the stability of the system in the presence of the actuator fault and mismatched disturbance. Figure 2 characterizes that the observer has a good performance of the disturbance.

Figure 1. Response of state $x\left(t\right)$

Figure 2. Estimation of disturbance $d\left(t\right)$

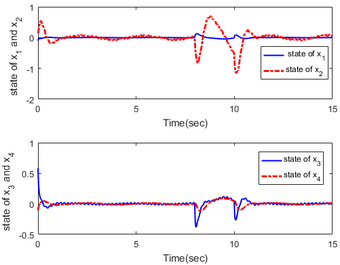
In order to illustrate the importance of the disturbance observer, the responses of the system are shown in Figure 3 without the disturbance observer. From the figure, we can see that the closed-loop system becomes unstable when removing the disturbance observer and compensator.

Figure 3. Response of state $x\left(t\right)$ without disturbance compensator

Example 2. In this section, the two-cart system which borrowed form is provided to illustrate the effectiveness of the proposed method [27].

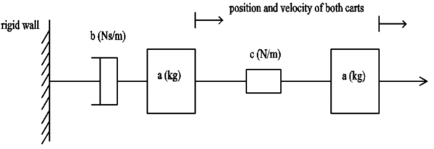
As shown in Figure 4, the first cart is connected to a rigid wall via a damper, and is connected to a second cart by a spring. The external force is applied to a second cart via an actuator. Both carts have a nominal mass of $a=1kg$, the damper has a constant of $b_{0}=1N/m$, and the spring constant $c_{0}=1N/m$. The time constant of the actuator $\tau =0.2$. The states are the force, velocities, and positions of the two carts. The actuator fault and mismatched disturbance are considered. The system parameters are given as follows

$A=\left[{\begin{array}{ccccc}-\displaystyle {\frac {1}{\tau }}&0&0&0&0\\0&-\displaystyle {\frac {b_{0}}{a}}&0&-\displaystyle {\frac {c_{0}}{a}}&\displaystyle {\frac {c_{0}}{a}}\\\displaystyle {\frac {1}{a}}&0&0&\displaystyle {\frac {c}{a}}&-\displaystyle {\frac {c_{0}}{a}}\\0&1&0&0&0\\0&0&1&0&0\end{array}}\right]$ , $B=\left[{\begin{array}{c}\displaystyle {\frac {1}{\tau }}\\0\\0\\0\\0\end{array}}\right]$ , $B_{F}=\left[{\begin{array}{c}\displaystyle {\frac {1}{\tau }}\\0\\0\\0\\0\end{array}}\right]$ , $C=\left[{\begin{array}{ccccc}0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\end{array}}\right]$ , $B_{d}=\left[{\begin{array}{cc}1&1\\0&0.2\\0&0.2\\0&0.1\\0&0.2\end{array}}\right]$.

Figure 4. Geometric structure of the two-cart system

The nonlinear unmodeled uncertainty and mismatched nonlinearity are assumed to be: $\Delta f\left(x,t\right)=\sin \left(x_{4}\right)$, $\xi \left(x,t\right)=\sin \left(x_{1}\right)$. The actuator fault and external are supposed to be as follows

$f\left(t\right)=\left\{{\begin{array}{c}0\left(0\leq t<{\mbox{25}}\right)\\{\mbox{0}}{\mbox{.5}}\sin \left(0.2t\right)\left({\mbox{25}}\leq t<4{\mbox{0}}\right)\\{\mbox{1}}\left(4{\mbox{0}}\leq t<{\mbox{80}}\right)\end{array}}\right.$ , $d_{1}\left(t\right){\mbox{=}}\left\{{\begin{array}{c}0\left(0\leq t<15\right)\\0.5\sin \left(t\right)\left(15\leq t<50\right)\\{\mbox{1}}\left({\mbox{5}}0\leq t<80\right)\end{array}}\right.$ , $d_{2}\left(t\right)=\left\{{\begin{array}{c}0.5\sin \left({\mbox{3}}t\right)\left(0\leq t<20\right)\\0.5\sin \left({\mbox{3}}t\right)\left(20\leq t<50\right)\\1\left(50\leq t<80\right)\end{array}}\right.$.

Choosing the matrix $D=\left[{\begin{array}{ccccc}1&0&0&0&0\end{array}}\right]$, we can check that $DB$ is invertible. By solving Eq.(50), we can obtain that

$P=\left[{\begin{array}{ccccc}{\mbox{0}}{\mbox{.0799}}&-0.000&-0.000&-0.000&-0.000\\-0.000&1.1046&0.000&-0.000&-0.000\\-0.000&0.000&1.1046&0.000&-0.000\\-0.000&-0.000&0.000&1.1046&0.000\\-0.000&-0.000&-0.000&0.000&1.1046\end{array}}\right]$.

Choose $\sigma \left(t\right)=2e^{-t}$ , the results of the simulation are as follows.

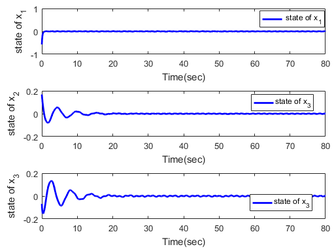
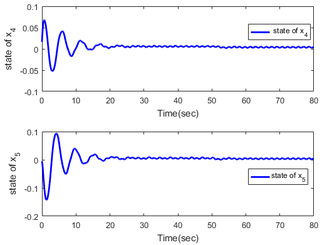
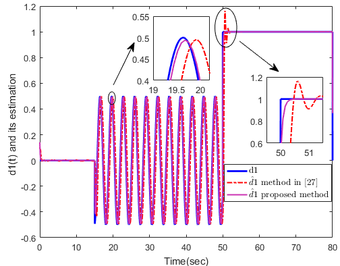
Figures 5 and 6 express the trajectories of the system. From Figures 5 and 6, we can see that the stability of the positions and velocities of the first and second carts can be guaranteed. Figure 7 shows the estimation of the external disturbance, we can check that the proposed method performs better than the intermediate method proposed in [27], precisely, the method proposed responds faster than the method in [27], and the proposed method has less chattering.

Figure 5. Response of state $x_{1}\left(t\right)$ , $x_{2}\left(t\right)$ and $x_{3}\left(t\right)$

Figure 6. Response of state $x_{4}\left(t\right)$ and $x_{5}\left(t\right)$

Figure 7. Estimation of disturbance $d\left(t\right)$

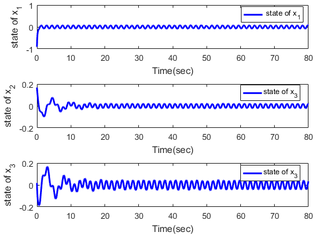
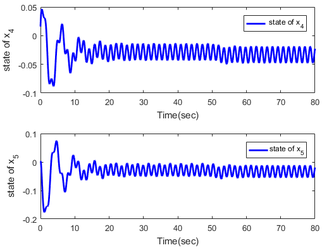
In order to illustrate the effectiveness of the proposed method, the responses of the system are shown in Figures 8 and 9 without the controller. From the figure, we can infer from this that the closed-loop system becomes unstable when removing the disturbance observer and compensator.

Figure 8. Response of state $x_{1}\left(t\right)$ , $x_{2}\left(t\right)$ and $x_{3}\left(t\right)$ without controller

Figure 9. Response of state $x_{\mbox{4}}\left(t\right)$ and $x_{\mbox{5}}\left(t\right)$ without controller

5. Conclusion

In this paper, the problem of a general Lipschitz nonlinear system with actuator fault and unmatched disturbance is investigated. Specifically, a disturbance observer is designed to estimate the mismatched disturbance first. Then, an observer-based integral sliding mode fault tolerant control scheme is proposed. In order to guarantee the stability of the system, three adaptive control laws are constructed because of the unknown nonlinear function parameters and the unmodeled uncertainty. Finally, two examples are given to illustrate the effectiveness of the proposed method. In our future work, we would like to focus on the fault-tolerant control methods for multiple faults and disturbances and their applications.

References

[1] Xiao B., Hu Q., Zhang Y. Adaptive sliding mode fault tolerant attitude tracking control for flexible spacecraft under actuator saturation, IEEE Trans. control Syst. Technol, 20(6):1605–1612, 2012.

[2] Wang R., Wang J. Passive actuator fault-tolerant control for a class of over actuated nonlinear systems and applications to electric vehicles, IEEE Trans. Veh. Technol., 62(3):972–985, 2013.

[3] Lin F.J., Hung Y.C., Tsai M.T. Fault-tolerant control for six-phase PMSM drive system via intelligent complementary sliding mode control using TSKFNN-AMF, IEEE Trans. Ind. Electron., 60(12):5747–5762, 2013.

[4] Shao J., Deng Z., Gu Y. Fault-tolerant control of position signals for switched reluctance motor drives, IEEE Trans Ind. Appli., 53(3):2959-2966, 2017.

[5] Wang Y., Xie L., de Souza C.E. Robust control of a class of uncertain nonlinear systems, Syst. Control Lett., 19(2):139–149, 1992.

[6] Shi P., Liu M., Zhang L. Fault-tolerant sliding mode observer synthesis of Markovian jump systems using quantized measurements, IEEE Trans. Ind. Electron., 62(9):5910–5918, 2015.

[7] Hu Q., Xiao B. Fault-tolerant sliding mode attitude control for flexible spacecraft under loss of actuator effectiveness, Nonlin. Dyn., 64(1):13–23, 2011.

[8] Kommuri S.K., Defoort M., Karimi H.R., Veluvolu K.C. A robust observer-based sensor fault-tolerant control for PMSM in electric vehicles, IEEE Trans. Ind. Electron., 63(12):7671–7681, 2016.

[9] Patan K. Neural network-based model predictive control: Fault tolerance and stability, IEEE Trans. Control Syst. Technol., 23(3):1147–1155, 2015.

[10] Yang G.H., Ye D. Reliable control of linear systems with adaptive mechanism, IEEE Trans. Autom. Control, 55(1):242–247, 2010.

[11] Wang W., Wen C.Y. Adaptive actuator failure compensation control of uncertain nonlinear systems with guaranteed transient performance, Automatica, 46(12):2082–2091, 2010.

[12] Ye D., Yang G.H. Adaptive fault-tolerant tracking control against actuator faults with application to flight control, IEEE Trans. Control Syst. Technol., 14:1088–1096, 2006.

[13] Zuo Z., Ho D.W.C., Wang Y. Fault tolerant control for singular systems with actuator saturation and nonlinear perturbation, Automatica, 46(3):569–576, 2010.

[14] Tong S.C., Huo B., Li Y.M. Observer-based adaptive decentralized fuzzy fault-tolerant control of nonlinear large-scale systems with actuator failures, IEEE Trans. Fuzzy Syst., 22(1):1–15, 2014.

[15] Li Y.X., Yang G.H. Robust adaptive fault-tolerant control for a class of uncertain nonlinear time delay systems, IEEE Trans. Syst, Man, Cybern, Syst., 47(7):1554-1563, 2017.

[16] Van M., Ge S.S., Ren H. Robust fault-tolerant control for a class of second-order nonlinear systems using an adaptive third-order sliding mode control, IEEE Trans. Syst, Man, Cybern, Syst., 47(2):221-228, 2017.

[17] Liang Y.W., Xu S.D., Tsai C.L. Study of VSC reliable designs with application to spacecraft attitude stabilization, IEEE Trans. Control Syst. Technol., 15(2):332–338, 2007.

[18] Kempf C.J., Kobayashi S. Disturbance observer and feed forward design for a high-speed direct-drive position table, IEEE Trans. Control Syst. Technol., 7(5):513–526, 1999.

[19] Chen X.S., Yang J., Li S.H., Li Q. Disturbance observer based multi-variable control of ball mill grinding circuits, J. Process Control, 19(7):1205–1213, 2009.

[20] Chen W.H. Disturbance observer based control for nonlinear systems, IEEE/ASME Trans. Mechatronics, 9(4):706–710, 2004.

[21] Yao X., Guo L. Composite anti-disturbance control for Markovian jump nonlinear systems via disturbance observer, Automatica, 49(8):2538–2545, 2013.

[22] Wu H.N., Liu Z.Y., Guo L. Robust $L_{\infty }$-gain fuzzy disturbance observer-based control design with adaptive bounding for a hypersonic vehicle, IEEE Trans. Fuzzy Syst., 22(6):1401–1412, 2014.

[23] Zhang H., Han J., Luo C., Wang Y. Fault-tolerant control of a nonlinear system based on generalized fuzzy hyperbolic model and adaptive disturbance observer, IEEE Trans. Syst, Man, Cybern, Syst., 47(8):2289-2300, 2017.

[24] Wei X.J., Guo L. Composite disturbance-observer-based control and H-infinity control for complex continuous models, Int. J. Robust Nonlinear Control, 20(1):106–118, 2009.

[25] Yang J., Li S., Yu X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer, IEEE Trans. Ind. Electron., 60 (1):160-169, 2013.

[26] Wu H.S. Adaptive robust tracking and model following of uncertain dynamical systems with multiple time delays, IEEE Trans. Autom. Control, 49(4):611–616, 2004.

[27] Zhu J.W., Yang G.H. Fault-tolerant control for linear systems with multiple faults and disturbances based on augmented intermediate estimator, IET Control Theory & Applications, 11(2):164-172, 2017.