Entropy generation in a micropolar fluid flow through an inclined channel

Abstract

In this paper the entropy generation is studied due to micropolar fluid flow through an inclined channel of parallel plates with constant pressure gradient. The lower plate is maintained at constant temperature and upper plate at a constant heat flux. The governing equations are solved by applying the spectral quasilinearization method. The velocity, microrotation and temperature profiles are obtained numerically and are used to calculate the entropy generation number. The influence of pertinent parameters on velocity, microrotation, temperature, entropy generation and Bejan number is discussed with the help of graphs. The results reveal that the entropy generation number increases with the increase in Brinkman number and angle of inclination. Further, it is observed that the increase in coupling number, Prandtl number and Reynolds number reduces the entropy generation number.

Keywords

Micropolar fluid; Spectral quasilinearization; Entropy; Bejan number

1. Introduction

The production of thermal and engineering devices is concerned by irreversible losses that lead to increase the entropy and decrease system efficiency. Thus it is important to find the factors that minimize the entropy generation and maximize the flow system efficiency. To analyze the irreversibilities in the form of entropy generation, the second law of thermodynamics is applied. Factors that are responsible for the irreversibility are heat transfer across finite temperature gradients, characteristics of convective heat transfer and viscous dissipation. Most of the energy related applications such as cooling of modern electronic systems, solar power collectors, and geothermal energy systems depend on entropy generation. Several investigations ([1], [2] and [3]) were carried out on entropy generation under various flow configurations.

Fluid flow and heat transfer inside channels with simple geometry and different boundary conditions is one of the fundamental areas of research in engineering. It has wide range of applications such as thermal insulation engineering, electronics cooling and water movement in geothermal reservoirs. Recently, a wide literature on fluid flow, heat transfer and entropy generation in various channels has been developed. Havzali et al. [4] investigated the entropy generation of incompressible, viscous fluid flow through an inclined channel with isothermal boundary conditions. They observed that the entropy generated in a small section is dominant on the total entropy produced in the entire system. Komurgoz et al. [5] discussed the entropy generation of porous-fluid layers contained in an inclined channel by using the differential transform method. Karamallah et al. [6] studied the consequence of differential heat isothermal walls on entropy generation of a vertical square channel saturated with porous media. Liu and Lo [7] performed a numerical analysis on the entropy generation within a mixed convection magneto hydrodynamic (MHD) flow in a parallel-plate vertical channel. They observed that the minimum entropy generation number and the maximum Bejan number occur at centerline region of the channel under asymmetric heating conditions. Makinde and Eegunjobi [8] addressed the irreversibility analysis in the flow of couple stress fluid through a porous medium. Damseh et al. [9] studied the presence of transverse magnetic field on entropy generation due to laminar forced convection flow in a channel. Das and Jana [10] investigated the combined effects of Navier slips, suction/injection and magnetic field on entropy generation in a porous channel by considering the constant pressure gradient. Chen and Liu [11] numerically investigated the viscous dissipation effect on entropy generation due to mixed convection nanofluid flow within a vertical channel.

The study of heat transfer has much importance in high temperature processes such as nuclear plants, gas turbines, thermal energy storage. Different kinds of boundary conditions are applied in heat transfer processes. Thermal boundary conditions, heat flux boundary conditions and convective boundary conditions are commonly encountered in heat transfer processes. The effects of these boundary conditions on entropy generation for any fluid flow of different geometries have been studied by several authors. Mahmud and Fraser [12] applied second law of thermodynamics to analyze the heat transfer and fluid motion in rotating concentric cylinders using heat flux boundary conditions. Iman [13] investigated the importance of thermal boundary conditions of the heated/cooled walls in the development of flow and heat transfer, and observed the characteristics of entropy generation in a porous enclosure. Antar and El-Shaarawi [14] investigated the effects of uniform heat flux boundary conditions on entropy generation over a rotating solid sphere with forced convection. Butt et al. [15] presented the effects of hydrodynamic slip on entropy generation in a viscous flow over a vertical plate with convective boundary conditions. Anandalakshmi and Basak [16] studied the effect of various heating patterns (different heating and Rayleigh–Benard convection) on entropy generation in a porous rhombic enclosure for different Pr and inclination angles. Anand [17] discussed the velocity slip effect on heat transfer and entropy generation of fully developed power law fluid flow in a micro channel. Mostafa and Ali [18] presented the effect of slip boundary condition on entropy generation for Newtonian and non-Newtonian fluid flows through a parallel plates channel. Ibanez [19] studied the combined effects of magnetic field, suction/injection Reynolds number and hydrodynamic slip on the entropy generation subjected to convective boundary conditions.

The majority of these studies deal with the traditional Newtonian fluids. The study of Newtonian fluids is not sufficient to characterize the flow properties of polymeric fluids, animal blood, coal slurries, mine tailings and mineral suspensions. Such properties are described in non-Newtonian fluid flow model. Many fluids in nature and industrial processes show a non-Newtonian fluid behavior. A number of mathematical models were proposed to explain the rheological behavior of non-Newtonian fluids. One among them is micropolar fluid introduced by Eringen [20] who exhibits certain microscopic effects arising from the local structure and microrotations of fluid elements. The Micropolar fluids accurately simulate the flow characteristics of geomorphological sediments, polymeric additives, colloidal suspensions, liquid crystals, lubricants, hematological suspensions, etc. The rotation of fluid particles in micropolar fluid model is governed by independent kinematic vector called the microrotation vector, which makes it different from other non-Newtonian fluids. Heat transfer in micropolar fluids is also important in the context of industrial manufacturing processes and aerospace engineering and also in chemical engineering.

Although the analysis of entropy generation in a micropolar fluid is important, very little work has been reported in the literature. Ramana Murthy and Srinivas [21] considered the problem of First and Second Law Analysis for the MHD Flow of Two Immiscible Couple Stress Fluids between Two Parallel Plates. Jangili and Murthy [22] analyzed the entropy generation on the steady Poiseuille flow of two immiscible incompressible micropolar fluids between two horizontal parallel plates of a channel with constant wall temperatures in terms of entropy generation. Though most of the work has been done on entropy generation, to the best of the authors’ knowledge, entropy generation analysis for micropolar fluid flow with heat flux boundary condition has not yet been addressed in the literature. Therefore, the objective of the present paper is to investigate the characteristics of micropolar fluid flow, heat transfer and entropy generation inside an inclined channel with constant pressure gradient and constant flux on the upper plate. The governing equations are solved using spectral quasilinearization method. The behavior of flow characteristics with pertinent flow parameters is discussed through graphs.

2. Mathematical formulation

Consider a steady laminar incompressible micropolar fluid flow bounded by two infinite inclined parallel plates separated by a distance ${\textstyle 2h}$. The channel is inclined at an angle α. Choose the cartesian coordinate system with x-axis aligned at the center of the channel in the direction of the flow and the y-axis perpendicular to the plates. The plates are of infinite length in x-direction so that the physical quantities do not depend on x. Therefore the physical variables are depending on y   only. Assume that the properties of the fluid are constant other than the variations of density in the buoyancy force term. Let ${\textstyle \left(u{\mbox{,}}v{\mbox{,}}0\right)}$ be the fluid velocity vector. The transpiration cross flow velocity ${\textstyle v_{0}}$ is constant, where ${\textstyle v_{0}>0}$ is the injection velocity and ${\textstyle v_{0}<0}$ is the suction velocity. In this study the upper plate of the channel is subjected to a constant uniform heat flux q   (isoflux) while the lower plate of the channel is kept at constant temperature${\textstyle T_{1}}$ (isothermal).

Under these assumptions and Boussinesq approximations the governing equations for the steady flow of micropolar fluid are

$v=v_{0}$

(1)

$(\mu +\kappa ){\frac {d^{2}u}{{dy}^{2}}}-\rho v_{0}{\frac {du}{dy}}+$$\kappa {\frac {d\sigma }{dy}}+\rho g^{_{\ast }}\beta (T-$$T_{1})sin(\alpha )-{\frac {\partial p}{\partial x}}=0$

(2)

$\gamma {\frac {d^{2}\sigma }{{dy}^{2}}}-\rho j^{_{\ast }}v_{0}{\frac {d\sigma }{dy}}-$$2\kappa \sigma -\kappa {\frac {du}{dy}}=0$

(3)

$K_{f}{\frac {d^{2}T}{{dy}^{2}}}-\rho C_{p}v_{0}{\frac {dT}{dy}}+(\mu +$$\kappa ){\left({\frac {du}{dy}}\right)}^{2}+2\kappa \left({\sigma }^{2}+\right.$$\left.\sigma {\frac {du}{dy}}\right)+\gamma {\left({\frac {d\sigma }{dy}}\right)}^{2}=$$0$

(4)

where u is the velocity component in the x direction, σ is the microrotation component in z direction, T is the temperature, ρ   and ${\textstyle j^{_{\ast }}}$ are the fluid density and gyration parameters, ${\textstyle \mu {\mbox{,}}\kappa }$ and γ are the material constants (viscosity coefficients), p   is pressure, ${\textstyle g^{_{\ast }}}$ is the acceleration due to gravity, ${\textstyle K_{f}}$ is the coefficient of thermal conductivity, β is the coefficient of thermal expansion.

The boundary conditions are

$u=0{\mbox{,}}\quad \sigma =0{\mbox{,}}\quad {\frac {dT}{dy}}=$${\frac {q}{K_{f}}}{\mbox{,}}\quad at\quad y=h$

(5a)

$u=0{\mbox{,}}\quad \sigma =0{\mbox{,}}\quad T=T_{1}{\mbox{,}}\quad at\quad y=$$-h$

(5b)

Introducing the following dimensionless quantities:

$\eta ={\frac {y}{h}}{\mbox{,}}\quad u=U_{0}f(\eta ){\mbox{,}}\quad \sigma =$${\frac {U_{0}}{h}}g(\eta ){\mbox{,}}\quad \theta (\eta )=$${\frac {T-T_{1}}{\frac {qh}{K_{f}}}}$

(6)

in Eqs. (1), (2), (3) and (4), we get the following nonlinear system of differential equations:

${\frac {1}{1-N}}f^{''}-{Rf}^{'}+{\frac {N}{1-N}}g^{'}+$${\frac {Gr}{Re}}sin(\alpha )\theta =A$

(7)

${\frac {2-N}{m^{2}}}g^{''}-a_{j}R\left({\frac {1-N}{N}}\right)g^{'}-$$2g-f^{'}=0$

(8)

${\theta }^{''}-RPr{\theta }^{'}+{\frac {Br}{1-N}}\left[f^{{'}2}+\right.$$\left.2N(g^{2}+{gf}^{'})+{\frac {N(2-N)}{m^{2}}}g^{{'}2}\right]=$$0$

(9)

where primes denote differentiation with respect to ${\textstyle \eta {\mbox{,}}U_{0}}$ is the characteristic velocity, ${\textstyle Pr={\frac {\mu C_{p}}{K_{f}}}}$ is the Prandtl number, ${\textstyle Re={\frac {\rho U_{0}h}{\mu }}}$ is the Reynolds number, ${\textstyle R={\frac {\rho v_{0}h}{\mu }}}$ is the suction/injuction Reynolds number, ${\textstyle N={\frac {\kappa }{\kappa +\mu }}}$ is the coupling number, ${\textstyle Gr={\frac {{\rho }^{2}g^{_{\ast }}\beta {qh}^{4}}{{\mu }^{2}K_{f}}}}$ is the Grashof number, ${\textstyle A={\frac {h^{2}}{\mu U0}}{\frac {dp}{dx}}}$ is the constant pressure gradient, ${\textstyle m^{2}={\frac {h^{2}\kappa (2\mu +\kappa )}{\gamma (\mu +\kappa )}}}$ is the micropolar parameter, ${\textstyle a_{j}={\frac {j^{_{\ast }}}{h^{2}}}}$ is the micro-inertial parameter, ${\textstyle Br={\frac {\mu U_{0}^{2}}{hq}}}$ is the Brinkman number.

The corresponding boundary conditions are as follows:

$f=0{\mbox{,}}\quad g=0{\mbox{,}}\quad {\theta }^{'}=$$1{\mbox{,}}\quad at\quad \eta =1$

(10a)

$f=0{\mbox{,}}\quad g=0{\mbox{,}}\quad \theta =0{\mbox{,}}\quad at\quad \eta =$$-1$

(10b)

3. Method of solution

The system of Eqs. (7), (8) and (9) along with the boundary conditions (10a) and (10b) is solved using the spectral quasilinearization method [23], [24] and [25]. Initially quasilinearization iteration scheme is applied to linearize the system of Eqs. (7), (8) and (9). This quasilinearization method is a generalization of the Newton–Raphson method and was proposed by Bellman and Kalaba [26] for solving nonlinear boundary value problems. In this method the iteration scheme is obtained by linearizing the nonlinear component of a differential equation using the Taylor series expansion. Chebyshev spectral collocation method is then used to solve the resulting scheme.

Let the ${\textstyle f_{r}{\mbox{,}}g_{r}}$ and ${\textstyle {\theta }_{r}}$ be an approximate current solution and ${\textstyle f_{r+1}{\mbox{,}}g_{r+1}}$ and ${\textstyle {\theta }_{r+1}}$ be an improved solution of the system of Eqs. (7), (8) and (9). By taking Taylors series expansion of nonlinear terms in (7), (8) and (9) around the current solution and neglecting the second and higher order derivative terms, we get the linearized equations as follows:

${\frac {1}{1-N}}f_{r+1}^{''}-{Rf}_{r+1}^{'}+{\frac {N}{1-N}}g_{r+1}^{'}+$${\frac {Gr}{Re}}sin(\alpha ){\theta }_{r+1}=A$

(11)

${\frac {2-N}{m^{2}}}g_{r+1}^{''}-a_{j}R\left({\frac {1-N}{N}}\right)g_{r+1}^{'}-$$2g_{r+1}-f_{r+1}^{'}=0$

(12)

${\theta }_{r+1}^{''}-RPr{\theta }_{r+1}^{'}+a_{1{\mbox{,}}r}f_{r+1}^{'}+$$a_{2{\mbox{,}}r}g_{r+1}^{'}+a_{3{\mbox{,}}r}g_{r+1}=$$a_{4{\mbox{,}}r}$

(13)

where the coefficients ${\textstyle a_{s{\mbox{,}}r}{\mbox{,}}\quad s=1{\mbox{,}}2{\mbox{,}}\ldots }$ are known functions calculated from previous iterations and are defined as

$a_{1{\mbox{,}}r}={\frac {2Br}{1-N}}\left[f_{r}^{'}+{Ng}_{r}\right]{\mbox{,}}\quad a_{2{\mbox{,}}r}=$${\frac {2Br}{1-N}}{\frac {N(2-N)}{m^{2}}}g_{r}^{'}{\mbox{,}}\quad a_{3{\mbox{,}}r}=$${\frac {2BrN}{1-N}}\left[f_{r}^{'}+2g_{r}\right]{\mbox{,}}\quad a_{4{\mbox{,}}r}=$${\frac {Br}{1-N}}\left[f_{r}^{{'}2}+2N(g_{r}^{2}+g_{r}f_{r}^{'})+\right.$$\left.{\frac {N(2-N)}{m^{2}}}g_{r}^{{'}2}\right]$

The above linearized Eqs. (11), (12) and (13) are solved using the Chebyshev spectral collocation method [27]. The approximations are done by using the Chebyshev interpolating polynomials for the unknown functions and further they are collocated at the Gauss-Lobatto points represented as

${\xi }_{j}=cos{\frac {\pi j}{J}}{\mbox{,}}\quad j=0{\mbox{,}}1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}J$

(14)

where J is the number of collocation points used.

The functions ${\textstyle f_{r+1}{\mbox{,}}g_{r+1}}$ and ${\textstyle {\theta }_{r+1}}$ are approximated at the collocation points by

$f_{r+1}(\xi )=\sum _{k=0}^{J}f_{r+1}({\xi }_{k})T_{k}({\xi }_{j}){\mbox{,}}\quad g_{r+1}(\xi )=$$\sum _{k=0}^{J}g_{r+1}({\xi }_{k})T_{k}({\xi }_{j}){\mbox{,}}\quad {\theta }_{r+1}(\xi )=$$\sum _{k=0}^{J}{\theta }_{r+1}({\xi }_{k})T_{k}({\xi }_{j}){\mbox{,}}\quad j=$$0{\mbox{,}}1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}J$

(15)

where ${\textstyle T_{k}}$ is the ${\textstyle k}$th Chebyshev polynomial defined by ${\textstyle T_{k}(\xi )=cos[k{cos}^{-1}\xi ]}$

The derivatives of the variables at the collocation points are represented as

${\frac {d^{a}f_{r+1}}{d{\eta }^{a}}}=\sum _{k=0}^{J}D_{jk}^{a}f_{r+1}({\xi }_{k}){\mbox{,}}\quad {\frac {d^{a}g_{r+1}}{d{\eta }^{a}}}=$$\sum _{k=0}^{J}D_{jk}^{a}g_{r+1}({\xi }_{k}){\mbox{,}}\quad {\frac {d^{a}{\theta }_{r+1}}{d{\eta }^{a}}}=$$\sum _{k=0}^{J}D_{jk}^{a}{\theta }_{r+1}({\xi }_{k}){\mbox{,}}\quad j=$$0{\mbox{,}}1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}J$

(16)

where ‘${\textstyle a}$’ is the order of differentiation and ${\textstyle D}$ being the Chebyshev spectral differentiation matrix. Substituting Eqs. (15) and (16) into Eqs. (11), (12) and (13) leads to the matrix equation

$A_{r}X_{r+1}=B_{r}{\mbox{.}}$

(17)

In Eq. (17), ${\textstyle A_{r}}$ is a ${\textstyle \left(3J+3)\times (3J+3\right)}$ square matrix and ${\textstyle X_{r+1}}$ and ${\textstyle B_{r}}$ are ${\textstyle (3J+3)\times 1}$ column vectors defined by

$A_{r}=\left[{\begin{array}{ccc}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{array}}\right]{\mbox{,}}\quad X_{r+1}=\left[{\begin{array}{c}F_{r+1}\\G_{r+1}\\{\Theta }_{r+1}\end{array}}\right]{\mbox{,}}\quad R_{r}=\left[{\begin{array}{c}r_{1{\mbox{,}}r}\\r_{2{\mbox{,}}r}\\r_{3{\mbox{,}}r}\end{array}}\right]$

(18)

where

${\begin{array}{l}F_{r+1}={\left[f_{r+1}({\xi }_{0}){\mbox{,}}f_{r+1}({\xi }_{1}){\mbox{,}}\ldots \ldots {\mbox{,}}f_{r+1}({\xi }_{J-1}){\mbox{,}}f_{r+1}({\xi }_{J})\right]}^{T}{\mbox{,}}\\G_{r+1}={\left[g_{r+1}({\xi }_{0}){\mbox{,}}g_{r+1}({\xi }_{1}){\mbox{,}}\ldots \ldots {\mbox{,}}g_{r+1}({\xi }_{J-1}){\mbox{,}}g_{r+1}({\xi }_{J})\right]}^{T}{\mbox{,}}\\{\Theta }_{r+1}={\left[{\theta }_{r+1}({\xi }_{0}){\mbox{,}}{\theta }_{r+1}({\xi }_{1}){\mbox{,}}\ldots \ldots {\mbox{,}}{\theta }_{r+1}({\xi }_{J-1}){\mbox{,}}{\theta }_{r+1}({\xi }_{J})\right]}^{T}{\mbox{,}}\\A_{11}={\frac {1}{1-N}}D^{2}-RD{\mbox{,}}\quad A_{12}=({\frac {N}{1-N}})D{\mbox{,}}\quad A_{13}={\frac {Gr}{Re}}sin\alpha I{\mbox{,}}\quad r_{1{\mbox{,}}r}=A{\mbox{,}}\\A_{21}=-D{\mbox{,}}\quad A_{22}={\frac {2-N}{m^{2}}}D^{2}-a_{j}R({\frac {1-N}{N}})D-2I{\mbox{,}}\quad A_{23}=0{\mbox{,}}\quad r_{2{\mbox{,}}r}=0{\mbox{,}}\\A_{31}=a_{1{\mbox{,}}r}D{\mbox{,}}\quad A_{32}=a_{2{\mbox{,}}r}D+a_{3{\mbox{,}}r}I{\mbox{,}}\quad A_{33}=D^{2}-RPrD{\mbox{,}}\quad r_{3{\mbox{,}}r}=a_{4{\mbox{,}}r}\end{array}}$

(19)

Here ${\textstyle I{\mbox{,}}0}$ represents ${\textstyle \left(J+1)\times (J+1\right)}$ identity matrix, zero matrix respectively.

The corresponding boundary conditions

$f_{r+1}({\xi }_{0})=0{\mbox{,}}\quad g_{r+1}({\xi }_{0})=$$0{\mbox{,}}\quad \sum _{k=0}^{J}D_{0k}{\theta }_{r+1}({\xi }_{k})=$$1$

(20a)

$f_{r+1}({\xi }_{J})=0{\mbox{,}}\quad g_{r+1}({\xi }_{J})=$$0{\mbox{,}}\quad {\theta }_{r+1}({\xi }_{J})=0$

(20b)

The boundary conditions (20a) and (20b) are incorporated in the matrix system (17), and thus the solution is obtained as

$X_{r+1}=A_{r}^{-1}B_{r}$

(21)

The initial approximations ${\textstyle f_{0}{\mbox{,}}g_{0}}$ and ${\textstyle {\theta }_{0}}$ are chosen to be functions that satisfy the boundary conditions (10a) and (10b) i.e.

$f_{0}(\eta )=0{\mbox{,}}\quad g_{0}(\eta )=0{\mbox{,}}\quad {\theta }_{0}(\eta )=$${\frac {{\eta }^{2}}{2}}-{\frac {1}{2}}$

(22)

4. Entropy generation

The volumetric rate of entropy generation for incompressible micropolar fluid is given as

$S_{G}={\frac {K_{f}}{T_{1}^{2}}}{\left({\frac {dT}{dy}}\right)}^{2}+$${\frac {\mu +\kappa }{T_{1}}}{\left({\frac {du}{dy}}\right)}^{2}+$${\frac {2\kappa }{T_{1}}}\left[{\sigma }^{2}+\sigma {\frac {du}{dy}}\right]+$${\frac {\gamma }{T_{1}}}{\left({\frac {d\sigma }{dy}}\right)}^{2}$

According to [3], the dimensionless entropy generation number ${\textstyle N_{s}}$ is the ratio of the volumetric entropy generation rate to the characteristic entropy generation rate. Thus the entropy generation number is given by

$N_{s}={\theta }^{{'}2}+{\frac {Br}{1-N}}L\left[f^{{'}2}+\right.$$\left.2N(g^{2}+{gf}^{'})+{\frac {N(2-N)}{m^{2}}}g^{{'}2}\right]$

(23)

where the characteristic entropy generation rate is ${\textstyle {\frac {q^{2}}{K_{f}T_{1}^{2}}}}$ and ${\textstyle L={\frac {K_{f}T_{1}}{hq}}}$ is the dimensionless value and it is a controlling parameter that depends on the heat flux, temperature of the fluid, length of the channel and the thermal conductivity. Eq. (23) can be expressed alternatively as follows:

$N_{s}=N_{h}+N_{v}$

(24)

The first term on the right hand side of this equation denotes the entropy generation due to heat transfer irreversibility and the second term represents the entropy generation due to viscous dissipation.

To evaluate the irreversibility distribution, the parameter Be (Bejan number), which is the ratio of entropy generation due to heat transfer to the overall entropy generation (24) is defined as follows

$Be={\frac {N_{h}}{N_{h}+N_{v}}}$

(25)

The Bejan number varies from 0 to 1. Subsequently, ${\textstyle Be=0}$ reveals that the irreversibility due to viscous dissipation dominates, whereas ${\textstyle Be=1}$ indicates that the irreversibility due to heat transfer is dominant. It is obvious that the ${\textstyle Be=0.5}$ is the case in which the irreversibility due to heat transfer is equal to viscous dissipation in the entropy production.

5. Results and discussion

In this section we present the results that were found using the spectral quasilinearization method (SQLM). The number of collocation points used is ${\textstyle J=100}$. To check the accuracy of our numerical scheme, we have compared our results with analytical solution of Ariman and Cakmak [28] in the absence of ${\textstyle R{\mbox{,}}\alpha }$ with the fixed values of ${\textstyle N=0.1{\mbox{,}}m=1}$ and ${\textstyle A=-1}$. The comparison in the above case is found to be in good agreement as shown in Table 1.

Table 1. Comparison analysis for the velocity and microrotation calculated by the present method and that of analytical solution [28] for ${\textstyle R=0}$ and ${\textstyle \alpha =0}$.

η	Velocity ${\textstyle f(\eta )}$		Microrotation ${\textstyle g(\eta )}$
	Analytical solution [28]	Present	Analytical solution [28]	Present
−1	0	0	0	0
−0.8090	0.1557	0.1557	−0.0204	−0.0204
−0.6129	0.2817	0.2817	−0.0275	−0.0275
−0.4258	0.3696	0.3696	−0.0248	−0.0248
−0.2181	0.4302	0.4302	−0.0147	−0.0147
0	0.4518	0.4518	0	0
0.2181	0.4302	0.4302	0.0147	0.0147
0.4258	0.3696	0.3696	0.0248	0.0248
0.6129	0.2817	0.2817	0.0275	0.0275
0.8090	0.1557	0.1557	0.0204	0.0204
1	0	0	0	0

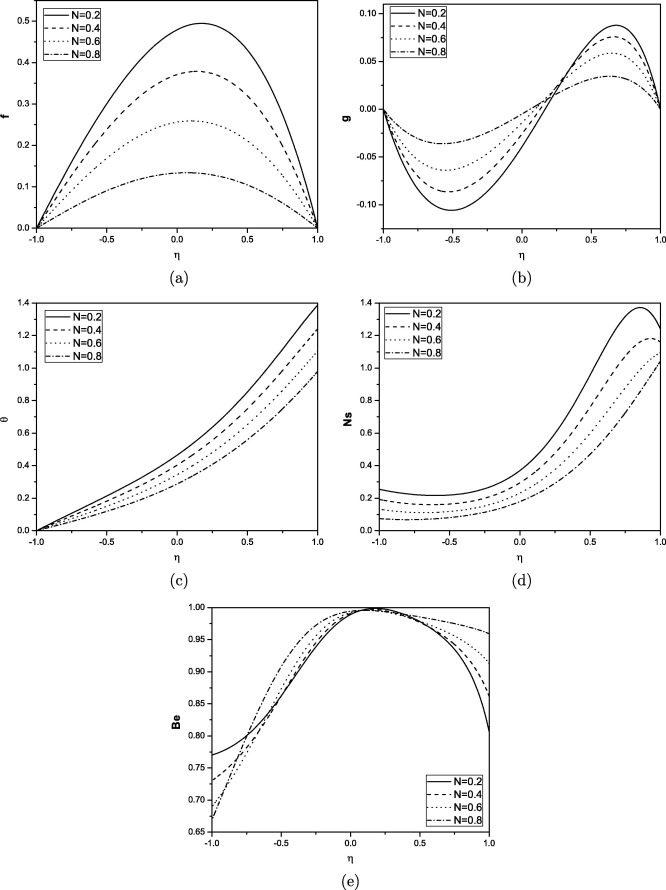
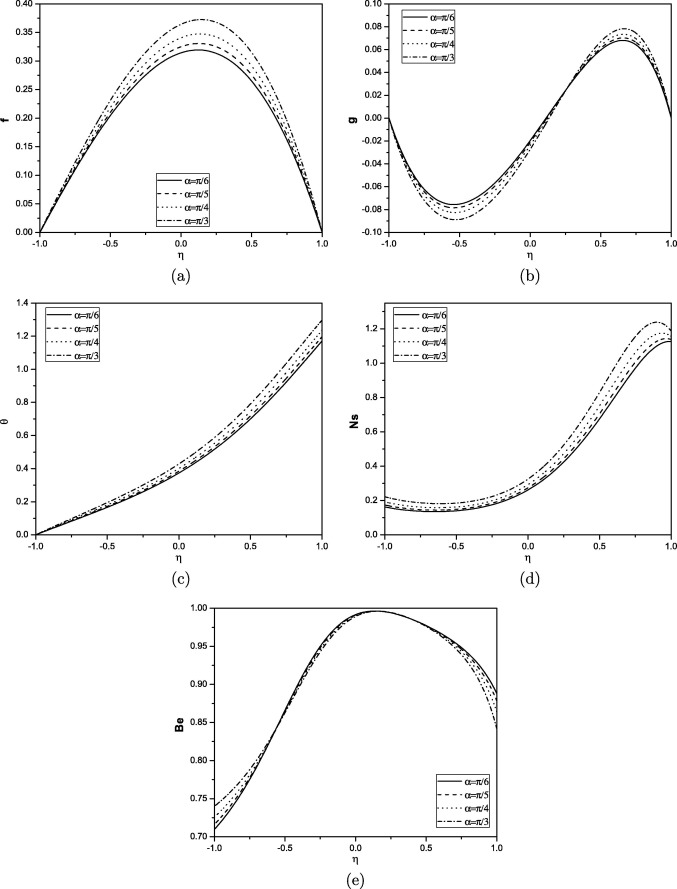
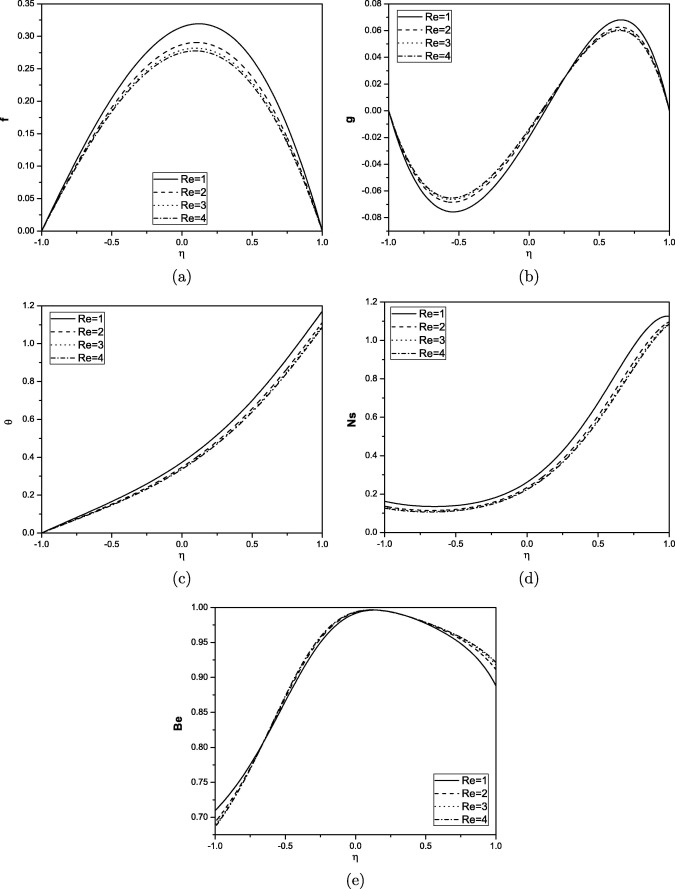
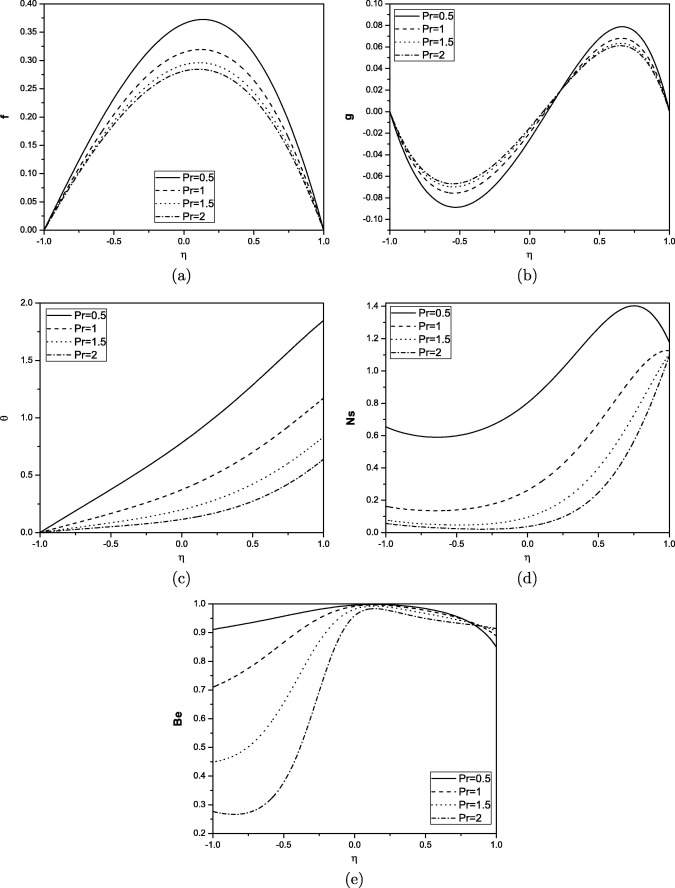
The solutions for the dimensionless velocity, microrotation, temperature, entropy generation and Bejan number are computed and are shown graphically in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. The effects of coupling number N, angle of inclination α, Brinkman number Br, Reynolds number Re and Prandtl number Pr   on the non-dimensional governing parameters are discussed. To study the effects of ${\textstyle N{\mbox{,}}\alpha {\mbox{,}}Br{\mbox{,}}Re}$ and Pr   computations were carried out by taking ${\textstyle aj=0.001{\mbox{,}}A=-1{\mbox{,}}m=2{\mbox{,}}Gr=1{\mbox{,}}L=}$$0.1$ and ${\textstyle R=1}$.

Figure 1. Effect of coupling number on velocity, microrotation, temperature, entropy generation and Bejan number for ${\textstyle Pr=1{\mbox{,}}Re=1{\mbox{,}}Br=1{\mbox{,}}\alpha =pi/6}$.

Figure 2. Effect of angle of inclination on velocity, microrotation, temperature, entropy generation and Bejan number for ${\textstyle Pr=1{\mbox{,}}Re=1{\mbox{,}}Br=1{\mbox{,}}N=0.5}$.

Figure 3. Effect of Reynolds number on velocity, microrotation, temperature, entropy generation and Bejan number for ${\textstyle Pr=1{\mbox{,}}N=0.5{\mbox{,}}Br=1{\mbox{,}}\alpha =pi/6}$.

Figure 4. Effect of Prandtl number on velocity, microrotation, temperature, entropy generation and Bejan number for ${\textstyle N=0.5{\mbox{,}}Re=1{\mbox{,}}Br=1{\mbox{,}}\alpha =pi/6}$.

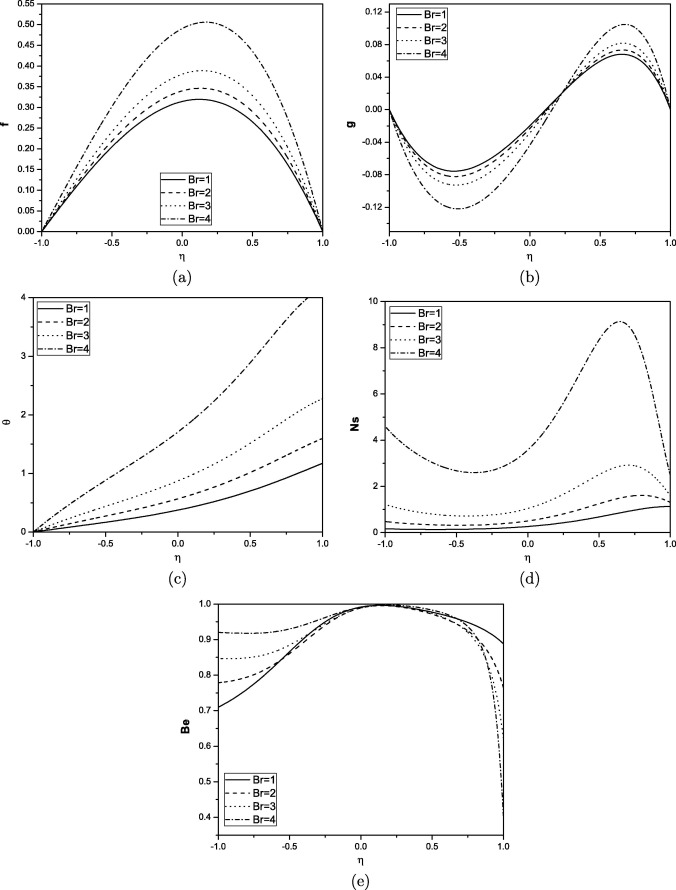
Figure 5. Effect of Brinkman number on velocity, microrotation, temperature, entropy generation and Bejan number for ${\textstyle Pr=1{\mbox{,}}Re=1{\mbox{,}}N=0.5{\mbox{,}}\alpha =pi/6}$.

The effect of the coupling number on velocity, microrotation, temperature, entropy generation and Bejan number of the fluid flow through an inclined channel is plotted in Fig. 1(a)–(e). The coupling of linear and rotational motion arising from the micromotion of the fluid molecules is characterized by coupling number. Hence, the coupling between the Newtonian and rotational viscosities is represented by N  . The microstructure effect is significant as ${\textstyle N\rightarrow 1}$, and for a smaller value of N   the substructure individuality is limited. The fluid is non-polar as its micropolarity is lost at ${\textstyle \kappa \rightarrow 0}$ i.e. ${\textstyle N\rightarrow 0}$. Thus, for viscous fluid ${\textstyle N\rightarrow 0}$. Generally a parabolic velocity profile is observed, with maximum velocity along the channel centerline and minimum velocity at the plates.

Fig. 1(a) shows the decreasing nature of velocity with increasing coupling number. The velocity for viscous fluid is more compared to micropolar fluid. It is observed from Fig. 1(b) that the component of microrotation increases near the lower plate and decreases near the upper plate with increase in the coupling number N. It is observed from Fig. 1(c) and (d) that the temperature and entropy generation decrease with increase in the value of coupling number. It is clear from Fig. 1(e) that the Bejan number increase with increase in the value of N. We observe that heat transfer irreversibility dominates around the centerline region of the channel, and the fluid friction dominates at the lower plate.

Fig. 2(a)–(e) present the effect of angle of inclination α on velocity, microrotation, temperature, entropy generation and Bejan number. It is noticed from Fig. 2(a) that the velocity increases with the increase in angle of inclination. It is shown from Fig. 2(b) that the microrotation component decreases near the lower plate and increases near the upper plate with an increase in the value of angle of inclination, showing a reverse rotation near the two boundaries. It is observed from Fig. 2(c) and (d) that the temperature and entropy generation increases with increase in the value of angle of inclination. We observe that the entropy-generation rate is less at the lower plate of the channel and increases quite rapidly to its maximum values at the upper plate of the channel for all the parameter variations. It is observed from Fig. 2(e) that the Bejan number is not much effected with increase in the value of α at the center of the channel but Be decreases at the upper plate and increases at the lower plate.

From Fig. 3(a)–(c), we observe that as the Reynolds number increases the velocity, microrotation(numerically) and temperature decrease. Fig. 3(d) displays the entropy generation as a function of Reynolds number Re. The entropy generation decreases with increase in Re. This may be attributed to the decrease in the velocity which results in the decrease in heat transfer and hence decrease in entropy generation. Fig. 3(e) shows that the Bejan number decreases as Re increases at the lower plate.

It is observed from Fig. 4(a) that the velocity decreases with increase in Prandtl number. It is shown from Fig. 4(b) that the microrotation component increases near the lower plate and decreases near the upper plate with an increase in the value of Prandtl number. Fig. 4(c) represents the Prandtl number effect on temperature. It is observed that the increase in Prandtl number causes a decrease in temperature. Fig. 4(d) shows that the increase in Prandtl number causes a decrease in entropy generation. Since the increase in Prandtl number reduces the fluid temperature as highlighted in Fig. 4(c), the entropy generation decreases. Fig. 4(e) shows that the Bejan number decreases as Prandtl number increases.

The effect of Brinkman number on velocity, microrotation, temperature, entropy generation and Bejan number is displayed in Fig. 5. Fig. 5(a) depicts that the non-dimensional velocity increases with an increase in the Brinkman number. It is seen from Fig. 5(b) that the microrotation component decreases near the lower plate and increases near the upper plate with an increase in the value of Brinkman number. It is observed from Fig. 5(c) and (d) that the temperature and entropy generation increase with increase in the value of Brinkman number. Brinkman number is related to heat conduction from a channel wall to a flowing fluid. The effect of viscous forces on entropy generation is significant in the region close to the channel walls. Ns profiles are similar in shape and are almost parallel to one another, for variation of all the parameters but they vary in magnitude. From Fig. 5(e) it is interesting to note that increasing values of Br result in an increase in dominant effect of fluid-friction irreversibility near the upper plate and decrease in dominant effect of fluid friction irreversibility near the lower plate.

6. Conclusions

In this study, the flow of micropolar fluid between two inclined parallel plates with the constant pressure gradient is studied. The solutions are obtained by applying the spectral quasilinearization method. The entropy generation number Ns at every point η between the channels is found. The effect of various parameters on entropy generation number (Ns) and Bejan number (Be) is studied through the graphs. The following are the observations from the present study:

• The presence of microstructure decreases the velocity, temperature and entropy generation.
• The entropy generation number increases with an increase in the Brinkman number and angle of inclination. Further, the increase in coupling number, Prandtl number and Reynolds number decreases the entropy generation number.
• Reynolds number has little effect on Bejan number.
• It is observed from the Bejan number profiles that the heat transfer irreversibility dominates around the center of the channel.
• The minimum values of Bejan number are observed at the lower plate and maximum value is at the center of the channel with increasing ${\textstyle N{\mbox{,}}\alpha {\mbox{,}}Re}$ and Pr.

References

1. [1] A. Bejan; A study of entropy generation in fundamental convective heat transfer; J. Heat Transfer, 101 (1979), pp. 718–725
2. [2] A. Bejan; Second law analysis in heat transfer and thermal design; Adv. Heat Transfer, 15 (1982), pp. 1–58
3. [3] A. Bejan; Entropy Generation Minimization; CRC Press, New York (1996)
4. [4] M. Havzali, A. Arikoglu, G. Komurgoz, H.I. Keser, R.O. Fraser; Analytical numerical analysis of entropy generation for gravity-driven inclined channel flow with initial transition and entrance effects; Phys. Scr., 78 (2008) 045401(1–7)
5. [5] G. Komurgoz, A. Arikoglu, E. Turker, I. Ozkol; Second-law analysis for an inclined channel containing porous-clear fluid layers by using the differential transform method; Numer. Heat Transfer, 57 (2010), pp. 603–623
6. [6] A.A. Karamallah, W.S. Mohammad, W.H. Khalil; Numerical study of entropy generation in a vertical square channel packed with saturated porous media; Eng. Tech. J., 29 (9) (2011), pp. 1721–1736
7. [7] C.C. Liu, C.Y. Lo; Numerical analysis of entropy generation in mixed-convection MHD flow in vertical channel; Int. Commun. Heat Mass Transfer, 39 (9) (2012), pp. 1354–1359
8. [8] O.D. Makinde, A.S. Eegunjobi; Entropy generation in a couple stress fluid flow through a vertical channel filled with saturated porous media; Entropy, 15 (2013), pp. 4589–4606
9. [9] R.A. Damseh, M.Q. Al-Odat, M.A. Al-Nimr; Entropy generation during fluid flow in a channel under the effect of transverse magnetic field; Heat Mass Transfer, 44 (2013), pp. 897–904
10. [10] S. Das, R.N. Jana; Entropy generation due to MHD flow in a porous channel with Navier slip; Ain Shams Eng. J., 5 (2014), pp. 575–584
11. [11] B.S. Chen, C.C. Liu; Heat transfer and entropy generation in fully-developed mixed convection nanofluid flow in vertical channel international; J. Heat Mass Transfer, 79 (2014), pp. 750–758
12. [12] S. Mahmud, R.A. Fraser; Second law analysis of heat transfer and fluid flow inside a cylindrical annular space; Exergy, 2 (4) (2002), pp. 322–329
13. [13] Z. Iman; On the importance of thermal boundary conditions in heat transfer and entropy generation for natural convection inside a porous enclosure; Int. J. Therm. Sci., 47 (2008), pp. 339–346
14. [14] M.A. Antar, M.A. El-Shaarawi; The entropy generation for a rotating sphere under uniform heat flux boundary condition in forced-convection flow; Int. J. Numer. Methods Heat Fluid Flow, 19 (3/4) (2009), pp. 396–410
15. [15] A.S. Butt, S. Munawar, A. Ali, A. Mehmood; Entropy generation in hydrodynamic slip flow over a vertical plate with convective boundary; J. Mech. Sci. Technol., 26 (9) (2012), pp. 2977–2984
16. [16] R. Anandalakshmi, T. Basak; Numerical simulations for the analysis of entropy generation during natural convection in porous rhombic enclosures; Numer. Heat Transfer, 63 (4) (2013), pp. 257–284
17. [17] V. Anand; Slip law effects on heat transfer and entropy generation of pressure driven flow of a power law fluid in a microchannel under uniform heat flux boundary condition; Energy, 76 (2014), pp. 716–732
18. [18] S. Mostafa, K. Ali; Convective heat transfer and entropy generation analysis on Newtonian and non-Newtonian fluid flows between parallel-plates under slip boundary conditions; Int. J. Heat Mass Transfer, 70 (2014), pp. 664–673
19. [19] G. Ibanez; Entropy generation in MHD porous channel with hydrodynamic slip and convective boundary conditions; Int. J. Heat Mass Transfer, 80 (2014), pp. 274–280
20. [20] A.C. Eringen; The theory of micropolar fluids; J. Math. Mech., 16 (1966), pp. 1–18
21. [21] J.V. Ramana Murthy, J. Srinivas; First and second law analysis for the mhd flow of two immiscible couple stress fluids between two parallel plates; Heat Transfer Asian Res., 44 (2014), p. 468487
22. [22] S. Jangili, J.V. Murthy; Thermodynamic analysis for the mhd flow of two immiscible micropolar fluids between two parallel plates; Front. Heat Mass Transfer (FHMT), 6 (1) (2015), pp. 1–11
23. [23] S.S. Motsa; A new spectral local linearization method for nonlinear boundary layer flow problems; J. Appl. Math., 2013 (2013), Article 423628 15 pp.
24. [24] S.S. Motsa, P.G. Dlamini, M. Khumalo; Spectral relaxation method and spectral quasilinearization method for solving unsteady boundary layer flow problems; Adv. Math. Phys., 2014 (2014), Article 341964 12 pp.
25. [25] S.S. Motsa; A new spectral relaxation method for similarity variable nonlinear boundary layer flow systems; Chem. Eng. Commun., 201 (2) (2014), pp. 241–256
26. [26] R.E. Bellman, R.E. Kalaba; Quasilinearisation and Non-Linear Boundary-Value Problems; Elsevier, New York, NY, USA (1965)
27. [27] C. Canuto, M.Y. Hussaini, A. Quarteroni, T.A. Zang; Spectral Methods in Fluid Dynamics; Springer, Berlin, Germany (1988)
28. [28] T. Ariman, A.S. Cakmak; Some basic viscous flows in micropolar fluids; Rheol. Acta, 7 (3) (1968), pp. 236–242