Effect of internal heat generation or absorption on MHD free convection from an isothermal truncated cone

Abstract

This paper examines the effect of heat generation or absorption on the free convection flow of an incompressible, electrically conducting fluid about an isothermal truncated cone in the presence of a transverse magnetic field. The non-linear coupled partial differential equations governing the flow and heat transfer have been solved numerically, using an efficient implicit finite-difference scheme along with quasilinearization technique. The nonsimilar solutions have been obtained for the problem overcoming numerical difficulties near the leading edge and in the downstream regime, for air (Pr = 0.72). The effects of various physical parameters on skin friction and heat transfer coefficients and, on velocity and temperature are shown graphically for different values of magnetic parameter (M) and heat generation/absorption parameter (Q). It is observed that, magnetic field decreases both skin friction and heat transfer coefficients. The effect of heat generation or absorption is found to be very significant on heat transfer, but its effect on skin friction is negligible.

Keywords

Free convection; MHD; Skin friction; Heat transfer; Truncated cone; Heat generation/absorption

1. Introduction

The problem of natural convection flow over the frustum of a cone without the transverse curvature effect (i.e., large cone angles when the boundary layer thickness is small compared to the local radius of the cone) has been treated by Na [1] for an isothermal surface. Hering and Grosh [2] studied the laminar natural convection from a non-isothermal cone and showed that similarity solutions exist when the cone wall temperature varies as a power of distance along a cone ray. Later, Hering [3] extended the analysis to investigate the flow for low Prandtl number fluids. Roy [4] extended the study of Hering and Grosh [2] to treat the case for fluids having high Prandtl numbers. Alamgir [5] used an integral method to study the overall heat transfer from vertical cones in laminar natural convection.

There has been a great interest in the study of magneto hydrodynamic (MHD) flow and heat transfer in any medium due to the effect of magnetic field on the boundary layer flow control and on the performance of many systems using electrically conducting fluids. This type of flow has attracted the interest of many researchers [6], [7], [8], [9], [10], [11], [12], [13] and [14] due to its applications in many engineering problems such as MHD generators, plasma studies, nuclear reactors, and geothermal energy extractions.

A large number of physical phenomena involve natural convection driven by heat generation. The study of heat generation (or absorption) in moving fluids is important in several physical problems dealing with chemical reactions and those concerned with dissociating fluids. Possible heat generation effects may alter the temperature distribution and therefore, the particle deposition rate. In addition, understanding the effects of internal heat generation is also significant in numerous applications that include reactor safety analysis, metal waste, spent nuclear fuel, fire and combustion studies and strength of radioactive materials.

The effect of heat generation/absorption on free convective flows has been studied by several authors [15], [16], [17], [18] and [19] and, motivated by these works; the present work aimed to study the effect of internal heat generation or absorption on free convection flow of an incompressible, electrically conducting fluid from an isothermal truncated cone in the presence of an applied magnetic field.

2. Mathematical model

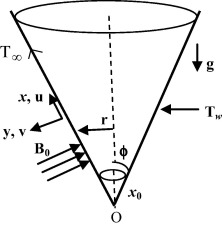
We consider the steady, two-dimensional laminar natural convection flow of a viscous incompressible fluid about an isothermal truncated cone in the presence of internal heat generation or absorption. Fig. 1 shows the flow model and physical coordinate system. The origin of the coordinate system is placed at the vertex of the full cone, where x is the coordinate along the surface of the cone measured from the origin, and y is the coordinate normal to the surface. It is assumed that the boundary layer to be sufficiently thin in comparison with the local radius of the truncated cone. The local radius to a point in the boundary layer can be replaced by the radius of the truncated cone r, r = xsin ϕ, where ϕ is semi vertical angle of the cone.

Figure 1. The flow geometry and the coordinate system.

A transverse magnetic field of strength B₀(x) is applied in the direction normal to the surface of the isothermal truncated cone and it is assumed that magnetic Reynolds number is small, so that the induced magnetic field can be neglected. The boundary layer is assumed to develop at the leading edge of the truncated cone (x = x₀) which implies that the temperature at the circular base is assumed to be the same as the ambient temperature T_∞. The temperature of the surface of the cone T_w is uniform and higher than the free stream temperature T_∞ (T_w > T_∞).

Under the above assumptions, the two-dimensional MHD boundary layer equations for natural convective flow of the electrically conducting fluid over a isothermal truncated cone, valid in the domain x₀ ⩽ x ⩽ ∞, are the continuity, momentum and energy equations, respectively given by

${\frac {\partial (ru)}{\partial x}}+{\frac {\partial (rv)}{\partial y}}=$$0$

(1)

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$${\frac {1}{\rho }}{\frac {\partial }{\partial y}}\left(\mu {\frac {\partial u}{\partial y}}\right)+$$g\beta cos\varphi (T-T_{\infty })-{\frac {\sigma B_{0}^{2}(x)}{\rho }}u$

(2)

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$$\alpha {\frac {{\partial }^{2}T}{\partial y^{2}}}+{\frac {Q_{0}}{\rho c_{p}}}(T-$$T_{\infty })$

(3)

where u, v are the components of velocity respectively in x- and y-directions, g the gravitational acceleration, μ coefficient of fluid viscosity, β the coefficient of thermal expansion, T the temperature inside the boundary layer, α the thermal diffusivity, ρ the density of the fluid, c_p the specific heat, and Q₀ is the heat generation or absorption coefficient.

2.1. Boundary conditions

The appropriate boundary conditions for the problem are given by

${\begin{array}{r}u=0{\mbox{,}}\quad v=0{\mbox{,}}\quad T=T_{w}\quad {\mbox{at}}\quad y=0\\u=0{\mbox{,}}\quad T=T_{\infty }\quad {\mbox{as}}\quad y\rightarrow \infty \end{array}}$

(4)

2.2. Method of solution

Introducing the following transformations:

${\begin{array}{c}\psi =\nu r\left({Gr}_{x^{_{\ast }}}^{1/4}\right)f(\xi {\mbox{,}}\eta ){\mbox{,}}\quad \eta ={\frac {y}{x^{_{\ast }}}}\left({Gr}_{x^{_{\ast }}}^{1/4}\right){\mbox{,}}\quad F=f^{'}={\frac {\partial f}{\partial \eta }}{\mbox{,}}\quad {\mbox{Pr}}={\frac {\nu }{\alpha }}{\mbox{,}}\quad \xi ={\frac {x^{_{\ast }}}{x_{0}}}={\frac {x-x_{0}}{x_{0}}}{\mbox{,}}\quad G={\frac {T-T_{\infty }}{T_{w}-T_{\infty }}}{\mbox{,}}\\M={\frac {\sigma B_{0}^{2}(x)x^{{_{\ast }}2}}{\rho {Gr}_{x^{_{\ast }}}^{1/2}}}{\mbox{,}}\quad ru={\frac {\partial \psi }{\partial y}}\quad \&\quad rv=-{\frac {\partial \psi }{\partial x}}{\mbox{,}}\quad {Gr}_{x^{_{\ast }}}={\frac {g\beta cos\varphi (T_{w}-T_{\infty })x^{{_{\ast }}3}}{{\nu }^{2}}}{\mbox{,}}\quad Q={\frac {x^{{_{\ast }}2}Q_{0}}{\rho {Gr}_{x^{_{\ast }}}^{1/2}c_{p}}}\end{array}}$

(5)

to Eqs. (1), (2) and (3), we find that continuity equation (1) is identically satisfied and the Eqs. (2) and (3) reduced, respectively transformed to

$F^{''}+\left({\frac {3}{4}}+{\frac {\xi }{1+\xi }}\right){fF}^{'}-$${\frac {1}{2}}F^{2}+G-MF=\xi ({FF}_{\xi }-F^{'}f_{\xi })$

(6)

${Pr}^{-1}G^{''}+\left({\frac {3}{4}}+{\frac {\xi }{1+\xi }}\right){fG}^{'}+$$QG=\xi ({FG}_{\xi }-G^{'}f_{\xi })$

(7)

Here ψ and f are dimensional and dimensionless stream functions, respectively; η is the pseudo similarity variable; F and G are, respectively, dimensionless velocity and temperature of the fluid in the boundary layer region. M non-dimensional magnetic parameter; Pr   is Prandtl number; ${\textstyle {Gr}_{x^{_{\ast }}}}$ is local Grashof number; x streamwise coordinate; x^∗ distance measured from the leading edge of the truncated cone; ξ dimensionless distance. Here (′) denotes derivative with respect to η. The subscripts w and ∞ denote conditions at wall and infinity respectively.

The heat generation or absorption parameter Q appearing in Eq. (7) is the non-dimensional parameter based on the amount of heat generated or absorbed per unit volume given by Q₀(T − T_∞), with Q₀ being constant coefficient that may take either positive or negative values. The source term represents the heat generation that is distributed everywhere when Q is positive (Q > 0) and the heat absorption when Q is negative (Q < 0); Q is zero, in case of no heat generation or absorption.

The boundary conditions for the above non dimensional equations (6) and (7) are given by

${\begin{array}{rr}f(\xi {\mbox{,}}0)=0{\mbox{,}}&F(\xi {\mbox{,}}0)=0{\mbox{,}}\quad G(\xi {\mbox{,}}0)=1{\mbox{,}}\quad {\mbox{at}}\quad \eta \rightarrow 0\\&F(\xi {\mbox{,}}\infty )=0{\mbox{,}}\quad G(\xi {\mbox{,}}\infty )=0\quad {\mbox{as}}\quad \eta \rightarrow \infty \end{array}}$

(8)

In practical applications, the physical quantities of principle interest are the shearing stress τ_w and the rate of heat transfer in terms of the skin friction coefficient (C_f) and Nusselt number (Nu), respectively, which can be written as

$C_{f}{Gr}_{x^{_{\ast }}}^{1/4}={\frac {2x^{{_{\ast }}2}{\tau }_{w}}{{Gr}_{x^{_{\ast }}}\rho }}=$${\frac {2x^{{_{\ast }}2}{\left(\mu {\frac {\partial u}{\partial y}}\right)}_{w}}{\rho {Gr}_{x^{_{\ast }}}}}=$$2F_{w}^{'}(\xi {\mbox{,}}0)$

(9)

${Nu}_{x^{_{\ast }}}{Gr}_{x^{_{\ast }}}^{-1/4}=-{\frac {x^{_{\ast }}{\left({\frac {\partial T}{\partial y}}\right)}_{w}}{\Delta T_{w}}}=$$-G_{w}^{'}(\xi {\mbox{,}}0)$

(10)

3. Numerical method

The system of coupled, non linear partial differential equations (6) and (7) along with the boundary conditions (8) using the relations (9) and (10) has been solved numerically employing an implicit finite difference scheme along with quasilinearization technique. Quasilinearization technique can be viewed as a generalization of the Newton–Raphson approximation technique in functional space. An iterative sequence of linear equations is carefully constructed to approximate the non-linear equations (6) and (7) under the boundary conditions (8) achieving quadratic convergence and monotonicity of the sequence of functions. With the help of quasilinearization technique, the non-linear coupled partial differential equations (6) and (7) with boundary conditions (8) are replaced by the following sequence of linear ordinary differential equations:

${}^{\left(k+1\right)}F^{''}+{}^{\left(k\right)}X_{1}{}^{\left(k+1\right)}F^{'}+$${}^{\left(k\right)}X_{2}{}^{\left(k+1\right)}F+{}^{\left(k\right)}X_{3}{}^{\left(k+1\right)}F_{\xi }+$${}^{\left(k\right)}X_{4}{}^{\left(k+1\right)}G={}^{\left(k\right)}U_{1}$

(11)

${}^{\left(k+1\right)}G^{''}+{}^{\left(k\right)}Y_{1}{}^{\left(k+1\right)}G^{'}+$${}^{\left(k\right)}Y_{2}{}^{\left(k+1\right)}G+{}^{\left(k\right)}Y_{3}{}^{\left(k+1\right)}G_{\xi }+$${}^{\left(k\right)}Y_{4}{}^{\left(k+1\right)}F={}^{\left(k\right)}U_{2}$

(12)

The coefficient functions with iterative index ‘k’ are known and the functions with iterative index ‘k + 1’ are to be determined.

The corresponding boundary conditions of Eq. (8) are given by

${\begin{array}{ll}{}^{\left(k+1\right)}F(\xi {\mbox{,}}0)=0{\mbox{,}}&{}^{\left(k+1\right)}G(\xi {\mbox{,}}0)=1\quad {\mbox{at}}\quad \eta =0\\{}^{\left(k+1\right)}F(\xi {\mbox{,}}\infty )=0{\mbox{,}}&{}^{\left(k+1\right)}G(\xi {\mbox{,}}\infty )=0\quad {\mbox{at}}\quad \eta ={\eta }_{\infty }\end{array}}$

(13)

The coefficients in Eqs. (11) and (12) are given by

${\begin{array}{l}{}^{\left(k\right)}X_{1}=G^{'}+\left[\left({\frac {3}{4}}+{\frac {\xi }{1+\xi }}\right)f+\xi f_{\xi }\right]\\{}^{\left(k\right)}X_{2}=-[M+F+\xi F_{\xi }]\\{}^{\left(k\right)}X_{3}=-\xi F\\{}^{\left(k\right)}X_{4}=1.0\\{}^{\left(k\right)}Y_{1}=\left({\frac {3}{4}}+{\frac {\xi }{1+\xi }}\right)fPr+Pr\xi f_{\xi }\\{}^{\left(k\right)}Y_{2}=PrQ\\{}^{\left(k\right)}Y_{3}=-PrF\xi \\{}^{\left(k\right)}Y_{4}=-Pr\xi G_{\xi }\\{}^{\left(k\right)}U_{1}=-\left[{\frac {1}{2}}F^{2}+\xi {FF}_{\xi }\right]\\{}^{\left(k\right)}U_{2}=-Pr\xi G_{\xi }F\end{array}}$

Since the method is presented for ordinary differential equations by Inouye and Tate [20] and for partial differential equations in a recent study by Jayakumar et al. [21], its description is omitted here for the sake of brevity. At each iteration step, the sequence of linear partial differential equations (11) and (12) along with boundary conditions (13) was expressed in different form, using central difference scheme in the η-direction. In each iteration step, the resulting equations were then reduced to a system of linear algebraic equations with a block tri-diagonal structure, which is solved by Varga’s algorithm [22]. To ensure the convergence of the numerical solutions to the exact solution, step sizes Δη   are optimized. To achieve this, the computed values of physical quantities ${\textstyle \left[F_{w}^{'}(\xi {\mbox{,}}0){\mbox{,}}G_{w}^{'}(\xi {\mbox{,}}0)\right]}$ with a step size Δη are compared with those obtained using reduced step sizes viz., (Δη/2), (Δη/4) and so on. In the present work, the optimal values of the step sizes Δη = 0.05 have been used for computation. The value of η_∞ (i.e. the edge of the boundary-layer) has been taken as 5.0 throughout the computation. A convergence criterion based on the relative difference between the current and previous iterations has been used. The solution is assumed to have converged and iterative process is terminated when

${\mbox{Max}}\left[\left|{\left(F_{w}^{'}(\xi {\mbox{,}}0)\right)}^{k+1}-\right.\right.$$\left.\left.{\left(F_{w}^{'}(\xi {\mbox{,}}0)\right)}^{k}{\mbox{,}}\quad {\left(G_{w}^{'}(\xi {\mbox{,}}0)\right)}^{k+1}-\right.\right.$$\left.\left.{\left(G_{w}^{'}(\xi {\mbox{,}}0)\right)}^{k}\right|\right]<{10}^{-4}$

It is remarked here that, the numerical solutions for the present problem are obtained using the aforementioned fast convergent numerical method involving implicit finite difference scheme, which is unconditionally stable.

4. Results and discussion

The computations have been carried out for various values of governing parameters viz., magnetic parameter (M) and heat generation or absorption parameter (Q). The computed results have been compared with those of Na and Chiou [1], for skin friction ${\textstyle F_{w}^{'}(0)}$ and heat transfer ${\textstyle G_{w}^{'}(0)}$ parameters in Table 1, Pr = 0.01 and 0.72, near the leading edge (ξ = 0). Our results are found to be in good agreement with those of [1], correct to four decimal places of accuracy (Table 1).

Table 1. Comparison of the values of ${\textstyle F_{w}^{'}(0)}$ and ${\textstyle G_{w}^{'}(0)}$ at ξ = 0.

Pr	Present results		Na and Chiou [1]
	${\textstyle F_{w}^{'}(0)}$	${\textstyle -G_{w}^{'}(0)}$	${\textstyle F_{w}^{'}(0)}$	${\textstyle -G_{w}^{'}(0)}$
0.01	1.39488	0.05741	1.39484	0.05742
0.72	0.95844	0.35338	0.95843	0.35338

The numerical results are obtained for various values of magnetic field parameter M (0 ⩽ M ⩽ 1.0) and heat generation or absorption parameter Q (Q > 0 or Q < 0) for Pr = 0.72, and are presented graphically in Figure 2, Figure 3, Figure 4 and Figure 5.

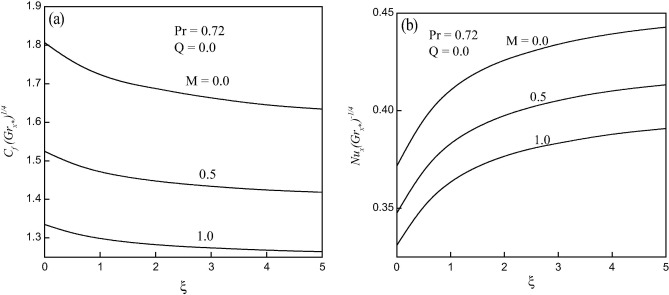
Figure 2. Effect of magnetic field on (a) skin friction and (b) heat transfer coefficients.

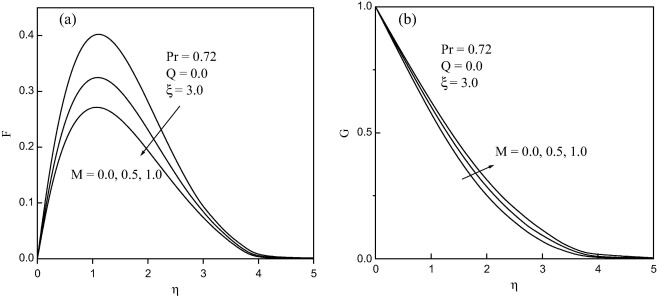
Figure 3. (a) Velocity and (b) temperature profiles for different values of M.

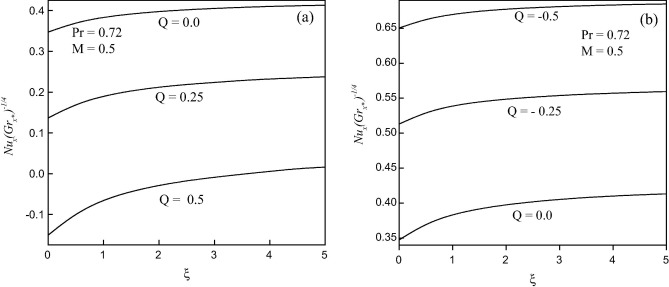
Figure 4. Effect of (a) heat generation and (b) heat absorption parameter (Q) on heat transfer coefficient.

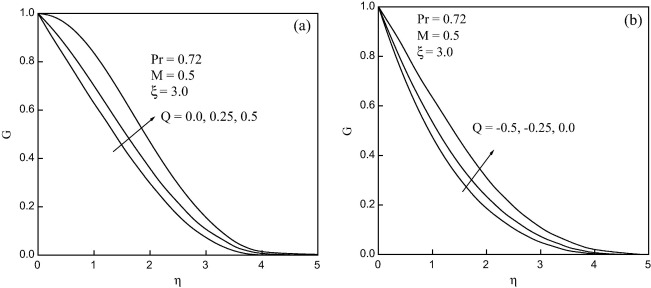
Figure 5. Temperature profiles for (a) heat generation (Q > 0) and (b) heat absorption (Q < 0).

The skin friction [C_f  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^1/4] and heat transfer [Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4] coefficients for various values of magnetic field M (=0.0, 0.5, 1.0) and Pr = 0.72 along the streamwise coordinate (ξ) are presented in Fig. 2(a) and (b), respectively. It is evident that both C_f  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^1/4 and Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4 found to decrease with increase of M. Also, C_f  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^1/4 is observed to decrease near the leading edge (ξ = 0), while Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4 exhibits an increasing trend near ξ = 0. The percentage of decrease in C_f  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^1/4 is 38.96% near ξ = 3.0, when M is increasing from M = 0.0 to 1.0. On the other hand, there is 5.08% decrease in the value of Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4 at the same streamwise location, in the range of 0 ⩽ M ⩽ 1.0.

Fig. 3 shows the velocity (F) and temperature (G) profiles for different values of M (0 ⩽ M ⩽ 1.0) for Pr = 0.72 at the streamwise coordinate ξ = 3.0. It is observed that velocity increases sharply near the wall whereas temperature decreases, with increase of magnetic parameter (M). Numerical results in these figures indicate that momentum boundary layer thickness decreases and thermal boundary layer thickness increases in terms of η at increasing distance from the leading edge. Also, velocity is found to increase with increasing η and reaches maximum value at η = 1.2 and later starts decreasing to the free stream conditions. The changes of velocity profile in η direction reveal velocity profiles for natural convection boundary layer flow, i.e. velocity is zero at the boundary wall then the velocity increases to the peak values as η increases and, finally, the velocity approaches to zero. The change in temperature profile (G), in the η-direction also shows the typical temperature profile for natural convection boundary wall where the temperature profiles decrease gradually along the η-direction for the values of M from 0.0 to 1.0. Indeed, the magnetic field normal to the flow of an electrically conducting fluid introduces a Lorentz force, which retards the flow. Consequently, the peak velocity decreases (see Fig. 3(a)) and, the temperature increases within the boundary layer, due to retarding effect (see Fig. 3(b)).

The influence of heat generation (Q > 0) or absorption parameter (Q < 0) on heat transfer coefficient [Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4] in the presence of the magnetic field (M = 0.5) is displayed in Fig. 4. It is observed that Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4 decreases with the increase of Q (−0.5 ⩽ Q ⩽ 0.5). On the other hand, there is a mild increase in Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4 during both heat generation (Q > 0) and heat absorption (Q < 0) along the streamwise coordinate (ξ). Indeed, the percentage of decrease of Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4 when Q increases from Q = 0.0 to Q = 0.5 at ξ = 3.0 is 44.39% while the percentage of increase of Nu  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^−1/4 when Q decreases from Q = 0.0 to Q = −0.5 at ξ = 3.0 is 27.58% (Fig. 4(a) and (b)). In fact, the presence of heat generation has the tendency to increase the temperature of the fluid in the boundary layer at the expense of reduced particle deposition level there. On the other hand, heat absorption produces the opposite effect; namely, decreases in the temperature and increases in the particle deposition level. In addition, the thermal boundary layer thickness increases for heat generation and decreases for heat absorption while the opposite behavior occurs for the concentration boundary layer thickness. Further, it is found that the direction of heat transfer gets reversed when Q = 0.5 (Fig. 4(a)). This is attributed to the fact that heat generation mechanism creates a layer of hot fluid near the surface and finally resultant temperature of the fluid exceeds the surface temperature resulting in the decrease of rate of heat transfer from the surface. The heat generation or absorption parameter doesn’t cause any significant effect on skin friction coefficient [C_f  (${\textstyle {Gr}_{x^{_{\ast }}}}$)^1/4] and hence it is not shown here.

Fig. 5 depicts the effect of heat generation or absorption parameter on temperature profile in the presence of magnetic field (M = 0.5). It is clearly observed that the thermal boundary layer thickness is increased in the presence of both heat generation and absorption. Further, it is evident from these figures that the present numerical results confirm to satisfy the thermal boundary layer conditions. The velocity profiles are unaffected by heat generation or absorption parameter and hence they are not shown here, for the sake of brevity.

5. Conclusions

For different values of relevant physical parameters including the magnetic parameter (M), the effect of natural convection flow of viscous incompressible fluid with heat generation or absorption parameter (Q) along isothermal truncated cone has been studied. From the present investigation the following conclusions may be drawn:

• The skin friction coefficient decreases and heat transfer coefficient increases with the increase of dimensionless distance along the truncated cone.
• Both skin friction and heat transfer coefficients show a decreasing trend with the increase of magnetic parameter. However, skin friction is found to decrease and heat transfer increases near the leading edge.
• The velocity decreases and temperature increases along the conical surface with the increase of magnetic parameter.
• The effect of increasing the heat generation/absorption parameter results in decreasing the heat transfer coefficient. Also, the direction of heat transfer gets reversed during heat generation.
• It is observed that the thermal boundary layer thickness is increased in the presence of both heat generation and absorption.

Acknowledgments

The authors wish to thank the anonymous reviewers for their helpful comments, which have greatly improved the quality of the manuscript. And, they are indebted to the principal and management of their respective institutions for providing them excellent facilities for research.

References

1. [1] T.Y. Na, J.P. Chiou; Laminar natural convection over a frustum of a cone; Appl. Sci. Res., 35 (1979), pp. 409–421
2. [2] R.G. Hering, R.J. Grosh; Laminar free convection from a non isothermal cone; Int. J. Heat Mass Transfer, 5 (1962), pp. 1059–1068
3. [3] R.G. Hering; Laminar free convection from a non isothermal cone at low Prandtl numbers; Int. J. Heat Mass Transfer, 8 (1965), pp. 1333–1337
4. [4] S. Roy; Free convection over a slender vertical cone at high Prandtl numbers; ASME J. Heat Transfer, 101 (1974), pp. 174–176
5. [5] M. Alamgir; Overall heat transfer from vertical cones in laminar free convection an approximate method ASME; J. Heat Transfer, 101 (1979), pp. 174–177
6. [6] K.B. Pavlov; Magnetohydrodynamic flow of an incompressible viscous fluid caused by the deformation of a plane surface; Magn. Gidrondin, 4 (1974), pp. 146–152
7. [7] A. Chakrabarthi, A.S. Gupta; A note on MHD flow over a stretching permeable surface; Q. Appl. Math., 37 (1979), pp. 73–78
8. [8] T. Chiam; Magneto hydrodynamic boundary layer flow due to a continuous moving flate plate; Comput. Math. Appl., 26 (1993), pp. 1–8
9. [9] V. Kumaran, A.K. Banerjee, A. Vanav Kumar, K. Vajravelu; MHD flow past a stretching permeable sheet; Appl. Math. Comput., 210 (2009), pp. 26–32
10. [10] M. Sheikholeslami, D.D. Ganji, M.M. Rashidi; Ferrofluid flow and heat transfer in a semi annulus enclosure in the presence of magnetic source considering thermal radiation; J. Taiwan Inst. Chem. Eng., 47 (2015), pp. 6–17
11. [11] M. Sheikholeslami, D.D. Ganji; Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method; Physica A, 417 (2015), pp. 273–286
12. [12] M. Sheikholeslami; Effect of uniform suction on nanofluid flow and heat transfer over a cylinder; J. Braz. Soc. Mech. Sci. Eng., 37 (2015), pp. 1623–1633
13. [13] M. Sheikholeslami, M. Gorji-Bandpy, K. Vajravelu; Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al₂O₃–water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder; Int. J. Heat Mass Transfer, 80 (2015), pp. 16–25
14. [14] M. Sheikholeslami, D.D. Ganji, M. Younus Javed, R. Ellahi; Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model; J. Magn. Magn. Mater., 374 (2015), pp. 36–43
15. [15] A.J. Chamkha; Effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface; Int. J. Numer. Methods Fluid Flow, 10 (2000), pp. 432–439
16. [16] M.M. Molla, M.A. Hossain, L.S. Yao; Natural convection flow along a vertical wavy surface with uniform surface temperature in the presence heat generation/absorption; Int. J. Therm. Sci., 34 (2004), pp. 157–163
17. [17] F.M. Hady, R.A. Mohamed, A. Mahdy; MHD free convection flows along a vertical wavy surface with heat generation or absorption effect; Int. Commun. Heat Mass Transfer, 33 (2006), pp. 1253–1259
18. [18] M.M. Molla, M.A. Hossain, M.C. Paul; Natural convection flow from an isothermal horizontal circular cylinder in the presence of heat generation; Int. J. Eng. Sci., 44 (2006), pp. 949–955
19. [19] S. Bagai; Effect of variable viscosity on free convection over a non-isothermal heat generation; Acta Mech., 169 (2004), pp. 186–187
20. [20] K. Inouye, A. Tate; Finite difference version of quasi-linearization applied boundary layer equations; AIAA J., 12 (1974), pp. 558–560
21. [21] K.R. Jayakumar, A.H. Srinivasa, A.T. Eswara; Axisymmetric MHD boundary-layer flow and heat transfer with variable viscosity; Int. J. Comput. Intell. Res. Appl., 3 (2009), pp. 271–276
22. [22] R.S. Verga; Matrix Iterative Analysis; Prentice-Hall (2000)