Application of discretization error estimators in stepped column buckling problems

Abstract

In order to reduce the discretization error, in this paper, Richardson’s Extrapolation and Convergence Error Estimator were used to investigating the buckling problem convergence. The main objective was to verify the convergence order of the stepped column problem and to define a consistent moment of inertia at the point of variation of the cross-section. The variable of interest was the critical buckling load obtained by the Finite Difference Method. The convergent solution obtained errors less than 10^-8, and this work showed that the best solution is not defined by excessive mesh refinement, but by the solution convergence analysis.

Keywords: Finite Difference Method, discretization error, convergence order, buckling analysis, Finite Element Method

1. Introduction

The use of techniques to reduce the numerical error is increasingly widespread, mainly due to the decrease in computational expenditure during the simulations. The reduction of the numerical error caused by discretization errors can be obtained in several ways: the mesh refinement and the increase in the precision order of the numerical solutions are some of these alternatives. However, there are disadvantages such as high computational cost and high level of complexity of the suggested model. In order to avoid such inconveniences, the use of extrapolation methods, such as Richardson Extrapolation (RE) [1] are very useful and applicable.

When RE is used successively, the technique is called Repeated Richardson Extrapolation (RRE). In this case, the numerical solution of the variable of interest must be defined in at least three different meshes, thus allowing two or more extrapolations. According to [2] there are many advantages when using the RRE technique that can be listed as: (a) Decreased of the discretization error; (b) Easy application and post-processing method, thus it does not interfere with the numerical solution obtained in a given mesh; (c) The computational cost (CPU time and RAM) is considered low; (d) Can be applied to existing codes or results obtained; (e) For different numerical methods and variables of interest is suitable; (f) It does not depend on priori analysis or the analytical solution of the problem; (g) Can be used in low-order numerical solutions to obtain higher-order numerical solutions.

The most interesting fact is that the technique allows defining a convergent numerical solution and its error estimators. In this sense, the true error and the estimated error of a numerical solution can be reliably reduced. In addition, the true discretization error is limited by the Richardson Error estimator [2–5].

Although the method is widely used in isotropic meshes, RE has also shown good results in improving the convergence rate (from fourth-order to sixth-order) in models of non-isotropic meshes using a finite difference compact method [6]. Furthermore, one worth noting that the convergence rates are strongly dependent on the order of the finite discrete scheme: finite schemes of a higher order lead to enriched constitutive laws of a higher order, with a higher convergence rate [7,8].

The variable of interest of this paper is the critical load of buckling in stepped columns simply supported. Columns of uniform cross section subjected to compressive loading may not be economical, so stability can be increased by removing a portion of material from the ends and increasing the cross section in the central region of the column [9]. Although the problem seems simple, several hypotheses of the stiffness in the coincident node between different cross sections can be approached, also, the convergence of the problem and the resolution method is relevant to be evaluated. According to the literature [10–13], the resolution of the problem by the Finite Differences Method (FDM) proved to be quite appropriate. Multiple-stepped beams are frequently discussed in literature to describe free vibration [14–16] or buckling behavior [17–20].

Despite the successful use of the RE method, Iremonger [21] warns that the application of FDM in the problem of stepped column presents some pitfalls: (a) the convergence pattern can change when the column is divided into an even or odd number of segments and (b) formulations using a fourth-order differential can lead to incorrect solutions. Although there is a need for caution in the use of FDM, for the proposed case, precise solutions for buckling load can be obtained using a small number of discretization divisions, especially if extrapolation techniques are used.

The purpose of this work is to verify the estimate of the discretization error when the apparent error order is monotonic converging to the asymptotic order of the error. Particularly, in this work assumed: (a) the FDM in solving a one-dimensional problem of stepped columns simply supported with isotropic grids, (b) the posteriori error estimation, (c) the RRE is used to decrease and estimate the discretization errors.

The outline of this paper is as follows. The exact solution for the stepped column buckling problem is introduced in section 2, subsequently, section 3 explains the FDM for discontinued section columns. The approach of the convergence analysis and error estimators is introduced in section 4. The problem description and numerical procedure are showed in section 5. Section 6 presents the numerical results obtained for stepped columns with different stiffness. Finally, section 7 presents the final considerations.

2. Timoshenko’s solution buckling column with section discontinuity

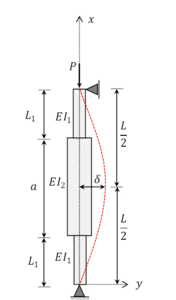
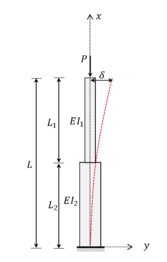
Considering a clamped-free column (Figure 1a) or the simply supported column (Figure 1b) and using the procedures developed in [9], it can be possible to define the exact solution of the stepped column problem.

(a)	(b)
Figure 1. Stepped Column. (a) clamped-free column. (b) Pinned-pinned column

In the stepped columns illustrated in Figures 1a and 1b, the bending rigidity ${\textstyle (EI)}$ changes suddenly; then, it is necessary to analyze each section separately. The governing differential equation in a clamped-free stepped column (Figure 1a), for section 1 of length ${\textstyle {L}_{1}}$, can be written as

${\frac {{d}^{2}{w}_{1}}{d{x}^{2}}}={\frac {P}{E{I}_{1}}}\left(\delta -{w}_{1}\right).$

(1)

Similarly, for the section 2, the differential equation can be expressed by

${\frac {{d}^{2}{w}_{2}}{d{x}^{2}}}={\frac {P}{E{I}_{2}}}\left(\delta -{w}_{2}\right),$

(2)

where ${\textstyle E{I}_{i}}$ is the bending rigidity in section ${\textstyle i}$, ${\textstyle P}$ is the axial compression, ${\textstyle \delta }$ is the deflection in the top of the column and ${\textstyle {w}_{i}}$ is the lateral displacement throughout section ${\textstyle i}$.

The general solution of the differential equations is known and given by

${\textstyle {w}_{1}=A\cos \left({\psi }_{1}x\right)+B\sin \left({\psi }_{1}x\right)+}$$\delta$,

(3)

${\textstyle {w}_{2}=C\cos \left({\psi }_{2}x\right)+D\sin \left({\psi }_{2}x\right)+}$$\delta$,

(4)

being ${\textstyle A}$, ${\textstyle B}$, ${\textstyle C}$ and ${\textstyle D\,}$ constants, and

${\psi }_{i}={\sqrt {\frac {P}{E{I}_{i}}}}.$

(5)

Applying the boundary conditions,

${\left({w}_{2}\right)}_{x=0}=0,\quad \quad \quad \quad \quad {\left({\frac {{dw}_{2}}{dx}}\right)}_{x=0}=$$0.$

(6)

From (4), the constants ${\textstyle C}$ and ${\textstyle \,D\,}$ are defined by

$C=-\delta ,\quad \quad \quad \quad \quad \quad \quad \quad \,\,D=0.$

(7)

Then, (4) results as

${\textstyle {w}_{2}=\delta [1-\cos \,\left({\psi }_{2}x\right)]}$.

(8)

One known that deflection is ${\textstyle \delta }$ for ${\textstyle x=L}$ and the same for ${\textstyle x={L}_{2}}$, one can be written

$\delta =A\cos \left({\psi }_{1}L\right)+B\sin \left({\psi }_{1}L\right)+\delta$

(9)

and

${\textstyle \delta \left[1-\cos \,\left({\psi }_{2}{L}_{2}\right)\right]=\,A\cos \left({\psi }_{1}{L}_{2}\right)+B\sin \left({\psi }_{1}{L}_{2}\right)+\delta }$.

(10)

From (9) and (10) can determine the constants,

$A=-B\tan \left({\psi }_{1}L\right),\quad \quad \quad \quad \quad \,B={\frac {\delta \cos \,\left({\psi }_{2}{L}_{2}\right)\mathrm {cos} \,\left({\psi }_{1}L\right)}{\sin \,{\psi }_{1}{L}_{1}}}.$

(11)

Since the tangent is the same to ${\textstyle x={L}_{2}}$ then,

${\textstyle \delta {\psi }_{2}\sin \,\left({\psi }_{2}{L}_{2}\right)=-A{\psi }_{1}\mathrm {sin} \,\left({\psi }_{1}{L}_{2}\right)+B{\psi }_{1}\cos \,({\psi }_{1}{L}_{2})}$.

(12)

Substituting (11) in (12) get the transcendental equation:

$\tan \left({\psi }_{1}{L}_{1}\right)\tan \,\left({\psi }_{2}{L}_{2}\right)={\frac {{\psi }_{1}}{{\psi }_{2}}}.$

(13)

Then, can write the equation in a more explicit form:

$\tan \left({\sqrt {\frac {P}{E{I}_{1}}}}{L}_{1}\right)\tan \,\left({\sqrt {\frac {P}{E{I}_{2}}}}{L}_{2}\right)={\sqrt {\frac {{I}_{2}}{{I}_{1}}}}.$

(14)

Substituting ${\textstyle {L}_{1}}$ for ${\textstyle (L-}$$a)/2$ and ${\textstyle {L}_{2}}$ for ${\textstyle a/2}$, the solution for the case of the Figure 1b is obtained as

$\tan \left({\sqrt {\frac {P}{E{I}_{1}}}}{\frac {(L-a)}{2}}\,\,\right)\tan \,\left({\sqrt {\frac {P}{E{I}_{2}\,}}}{\frac {a}{2}}\,\,\right)={\sqrt {\frac {{I}_{2}}{{I}_{1}}}}.$

(15)

The load ${\textstyle P}$ that satisfies the transcendental equation is called the buckling critical load. The solution of this equation can be obtained by numerical methods, for example, the Newton-Raphson Method. Further details for several cases can be achieved in classic literature [9].

3. Finite difference applied to buckling column with section discontinuity

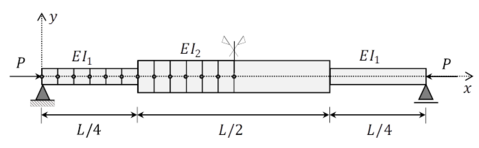
The simply supported column (Figure 2a) consists of three segments proportional to bending rigidities ${\textstyle EI}$. Focusing only on the first buckling mode, it is sufficient to model a half column, as described in Figure 2b.

(a)

(b)

Figure 2. Simplified finite difference model representation of stepped column. (a) Geometric description. (b) Finite difference discretization (${\textstyle m=n/2)}$

The differential equation for lateral displacement ${\textstyle w(x)}$ is stated as

${\frac {d}{dx}}\left(EI\left(x\right){\frac {dw\left(x\right)}{dx}}\right)+P\,w\left(x\right)=0,$

(16)

where ${\textstyle EI(x)}$ is the bending rigidity as a function of coordinate ${\textstyle x}$, ${\textstyle P}$ is the axial compressive load. The boundary conditions are described by

$w\left(0\right)={w}^{'}\left(0\right)=0,$

(17)

where ${\textstyle {w}^{'}\left(x\right)=dw\left(x\right)/dx}$.

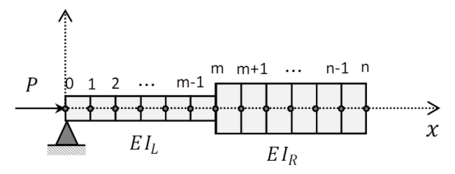
Applying the FDM, we replace the derivatives of ${\textstyle w\left(x\right)}$ by central finite difference of error order ${\textstyle O\left(\Delta {x}^{2}\right)}$ at the interior nodes ${\textstyle i}$ (nodes ${\textstyle 1}$ to ${\textstyle n}$):

$EI\left(x\right)\left({w}_{i-1}-2{w}_{i}+{w}_{i+1}\right)+P\Delta {x}^{2}\,{w}_{i}=$$0,$

(18)

where ${\textstyle {w}_{i}=w\left(i\,\Delta x\right)}$, for ${\textstyle i\in 1}$ to ${\textstyle n}$.

At point ${\textstyle m}$ (Figure 2b), we have difficulty determining flexural inertia ${\textstyle EI\left(x\right)}$ for finite difference operator. As related by [12] and [21], the numerical free vibration analysis or linear buckling load determination of stepped beams using finite difference formulation need special attention at step discontinuity. If flexural rigidity average is chosen, we observe an increase of numerical error of the finite difference model. This approach does not respect the continuity conditions of bending moment for each segment. In literature, a consistent approach to discretizing the stepped beam joint by an equivalent moment of inertia is proposed as follows.

For example, to applying the differential operator (18) at step discontinuity (point ${\textstyle m}$), one proposed creation of two ghost points: (a) one ghost point at the right of the thin beam (with flexural rigidity ${\textstyle E{I}_{L}}$), and (b) one ghost at the left of the thick beam (with flexural rigidity ${\textstyle E{I}_{R}}$). Both differential operators are described, to thin beam:

$E{I}_{L}\left({w}_{i-1}-2{w}_{i}+{w}_{a}\right)+P\Delta {x}^{2}\,{w}_{i}=0$

(19)

and to thick beam:

${\textstyle E{I}_{R}\left({w}_{b}-2{w}_{{i}^{'}}+{w}_{{i}^{'}+1}\right)+P\Delta {x}^{2}\,{w}_{{i}^{'}}=0}$.

(20)

To assure the displacement and bending moment continuity, respectively, we applying the following boundary conditions:

${w}_{i}={w}_{{i}^{'}}\,,$

(21)

${\frac {\partial {w}_{i}}{\partial x}}={\frac {\partial {w}_{{i}^{'}}}{\partial x}}\,\Rightarrow {w}_{i-1}+{w}_{i+1}={w}_{b}+{w}_{a}.$

(22)

Adding the expressions (19) and (20) applying the boundary conditions (21) and (22), we have:

$\left({w}_{i-1}-2{w}_{i}+{w}_{i+1}\right)+{\frac {P\Delta {x}^{2}}{E{I}_{eq}}}\,{w}_{i}=0,$

(23)

where the equivalent moment of inertia ${\textstyle {I}_{eq}}$ is expressed as

${I}_{eq}={\frac {2{I}_{L}{I}_{R}}{{I}_{L}+{I}_{R}}}.$

(24)

In literature, there are other non-consistent equivalent moments of inertia ${\textstyle {I}_{eq}}$ possibilities described as

${I}_{eq}\simeq {I}_{L},$

(25)

${I}_{eq}\simeq {I}_{R},$

(26)

${I}_{eq}\simeq {I}_{avg}={\frac {1}{2}}\left({I}_{L}+{I}_{R}\right).$

(27)

This work proposes to analyse each one of these moments of inertia (24)-(27) at the point ${\textstyle m\,}$ of the intersection of the stepped column, in this way, it will be possible to verify the consistency in the numerical modelling in each case.

4. Convergence analysis and grid convergence index

A reliable numerical solution should have a null error or very close to zero. In order to reduce the numerical error caused by discretization problems, the Richardson Error Estimator and Convergent Error Estimator were used to verify the convergence for FDM approaches. To perform the convergence methods analysis, one necessary to define 3 different meshes: coarse ${\textstyle ({\phi }_{3})}$, medium ${\textstyle ({\phi }_{2})}$ and fine ${\textstyle {(\phi }_{1})}$, with grades ${\textstyle \Delta {h}_{3}}$, ${\textstyle \Delta {h}_{2}}$ e ${\textstyle \Delta {h}_{1}}$, respectively.

According to Marchi and Silva [4,5] the error estimation could be performed following the steps.

4.1 Richardson error estimator

The true numerical error is determined through the equation (28) where ${\textstyle \Phi }$, is the exact analytical solution and ${\textstyle \phi }$ is the proposed numerical solution:

$\epsilon \,({\phi }_{1})=\Phi -{\phi }_{1}.$

(28)

The estimative of the analytical solution ${\textstyle (\Phi )}$ could be performed through

${\phi }_{\infty }\left(PL\right)={\phi }_{1}+\left({\frac {{\phi }_{1}-{\phi }_{2}}{{r}^{PL}-1}}\right),$

(29)

where ${\textstyle r}$ is the grid refinement ratio:

$r={\frac {\Delta {h}_{2}}{\Delta {h}_{1}}}=\,{\frac {\Delta {h}_{3}}{\Delta {h}_{2}}}$

(30)

and ${\textstyle PL}$ is the asymptotic order of the discretization error.

The apparent order of the uncertainty (${\textstyle PU}$) is calculated through

$PU={\frac {\mathrm {log} \,\left({\frac {{\phi }_{2}-{\phi }_{3}}{{\phi }_{1}-{\phi }_{2}}}\right)}{\mathrm {log} \,(r)}}$

(31)

and the estimative of the numerical solution ${\textstyle {\phi }_{\infty }\left(PU\right)}$ could be obtained by

${\phi }_{\infty }\left(PU\right)={\phi }_{1}+\left({\frac {{\phi }_{1}-{\phi }_{2}}{{r}^{PU}-1}}\right).$

(32)

If the apparent order of the error is monotonic convergent, so the analytical solution ${\textstyle (\Phi )}$ is between ${\textstyle {\phi }_{\infty }\left(PL\right)}$ and ${\textstyle {\phi }_{\infty }\left(PU\right)}$.

Equations (29) and (32) are generalized Richardson Extrapolation. The error estimative of numerical solution ( ${\textstyle {\phi }_{1}}$) could be given by the Richardson Error Estimator (${\textstyle {U}_{Ri}}$), calculated by

${U}_{Ri}\left({\phi }_{1}\right)=\,sg\left({\phi }_{1}-{\phi }_{2}\right)\mathrm {max} \,\left\{\left|{U}_{Ri}\left({\phi }_{1},PL\right)\right|;\left|{U}_{Ri}\left({\phi }_{1},PU\right)\right|\right\},$

(33)

been the maximum absolute value between the numerical solution error estimator, obtained by asymptotic error order is

${U}_{Ri}\left({\phi }_{1},PL\right)=\left|{\frac {{\phi }_{1}-{\phi }_{2}}{{r}^{PL}-1}}\right|$

(34)

and by apparent error order is

${U}_{Ri}\left({\phi }_{1},PU\right)=\left|{\frac {{\phi }_{1}-{\phi }_{2}}{{r}^{PU}-1}}\right|.$

(35)

One can be said the estimated error ${\textstyle U}$ is reliable if the condition founded

$\left|{\frac {{U}_{Ri}\left({\phi }_{1}\right)}{\epsilon \,({\phi }_{1})}}\right|\geq 1$

(36)

is fulfilled. In other words, the ratio between the estimated error ${\textstyle U}$ and the true error ${\textstyle \epsilon \,}$ is greater or equal to the unit.

If the aim is obtaining a reliably estimated error, the numerical solution of the variable could be calculated through

$\phi ={\phi }_{1}+{U}_{Ri}({\phi }_{1}).$

(37)

4.2 Convergent error estimator

Using the same numerical solutions (${\textstyle {\phi }_{1},\,{\phi }_{2},\,{\phi }_{3}}$), is possible to calculate an estimative of the convergent numerical solution that allows minimizing the true discretization error. The numerical convergent solution can be calculated by

${\phi }_{c}={\frac {{\phi }_{\infty }\left(PL\right)+{\phi }_{\infty }\left(PU\right)}{2}},$

(38)

where ${\textstyle {\phi }_{\infty }\left(PL\right)}$ and ${\textstyle {\phi }_{\infty }\left(PU\right)}$ have already been determinate in equations (29) and (32) by Richardson extrapolation.

The convergent error estimative of the convergent numerical solution could be determined by:

${U}_{c}\left({\phi }_{c}\right)=\left|{\frac {{\phi }_{\infty }\left(PL\right)-{\phi }_{\infty }\left(PU\right)}{2}}\right|$

(39)

and the true discretization error is calculated through

$\epsilon \,\left({\phi }_{c}\right)=\Phi -{\phi }_{c}.$

(40)

In this case, the estimated error ${\textstyle {U}_{c}}$ is reliable if satisfy what is proposed by

$\left|{\frac {{U}_{c}\left({\phi }_{c}\right)}{\epsilon \,({\phi }_{c})}}\right|\geq 1.$

(41)

The numerical solution of the analyzed variable can be defined by

$\phi ={\phi }_{c}\pm {U}_{c}\left({\phi }_{c}\right).$

(42)

One important to highlight, according to Marchi and Silva [4,5], in a convergent interval of ${\textstyle Pu}$, is recommended using a numerical convergent solution ${\textstyle {\phi }_{c}}$ instead using ${\textstyle {\phi }_{1}}$, so the true error ${\textstyle \epsilon \,({\phi }_{c})}$ is smaller than ${\textstyle \epsilon \,({\phi }_{1})}$.

5. Problem description and numerical procedure

This work analyzed the convergence of the critical buckling load in a stepped column using FDM. The cross-section of the column was square and the length (${\textstyle L}$) was equal to ${\textstyle 100mm}$, being composed of different cross-sections in which the intermediate section (section 2) has a moment of inertia greater than the extremity sections (Figure 2). The material used had Young's modulus equal to ${\textstyle 200GPa\,}$ and Poisson's coefficient equal to ${\textstyle 0.3}$.

The moment of inertia (${\textstyle {I}_{L}}$) to the left of point ${\textstyle m}$ was kept constant and equal to ${\textstyle 0.5m{m}^{4}}$. To validate the methodology, two cases were investigated. CASE 1 considering the ratio between cross-section moments of inertia (${\textstyle {I}_{R}}$/ ${\textstyle {\,I}_{L}}$) equal to ${\textstyle 1.5}$ and CASE 2 equal to ${\textstyle 2}$. Moreover, four different moments of inertia (${\textstyle {I}_{L},\,{I}_{R},\,{I}_{avg},\,{I}_{eq})\,}$ - discussed in section 3 - were considered in node ${\textstyle m}$ of the intersection (Figure 2b) and the consistency of the modeling was verified in each case.

The FDM implementation was developed in MATLAB® and for validation, one was also simulated in ANSYS APDL® by Finite Element Method (FEM). Initially, Newton Raphson's method was used to obtain the exact solution of the transcendental equation for the buckling problem. After the numerical simulations (FDM and FEM), the data post-processing were used for the convergence analysis (discussed in section 4). Finally, the asymptotic behavior of the discretization error and possible numerical instabilities were investigated in each case of the problem proposed.

6. Numerical results

This section presents a comparison between the discretization error by FEM using commercial software (ANSYS®) and FDM, posteriorly the results by FDM are showed for each moment of inertia considered in this study. Then, the analysis of the results allows verifying the convergence of the proposed problem.

6.1 Buckling of stepped column

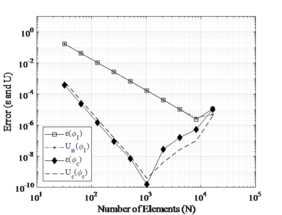
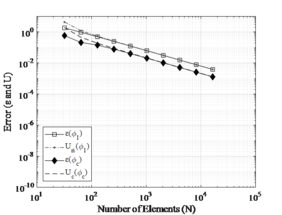
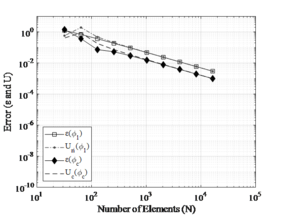
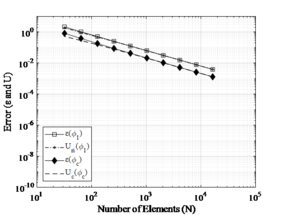
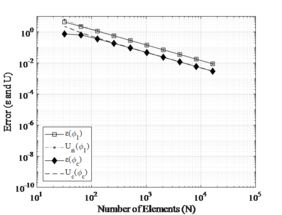
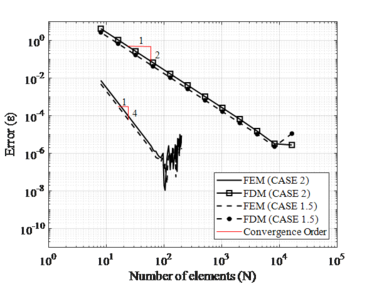
Figure 3 shows a comparison between the FEM and FDM. One can be noted that convergence by FEM is the 4^th order and by FDM is the 2^nd order. This occurs because the approximation for the finite difference operator is 2^nd order and the deflection approximation used in ANSYS® is 4^th order.

Figure 3. Convergence analysis by FEM and FDM for stepped column (CASE 1 and CASE 2)

From Figure 3, one can be seen that the two numerical models showed monotonic convergence until reaching the computational limit of approximately ${\textstyle \,{10}^{-6}}$. Moreover, it is clearly visible that the FDM needs further refinement of the mesh compared to the FEM. For example, to obtain an error of ${\textstyle {10}^{-4}}$, the FDM needed approximately 1100 elements while the FEM used only 20 elements. Nevertheless, the use of extrapolation methods can cause the FDM to reach the order of convergence of the FEM from the determination of the convergent solution. This will consequently lead the FDM to achieve much smaller errors than those presented by the FEM (see section 6.2).

In both cases, there is a numerical instability is generated by the computational limit. In this case, it is advisable to always choose to use solutions outside the numerical instability zone, in addition to checking the error considered reliable for each type of problem. Finally, the convergent monotonic order is considered consistent according to the numerical model proposed by FEM and FDM.

6.2 Convergence analysis of inertia models by finite difference method

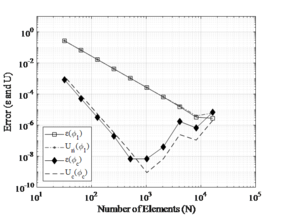
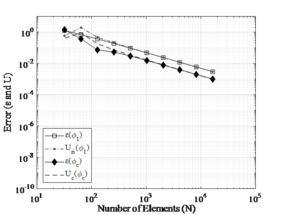
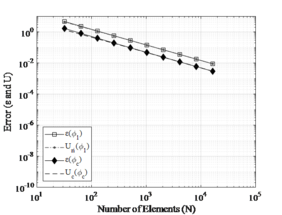
The discretization true error ${\textstyle (\epsilon )}$ and the estimated error ${\textstyle (U)}$ for CASE 1 and CASE 2 are shown in Figures 4 and 5, respectively. The results considered four different moments of inertia ( ${\textstyle {I}_{L},\,{I}_{R},\,{I}_{avg},\,{I}_{eq})\,}$ in node ${\textstyle m}$ of the intersection.

(a)	(b)
(c)	(d)
Figure 4. Estimated error (${\textstyle U}$) and true error (${\textstyle \epsilon }$) for stepped column: CASE 1. (a) ${\textstyle {I}_{eq}}$. (b) ${\textstyle {I}_{R}}$. (c) ${\textstyle {I}_{avg}}$. (d) ${\textstyle {I}_{L}}$

(a)	(b)
(c)	(d)
Figure 5. Estimated error (${\textstyle U}$) and true error (${\textstyle \epsilon }$) for stepped column: CASE 2. (a) ${\textstyle {I}_{eq}}$. (b) ${\textstyle {I}_{R}}$. (c) ${\textstyle {I}_{avg}}$. (d) ${\textstyle {I}_{L}}$

According to the results presented, the convergence behavior between the stepped columns (CASE 1 and CASE 2) is quite similar. The results were consistent and convergent when the equivalent moment of inertia (${\textstyle {I}_{eq}}$) was used, reaching 2^nd convergence order for the Richardson Error Estimator and 4^th convergence order using Convergence Error Estimator. Numerical instability occurs approximately for similar meshes, in both cases, that indicated an instability for computational limit.

In addition, one could be seen that the results of the convergent solution (${\textstyle {\phi }_{c})}$ for CASE 1 obtained an error approximately to ${\textstyle {10}^{-10}}$ and for CASE 2 the error was about ${\textstyle {10}^{-8}}$, which the best convergence value occurs for 1024 elements. It is valid to emphasize that the matrices generated for a much large number of elements are robust, and the convergence is constrained by the computer precision used in the simulation.

As expected, using moment of inertia (${\textstyle {I}_{R}}$, ${\textstyle {I}_{avg}}$ and ${\textstyle {I}_{L}}$) have inconsistent results with errors between ${\textstyle {10}^{-3}}$ and ${\textstyle {10}^{-2}}$. This happens because the continuity conditions on bending moment are not satisfied at the point ${\textstyle m}$of intersection between different cross-sections [12], therefore, the apparent order of convergence does not reach the asymptotic order of error.

Lastly, the results confirmed what Marchi and Silva [4] reinforced, that is in an interval convergent ${\textstyle Pu}$ is advisable to use ${\textstyle {\phi }_{c}}$ instead ${\textstyle {\phi }_{1}}$ because the true discretization error ${\textstyle \epsilon ({\phi }_{c})}$ is less than ${\textstyle \epsilon ({\phi }_{1})}$. Furthermore, this work presented that the use of extrapolation in FDM provides better results when compared with conventional FEM results.

7. Conclusions

This article verified the order of convergence of the critical buckling load of a simply supported stepped column. For this, Richardson's Extrapolation and the Convergence Error Estimator were used to estimating and reducing the numerical error of the buckling problem by the Finite Difference Method.

The study contemplated two cases with different ratios between the moment of inertia of the cross-sections and evaluated the consistency of the results at the intersection of the sections (the point at which the change in the cross-section of the column occurs). To verify the consistency of the solution, different moments of inertia were proposed at the point of intersection for both cases.

The methodology using the equivalent moment of inertia at the intersection node proved to be monotonic convergent with asymptotic order 2^nd for Richardson's Error Estimator and asymptotic order 4^th for Convergence Error Estimator, being considered consistent. These results showed that, for the same number of elements, the convergent solution has errors twice as small as that of the numerical solution. In this case, the error of the numerical solution was approximately 10^-4 and the error of the convergent solution was 10^-8 and 10^-10, depending on the ratio between moments of inertia.

This work also showed that using inconsistent moments of inertia at the point of intersection precludes the apparent order of error from reaching the asymptotic order of the proposed problem. This confirmed that the study of convergence is extremely necessary for the analysis of possible inconsistencies or numerical modeling problems.

Finally, the use of error estimators proved to be adequate to verify the reliability of the discretization errors for the proposed problem, in addition to being possible to define the regions with asymptotic or unstable behavior of the numerical solutions. Moreover, applied extrapolations technics in FDM can be possible reaching minor errors than the model by FEM using commercial software.

Acknowledgements

This study was financed in part by the Coordination for the Improvement of Higher Education Personnel – Brazil (CAPES), Brazilian Council for Scientific and Technological Development (CNPq) and Research Support Foundation of Federal District (FAPDF). The authors are grateful to Group of Experimental and Computational Mechanics (UnB-FGA/GMEC) for provide computational resources and become possible the work development. The second author acknowledges Laboratory of Vibration and Dynamic Metrology and Group of Dynamics of Systems (UnB-FT/EnM/GDS) for its support to make possible the present experiments.

References

[1] Richardson L.F. IX. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Philos. Trans. R. Soc. London. Ser. A, Contain. Pap. a Math. or Phys. Character, 210:307–357, 1911. 10.1098/rsta.1911.0009.

[2] Marchi C.H., Novak L.A., Santiago C.D., Vargas A.P. da S. Highly accurate numerical solutions with repeated Richardson extrapolation for 2D laplace equation. Appl. Math. Model., 37(12–13):7386–7397, 2013. 10.1016/j.apm.2013.02.043.

[3] Marchi C.H. et al. Polynomial interpolation with repeated Richardson extrapolation to reduce discretization error in CFD. Appl. Math. Model, 40(21–22):8872–8885, 2016. 10.1016/j.apm.2016.05.029.

[4] Marchi C.H., Silva A.F.C. Multi-dimensional discretization error estimation for convergent apparent order. J. Brazilian Soc. Mech. Sci. Eng., 27(4):432–439, 2005. 10.1590/S1678-58782005000400012.

[5] Marchi C.H., Silva A.F.C. Unidimensional numerical solution error estimation for convergent apparent order. Numer. Heat Transf. Part B Fundam., 42(2):167–188, 2002. 10.1080/10407790190053888.

[6] Wang Y.M. Error analysis of a compact finite difference method for fourth-order nonlinear elliptic boundary value problems. Appl. Numer. Math., 120(13):53–67, 2017. 10.1016/j.apnum.2017.04.011.

[7] Challamel N., Picandet V., Elishakoff I., Wang C.M., Collet B., Michelitsch T. On nonlocal computation of eigenfrequencies of beams using finite difference and finite element methods. Int. J. Struct. Stab. Dyn., 15(7):1–18, 2015. 10.1142/S0219455415400088.

[8] Challamel N., Picandet V., Collet B., Michelitsch T., Elishakoff I., Wang C.M. Revisiting finite difference and finite element methods applied to structural mechanics within enriched continua. Eur. J. Mech. A/Solids, 53:107–120, 2015. 10.1016/j.euromechsol.2015.03.003.

[9] Timoshenko S.P., Gere J.M. Theory of elastic stability. Dover Publications, pp. 113–117, 1963.

[10] Soltani M., Sistani A. Elastic stability of columns with variable flexural rigidity under arbitrary axial load using the finite difference method. Journals Numer. Method Civ. Eng., 1(4):23–31, 2017. [Online]. Available: http://nmce.kntu.ac.ir/article-1-91-en.pdf%0Ahttp://nmce.kntu.ac.ir/browse.php?a_code=A-10-50-3&sid=1&slc_lang=en.

[11] O’Rourke M., Zebrownski T. Buckling load for nonuniform columns. Comput. Struct., 7(4):717–720, 1977.

[12] Krishnan A., George G., Malathi P. Use of finite difference method in the study of stepped beams. Int. J. Mech. Eng. Educ., 26(1):11-24, 1998.

[13] Lu X., Wu Q., Khan Y. The analysis of dynamic buckling of an impacted column using difference methods. Int. J. Comput. Methods, 15(4):1850025, 2018. 10.1142/S0219876218500251.

[14] Lu Z.R., Huang M., Liu J.K., Chen W.H., Liao W.Y. Vibration analysis of multiple-stepped beams with the composite element model. J. Sound Vib., 322(4–5):1070–1080, 2009. 10.1016/J.JSV.2008.11.041.

[15] Dang T.D., Kapania R.K., Patil M.J. Ritz analysis of discontinuous beams using local trigonometric functions. Comput. Mech., 47(3):235–250, 2011. 10.1007/s00466-010-0540-y.

[16] Baǧdatli S.M., Özkaya E., Özyiǧit H.A., Tekin A. Non linear vibrations of stepped beam systems using artificial neural networks. Struct. Eng. Mech., 33(1):15–30, 2009. 10.12989/sem.2009.33.1.015.

[17] Yao F., Meng W., Zhao J., She Z., Shi G., Liu H. Buckling theoretical analysis on all-terrain crane telescopic boom with n-stepped sections. J. Mech. Sci. Technol., 32(8):3637–3644, 2018. 10.1007/s12206-018-0715-6.

[18] Salama M.I. Elastic buckling of single-stepped columns with end and intermediate axial loads. Comput. Eng. Phys. Model., 1(4):25–35, 2019. 10.22115/CEPM.2018.147218.1046.

[19] Fliegner B., Marcinowski J., Sakharov V. Buckling resistance of two-segment stepped steel columns. Materials, 14(4):1046, 2021. 10.3390/ma14041046.

[20] Tian W., Hao J., Zhong W. Buckling of stepped columns considering the interaction effect among columns. J. Constr. Steel Res., 177:106416, 2021. 10.1016/j.jcsr.2020.106416.

[21] Iremonger M.J. Finite difference buckling analysis of non-uniform columns. Comput. Struct., 12(5):741-748, 1980.