An algorithm for the design of a feedforward controller in canals

Resumen

Cuando se realiza cualquier movimiento de compuerta u otro mecanismo de control de un canal en lámina libre, se produce una respuesta del flujo que puede tardar mucho tiempo en notarse en el lugar del canal en que se generó la necesidad de aumentar o reducir el caudal de riego, por ejemplo. Por otro lado, a veces existen variaciones del caudal de riego que están programadas dentro de un horizonte futuro por lo que la acción de control puede programarse también. En este trabajo, se presenta un algoritmo de control en lazo abierto que planifica los movimientos de compuerta ante unas demandas programadas de caudal en los puntos de salida lateral del canal en un horizonte de predicción. La matriz de influencia hidráulica (HIM) o matriz de sensibilidad de las condiciones hidrodinámicas en un canal a cambios de los parámetros definitorios de las trayectorias de compuerta es una herramienta que se muestra muy eficaz en el control de canales en lazo abierto. El trabajo define el concepto, presenta la forma de calcular y compilar la HIM a partir de las ecuaciones completas de Saint-Venant en su forma en curvas características. Posteriormente, se presenta el algoritmo GoRoSo en que se utiliza dicha matriz: un controlador en lazo abierto para el cálculo anticipado de las trayectorias óptimas de compuerta en un horizonte de predicción con el objetivo de mantener constante el calado en los puntos de salida lateral por gravedad.

Abstract

When it is carried out any movement of a gate or another mechanism of control of a canal in free surface flow, an answer of the flow can take a lot of time in being noticed in the place of the canal takes place in which it was generated the necessity to increase or to reduce the irrigation demand, for example. Usually, the scheduled perturbations of the flow can be programmed for a future horizon. In this manner, the control action can also be programmed. This work, it shows a feedforward control algorithm that plans the gate trajectories when the demand at offtakes are programmed in a prediction horizon. The Hydraulic Influence Matrix (HIM) or matrix of sensibility of the hydrodynamic conditions in the canals to changes in the parameters of the gate trajectories is a tool that is shown very effective in the control of canals in open loop. The work defines the concept, it presents the form of to calculate and to compile the HIM starting from the complete equations of Saint-Venant in their characteristic form. Later on, it shows up an algorithm in that HIM is used: a feedforward controller algorithm so-called GoRoSo. Known the water demands at offtakes, the algorithm calculates the optimal gate trajectories in advance for a prediction horizon with the objective of keeping constant the water depth at gravity offtakes.

Palabras clave

Método de las caracteristicas ; Control en lazo abierto ; Control con modelos predictivos ; Canales de riego ; Optimización no lineal

Keywords

Method of characteristics ; Feedforward control ; Model Predictive Control ; Irrigation canals ; Nonlinear optimization

1. Introducción y objetivos

En la gestión del agua en algunos canales de regadío se ha demostrado la necesidad de planificar las operaciones de abertura y cierre de las compuertas ante cambios significativos de la demanda de caudal de riego. La causa principal de esta necesidad se encuentra en el importante retraso existente entre la operación de compuerta (acción de control) y la consiguiente modificación del caudal transportado (respuesta del canal) en el punto de cambio de demanda (punto de consigna). Este desfase puede llegar a ser de varios días y depende de la longitud del canal. En estos casos, cuando no se aplica ningún tipo de planificación de las operaciones, se produce una pérdida de eficiencia en el transporte y distribución de agua que habitualmente lleva al despilfarro de este preciado recurso. Con la presentación del algoritmo objeto de este trabajo se aporta una herramienta encaminada a ayudar a la solución de esta problemática.

Cuando se abre una toma de un canal por la que sale una parte del caudal que transporta el canal principal, se produce una perturbación sobre el flujo (cambios de nivel y velocidad de transporte) que se traslada tanto aguas abajo como aguas arriba. Si la distancia entre la toma y la cabecera del canal es muy grande, el tiempo que tarda la perturbación en hacer notar sus efectos en cabecera es muy grande. Posteriormente, los efectos de la consiguiente abertura de la compuerta de cabecera para la recuperación de las condiciones del flujo vuelven a tardar en volver a la toma. Puede pasar que durante todo este periodo de tiempo el tramo donde se ubica la salida lateral se vacíe excesivamente, perdiendo la capacidad de suministrar agua a las demás tomas por falta de cota. En estas circunstancias, resulta muy interesante abrir la compuerta de cabecera antes de abrir la toma de manera que cuando los efectos de la abertura lleguen a la toma, ésta se abra. Lo único que se tiene que saber es el momento en que se abrirá la toma y en qué cantidad, es decir, conocer de antemano la programación de las demandas de todas las salidas laterales.

El algoritmo GoRoSo es una herramienta de ayuda al cálculo de las trayectorias de compuerta de un canal (entendiendo como trayectoria una secuencia temporal de posiciones de compuerta) ante un escenario futuro en el que las demandas a suministar en las tomas están perfectamente programadas. Por lo tanto, se trata de un controlador en lazo abierto. El algoritmo utiliza técnicas de optimización matemática para la resolución del problema. El objetivo principal de este trabajo es la presentación del algoritmo.

En la sección 2, se describe el «método de las curvas características» para la resolución numérica de las ecuaciones de Saint-Venant en su forma completa, que es el método utilizado para la simulación de flujo en lámina libre en canales. La aplicación de este método da como resultado un modelo predictivo en tiempo discreto. También se define, se indica cómo se calcula y se muestra el sentido físico de un concepto nuevo: la matriz de influencia hidráulica (denotada en adelante con el acrónimo HIM). Se entiende por influencia hidráulica de un parámetro, la capacidad de dicho parámetro para modificar el flujo (calado/velocidad). El cálculo de la HIM está íntimamente ligado al de las ecuaciones del modelo de simulación, razón por la cual se presentan en la misma sección.

En la sección 3 se presenta el algoritmo GoRoSo . En una primera parte, se plantea el problema de control en lazo abierto como un problema de optimización con restricciones cuyas incógnitas a resolver son los parámetros definitorios de la trayectorias de compuerta. Y posteriormente, se establecen los pasos de que consta el algoritmo, cuya base es el algoritmo de descenso denominado «Problema cuadrático secuencial» (en inglés, «Sequential Quadratic Problem») porque resuelve un problema cuadrático en cada interación. Para la resolución del problema cuadrático que se plantea, se utiliza la estrategia de las restricciones activas (en inglés, «Active Set Method»).

Aunque el algoritmo GoRoSo actúe off-line , puede considerarse también como un controlador predictivo en tiempo discreto como los utilizados en control predictivo en [1] y podría ser presentado formalmente como tal. A pesar de ello, se ha preferido el punto de vista numérico porque la aportación principal del trabajo es el concepto de matriz de influencia y su sentido físico.

2. La matriz de influencia hidráulica: concepto y obtención

2.1. La influencia hidráulica de un movimiento de compuerta en un instante sobre una sección del canal

2.1.1. Las ecuaciones del flujo en lámina libre

Las ecuaciones de Barré de Saint-Venant (1871) describen el flujo de agua en lámina libre en canales y son el resultado de la aplicación de los principios de conservación de la masa y de la cantidad de movimiento en un volumen de control que se extiende transversalmente en la dirección del flujo para toda la sección del canal. Una deducción rigurosa de estas ecuaciones para canales prismáticos se puede encontrar en Walker y Skogerboe [2] . El sistema resultante está constituido por el siguiente sistema de dos ecuaciones diferenciales de primer orden en derivadas parciales:

${\begin{array}{c}{\frac {\partial y}{\partial t}}+v{\frac {\partial y}{\partial x}}+{\frac {A\left(y\right)}{T\left(y\right)}}{\frac {\partial v}{\partial x}}=0\\{\frac {\partial v}{\partial t}}+v{\frac {\partial v}{\partial x}}+g{\frac {\partial y}{\partial x}}=g\left[S_{0}-S_{f}\left(y,v\right)\right]\end{array}}$

( 1)

donde x y t son las variables independientes espacio y tiempo, y   es el calado o nivel de la superficie libre repecto la solera del canal, ${\textstyle v}$ es la velocidad media ponderada de todas las partículas de una sección transversal al flujo, ${\textstyle A\left(y\right)}$ es el área de la sección mojada que depende del calado, ${\textstyle T\left(y\right)}$ es el ancho de la lámina libre que también depende del calado, S₀ es la pendiente de la solera del canal y finalmente, ${\textstyle S_{f}\left(y,v\right)}$ es la pendiente de rozamiento.

El sistema de ecuaciones (1) es aplicable si se cumplen las siguientes hipótesis:

• La curvatura de la lámina es pequeña, con lo que se desprecian las aceleraciones verticales y la distribución de presiones a lo largo de una línea vertical es la misma que en condiciones hidrostáticas.
• La pendiente se supone suficientemente pequeña como para que el seno del ángulo que forma con la horizontal sea prácticamente nulo.
• El término de disipación de energía será especificado mediante la ecuación de Manning, que fue obtenida en condiciones de régimen estacionario:

$S_{f}\left(y,v\right)=n^{2}{\frac {v\left|v\right|}{R_{H}^{4/3}}}\quad con\quad R_{H}=$${\frac {A\left(y\right)}{P\left(y\right)}}$

( 2)

donde n   es el coeficiente de Manning y ${\textstyle P\left(y\right)}$ es el perímetro mojado que es función del calado.

• Los cambios de las condiciones de flujo no son suficientemente rápidos como para generar frentes de onda.
• El canal es de sección prismática.

Estas ecuaciones no son susceptibles de ser resueltas analíticamente y, en cambio, sí que lo son numéricamente. Por ello, existe un conjunto de métodos numéricos que permiten resolver el sistema (1) que pueden encontrarse en Gómez [3] . Según Wylie [4] todos los métodos numéricos de resolución ya sean explícitos, implícitos o mediante curvas características presentan unos resultados parecidos cuando se comparan con la realidad, dependiendo más la exactitud de los resultados de los datos de entrada que de las diferencias metodológicas. Teniendo en cuenta este factor clave, en el presente trabajo se ha utilizado el método de las características porque ayuda a la comprensión física del fenómeno de onda subyacente en el flujo en lámina libre. No obstante, la elección de un método de resolución no particulariza lo que aquí se expone por lo que sería perfectamente aplicable con cualquier método numérico utilizado.

Los ejes a lo largo de los cuales se discretiza el sistema hiperbólico (1) son los clásicos de espacio y tiempo (x /t   ) pero, si se discretiza a lo largo de curvas características del sistema denotadas paramétricamente con ${\textstyle x^{+}\left(t\right)}$ y ${\textstyle x^{-}\left(t\right)}$ y que cumplen localmente las dos siguientes ecuaciones diferenciales ordinarias,

${\begin{array}{c}{\frac {{dx}^{+}}{dt}}=v+c\left(y\right)\\{\frac {{dx}^{-}}{dt}}=v-c\left(y\right)\end{array}}$

( 3)

entonces, (1) queda transformado en el siguiente sistema en derivadas totales:

${\begin{array}{c}{\frac {dv}{dt}}+{\frac {g}{c\left(y\right)}}{\frac {dy}{dt}}=g\left[S_{0}-S_{f}\left(y,v\right)\right]\\{\frac {dv}{dt}}-{\frac {g}{c\left(y\right)}}{\frac {dy}{dt}}=g\left[S_{0}-S_{f}\left(y,v\right)\right]\end{array}}$

( 4)

donde la primera ecuación es válida a lo largo de la curva ${\textstyle x^{+}\left(t\right)}$ y la segunda a lo largo de la ${\textstyle x^{-}\left(t\right)}$ , ${\textstyle c\left(y\right)={\sqrt {\frac {gA\left(y\right)}{T\left(y\right)}}}}$ es la celeridad de onda.

La dificuldad de dicha tranformación radica en el hecho de que el sistema se tiene que resolver a lo largo de las curvas características o ejes locales que son solución del propio sistema y al tratarse de un sistema no lineal se obliga a resolver las cuatro ecuaciones simultáneamente. Por suerte, en las condiciones de flujo subrítico (${\textstyle {\frac {{dx}^{+}}{dt}}>0}$ y ${\textstyle {\frac {{dx}^{-}}{dt}}<0}$ ) que se dan habitualmente en el contexto del control de canales, las curvas ${\textstyle x^{+}\left(t\right)}$ y ${\textstyle x^{-}\left(t\right)}$ siempre se cruzan —a pesar de no ser ortogonales— y por lo tanto, se asegura la solución y su unicidad.

En resumen, solucionar el sistema de dos ecuaciones en derivadas parciales (1) equivale a resolver el siguiente sistema de cuatro ecuaciones en derivadas totales:

${\begin{array}{r}{\frac {dv}{dt}}+{\frac {g}{c\left(y\right)}}{\frac {dy}{dt}}=g\left[S_{0}-S_{f}\left(y,v\right)\right]\quad \quad (a)\\{\frac {{dx}^{+}}{dt}}=v+c\left(y\right)\quad \quad \quad \quad \quad (b)\\{\frac {dv}{dt}}-{\frac {g}{c\left(y\right)}}{\frac {dy}{dt}}=g\left[S_{0}-S_{f}\left(y,v\right)\right]\quad \quad (c)\\{\frac {{dx}^{-}}{dt}}=v-c\left(y\right)\quad \quad \quad \quad \quad (d)\end{array}}$

( 5)

El proceso matemático de transformación de (1) en (5) se puede encontrar en muchas referencias bibliográficas [3] , [5] , [6]  and [7] . (5) describe las condiciones de flujo en un canal de la misma forma que (1) porque no se añaden nuevas hipótesis en la transformación. No obstante, (5) tiene restricciones en la forma de ser aplicado. La variable x , que inicialmente era independiente, ahora es dependiente de t según se desprende de (3) ; entonces (5 -(a)) será cierta a lo largo de las curvas que cumplen (5 -(b)) y paralelamente, (5 -(c)) será cierta a lo largo de las curvas que cumplen (5 -(d)).

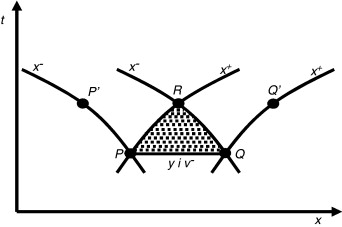
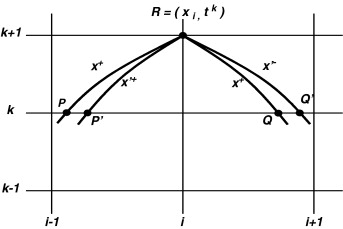
El sistema (5) puede ser representado en el plano x /t ( fig. 1 ) donde en el punto de intersección R coinciden las cuatro ecuaciones y por tanto se pueden encontrar las cuatro incógnitas x , t , y   , ${\textstyle v}$ . Si se conocen las condiciones de flujo sobre la recta que une los puntos P y Q , se podrá encontrar la posición del punto R (x , t ) y las condiciones de flujo (y   ,${\textstyle v}$ ).

Figura 1. Esquema del dominio de dependencia del punto R y representación para el anunciado del primer teorema de unicidad.

Esto se puede asegurar gracias al primero de los teoremas de unicidad planteados en [8] , donde se asegura que si sobre una curva del plano x /t que no sea una característica —como la recta PQ de la figura 1 — se conocen las condiciones de flujo y   , ${\textstyle v}$ , entonces el sistema (5) determina la solución con unicidad en la zona punteada PQR ; zona que se denomina dominio de dependencia del punto R porque cualquier perturbación introducida en esta zona afectará a la posición del punto R y sus condiciones hidrodinámicas.

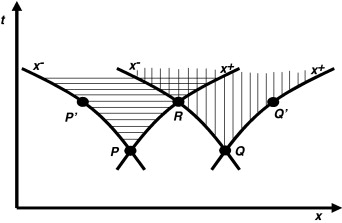
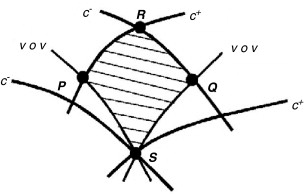
Un concepto complementario al anterior es el dominio de influencia . En la figura 2 se puede ver el dominio de influencia del punto P , que es el conjunto de puntos del plano x /t de la zona tramada horitzontalmente que se ven afectados por las condiciones de flujo existentes en P . De la misma forma, la zona tramada verticalmente es el dominio de influencia de Q y la zona doblemente tramada es el dominio de influencia de R .

Figura 2. Dominios de influencia de los puntos P, Q y R.

Se denomina dominio de influencia de P porque una variación en las condiciones de flujo en este punto afectará a todos los puntos del dominio, de entre ellos, los puntos P ′ y R . De la misma manera Q influencia Q ′ y R .

Una vez introducidos los conceptos de dominio de influencia y dominio de dependencia se está en disposición de presentar el objetivo básico del siguiente apartado. Cuando se provoca un movimiento de compuerta, se producen una serie de cambios en las condiciones de flujo, primero en las proximidades de la compuerta y después más lejos. Si el movimiento es considerado como una perturbación, entonces podemos hablar del dominio de influencia de la perturbación y por extensión, del dominio de influencia de un movimiento de compuerta. Así, la presentación de una forma de cálculo y cuantificación de la variación sufrida por las condiciones del punto R —denotadas con ▵y_R , ${\textstyle \vartriangle v_{R}}$ — cuando se introducen perturbaciones en los puntos P y Q —denotadas con ▵y_P , ${\textstyle \vartriangle v_{P}}$ , ▵y_Q , ${\textstyle \vartriangle v_{Q}}$ — es el objetivo de la seguiente sección.

2.1.2. La discretización de las ecuaciones en características

Como ya se ha comentado anteriormente, (1) y su equivalente (5) no tienen solución analítica conocida y, por consiguiente, el uso de técnicas numéricas es obligatorio. Existen muchos esquemas numéricos susceptibles de ser utilizados en la discretización. En este trabajo, se ha utilizado un esquema concreto y se han hecho los desarrollos matemáticos pertinentes sobre el resultado de esta discretización.

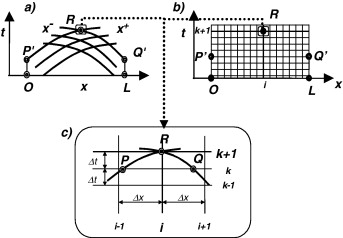
Con el objetivo de conseguir pasos de tiempo de integración lo más largos posible sin pérdida de precisión de los resultados, se ha optado por un esquema en diferencias finitas de segundo orden, denominado método de las características curvas en [3] . Este es un método parcialmente implícito que supone el trozo de característica como una parábola, es decir, un «spline»de segundo orden. La necesidad de utilización de este esquema de paso largo se verá claro más adelante. Si se aplica este esquema a (5) y se tiene en cuenta la nomenclatura presentada en la figura 3 , resulta el siguiente sistema de ecuaciones algebraicas:

${\begin{array}{l}{\frac {v_{R}-v_{P}}{t_{R}-t_{P}}}+\left[\theta {\frac {g}{c_{R}}}+\left(1-\theta \right){\frac {g}{c_{P}}}\right]{\frac {y_{R}-y_{P}}{t_{R}-t_{P}}}\\={gS}_{0}-g\left[\theta S_{f_{R}}+\left(1-\theta \right)S_{f_{P}}\right]\\{\frac {x_{R}-x_{P}}{t_{R}-t_{P}}}=\theta \left[v_{R}+c_{R}\right]+\left(1-\theta \right)\left[v_{P}+c_{P}\right]\\{\frac {v_{R}-v_{Q}}{t_{R}-t_{Q}}}-\left[\theta {\frac {g}{c_{R}}}+\left(1-\theta \right){\frac {g}{c_{Q}}}\right]{\frac {y_{R}-y_{Q}}{t_{R}-t_{Q}}}\\={gS}_{0}-g\left[\theta S_{f_{R}}+\left(1-\theta \right)S_{f_{Q}}\right]\\{\frac {x_{R}-x_{Q}}{t_{R}-t_{Q}}}=\theta \left[v_{R}-c_{R}\right]+\left(1-\theta \right)\left[v_{Q}-c_{Q}\right]\end{array}}$

( 6)

donde ${\textstyle S_{f_{R}}=S_{f}\left(y_{R},v_{R}\right)}$ , ${\textstyle S_{f_{P}}=S_{f}\left(y_{P},v_{P}\right)}$ , ${\textstyle S_{f_{Q}}=S_{f}\left(y_{Q},v_{Q}\right)}$ y 0 ≤ θ  ≤ 1 es el coeficiente de ponderación temporal que indica el tipo de esquema usado; cuando θ  = 1 el esquema es implícito, cuando θ  = 0 es explícito y cuando ${\textstyle \theta ={\frac {1}{2}}}$ el esquema es en diferencias centradas o de características curvas.

Figura 3. Esquema de interpolación con «splines» de segundo orden.

Si se conocen las condiciones de flujo en los puntos P y Q , entonces de (6) se conocen x_P , t_P , y_P , ${\textstyle v_{P}}$ y x_Q , t_Q , y_Q , ${\textstyle v_{Q}}$ y quedan como incógnitas x_R , t_R , y_R , ${\textstyle v_{R}}$ , las cuales se pueden encontrar mediante cualquier método de resolución de ceros de ecuaciones algebraicas no lineales, como por ejemplo el método de Newton-Raphson . Reordenando (6) , se obtiene:

${\begin{array}{l}f_{1}\equiv x_{R}-x_{P}-{\frac {\Delta t}{2}}\left[v_{R}+c_{R}+v_{P}+c_{P}\right]=0\\f_{2}\equiv \left(v_{R}-v_{P}\right)+{\frac {g}{2}}{\frac {c_{R}+c_{P}}{c_{R}c_{P}}}\left(y_{R}-y_{P}\right)+\\\quad +g\Delta t\left({\frac {S_{f_{R}}+S_{f_{P}}}{2}}-S_{0}\right)=0\\f_{3}\equiv \left(v_{R}-v_{Q}\right)-{\frac {g}{2}}{\frac {c_{R}+c_{Q}}{c_{R}c_{Q}}}\left(y_{R}-y_{Q}\right)+\\\quad +g\Delta t\left({\frac {S_{f_{R}}+S_{f_{Q}}}{2}}-S_{0}\right)=0\\f_{4}\equiv x_{R}-x_{Q}-{\frac {1}{2}}\Delta t\left[v_{R}-c_{R}+v_{Q}-c_{Q}\right]=0\end{array}}$

( 7)

donde Δt  = t_R  − t_P  = t_R  − t_Q (fig. 3 c)) y ζ  = 1/2.

Un vez resuelto (7) , uno ya puede hacerse la siguiente pregunta: ¿cuál hubiera sido la solución si en lugar de tener en P   por ejemplo las condiciones ${\textstyle \left(y_{P},v_{P}\right)}$ se hubiesen tenido ${\textstyle \left(y_{P}+\vartriangle y_{P},v_{P}\right)}$ ? Es decir, una vez introducida una perturbación en el calado. Una pregunta como esta tiene fácil solución y está íntimamente relacionada con el concepto de influencia hidráulica .

Cabe decir que el grado de influencia depende tanto de las propias condiciones de P como de las de R . Así, una misma modificación de las condiciones en P tendrá un efecto perturbador mayor sobre R a medida que en P se tengan unos calados y velocidades bajas.

Para responder la pregunta planteada, supongamos que todas las variables de (7) dependen implícitamente de y_P , esto es: ${\textstyle y_{R}\left(y_{P}\right)}$ , ${\textstyle v_{R}\left(y_{P}\right)}$ , ${\textstyle t_{R}\left(y_{P}\right)}$ y ${\textstyle x_{R}\left(y_{P}\right)}$ y con este supuesto se aplica el teorema de la función implícita. Entonces, resolviendo el sistema 4 × 4:

$\left[{\begin{array}{cccc}{\frac {\partial f_{1}}{\partial x_{R}}}&{\frac {\partial f_{1}}{\partial y_{R}}}&{\frac {\partial f_{1}}{\partial v_{R}}}&{\frac {\partial f_{1}}{\partial t_{R}}}\\{\frac {\partial f_{2}}{\partial x_{R}}}&{\frac {\partial f_{2}}{\partial y_{R}}}&{\frac {\partial f_{2}}{\partial v_{R}}}&{\frac {\partial f_{2}}{\partial t_{R}}}\\{\frac {\partial f_{3}}{\partial x_{R}}}&{\frac {\partial f_{3}}{\partial y_{R}}}&{\frac {\partial f_{3}}{\partial v_{R}}}&{\frac {\partial f_{3}}{\partial t_{R}}}\\{\frac {\partial f_{4}}{\partial x_{R}}}&{\frac {\partial f_{4}}{\partial y_{R}}}&{\frac {\partial f_{4}}{\partial v_{R}}}&{\frac {\partial f_{4}}{\partial t_{R}}}\end{array}}\right]\left({\begin{array}{c}{\frac {\partial x_{R}}{\partial y_{P}}}\\{\frac {\partial y_{R}}{\partial y_{P}}}\\{\frac {\partial v_{R}}{\partial y_{P}}}\\{\frac {\partial t_{R}}{\partial y_{P}}}\end{array}}\right)=-\left({\begin{array}{c}{\frac {\partial f_{1}}{\partial y_{P}}}\\{\frac {\partial f_{2}}{\partial y_{P}}}\\0\\0\end{array}}\right)$

( 8)

se puede encontrar los valores ${\textstyle {\frac {\partial x_{R}}{\partial y_{P}}}}$ , ${\textstyle {\frac {\partial y_{R}}{\partial y_{P}}}}$ , ${\textstyle {\frac {\partial v_{R}}{\partial y_{P}}}}$ y ${\textstyle {\frac {\partial t_{R}}{\partial y_{P}}}}$ .

Obviamente, la matriz del sistema se evalúa en x_P , t_P , y_P , ${\textstyle v_{P}}$ , x_Q , t_Q , y_Q y ${\textstyle v_{Q}}$ . Linealizando en el entorno de y_P podemos escribir una aproximación en serie de Taylor de primer orden:

$y_{R}\left(y_{P}+\vartriangle y_{P}\right)=y_{R}\left(y_{P}\right)+$${\frac {\partial y_{R}}{\partial y_{P}}}\vartriangle y_{P}+$$O\left(\vartriangle y_{P}^{2}\right)$

( 9)

lo que permite la obtención de y_R perturbado tal y como se quería.

Existen expresiones similares a (9) para el resto de variables x_R , ${\textstyle v_{R}}$ y t_R . Cabe decir que, dado que (8) es el resultado de la aplicación del teorema de la función implícita sobre (7) , hace falta que se cumpla la condición necesaria y suficiente de que la matriz de (8) sea invertible, es decir, que su determinante sea diferente de cero. Se puede demostrar que en presencia de flujo se tiene esta condición, y por lo tanto, los valores de las derivadas implícitas ${\textstyle {\frac {\partial x_{R}}{\partial y_{P}}}}$ , ${\textstyle {\frac {\partial y_{R}}{\partial y_{P}}}}$ , ${\textstyle {\frac {\partial v_{R}}{\partial y_{P}}}}$ y ${\textstyle {\frac {\partial t_{R}}{\partial y_{P}}}}$ siempre existen y de forma única. Se pueden realizar análisis similares para el resto de variables perturbables ${\textstyle v_{P}}$ , y_Q y ${\textstyle v_{Q}}$ .

En general y de cara a posteriores desarrollos, se hablará de un parámetro genérico ϕ para denotar variables de caracterización del flujo como son los calados, las velocidades, los coeficientes físicos como la rugosidad, posiciones de compuerta, etcétera. Entonces se puede escribir:

$\left[{\boldsymbol {\mbox{M}}}\right]{\frac {\partial }{\partial \phi }}\left({\begin{array}{c}x_{R}\\y_{R}\\v_{R}\\t_{R}\end{array}}\right)=-\left[{\boldsymbol {\mbox{N}}}\right]{\frac {\partial }{\partial \phi }}\left({\begin{array}{c}y_{P}\\v_{P}\\y_{Q}\\v_{Q}\end{array}}\right)$

( 10)

donde

$\left[{\boldsymbol {\mbox{M}}}\right]=\left[{\frac {\partial \left(f_{1},f_{2,}f_{3},f_{4}\right)}{\partial \left(x_{R},y_{R},v_{R},t_{R}\right)}}\right];\left[{\boldsymbol {\mbox{N}}}\right]=$$\left[{\frac {\partial \left(f_{1},f_{2,}f_{3},f_{4}\right)}{\partial \left(y_{P},v_{P},y_{Q},v_{Q}\right)}}\right]$

Hay que hacer notar que (8) equivale a (10) cuando ϕ  = y_P con lo que se tiene un carácter más general. Desde un punto de vista físico (10) «traslada»y «modifica»la influencia hidráulica de un parámetro ϕ desde los puntos P y Q al punto R .

2.1.3. Aplicación sobre una malla estructurada

Por lo que se ha dicho hasta el momento, la solución se encuentra en aquellos puntos de coordenadas x_R y t_R que son solución del sistema. En la figura 3 , se puede ver como a partir de la superposición de la malla de curvas características (fig. 3 a)) y de una malla estructurada (fig. 3 b)) se obtiene un esquema donde se interpolan las variables en los puntos P y Q ( fig. 3 c)) y de esta forma se obtienen las condiciones de flujo en el punto fijo R . Obviamente, se resuelve el mismo conjunto de ecuaciones que en (7) , pero ahora con las nuevas incógnitas ${\textstyle x_{P},y_{R},v_{R}}$ y x_Q .

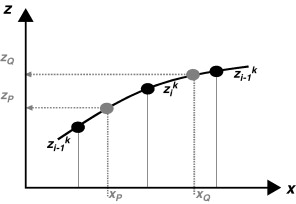
Esta malla estructurada da lugar a una nueva nomenclatura en que cualquier variable queda doblemente indexada con el índice temporal k y el índice espacial i   . Así, ${\textstyle y_{i}^{k}}$ y ${\textstyle v_{i}^{k}}$ representan los valores de nivel de agua y velocidad media en el punto de coordenadas x_i  = i Δx y t^k  = k Δt donde Δx y Δt toman valores predeterminados. Dado que se ha elegido un esquema de discretización de segundo orden, la interpolación también deberá serlo por coherencia. Se ha optado por el uso de los denominados factores de Lagrange —una manera de representar los «splines» cuadráticos— que para una variable cualquiera z resulta ( fig. 4 ):

$s^{k}\left(x,z_{i-1}^{k},z_{i}^{k},z_{i+1}^{k}\right)=\left({\frac {x-x_{i}}{\Delta x}}\right)\left({\frac {x-x_{i-1}}{2\Delta x}}\right)z_{i+1}^{k}+$ $+\left({\frac {x-x_{i-1}}{\Delta x}}\right)\left({\frac {x-x_{i+1}}{-\Delta x}}\right)z_{i}^{k}+$$\left({\frac {x-x_{i}}{-\Delta x}}\right)\left({\frac {x-x_{i+1}}{-2\Delta x}}\right)z_{i-1}^{k}$

( 11)

Figura 4. Esquema de interpolación con «splines»de segundo orden.

De esta forma las variables ${\textstyle y_{P},v_{P},y_{Q}}$ y ${\textstyle v_{Q}}$ pasan a ser funciones interpoladas en las abcisas x_P y x_Q :

$y_{P}\left(x_{P}\right)=s_{y_{P}}\left(x_{P},y_{i-1}^{k},y_{i}^{k},y_{i+1}^{k}\right)$ $v_{P}\left(x_{P}\right)=s_{v_{P}}\left(x_{P},v_{i-1}^{k},v_{i}^{k},v_{i+1}^{k}\right)$ $y_{Q}\left(x_{Q}\right)=s_{y_{Q}}\left(x_{Q},y_{i-1}^{k},y_{i}^{k},y_{i+1}^{k}\right)$ $v_{Q}\left(x_{Q}\right)=s_{v_{Q}}\left(x_{Q},v_{i-1}^{k},v_{i}^{k},v_{i+1}^{k}\right)$

( 12)

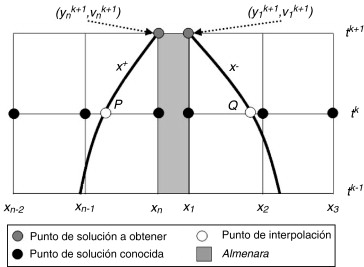
A partir de ahora hace falta determinar el sistema a resolver para encontrar la evolución de la influencia de un parámetro a través de la malla estructurada, de la misma forma como se ha hecho para encontrar (10) . Al contrario de lo que parece, encontrar el «traslado» de las influencias —o evolución de la influencia tanto en el tiempo como en el espacio— en una malla estructurada simplifica el problema. La causa de ésto es que la influencia del parámetro sobre la posición y el instante —es decir, los valores ${\textstyle {\frac {\partial x_{R}}{\partial \phi }}=}$${\frac {\partial x_{i}}{\partial \phi }}$ y ${\textstyle {\frac {\partial t_{R}}{\partial \phi }}=}$${\frac {\partial t^{k+1}}{\partial \phi }}$ — pierden el sentido porque se quiere encontrar la solución en una abscisa y una ordenada determinadas (fig. 5 ). Así, si se introduce una perturbación en cualquier variable hidráulica del instante k , entonces resolviendo (7) con x_P , ${\textstyle y_{i}^{k+1}}$ , ${\textstyle v_{i}^{k+1}}$ y x_Q como incógnitas se obtienen dos juegos de caracterísiticas —x⁺ , x^′+ y x⁻ , x^′− —, dos soluciones para el punto R   —${\textstyle \left(y_{i}^{k+1},v_{i}^{k+1}\right)}$ y ${\textstyle {\left(y_{i}^{k+1},v_{i}^{k+1}\right)}^{'}}$ — y dos juegos de abscisas de interpolación —x_P , x_Q y ${\textstyle x_{P^{'}},x_{Q^{'}}}$ —, resultando inalterada la posición del punto R .

Figura 5. Par de curvas características pasando por el punto R.

Volviendo a aplicar el teorema de la función implícita sobre las mismas ecuaciones (7) con el supuesto que ${\textstyle y_{i-1}^{k}}$ , ${\textstyle v_{i-1}^{k}}$ , ${\textstyle y_{i}^{k}}$ , ${\textstyle v_{i}^{k}}$ , ${\textstyle y_{i+1}^{k}}$ , ${\textstyle v_{i+1}^{k}}$ , ${\textstyle y_{i}^{k+1}}$ y ${\textstyle v_{i}^{k+1}}$ dependen ahora de un parámetro genérico ϕ , se encuentra el siguiente sistema:

$\left[{\boldsymbol {\mbox{M}}}\right]{\frac {\partial }{\partial \phi }}\left({\begin{array}{c}x_{P}\\y_{i}^{k+1}\\v_{i}^{k+1}\\x_{Q}\end{array}}\right)=-\left[{\boldsymbol {\mbox{N}}}\right]\left[{\boldsymbol {\mbox{S}}}\right]{\frac {\partial }{\partial \phi }}\left({\begin{array}{c}y_{i-1}^{k}\\v_{i-1}^{k}\\y_{i}^{k}\\v_{i}^{k}\\y_{i+1}^{k}\\v_{i+1}^{k}\end{array}}\right)$

( 13)

siendo ahora

$\left[{\boldsymbol {\mbox{M}}}\right]=\left[{\frac {\partial \left(f_{1},f_{2,}f_{3},f_{4}\right)}{\partial \left(x_{P},y_{R},v_{R},x_{Q}\right)}}\right];\left[{\boldsymbol {\mbox{N}}}\right]=$$\left[{\frac {\partial \left(f_{1},f_{2,}f_{3},f_{4}\right)}{\partial \left(y_{P},v_{P},y_{Q},v_{Q}\right)}}\right]$ $\left[{\boldsymbol {\mbox{S}}}\right]=\left[{\frac {\partial \left(s_{y_{P}},s_{v_{P}},s_{y_{Q}},s_{v_{Q}}\right)}{\partial \left(y_{i-1}^{k},v_{i-1}^{k},y_{i}^{k},v_{i}^{k},y_{i+1}^{k},v_{i+1}^{k}\right)}}\right]$

De los cuatro valores obtenidos (${\textstyle {\frac {\partial x_{P}}{\partial \phi }}}$ , ${\textstyle {\frac {\partial y_{i}^{k+1}}{\partial \phi }}}$ , ${\textstyle {\frac {\partial v_{i}^{k+1}}{\partial \phi }}}$ y ${\textstyle {\frac {\partial x_{Q}}{\partial \phi }}}$ ) solamente interesa conservar ${\textstyle {\frac {\partial y_{i}^{k+1}}{\partial \phi }}}$ y ${\textstyle {\frac {\partial v_{i}^{k+1}}{\partial \phi }}}$ de cada intante de tiempo para poder encontrar la solución en el siguiente instante ya que en ningún caso los otros dos valores intervienen en la parte derecha de (13) .

Como novedad respecto de (10) hay que destacar la presencia de la matriz ${\textstyle \left[S\right]}$ , cuyos valores pueden obtenerse fácilmente a partir de (12) y cabe destacar también como a partir de los valores conocidos de la influencia del parámetro ϕ en el instante k   : ${\textstyle {\frac {\partial y_{i-1}^{k}}{\partial \phi }}}$ , ${\textstyle {\frac {\partial v_{i-1}^{k}}{\partial \phi }}}$ , ${\textstyle {\frac {\partial y_{i}^{k}}{\partial \phi }}}$ , ${\textstyle {\frac {\partial v_{i}^{k}}{\partial \phi }}}$ , ${\textstyle {\frac {\partial y_{i+1}^{k}}{\partial \phi }}}$ y ${\textstyle {\frac {\partial v_{i+1}^{k}}{\partial \phi }}}$ , se obtiene la influencia en el instante k  + 1: ${\textstyle {\frac {\partial y_{i}^{k+1}}{\partial \phi }}}$ y ${\textstyle {\frac {\partial v_{i}^{k+1}}{\partial \phi }}}$ , haciendo evidente el concepto de dominio de influencia y de dominio de dependencia .

La inversión de la matriz ${\textstyle \left[{\boldsymbol {\mbox{M}}}\right]}$ no añade demasiados cálculos adicionales si se resuelve (13) immediatamente después de la resolución del sistema (7) puesto que es la misma matriz que la utilizada en la última iteración del proceso de Newton-Raphson —véase parte izquierda de (8) —, incluso se puede utilizar la misma descomposición LU .

Para cada punto de la malla estructurada, se puede resolver un sistema del tipo (13) a excepción de los puntos interiores con compuerta y en las condiciones de contorno. El tratamiento de estos puntos será objeto de las dos secciones siguientes.

2.1.4. Las ecuaciones de una compuerta

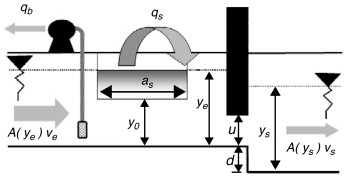
Existen muchas estructuras de control del flujo en los canales que permiten moldearlo según el deseo del operador de compuertas. Prácticamente todas las estructuras presentes en canales, a excepción del propio revestimiento, pueden ser consideradas estructuras de control. El estudio particular de cada una de éstas es inabordable en este trabajo y no es tampoco un objetivo. A pesar de ello, se presentará a modo de ejemplo una estructura compuesta que se denominará punto de control o almenara donde se puede encontrar, además de una compuerta de deslizamiento vertical, un vertedero y un bombeo directo, tal como puede verse en la figura 6 .

Figura 6. Esquema de un punto de control o almenara.

La forma de interactuar con el flujo que tiene esta superestructura de control denominada almenara puede ser descrita en base a los principios de conservación de la masa y de la energía, los cuales establecen dos relaciones matemáticas entre las condiciones de flujo justo aguas arriba del punto y las condiciones justo aguas abajo:

${\begin{array}{l}A\left(y_{e}\right)v_{e}=A\left(y_{s}\right)v_{s}+q_{b}+q_{s}\left(y_{e}\right)\\A\left(y_{s}\right)v_{s}=k_{c}\times u\times {\sqrt {y_{e}+d-y_{s}}}\quad si\quad \quad y_{s}>d+{\frac {1}{2}}u\\A\left(y_{s}\right)v_{s}=k_{c}\times u\times {\sqrt {y_{e}-{\frac {1}{2}}u}}\quad \quad si\quad \quad y_{s}\leq d+{\frac {1}{2}}u\end{array}}$

( 14)

donde ${\textstyle A\left(y_{e}\right)v_{e}}$ y ${\textstyle A\left(y_{s}\right)v_{s}}$ son el caudal entrante definido en términos de calado y velocidad de entrada y el de salida, respectivamente, q_b es el caudal de salida por bombeo programado, ${\textstyle q_{s}\left(y_{e}\right)=C_{s}a_{s}{\left(y_{e}-y_{0}\right)}^{\frac {3}{2}}}$ es el caudal desaguado por la salida lateral a través del vertedero, siendo C_s el coeficiente de desagüe, a_s la longitud del labio y y₀ su altura respecto del fondo del canal, ${\textstyle k_{c}={\sqrt {2g}}C_{c}a_{c}}$ siendo C_c el coeficiente de desagüe de la compuerta y a_c su ancho supuesta rectangular, d es la caída de la compuerta y u su abertura.

Desde el punto de vista del control, hay que hacer notar la diferencia que existe entre ambos tipos de salida lateral: la primera, representada por el bombeo, que está prefijada de antemano por el programador de compuertas y la segunda, simbolizada por el vertedero que depende del calado existente aguas arriba del punto de control y por lo tanto, controlada por éste. La diferencia radica en el hecho de que con el bombeo se podrá suministrar el caudal deseado con la única condición de que baje agua suficiente y a través del vertedero lateral el agua suministrada dependerá del calado que se consiga mantener de manera que resultará mucho más difícil su control. Fuera de los casos en que el bombeo es obligado por cuestiones de cota, principalmente el vertedero es el mecanismo de reparto de agua preferido por tener menor coste energético pero tiene la dificultad de un peor control.

2.1.5. La discretización de las ecuaciones de una almenara

La presencia de almenaras a lo largo de un canal conduce a la subdivisión del mismo en tramos de manera que entre dos de ellas se define un tramo y entre dos tramos una almenara   . Así, se denota ${\textstyle y_{n}^{k+1}}$ como el calado existente en el nodo n del tramo aguas arriba de la almenara en el instante k  + 1 y se define ${\textstyle y_{1}^{k+1}}$ como el calado existente en el primer nodo del tramo aguas abajo de la almenara en k  + 1 (fig. 7 ). Y también para las velocidades ${\textstyle v_{n}^{k+1}}$ y ${\textstyle v_{1}^{k+1}}$ .

Figura 7. Esquema de un punto de control o almenara.

Si se discretizan (14) y se reúnen con (7) se llega al sistema de seis ecuaciones con seis incógnitas siguiente:

${\begin{array}{l}f_{1}\equiv \quad x_{n}-x_{P}-{\frac {1}{2}}\Delta t\left[v_{n}^{k+1}+\quad c_{n}^{k+1}+v_{P}+c_{P}\right]=0\\f_{2}\equiv \left(v_{n}^{k+1}-v_{P}\right)+{\frac {g}{2}}{\frac {c_{n}^{k+1}+c_{P}}{c_{n}^{k+1}c_{P}}}\left(y_{n}^{k+1}-y_{P}\right)+g\Delta t\left({\frac {S_{f}{}_{n}^{k+1}+S_{f_{P}}}{2}}-S_{0}\right)=0\\f_{3}\equiv \left(v_{1}^{k+1}-v_{Q}\right)-{\frac {g}{2}}{\frac {c_{1}^{k+1}+c_{Q}}{c_{1}^{k+1}c_{Q}}}\left(y_{1}^{k+1}-y_{Q}\right)+g\Delta t\left({\frac {S_{f}{}_{1}^{k+1}+S_{f_{Q}}}{2}}-S_{0}\right)=0\\f_{4}\equiv x_{n}-x_{Q}-{\frac {1}{2}}\Delta t\left[v_{1}^{k+1}-c_{1}^{k+1}+v_{Q}-c_{Q}\right]=0\\f_{5}\equiv A\left(y_{n}^{k+1}\right)v_{n}^{k+1}-A\left(y_{1}^{k+1}\right)v_{1}^{k+1}-q_{b}-q_{s}\left(y_{n}^{k+1}\right)=0\\f_{6}\equiv A\left(y_{1}^{k+1}\right)v_{1}^{k+1}-k_{c}u{\left(y_{n}^{k+1}-y_{1}^{k+1}+d\right)}^{\frac {1}{2}}=0\end{array}}$

( 15)

donde

$\Delta t=t^{k+1}-t_{P}=t^{k+1}-t_{Q}$ $y_{P}=s_{y_{P}}\left(x_{P},y_{n-2}^{k},y_{n-1}^{k},y_{n}^{k}\right)$ $v_{P}=s_{y_{P}}\left(x_{P},v_{n-2}^{k},v_{n-1}^{k},v_{n}^{k}\right)$ $y_{Q}=s_{y_{Q}}\left(x_{Q},y_{1}^{k},y_{2}^{k},y_{3}^{k}\right)$ $v_{Q}=s_{y_{Q}}\left(x_{Q},v_{1}^{k},v_{2}^{k},v_{3}^{k}\right)$ $c_{1}^{k+1}=c\left(y_{1}^{k+1}\right)\quad y\quad c_{n}^{k+1}=$$c\left(y_{n}^{k+1}\right)$ $S_{f}{}_{n}^{k+1}=S_{f}\left(y_{n}^{k+1},v_{n}^{k+1}\right)\quad y\quad S_{f}{}_{1}^{k+1}=$$S_{f}\left(y_{1}^{k+1},v_{1}^{k+1}\right)$

y donde las incógnitas son x_P , ${\textstyle y_{n}^{k+1}}$ , ${\textstyle v_{n}^{k+1}}$ ,${\textstyle y_{1}^{k+1}}$ , ${\textstyle v_{1}^{k+1}}$ y x_Q .

Si se supone que ϕ   es un parámetro que define de alguna manera la posición de compuerta —ésto es ${\textstyle u\left(\phi \right)}$ — y que las incógnitas x_P , ${\textstyle y_{n}^{k+1}}$ , ${\textstyle v_{n}^{k+1}}$ ,${\textstyle y_{1}^{k+1}}$ , ${\textstyle v_{1}^{k+1}}$ y x_Q también dependen de ϕ , entonces, volviendo a aplicar el teorema de la función implícita sobre (15) , se obtiene:

$\left[{\boldsymbol {\mbox{M}}}\right]{\frac {\partial }{\partial \phi }}\left({\begin{array}{c}x_{P}\\y_{n}^{k+1}\\v_{n}^{k+1}\\y_{1}^{k+1}\\v_{1}^{k+1}\\x_{Q}\end{array}}\right)=\left[{\boldsymbol {\mbox{N}}}\right]\left[{\boldsymbol {\mbox{S}}}\right]{\frac {\partial }{\partial \phi }}\left({\begin{array}{c}y_{n-2}^{k}\\v_{n-2}^{k}\\y_{n-1}^{k}\\v_{n-1}^{k}\\y_{n}^{k}\\v_{n}^{k}\\y_{1}^{k}\\v_{1}^{k}\\y_{2}^{k}\\v_{2}^{k}\\y_{3}^{k}\\v_{3}^{k}\end{array}}\right)+\left({\boldsymbol {\mbox{L}}}\right){\frac {\partial u}{\partial \phi }}$

( 16)

donde ahora

$\left[{\boldsymbol {\mbox{M}}}\right]=\left[{\frac {\partial \left(f_{1},f_{2},f_{3},f_{4},f_{5},f_{6}\right)}{\partial \left(x_{P},y_{n}^{k+1},v_{n}^{k+1},y_{1}^{k+1},v_{1}^{k+1},x_{Q}\right)}}\right]$ $\left[{\boldsymbol {\mbox{N}}}\right]=-\left[{\frac {\partial \left(f_{1},f_{2},f_{3},f_{4},f_{5},f_{6}\right)}{\partial \left(y_{P},v_{P},y_{Q},v_{Q}\right)}}\right]$ $\left({\boldsymbol {\mbox{L}}}\right)=-{\left(0,0,0,0,0,{\frac {\partial f_{6}}{\partial u}}\right)}^{T}$ $\left[{\boldsymbol {\mbox{S}}}\right]=\left[{\frac {\partial \left(y_{P},v_{P},y_{Q},v_{Q}\right)}{\partial \left(y_{n-2}^{k},v_{n-2}^{k},y_{n-1}^{k},v_{n-1}^{k},y_{n}^{k},v_{n}^{k},y_{1}^{k},v_{1}^{k},y_{2}^{k},v_{2}^{k},y_{3}^{k},v_{3}^{k}\right)}}\right]$

Hasta el momento, se ha hablado de la influencia de un parámetro genérico ϕ   sin entrar en detalles de qué puede llegar a representar y es ahora cuando aparece por primera vez representado explícitamente a través de la descripción de la abertura de compuerta a través de ${\textstyle u\left(\phi \right)}$ . A pesar de que, a estas alturas, la forma particular de esta función es desconocida, en (16) se muestra que la influencia de ϕ sobre las condiciones de flujo en el instante k  + 1 (parte izquierda de la igualdad) es la suma de la influencia indirecta de las condiciones en el instante k (primer sumando de la parte derecha de la igualdad) y la influencia directa de la abertura en el instante k  + 1 (segundo sumando) a través del término ${\textstyle {\frac {\partial u}{\partial \phi }}}$ que representa la variación de la abertura cuando varía ϕ .

2.1.6. Las trayectorias de compuerta

En un modelo descriptivo de un fenómeno físico como el flujo de agua en canales regulados, existen los parámetros empíricos, las variables de control y las variables observables que son dependientes de las anteriores. Habitualmente, el proceso de identificación de parámetros, primeramente, consiste en tomar medidas de las variables observables (en el presente caso serían el caudal, la velocidad y/o calados). Después, se tiene que intentar ajustar el valor de los parámetros de tal manera que una vez introducido en las ecuaciones del modelo, éstas hagan una previsión lo más parecida posible al comportamiento medido. Durante este proceso, que se denomina resolución del problema inverso, es necesario conocer la matriz de sensibilidad a los parámetros. Una de las novedades que presenta este trabajo es la de considerar como incógnitas del problema inverso las variables de control, que en este caso son las trayectorias de compuerta, con lo que la matriz de sensibilidad acaba siendo la matriz de influencia hidráulica y el comportamiento medido pasa a ser un comportamiento deseado.

Así pues, el objetivo consiste en encontrar las trayectorias de compuerta que generan un comportamiento del canal lo más parecido al deseado. Por lo tanto, la existencia de esta forma analítica de encontrar la matriz de influencia hidráulica resulta una inestimable ayuda para cuantificar el grado de sensibilidad a los parámetros.

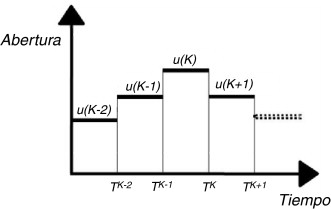
En el control de los canales de regadío, el tiempo que dura un movimiento de compuerta se puede considerar despreciable si se compara con el tiempo en que la compuerta está parada. La causa de que una compuerta no esté permanentemente en movimiento es que cualquier reposicionamiento de compuerta tiene sus costes¹ . Por este motivo, la mejor forma de representar matemáticamente una trayectoria de compuerta es mediante una función temporal constante a tramos con la forma ilustrada en la figura 8 .

Figura 8. Representación de una trayectoria de compuerta mediante una función a tramos.

Esta representación matemática facilita la parametrización del problema, que es el proceso de identificación de las incógnitas, porque simplemente identificando como ϕ   la posición de compuerta ${\textstyle u\left(K\right)}$ existente durante el periodo de tiempo K comprendido entre los instantes t^{K −1} y t^K ya se tiene la parametrización. No obstante, hay otras representaciones posibles de trayectoria de compuerta que son susceptibles de ser parametrizadas.

Se define una trayectoria de compuerta como el siguiente vector de parámetros:

${\boldsymbol {\mbox{U}}}=\left[{\begin{array}{ccccc}u\left(K_{I}+1\right)&\cdots &u\left(K\right)&\cdots &u\left(K_{F}\right)\end{array}}\right]$

( 17)

donde K_I es el periodo de muestreo en el que se está en cuyo final se resolverá el problema de optimización, K_F  = K_I  + λ siendo λ el número de intervalos de muestreo u horizonte de predicción que se corresponde con el último intervalo en que está definida la función.

Una descripción matemática de este tipo lleva consigo las siguientes consecuencias:

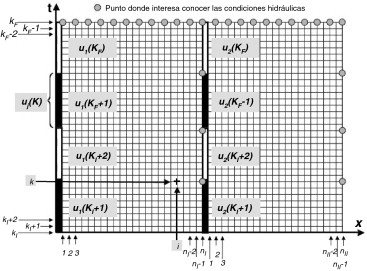
• Para resolver el problema se utiliza el método de las características . Este método está sujeto a la condición de estabilidad de Courant-Friedrichs-Levy que se resume diciendo que el incremento de tiempo de integración numérica Δt tiene que ser menor que el tiempo que tarda en viajar una onda el incremento de espacio de integración Δx . Por otro lado, como ya se ha dicho anteriormente, las compuertas se mantienen paradas la mayor parte del tiempo con lo que el periodo de muestreo es muy superior al de integración numérica. Por este motivo se tiene que establecer una discretización temporal de la trayectoria de compuerta independiente del intervalo de integración numérica. Para denotar esta diferencia se utilizará el superíndice K (en mayúscula) para la discretización temporal de las trayectorias de compuerta y el k (en minúscula) para el intervalo de integración numérica, tal y como puede verse en la figura 9 .

Figura 9. Esquema de las dos discretizaciones utilizadas. Los círculos grises indican los puntos donde interesa conocer las condiciones hidráulicas (observador discreto).

• La derivada ${\textstyle {\frac {\partial u\left(K\right)}{\partial \phi }}=}$$1$ en el sistema (16) . Así que a partir de ahora se referirá como parámetro genérico la abertura ${\textstyle u\left(K\right)}$ en lugar de ϕ como hasta ahora.
• Con (17) se dota a los parámetros de cierto carácter temporal que permite afirmar:

${\frac {\partial y_{i}^{k}}{\partial u\left(K\right)}}=0\quad si\quad t^{k}<T^{K}$

2.1.7. Las condiciones de contorno

Para concluir el estudio de la influencia hidráulica de un único movimiento de compuerta sobre el flujo en un punto del canal en un instante determinado de esta sección, hace falta describir las condiciones de contorno y también descubrir cómo evoluciona la influencia cuando se traslada a los extremos del canal y «rebota». En [8] se demuestra un segundo teorema de unicidad para sistemas de segundo orden como el estudiado aquí. El teorema dice lo siguiente (fig. 10 ): «Conocidas las condiciones de flujo en una intersección S   de características y conocida una sola variable de las dos curvas no características ${\textstyle {\tilde {SP}}}$ y ${\textstyle {\tilde {SQ}}}$ , entonces se asegura solución y unicidad en la zona tramada ${\textstyle {\tilde {SPRQ}}}$ ».

Figura 10. Esquema para el enunciado del segundo teorema de unicidad.

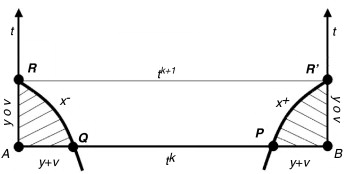
La aplicación conjunta de este teorema y el principio planteado anteriormente (fig. 1 ) permite asegurar unicidad de la solución en las zonas tramadas de la figura 11 si se establen dos condiciones, una en cada extremo del canal. Es decir, si se conocen las condiciones de flujo en los puntos A y B del instante k   , y una condición en los segmentos no característicos ${\textstyle {\overline {AR}}}$ y ${\textstyle {\overline {{BR}^{'}}}}$ de los ejes de ordenadas correspondientes a los extremos del canal, se puede encontrar solución en los puntos R y R ′.

Figura 11. Esquema para el establecimiento de las condiciones de contorno en condiciones de flujo subcrítico.

Esto concuerda con el hecho de que en régimen subcrítico se tiene que establecer una condición en cada extremo de canal porque las pendientes de las curvas características x⁺ y x⁻ tienen signo contrario ya que la celeridad de la onda es superior a la velocidad del medio por donde viaja. Por lo tanto, de (3) resulta:

${\frac {{dx}^{+}}{dt}}>0$ ${\frac {{dx}^{-}}{dt}}<0$

Existe un gran número de condiciones de contorno que pueden establecerse en los extremos de un canal y que se pueden representar de forma general de la siguiente manera:

$f_{7}\left(y_{1}^{k+1},v_{1}^{k+1}\right)\equiv 0\quad condici{\acute {o}}n\quad de\quad \quad aguas\quad arriba$ $f_{8}\left(y_{n_{S}}^{k+1},v_{n_{S}}^{k+1}\right)\equiv 0\quad condici{\acute {o}}n\quad de\quad aguas\quad abajo$

( 18)

donce n_S es el número total de secciones en que se ha subdividido el canal.

Tomando la tercera y cuarta ecuaciones de (15) y la primera de (18) resulta el siguiente sistema a resolver para encontrar las condiciones de flujo en el extremo de aguas arriba:

${\begin{array}{l}f_{3}\equiv \left(v_{1}^{k+1}-v_{Q}\right)-{\frac {g}{2}}{\frac {c_{1}^{k+1}+c_{Q}}{c_{1}^{k+1}c_{Q}}}\left(y_{1}^{k+1}-y_{Q}\right)\\\quad +g\Delta t\left({\frac {S_{f_{1}}^{k+1}+S_{f_{Q}}}{2}}-S_{0}\right)=0\\f_{4}\equiv x_{n}-x_{Q}-{\frac {1}{2}}\Delta t\left[v_{1}^{k+1}-c_{1}^{k+1}+v_{Q}-c_{Q}\right]=0\\f_{7}\left(y_{1}^{k+1},v_{1}^{k+1}\right)\equiv 0\end{array}}$

( 19)

Manipulando de la misma forma se pueden encontrar las condiciones de contorno de aguas abajo:

${\begin{array}{l}f_{1}\equiv \quad x_{n_{S}}-x_{P}-{\frac {1}{2}}\Delta t\left[v_{n_{S}}^{k+1}+\quad c_{n_{S}}^{k+1}+v_{P}+c_{P}\right]=0\\f_{2}\equiv \left(v_{n_{S}}^{k+1}-v_{P}\right)+{\frac {g}{2}}{\frac {c_{n_{S}}^{k+1}+c_{P}}{c_{n_{S}}^{k+1}c_{P}}}\left(y_{n_{S}}^{k+1}-y_{P}\right)+\\\quad +g\Delta t\left({\frac {S_{f}{}_{n_{S}}^{k+1}+S_{f_{P}}}{2}}-S_{0}\right)=0\\f_{8}\left(y_{n_{S}}^{k+1},v_{n_{S}}^{k+1}\right)\equiv 0\quad \end{array}}$

( 20)

Volviendo con la hipótesis de que todas las variables son dependientes de una abertura de compuerta ${\textstyle u\left(K\right)}$ , se puede escribir para el contorno de aguas arriba:

$\left[{\boldsymbol {\mbox{M}}}\right]{\frac {\partial }{\partial u\left(K\right)}}\left({\begin{array}{c}y_{1}^{k+1}\\v_{1}^{k+1}\\x_{Q}\end{array}}\right)=\left[{\boldsymbol {\mbox{N}}}\right]\left[{\boldsymbol {\mbox{S}}}\right]{\frac {\partial }{\partial u\left(K\right)}}\left({\begin{array}{c}y_{1}^{k}\\v_{1}^{k}\\y_{2}^{k}\\v_{2}^{k}\\y_{3}^{k}\\v_{3}^{k}\end{array}}\right)+\left(L\right)$

( 21)

donde ahora

$\left[{\boldsymbol {\mbox{M}}}\right]=\left[{\frac {\partial \left(f_{3},f_{4},f_{7}\right)}{\partial \left(y_{1}^{k+1},v_{1}^{k+1},x_{Q}\right)}}\right]\quad y\quad \left[{\boldsymbol {\mbox{N}}}\right]=$$-\left[{\frac {\partial \left(f_{3},f_{4},f_{7}\right)}{\partial \left(y_{Q},v_{Q}\right)}}\right]$ $\left({\boldsymbol {\mbox{L}}}\right)=-{\left(0,0,{\frac {\partial f_{7}}{\partial u\left(K\right)}}\right)}^{T}\quad y\quad \left[{\boldsymbol {\mbox{S}}}\right]=$$\left[{\frac {\partial \left(y_{Q},v_{Q}\right)}{\partial \left(y_{1}^{k},v_{1}^{k},y_{2}^{k},v_{2}^{k},y_{3}^{k},v_{3}^{k}\right)}}\right]$

y para el contorno de aguas abajo:

$\left[{\boldsymbol {\mbox{M}}}\right]{\frac {\partial }{\partial u\left(K\right)}}\left({\begin{array}{c}y_{n_{S}}^{k+1}\\v_{n_{S}}^{k+1}\\x_{P}\end{array}}\right)=\left[{\boldsymbol {\mbox{N}}}\right]\left[{\boldsymbol {\mbox{S}}}\right]{\frac {\partial }{\partial u\left(K\right)}}\left({\begin{array}{c}y_{n_{S}-2}^{k}\\v_{n_{S}-2}^{k}\\y_{n_{S}-1}^{k}\\v_{n_{S}-1}^{k}\\y_{n_{S}}^{k}\\v_{n_{S}}^{k}\end{array}}\right)+\left({\boldsymbol {\mbox{L}}}\right)$

( 22)

donde ahora

$\left[{\boldsymbol {\mbox{M}}}\right]=\left[{\frac {\partial \left(f_{1},f_{2},f_{8}\right)}{\partial \left(y_{n_{S}}^{k+1},v_{n_{S}}^{k+1},x_{P}\right)}}\right]\quad y\quad \left[{\boldsymbol {\mbox{N}}}\right]=$$-\left[{\frac {\partial \left(f_{1},f_{2},f_{8}\right)}{\partial \left(y_{P},v_{P}\right)}}\right]$ $\left({\boldsymbol {\mbox{L}}}\right)=-{\left(0,0,{\frac {\partial f_{8}}{\partial u\left(K\right)}}\right)}^{T}$ $\left[{\boldsymbol {\mbox{S}}}\right]=\left[{\frac {\partial \left(y_{P},v_{P}\right)}{\partial \left(y_{n_{S}-2}^{k},v_{n_{S}-2}^{k},y_{n_{S}-1}^{k},v_{n_{S}-1}^{k},y_{n_{S}}^{k},v_{n_{S}}^{k}\right)}}\right]$

2.2. Influencia hidráulica de un parámetro de trayectoria de compuerta sobre el vector de estado

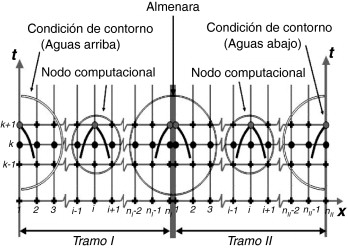
A modo de ejemplo, en la malla estructurada de la figura 12 , se puede ver una discretización espacio-temporal de un canal constituido por dos tramos, el Tramo I subdividido en n_I  − 1 celdas y el Tramo II subdividido en n_II  − 1 celdas. También se puede ver como a partir de la solución en el instante k se puede encontrar la solución de la totalidad de los n_S  = n_I  + n_II nodos computacionales en el instante k  + 1.

Figura 12. Ejemplo de canal con dos tramos para el establecimiento de las condiciones interiores y de contorno.

La lógica de la programación permite obtener la solución de todos los nodos en k  + 1 a partir de la solución en k , de foma secuencial para todo el horizonte de predicción. Ello se hace identificando cada tipo de nodo y resolviendo el correspondiente sistema. Paralelamente al cálculo de la solución, se van actualizando las influencias. Los sistemas involucrados para cada tipo de nodo son:

	Solución	Influencia
Nodo aguas arriba de${\textstyle I}$	(19)	(21)
Nodo computacional de${\textstyle I}$	(7)	(13)
Almenara entre${\textstyle I}$   y ${\textstyle II}$	(15)	(16)
Nodo computacional de${\textstyle II}$	(7)	(13)
Nodo aguas abajo de${\textstyle II}$	(20)	(22)

El conjunto de todas las matrices constituyentes de estos sistemas para cada nodo se puede compilar adecuadamente en un solo sistema que puede representarse de la siguiente manera:

${\frac {\partial {\boldsymbol {\mbox{x}}}^{k+1}}{\partial u\left(K\right)}}=$$\left[{\boldsymbol {\mbox{A}}}\right]{\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u\left(K\right)}}+$${\boldsymbol {\mbox{b}}}\left[{\boldsymbol {\mbox{x}}}^{k+1},u\left(K\right)\right]$

( 23)

donde ${\textstyle \left[{\boldsymbol {\mbox{A}}}\right]=}$${\boldsymbol {\mbox{A}}}\left[x^{k+1},x^{k},u\left(K\right)\right]$ es una matriz cuadrada de orden ${\textstyle \left(2\times n_{S}\right)\times \left(2\times n_{S}\right)}$ siendo n_S el número total de secciones de cálculo de la simulación, ${\textstyle {\boldsymbol {\mbox{b}}}\left[x^{k+1},u\left(K\right)\right]}$ es el vector de influencia directa de 2 × n_S componentes y x es el vector de estado de dimensión 2 × n_S que en los instantes k y k  + 1 vale:

${\boldsymbol {\mbox{x}}}^{k+1}={\left({\begin{array}{cccccccc}y_{1}^{k+1}&v_{1}^{k+1}&\cdots &y_{i}^{k+1}&v_{i}^{k+1}&\cdots &y_{n_{S}}^{k+1}&v_{n_{S}}^{k+1}\end{array}}\right)}^{T}$ ${\boldsymbol {\mbox{x}}}^{k}={\left({\begin{array}{cccccccc}y_{1}^{k}&v_{1}^{k}&\cdots &y_{i}^{k}&v_{i}^{k}&\cdots &y_{n_{S}}^{k}&v_{n_{S}}^{k}\end{array}}\right)}^{T}$

( 24)

Por suerte, cuando la red de canales está constituida por un único canal principal, la matriz ${\textstyle \left[{\boldsymbol {\mbox{A}}}\right]}$ puede almacenarse en forma de matriz banda.

La expresión (23) pone de manifiesto que la influencia del parámetro de compuerta ${\textstyle u\left(K\right)}$ sobre el vector de estado en el instante k  + 1 es la suma de la actualización de la influencia en el instante k   más la influencia directa de ${\textstyle u\left(K\right)}$ . De esta forma, si en lugar de implementar en el canal la posición ${\textstyle u\left(K\right)}$ , se hubiese implementado otra un poco modificada ${\textstyle u\left(K\right)+\Delta u\left(K\right)}$ , entonces el vector de estado habría sido ${\textstyle {\boldsymbol {\mbox{x}}}^{k+1}+}$${\frac {\partial {\boldsymbol {\mbox{x}}}^{k+1}}{\partial u\left(K\right)}}\Delta u\left(K\right)$ .

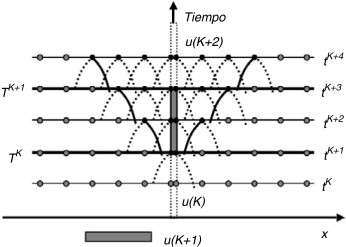
A la vista del esquema de la figura 13 , hay que destacar las seguientes consideraciones:

• Cuando t^{k +1}  < T^K , entonces ${\textstyle {\frac {\partial {\boldsymbol {\mbox{x}}}^{k+1}}{\partial u\left(K\right)}}=}$${\boldsymbol {0}}$ y no hace falta actualizar porque el dominio de influencia hacia atrás en el tiempo es nula.
• En el momento en que t^{k +1}  = T^K , (23) resulta

${\frac {\partial {\boldsymbol {\mbox{x}}}^{k+1}}{\partial u\left(K\right)}}=$${\boldsymbol {\mbox{b}}}\left[{\boldsymbol {\mbox{x}}}^{k+1},u\left(K\right)\right]\quad si\quad t^{k}=$$T^{K}$

ya que ${\textstyle {\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u\left(K\right)}}=}$${\boldsymbol {0}}$ . El planteamiento de este sistema sirve para encontrar el valor inicial de la influencia de ${\textstyle u\left(K\right)}$ sobre las condiciones de flujo x^{k +1} , es decir, la influencia directa.

• Cuando T^K  < t^{k +1}  ≤ T^{K +1} , (23) se usa completa.
• Finalmente, cuando t^{k +1}  > T^{K +1} , (23) pierde la influencia directa y por tanto

${\frac {\partial {\boldsymbol {\mbox{x}}}^{k+1}}{\partial u\left(K\right)}}=$$\left[{\boldsymbol {\mbox{A}}}\right]{\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u\left(K\right)}}$

Figura 13. Evolución de la influencia hidráulica del parámetro de compuerta u(K). Los puntos grises no tienen influencia y los negros sí.

Una vez determinados los valores que va tomando el vector de estado mediante la aplicación recursiva de los sistemas correspondientes, queda descrito y cuantificado el dominio de influencia   del parámetro ${\textstyle u\left(K\right)}$ , tal y como se representa con los puntos negros de la figura 13 . En la figura también puede verse como evoluciona la influencia sobre los arcos de característica y como se ensancha el dominio de influencia en el tiempo.

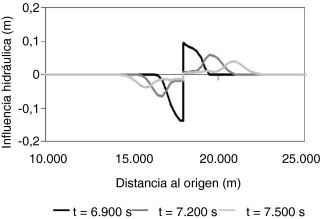
Para ilustrar todavía más el concepto de influencia de un parámetro de trayectoria de compuerta sobre el vector de estado, es decir, sobre todas las secciones del canal, se propone un ejemplo numérico basado en una simulación hecha sobre un canal de 28 Km de longitud y ocho almenaras con sus correspondientes compuertas. En el ejemplo, existe un punto de control a 18.000 m del origen que tiene una compuerta que se mueve según una trayectoria. Se computó el valor de la influencia del parámetro u (23) —que se corresponde con la abertura existente entre los instantes de tiempo T²²  = 22 × ▵ T  = 22 × 300 s  = 6.600 s y T²³  = 23 × ▵ T  = 23 × 300 s  = 6.900 s de la definición de la trayectoria de la compuerta hecha a tramos de ΔT  = 300 s — sobre el vector de estado en los instantes 6.900 s , 7.200 s y 7.500 s , esto es, x⁶⁹⁰⁰ , x⁷²⁰⁰ y x⁷⁵⁰⁰ . Los resultados se presentan en la figura 14 donde se puede ver cómo la influencia del parámetro u (23) evoluciona instantes después.

Figura 14. Evolución de la influencia hidráulica sobre los calados del parámetro u(23) (posición de compuerta entre los instantes 6.660 s y 6.900 s).

A la vista de la figura 14 cabe destacar que:

• Un pequeño movimiento de compuerta influye en las condiciones de flujo tanto en sentido aguas abajo como aguas arriba, tal como se podía esperar de un flujo en régimen subcrítico.
• La influencia es menor a medida que evoluciona tanto en el tiempo como en el espacio. Ésto se puede ver porque la curva de influencia es cada vez más suave.
• Si por ejemplo se produce una abertura —o sea, un Δu (23) > 0— se producirá un descenso de calado que viajará aguas arriba y un aumento aguas abajo. Y vice-versa , si se produce un cierre —o sea, un Δu (23) < 0—.

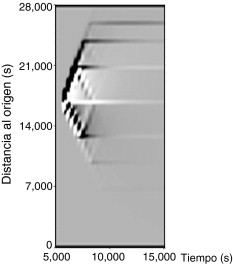
La gráfica de la figura 14 es un perfil tomado en tres instantes de tiempo de la influencia del parámetro ${\textstyle u\left(23\right)}$ . Si se dibujan todos los perfiles de la influencia de este parámetro sobre el vector de estado en todos los instantes de tiempo, es decir, sobre todo el dominio de integración —que va de los 0 s a los 15.000 s y de 0 m a 28.000 m — y se extrae la parte que va desde el instante 6.300 s al 15.000 s , el resultado se puede ver en la imagen de la figura 15 .

Figura 15. Evolución de la influencia hidráulica sobre los calados del parámetro u(23) (posición de compuerta entre los instantes 6.660 s y 6.900 s). La tonalidad gris representa que no hay influencia, la blanca representa influencia negativa (descenso de calado) y la negra influencia positiva (ascenso de nivel).

Si se analiza la imagen de la figura 15 , se detectan una serie de puntos que cabe remarcar:

• Hay un «remanente de influencia» que queda en todo el dominio de influencia que hace que no se recupere el estado inicial de color gris hasta al cabo de mucho tiempo después del instante 6.900 s en que desaparece la influencia directa.
• La influencia llega al siguiente punto de control, parte «rebota»—cambia de sentido— y parte continúa en el mismo sentido.

Si se define el vector predicción  ${\textstyle {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}}$ , como la compilación de todos los valores que toma el vector de estado x^k desde el instante inicial k  = k_I  + 1 hasta el final k  = k_F :

${\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}=\left({\begin{array}{l}{\boldsymbol {\mbox{x}}}^{k_{I}+1}\\\vdots \\{\boldsymbol {\mbox{x}}}^{k}\\\vdots \\{\boldsymbol {\mbox{x}}}^{k_{F}}\end{array}}\right)$

( 25)

entonces se puede compilar todos los valores de la influencia de un parámetro de trayectoria de compuerta cualquiera ${\textstyle u\left(K\right)}$ sobre el vector de estado en un solo vector:

${\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}}{\partial u\left(K\right)}}=$${\frac {\partial }{\partial u\left(K\right)}}\left({\begin{array}{l}{\boldsymbol {\mbox{x}}}^{k_{I}+1}\\\vdots \\{\boldsymbol {\mbox{x}}}^{k}\\\vdots \\{\boldsymbol {\mbox{x}}}^{k_{F}}\end{array}}\right)$

( 26)

2.3. La matriz de influencia hidráulica (HIM)

2.3.1. Definición

Llegados a este punto, ya es posible definir la denominada matriz de influencia hidráulica . Si se reúnen todos los vectores (26) de todos los parámetros de una trayectoria de compuerta cualquiera j(17) se obtiene la matriz de influencia hidráulica :

$\left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}_{j}\right)\right]=$$\left[{\begin{array}{ccccc}{\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}}{\partial u_{j}\left(K_{I}+1\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}}{\partial u_{j}\left(K\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}}{\partial u_{j}\left(K_{F}\right)}}\end{array}}\right]=$ $=\left[{\begin{array}{ccccc}{\frac {\partial {\boldsymbol {\mbox{x}}}^{k_{I}+1}}{\partial u_{j}\left(K_{I}+1\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{x}}}^{k_{I}+1}}{\partial u_{j}\left(K\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{x}}}^{k_{I}+1}}{\partial u_{j}\left(K_{F}\right)}}\\\vdots &\ddots &\vdots &&\vdots \\{\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u_{j}\left(K_{I}+1\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u_{j}\left(K\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u_{j}\left(K_{F}\right)}}\\\vdots &&\vdots &\ddots &\vdots \\{\frac {\partial {\boldsymbol {\mbox{x}}}^{k_{F}}}{\partial u_{j}\left(K_{I}+1\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{x}}}^{k_{F}}}{\partial u_{j}\left(K\right)}}&\cdots &{\frac {\partial {\boldsymbol {\mbox{x}}}^{k_{F}}}{\partial u_{j}\left(K_{F}\right)}}\end{array}}\right]$

( 27)

De esta matriz destacan los siguientes puntos:

• El número de filas es muy superior al de columnas porque cada elemento ${\textstyle {\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u_{j}\left(K\right)}}}$ es un vector de 2 × n_S filas.
• No todos los elementos tienen un valor diferente de cero. Como ya se ha comentado, todos los elementos ${\textstyle {\frac {\partial {\boldsymbol {\mbox{x}}}^{k}}{\partial u_{j}\left(K\right)}}}$ que cumplen que t^k  < T^K son nulos. Ello es debido a la componente temporal que tienen los parámetros. La disposición hecha en (27) provoca que los elementos no nulos de la matriz se encuentren en la parte triangular subdiagonal por bloques.
• Cuando son muchas las compuertas que regulan el canal, se tiene que compilar las ${\textstyle \left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}_{j}\right)\right]}$ para j  = 1, . . . , n_G en una sola:

$\left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}\right)\right]=$$\left[{\begin{array}{ll}{\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}{\partial u_{1}\left(K_{I}+1\right)}}\cdots {\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}{\partial u_{nG}\left(K_{I}+1\right)}}&\cdots {\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}{\partial u_{1}\left(K_{F}\right)}}\cdots {\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}{\partial u_{n_{G}}\left(K_{F}\right)}}\end{array}}\right]$

( 28)

donce n_G es el número total de compuertas y ${\textstyle {\boldsymbol {\mbox{U}}}={\left(u_{1}\left(K_{I}+1\right),\ldots ,u_{G}\left(K_{F}\right)\right)}^{T}}$ es el vector de trayectorias .

2.3.2. El observador discreto

En la mayoría de casos solamente se necesita saber los valores de la simulación y de la influencia en determinados puntos del canal e instantes. En la representación sobre el plano x /t de la figura 9 se puede ver un ejemplo de dos tramos de canal con dos compuertas de regulación. También se puede ver en la gráfica que existe un número de secciones n_S  = n_I  + n_II  = 23 + 22 = 45 de discretización y un número total de pasos de tiempo de integración n_T  = k_F  − k_I  = 33 que depende de la condición de CFL . Por lo que hace referencia a la discretización de las trayectorias de compuerta, hay que decir que se tiene un número de compuertas n_G  = 2, cada una de la cuales tiene definida su trayectoria mediate cuatro intervalos λ  = 4 y por consiguiente el número total de parámetros es n_U  = λ  × n_G  = 8.

En el ejemplo gráfico también se puede ver que hay una serie de n_Y  = 29 puntos coloreados de gris de los cuales se desea conocer información. De esta forma, las dimensiones de los vectores y matrices del ejemplo son las siguientes:

• Vector simulación ${\textstyle {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}}$ : n_X  = 2 × n_T  × n_S  = 2.970
• Vector de parámetros U : n_U  = λ  × n_G  = 8
• Matriz de influencia hidráulica ${\textstyle {\left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}\right)\right]}_{\boldsymbol {\mbox{X}}}}$ : n_X × n_U  = (2.970 × 8)
• Número de puntos de observación discreta ${\textstyle {\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}$ : n_Y  = 29
• Matriz influencia hidráulica sobre el conjunto de puntos de observador discreto ${\textstyle {\left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}\right)\right]}_{\boldsymbol {\mbox{Y}}}}$ : n_Y  × n_U  = 29 × 8

Para expresar matemáticamente este subconjunto de información, hay que introducir una nueva matriz denominada «matriz de observador discreto» que se denota con ${\textstyle \left[{\boldsymbol {\mbox{C}}}\right]}$ . Esta matriz, que tiene carácter puramente formal por lo que no se compila, está compuesta exclusivamente de «ceros» y «unos» de manera que:

${\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)=$$\left[{\boldsymbol {\mbox{C}}}\right]{\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)$

( 29)

representan, respectivamente, el comportamiento simulado en ciertos puntos del canal en ciertos instantes y la matriz de influencia de las trayectorias sobre estos puntos.

2.3.3. Verificación de la matriz de influencia hidráulica: un punto de vista numérico

Para poder verificar el valor de las componentes de la HIM que se obtenían con la subrutina de cálculo de dicha matriz, se llevó a cabo un ensayo numérico que consistió en aplicar numéricamente la definición matemática de infuencia hidráulica, que es:

${\frac {\partial {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}{\partial u_{j}\left(K\right)}}\approx {\underset {\left\|{\boldsymbol {\Delta {\mbox{U}}}}\right\|\rightarrow 0}{Lim}}{\frac {{\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}+{\boldsymbol {\Delta {\mbox{U}}}}\right)-{\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}{\left\|{\boldsymbol {\Delta {\mbox{U}}}}\right\|}}$

( 31)

donce ${\textstyle {\boldsymbol {\Delta {\mbox{U}}}}=}$${\left[{\begin{array}{ccccc}0&\cdots &\Delta u_{j}\left(K\right)&\cdots &0\end{array}}\right]}^{T}$ (Aquí, los elementos la izquierda son encontrados analíticamente y los de la derecha, numéricamente).

Dicho de otro modo, si se simula una vez y se encuentra ${\textstyle {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)}$ y luego repite la operación con otro vector de trayectorias   perturbado en alguna de sus componentes para obtener ${\textstyle {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {{\mbox{U}}+\Delta {\mbox{U}}}}\right)}$ , entonces la diferencia entre simulaciones ${\textstyle {\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {{\mbox{U}}+\Delta {\mbox{U}}}}\right)-}$${\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)$ se puede atribuir exclusivamente a la influencia del parámetro perturbado.

Todos los resultados obtenidos en los numerosos ensayos de verificación —∀K  = 1, …, λ y ∀j  = 1, …, n_C — aplicados sobre ejemplos particulares tuvieron una margen de error inferior a 10⁻⁶ , cosa que dió gran confianza y alto nivel de exactitud en el cálculo de los elementos de la HIM .

3. Algoritmo GoRoSo

Con el objetivo de mantener constante el calado en ciertos lugares del canal donde existen salidas laterales por gravedad tales como orificios en flujo a presión o acequias laterales controladas por sus correspondientes compuertas de deslizamiento vertical. El caudal desaguado por este tipo de salidas es muy sensible al nivel de lámina existente dentro del canal con lo que manteniéndolo constante es posible repartir bien el caudal según una demanda prevista.

Por otro lado, el caudal circulante por el canal varía a lo largo del tiempo en función de las demandas integradas que se derivan a las acequias laterales y ello se consigue mediante la regulación de las compuertas en línea. En este contexto, el algoritmo calcula las trayectorias de compuerta a lo largo de un horizonte de predicción para conseguir repartir el caudal entre las salidas laterales según una programación de demandas y manteniendo los niveles en los puntos de control. Se trata, pues, de un algoritmo de control de canales en lazo abierto.

3.1. Definiciones

Para poder realizar un planteamiento matemático riguroso del problema de optimización no-lineal subyacente en el algoritmo GoRoSo como controlador en lazo abierto es necesario realizar algunas definiciones previas, algunas de la cuales ya han sido planteadas anteriormente. A pesar de esta redundancia, creemos conveniente volverlas a proponer aquí.

• Se define vector de estado como aquel vector que contiene la solución numérica de todo el canal en el instante k :

${\boldsymbol {\mbox{x}}}\left(k\right)={\left({\begin{array}{lll}y_{1}\left(k\right),v_{1}\left(k\right),&\ldots &,y_{n_{S}}\left(k\right),v_{n_{S}}\left(k\right)\end{array}}\right)}^{T}$

( 32)

donce ${\textstyle y_{i}\left(k\right),v_{i}\left(k\right)}$ son el calado y la velocidad media de la sección i y n_S es el número de puntos en que el canal ha sido discretizado.

• Se pueden inlcuir todos los vectores de estado como (32) de todos los instantes k del horizonte de predicción en un solo que se denominado vector de predicción :

${\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}={\left({\begin{array}{lllll}{\boldsymbol {\mbox{x}}}{\left(k_{I}+1\right)}^{T}&\cdots &{\boldsymbol {\mbox{x}}}\left(k\right)^{T}&\cdots &{\boldsymbol {\mbox{x}}}{\left(k_{F}\right)}^{T}\end{array}}\right)}^{T}$

( 33)

donde k_I  + 1 y k_F son los instantes inicial y final del horizonte de predicción y por lo tanto su longitud será l  = k_F  − k_I . La dimensión del vector será: n_X  = (2 × n_S ) × l .

• Normalmente, se desea controlar el calado en los puntos donde existen almenaras por razones que no vienen al caso aquí. Así, hay que definir un nuevo vector que contenga los valores simulados por el modelo en estos puntos:

${\boldsymbol {\mbox{y}}}\left(k\right)={\left({\begin{array}{lllll}y_{1}\left(k\right)&\ldots &y_{i}\left(k\right)&\ldots &y_{n_{C}}\left(k\right)\end{array}}\right)}^{T}$

( 34)

donde n_C es el número de puntos de control. Este vector está constituído por valores provinientes del vector de estado.

• También podemos considerar un grupo de valores de calados simulados en todas las secciones del canal —que constituyen una curva de remanso— al final del horizonte de predicción (fig. 9 ):

${\boldsymbol {\mbox{y}}}\left(k_{F}\right)={\left({\begin{array}{lllll}y_{1}\left(k_{F}\right)&\ldots &y_{i}\left(k_{F}\right)&\ldots &y_{n_{S}}\left(k_{F}\right)\end{array}}\right)}^{T}$

( 35)

• Ahora, podemos reunir los vectores (34) de todos los instantes de tiempo del horizonte de predicción conjuntamente con la curva de remanso (35) en el vector que se denominará vector de salidas :

${\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}={\left({\begin{array}{llll}{\boldsymbol {\mbox{y}}}{\left(k_{I}+1\right)}^{T}&\cdots &{\boldsymbol {\mbox{y}}}{\left(k_{F}-1\right)}^{T}&{\boldsymbol {\mbox{y}}}{\left(k_{F}\right)}^{T}\end{array}}\right)}^{T}$

( 36)

La dimensión de este vector es n_Y  = (l  − 1) × n_C  + n_S .

• El vector de salidas está realacionado claramente con el vector de predicción de la siguiente manera:

${\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}=\left[{\boldsymbol {\mbox{C}}}\right]{\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}$

( 37)

donce ${\textstyle \left[{\boldsymbol {\mbox{C}}}\right]}$ es la matriz de observador discreto de dimensión n_Y  × n_X y sus componentes son exclusivamente «ceros»y «unos».

• Ahora, se va a definir un nuevo vector que contiene los valores de calado que se desea mantener constante en los mismos puntos de control que en el vector de salidas y para el instante k :

${\boldsymbol {\mbox{y}}}^{\ast }\left(k\right)={\left({\begin{array}{lllll}y_{1}^{\ast }\left(k\right)&\ldots &y_{i}^{\ast }\left(k\right)&\ldots &y_{n_{C}}^{\ast }\left(k\right)\end{array}}\right)}^{T}$

( 38)

• De la misma manera que (35) donde se ha compilado la curva de remanso final simulada, ahora se compilará la curva de remanso final a la que se desea llegar al final del horizonte de predicción:

${\boldsymbol {\mbox{y}}}^{\ast }\left(k_{F}\right)={\left({\begin{array}{lllll}y_{1}^{\ast }\left(k_{F}\right)&\ldots &y_{i}^{\ast }\left(k_{F}\right)&\ldots &y_{n_{S}}^{\ast }\left(k_{F}\right)\end{array}}\right)}^{T}$

( 39)

• Se puede reunir los vectores (38) de todos los instantes de tiempo del horizonte de predicción conjuntamente con la curva de remanso (39) en el vector que se denominará vector de comportamiento deseado :

${\boldsymbol {\mbox{Y}}}^{\ast }={\left({\begin{array}{llll}{\boldsymbol {\mbox{y}}}^{\ast }{\left(k_{I}+1\right)}^{T}&\cdots &{\boldsymbol {\mbox{y}}}^{\ast }{\left(k_{F}-1\right)}^{T}&{\boldsymbol {\mbox{y}}}^{\ast }{\left(k_{F}\right)}^{T}\end{array}}\right)}^{T}$

( 40)

La dimensión de este vector es exactamente n_Y .

• Tal como muestra la figura 8 y se ha descrito anteriormente, la trayectoria de una compuerta puede definirse mediante una función temporal a tramos. Si se define u_j (K ) como la posición de la compuerta j durante el periodo de muestreo: [T^{K −1} , T^K ) con T^K  = K  × ΔT donde ΔT es la longitud del periodo de muestreo, entonces definimos el vector de trayectorias juntando todas las posiciones de todas las compuertas y para todos los periodos de muestreo de la siguiente manera:

${\boldsymbol {\mbox{U}}}=\left({\begin{array}{l}u_{1}\left(K_{I}+1\right)\\\vdots \\u_{n_{G}}\left(K_{I}+1\right)\\\vdots \\u_{1}\left(K_{F}\right)\\\vdots \\u_{n_{G}}\left(K_{F}\right)\end{array}}\right)$

( 41)

donce n_G es el número de compuertas del canal. La dimensión de este vector es n_U  = n_G  × λ con λ  = K_F  − K_I siendo el número de periodos de muestreo entre los cuales se ha dividido el horizonte de predicción.

• Dadas unas condiciones iniciales x (k_I ) y unas condiciones de contorno, tanto el vector de salidas como el vector de predicción están unívocamente determinados por el vector de trayectoriasU . Por consiguiente, (37) puede reescribirse como:

${\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)=$$\left[{\boldsymbol {\mbox{C}}}\right]{\boldsymbol {\mbox{X}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)$

( 42)

De esta forma, solamente U determina el comportamiento del canal a lo largo del intervalo de operación y cuando las trayectorias de compuerta son implementadas en el canal, el flujo responde de forma única. Y vice-versa , un comportamiento del canal es causado por un determinado vector de trayectorias .

3.2. Función objetivo

Desde el punto de vista matemático, el objetivo del algoritmo GoRoSo consiste en encontrar aquel comportamiento simulado (expresado en términos del vector de salidas ) lo más parecido al deseado (expresado en términos del vector de comportamiento deseado ) modificando el vector de trayectorias . En otras palabras, se desea encontrar aquel U que minimiza el siguiente índice de rendimiento o función objectivo:

$J\left({\boldsymbol {\mbox{U}}}\right)={\frac {1}{2}}{\left({\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)-{\boldsymbol {\mbox{Y}}}^{\ast }\right)}^{T}\left[{\boldsymbol {\mbox{Q}}}\right]\left({\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)-\right.$$\left.{\boldsymbol {\mbox{Y}}}^{\ast }\right)$

( 43)

donce ${\textstyle \left[{\boldsymbol {\mbox{Q}}}\right]}$ es una matriz de ponderación de dimensiones n_Y  × n_Y . Cuando esta matriz es la identidad, entonces el funcional (43) es el conocido de mínimos cuadrados.

3.3. Restricciones

Valores negativos o anormalmente grandes de una posición de compuerta no son posibles. Entonces hay que introducir explícitamente restricciones:

$U_{\underset {j}{min}}\leq u_{j}\left(K\right)\leq U_{\underset {j}{max}}$

( 44)

donce ${\textstyle U_{{max}_{j}}}$ es la máxima abertura de la compuerta y ${\textstyle U_{min{}_{j}}}$ es la mínima abertura. Éstas se denominan «restricciones de conjunto» en la literatura de optimización [8] , [9]  and [10] .

Por otro lado, grandes movimientos de compuerta pueden producir frentes de onda indeseables, desbordamientos y secados excesivos del canal. Por este motivo, es recomendable la introducción de restricciones al movimiento de las compuertas:

$\left|u_{j}\left(K\right)-u_{j}\left(K-1\right)\right|\leq {DU}_{\underset {j}{max}}$

( 45)

donce DU_j es el movimiento de compuerta permitido en la compuerta j entre dos periodos consecutivos de muestreo. Éstas se denominan «restricciones funcionales»en la literatura de optimización.

3.4. Planteamiento del problema

A modo de resumen de esta sección, seguidamente se plantea el problema de optimización con restricciones que es resuelto por el algoritmo GoRoSo para conformar el controlador en lazo abierto de canales:

Minimizar:

$J\left({\boldsymbol {\mbox{U}}}\right)={\frac {1}{2}}{\left({\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right)-{\boldsymbol {\mbox{Y}}}^{\ast }\right)}^{T}\left[{\boldsymbol {\mbox{Q}}}\right]\left({\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}\right){\boldsymbol {-{\mbox{Y}}}}^{\ast }\right)$

( 46)

Sujeto a:

$r_{1i}\equiv U_{{max}_{j}}-u_{j}\left(K\right)\geq 0;i=$$1,...,n_{U}$ $r_{2i}\equiv u_{j}\left(K\right)-U_{{min}_{j}}\geq 0;i=$$1,...,n_{U}$ $r_{3i}\equiv {DU}_{{max}_{j}}-\left[u_{j}\left(K+1\right)-\right.$$\left.u_{j}\left(K\right)\right]\geq 0;i=1,...,n_{U}-$$1$

( 47)

3.5. Algoritmo GoRoSo

El problema planteado en la sección 3.4 es el problema clásico de optimización no lineal con restricciones lineales. Existen muchas técnicas numéricas para resolverlo en la literatura de optimización. Han habido muchas contribuciones a la teoría de optimización con restricciones y el concepto más importante de esta teoría es sin duda el de los multiplicadores de lagrange . Se ha planteado la resolución del problema como un problema de optimización de la función lagrangiana sin restricciones. Para resolverlo, se ha utilizado el método denominado «problema cuadrático secuencial» (PCS ) y se ha utilizado la estrategia del «método del conjunto activo» (MCA ) para resolver el problema cuadrático que se presenta en cada interación del PCS.

El método utilizado para la resolución ha sido uno de los denominados «métodos de lagrange»en [11] para la resolución de problemas de minimización con restricciones no lineales. A pesar de que las restricciones (47) son lineales, se ha optado por el método con restricciones no lineales porque, primero, resuelve también los casos con restricciones lineales y segundo, para facilitar la introducción de futuras restricciones no lineales. Seguidamente, se presentan los pasos que sigue el algoritmo.

• Inicialización del bucle exterior (PCS ):
• l  = 0 (contador de iteraciones del bucle exterior)
• U₁ = U₀ (primera estimación del vector de trayectorias)
• Cálculo de matrices y vectores :

$l=l+1$ $J_{l}={\frac {1}{2}}{\left({\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}_{l}\right)-{\boldsymbol {\mbox{Y}}}^{\ast }\right)}^{T}\left[{\boldsymbol {\mbox{Q}}}\right]\left({\boldsymbol {\mbox{Y}}}_{k_{I}+1}^{k_{F}}\left({\boldsymbol {\mbox{U}}}_{l}\right)-\right.$$\left.{\boldsymbol {\mbox{Y}}}^{\ast }\right)$ ${\boldsymbol {\mbox{g}}}_{l}={\left(\left[{\boldsymbol {\mbox{C}}}\right]\left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}_{l}\right)\right]\right)}^{T}\left[{\boldsymbol {\mbox{Q}}}\right]\left(\left[{\boldsymbol {\mbox{C}}}\right]{\boldsymbol {\mbox{X}}}\left({\boldsymbol {\mbox{U}}}_{l}\right){\boldsymbol {-{\mbox{Y}}}}^{\ast }\right)$ ${\boldsymbol {\mbox{G}}}_{l}={\left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}_{l}\right)\right]}^{T}\left\{\left[{\boldsymbol {\mbox{C}}}\right]^{T}\left[{\boldsymbol {\mbox{Q}}}\right]\left[{\boldsymbol {\mbox{C}}}\right]\right\}\left[{\boldsymbol {\mbox{HIM}}}\left({\boldsymbol {\mbox{U}}}_{l}\right)\right]+$$\nu {\boldsymbol {\mbox{I}}}$

donde J_l es la función objetivo, g_l es el vector gradiente y G_l es una aproximación a la matriz hessiana.

• Inicialización bucle interior (MCA ):

$k=0$ ${\boldsymbol {\delta {\mbox{x}}}}_{l}{\boldsymbol {=0}}$ $A_{k}=\varnothing$

donde A_k es el conjunto activo que contiene los índices de las restricciones que se encuentran activas.

• Resolución del problema cuadrático :
• k  = k  + 1
• Adición de la información sobre restricciones activas :

${\boldsymbol {\mbox{H}}}_{k}={\boldsymbol {\mbox{G}}}_{l}-\sum _{i=1,...,m_{k};i\in A_{k}}{\lambda }_{i}\left[{\boldsymbol {\nabla }}_{\boldsymbol {\mbox{UU}}}^{2}{\boldsymbol {\mbox{r}}}_{i}\left({\boldsymbol {\mbox{U}}}_{l}\right)\right]$ ${\boldsymbol {\mbox{h}}}_{k}{={\boldsymbol {\mbox{g}}}}_{l}$

donce m_k es el número total de restricciones activas igual al número de elementos del conjunto activo.

• Compilación de matrices y resolución del sistema :

$\left[{\begin{array}{cc}{\boldsymbol {\mbox{H}}}_{k}&-{\boldsymbol {\nabla }}_{\boldsymbol {\mbox{U}}}{\boldsymbol {\mbox{r}}}\left({\boldsymbol {\mbox{U}}}_{l}\right)\\-{\nabla }_{\boldsymbol {\mbox{U}}}{\boldsymbol {\mbox{r}}}{\left({\boldsymbol {\mbox{U}}}_{l}\right)}^{T}&0\end{array}}\right]\left({\begin{array}{c}{\boldsymbol {\delta \delta {\mbox{x}}}}_{k}\\{\boldsymbol {\lambda }}\end{array}}\right)=-\left({\begin{array}{c}{\boldsymbol {\mbox{h}}}_{k}\\{\boldsymbol {0}}\end{array}}\right)$

• Si${\textstyle {M{\acute {a}}x}_{i}{\left(\delta \delta x_{k}\right)}_{i}\geq Tol}$calcula :

${\alpha }_{k_{i_{m{\acute {\imath }}n}}}={\underset {\left({\boldsymbol {\nabla }}_{U}{\boldsymbol {\mbox{r}}}_{i}\right){\left({\boldsymbol {\delta \delta {\mbox{x}}}}_{k}\right)}_{i}<0;\quad i\not \in A_{k}}{M{\acute {\imath }}nimo}}\left\{1,{\frac {h_{k_{i}}-\left({\boldsymbol {\nabla }}_{\boldsymbol {\mbox{U}}}{\boldsymbol {\mbox{r}}}_{i}\right){\left({\boldsymbol {\delta {\mbox{x}}}}_{l}\right)}_{i}}{\left({\boldsymbol {\nabla }}_{\boldsymbol {\mbox{U}}}{\boldsymbol {\mbox{r}}}_{i}^{T}\right){\left({\boldsymbol {\delta \delta {\mbox{x}}}}_{k}\right)}_{i}}}\right\}$

• Actualiza :

${\boldsymbol {\delta {\mbox{x}}}}_{l}={\boldsymbol {\delta {\mbox{x}}}}_{l}+$${\alpha }_{k_{i_{m{\acute {\imath }}n}}}\times {\boldsymbol {\delta \delta {\mbox{x}}}}_{k}$

• Si${\textstyle {\alpha }_{k_{i_{m{\acute {\imath }}n}}}\leq 1}$ :

$m_{k+1}=m_{k}+1$ $A_{k+1}=A_{k}+\left\{i_{m{\acute {\imath }}n}\right\}$ $Vuelve\quad a\quad 4a)$

• Si${\textstyle {M{\acute {\imath }}nimo}_{i\in A_{k}}\left\{{\lambda }_{i}\right\}<0}$ :

$m_{k+1}=m_{k}-1$ $A_{k+1}=A_{k}-\left\{i_{m{\acute {\imath }}n}\right\}$ $Vuelve\quad a\quad 4a)$

• Actualiza :

${\boldsymbol {\mbox{U}}}_{l}={\boldsymbol {\mbox{U}}}_{l}+{\boldsymbol {\delta {\mbox{x}}}}_{l}$ $Vuelve\quad a\quad 2$

Gracias a la presencia de restricciones que obligan a hacer pasos de descenso muy pequeños, el método se estabiliza. A pesar de ello, la eficiencia mejora mucho en las primeras iteraciones se se añade cierta cantidad ν a la diagonal de la matriz G_l . Eso pasa porque la matriz:

$\left[{\begin{array}{cc}{\boldsymbol {\mbox{H}}}_{k}&-{\boldsymbol {\nabla }}_{\boldsymbol {\mbox{U}}}{\boldsymbol {\mbox{r}}}\left({\boldsymbol {\mbox{U}}}_{l}\right)\\-{\boldsymbol {\nabla }}_{\boldsymbol {\mbox{U}}}{\boldsymbol {\mbox{r}}}{\left({\boldsymbol {\mbox{U}}}_{l}\right)}^{T}&{\boldsymbol {0}}\end{array}}\right]$

es definida positiva si y solo si G_l también lo es.

Existen dos razones por las cuales es necesaria la introducción del parámetro de Marquardt ν   en la diagonal de la matriz ${\textstyle \left[{\boldsymbol {\mbox{G}}}_{l}\right]}$ compilada en el paso 2d ):

• ${\textstyle \left[{\boldsymbol {\mbox{G}}}_{l}\right]}$ está muy mal condicionada porque en ella conviven posiciones de compuerta que tienen una gran influencia sobre el flujo y otras con una de muy pequeña.
• ${\textstyle \left[{\boldsymbol {\mbox{G}}}_{l}\right]}$ es solamente una aproximación a la matriz hessiana de la función objectivo (43) . Durante las primeras iteraciones del algoritmo en que U se encuentra muy alejada de la solución final de manera que la aproximación a la matriz hessiana no es suficientemente buena a causa de que está construida solamente con derivadas de primer orden.

Una buena elección del valor de ν permite llegar a la solución con menor número de iteraciones. La cuestión es que depende de cada problema en particular.

La «American Society of Civil Engineers »(ASCE) creó un comité de desarrollo de algoritmos para la automatización de canales. Este comité ha establecido una serie de casos para examinar la versatilidad de diferentes esquemas de control [12] que abarcan situaciones hidráulicas extremas representativas de un amplio rango de situaciones reales. Concretamente en [12] se presentan dos escenarios diferentes: un canal, el Maricopa Stanfield, de elevada pendiente y poca capacidad de almacenamiento, en el cual los cambios de las condiciones de flujo suceden rápidamente, incluidos cambios de régimen, y el Corning Canal, de poca pendiente y gran capacidad de transporte, en el que los cambios suceden muy lentamente dada la gran capacidad de amortiguamiento del canal. El algoritmo GoRoSo ha sido utilizado con éxito para la resolución de los casos que son programables [13] .

GoRoSo también ha sido utilizado con éxito en el cálculo de las trayectorias de compuerta para el cierre cuasi instantáneo de un canal en caso de emergencia por la entrada en cabecera de una avenida contaminante [14] .

4. Resumen y conclusiones

Seguidamente se enumeran las conclusiones del presente trabajo.

• Con la presentación del algoritmo GoRoSo se ha aportado una herramienta de ayuda a la planificación de las operaciones de control en un canal de regadío para maximizar la eficiencia en el transporte y distribución de agua entre las diferentes tomas de canal. Ello se consigue mediante un buen ajuste del caudal transportado por el canal y la demanda de riego variable a lo largo del tiempo.
• Se ha presentado el algoritmo de control en lazo abierto para la definición de las trayectorias que hay que seguir en las aberturas de compuerta de un canal, con objeto de satisfacer unas consignas de nivel y unas demandas de caudal conocidas a lo largo de un cierto horizonte de tiempo.
• El algoritmo se basa en la minimización de la función objetivo de mínimos cuadrados obtenida como diferencia entre los niveles existentes en el canal (simulados) y los niveles deseados (consignas). El problema se ha planteado como un problema de optimización no lineal con restricciones y ha sido resuelto minimizando la función lagrangiana madiante el algoritmo «problema cuadrático secuencial» empleando la estartégia del «método del conjunto activo» para la resolución del problema cuadrático que se presenta en cada iteración.
• En el proceso de minimización de esta función objetivo se utiliza la matriz HIM que representa las influencias sobre todas las secciones en que se discretiza el canal de cualquier abertura de compuerta. Dicha matriz se obtiene a partir de un proceso numérico de discretización en diferencias finitas de un esquema de características curvas que representa las ecuaciones de Saint-Venant. Se presenta detalladamente el proceso de compilación de dicha matriz.
• La matriz HIM puede considerase una linealización de las ecuaciones del flujo en el entorno de la U y por lo tanto es suceptible de ser utilizada como «modelo predictivo»en un controlador en lazo cerrado en tiempo real. Ésto puede considerarse como una linea nueva de investigación para futuros trabajos en control de canales.

References

1. [1] J. Rodellar, A.H. Barbat, Control digital predictivo de la respuesta sísmica de estructuras, Revista internacional de métodos numéricos para el cálculo y el dise no en ingeniería, 1(1) (1985) 55-66, Barcelona, España.
2. [2] W.R. Walker, G.V. Skogerboe; Surface Irrigation. Theory and Practice, Prentice-Hall, Inc. Englewood Cliffits, New Jersey, US (1987)
3. [3] M. Gómez, Contribución al estudio del movimiento variable en lámina libre, en las redes de alcantarillado. Aplicaciones, Tesis doctoral UPC, Barcelona (1988).
4. [4] E.B. Wylie; Control of transient free-surface flow; Jour. of the Hydr. Div. (ASCE) (1969), pp. 347–361
5. [5] J. Soler, Integració de les equacions de Saint-Venant: aplicació al reg superficial per taules, Proj. Final de Carrera, Universitat de Lleida, Lleida (1996).
6. [6] P. Ducheteau, D.W. Zachmann; Ecuaciones diferenciales parciales, Ed. McGraw-Hill, Mèxic (1988)
7. [7] W.F. Ames; Numerical Methods for Partial Differential Equations, Academic Press Inc, Orlando, Florida, US (1977)
8. [8] S.H. Crandall; Engineering Analisys-A Survey of Numercial Procedures, Willey (Interescience), New York, US (1956)
9. [9] R. Fletcher; Practical Methods of Optimization (2nd. Ed.), John Viley & Sons, U.K (1987)
10. [10] P.E. Gill, W. Murray, M.H. Wright; Practical Optimization, Academic Press Inc, Scotland (1981)
11. [11] D.G. Luemberger; Linear and Nonlinear Programming (2nd. Ed.), Addison-Wesley, Massachusetts (1984)
12. [12] A.J. Clemmens, B. Grawitz, W. Schuurmans; Test Cases for Canal Control Algorithms; J. Irrig. and Drain. Engrg., ASCE, 124 (1) (1998), pp. 23–30
13. [13] J. Soler, M. Gómez, y J. Rodellar; «Una herramienta de control de transitorios en canales de regadío»; Revista Ingeniería del agua, 11 (3) (2004), pp. 297–313
14. [14] J. Soler, M. Gómez, J. Rodellar; «Estudio hidráulico para el Plan de Emergencia del Canal de la Margen Izquierda del Delta del Ebro», artículo para la revista; Ingeniería del agua, 17 (2) (2009), pp. 171–186

Notes

1. Tanto si una compuerta la reposiciona un operador como si es movida automáticamente por un motor eléctrico con cierta vida útil, cada operación de reajuste tiene su coste de desgaste de juntas y partes móviles que puede ser evaluado. Por consiguiente, existe el dilema entre conseguir el mejor control y realizar el menor número de operaciones y reducir la importancia de los mismos.