Study of demagnetization risk for a 12 kW direct driven permanent magnet synchronous generator for wind power

Abstract

One of the main aspects when designing a permanent magnet (PM) generator is to choose suitable PMs, both in terms of achieving the required flux in the generator but also of withstanding high demagnetizing fields, that is, having sufficiently high coercivity. If the coercivity is too low, the magnets are at risk of demagnetizing, fully or partially, at the event of a short circuit and/or an increase in temperature. This study aims to determine the risk of demagnetization for a 12 kW direct driven permanent magnet synchronous generator. Furthermore, as the prices on PMs have increased drastically the last few years the possibility to use smaller and/or cheaper PMs of different grades has been investigated. A new proprietary finite element method (FEM) model has been developed, which is also presented. The study is based on simulations from this FEM model and is focused on NdFeB magnets. Results show that the reference magnet can withstand a two-phase short circuit at both the temperatures tested and in both geometries. The use of cheaper magnets, smaller air gap and in the event of a two-phase short circuit often results in partial irreversible demagnetization. However, magnets with lower coercivity are easier demagnetized.

Introduction

Permanent magnet (PM) machines are designed to retain their magnetization. However, sometimes the worst case scenarios are overseen due to development and manufacturing costs or that the worst case scenarios seem too unlikely to be worth considering. A typical critical scenario could be a short circuit at an elevated temperature [2-4]. A short circuit in the armature winding can result in a high counteracting magnetic field and an increased temperature will lower the coercivity of the magnet. In a badly designed machine or if inferior magnets are used, the magnets can be partly or fully demagnetized at such an event.

This study is focused on a 12 kW direct driven permanent magnet synchronous generator (DDPMSG), which is connected to a vertical axis wind turbine. The weight of a direct driven permanent magnet generator can be pointed out as a disadvantage [3]. The weight of the generator when using a vertical axis wind turbine is not an issue as the generator can be placed on the ground [5]. With horizontal axis wind turbines the weight is a big concern as the generator is mounted on top of the wind turbine tower.

Although much work have been done on the electrical properties for this 12 kW DDPMSG [7, 8], very little have been documented on the demagnetization risk. Therefore, the demagnetization risk for this 12 kW DDPMSG has been studied for three different NdFeB magnet grades. The study has been performed with a proprietary finite element method (FEM) model, also presented in this paper. Furthermore, as the price on NdFeB magnets has increased and fluctuated considerably the last few years, an alternative geometry with smaller magnets and air gap has also been investigated. The magnet grades selected for this study are also all cheaper than the magnet grade used in the built generator, the magnet grade in the built generator is used as reference. The study is based on simulations and intends to determine if there is any risk of demagnetizing the magnets included in the study in any of the two geometries, that is, investigating if any of the cheaper magnets have sufficient properties to replace the reference magnet under the assumed conditions.

The Hysteresis Curve

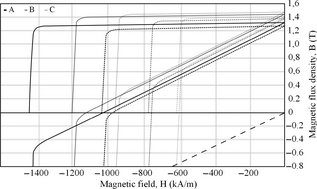
A hysteresis curve or BH curve is a plot of the magnetic flux density, B, as a function of the magnetic field, H. In Figure 1, the second and part of the third quadrant of several hysteresis plots are depicted. In this figure, both the normal and the intrinsic BH curves are included, the figure is based on data from [9]. The intrinsic curve is the normal curve but with an additional ${\textstyle {\mu }_{0}H}$ term. With this extra term, the intrinsic curve represents the total coercivity of the magnet, that is, the total magnetic field needed to reduce the magnetization to zero.

The most important properties that can be extracted from a BH curve is the remanence, ${\textstyle B_{r}}$ , the coercivity, ${\textstyle H_{c}}$ , and the intrinsic coercivity, ${\textstyle H_{ic}}$ .

Study

Generator

Design of the simulated generator was done with a FEM model presented in [6]. Geometrical and electrical parameters for the finished generator [6] are listed in Table 1. As the efficiency is high, there will be little heat generated in the generator and the magnets is not expected to reach very high temperatures. The generator is passively air cooled and the rated maximum temperature of the stator winding is ${\textstyle {70}^{\circ }}$ C. Hence, the maximum allowed temperature of the generator has been set to ${\textstyle {60}^{\circ }}$ C. This high temperature would only occur if the air exchange of the generator housing was insufficient. The properties of the generator have not been thoroughly optimized, as the goal was to build a simple to work with generator for scientific and educational purposes. The generator is more thoroughly described in [6]. This 12 kW generator was used as a reference model in this study.

Table 1. Geometric and electromagnetic parameters of the built generator.

Characteristics
Rotational speed (rpm)	127
Number of poles	32
Number of slots per pole and phase	5/4
Stator inner diameter (mm)	760
Air gap width (mm)	10
Generator length (mm)	222
Magnet width (mm)	54
Magnet height (mm)	14
Power (kW)	12.0
Efficiency, η (%)	95.9
Phase voltage (V) rms	156
Electrical frequency (Hz)	33.9
Load angle, δ ( ${\textstyle {}^{\circ }}$ )	5.3

By reducing the air gap to half and the magnet height to 6.5 mm, an alternative generator with similar electrical properties as the reference generator was found using the FEM model described in [6]. All stator parameters were kept the same, whereas the rotor diameter had to be increased for the rotor to fit after the air gap and magnet height had been reduced. With the reduction in the magnet size, the weight of the magnets for the alternative geometry was reduced from 41 to 19 kg.

Magnets

Three different PM grades were selected for the study. Data for the magnets were collected from the manufacturer [9] and are listed in Table 2. The notation TP and HR, in Table 2, refers to that the magnet was pressed either tangentially or hydrostatic, respectively, with respect to the magnetization direction during production. BH curves for the selected magnets are depicted in Figure 1, based on data from [9]. The demagnetization point has, in this study, been defined as the point on the BH curve where the distance to an extrapolation of the linear part of the BH curve is 0.01 T. The demagnetization points for all magnets and temperatures are listed in Table 3.

Table 2. Data for the selected magnets in the study at ${\textstyle {20}^{\circ }}$ C.

Magnet (Vacodym)	Br (T)	Hc (kA/m)	Hic (kA/m)	BHmax (kJ/m ${\textstyle {}^{3}}$ )	Temperature coefficient (% B ${\textstyle {}_{r}}$ / ${\textstyle {}^{\circ }}$ C)	Cost
A - 633 TP	1.32	1020	1432	335	−0.095	1
B - 745 HR	1.44	1115	1200	400	−0.115	0.95
C - 722 HR	1.47	915	955	415	−0.095	0.89

The price of the magnets [9], also in Table 2, is presented in per units of magnet A, the magnet grade used in the built generator, and the magnet used as reference. One objective of this study was to investigate if it is possible to reduce the cost of the PMs and still have satisfying magnetic properties, in the given generator geometries. Therefore, are all the chosen magnets a bit cheaper than the reference magnet.

Table 3. Critical limits for the magnetic field, for the magnetic grades at ${\textstyle {20}^{\circ }}$ C and ${\textstyle {60}^{\circ }}$ C.

Magnet	${\textstyle H_{knee}^{{20}^{\circ }c}}$ (kA/m)	${\textstyle H_{knee}^{{60}^{\circ }c}}$ (kA/m)
A	−1399	−988
B	−1167	−747
C	−921	−587

As the price of NdFeB magnets has been fluctuating considerably the last few years, a normalized price of 40 €/kg has been set for manufactured magnets of type A to be able to compare the total price differences between the generators.

Figure 1. BH curves for all the magnets tested, both at ${\textstyle {20}^{\circ }}$ C (solid) and ${\textstyle {60}^{\circ }}$ C (dotted). The curves with high initial slopes are the normal BH curves and the others the intrinsic BH curves. The dashed line is ${\textstyle {\mu }_{0}H}$ .

FEM model

The main simulation model used in the study was developed in Comsol Multiphysics which is a commercial FEM software capable of performing multiphysics simulations in different study domains.

With the 2D FEM model presented in this section, stationary electromagnetic simulations at different magnet temperatures can be performed. The model focuses on determining the magnetization inside the magnets at a user-defined load case. 3D effects, such as eddy currents and end effects at the generator edges, were neglected in this model.

A typical load case could be a short circuit in the armature winding at an elevated magnet temperature. The model does not account for the recovery of the magnets when the current is returned to normal levels, that is, the results are given for the exact moment and conditions set by the user.

Electromagnetic model

The electromagnetic field in the FEM model is derived from Maxwells equations and results in:

$\nabla \times ({\mu }_{0}^{-1}\nabla \times A-M)-\sigma v\times (\nabla \times A)=$$J^{e},$

(1)

where, ${\textstyle {\mu }_{0}}$ is the permeability, A is the magnetic vector potential, M is the magnetization, v is the velocity of the conductor and ${\textstyle J^{e}}$ is an externally applied current density. The velocity term is always zero in the stationary case and the model is assumed to be axisymmetric which results in that the magnetic vector potential and the external current density only have components in the z direction. Equation (1) is thereby reduced to

$\nabla \times ({\mu }_{0}^{-1}\nabla \times A_{z}-M)=J_{z}^{e}$

(2)

which is the equation solved in the FEM model.

Magnets

The magnetization of the magnets are modeled with an interpolation function of M as a function of B, M(B). The easy axis of the magnet is directed radially out from the rotor axis. The interpolation function uses the easy axis component of the magnetic flux density as input and return the magnetization in the easy axis direction of the magnet. The interpolation function is applied in every mesh node inside the magnets.

The M(B) function can be derived from the BH curve of the used PM. This means that only homogeneous magnet temperatures can be studied. However, the temperature inside a generator is fairly homogeneous and can be controlled with a cooling system.

In [[[#ese316-bib-0004|[4]]], [10, 11]] the demagnetization has been studied as a function of the applied magnetic fields angle relative to the magnetization direction. The conclusions were that only the parallel component of the magnetic field is not sufficient to model demagnetization behavior in all cases. However, in [10] an overloaded multipole machine was tested both with a similar model presented here, only using the parallel magnetic field, and a model taking the inclined field into account. The results from the two models were the same for the multipole machine. The FEM model presented in this paper will primarily be used for multipole machines with low load angles; hence, inclined fields do not need to be considered. Therefore, only the demagnetization field parallel to the magnetization is taken into account, that is, the M(B) function is only applied in the magnetization direction of the magnet. As a sintered NdFeB magnet is anisotropic, a M(B) function would be needed for all angles of the inclined field to be able to use the methodology in this FEM model. An alternative way would be to apply an analytic function of how the knee point is affected by an inclined field as Ruoho and Arkkio propose in [10].

If there is no explicit data available for the BH curve, that is, only the plot, B(H) can be approximated with an analytic function [12]

$B=B_{r}+{\mu }_{0}{\mu }_{r}H+{Ee}^{K_{1}(K_{2}+H)}$

(3)

where, ${\textstyle B_{r}}$ is the remanent flux density, ${\textstyle {\mu }_{0}}$ is the permeability, ${\textstyle {\mu }_{r}}$ is the relative permeability, H is the magnetic field, E is a unit conversion factor and it is 1 T. The parameter ${\textstyle K_{2}}$ is calculated from:

$K_{2}={\frac {ln[(B_{r}+({\mu }_{r}-1)\cdot {\mu }_{0}\cdot H_{ic})\cdot {\frac {1}{E}}]}{K_{1}}}-$$H_{ic}.$

(4)

The K₁ parameter sets the shape of the knee point in the BH curve, where a larger value gives a sharper knee. A fairly good agreement with the original BH curve was achieved with a ${\textstyle K_{1}}$ value of ${\textstyle -1.5\cdot {10}^{-4}}$ m/A. The magnetization can then be calculated with:

$M={\frac {B}{{\mu }_{0}}}-H.$

(5)

Boundary conditions

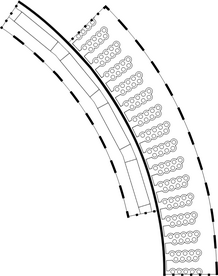
On the inner and outer boundary of the generator model, a homogeneous Dirichlet boundary condition is used which do not allow any flux through its boundary. As only the smallest periodic part of the generator is modeled, there is a continuity boundary condition on the edges where the generator is supposed to continue. This sets the magnetic vector potential equal on the two boundaries. To be able to move the rotor relative to the stator (without remeshing), a sector symmetry boundary condition, which also acts as a continuity boundary condition, is set along a line in the air gap. The simulated sector of the generator geometry together with all boundary conditions is depicted in Figure 2.

Figure 2. The solid, dashed and dotted lines represent sector symmetry, homogeneous Dirichlet and continuity boundary conditions, respectively.

Mesh

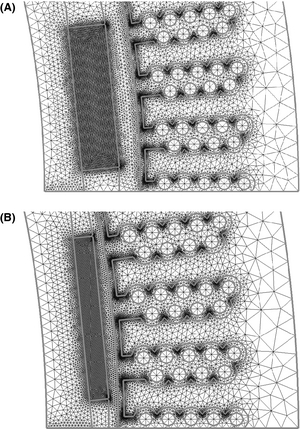
In the reference generator geometry used in this study the mesh is built out of ∼133 000 triangular elements and in the smaller geometry it has ∼115 000 elements. The mesh is finer close to geometrically detailed parts of the design and at parts that are critical to the study. The mesh in a small part of the two generator geometries is depicted in Figure 3.

Figure 3. The mesh in a small part in (A) for the reference geometry and in (B) for the alternative geometry.

Simulations

Three different NdFeB grades were simulated for two different generator geometries. In total, six unique generators were simulated.

All generators were tested with the same four simulation cases, first, the short-circuit current, ${\textstyle I_{sc}}$ , was determined for all generators using the FEM model [6] used for designing the generator. The short-circuit current is here defined as the worst-case maximum phase current of the phase that is not short circuited, for example, the phase current when the currents in the two other phases are equal. During simulations one phase had a current of ${\textstyle I_{sc}}$ and the other two had each a current of ${\textstyle -I_{sc}/2}$ . The resulting magnetic field was determined for both rated and short-circuit current with a magnet temperature of ${\textstyle {20}^{\circ }}$ C and ${\textstyle {60}^{\circ }}$ C, respectively. The simulation cases are summarized in Table 4. Each geometry and case was simulated at different stationary rotor positions; the rotor was rotated with an angle of ${\textstyle 1^{\circ }}$ (16 el ${\textstyle {}^{\circ }}$ ) per simulation, with a total rotation of ${\textstyle {45}^{\circ }}$ (720 el ${\textstyle {}^{\circ }}$ ). In this way, the worst possible position of the rotor could be found for every simulation case.

Table 4. The magnet temperature and the amplitude of the current for the four simulation cases.

Case	T ( ${\textstyle {}^{\circ }}$ C)	I (A)
1	20	37
2	20	${\textstyle I_{sc}}$
3	60	37
4	60	${\textstyle I_{sc}}$

Results

The results from the study are summarized in Table 5. The load angle, δ, is low and in the same order of magnitude for all generators, which makes them comparable. A generator with low load angle has good overload capability which is needed when electrical breaking is used [13]. The load angle was determined with the same FEM model used to design the reference generator.

Table 5. The minimum magnetic field inside the magnets for all simulation cases and rotor positions. Gray background indicates that the magnets will be partly irreversibly demagnetized. ${\textstyle I_{sc}}$ is the maximum amplitude of the short circuit current. The presented price only represents the price of the PMs.

Grade	${\textstyle H_{min}^{mag}}$ (kA/m)				Isc	δrated	Price
	Case 1	Case 2	Case 3	Case 4	(A)	( ${\textstyle {}^{\circ }}$ )	(€)
A	−498	−742	−467	−716	619	5.3	1640
A (thin)	−570	−945	−533	−914	550	6.2	760
B	−550	−799	−520	−753	651	5.0	1558
B (thin)	−632	−1023	−598	−774	590	5.8	722
C	−561	−806	−515	−611	651	4.9	1460
C (thin)	−644	−942	−586	−617	600	5.8	676

In the alternative geometry, with the reduced magnet and air gap size, the weight of the magnets was reduced from 41 to 19 kg. The total price for the PMs in each generator is presented in Table 5.

Resulting field

In Table 5, the minimum magnetic field inside the magnets for each generator and simulation case is presented. Results which will cause irreversible demagnetization are marked with a gray background.

The reference grade A magnet performed well for the two tested geometries and did not show any sign of irreversible demagnetization even at an elevated temperature.

The grade B magnet showed satisfying results at rated temperature, but at an elevated temperature it suffered from irreversible demagnetization when the generator was short circuited.

The reference geometry grade C magnet only suffered from irreversible demagnetization when the temperature was increased and a short-circuit occurred. The thin grade C magnet performed worst of the tested magnets and was partly irreversible demagnetized in both short-circuit cases.

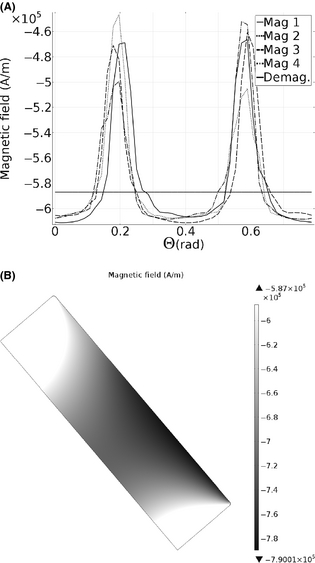
In Figure 4A, the minimum magnetic field inside four magnets is plotted versus the rotational angle of the rotor for the reference size grade C magnet and simulation case 4. In Figure 4B, the result of demagnetization for the worst affected magnet, at the worst angle 0.018 rad, is depicted. The gray shaded area in Figure 4B represents the area that will suffer from irreversible demagnetization. The white areas of the magnet represent values over 97%, which represent the linear part of the BH curve before the knee point, that is, will not be irreversibly demagnetized. The dark area will be the most damaged. In this case the demagnetization point was −587 kA/m, represented by the horizontal line in Figure 4A.

Figure 4. (A) The magnetic field as a function of rotational angle relative the stator. The horizontal line represents the value of the demagnetization point. (B) A plot of the remaining magnetization in the worst affected magnet, Mag 1, at angle 0.018 rad.

Discussion

In the case with the smaller alternative geometry, the diameter of the rotor is a bit larger than in the reference geometry to compensate for the smaller air gap and thinner magnets. The extra space given on the periphery of the rotor could be used for wider magnets. In this case the change was small +1.2 mm/magnet and the same magnet width was used for both geometries. If the change had been larger, the PM width should be compensated to keep the same power [14].

For the smaller generator geometry the total weight of the magnets is less than half than for the standard geometry. This also reduces the price of the magnets aliquot. Since the price of NdFeB magnets has increased substantially the last few years, the use of smaller magnets and air gap is one way to reduce the cost for PM generators.

The results from this study show that the best alternative, if one were to build a similar generator, is to choose the smaller geometry with the grade A magnets. The cost for the PMs is then reduced by ∼54%, compared to the reference generator. The price difference to the small grade B magnet is small and thereby hard to motivate with the better performing grade A magnet.

On the other hand, when a smaller air gap is used, more consideration is needed to the choice of PMs. Further, when the air gap width is decreased, higher demands are placed on tolerances of the construction, increasing the cost. Even small errors in tolerance can propagate throughout the construction and cause severe problems in other parts of the structure. This might increase the cost for the supporting structure of the generator.

Even though the event of a short circuit is very critical for a generator it is sometimes not worth protecting the magnets against these events if the event is very unlikely or leads to complete destruction. This could motivate the use of one of the cheaper magnet grades.

The goal with the design of the alternative generator was to get similar electrical properties as the reference generator. A negative aspect of this design is that the load angle increases when smaller magnets are used, this could be compensated by adding 15–20% more PM material. The alternative design would still be much cheaper and the induced voltage would also increase a bit due to larger magnets.

Conclusions

A new proprietary FEM model has been presented and shows in this study that there is no risk of demagnetizing the magnets in the built 12 kW PM generator, under the assumed conditions. However, the cheaper magnets in the study suffered from partial irreversible demagnetization in most of the short-circuit cases.

In conclusion, designing a generator to avoid demagnetization is a cost optimization process considering magnet material, cooling equipment, and construction tolerances.

Acknowledgment

This work has been carried out with funding from the Swedish Research Council, grant number 2010-3950.

Conflict of Interest

None declared.

References

1. Sebastian, T., and G. Slemon. 1987. Transient torque and short circuit capabilities of variable speed permanent magnet motors. IEEE Trans. Magn.23:3619–3621.
2. Ruoho, S., J. Kolehmainen, J. Ikheimo, and A. Arkkio. 2010. Interdependence of demagnetization, loading, and temperature rise in a permanent-magnet synchronous motor. IEEE Trans. Magn.46:949–953.
3. Goldemberg, C., L. Lebensztajn, and O. S. Lobosco. 1997. Analysis of short-circuit transients of a PM machine. WB2/13.1–WB2/13.3in1997 IEEE International Electric Machines and Drives Conference Record, February, Milwaukee, WI, 18–21 May 1997.
4. Thelin, P.2002. Short circuit fault conditions of a buried PMSM investigated with FEM. Proceedings of the Nordic Workshop on Power and Industrial Electronics, NORpie 2002, August, Stockholm, Sweden.
5. Eriksson, S.2008. Direct driven generators for vertical axis wind turbines. Ph.D. diss. Comprehensive summaries of Uppsala dissertations from the Faculty of Science and Technology 547. Acta Universitatis Upsaliensis, Uppsala, Sweden, ISBN: 978-91-554-7264-1.
6. Eriksson, S., A. Solum, M. Leijon, and H. Bernhoff. 2008. Simulations and experiments on a 12 kW direct driven PM synchronous generator for wind power. Renew. Energy33:674–681.
7. Eriksson, S., H. Bernhoff, and M. Leijon. 2009. FEM simulations and experiments of different loading conditions for a 12 kW direct driven PM synchronous generator for wind power. Int. J. Emerg. Electr. Power Syst.10: Article 3.
8. Deglaire, P., S. Eriksson, J. Kjellin, and H. Bernhoff. 2007. Experimental results from a 12 kW vertical axis wind turbine with a direct driven PM synchronous generator. inProceedings of EWEC 2007 - European Wind Energy Conference & Exhibition, Milan, Italy, 7–10 May.
9. Vacuumschmelze GmbH. 2012http://www.vacumschmelze.com/(accessed 17 August 2012).
10. Ruoho, S., and A. Arkkio. 2008. Partial demagnetization of permanent magnets in electrical machines caused by an inclined field. IEEE Trans. Magn.44:1773–1778.
11. Katter, M.2005. Angular dependence of the demagnetization stability of sintered Nd-Fe-B magnets. IEEE Trans. Magn.41:3853–3855.
12. Ruoho, S., E. Dlala, and A. Arkkio. 2007. Comparison of demagnetization models for finite- element analysis of permanent-magnet synchronous machines. Magnetics43:3964–3968.
13. Eriksson, S., and H. Bernhoff. 2011. A 225 kW direct driven PM generator adapted to a vertical axis wind turbine. Adv. Power Electron. 2011.
14. Wang, F., J. Pan, Y. Zhang, X. Cai, and J. Du. 2011. Design and performance of large scale direct-driven permanent magnet wind generators. 1–5inProceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, February.