Resumo
A otimização de um componente mecânico é um importante aspecto do processo de engenharia; um sistema bem projetado irá permitir uma redução do custo durante a fase de operação do equipamento. Em refinarias de petróleo e em plantas petroquímicas, fornos são incorporados ao processo para suprir energia térmica (calor) gerada pela combustão do combustível, que é transmitida para o fluido que escoa no interior da serpentina. Um importante componente interno de um forno de refinaria de petróleo é o sistema que suporta a serpentina de tubos. Este trabalho faz parte de uma pesquisa cuja meta é gerar uma nova metodologia para o projeto de suportes da zona de radiação de fornos de refinaria. Essa metodologia representa no seu conjunto a possibilidade de aplicação de alguns algoritmos evolutivos na área de projeto mecânico de fornos. Para a otimização de suportes laterais são utilizados 2 algoritmos evolutivos, o algoritmo genético e enxame de partículas. Neste estudo é realizada uma comparação entre os 2 métodos de otimização escolhidos. Recentes técnicas de penalidade dinâmica, especificamente o método da penalidade adaptativa, são incorporadas ao algoritmo. Os requisitos de resistência e operacionalidade são considerados no projeto como especificados pela norma API560. Os resultados mostram que o modelo converge para uma solução muito eficiente. Um exemplo real é incluído para demonstrar a eficiência do algoritmo.
Abstract
Optimization of mechanical components is an important aspect of the engineering process; a well designed system will lead to money saving during the production phase and better machine life. In oil refineries and petrochemical plants, furnaces are incorporated into the process to supply thermal energy (heat) generated by fuel combustion, which is transmitted to a fluid flowing within a tube bundle, i.e., a coil. An important internal component of the furnace oil refinery is the system that supports the tube coil. This work is part of a research whose goal is to generate a new methodology for the investigation and search of the supports of the radiation zone refining furnace. This methodology represents as a whole the possibility of application of some evolutionary algorithms in the area of mechanical design of furnaces. For the optimization of the lateral supports two evolutionary algorithms are used, genetic algorithm and particle swarm algorithm. In this work a comparison between the two optimization methods chosen is carried out. Recent techniques of dynamic penalty, specifically adaptive penalty method are incorporated into the algorithms. The serviceability and strength requirements are considered in the design problem as specified in API560. The results show that the model converges to a very efficient solution without any engineer intervention. A real example is included to demonstrate the efficiency of the algorithm.
Palavras‐chave
Algoritmos evolutivos ; Suportes de tubos ; Fornos de refinaria ; Projeto mecânico
Keywords
Evolutionary algorithms ; Tube supports ; Fired heaters ; Mechanical design
1. Introdução
Devido à crescente demanda no Brasil por derivados do petróleo existe a necessidade de expansão do refino. Logo, novas refinarias serão construídas e os fornos podem representar mais de 20% do investimento de uma unidade do refino. Dentro deste contexto, melhorias no projeto deste equipamento e de suas estruturas representam um aumento da segurança operacional e uma redução do custo total do projeto.
O projeto de fornos de refinaria de petróleo é complexo e envolve diversos sistemas. Um subgrupo destes sistemas inclui os componentes internos que estão expostos a altas temperaturas. Um componente interno importante é o sistema de suportação da serpentina de tubos.
Aproximadamente 40% das interrupções não planejadas na operação de fornos são causadas por falhas no sistema de suportação de tubos. Adicionalmente, estes suportes são fabricados a partir de um material com um custo elevado. O projeto de um suporte que considera aspectos relacionados à segurança operacional e à redução do peso do mesmo permitirá uma redução de custo significativa. No presente estudo é realizada apenas a otimização dos suportes laterais. Para a otimização dos suportes laterais são utilizados 2 algoritmos evolutivos, o algoritmo genético (AG) e o algoritmo enxame de partículas (particle swarm optimization – PSO).
Em diversos trabalhos recentes outros tipos de problema foram abordados, sempre utilizando algoritmos evolutivos. Nestes estudos foram feitas, de forma eficiente, uma otimização em um projeto mecânico, considerando um determinado componente, como uma turbina [1] , um domo [2] , um tanque cônico [3] ou um riser [4] and [5] . Logo, os diversos algoritmos evolutivos, como os AG e o PSO, têm grande flexibilidade e aplicabilidade, pois permitem exploração e explotação do espaço de busca.
Este trabalho faz parte de uma pesquisa cujo objetivo é a implementação de alguns algoritmos evolutivos na área de projeto mecânico de fornos [6] .
A redução do peso do suporte, que é a meta deste estudo, possibilitará uma redução no custo na etapa da fabricação destes componentes. O que pode ser significativo se considerarmos que o forno da Refinaria Gabriel Passos (REGAP) possui 640 suportes fundidos.
O projeto dos suportes laterais é realizado utilizando‐se uma abordagem analítica, através do programa SuporteLForno, que foi desenvolvido por técnicos da Petrobras. Logo, utilizou‐se uma metodologia analítica como método de cálculo das restrições estruturais.
A abordagem analítica considera tensões decorrentes do peso dos tubos, associados à tensão de longa duração, e a tensões relacionadas à dilatação dos tubos, associados à tensão de curta duração. O projeto é baseado na norma API STANDARD 560 [7] , específica para o projeto de fornos industriais. Esta norma contém diversas recomendações e procedimentos para o projeto de suportes dos tubos que passam pelo interior do forno, considerando que os suportes trabalham sob severo regime de fluência.
Neste trabalho realiza‐se uma comparação entre os 2 métodos de otimização escolhidos para a otimização deste projeto.
Recentes técnicas de penalização dinâmica são incorporadas ao algoritmo, mais especificamente o método de penalidade adaptativa (APM) de Lemonge e Barbosa [8] . Esse método é robusto e eficiente. O tratamento é totalmente adaptativo, não precisando ser parametrizado.
Através dos resultados obtidos com os algoritmos de otimização realizou‐se uma comparação com um projeto de um forno real para a refinaria REGAP da Petrobras.
2. Algoritmo enxame de partículas
O método de otimização PSO foi originalmente desenvolvido por Kennedy e Eberhart [8] . A técnica PSO é inspirada no voo de pássaros, que são denominados de partículas.
Esse método se inicializa aleatoriamente, através de um conjunto de partículas com velocidades e posições aleatórias. Após essa inicialização os indivíduos são avaliados através da função de avaliação. Em um algoritmo PSO existe um conjunto de vetores cujas trajetórias oscilam em torno de uma região definida por cada melhor posição individual (PBEST) e a melhor posição dos outros (GBEST).
A posição da partícula, xi , vai sendo atualizada de acordo com a equação:
|
|
( 1) |
Na equação (1), vi (t) representa o vetor velocidade da partícula i no tempo t, w é o fator de inércia, rnd representa números aleatórios de distribuição uniforme entre 0‐1, C1 e C2 representam respectivamente os parâmetros social e cognitivo, PBEST é a melhor posição individual e GBEST é a melhor posição social. Os parâmetros C1 e C2 ajustam o balanço entre a influência social e a aprendizagem da partícula individual.
No algoritmo básico inicial do PSO, proposto por Kennedy e Eberhart [7] , C1 = C1 = 2. Trabalhos posteriores [9] , [10] and [11] indicam a preferência pelo uso de outros valores para os parâmetros cognitivo e social.
Kennedy e Eberhart [9] sugerem que se definam limites para a velocidade máxima de cada partícula, limitada ao valor limite de cada variável (xmáx. ‐ xmin. ). Mas, estudos indicavam a necessidade de um controle da velocidade mais elaborado.
Desta forma, introduziu‐se na equação (1) o fator de inércia w [12] .
3. Algoritmo genético
Os AG são inspirados na teoria da evolução natural e também em conceitos posteriores sobre genética e foram originalmente propostos por Holland [13] .
Inicialmente, para o processo de otimização, cada indivíduo é definido em função das variáveis de projeto. Pode‐se escolher a codificação binária ou real. Define‐se os limites de cada variável, o que gera um espaço de busca para o processo. A população da primeira geração é obtida de maneira aleatória. Posteriormente cada indivíduo da geração atual é avaliado pela função de avaliação.
Em geral é possível na própria função de avaliação incorporar uma função de penalidade, que será capaz de avaliar e penalizar os indivíduos que eventualmente violem as restrições do problema. Para o cálculo das restrições podem ser utilizados diversos tipos de funções de penalidades. Nesta pesquisa utilizou‐se a penalidade adaptativa [8] .
Posteriormente a metodologia verifica se um determinado critério de parada foi atingido. Podem ser utilizados um determinado número de gerações, um valor para o melhor indivíduo ou até um determinado tempo para o processo de otimização.
Após a avaliação de cada indivíduo da população e se o critério de parada não for satisfeito realiza‐se a seleção dos pares de indivíduos para a reprodução. Os indivíduos mais adaptados são selecionados probabilisticamente. Após esta etapa, são aplicados os operadores de cruzamento e mutação com uma probabilidade pré‐definida, pc e pm , respectivamente. O ciclo reinicia‐se novamente até que o critério de parada seja satisfeito.
Vários tipos de operadores de crossover e mutação podem ser testados e explorados. Adotando‐se a codificação real, podem‐se utilizar, entre outros, os seguintes operadores de crossover: média [14] , média geométrica, BLX‐α [15] e aritmético [16] . Para o operador mutação, também para a representação real, apresenta‐se os seguintes operadores: uniforme, gaussiana e limite [16] .
No crossover aritmético [16] , dado 2 cromossomos p1 e p2 , são produzidos 2 cromossomos c1 e c2 da seguinte forma:
|
|
( 2) |
|
|
( 3) |
onde β ∈ U (0, 1).
A mutação uniforme e a gaussina, realizadas para cada cromossomo de um indivíduo, são, respectivamente, a substituição de um gene por um número aleatório e por um número aleatório de uma distribuição normal. A substituição do gene deve sempre respeitar os limites definidos para as variáveis de projeto. A mutação limite [16] é a substituição do gene por um dos limites do intervalo permitido.
4. Nova abordagem para o projeto de suportes laterais
4.1. Variáveis
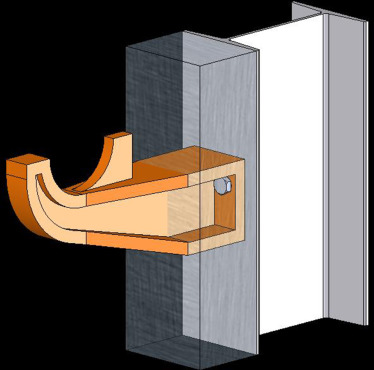
Por possuírem algumas características distintas, os suportes dos tubos de fornos são tratados em 3 itens separados: suportes da radiação, suportes intermediários da convecção (espelhos) e suportes terminais da convecção. Este trabalho aborda os suportes da radiação, esses suportes podem assumir diversas geometrias, dependendo da posição dos tubos no interior do forno. Na situação em que os tubos tangenciam horizontalmente a parede do forno o suporte empregado é o suporte lateral. Uma das possíveis geometrias para o suporte lateral de fornos é mostrada na figura 1 abaixo.
|
|
|
Figura 1. Suporte lateral de fornos. |
O estudo de otimização realizado neste trabalho adota a geometria mostrada na figura 1 acima para a geometria do suporte lateral, esse tipo de geometria é adotado em grande parte das refinarias da Petrobras no Brasil. O programa SuporteLForno, utilizado no projeto do suporte, considera as variáveis necessárias para a especificação de um suporte lateral com uma geometria de acordo com a figura 1 .
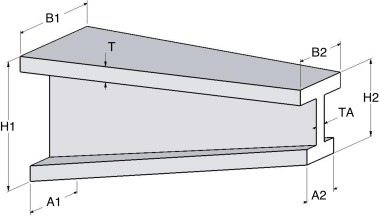
As variáveis A1, A2, B1, B2, H1, H2, T e TA representam os parâmetros geométricos de um suporte lateral. Essas variáveis são definidas no projeto de um determinado suporte, mostrado na figura 1 . São as variáveis de projeto escolhidas para o estudo de otimização proposto neste trabalho. Estas variáveis definem um indivíduo ou uma partícula. As variáveis de projeto são mostradas na figura 2 abaixo.
|
|
|
Figura 2. Variáveis de projeto. |
Os limites destas variáveis definem o espaço de busca adotado nas diversas simulações de otimização através de um AG e de um algoritmo por PSO, no intuito de se obter o ótimo global dos diversos casos analisados.
Alguns dados reais, fornecidos por empresas que fabricam os suportes de fornos de refinaria, foram incorporados aos algoritmos de otimização. Os suportes da zona de radiação são fabricados através do processo de fundição e, consequentemente, existem valores extremos para as variáveis de projeto do componente que a fundidora impõe como condição para a fabricação do suporte.
A tabela a seguir mostra esses parâmetros, definidos para as variáveis geométricas do suporte, que são as variáveis de projeto. A tabela 1 apresenta os limites das variáveis de projeto.
| Variável de projeto | Limite inferior (mm) | Limite superior (mm) |
|---|---|---|
| A1 | 15 | 180 |
| A2 | 15 | 90 |
| B1 | 60 | 180 |
| B2 | 30 | 90 |
| H1 | 70 | 230 |
| H2 | 40 | 120 |
| T | 10 | 50 |
| TA | 10 | 50 |
Ao longo do processo de otimização, quando um dos limites (inferior ou superior) de cada variável de projeto for violado, o algoritmo impõe como valor para a variável de projeto o próprio valor do limite inferior ou superior, o que for violado.
Para o presente estudo foram consideradas algumas constantes, necessárias ao estudo de otimização. Adotaram‐se os seguintes parâmetros constantes, que foram considerados para o projeto do suporte lateral do forno F‐01 da refinaria REGAP, para a otimização do suporte: L = 228 mm, VAO = 5 mm, REFR = 140 mm, SLQ = 5,39 MPa, SSQ = 10,79 MPa, C = 1,3 mm, P = 1.402,35 N. A seguir apresenta‐se uma breve explicação desses parâmetros constantes.
Para a representação geométrica do suporte deve‐se definir o valor de L, que é em geral um parâmetro fixo, pois depende da posição do tubo na estrutura interna do forno e não do projeto mecânico do suporte.
O parâmetro REFR representa a espessura do refratário utilizado no projeto do suporte.
Em geral é utilizado um valor fixo para o parâmetro VAO, um parâmetro geométrico para estabilização do tubo no suporte.
A constante C representa uma sobre‐espessura de corrosão, ou seja, diminui‐se o valor de 2 XC dos valores das variáveis geométricas de projeto. Desta forma considera‐se no cálculo das tensões que a peça está no fim de sua vida útil em relação ao fenômeno de corrosão.
A constante P representa a carga aplicada no suporte e o PESO o próprio peso do suporte, esses parâmetros são descritos respectivamente, nas seções 4.2 e 4.3 deste artigo.
As constantes SSQ, a tensão admissível de longa duração, e SLQ, a tensão admissível de curta duração, são obtidas da norma API560, que define em função da temperatura atuante no suporte as tensões admissíveis para um determinado material.
Finalmente, SLM, a tensão máxima de longa duração, SSM, a tensão máxima de curta duração, são obtidas a partir de formulações analíticas para o cálculo das tensões atuantes ao longo dos suportes.
4.2. Restrições estruturais
O projeto do suporte lateral de fornos é baseado na norma API STANDARD 560, específica para o projeto de fornos industriais. Esta norma contém diversas recomendações e procedimentos para o projeto de suportes dos tubos que passam pelo interior do forno, considerando que os suportes trabalham sob severo regime de fluência. A API STANDARD 560 [7] estabelece que os suportes sejam dimensionados considerando‐se 2 tipos de carregamentos: longa duração (peso próprio dos tubos) e curta duração (peso próprio dos tubos + atrito causado pela dilatação momentânea dos tubos apoiados).
O código estabelece tensões admissíveis para cada um desses carregamentos e na grande maioria dos casos a condição de curta duração é a dimensionante. O que a norma estabelece é que para os cálculos da tensão de curta duração uma força horizontal de 0,3 vezes a força vertical é adicionada ao carregamento.
Portanto, as tensões ao longo do suporte são calculadas para 2 situações distintas. Para o caso da tensão de longa duração apenas o peso irá atuar, calcula‐se a força atuante no suporte considerando‐se uma configuração real do forno, onde é feito um modelo matemático que calcula a reação de apoio no suporte. A reação de apoio obtida é equivalente ao peso que atua em um único suporte lateral, que não deve ser confundido com a variável PESO do suporte.
Este modelo matemático considera para o cálculo da reação, onde o peso do tudo e o peso do fluido contido no seu interior são considerados, que os suportes e os carregamentos impostos podem ser representados por uma viga hiperestática. Cada vão representa o espaço livre entre os suportes no interior do forno e as cargas concentradas e distribuição representam condições atuantes no equipamento, como flanges e o peso do fluido e do tubo.
O método de cálculo utilizado para a solução da viga hiperestática é dos 3 momentos [17] . A figura 3 abaixo mostra uma viga hiperestática que representa um caso real de um forno, utilizada para se obter a carga atuante no suporte.
|
|
|
Figura 3. Viga hiperestática para o cálculo das cargas. |
As forças consideradas, que atuam no suporte, para cada caso de tensão causam esforços de flexão e cortante, esses esforços estão associados com tensões, de tração, compressão e cisalhamento. Essas tensões serão comparadas, através de critérios de resistência, com o valor da tensão admissível especificado, após a escolha do material a ser utilizado, pela norma API560 [7] .
A seção reta do suporte lateral varia ao longo do mesmo, logo, subdividiu‐se o componente em 100 partes iguais e obtiveram‐se para cada caso de tensão as tensões máximas atuantes, SLM e SSM, que devem ser comparadas com as tensões admissíveis, SSQ e SLQ. Elas devem ser necessariamente menores do que SLQ e SSQ para que um indivíduo ou partícula qualquer sejam considerados viáveis. Logo, são utilizadas formulações analíticas para o cálculo das tensões atuantes ao longo dos suportes.
Essas formulações analíticas podem ser obtidas a partir de considerações a respeito do cálculo de tensões em vigas com seção reta variável [18] .
Essa metodologia analítica não é apresentada neste trabalho devido ao elevado número de equações, entretanto este equacionamento pode ser realizado no intuito de se reproduzir os resultados apresentados neste artigo.
Em cada caso de tensão, após a obtenção das tensões máximas atuantes, as 2 restrições poderão ser obtidas. Estas restrições estruturais são incorporadas à função objetivo para formar a função de avaliação através de funções de penalidade.
As restrições estruturais referem‐se às tensões de longa e de curta duração e podem ser obtidas através das seguintes equações:
|
|
|
|
4.3. Função de avaliação
Para determinar uma configuração para um suporte que atenda a requisitos técnicos da norma e critérios de projeto e que também possibilite o menor custo de fabricação, a função objetivo deve envolver a busca pelo peso mínimo do suporte. O peso do suporte, variável PESO, é a função objetivo do problema analisado, Fpeso .
O peso do suporte é obtido através de um cálculo aproximado, subdividindo‐se a estrutura em diversas partes e obtendo‐se o volume aproximado do suporte. Para se obter o peso do componente basta multiplicar o volume total pelo peso específico, no valor de 8 x 10‐6 kgf/mm3 . As equações (4)‐(10), mostradas a seguir, são utilizadas para se obter inicialmente o volume do suporte (equação (9)) e posteriormente, através da equação (10), se obter o peso do suporte, multiplicando‐se o volume pelo peso específico.
|
|
( 4) |
|
|
( 5) |
|
|
( 6) |
|
|
( 7) |
|
|
( 8) |
|
|
( 9) |
|
|
( 10) |
Neste trabalho as restrições de projeto são implementadas através de funções de penalidade adaptativas, método APM [8] . A variável x representa o conjunto de variáveis de projeto que definem um suporte e as formulas a seguir são sempre aplicadas para cada indivíduo. A aptidão F(x) de cada solução candidata é dada por:
|
|
( 11) |
onde é o valor médio da função objetivo, Fpeso, para a população atual. Os parâmetros de penalização, k1 (i = 1) e k2 (i = 2), são definidos para cada geração por:
|
|
( 12) |
onde é a média das restrições, para cada caso de tensão, na geração considerada. O denominador do segundo termo da equação (12) é o mesmo para o cálculo dos 2 parâmetros de penalização e representa a soma da média das restrições para uma determina geração elevado a potência de 2.
Considerando‐se a função de penalidade adaptativa adotada (11), uma determinada solução candidata com violações pequenas é menos penalizada do que outra com violação considerável das restrições. Isto evita que uma partícula ou um indivíduo próximos ao ótimo se afastem do mesmo dificultando a busca da solução desejada. Além de não desconsiderar soluções inviáveis, o tratamento é totalmente adaptativo, não precisando de nenhum parâmetro a ser ajustado pelo usuário.
4.4. Otimização através de um algoritmo genético
Diversas considerações são adotadas para o AG utilizado neste trabalho. As variáveis de projeto foram representadas através de uma codificação real. Alguns parâmetros adotados para o AG foram baseados em recomendações de trabalhos na área de otimização [1] e também foram escolhidos a partir de evidências empíricas.
A população inicial, com 100 candidatos, é escolhida aleatoriamente, considerando os limites definidos para as variáveis de projeto. Após a avaliação de cada indivíduo da população é realizada a seleção dos pares de indivíduos para a reprodução, os indivíduos mais adaptados são selecionados probabilisticamente. Realiza‐se uma seleção por torneio, com 2 indivíduos competindo.
Após esta etapa, são aplicados os operadores de cruzamento e mutação com uma probabilidade pré‐definida, pc e pm , respectivamente, com valores de 0,9 e 0,003. Neste trabalho utilizaram‐se os seguintes operadores: crossover aritmético [16] e mutação uniforme. O critério de convergência adotado foi o número máximo de gerações pré‐determinado, estipulado em 100 gerações.
Depois do processo de atuação dos operadores, uma nova geração é obtida. Neste trabalho é utilizado um AG geracional. O melhor indivíduo obtido em todas as gerações representa a solução obtida ao longo do processo. Durante o procedimento computacional de otimização a técnica de elitismo é empregada, o melhor indivíduo em cada geração substitui o pior indivíduo da próxima geração.
4.5. Otimização através do algoritmo enxame de partículas
São adotadas para o algoritmo enxame de partículas utilizado neste trabalho algumas considerações obtidas a partir da literatura. Inicialmente as variáveis de projeto foram representadas através de uma codificação real.
A população inicial, com 100 candidatos, é escolhida aleatoriamente, considerando os limites definidos para as variáveis de projeto. No algoritmo básico inicial do PSO, proposto por Kennedy e Eberhart [8] , C1 = C1 = 2. Nesta pesquisa é utilizado o valor de 2 para C1 e C2.
Para controlar‐se a velocidade de cada partícula, limita‐se seu valor máximo ao valor limite de cada variável. Além disso, o valor de 0,5 para w, o fator de inércia, é utilizado.
Assim como no AG desenvolvido nesta pesquisa, é explorado para o algoritmo PSO a penalidade adaptativa [8] como técnica de tratamento das restrições, essa função de penalidade é incorporada à função de avaliação, que é a maneira como os algoritmos evolutivos irão avaliar cada indivíduo ou partícula.
Ao longo do processo de otimização a técnica de elitismo é empregada. O critério de convergência adotado foi o número máximo de gerações pré‐determinado, estipulado em 100 gerações.
5. Experimentos
Neste trabalho escolheu‐se um projeto já realizado, para um forno da refinaria REGAP da Petrobras, para se comparar o resultado obtido para o peso do suporte lateral através dos algoritmos genético e PSO com o peso do suporte projetado anteriormente. No projeto da REGAP, o material do forno F‐2102 A/B foi identificado como ASTM A297, Grau HP (25Cr‐35Ni+Nb).
Foram feitas 30 execuções independentes para cada algoritmo de otimização adotado, os AG e PSO, com o objetivo de se ter um suporte lateral com um peso mínimo para produção e que atendessem as restrições impostas, o que representa o melhor resultado.
Em 27 das execuções realizadas o peso obtido através do AG foi menor do que o algoritmo PSO. Os resultados do menor valor viável obtido do peso do suporte para cada algoritmo, a média de todo os pesos viáveis obtidos, a execução, a geração e o número de soluções factíveis (nsf) para este melhor indivíduo obtido são expostos na tabela 2 .
| Algoritmo | Viáveis (melhor) | Viáveis (média) | Execução | Geração (melhor) | NSF |
|---|---|---|---|---|---|
| AG | 7,70kgf | 11,43kgf | 20 | 90 | 6.943 |
| PSO | 8,62kgf | 10,63kgf | 22 | 18 | 5.201 |
A tabela 3 apresenta as variáveis obtidas através dos algoritmos de otimização desenvolvidas para este estudo para os casos apresentados na tabela 2 . A última linha da tabela apresenta o PESO do suporte, para o melhor indivíduo, ao final de 100 gerações. Os valores apresentados na coluna «Projeto de referência» representam os parâmetros geométricos do suporte existente no forno da refinaria REGAP.
| Variáveis | Projeto de referência | GA | PSO1 |
|---|---|---|---|
| A1 (mm) | 19 | 43 | 60 |
| A2 (mm) | 19 | 26 | 17 |
| B1 (mm) | 110 | 84 | 89 |
| B2 (mm) | 40 | 37 | 30 |
| H1 (mm) | 130 | 120 | 103 |
| H2 (mm) | 60 | 65 | 115 |
| T (mm) | 25 | 15 | 13 |
| TA (mm) | 19 | 10 | 13 |
| Peso (kgf) | 12,4kgf | 7,70kgf | 8,62kgf |
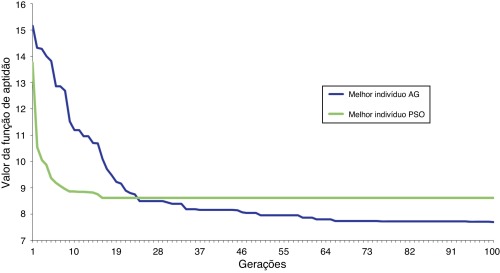
A figura 4 mostra a evolução do melhor experimento realizado para cada algoritmo de otimização, apresentados nas Tabela 2 and Tabela 3 . A partir da décima primeira geração o valor da função de aptidão do melhor indivíduo é mantido constante até a centésima geração, para o algoritmo PSO. O melhor indivíduo obtido ao longo dos processos não viola nenhuma das restrições estruturais. Este gráfico é representativo das diversas execuções realizadas, ou seja, é típico.
|
|
|
Figura 4. Evolução dos experimentos. |
6. Conclusão
Ao final do processo de otimização obteve‐se respectivamente, para os algoritmos genético e PSO, uma redução do peso da estrutura de 37,9 e 30,5%, considerando que o peso atual dos suportes da refinaria REGAP da Petrobras projetados pela equipe de engenheiros da companhia é de 12,4 kgf.
Comparando‐se os 2 métodos de otimização utilizados neste estudo pode‐se concluir que o AG é mais eficaz e possibilitou que se encontrasse o melhor ótimo viável para o problema de otimização de um suporte lateral de um forno de refinaria da Petrobras.
Os algoritmos apresentados neste estudo permitem a obtenção de um suporte lateral de fornos de refinaria com um peso mínimo e que atenda as 2 restrições estruturais apresentadas na seção 4.2 deste artigo. Essas restrições foram implementadas como funções de penalidade adaptativa (APM) de Lemonge e Barbosa [8] , [19] and [20] de maneira eficiente.
Alguns dados reais, fornecidos por empresas que fabricam os suportes de fornos de refinaria, foram incorporados aos algoritmos de otimização. Os suportes da zona de radiação são fabricados através do processo de fundição e, consequentemente, existem valores extremos para as variáveis de projeto do componente que a fundidora impõem como condição para a fabricação do suporte. Logo, o processo de otimização gerou uma solução viável quanto à fabricação do componente.
Referências
- [1] G. Corriveau, R. Guilbault, A. Tahan; Genetic algorithms and finite element coupling for mechanical optimization; Adv. Eng. Softw., 41 (3) (2010), pp. 422–426
- [2] E.S. Kameshki, M.P. Saka; Optimum geometry design of nonlinear braced domes using genetic algorithm; Comput. Struct., 41 (1–2) (2007), pp. 71–79 85
- [3] A.M. ElAnsary, A.A. ElDamatty, A.O. Nassef; A coupled finite element genetic algorithm technique for optimum design of steel conical tanks; Thin Wall. Struct., 41 (4) (2011), pp. 482–494 49
- [4] Silva, R.F. da; Teófilo, F.A. F.; Parente, E.; Melo, A.M. C. de; Holanda, A.S. de. Optimization of composite catenary risers. Marine Structures, 33, 1‐20, 2013.
- [5] A. Pina, C. Albrecht, B.S.L.P. Lima, B. Jacob; Tailoring the particle swarm optimization algorithm for the design of offshore oil production risers; Optim. Eng., 12 (5) (2010), pp. 215–235
- [6] G.J. Simões, B.S.L.P. Lima; Optimization of furnace lateral supports through genetic algorithms; 21st Brazilian Congress of Mechanical Engineering, Natal, RN, Brazil (October 24‐28 2011)
- [7] API Standard 560. Third Edition, May 2001. American Petroleum Institute.
- [8] A.C.C. Lemonge, H.J.C. Barbosa; An adaptive penalty scheme for genetic algorithms in structural optimization; Int. J. Numer. Meth. Eng., 59 (5) (2004), pp. 703–736
- [9] J. Kennedy, R.C. Eberhart; Swarm Intelligence; Morgan Kaufmann P ublishers (2001) ISBN: 1‐55860‐595‐9
- [10] K. Parsopoulos, M. Vrahatis; Recent Approaches to Global Optimization Problems Through Particle Swarm, In Natural Computing1:; Kluwer Academic Publishers (2002), pp. 232–306
- [11] Carlisle, A., Dozier, G., An off‐The‐Shelf PSO. In Proceedings of the Particle Swarm, Optimization Workshop, pp. 1‐6. Indianapolis, IN: Purdue School of Engineering and Technology, IUPUI (in press), 2001.
- [12] R.C. Eberhart, Y. Shi; Comparing inertia weights and constriction factors in particle swarm optimization, IEEE International Conference on Evolutionary Computation; San Diego, California (2000), pp. 84–88
- [13] J.H. Holland; Adaptation in natural and artificial systems; University of Michigan Press, Ann Arbor, MI (1975)
- [14] L. Davis; Handbook of genetic algorithms; Van Nostrand Reinhold (1991)
- [15] L.J. Eshelman, D.J. Shaffer; Real‐ coded genetic algorithms and interval‐ schemata; D.L. Whitley (Ed.), Foundations of Genetic Algorithms 3, Morgan Kaufman, San Mateo, CA (1992), pp. 187–203
- [16] Michalewicz, Z.; Fagel, D.B. In:;1. How to solve it: modern heuristics. 2 nd ed., rev. and extended ed. Berlin, New York: Springer; 2004.
- [17] V.I. Féodosiev; Resistencia de materiales; (2 ed.)Editorial MIR, Moscou (1980)
- [18] D. Lardner Crandall; An introduction to the mechanics of solids; McGraw‐Hill (1978)
- [19] H.J.C. Barbosa, A.C.C. Lemonge; An adaptive penalty scheme in genetic algorithms for constrained optimization problems; Proceedings of the Genetic and Evolutionary Computation Conference ‐ GECCO, Morgan Kaufmann Publishers, New York (9‐13 July 2002), pp. 287–294
- [20] H.J.C. Barbosa, A.C.C. Lemonge; A new adaptive penalty scheme for genetic algorithms; Inform. Sciences, 156 (5) (2003), pp. 215–251
Document information
Published on 01/03/16
Accepted on 14/07/14
Submitted on 29/01/14
Volume 32, Issue 1, 2016
DOI: 10.1016/j.rimni.2014.07.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?