Damage detection in a fiber reinforced polymers based tower of a floating offshore wind and tidal power platform using structural dynamic parameters

1 INTRODUCTION

Offshore renewable energy is a cornerstone of the clean energy transition in the EU. It consists of many different sources that are abundant, natural and clean, obtaining energy from wind, wave and tidal. This can be harnessed by modern technologies without emitting any greenhouse gases, (European Commission 2020). There is no doubt that the offshore renewable energy exploitation has a large potential to grow. However, the open sea is a very aggressive environment, which may largely affect the maintenance costs of the installations and therefore the overall cost of offshore energy generation. The owners of offshore assets are aware of that and are paying a steep price. A massive amount of steel goes into those assets, and all this metal is subject to degradation, which explains why corrosion accounts for approximately 60% of offshore maintenance costs. In order to address this problem, the main objective of the EU H2020 952966 FIBREGY project, (EU 2023), is enabling the extensive use of FRP materials in the structure of the next generation of large Offshore Wind and Tidal Power (OWTP) platforms, due to the convenient immunity to corrosion and superior fatigue performance of these materials. Another innovative aspect that will be considered is the use of multifunctional FRP materials in the OWTP structure, by embedding sensors in the material for continuous SHM.

During FIBREGY project, a scale (1:50) of an FRP tower with an embedded SHM system will be tested. In this paper, a dynamic numerical analysis of this scaled structure is carried out. A FEM is made and analysed to obtain its dynamic behaviour, characterized by frequencies and modal shapes. Also, a model updating and optimization based damage detection method is proposed for this structure and tested using a numerical damaged scenario.

2 Numerical Model

2.1 Geometry

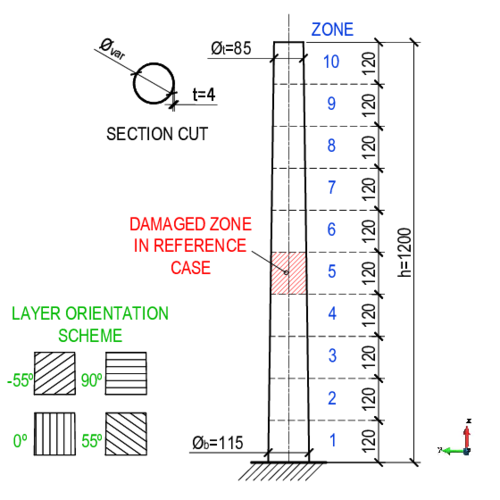
The structure under study is a cone with the following geometric characteristics, showed in Fig. 1. The bottom face of the tower is fully fixed (displacement in x, y and z).

• Height: ${\textstyle h=1200\ mm}$
• Bottom external diameter: ${\textstyle \Phi _{b}=117\ mm}$
• Top external diameter: ${\textstyle \Phi _{t}=84\ mm}$
• Thickness: ${\textstyle t=4\ mm}$

The tower is divided into ${\textstyle 10}$ sectors in its height (x axis) and in ${\textstyle 6}$ layers evenly distributed in the thickness, in correspondence with the laminate that forms it, resulting in ${\textstyle 60}$ volumes.

Figure 1: Geometry of the analysed tower, dimensions in mm.

The FEM design is done with GiD,(CIMNE 2020), a pre and post processor for numerical simulations in science and engineering. The structure is discretized in ${\textstyle 54\,096}$ nodes and ${\textstyle 46\,080}$ hexahedra linear elements and, as it is shown in Fig. 2.

Figure 2: Numerical model discretization

2.2 Material

The FRP used in the scaled tower is composed of a vinylester based resin with glass fibre reinforcement, with a ${\textstyle 20\%}$ of fibre volume fraction. The main characteristics are listed in Tab 1. The composite has ${\textstyle 6}$ layers of unidirectional fibres in the following orientations, from external to internal layer: [${\textstyle 0^{\circ }/55^{\circ }/0^{\circ }/{-55}^{\circ }/0^{\circ }/90^{\circ }}$], angles from the axis of the tower, see Fig. 1. .

Table. 1 Materials properties

Material	Young's Modulus	Poisson	Density
	E (MPa)	$\nu$	$\rho \left({\frac {t}{m^{3}}}\right)$
Resin	$3\,350$	$0.260$	$1.12$
Fibre	$73\,100$	$0.238$	$2.62$

2.3 Numerical Analysis

A dynamic analysis of the model is done using an in-house multi-physics FEM code, FEMUSS, developed by the International Centre for Numerical Methods in Engineering (CIMNE) and the Polytechnical University of Catalunya (UPC). The different orthotropic composite layers, are treated using the Serial-Parallel mixing theory, (Martinez, et al. 2008).

2.4 Damaged Case

A reference damaged tower is proposed to observe changes in the dynamic behaviour of the model and to use its modal frequencies as input data in the damage detection method. Numerically, the damaged is represented by a reduction of the Young's Modulus of both materials, fibre and resin, in layers ${\textstyle 1}$, ${\textstyle 3}$, and ${\textstyle 5}$ (zero degree fibre orientation layers of the laminate), to ${\textstyle 100MPa}$ in the sector ${\textstyle 5}$ of the tower, as shown in Fig. 1.

3 Dynamic behaviour

The embedded SHM system that is going to be used in tests allows up to ${\textstyle 1\,000\ Hz}$ of sampling rate. In consequence, the analysis is limited to ${\textstyle 500\ Hz}$, the half of the sampling rate value, corresponding to the Nyquist frequency. This value defines the bandwith by Fourier transform based analysis.

In this range, ${\textstyle 7}$ modes were found. The frequency values obtained in the analysis of the undamaged scenario and the described damaged reference case, are listed and compared in Tab. 2. Due to the rotational symmetry of the structure, modes 1-2, 3-4 and 6-7 have almost the same values between them, but not equal because the asymmetry in the fibre's orientation. These are flexural modes, while mode 5 is expansive, as is shown in Figs. 3 and 4. There, dark blue colour represents no displacement, red biggest displacement.

Table. 2 Frequencies, in $[Hz]$

Mode	Main	Undamaged	Damaged	$\Delta _{rel}$
	Direction	Case	Case	$[\%]$
1	Z	43.16	37.97	12.02
2	Y	43.34	38.07	12.14
3	Z	209.12	177.76	14.99
4	Y	209.82	178.49	14.93
5	-	292.47	279.26	4.51
6	Z	488.72	470.05	3.81
7	Y	489.78	470.93	3.84

Figure 3: Modal shapes of selected modes in undamaged tower.

Figure 4: Modal shapes of selected modes in reference damaged tower.

The first ${\textstyle 4}$ modes are more affected for the damage, with changes in frequencies above ${\textstyle 10\%}$, than the last 3 modes analysed. That is because the damage is located close to a nodal point of the modal shape in modes ${\textstyle 6}$ and ${\textstyle 7}$ and minimally affects the pressure stiffness, observed in mode ${\textstyle 5}$.

From this analysis is concluded that the frequencies are sensitive to the damage and its location is related to the more affected modes. So, this parameter can be used in a damage detection method.

4 Damage detection

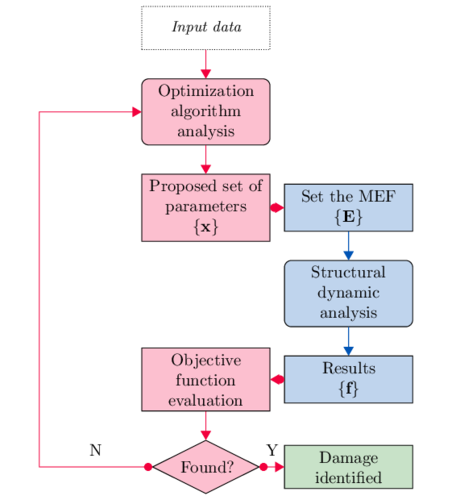
In this paper, structural damage is detected using changes in the natural frequencies. The method is a FEM updating based, that consist in modifying the mass, stiffness and damping parameters of the numerical model to match the behaviour in the model as in the test. To find it, an optimization algorithm is used, described in section 4.1. The problem is converted to a minimization of an objective function ${\textstyle f\mathbf {(x)} }$, where ${\textstyle \mathbf {(x)} }$ are the design variables, in this case the Young modulus of different volumes of the FEM. The basic scheme of the method is illustrated in Fig. 5, where ${\textstyle \left\lbrace \mathbf {f} \right\rbrace }$ is the vector of natural frequencies.

Figure 5: Damage detection method scheme

Several interfaces have been developed to couple the optimization algorithm with the structural analysis software. For example, to convert the proposed numerical design variables ${\textstyle \mathbf {x} }$ by the optimizer in an valid analysable FEM by FEMUSS, other to read the results of the dynamic analysis and evaluate the objective function.

4.1 Optimization

The general optimization problem can be formulated as solving the function:

$minimize\quad f\mathbf {(x)} ,\quad \mathbf {x} =[x_{1},x_{2},\dots ,x_{n}]$

(1)

Where ${\textstyle f\mathbf {(x)} }$ is the objective function, ${\textstyle n}$ is the dimension of the problem and ${\textstyle (x_{1},x_{2},\dots ,x_{n})}$ are the design variables. These may be subject to constraints in order to preserve physical sense.

$lb_{i}\leq x_{i}\leq ub_{i}\quad for\quad i=1,2,\dots ,n$

(2)

There ${\textstyle lb}$ and ${\textstyle ub}$ represents the lower and upper bound limit, respectively. The global optimization is referred to find the set of ${\textstyle \mathbf {x} }$ that minimize ${\textstyle f\mathbf {(x)} }$ over the entire feasible region. The problem is harder as the dimension ${\textstyle n}$ increases and, in cases when the behaviour of the objective function is unknown, is not possible to be certain whether one has found the true global optimum.

Several global optimization algorithms were developed that are more or less efficient, depending on the behaviour of the problem. In this paper, the Multi Level Single Linkage (MLSL) algorithm for global optimization from the NLopt library, (Johnson 2020), is used for the damage detection problem. It consist of a sequence of local optimizations starting from random points, proposed by Rinnooy Kan & Timmer (1987a), (1987b). An alternative implementation is applied and it uses a Sobol low discrepancy sequence as starting points, instead of random numbers, providing more accurate results, practically and theoretically guaranteed. This application was presented by Kucherenko & Sytsko (2005). The local optimization is carried out by the derivative - free and bound - constrained BOBYQUA local optimizer. This algorithm was presented by Powell (2009). It consist of a quadratic approximation of the objective function, constructed iteratively.

4.2 Design variables

In this numerical case, the design variables represent changes in the Young's modulus of the materials that are in the composite, fibre and resin. These variables can take any value between ${\textstyle 0}$ and ${\textstyle 1}$.

$\mathbf {x} =[x_{1},x_{2},\dots ,x_{n}],\quad x_{i}\in \left[0,1\right]$

(3)

The zero value represents no damage, so the ${\textstyle \mathbf {E} }$ remains unalterable, with the values listed in Tab. 1. A value of one, represents fully damaged, to avoid convergence problems in the numerical analysis, the ${\textstyle \mathbf {E} }$ is reduced to ${\textstyle 100MPa}$ for both, the resin and the fibre. Intermediate values are linearly interpolated, as shown in Tab. 3, with ${\textstyle x=0.5}$.

Table. 3 Young's Modulus in function of design variable

$x_{i}$	Fibre	Resin
	$\mathbf {E}$ [MPa]	$\mathbf {E}$ [MPa]
$0$	$73\,100$	$3\,350$
$0.5$	$36\,600$	$1\,725$
$1$	$100$	$100$

At first, a simpler scenario is evaluated, where are only ${\textstyle 10}$ design variables. Each one of these represents the ${\textstyle 3}$ layers with ${\textstyle 0^{\circ }}$ fibre orientation of ${\textstyle 1}$ zone in the structure, see Fig. 1. If, for example, the design variable ${\textstyle x_{7}=1}$, it implies that the ${\textstyle 3}$ layers ${\textstyle 0^{\circ }}$ in zone ${\textstyle 7}$ are damaged, so it's Young's modulus is equal to ${\textstyle 100MPa}$. The damaged case, described in Section 2.4, is represented by the vector of Eq. 4.

$\mathbf {x} =[0.0,0.0,0.0,0.0,1.0,0.0,0.0,0.0,0.0,0.0]$

(4)

Another scenario is considered, with ${\textstyle 60}$ design variables. These are correlated with the material properties of each one of the volumes that the structure is divided. So, first ${\textstyle 10}$ variables represent the external layer, of ${\textstyle 0^{\circ }}$ fibre orientation, in the different zones. From ${\textstyle 11}$ to ${\textstyle 20}$, the second layer, of ${\textstyle 55^{\circ }}$ fibre orientation, and so on for the following variables. The damaged case, described in Section 2.4, is represented by all values equal to ${\textstyle 0.0}$, except the listed in Eq. 5.

$x_{5}=1.0,\quad x_{25}=1.0,\quad x_{45}=1.0$

(5)

4.3 Objective function

The aim of the optimization process is to obtain the set of variables which minimize the objective function, Eq. 1. The success of the process depends on the correct behaviour of this function. This function must compare measurable values of a damaged structure (reference - ref), with the results of a proposed by the optimizer model of the structure (evaluation - ev).

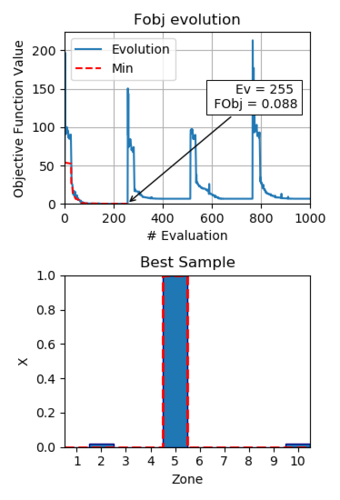
Figure 6: Results optimization with $10$ design variables

In this paper the Eigenfrequencies Method is used. The natural frequencies of the structure are very sensitive to the damage and it is easy to implement a monitoring system, thus is widely used. The variations in the frequencies and which mode is more or less affected depends on the position and severity of the damage. But it represents the global behavior of the structure, since doesn't use spatial information. The proposed objective function is Eq. 6.

$f_{(\mathbf {x} )}=\left\|\mathbf {f} _{ref}-\mathbf {f} _{ev}\right\|$

(6)

$\mathbf {f} _{ref}=[f_{ref,1},f_{ref,2},\dots ,f_{ref,7}]=[37.97,38.07,\dots ,470.93]Hz$

(7)

$\mathbf {f} _{ev}=[f_{ev,1},f_{ev,2},\dots ,f_{ev,7}]$

(8)

Where ${\textstyle \mathbf {f} _{ref}}$ and ${\textstyle \mathbf {f} _{ev}}$ are vectors of the first ${\textstyle 7}$ natural frequencies of the reference damaged structure and the results of the evaluation, respectively. This function is ${\textstyle 0}$ and is the global minimum when the vectors are equal, so the structure proposed and the damaged case matches.

4.4 Results

In the first scenario, with ${\textstyle 10}$ design variables as explained before, the optimization process is set up with a limit of ${\textstyle 1\,000}$ evaluations. In that range, the algorithm found a minimum in the evaluation ${\textstyle 255}$, with an objective function value of ${\textstyle 0.088}$. The evolution of the objective function value is shown in Fig. 6.

The design variables corresponding with the obtained minimum are listed in Eq. 9 and plotted in the histogram of Fig. 6. Except for minimal differences in zones ${\textstyle 2}$ and ${\textstyle 10}$ (less than ${\textstyle 2\%}$), the obtained structure and the damaged case are equal, so the damage is found.

$\mathbf {x} _{res}=[0.000,0.020,0.000,0.000,0.998,0.000,0.000,0.000,0.000,0,019]$ (9)

In the ${\textstyle 60}$ design variables scenario, the optimization is limited to ${\textstyle 3\,500}$ evaluations. In this scenario the minimum value of the objective function was found in the evaluation ${\textstyle 2\,801}$, with an objective function value of ${\textstyle 1.148}$. Although this value is bigger than the obtained before, is acceptable, due the problem is harder to solve. The evolution of this function and the histogram representing the best sample found are shown in Fig. 7.

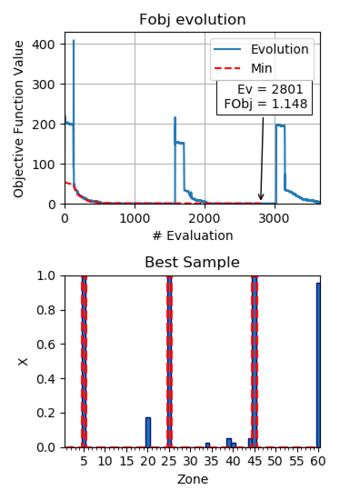
Figure 7: Results optimization with $60$ design variables

The damage in zones ${\textstyle 5}$, ${\textstyle 25}$ and ${\textstyle 45}$ of the reference damaged case are well captured, but, there are also significant damage values in zones ${\textstyle 60}$ and ${\textstyle 20}$, ${\textstyle 0.956}$ and ${\textstyle 0.175}$ respectively. The error in the remaining values is negligible, less than ${\textstyle 0.051}$. To obtain better results, the optimization algorithm needs more evaluations, but the obtained results can be considered acceptable, considering the difficulty of the problem.

5 Conclusions

In this paper a numerical model of offshore windmill FRP tower is presented and its dynamic behaviour is characterized by its natural frequencies and modal shapes. A reference damaged case of the tower is analysed. The sensitivity to damage of the natural vibration frequencies of the structure has been verified.

Also, a damage detection method is presented, based on optimization algorithms and model updating techniques. This method includes detection, localization and extension of the damage. Based on the comparison of the natural frequencies, ${\textstyle 2}$ cases are evaluated with different space discretization. One with the structure divided into ${\textstyle 10}$ zones to apply damage, while in the second scenario into ${\textstyle 60}$ zones. In both, satisfactory results were obtained. Its demonstrated that the proposed damage detection method could be used in SHM process for this kind of structures. These monitoring strategies periodically evaluates possibles structural damages, improving the operational safety of the structure and reducing its maintenance costs.

6 Acknowledgments

The founding of FIBREGY, “Development, engineering, production and life-cycle management of improved FIBRE-based material solutions for structure and functional components of large offshore wind enerGY and tidal power platform” an H2020 project under agreement 952966 is gratefully acknowledged.

BIBLIOGRAPHY

CIMNE (2020, Sep. 30, 2020). GiD. https://www.gidhome.com.

EU (2021-2023). H2020 952966 FIBREGY - Development, engineering, production and life-cycle management of improved FIBRE-based material solutions for structure and functional components of large offshore wind enerGY and tidal power platform. https://fibregy.eu/.

European Commission (2020). An eu strategy to harness the potential of offshore renewable energy for a climate neutral future. Technical report, Commision to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the regiions. https://eur-lex.europa.eu/legalcontent/EN/TXT/?uri=COM:2020:741:FIN&qid=1605792629666.

Johnson, S. G. (2020, Sep. 30, 2020). NLopt - the NonLinear - optimization package. http://github.com/stevengj/nlopt.

Kucherenko, S. & Y. Sytsko (2005). Application of Deterministic Low-Discrepancy Sequences in Global Optimization. Computational Optimization and Applications 30, 297–318.

Martinez, X., S. Oller, F. Rastellini, & A. Barbat (2008). A numerical procedure simulating RC structures reinforced with FRP using the serial/parallel mixing theory. Computers and Structures 86, 1604–1618.

Powell, M. (2009). The BOBYQA Algorithm for Bound Constrained Optimization without Derivatives. Technical report, Department of Applied Mathematics and Theoretical Physics.

Rinnooy Kan, A. H. G. & G. T. Timmer (1987a). Stochastic global optimization methods part I: Clustering methods. Mathematical Programming 39, 27–56.

Rinnooy Kan, A. H. G. & G. T. Timmer (1987b). Stochastic global optimization methods part II: Multi level methods. Mathematical Programming 39, 57–78.