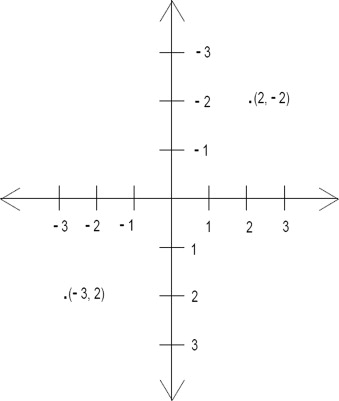Algorithm for constructing an optimally connected rectangular floor plan

Abstract

In most applications, such as urbanism and architecture, randomly utilizing given spaces is certainly not favorable. This study proposes an explicit algorithm for utilizing the given spaces inside a rectangle with satisfactory results. In the literature, connectivity is not considered as a criterion for floor plan design, but it is deemed essential in architecture. For example, dining rooms are preferably connected to kitchens, toilets should be connected to many rooms, and each bedroom should be separated from the other rooms. This paper describes adjacency among spaces and proves that the obtained rectangular floor plan is one of the best ones in terms of connectivity. An architectural and mathematical object called extra spaces is introduced by the proposed algorithm and is subsequently examined in this work.

Keywords

Floor plan ; Extra space ; Algorithm ; Adjacency

1. Introduction

The floor plan is the most fundamental architectural diagram. Similar to a map, it is an aerial view of the arrangement of spaces in a building but with focus on the arrangement at a particular level (floor). In architectural terms, an arrangement has two basic elements. The first element is geometry (position). The position of spaces is always considered when organizing them. Examples of geometric arrangements are furniture organized in the most functional way, the famous Rubik׳s Cube, and the arrangement of squares in the golden rectangle. The second essential element is the topology (similarity) of spaces. Elements with similar shapes, reactions, functions, and orientations or directions are often grouped together. For example, noble gases in the periodic table are arranged based on the chemical properties they share. In designing a house, architects place the dining room and kitchen close together. In the context of the present study, a floor plan is an aerial view of the arrangement of spaces and extra spaces (waste spaces) in a building.

Given spaces as well as extra spaces are important in a floor plan. For example, houses require extra spaces, such as storerooms and balconies. Therefore, the problem addressed in this study is establishing a way to arrange a finite collection of rectangular spaces of various sizes inside a rectangular frame in an optimal manner as well as introducing necessary additional space for filling given certain geometric or topological constraints.

The rectangular frame in the aforementioned problem is referred to as a rectangular floor plan denoted by ${\textstyle R^{F}}$ . The given spaces represent the different elements of a building, e.g., rooms, offices, kitchens, bathrooms, and toilets.

An algorithm is a step-by-step procedure or formula that is used to solve a problem. The literature describes several algorithms for constructing floor plans. Galle (1981) proposed an algorithm for generating rectangular plans on modular grids to provide a large number of possible solutions. Lai (1988) used graph theory for floor plan design in a study where the rectangular dualization problem was reduced to a matching problem on bipartite graphs. The dual graph of a plane graph G has a vertex corresponding to each face of G and an edge joining two neighboring faces for each edge in G . A plane graph can be embedded in the plane, i.e., it can be drawn in such a way that no edges cross each other. A plane graph is termed rectangular if each of its edges is oriented in either the horizontal or the vertical direction, each of its regions has exactly four sides, and the whole graph can fit a rectangular enclosure. A bipartite graph is a graph whose vertices can be divided into two independent sets, A and B , such that every edge (a , b ) connects either a vertex from A to B or a vertex from B to A . Stiny (2013) proposed the construction of floor plans using shape grammar. Shape grammar is a procedure for generating different geometric shapes. Terzidis (2007–08) developed a computer program called autoPLAN that generates architectural plans for the boundary and adjacency matrix of a given site.

Since ancient times, architectural forms composed of mathematical and geometrical relationships have generated great interest (Dabbour, 2012 ). In the present study, we propose an algorithm for the construction of a rectangular floor plan and use mathematical tools to prove that the obtained floor plan is optimally connected.

2. Constructing a rectangular floor plan

In this section, we provide an algorithm for constructing a rectangular floor plan called the spiral-based rectangular floor plan, which is denoted by ${\textstyle R_{S}^{F}}$ . A ${\textstyle R_{S}^{F}}$ with n   given spaces is termed as ${\textstyle R_{S}^{F}}$ of order n   and is denoted by ${\textstyle R_{S}^{F}(n)}$ .

2.1. Spiral-based sequence

The golden ratio, one of the keystones of sacred geometry, is related to the Fibonacci sequence, which is a numerical series where the next number is the sum of the previous two numbers (Dabbour, 2012 ). We use the Fibonacci sequence to obtain a “spiral-based sequence” that calculates the width and height of a spiral-based rectangular floor plan. Using this sequence, the width and height of ${\textstyle R_{S}^{F}}$ are calculated as follows:

• For odd i   , i.e., after drawing the 1st, 3rd, … spaces, the width of the obtained rectangular floor plan ${\textstyle R_{S}^{F}(i)}$ is the sum of the widths of ${\textstyle R_{S}^{F}(i-1)}$ and the i th space R_i , and the height of ${\textstyle R_{S}^{F}(i)}$ is the sum of the maximum heights of R_i and ${\textstyle R_{S}^{F}(i-1)}$ .
• For even i   , i.e., after drawing the 2nd, 4th, … spaces, the width of ${\textstyle R_{S}^{F}(i)}$ is the sum of the maximum widths of ${\textstyle R_{S}^{F}(i-1)}$ and R_i , and the height of ${\textstyle R_{S}^{F}(i)}$ is the sum of the heights of ${\textstyle R_{S}^{F}(i-1)}$ and R_i .

If l_i and h_i are the width and height, respectively, of R_i and if L_i and H_i are the width and height, respectively, of ${\textstyle R_{S}^{F}(i)}$ , then the spiral-based sequence is given numerically as follows:

• For i =1, 3, 5,…,

$L_{i}=L_{i-1}+l_{i},H_{i}=\quad max(H_{i-1},h_{i}).$

• For i =2, 4, 6,…,

$L_{i}=\quad max(L_{i-1},l_{i}),H_{i}=H_{i-1}+h_{i}.$

Here, L₀ =0, and H₀ =0.

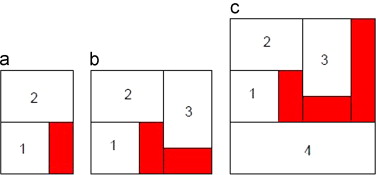
The concept of a spiral-based sequence is shown in Figure 1 , where the shaded rectangles represent the extra spaces, and the white rectangles represent the given spaces.

Figure 1. Calculating the width and height of a rectangular floor plan.

In Figure 1 (a), i =2. Therefore, we compute L₂ and H₂ . Here, ${\textstyle L_{2}=\quad max(L_{1},l_{2})=\quad max(l_{1},l_{2})=l_{2}}$ , and ${\textstyle H_{2}=H_{1}+h_{2}=h_{1}+h_{2}}$ .

In Figure 1 (b), a new space is added to the obtained ${\textstyle R^{F}(2)}$ . Hence, i =3, L₃ =L₂ +l₃ =l₂ +l₃ , and ${\textstyle H_{3}=\quad max(H_{2},h_{3})=\quad max(h_{1}+h_{2},h_{3})=h_{1}+}$$h_{2}$ .

In Figure 1 (c), i   =4, ${\textstyle L_{4}=\quad max(L_{3},l_{4})=\quad max(l_{2}+l_{3},l_{4})=l_{4}}$ , and ${\textstyle H_{4}=H_{3}+h_{4}=h_{1}+h_{2}+h_{4}}$ .

2.2. Spiral-based algorithm for obtaining a rectangular floor plan

In this algorithm, we draw the given spaces one by one. If the composition of the drawn spaces is rectangular with width L_i and height H_i after drawing each space R_i , then we draw the next space. Otherwise, we draw an extra space to obtain a rectangular composition ${\textstyle R_{S}^{F}(i)}$ with width L_i and height H_i .

Here, we consider three kinds of rectangles. Each type of rectangle is determined by its position, which in turn is determined by the upper left vertex. The size of the rectangle is determined by its width and height.

The first kind of rectangle is the new space R_i drawn at Stage i   of the construction process and whose position and size are denoted by ${\textstyle (x_{i},y_{i})}$ and the given pair ${\textstyle (l_{i},h_{i})}$ , respectively. ${\textstyle (x_{i},y_{i})}$ represents a point on a Cartesian plane, as depicted in Figure 2 . The Cartesian plane consists of a set of two perpendicular lines intersecting each other at origin (0,0). The horizontal line is the x -axis, and the vertical line is the y -axis. The location of any point on the Cartesian plane is denoted by an ordered pair (x ,y ), where x is the horizontal distance from the origin, and y is the vertical distance from the origin.

Figure 2. Cartesian plane for the position of rectangles.

The second kind of rectangle is extra space E_i , which may be empty. We denote its position by ${\textstyle (t_{i},u_{i})}$ and its size by the pair ${\textstyle ({\lambda }_{i},{\mu }_{i})}$ . In ${\textstyle R_{S}^{F}}$ , an extra space is a rectangle generated by the difference in either the widths or the heights of the spaces.

The last kind of rectangle is the new rectangular composition ${\textstyle R_{S}^{F}(i)}$ . Its position also depends on i   and is denoted by ${\textstyle (X_{i},Y_{i})}$ . The size of ${\textstyle R_{S}^{F}(i)}$ is the pair ${\textstyle (L_{i},H_{i})}$ .

The steps for constructing ${\textstyle R_{S}^{F}}$ are as follows:

Step 1: All the given spaces are arranged in the order of increasing areas, i.e., we start with the space that has the smallest area; the space with the greatest area is placed last.

Step 2: The process starts with i =0, with all numbers set to 0. The first space is then placed to the left of (0,0). For example, we draw R₁ with width l₁ and height h₁ at position ${\textstyle (x_{1},y_{1})}$ , as shown in Figure 3 .

Figure 3. Placing the first space.

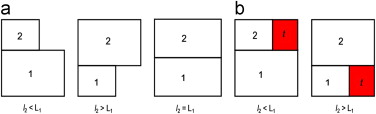
Step 3: R₂ is drawn above R₁ in such a way that its lower left vertex is the upper left vertex of ${\textstyle R_{S}^{F}(1)}$ , as shown in Figure 4 (a).

Figure 4. Placing the second space above the first space.

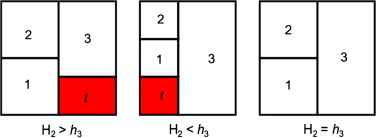
Given the difference between l₁ and l₂ , three cases are possible. An extra space is drawn if either l₂ >L₁ or l₂ <L₁ because the composition of spaces in both cases is not rectangular. To obtain ${\textstyle R_{S}^{F}(2)}$ , an extra space t is drawn, as shown in Figure 4 (b).

In general, if ${\textstyle i\equiv 1(mod\quad 4)}$ , then ${\textstyle (x_{i},y_{i})=(X_{i-1}-l_{i},Y_{i-1}),(X_{i},Y_{i})=(x_{i},y_{i})}$ , i.e., R_i is drawn to the left of ${\textstyle R_{S}^{F}(i-1)}$ in such a way that its upper right vertex is the upper left vertex of ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle h_{i}<H_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(x_{i},y_{i}+h_{i})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(l_{i},H_{i-1}-h_{i})}$ . An extra space is drawn below R_i and to the left of ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle h_{i}>H_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(X_{i-1},Y_{i-1}+H_{i-1})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(L_{i-1},h_{i}-H_{i-1})}$ . An extra space is drawn below ${\textstyle R_{S}^{F}(i-1)}$ and to the right of R_i .

Step 4: R₃ is drawn to the right of ${\textstyle R_{S}^{F}(2)}$ in such a way that its upper left vertex is the upper right vertex of ${\textstyle R_{S}^{F}(2)}$ .

The positioning of R₃ with extra space t is shown in Figure 5 . Illustrating all possible cases is not feasible. Hence, Figure 5 assumes that l₂ =l₁ .

Figure 5. Placing the third space to the right of the second space.

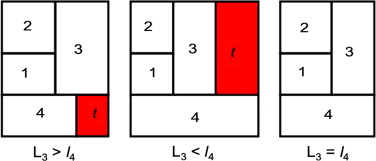
In general, if ${\textstyle i\equiv 2(mod\quad 4)}$ , then ${\textstyle (x_{i},y_{i})=(X_{i-1},Y_{i-1}-h_{i}),(X_{i},Y_{i})=(x_{i},y_{i})}$ , i.e., R_i is drawn above ${\textstyle R_{S}^{F}(i-1)}$ in such a way that its lower left vertex is the upper left vertex of ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle l_{i}<L_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(x_{i}+l_{i},y_{i})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(L_{i-1}-l_{i},h_{i})}$ . Here, an extra space is drawn to the right of R_i and above ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle l_{i}>L_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(X_{i-1}+L_{i-1},Y_{i-1})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(l_{i}-L_{i-1},H_{i-1})}$ . Here, an extra space is drawn to the right of ${\textstyle R_{S}^{F}(i-1)}$ and below R_i .

Step 5: R₄ is drawn below ${\textstyle R_{S}^{F}(3)}$ such that its upper left vertex is the lower left vertex of ${\textstyle R_{S}^{F}(3)}$ .

The construction of R₄ with an extra space t is shown in Figure 6 . In this figure, l₂ =l₁ and H₂ =h₃ are assumed; however, other possible scenarios also exist.

Figure 6. Placing the fourth space below the third space.

In general, if ${\textstyle i\equiv 3(mod\quad 4)}$ , then ${\textstyle (x_{i},y_{i})=(X_{i-1}+L_{i-1},Y_{i-1}),(X_{i},Y_{i})=(X_{i-1},Y_{i-1})}$ , i.e., R_i is drawn to the right of ${\textstyle R_{S}^{F}(i-1)}$ in such a way that its upper left vertex is the upper right vertex of ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle h_{i}<H_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(x_{i},y_{i}+h_{i})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(l_{i},H_{i-1}-h_{i})}$ . Here, an extra space is drawn below R_i and to the right of ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle h_{i}>H_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(X_{i-1},Y_{i-1}+H_{i-1})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(L_{i-1},h_{i}-H_{i-1})}$ . Here, an extra space is drawn below ${\textstyle R_{S}^{F}(i-1)}$ and to the left of R_i .

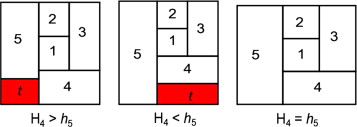
Step 6: R₅ is drawn to the left of ${\textstyle R_{S}^{F}(4)}$ in such a way that its upper right vertex is the upper left vertex of ${\textstyle R_{S}^{F}(4)}$ .

R₅ with an extra space t is shown in Figure 7 . For demonstration purposes, l₂ =l₁ , H₂ =h₃ , and L₃ =l₄ are taken into consideration, but other possible cases also exist.

Figure 7. Placing the fifth space to the left of the fourth space.

In general, if ${\textstyle i\equiv 0(mod\quad 4)}$ , then ${\textstyle (x_{i},y_{i})=(X_{i-1},Y_{i-1}+H_{i-1}),(X_{i},Y_{i})=(X_{i-1},Y_{i-1})}$ , i.e., R_i is drawn below ${\textstyle R_{S}^{F}(i-1)}$ in such a way that its upper left vertex is the lower left vertex of ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle l_{i}<L_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(x_{i}+l_{i},y_{i})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(L_{i-1}-l_{i},h_{i})}$ . Here, an extra space is drawn to the right of R_i and below ${\textstyle R_{S}^{F}(i-1)}$ .

If ${\textstyle l_{i}>L_{i-1}}$ , then ${\textstyle (t_{i},u_{i})=(X_{i-1}+L_{i-1},Y_{i-1})}$ , and ${\textstyle ({\lambda }_{i},{\mu }_{i})=(l_{i}-L_{i-1},H_{i-1})}$ . Here, an extra space is drawn to the right of ${\textstyle R_{S}^{F}(i-1)}$ and above R_i .

Step 7: Repeat Steps 3–6 until all the spaces are arranged.

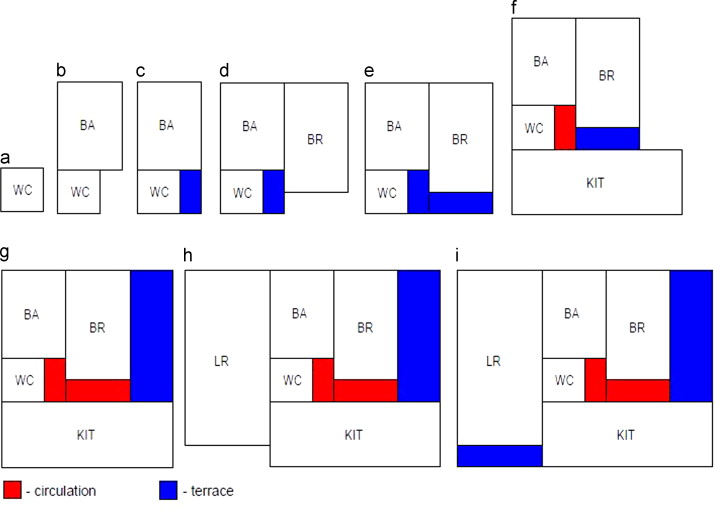
The steps of this algorithm clearly show that the spaces are arranged along a spiral, hence the name “spiral-based algorithm.” For an enhanced understanding of this algorithm, we use the following example. Consider five different spaces with the following widths and heights:

BR – bedroom (3×4), KIT – kitchen (6×4), BA – bathroom (2×3), WC (1.5×1.5), and LR – living room (5×8).

The construction of the spiral-based rectangular floor plan with the following spaces is shown in Figure 8 , where Figure 8 (i) indicates the required ${\textstyle R_{S}^{F}(5)}$ .

Figure 8. Step-by-step construction of a spiral-based rectangular floor plan for the given spaces.

In a rectangular floor plan, an extra space adjacent to the outside is considered a terrace; otherwise, it is a circulation. A terrace is an outdoor living space or a storeroom, and a circulation refers to the way people move through and interact within a house. The circulations and terraces are marked in Figure 8 . In this figure, the extra spaces in some sub-figures have been initially considered as terraces, but they have been marked subsequently as circulations.

2.3. Seven additional spiral-based rectangular floor plans

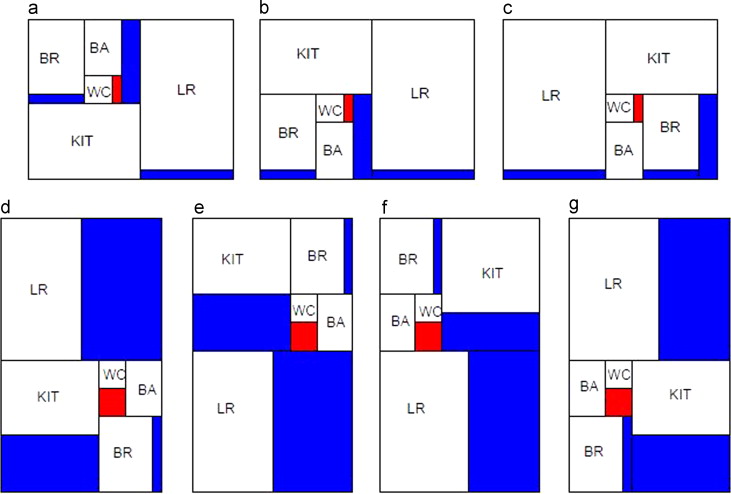
Seven additional spiral-based rectangular floor plans can be obtained by slightly changing the spiral-based algorithm (Section 2.2 ) as follows:

• By considering the anticlockwise movement as a replacement for the clockwise movement (e.g., refer to Figure 9 [a])

Figure 9. Seven different spiral-based rectangular floor plans.

• By interchanging the positions of R₁ and R₂ in the above step and then following the clockwise movement (e.g., refer to Figure 9 [b])
• By considering the anticlockwise movement in the above step (e.g., refer to Figure 9 [c])
• By positioning R₁ and R₂ side by side in the spiral-based algorithm and then following the clockwise movement (e.g., refer to Figure 9 [d])
• By considering the anticlockwise movement in the above step (e.g., refer to Figure 9 [e])
• By interchanging the positions of R₁ and R₂ in Step 4 and then following the clockwise movement (e.g., refer to Figure 9 [f])
• By considering the anticlockwise movement in the above step (e.g., refer to Figure 9 [g])

In Figure 9 , we consider the same spaces as those in the example in Section 2.2 .

3. Connectivity of a rectangular floor plan

3.1. Adjacency among the spaces

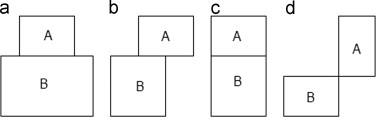
A wall is one side of a rectangle. If W is a wall with side length j , a sub-wall of W is a properly connected part of W . Hence, a closed interval of length k is strictly included in W , i.e., 0<k <j . Two rectangles are adjacent if they share a wall or a sub-wall. Figure 10 illustrates the concept of adjacency for rectangles A and B. In Figure 10 (a) and (c), A and B share a wall; in Figure 10 (b), A and B share a sub-wall; in Figure 10 (d), A and B share neither a wall nor a sub-wall. Hence, in Figure 10 , A is adjacent to B in cases a, b, and c but not in case d.

Figure 10. Four cases that define adjacency among rectangles.

The adjacency graph of a rectangular floor plan is a simple undirected graph obtained by representing each space as a vertex and then drawing an edge between any two vertices if the corresponding spaces are adjacent (Gross, 2006 ). The adjacency graph of the spiral-based rectangular floor plans obtained in Figure 8  ;  Figure 9 is shown in Figure 11 .

Figure 11. Graph of the eight spiral-based rectangular floor plans.

3.2. Optimally connected rectangular floor plan

The degree of connectivity of a rectangular floor plan is defined by the adjacency among the different spaces and is given in terms of the connectivity of the corresponding adjacency graph. Therefore, the connectivities of different rectangular floor plans are compared based on the connectivities of the corresponding adjacency graphs.

Several measures can be used to compare the connectivity of two graphs (Rodrigue et al., 2006 ). In this study, we consider the number of edges as a measure of connectivity. If two connected adjacency graphs have the same number of vertices, then the adjacency graph with many edges is considered to be closely connected.

Let n   be the number of spaces in a rectangular floor plan or the number of vertices in the corresponding graph. For a ${\textstyle R_{S}^{F}(n)}$ , the number of edges in the corresponding graph when n >3 is equal to 3n –7 ( Shekhawat, 2013 ; Theorem 3.13); this theorem has been proven mathematically. In Figure 10 , n =5; hence, the number of edges is equal to 3n   –7=3×5–7=8. For any ${\textstyle R^{F}(n)}$ , the number of edges in the corresponding graph when n >3 is always less than 3n −6 ( Shekhawat, 2013 ; Theorem 3.24); this theorem has also been proven mathematically.

Based on the results above, we can deduce that any graph of a rectangular floor plan cannot have more than 3n –7 edges and that the graph of a spiral-based rectangular floor plan has exactly 3n –7 edges. Therefore, the spiral-based rectangular floor plan is one of the best rectangular floor plans in terms of connectivity.

4. Conclusion and future work

A spiral-based rectangular floor plan starts from the smallest space, i.e., the smallest space is always at the center of a floor plan. In a house, toilets are among the smallest spaces, and users want these rooms to be in the center and connected to a maximum number of spaces. Moreover, the position of extra spaces indicates the position of the doors.

In this work, we constructed eight different spiral-based rectangular floor plans that offer a number of choices to users. The results revealed that spiral-based rectangular floor plans are the best in terms of connectivity. For our future work, we can use the concept of spiral-based rectangular floor plans to construct other floor plans of different shapes.

A number of extra spaces are known to exist in a rectangular floor plan. As far as applications are concerned, extra spaces are valuable, but their sizes must be reduced. In the future, we will find methods for reducing the sizes of extra spaces to maintain connectivity and the number of extra spaces.

References

1. Dabbour, 2012 Dabbour; Geometric proportions: the underlying structure of design process for Islamic geometric patterns; Front. Archit. Res. (2012), pp. 382–383
2. Galle, 1981 Galle; An algorithm for exhaustive generation of building floor plans; Commun. ACM, 24 (12) (1981), pp. 813–825
3. Gross, 2006 Yellen Gross; Graph Theory and Its Applications; (second ed.)Chapman & Hall/CRC, Boca Raton (2006)
4. Lai, 1988 Leinwand Lai; Algorithms for floorplan design via rectangular dualization; IEEE Trans. Comput. Aided Des., 7 (12) (1988), pp. 1278–1289
5. Rodrigue et al., 2006 Rodrigue, Comtois, Slack; The Geography of Transport Systems; Routledge, New York (2006)
6. Shekhawat and Rectangle, 2013 Shekhawat, Rectangle Tilings, Connectivity and Associated Covariants, Thèse no. 4570, 2013, Section de Mathématiques, Université de Genève, Genève.
7. Stiny Stiny; Shape (Talking about Seeing and Doing); The MIT Press, Cambridge (2013)
8. Terzidis, 2007–08 Terzidis; AutoPLAN: a stochastic generator of architectural plans from a building program; form\cdotZ Jt. Study J. (2007–08), pp. 84–85