Flaw-Bridging in Composite Materials

1 Introduction

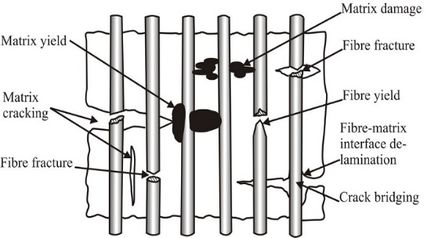
The reinforcement of a brittle matrix by fibres is a fundamental concept in the theory of composite materials. Although fibre-reinforcement is intended to enhance the strength and deformability characteristics of a composite, the processes of defect development in composites can range from matrix damage, fibre-matrix interface delamination, fibre fracture, matrix cracking, fibre yield, etc. (Fig. 1). The brittle matrix usually consists of epoxies, resins and other cementitious materials that are prone to development of micro-mechanical defects, which can result in the development of discrete fractures at the macro-scale

In instances where the damage to the matrix also results in damage to the fibres, the defect will simply constitute a crack and the stress states at the extremities of these defects can be examined by appeal to the conventional theory of fracture mechanics applicable to either anisotropic or transversely isotropic elastic media [1-3]. When the matrix experiences damage leading to a crack but the fibres remain intact, it results in a process referred to as fibre-bridging. The topic of crack bridging has been investigated by a number of authors and extensive discussions and references to these developments are given in [4-12]. The continuity of the fibre exerts a kinematic constraint across the matrix crack, changing the mechanics of the crack and, in particular, the stress intensity factor at the crack tip. This paper examines the basic problem of a circular bridged penny-shaped crack that is located at the interior of a fibre-reinforced composite.

Figure 1. Defects in a uni-directionally fibre-reinforced composite.

2 Elastic behaviour of unidirectionally reinforced composites

We consider the problem of a unidirectonally fibre-reinforced composite consisting of isotropic elastic fibres embedded in an isotropic elastic matrix. The spatial arrangement of the fibres is assumed to be such that there is regular separation between the fibres. In reality the fibres could experience irregular spacing including contact between fibres that can contribute to inadequate contiguity, resulting in generation of defects. Despite these limitations, the effective elastic behaviour of the unidirectionally fibre-reinforced composite can be modelled as a transversely isotropic elastic material where the plane of isotropy is normal the direction of the aligned unidirectional fibres. Referring to the axisymmetric cylindrical polar coordinate system ${\textstyle \left(r,z\right)}$ it can be shown (Green and Zerna [13]) that the displacement and stress fields in the transversely isotropic elastic medium can be expressed in terms of two functions ${\varphi }_{\alpha }(r,z){\mbox{ }}(\alpha =1,2)$ , which are solutions of

$\left({\frac {{\partial }^{2}}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial }{\partial r}}+\right.\left.{\frac {{\partial }^{2}}{\partial z_{\alpha }^{2}}}\right){\varphi }_{\alpha }(r,z)=0$

(1)

where $z_{\alpha }=z/{\sqrt {{\nu }_{\alpha }}}$ and ${\nu }_{\alpha }$ are the roots of the characteristic equation

$c_{11}c_{44}{\nu }^{2}+\left\{c_{13}(2c_{44}+c_{13})-\right.\left.c_{11}c_{33}\right\}\nu +c_{33}c_{44}=0$

(2)

In (2), $c_{ij}$ are the elastic constants of the transversely isotropic elastic model of the unidirectionally fibre reinforced solid. These elastic constants can be expressed in terms of the isotropic elastic constants of the fibre and the matrix phases and their respective volume fractions. These expressions are given by Hashin and Rosen [14]. The displacement and stress fields in the transversely isotropic elastic material that are relevant to the formulation of the bridged crack problem can be expressed in terms of ${\varphi }_{\alpha }(r,z){\mbox{ }}$ .

3 The penny-shaped bridged crack

Penny-shaped cracks with displacement-dependent traction boundary conditions on the crack faces were first examined by Atkinson [15] using an iterative technique. We examine the problem of a penny-shaped matrix crack that is located in a unidirectional fibre-reinforced material, where the fibres exhibit continuity across the faces of the crack.

This assumption gives rise to a displacement constraint, which is derived from a fibre that has a finite length at the crack tip. The axisymmetric bridged crack problem can be formulated in relation to a halfspace region, where the surface of the halfspace region is subjected to mixed boundary conditions

(3) $u_{z}(r,0)=0{\mbox{ }},{\mbox{ }}b\leq r<\infty$ (4) ${\sigma }_{zz}(r,0)=-p^{\ast }(r)+{\frac {E_{f}V_{f}}{l}}u_{z}(r,0){\mbox{ }};{\mbox{ }}0<r<b$ (5) ${\sigma }_{rz}(r,0)=0{\mbox{ }};{\mbox{ }}0\leq r\leq \infty$

(5)

where $p^{\ast }(r)$ is the tensile traction induced on the plane $z=0$ of the intact composite due to the action of the external stress state. For the analysis of the mixed boundary value problem posed by (3) to (5), we seek solutions of (1), which are based on Hankel transform developments (Sneddon [16], Selvadurai [17]). The relevant solutions that satisfy the regularity conditions applicable to a halfspace region are

${\varphi }_{i}(r,z)={\frac {1}{b^{2}}}{\int }_{{\mbox{ }}0}^{{\mbox{ }}\infty }\xi {\mbox{ }}A_{i}(\xi ){\mbox{ }}e^{-{\eta }_{i}z}{\mbox{ }}J_{0}(\xi r/b){\mbox{ }}d\xi$

(6)

where $A_{i}(\xi )$ are arbitrary functions and ${\eta }_{i}=\xi /b{\sqrt {{\nu }_{i}}}$ . The mixed boundary conditions (3) to (5) can be reduced to a system of dual integral equations for a single unknown function. Using a finite Fourier transform, we can further reduce the dual system to a single Fredholm integral equation of the second-kind for an unknown function $\Phi (t)$ , which takes the form:

$\Phi (t)-{\frac {\beta }{\pi }}{\int }_{{\mbox{ }}0}^{{\mbox{ }}1}K(t,\tau ){\mbox{ }}\Phi (\tau ){\mbox{ }}d\tau =$$g(t)$

(7)

where the kernel function $K(t,\tau )$ is given by

$K(t,\tau )=2{\int }_{{\mbox{ }}0}^{{\mbox{ }}\infty }{\vartheta }^{-1}sin(\vartheta t){\mbox{ }}sin(\vartheta \tau ){\mbox{ }}d\vartheta$

(8)

The constant $\beta$ depends on the elasticity of the composite and the function $g(t)$ depends only on the nature of the axisymmetric external loading. For example, when the composite is subjected to a uniform tensile stress field at infinity

$g(t)=t$

(9)

It should be noted that the function $\Phi (t)$ will contain a multiplier that takes into account the magnitude and nature of the loading. The mathematical analysis of the bridged penny-shaped crack problem (for $t\in {\mbox{ }}{\mbox{real}}$ and $\tau \in {\mbox{ }}{\mbox{real}}$ ) is formally reduced to the solution of the integral equation

$\Phi (t)-{\frac {\beta }{\pi }}{\int }_{{\mbox{ }}0}^{{\mbox{ }}1}{log}_{e}\left({\frac {t+\tau }{t-\tau }}\right){\mbox{ }}\Phi (\tau ){\mbox{ }}d\tau =g(t){\mbox{ }};{\mbox{ }}t>\tau \geq 0$

(10)

The solution of (10) provides results of importance to the idealized bridged penny-shaped crack with a bridged region of constant length $2l$ over the entire crack surface. The result of particular interest to fracture mechanics of composites relates to the Mode I stress intensity factor at the crack tip, defined by

${\mbox{K}}_{\mbox{I}}={\underset {r\rightarrow b^{+}}{\mbox{Lim}}}{\mbox{ }}{\left[2(r-b)\right]}^{1/2}{\sigma }_{zz}(r,0)$

(11)

Considering the result for the axial stress expressed in terms of $\Phi (t)$ , it can be shown that for a penny-shaped crack in a unidirectional fibre reinforced material with crack bridging and subjected to a uniform far-field axial stress ${\sigma }_{0}$ ,

${\mbox{K}}_{\mbox{I}}={\frac {2{\mbox{ }}{\sigma }_{0}{\sqrt {b}}}{\pi }}\Phi (1)$

(12)

In the limiting case when the elasticity of the bridging fibres $E_{f}\rightarrow 0$ , $\beta \rightarrow 0$ and we have a penny-shaped crack located in a matrix with unidirectional cavities where originally there were fibres. Since the resulting material is still transversely isotropic and $\Phi (1)=1$ , the expression (12) gives

${\mbox{K}}_{\mbox{I}}={\frac {2{\mbox{ }}{\sigma }_{0}{\sqrt {b}}}{\pi }}$

(13)

which is the classical result [1-3]. Consider the limiting case when the unidirectional fibre-reinforced material is reinforced with inextensible fibres (i.e. $E_{f}\rightarrow \infty$ ): This is an idealization that was proposed by Adkins and Rivlin [18] and successfully developed and extended by Spencer [19,20] and others (see e.g. [12]).

In the limit of fibre inextensibility, the integral equation (10) reduces to

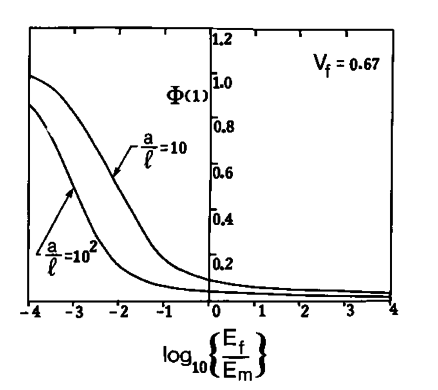
${\int }_{{\mbox{ }}0}^{{\mbox{ }}1}{log}_{e}\left({\frac {t+\tau }{t-\tau }}\right){\mbox{ }}\Phi (\tau ){\mbox{ }}d\tau =0$$0$ (14) which has a trivial solution $\Phi (t)=0$ . Consequently, ${\mbox{K}}_{\mbox{I}}\equiv 0$ , and the stress intensity factor is completely suppressed. For arbitrary values of the elastic properties of the fibre-reinforced composite, the integral equation (10) has a non-degenerate solution. There appears to be no closed form solution of this equation and the Fredholm integral equation can be solved using quadrature techniques that reduce the integral equation to a matrix equation [21-23]. Details of the method are well documented in the literature [24-27]). Figure 2 illustrates the influence of the fibre-matrix elastic modular ratio and the geometry of the bridging zone on the Mode I stress intensity factor for the bridged penny-shaped crack. It is evident that as the fibre-matrix modular ratio increases and the bridging region geometry in terms of the fibre length decreases, the Mode I stress intensity factor for the bridged penny-shaped crack decreases. The general modelling approach for examining bridging action at penny-shaped flaws subjected to loading by a dipole of forces is presented in [5] and a similar problem for the bridged external circular crack is given in [11]. Analogous results for the case of the bridged plane crack are also presented in [9].

Variational procedures that assign displacement fields in the bridged región that take into consideration the limiting cases of complete fibre felxibility and fibre inextensibility can be used to examine the mechanics of bridged cracks. Such variational techniques have been successfully adopted for the solution of complex mixed boundary value problems in contact mechanics [29-33].

Figure 2. The influence of flaw bridging and bridging length on the stress intensity factor at the tip of the penny-shaped crack.

4 Conclusions

Flaw-bridging in composite materials can influence the development of stress intensity factors at crack tips. The paper considers a relatively straighforward problem where the bridging by intact fibres occurs across a penny-shaped crack. The loading of the composite is restricted to situations where the Mode I stress intensity factor is examined. The bridging action has a significant influence in suppressing the Mode I Stress Intensity factor at the tip of the penny-shaped crack. For most fibre reinforced composites, the fibre-matrix modular ratio can be in excess of $(E_{f}/E_{m})>>{10}^{4}$ , which would suggest that the Mode I stress intensity factor can be almost completely suppressed.

Acknowledgements

The work described in this paper was supported by a Discovery Grant awarded by the Natural Sciences and Engineering Research Council of Canada and the James McGill Research Chairs Program.

References

[1] H. Liebowitz (Ed.) Fracture Vols. !-V, Academic Press, NY (1968)

[2] I.N. Sneddon, M. Lowengrub, Crack Problems in the Classsical Theory of Elasticity, John Wiley, NY (1969)

[3] G.C. Sih (Ed.), Mechanics of Fracture Vols. I-V, Noordhoff International, Leyden

[4] A.P.S. Selvadurai, Proceedings of the International Symposium on Mechanics of Structured Media, Developments in Mechanics, Elsevier Scientific Publ., Amsterdam 5A: 59-72. (1981)

[5] A.P.S. Selvadurai, International Journal of Fracture 21:149-159 (1983)

[6] A.P.S. Selvadurai, Journal of Applied Mathematics and Physics 34:51-64(1983)

[7] A.P.S. Selvadurai, Journal of Engineering Materials and Technology, ASME 119:398-402 (1994)

[8] A.P.S. Selvadurai, M.C. Au, B.M. Singh Journal of Applied Mechanics, ASME 118:639-649 (1996)

[9] A.P.S. Selvadurai, Advances in Boundary Element Techniques (A.P.S. Selvadurai, C.L. Tan and M.H. Aliabadi, Eds.), EIC Ltd, 89-94 (2005)

[10] A.P.S. Selvadurai, Journal of Engineering Mathematics 68: 5-14 (2010)

[11] A.P.S. Selvadurai, Composite Structures 92:1512-1516 (2010)

[12] A.P.S. Selvadurai, Journal of Engineering Mathematics 95:359–380 (2015)

[13] A. E. Green, W. Zerna, Theoretical Elasticity, Clarendon Press, Oxford (1968)

[14] Z. Hashin, B.W. Rosen, Journal of Applied Mechanics, ASME 31:223–232 (1964)

[15] C. Atkinson, International Journal of Fracture 6:193–198 (1970)

[16] I.N. Sneddon, Fourier Transforms, McGraw-Hill, NY (1951)

[17] A.P.S. Selvadurai, Partial Differential Equations in Mechanics. Vol. 2. The Bi-harmonic Equations, Poisson’s Equation, Springer Verlag, Heidelberg (2000)

[18] J.E. Adkins, R.S. Rivlin, Philosophical Transactions of the Royal Society, A 248:201–223 (1955)

[19] A.J.M. Spencer, Deformations of Fibre-Reinforced Materials, Clarendon Press, Oxford (1970)

[21] A.J.M. Spencer, International Journal of Solids and Structures 10:1103–1123 (1974)

[22] C.T.H. Baker, The Numerical Treatment of Integral Equations, Clarendon Press, Oxford (1977)

[23] L.M. Delves, J.L. Mohamed, Computational Methods for Integral Equations, Cambridge University Press, Cambridge (1985)

[24] K.E. Atkinson, The Numerical Solution of Integral Equations of the Second-Kind, Cambridge University Press, Cambridge (1996)

[25] A.P.S. Selvadurai, International Journal for Numerical and Analytical Methods in Geomechanics 17: 343-353 (1993)

[26] A.P.S. Selvadurai, Journal of Engineering Mathematics 37: 155-170 (2000)

[27] A.P.S. Selvadurai, International Journal of Geomechanics 1: 149-174 (2001)

[28] A.P.S. Selvadurai, International Journal of Solids and Structures 39:6035-6053 (2002)

[29] A.P.S. Selvadurai, Journal of Structural Mechanics 7: 231-246 (1979)

[30] A.P.S. Selvadurai, International Journal for Numerical and Analytical Methods in Geomechanics 3: 285-292 (1979)

[31] A.P.S. Selvadurai, International Journal of Solids and Structures 16:167-176 (1980)

[32] A.P.S. Selvadurai, Acta Materialia 55: 4679-4687 (2007)

[33] A.P.S. Selvadurai, N.A. Dumont, Journal of Elasticity 105: 253-269 (2011)