Considering functional dimensioning in architectural design

Abstract

This paper presents an overview of the functional dimensioning (FD) concept applied to the construction sector. FD addresses the issue of tolerance; construction involves several trades working together while each trade has its own construction tolerances. To investigate this problem, three case studies are investigated. The first one describes a classic case of a window in a bay and the way constructors solved the resulting tolerance problems. The second case study describes the notion of chain dimension. The last case study presents the notion of wedge as a solution to solve problems related to tolerance gap accumulation. This paper is of interest to the scientific community that is working to industrialize the construction sector and also to architects (in the design), construction managers (onsite), and manufacturers (construction trades).

Keywords

Tolerance ; Architecture ; Construction ; Dimensioning ; Quotation

1. Introduction

Functional dimensioning (FD) is a dimensioning system designed to define the dimensions of an element so that its function (e.g., sliding of the piston in its support or a drawer) can be ensured regardless of the incoming part and the receiving one. Another definition by Ciurana et al. (2003 ) is the selection of the correct dimension and tolerance to optimize the parts according to the definition of the mechanical assembly for their functional purpose.

Until the end of the nineteenth century, production could be realized without a deep understanding of FD. Drawings were exploited without an advanced level of details unlike in today׳s industry (Campbell, 2004 ), especially with the advent of product flexibility and customization needs of the client (Khalili-Araghi and Kolarevic, 2016 ). The questions related to product fabrication tolerances were first investigated after the mass production of the Ford Model T; industrialization was launched hand in hand with product quality control. Now that precision is compulsory for different industries (nanoprecision), software is now used to solve complex geometrical tolerance problems (Islam, 2004  ;  Khajehdehi and Panahshahi, 2016 ).

One may wonder why the construction has not adopted such a concept because in many cases, “know-how” knowledge contains results that come from experience, and such results could support an FD reasoning. In their paper, Cavalaro et al. (2012 ) investigate a complex construction: concrete tunnels. The latter is composed of several elements, and each element has its own tolerance limits, thereby making global construction difficult to assess.

The construction industry is moving toward a more industrialized process. The advent of lean construction in the 1990s (Koskela, 1992 ) was a turning point in how construction is seen. Lean construction is a philosophy adopted from the Toyota Production System, which aims to eliminate waste (physical and information) throughout the construction value chain while maximizing value to the client. Directly copying the applications from manufacturing would not be feasible because of the differences between the two industries (Tezel and Nielsen, 2013 ). Ballard and Howell (1993 ) pointed out the challenges faced by the construction industry and found that more than 40% of tasks scheduled weekly onsite were not realized. A real concern with regard to the productivity of the construction sector was raised (Park et al ., 2005  ;  Tucker, 1986 ).

Many studies investigated tolerance issues in construction under the lean construction perspective (Alexandridis and Gardner, 1992 ; Iwashita et al ., 2012  ;  Milberg and Tommelein, 2010 ). Milberg and Tommelein (2003 ) explored tolerance problems of partition walls and found that geometric tolerances related to products and processes can have negative effects on project outcomes. A proposed solution to mitigate risks is the use of maps. Milberg and Tommelein (2005 ) explained, “Tolerance maps are a tool for specifying, analyzing and allocating tolerances for both product and process design.”

With the changes made by building information modeling (BIM) in the way construction is designed, the construction sector should clearly consider FD and begin to incorporate this way of reasoning in various stages of design. The “as-built” concept is now investigated through BIM (Woo et al., 2010 ) to match the design to construction as accurately as possible while resolving design issues upstream.

2. Concept of tolerance in construction

Architectural engineering and construction introduced the concept of tolerance according to the different existing trades:

• The mason works with a +/−10 mm tolerance.
• The carpenter works with a +/−5 mm tolerance.
• Some trades have lower tolerances.

Every construction trade must respect the tolerances because they are part of the professional “know-how” and the expected quality (cf. DTU and best practices).

However, are current efforts sufficient? What is happening in reality?

The performance required for each trade corresponds to the potential performance observed in the execution phase at the worksite. In the next section of the paper, we introduce FD by following these steps:

• Identifying the functional dimensioning challenges induced during the design phase;
• Exploring how the experience of contractors helped envision potential solutions.

To illustrate the situation, we consider three case studies. The first one is a classic case encountered in building construction: an element designed to fit into a reservation in the wall. The second case study deals with tolerance problems related to bathroom construction. The last part investigates FD and design by using an elevator case study.

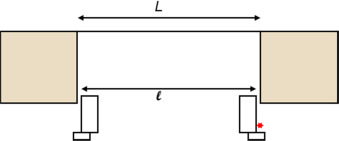
2.1. Case study 1: Window in the bay

We will consider a window in a 900 mm × 900 mm bay (Fig. 1 ). The carpenter has 900 mm and the mason has 900 mm for the structural work for the bay. According to 36.5, 2010  ;  P18-201, 2004 ), each of the two trades have the following tolerances:

• +/−10 mm for concrete (in the extension for the bay);
• +/−5 mm for carpentry.

Fig. 1. Window (L ) and bay׳s (l ) dimensions.

The results of the minimum and maximum dimensions are presented in Table 1 .

Table 1. Minimum and maximum length for the bay and the window according to DTU code.

	Length+ tolerance	Minimal length (mm)	Maximal length (mm)
Bay	L =900+/−10 mm	Lmin =890	Lmax =910
Window	l =900+/− 5 mm	lmin =895	lmax =905

The bays can range from 890 mm to 910 mm. The windows can range from 895 mm to 905 mm. This result generates a dimensioning problem. Large windows that measure 905 mm do not fit in the small bays of 890 mm; a 15 mm (10 mm+5 mm) gap exists.

Using this example, we showed that the gap between the largest window and the narrowest bay is equal to the sum of tolerances of the carpenter and the mason (10 mm+5 mm).

In a practical way, we will ask the most accurate trade (i.e., the carpenter) to dimension his work to avoid conflict with the mason׳s tolerances. The mason will continue to dimension the 900 mm bay while knowing that the expected produced bays could range from 890 mm to 910 mm.

The carpenter can start from this assertion to make sure that his largest window (5 mm more than the targeted dimension) can fit into the smallest bay that could be produced (890 mm).

The targeted dimension will then be 890 mm−5 mm =885 mm.

We note that 885 mm is 900–10 mm (mason tolerance) −5 mm (carpenter tolerance), which brings us to the following result:

The mason, with his 900 mm bay, will produce bays 890–910 mm wide. The carpenter targeted a length of 885 mm; therefore, he will produce a window with a length that ranges from 880 mm to 890 mm (Table 2 ).

Table 2. Minimum and maximum length for the bay and the window after reviewing tolerances.

	Length+ tolerance	Minimal length (mm)	Maximal length (mm)
Bay	L =900+/−10 mm	Lmin =890	Lmax =910
Window	l =885 +/− 5 mm	lmin =880	lmax =890

Large windows that measure 890 mm fit in the small bays of 890 mm. The maximum clearance between a large bay and a small window will be 30 mm; (5 mm+10 mm) × 2 is the sum of total tolerances.

The produced windows could fit into any encountered bay. However, a play exists between the window and the bay, with the largest play game being 30 mm. This play may be distributed left or right; therefore, a cover joint of 15 mm in each side is expected for sealing purposes. The use of joinery (Eq. (1) ) is an example of a well-known solution used in practice to overcome FD challenges.

$30\quad mm/2=15\quad mm+the\quad desired\quad recovery$

( 1)

This example shows that errors add up in absolute values (Eq. (2) ).

$\Delta (L-l)=\Delta L+\Delta l$

( 2)

Eq. (2) could be generalized as follows:

If we use X_max =X +ΔX for the greatest tolerance and Y_min =Y −ΔY for the smallest tolerance, then the total tolerance is

$X_{max}-Y_{min}=\Delta X+\Delta Y$

( 3)

Examples of construction applications that can use FD include but are not limited to

• Windows or doors and their cover seals.
• False ceiling plates and rails.
• Plinth tiles of bank.
• The bath between two walls and tiles.

3. Notion of chain dimension

We have seen a case of an object made by a trade and a receptacle made by another trade and how conflicts can be prevented by a simple dimensioning. Now the situation to be addressed is one in which multiple elements are placed in a container. We investigate the case of a bathroom with a bathtub, a sink, a washing machine, and the turning radius of a wheelchair. This example is common because it is encountered in each apartment/house. Moreover, the case is of educational interest: bathroom walls are the receptacle, while the washing machine, sink, and bathtub are the constituent parts of the function “bathroom,” and the condition related to the chair׳s radius of gyration will be a “functionality condition.” For this scheme to work properly, the manufactured container (with its dimensional tolerance) should be able to fit the constituent parts of the function (with their dimensional constraints) while respecting the functionality condition.

3.1. Case study 2: Bathroom

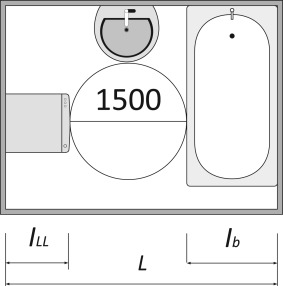
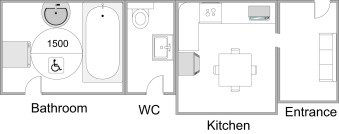
Fig. 2 presents the function (bathroom) and its constituent parts (a bathtub, a sink, and a washing machine) and the functionality condition (radius of a wheelchair).

Fig. 2. Function (bathroom) and its constituent parts (bathtub, a sink, and a washing machine) and the functionality condition (radius of a wheelchair).

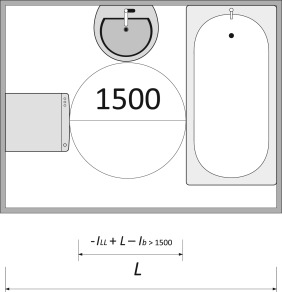
Knowing that the remaining distance for the turning circle must be greater than 1500 mm, the functionality condition (Fig. 3 ) could be written as follows:

$L-l_{LL}-l_{b}>1500\quad mm$

( 4)

Fig. 3. Functionality condition of the bathroom.

In the case of a larger element in the smallest container (i.e., the worst scenario),

$L_{min}-l_{LLmax}-l_{bmax}>1500$

( 5)

The functionality condition is written as follows:

$L_{min}-l_{LLmax}-l_{bmax}>1500$

( 6)

which could be written as

$L-\Delta L-(l_{LL}+\Delta l_{LL})-(l_{b}+\Delta l_{b})>1500$

( 7)

$L>1500+l_{LL}+l_{b}+\Delta l_{LL}+\Delta L+\Delta l_{b}$

( 8)

If we take l_LL =600 mm and l_b =600 mm with a +/−5 mm tolerance, then

≪ L ≫ should be superior to 1500+1200+10+5+5=2720 mm.

Errors are additive, which means that the receptacle (function) dimension must include the sum of the constituent parts tolerances.

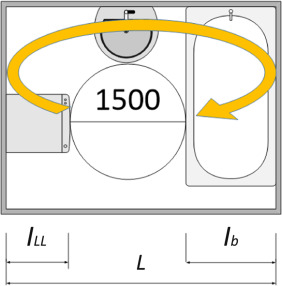
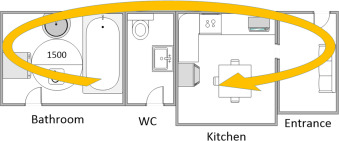
The functionality condition (Eq. (4) ) therefore constitutes what we can call the chain dimension (Fig. 4 ).

Fig. 4. Chain dimension of the bathroom.

The treatment applied in the bathroom for the length of the room should be duplicated for the width. Once completed, we obtain the FD of the bathroom.

4. Concept of wedge

The concept of wedge consists of creating a referenced fixed point with a known tolerance and an enhanced control.

In this part, we discuss how to minimize tolerance issues when different elements are superposed. The following example consists of a kitchen, a toilet, a bathroom, and an entrance as presented in Fig. 5 .

Fig. 5. Assembled elements: a kitchen, a toilet, a bathroom, and an entrance.

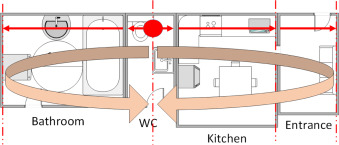
Knowing that each element has its own dimensional constraints, the overall length of the elements will come out with a tolerance (min/max) according to the precedent affirmation “errors add up” (Fig. 6 ). This total tolerance is expected to be great, which is problematic.

Fig. 6. Sum of tolerance of each element should theoretically constitute the total tolerance.

This problem could be solved using the concept of wedge. The issue now is how the position of this point is chosen in construction.

We will choose as a fixed point (wedge) the position of the rising column in the water closet (WC) for example (Fig. 7 ) because this point should be referred to in the different floors and have some verticality as well.

Fig. 7. Choice of the fixed point (wedge) in the position of the rising column in WC.

An important detail to note that the wedge itself has its own tolerance. The wedge is a reference point, which means that the objective is to come up with relative tolerances for other elements so that they can be built next to each other. Doing so ensures that the chain dimension (and the gaps) is (are) divided by two, and we create a fixed reference point per floor.

The dimensioning of plans should take into account this design choice. The position of the wedge will be listed, and the dimensioning of the elements will be calculated as a consequence.

5. FD and design

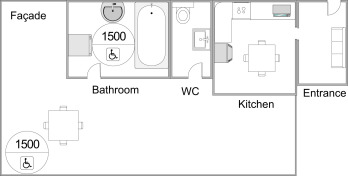
In the case of housing, the issue to be addressed is how wedge points are positioned and what dimension to use. Therefore, we will first build upon the precedent case study: a zone that constitutes an area of damp rooms, including the entrance. Façades inherently include manufactured elements with different tolerances. The next step is to constitute a group façade with a wedge in a corner. The room with the constraint linked to the disabled population will be examined in this corner. These dispositions create two distinct groups, and between these two groups, dimensions will be free of tolerance constraints. We therefore obtain the following operating principle in Fig. 8 :

Fig. 8. Use of two wedges for two groups: damp rooms and façades.

Using this example, we set the first base for the elements of housing. The next part deals with a building composed of five floor levels that contain four apartments each.

The apartments will be assembled around an ascending point composed of a staircase, an elevator, sleeves, and bearings. This set (duct + elevator + stairs + bearing) constitutes a group. Each element of the set needs to be dimensioned while taking into account each element׳s size constraints.

In this set, we consider only the case of the elevator. The latter is made up of the following elements:

• A cabin with its rails and calibrations in a duct
• A landing door attached to the cabin on each floor with a window in the shell of the elevator shaft with a finishing trim

In this case study, we are interested in the finishing trim.

5.1. Case study 3: Elevator

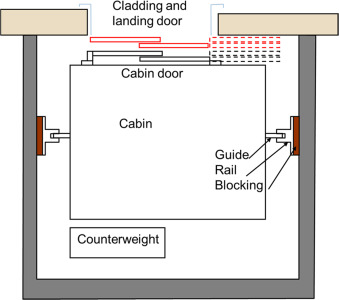
The case study (Fig. 9 ) is composed of the following characteristics:

• The landing door in the bay with its finishing appears to be a classic case.
• The cabin in its cage can appear as a classic case, too. The cage׳s width must be greater than the cabin׳s width.

Fig. 9. Elevator components.

The sum of the cage construction tolerances on one hand and jig/rail/guide tolerances on the other hand constitute the maximum and minimum gaps and thus help in dimensioning the wedges.

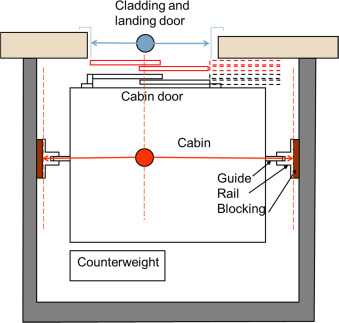
The situation is not different, except that tolerances will be checked on every floor and the elevator contractor will encounter a distribution gap and is thus obliged to choose a midpoint position of his cabin in the cage.

This point will be a single wedge (a point itself is a position of tolerance determined retrospectively and with a clear calculation method) that sets the calculation point tolerances for each floor (Fig. 10 ).

Fig. 10. Design of a wedge for the elevator case study.

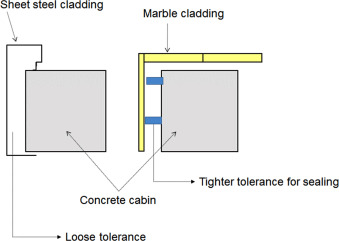
We will consider a reference point of floor bay tolerances with its own tolerance as a basis for calculating the bay and the side cladding panels. As tolerance gaps add up, the calculation incorporates the sum of the point position tolerances of the bay and the cabin door. This problem could be solved with stainless steel trim. Such a design ensures that the gaps in tolerance can be absorbed easily. However, such absorption becomes more difficult with marble cladding (Fig. 11 ).

Fig. 11. Sheet steel and marble claddings.

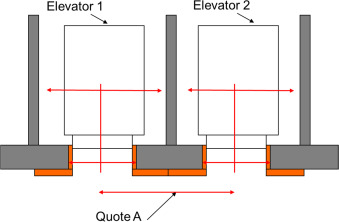
In the case of two neighboring elevators on the landing (Fig. 12 ), the problem could be made even more difficult to solve by reversing the constraint dimensions. Creating working drawings of marble finishing can reverse the problem.

Fig. 12. Case of two neighboring elevators.

Fig. 12 explains this phenomenon as follows: marble drawings makes the dimension between cabin axes predominant.

Quote A shown in Fig. 12 will be subjected to the precision of the stone mason, the stone seal, and the landing side door of the elevator (a few mm). This dimension will guide the windows’ design. The wedging in the ducts is relatively easy.

With the example of the elevator, we could also build the argument that integrates vertical tolerances of technical ducts. Referring to the DTU structural code to analyze tolerances allowed in width dimension and verticality (DTU indicates a height of 5 mm and a width of 10 mm), the acceptable dimensions under the tolerances allowed for duct construction by the structural contractor can be defined.

The axis taken by the elevator contractor should be an acceptable median axis because of its verticality and could be different from the theoretical axis that was determined in the design phase.

FD helps to calculate positions and determine the correct manufacturing dimensions for each trade.

6. Conclusion

By relying on elementary case studies in the design and construction phases, we demonstrated the potential use and mastery of FD in the construction sector. We detailed how dimensioning could account for tolerances and therefore give construction stakeholders the correct manufacturing dimensions. We also introduced the concept of chain dimension, which states that the dimensioning is the result of a desired functionality.

The notion of wedge and its position that was fixed during the design phase will guide the dimensioning system for each floor level and provide guidance during the construction phase. The elevator׳s case study suggests an additional opportunity offered by FD.

BIM will provide all the results needed by the profession (quality improvement, built-in quality) and therefore save time and money. All the stakeholders involved in the design phase need to acquire solid knowledge of FD techniques. These techniques range from simple ones (considering tolerance to establish a dimension) to more advanced ones (the dimensioning system and the notion of wedge, among others).

References

1. 36.5, 2010 36.5, N.D., 2010. NF DTU 36.5 – Travaux de bâtiment – Mise en oeuvre des fenêtres et portes extérieures. France.
2. Alexandridis and Gardner, 1992 A. Alexandridis, N.J. Gardner; Tolerance limits for geometric imperfections in hyperbolic cooling towers; J. Struct. Eng., 118 (1992), pp. 2082–2100 http://doi.org/10.1061/(ASCE)0733-9445(1992)118:8(2082)
3. Ballard and Howell, 1993 G. Ballard, G.A. Howell; Lean project management; Int. J. Proj. Manag., 11 (1993), pp. 3–4 http://doi.org/10.1016/0263-7863(93)90002-5
4. Campbell, 2004 R.G. Campbell; Integrated product design and manufacturing using geometric dimensioning and tolerancing; Ind. Robot Int. J., 31 (2004), pp. 375–376 http://doi.org/10.1108/ir.2004.31.4.375.2
5. Cavalaro et al., 2012 S.H.P. Cavalaro, C.B.M. Blom, A. Aguado, J.C. Walraven; New design method for the production tolerances of concrete tunnel segments; J. Perform. Constr. Facil., 26 (2012), pp. 824–834 http://doi.org/10.1061/(ASCE)CF.1943-5509.0000291
6. Ciurana et al., 2003 J. Ciurana, C. Riba, M.L.G. Romeu; Implementation of unidirectional functional dimensioning and tolerancing algorithm in CAD systems; Integr. Manuf. Syst., 14 (2003), pp. 468–476 http://doi.org/10.1108/09576060310477870
7. Islam, 2004 M.N. Islam; Functional dimensioning and tolerancing software for concurrent engineering applications; Comput. Ind., 54 (2004), pp. 169–190 http://doi.org/10.1016/j.compind.2003.09.006
8. Iwashita et al., 2012 T. Iwashita, J.A. Packer, J.-C. de Oliveira; Defect tolerance for cast steel connections in braced frames; J. Struct. Eng., 138 (2012), pp. 1455–1464 http://doi.org/10.1061/(ASCE)ST.1943-541X.0000583
9. Khajehdehi and Panahshahi, 2016 R. Khajehdehi, N. Panahshahi; Effect of openings on in-plane structural behavior of reinforced concrete floor slabs; J. Build. Eng., 7 (2016), pp. 1–11 http://doi.org/10.1016/j.jobe.2016.04.011
10. Khalili-Araghi and Kolarevic, 2016 S. Khalili-Araghi, B. Kolarevic; Development of a framework for dimensional customization system: a novel method for customer participation; J. Build. Eng., 5 (2016), pp. 231–238 http://doi.org/10.1016/j.jobe.2016.01.001
11. Koskela, 1992 L. Koskela; Application of the new production philosophy to construction; Tech. Rep. (1992), pp. 37–62
12. Milberg and Tommelein, 2005 C., D. Milberg, I. Tommelein; Application of tolerance mapping in AEC systems; I. D. Tommelein (Ed.), Construction Research Congress 2005: Broadening Perspectives, American Society of Civil Engineers, San Diego, California (2005), pp. 1–10
13. Milberg and Tommelein, 2003 Milberg, C., Tommelein, I., 2003. Application of tolerance analysis and allocation in work structuring: partition wall case, In: Proceedings of the 11th Annual Conference of the International Group for Lean Construction. Virginia, USA.
14. Milberg and Tommelein, 2010 C.T. Milberg, I.D. Tommelein; Tolerance and constructability of soldier piles in slurry walls; J. Perform. Constr. Facil., 24 (2010), pp. 120–127 http://doi.org/10.1061/(ASCE)CF.1943-5509.0000079
15. P18-201, 2004 P18-201, N., 2004. NF P18-201 – DTU 21 – Travaux de bâtiment – Exécution des ouvrages en béton. France.
16. Park et al., 2005 H.-S. Park, S.R. Thomas, R.L. Tucker; Benchmarking of construction productivity; J. Constr. Eng. Manag., 131 (2005), pp. 772–778 http://doi.org/10.1061/(ASCE)0733-9364(2005)131:7(772)
17. Tezel and Nielsen, 2013 A. Tezel, Y. Nielsen; Lean construction conformance among construction contractors in Turkey; J. Manag. Eng., 29 (2013), pp. 236–250 http://doi.org/10.1061/(ASCE)ME.1943-5479.0000145
18. Tucker, 1986 R.L. Tucker; Management of construction productivity; J. Manag. Eng., 2 (1986), pp. 148–156 http://doi.org/10.1061/(ASCE)9742-597X(1986)2:3(148)
19. Woo et al., 2010 J. Woo, J. Wilsmann, D. Kang; Use of as-built building information modeling; J. Ruwanpura, Y. Mohamed, S. Lee (Eds.), Construction Research Congress 2010: Innovation for Reshaping Construction Practice., American Society of Civil Engineers, Banff, Albert (2010), pp. 538–548