Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions

Abstract

In this paper we report on combined Dufour and Soret effects on the heat and mass transfer in a Casson nanofluid flow over an unsteady stretching sheet with thermal radiation and heat generation. The effects of partial slip on the velocity at the boundary, convective thermal boundary condition, Brownian and thermophoresis diffusion coefficients on the concentration boundary condition are investigated. The model equations are solved using the spectral relaxation method. The results indicate that the fluid flow, temperature and concentration profiles are significantly influenced by the fluid unsteadiness, the Casson parameter, magnetic parameter and the velocity slip. The effect of increasing the Casson parameter is to suppress the velocity and temperature growth. An increase in the Dufour parameter reduces the flow temperature, while an increase in the value of the Soret parameter causes increase in the concentration of the fluid. Again, increasing the velocity slip parameter reduces the velocity profile whereas increasing the heat generation parameter increases the temperature profile. A validation of the work is presented by comparing the current results with existing literature.

Keywords

Casson nanofluid; Navier slip; Soret and Dufour parameters; Spectral relaxation method

1. Introduction

The concept of nanofluids was introduced by Choi [1] where he proposed the suspension of nanoparticles in a base fluid such as water, oil, and ethylene glycol. Buongiorno [2] attempted to explain the increase in the thermal conductivity of such fluids and developed a model that took into account the particle Brownian motion and thermophoresis.

Noghrehabadi et al. [3] investigated the effects of the slip boundary condition on the heat transfer characteristics for a stretching sheet subjected to convective heat transfer in the presence of nanoparticles. They found that the flow velocity and the surface shear stress on the stretching sheet are strongly influenced by the slip parameter with a decrease in the momentum boundary layer thickness and increase in thermal boundary layer thickness. Khan and Pop [4] studied the problem of laminar fluid flow which results from a stretching of a flat surface in a nanofluid. They analyzed the development of the steady boundary layer flow, heat transfer and nanoparticle volume fraction over a stretching surface in the nanofluid. They observed that the reduced Nusselt number decreased while the reduced Sherwood number increased with the parameters considered in the study. They further obtained linear regression estimations in terms of Brownian and thermophoresis parameters for both the reduced Nusselt and Sherwood numbers. Nadeem et al. [5] studied two-dimensional boundary layer flow and heat transfer in steady incompressible Oldroyd-B nanofluid due to a stretching sheet. They showed that an increase in the Brownian motion parameter reduced the local Nusselt number while the local Sherwood number increased. Makinde et al. [6] studied the combined effects of buoyancy force, convective heating, Brownian motion, thermophoresis and a magnetic field on stagnation point flow and heat transfer due to a nanofluid flow from a stretching/shrinking sheet under the assumption that the magnetic Reynolds number was small. Their results showed that dual solutions exist for the shrinking case and an increase in the buoyancy force reduced both the skin friction coefficient and the local Sherwood number while the local Nusselt number increased. Haroun et al. [7] studied the heat and mass transfer in magnetohydrodynamic mixed convection flow of a nanofluid over an unsteady stretching/shrinking sheet. The flow considered was subject to a heat source and viscous dissipation. Soret and Dufour effects were assumed to be significant. They further assumed that the nanoparticle volume fraction at the wall could be actively controlled. The resulting fluid model equations were solved using the spectral relaxation method, an accurate technique for solving nonlinear boundary value problems. Recently, Haroun et al. [8] investigated magnetohydrodynamic nanofluid flow past an impulsively stretching surface with a chemical reaction and an applied magnetic field using the spectral relaxation method.

Casson fluid is classified as a non-Newtonian fluid due to its rheological characteristics in relation to the shear stress–strain relationship. It behaves like an elastic solid at low shear strain and above a critical stress value, it behaves like a Newtonian fluid. A Casson fluid can best be described as a shear thinning liquid with infinite viscosity at zero shear rate, and zero viscosity at an infinite rate of shear. Some common examples of liquids that exhibit Casson fluid characteristics include tomato sauce, honey, soup, orange juice and human blood.

Mustafa et al. [9] used the homotopy analysis method of solution to study the boundary layer flow of a Casson fluid near the stagnation-point on a stretching surface and presented results for the limiting case when the Casson parameter tends to infinity. Mustafa et al. [10] studied the momentum and thermal boundary layer development in a Casson fluid flow over a semi-infinite flat plate when both the ambient fluid and the flat plate are impulsively set in motion at the same time and the temperature of the flat plate is suddenly raised from that of the surrounding fluid. They derived parabolic partial differential equations which were solved analytically using the homotopy analysis method. Nandy [11] investigated the hydromagnetic boundary layer flow and heat transfer in a non-Newtonian Casson fluid with a stagnation point over a stretching surface in the presence of velocity and thermal slip boundary condition and the results indicated that the flow and temperature fields were greatly affected by the slip parameters on the velocity and thermal boundary conditions respectively. Makanda et al. [12] considered two-dimensional flow and diffusion of a chemically reactive species in Casson fluid from an unsteady stretching surface in the presence of magnetic field. It was generally noted that increasing the magnetic and permeability parameters reduced the velocity profiles, the coefficient of heat transfer and the concentration profiles while the skin friction increased. Bhattacharyya [13] considered two-dimensional magnetohydrodynamic stagnation point flow of an electrically conducting Casson fluid and heat transfer due to a stretching sheet under the effect of thermal radiation. They pointed out that the velocity boundary layer thickness for Casson fluid is larger than that of Newtonian fluids due to the plasticity of the Casson fluid. Mukhopadhyay et al. [14] studied Casson fluid flow over an unsteady stretching surface by extending the earlier work of Andersson et al. [15]. Hayat et al. [16] presented Soret and Dufour effects on two-dimensional flow of a Casson fluid induced by a stretching surface that is electrically conducting. They used the homotopy analysis method to solve the nonlinear system of ordinary differential equations. Nadeem [17] studied magnetohydrodynamic three dimensional Casson fluid flow past a porous linearly stretching sheet and they concluded that due to viscosity effects, the Newtonian fluid has less friction at the wall compared to the non-Newtonian fluid. Bhattacharyya [18] obtained analytical solutions for magnetohydrodynamic boundary layer flow of Casson fluid over a permeable stretching/shrinking sheet with wall mass transfer. Nadeem et al. [19] investigated the magnetohydrodynamic boundary layer flow of a Casson fluid over an exponentially permeable shrinking sheet. Nadeem et al. [20] discussed enhancement in the heat and mass transfer of a three dimensional magnetohydrodynamic Casson nanofluid and adjusted the hot fluid along the lower surface of the wall by introducing a convective boundary condition. They showed that a Newtonian nanofluid produces low skin friction at the wall compared to the Casson nanofluid and that there is low thermal conductivity for a higher Prandtl numbers. Mukhopadhyay [21] examined the effects of thermal radiation on Casson fluid flow and heat transfer over an unsteady stretching surface subjected to suction/blowing and they concluded that the Prandtl number can be used to increase the rate of cooling in the Casson fluid flow, temperature profile is intensified with increase in the radiation parameter, while the Casson parameter reduced the momentum boundary layer thickness and enhanced the thermal boundary layer thickness. Raju et al. [22] analyzed the flow, heat and mass transfer behavior of a Casson fluid past an exponentially permeable stretching surface in the presence of thermal radiation, a magnetic field, viscous dissipation, a heat source and chemical reaction, and they showed that increasing the heat source parameter reduced the temperature profiles in the boundary layer.

Recently, Kuznetsov and Nield [23] revisited their model on the natural convective boundary layer flow of a nanofluid over a vertical plate by including the effects of Brownian motion and thermophoresis. For the new model they argued that the nanofluid particle fraction at the boundary should be passively rather than actively controlled in order for the model to be physically realistic. This recent boundary condition provides one of the motivations for the present research.

The study of unsteady flow of Casson nanofluid has not been given much consideration so far. The aim of this paper is to study the fluid flow, heat and mass transfer in a Casson nanofluid, the Casson fluid being the base fluid. The traditional Casson nanofluid model is revised to include the effect of thermophoresis and Brownian motion. In this paper we have studied the effects of various parameters (such as Soret, Dufour, thermal radiation, heat generation and unsteadiness parameters) on the fluid flow, heat and mass transfer profiles with Navier slip and thermal convective boundary conditions. The model equations are solved using the spectral relaxation method proposed by Motsa [24]. The spectral relaxation method has the characteristics of fast convergence and good accuracy as shown in some recent studies (see [25] and [26]). We give qualitative and quantitative comparisons with previously published work to show that our results are accurate.

2. Governing equations and boundary conditions

Consider the unsteady two-dimensional laminar flow and heat transfer of an incompressible Casson nanofluid past a stretching sheet with stretching velocity ${\textstyle u(x{\mbox{,}}t)=cx/(1-\lambda t)}$, where ${\textstyle c>0{\mbox{,}}\quad \lambda \geqslant 0}$ are constants and t   is time. The unsteady stretching surface has a uniform temperature and nanoparticle concentration ${\textstyle T_{w}}$ and ${\textstyle C_{w}}$ respectively. The temperature and nanoparticle concentration far from the surface is ${\textstyle T_{\infty }}$ and ${\textstyle C_{\infty }}$ respectively.

The rheological equation of state for an isotropic and incompressible flow of a Casson fluid is expressed (see [11] and [27]) as:

${\tau }_{ij}={\begin{array}{ll}2\left(k_{c}+{\frac {{\tau }_{0}}{\sqrt {2\pi }}}\right)e_{ij}&if\quad \pi >{\pi }_{c}\\2\left(k_{c}+{\frac {{\tau }_{0}}{\sqrt {2{\pi }_{c}}}}\right)e_{ij}&if\quad \pi <{\pi }_{c}{\mbox{,}}\end{array}}$

(1)

where

$e_{ij}={\frac {1}{2}}\left({\frac {\partial u_{i}}{\partial x_{j}}}+\right.$$\left.{\frac {\partial u_{j}}{\partial x_{i}}}\right){\mbox{,}}$

(2)

is the rate of strain tensor, ${\textstyle {\tau }_{ij}}$ is the component of stress tensor, ${\textstyle k_{c}}$ is the Casson coefficient of viscosity, ${\textstyle \pi =e_{ij}e_{ij}}$ is the product of the rate of strain tensor with itself, ${\textstyle {\pi }_{c}}$ is the critical value of the product of the rate of strain tensor with itself, ${\textstyle {\tau }_{0}}$ is the yield stress of the fluid and ${\textstyle u_{i}}$ are the velocity components. It is assumed that both temperature and concentration at the surface vary with distance and time from the origin, thus the temperature ${\textstyle T_{w}}$ and concentration ${\textstyle C_{w}}$ at the surface are given by:

$T_{w}(x{\mbox{,}}t)=T_{\infty }+{\frac {{bx}^{2}}{{\left(1-\lambda t\right)}^{2}}}{\mbox{,}}\quad C_{w}(x{\mbox{,}}t)=$$C_{\infty }+{\frac {b_{1}x^{2}}{{\left(1-\lambda t\right)}^{2}}}$

(3)

where b   and ${\textstyle b_{1}}$ are constants. It should be noted that the expressions ${\textstyle u_{w}(x{\mbox{,}}t){\mbox{,}}T_{w}(x{\mbox{,}}t)}$, and ${\textstyle C_{w}(x{\mbox{,}}t)}$ are valid only for time ${\textstyle t<{\lambda }^{-1}}$, but not when ${\textstyle \lambda =0}$.

The continuity, momentum, energy and concentration equations of the unsteady incompressible Casson nanofluid boundary layer flow are as follows (see [11]):

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0{\mbox{,}}$

(4)

${\frac {\partial u}{\partial t}}+u{\frac {\partial u}{\partial x}}+$$v{\frac {\partial u}{\partial y}}=U{\frac {dU}{dx}}+\nu \left(1+\right.$$\left.{\frac {1}{\beta }}\right){\frac {{\partial }^{2}u}{\partial y^{2}}}+$${\frac {\sigma B_{0}^{2}}{\rho }}(U-u){\mbox{,}}$

(5)

${\frac {\partial T}{\partial t}}+u{\frac {\partial T}{\partial x}}+$$v{\frac {\partial T}{\partial y}}={\frac {k_{0}}{\rho c_{p}}}{\frac {{\partial }^{2}u}{\partial y^{2}}}+$${\frac {\nu }{c_{p}}}\left(1+{\frac {1}{\beta }}\right){\left({\frac {\partial u}{\partial y}}\right)}^{2}+$${\frac {\sigma B_{0}^{2}}{\rho }}{\left(U-u\right)}^{2}-{\frac {1}{\rho c_{p}}}{\frac {\partial q_{r}}{\partial y}}+$${\frac {Q_{0}}{\rho c_{p}}}(T-T_{\infty })+\tau \left[D_{B}{\frac {\partial C}{\partial y}}{\frac {\partial T}{\partial y}}+\right.$$\left.{\frac {D_{T}}{T_{\infty }}}{\left({\frac {\partial T}{\partial y}}\right)}^{2}\right]+$${\frac {D_{m}k_{0}}{c_{s}c_{p}}}{\frac {{\partial }^{2}C}{\partial y^{2}}}{\mbox{,}}$

(6)

${\frac {\partial C}{\partial t}}+u{\frac {\partial C}{\partial x}}+$$v{\frac {\partial C}{\partial y}}=D_{B}{\frac {{\partial }^{2}C}{\partial y^{2}}}+$${\frac {D_{T}}{T_{\infty }}}{\frac {{\partial }^{2}T}{\partial y^{2}}}+$${\frac {D_{m}k_{0}}{T_{m}}}{\frac {{\partial }^{2}T}{\partial y^{2}}}{\mbox{,}}$

(7)

where u and v are the velocity components along the x- and y  -directions, respectively, ${\textstyle \nu }$ is the kinematic Casson fluid viscosity, ${\textstyle \rho }$ is the density of the fluid, ${\textstyle \sigma }$ is the electrical conductivity, ${\textstyle B_{0}}$ is the uniform magnetic field along y  -axis, ${\textstyle c_{p}}$ is the specific heat at constant pressure and ${\textstyle \beta =k_{c}{\sqrt {2{\pi }_{c}}}/{\tau }_{0}}$ is the non-Newtonian Casson parameter. ${\textstyle k_{0}}$ is the thermal diffusivity, ${\textstyle q_{r}}$ is the radiation heat flux, ${\textstyle Q_{0}}$ is the heat generation constant, ${\textstyle \tau ={\left(\rho c\right)}_{p}/{\left(\rho c\right)}_{f}}$ is the ratio of the heat capacity of the nanoparticle material and the heat capacity of the fluid, ${\textstyle D_{B}}$ is the Brownian diffusion coefficient, ${\textstyle D_{T}}$ is the thermophoretic diffusion coefficient, ${\textstyle D_{m}}$ is the mass diffusivity, ${\textstyle c_{s}}$ is the concentration susceptibility, and ${\textstyle T_{m}}$ is the mean temperature.

The dimensional boundary conditions are:

${\begin{array}{rl}&u=u_{w}(x{\mbox{,}}t)+u_{slip}(x{\mbox{,}}t){\mbox{,}}\quad v=0{\mbox{,}}\quad -k^{_{\ast }}{\frac {\partial T}{\partial y}}=h_{f}(T_{w}-T){\mbox{,}}\\&D_{B}{\frac {\partial C}{\partial y}}+{\frac {D_{T}}{T_{\infty }}}{\frac {\partial T}{\partial y}}=0\quad at\quad y=0{\mbox{,}}\end{array}}$

(8)

$u\rightarrow U(x{\mbox{,}}t)={\frac {ax}{1-\lambda t}}{\mbox{,}}\quad {\frac {\partial u}{\partial y}}\rightarrow 0{\mbox{,}}\quad T\rightarrow T_{\infty }{\mbox{,}}\quad C\rightarrow C_{\infty }\quad as\quad y\rightarrow \infty {\mbox{,}}$

(9)

where

$u_{w}(x{\mbox{,}}t)={\frac {cx}{1-\lambda t}}{\mbox{,}}\quad u_{slip}(x{\mbox{,}}t)=$$L\nu {\frac {\partial u}{\partial y}}\quad and\quad L=$$N{\left(1-\lambda t\right)}^{\frac {1}{2}}{\mbox{,}}$

(10)

is the slip velocity factor, ${\textstyle k^{_{\ast }}=k_{0}{\left(1-\lambda t\right)}^{\frac {1}{2}}}$ is the thermal conductivity and ${\textstyle h_{f}}$ is the convective heat transfer coefficient.

We introduce the stream function ${\textstyle \psi }$ defined in the usual way in terms of the velocity components, a similarity variable ${\textstyle \eta }$ and the following similarity transformations;

${\begin{array}{rl}&\eta ={\sqrt {\frac {c}{\nu (1-\lambda t)}}}{\mbox{,}}\quad \psi ={\sqrt {\frac {c\nu }{\left(1-\lambda t\right)}}}\quad x\quad f(\eta ){\mbox{,}}\quad T_{w}=T_{\infty }+{\frac {{bx}^{2}}{{\left(1-\lambda t\right)}^{2}}}\quad \theta (\eta ){\mbox{,}}\\&C_{w}=C_{\infty }+{\frac {b_{1}x^{2}}{{\left(1-\lambda t\right)}^{2}}}\quad \phi (\eta ){\mbox{.}}\end{array}}$

(11)

where ${\textstyle f(\eta ){\mbox{,}}\theta (\eta )}$ and ${\textstyle \phi (\eta )}$ are the non-dimensional velocity, temperature and concentration respectively. Substituting into Eqs. (4), (5), (6) and (7), gives the non-dimensional equations;

$\left(1+{\frac {1}{\beta }}\right)f^{'''}+{ff}^{''}-$$f^{{'}2}-A\left(f^{'}+{\frac {\eta }{2}}f^{''}\right)+$${\alpha }^{2}+M(\alpha -f^{'})=0{\mbox{,}}$

(12)

${\frac {1}{Pr}}\left(1+N_{R}\right){\theta }^{''}-A\left(2\theta +\right.$$\left.{\frac {\eta }{2}}{\theta }^{'}\right)-2f^{'}\theta +$$f{\theta }^{'}+He\theta +Nt{\theta }^{{'}2}+Nb{\theta }^{'}{\phi }^{'}+$$\left(1+{\frac {1}{\beta }}\right){Ecf}^{{''}2}+MEc{\left(\alpha -f^{'}\right)}^{2}+$$Df{\phi }^{''}=0{\mbox{,}}$

(13)

${\phi }^{''}-Sc\left[A(2\phi +{\frac {\eta }{2}}{\phi }^{'})+\right.$$\left.2f^{'}\phi -f{\phi }^{'}-Sr{\theta }^{''}\right]+$${\frac {Nt}{Nb}}{\theta }^{''}=0{\mbox{,}}$

(14)

subject to the boundary conditions

$f(0)=0{\mbox{,}}\quad f^{'}(0)=1+\delta f^{''}(0){\mbox{,}}\quad f^{'}(\infty )=$$\alpha {\mbox{,}}\quad f^{''}(\infty )=0{\mbox{,}}$

(15)

${\theta }^{'}(0)=-Bi(1-\theta (0)){\mbox{,}}\quad \theta (\infty )=$$0{\mbox{,}}$

(16)

$Nb{\phi }^{'}(0)+Nt{\theta }^{'}(0)=0{\mbox{,}}\quad \phi (\infty )=$$0{\mbox{,}}$

(17)

where differentiation is with respect to ${\textstyle \eta }$ and ${\textstyle A=\lambda /c}$ is the unsteadiness parameter, ${\textstyle \alpha =a/c}$ is the dimensionless velocity ratio parameter, ${\textstyle M={\frac {\sigma B^{2}}{c\quad \rho }}}$ is the magnetic parameter, ${\textstyle Pr=\nu \rho c_{p}/k_{0}}$ is the Prandtl number, ${\textstyle Sc=\nu /D_{B}}$ is the Schmidt number, ${\textstyle He=Q/c\quad \rho c_{p}}$ is the heat generation parameter, ${\textstyle Nb=\tau D_{B}(C_{w}-C_{\infty })/\nu }$ is the Brownian motion parameter, ${\textstyle Nt=\tau D_{T}(T_{w}-T_{\infty })/\nu T_{\infty }}$ is the thermophoresis parameter, ${\textstyle Df={\frac {D_{m}k_{0}(C_{w}-C_{\infty })}{c_{s}c_{p}\nu (T_{w}-T_{\infty })}}}$ is the Dufour number, ${\textstyle N_{R}={\frac {16{\sigma }^{_{\ast }}T_{\infty }^{3}}{3k^{_{\ast }}\nu \rho c_{p}k_{0}}}}$ is the radiation parameter, ${\textstyle Ec=c^{2}/{bc}_{p}}$ is the Eckert number, ${\textstyle Sr={\frac {D_{m}k_{0}(T_{w}-T_{\infty })}{T_{m}\nu (C_{w}-C_{\infty })}}}$ is the Soret number, ${\textstyle \delta =N{\sqrt {c\nu }}}$ is the dimensionless velocity slip parameter and ${\textstyle Bi={\sqrt {\nu /c}}\quad h_{f}/k_{0}}$ is the Biot number.

3. Method of solution

In this section, the spectral relaxation method (SRM) is used to solve the nonlinear differential Eqs. (12), (13) and (14). The SRM algorithm (see [24], [25] and [26]) first decouples the system of equations and an iteration scheme is then developed from the decoupled equations by evaluating linear terms at the current iteration level ${\textstyle r+1}$. To use this method, we first reduce the order of the equations as follows;

$f_{r+1}^{'}=g_{r}{\mbox{,}}\quad f_{r+1}(0)=0{\mbox{,}}$

(18)

$\left(1+{\frac {1}{\beta }}\right)g_{r+1}^{''}+\left(f_{r+1}-\right.$$\left.A{\frac {\eta }{2}}\right)g_{r+1}^{'}-(A+M)g_{r+1}=$$g_{r}^{2}-{\alpha }^{2}-M\alpha {\mbox{,}}$

(19)

${\frac {1}{Pr}}\left(1+N_{R}\right){\theta }_{r+1}^{''}+$$\left(f_{r+1}-A{\frac {\eta }{2}}+Nb{\phi }_{r}^{'}\right){\theta }_{r+1}^{'}-$$2g_{r+1}{\theta }_{r+1}-(2A-He){\theta }_{r+1}=-Nt{\theta }_{r}^{{'}2}-$$\left(1+{\frac {1}{\beta }}\right)Ec\quad g_{r+1}^{{'}2}-$$MEc{\left(\alpha -g_{r+1}\right)}^{2}-Df{\phi }_{r}^{''}{\mbox{,}}$

(20)

${\phi }_{r+1}^{''}+Sc\left(f_{r+1}-A{\frac {\eta }{2}}\right){\phi }_{r+1}^{'}-$$2{Scg}_{r+1}{\phi }_{r+1}-2ASc{\phi }_{r+1}=-(SrSc+$$Nt/Nb){\theta }_{r+1}^{''}{\mbox{,}}$

(21)

subject to

$g_{r+1}(0)=1+\delta g_{r+1}^{'}(0){\mbox{,}}\quad g_{r+1}(\infty )=$$\alpha {\mbox{,}}\quad g_{r+1}^{'}(\infty )=0{\mbox{,}}$

(22)

${\theta }_{r+1}^{'}(0)=-Bi(1-{\theta }_{r+1}(0)){\mbox{,}}\quad {\theta }_{r+1}(\infty )=$$0{\mbox{,}}\quad Nb{\phi }_{r+1}^{'}(0)+Nt{\theta }_{r+1}^{'}(0)=$$0{\mbox{,}}{\phi }_{r+1}(\infty )=0{\mbox{.}}$

(23)

Eqs. (18), (19), (20), (21) and (22) are solved using the Chebyshev pseudo-spectral method [24]. The unknown functions are defined by Chebyshev interpolating polynomials with Gauss–Lobatto points defined by

${\xi }_{i}=cos{\frac {\pi i}{N}}{\mbox{,}}\quad i=0{\mbox{,}}1{\mbox{,}}\ldots {\mbox{,}}N{\mbox{;}}\quad -$$1\leqslant \xi \leq 1{\mbox{,}}$

(24)

where N   is the number of collocation points used. The semi-infinite domain is approximated by the truncated domain ${\textstyle \left[0{\mbox{,}}L\right]}$ for convenience of numerical computations. Using the linear transformation ${\textstyle \eta =L(\xi +1)/2}$, the interval [${\textstyle 0{\mbox{,}}L}$] is transformed into the interval ${\textstyle \left[-1{\mbox{,}}1\right]}$, where L   is a scaled parameter used as the boundary condition value at infinity. It is a large but finite number chosen to represent the behavior of the flow properties when ${\textstyle \eta }$ is very large.

The differentiation matrix D used to approximate the derivatives of the unknown variables is defined by:

${\frac {df}{d\eta }}={\Sigma }_{k=0}^{N}D_{ik}f({\xi }_{k})=$$Df{\mbox{,}}\quad i=1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}N{\mbox{,}}$

(25)

where ${\textstyle D=2D/L}$ and ${\textstyle f={\left[f({\xi }_{0}){\mbox{,}}f({\xi }_{1}){\mbox{,}}\ldots {\mbox{,}}f({\xi }_{N})\right]}^{T}}$ is the vector function at the collocation points. Discretizing Eqs. (18), (19), (20), (21) and (22) using the spectral relaxation method, we obtain the following matrix equations:

$A_{1}f_{r+1}=B_{1}{\mbox{,}}\quad f_{r+1}({\xi }_{N})=0{\mbox{,}}$

(26)

$A_{2}g_{r+1}=B_{2}{\mbox{,}}\quad g_{r+1}({\xi }_{N})=1+\delta g_{r+1}^{'}({\xi }_{N}){\mbox{,}}\quad g_{r+1}({\xi }_{0})=$$\alpha {\mbox{,}}\quad g_{r+1}^{'}({\xi }_{0})=0{\mbox{,}}$

(27)

$A_{3}{\Theta }_{r+1}=B_{3}{\mbox{,}}\quad {\theta }_{r+1}^{'}({\xi }_{N})=$$-Bi(1-{\theta }_{r+1}({\xi }_{N})){\mbox{,}}\quad {\theta }_{r+1}({\xi }_{0})=$$0{\mbox{,}}$

(28)

$A_{4}{\Phi }_{r+1}=B_{4}{\mbox{,}}\quad Nb{\phi }_{r+1}^{'}({\xi }_{N})+$$Nt{\theta }_{r+1}^{'}({\xi }_{N})=0{\mbox{,}}\quad {\phi }_{r+1}({\xi }_{0})=$$0{\mbox{,}}$

(29)

where

$A_{1}=D{\mbox{,}}\quad B_{1}=g_{r}$

(30)

$A_{2}=\left(1+{\frac {1}{\beta }}\right)D^{2}+diag\left[f_{r+1}-\right.$$\left.A{\frac {\eta }{2}}\right]D-(A+M)I{\mbox{,}}\quad B_{2}=$$g_{r}^{2}-{\alpha }^{2}-M\alpha {\mbox{,}}$

(31)

$A_{3}={\frac {1}{Pr}}(1+N_{R})D^{2}+diag\left[f_{r+1}-A{\frac {\eta }{2}}+\right.$$\left.Nb{\Phi }_{r}^{'}\right]D-2diag\left[g_{r+1}\right]-$$(2A-He)I{\mbox{,}}$

(32)

$B_{3}=-Nt{\theta }_{r}^{{'}2}-\left(1+{\frac {1}{\beta }}\right)Ecg_{r+1}^{{'}2}-$$MEc{\left(\alpha -g_{r+1}\right)}^{2}-Df{\Phi }_{r}^{''}{\mbox{,}}$

(33)

$A_{4}=D^{2}+Scdiag\left[f_{r+1}-A{\frac {\eta }{2}}\right]D-$$2Scdiag\left[g_{r+1}\right]-2AScI{\mbox{,}}$

(34)

$B_{4}=-(SrSc+Nt/Nb){\Theta }_{r+1}^{''}{\mbox{.}}$

(35)

Here I   is an ${\textstyle \left(N+1)\times (N+1\right)}$ identity matrix, ${\textstyle diag[]}$ denotes a diagonal matrix and ${\textstyle f{\mbox{,}}\quad g{\mbox{,}}\quad \Theta {\mbox{,}}\quad and\quad \Phi }$ are the values of functions ${\textstyle f{\mbox{,}}\quad g{\mbox{,}}\quad \theta }$ and ${\textstyle \phi }$ respectively when evaluated at the collocation points. The matrix systems (26), (27), (28) and (29) constitute the SRM scheme in which the equations are solved iteratively starting with suitable initial guesses ${\textstyle f_{0}(\eta ){\mbox{,}}\quad g_{0}(\eta ){\mbox{,}}\quad {\theta }_{0}(\eta )}$ and ${\textstyle {\phi }_{0}(\eta )}$.

4. Results and discussion

In this study the governing equations were solved using the spectral relaxation method. Extensive calculations were performed to obtain the velocity, temperature, concentration profiles as well as the skin friction, the local Nusselt number and the local Sherwood number for various physical parameters values. Tables 1 to 4 give a comparison of the skin friction coefficient with the previously published results. Table 1 shows the skin friction coefficient for various values of the unsteadiness parameter A   for a Newtonian fluid (i.e., when ${\textstyle \beta \rightarrow \infty }$) which is compared with previously published results [14], [28] and [29] when the other parameter values remain same. Table 2 displays the skin friction coefficient for various values of ${\textstyle \alpha }$ when ${\textstyle \beta \rightarrow \infty }$ which are compared with previously published results [9], [30] and [31] when the other parameter values remain unchanged. Table 3 depicts the skin friction coefficient for various values of ${\textstyle \beta }$ and M and compares these values with those of Nadeem et al. [19] when ${\textstyle \alpha =0}$ and other parameters are remain unchanged. Table 4 shows the skin friction coefficient for various values of ${\textstyle \delta }$ when compared with results in Noghrehabadi et al. [3] and Sahoo and Do [32]. It is seen that a very good agreement with the previously published results is achieved thus validating the accuracy of the current numerical results.

Table 1. The values of ${\textstyle f^{''}(0)}$ for various values of unsteadiness parameter A for Newtonian fluid.

A	Present results	Sharidan et al. [28]	Chamka et al. [29]	Mukhopadhyay et al. [14]
0.8	−1.261043	−1.261042	−1.261512	−1.261479
1.2	−1.377725	−1.377722	−1.378052	−1.377850

Table 2. Comparison of values of ${\textstyle f^{''}(0)}$ with those of existing literature for various values of ${\textstyle \alpha }$ when ${\textstyle \beta \rightarrow \infty }$.

${\textstyle \alpha }$	Present	Mustafa et al. [9]	Mahapatra and Gupta [30]	Ishak et al. [31]
0.01	−0.99782	−0.99802	–	−0.9980
0.10	−0.96937	−0.96939	−0.9694	−0.9694
0.20	−0.918111	0.918107	0.9181	0.9181
0.50	−0.66726	−0.66735	−0.6673	−0.6673
2.00	2.01750	2.01757	2.0175	2.0175
3.00	4.72928	4.72964	4.7294	4.7294

Table 3. Comparison of values for skin friction coefficient for various values of ${\textstyle \beta }$ and M with those of Nadeem et al. [19] when ${\textstyle \alpha =0}$.

${\textstyle \beta }$	M	Present	Nadeem et al. [19]
${\textstyle \infty }$	0	1.00000	1.0042
5		−1.09544	−1.0954
1		−1.41421	−1.4142
${\textstyle \infty }$	10	−3.31662	−3.3165
5		−3.63318	−3.6331
1		−4.69042	−4.6904
${\textstyle \infty }$	100	−10.04987	−10.049
5		−11.00909	−11.0091
1		−14.21267	−14.2127

Table 4. Comparison of results for ${\textstyle -f^{''}(0)}$ with the slip factor ${\textstyle \delta }$.

${\textstyle \delta }$	Present results	Noghrehabadi et al. [3]	Sahoo and Do [32]
0	1.000000	1.0	1.001154
0.1	0.872083	0.872082	0.871447
0.2	0.776377	0.776377	0.774933
0.3	0.701548	0.701548	0.699738
0.5	0.591195	0.591195	0.589195
1.0	0.430160	0.430160	0.428450
2.0	0.283979	0.283980	0.282893
3.0	0.214054	0.214055	0.213314
5.0	0.144714	0.144841	0.144430
10	0.080932	0.081243	0.081091
20	0.043569	0.043790	0.043748

Table 5 displays the computed values of the skin friction coefficient, the heat transfer coefficient and the mass transfer coefficient when ${\textstyle A=0.8{\mbox{,}}\quad Bi=0.5{\mbox{,}}\quad Pr=Sc=1{\mbox{,}}\quad Nt=}$$0.5{\mbox{,}}\quad Nb=0.3{\mbox{,}}\quad He=0.3{\mbox{,}}\quad Ec=$$0.3{\mbox{,}}\quad \alpha =0.2$ and ${\textstyle \delta =0.1}$, for different values of ${\textstyle \beta {\mbox{,}}M{\mbox{,}}Df{\mbox{,}}Sr}$ and ${\textstyle N_{R}}$. We note that an increase in ${\textstyle \beta }$ increases the skin-friction coefficient whereas increasing M   reduces the skin-friction coefficient. The local Nusselt number is reduced by increasing ${\textstyle \beta }$ and Df   while the local Sherwood number increases when ${\textstyle \beta }$ and Df are increased, whereas local Nusselt number increases by increasing M but the opposite trend is observed in case of the local Sherwood number. Again, the local Nusselt number increases and local Sherwood number decreases when increasing the values of Sr   and ${\textstyle N_{R}}$.

Table 5. Computed values of Skin friction coefficient, heat transfer coefficient and mass transfer coefficient when ${\textstyle A=0.8{\mbox{,}}\quad Bi=0.5{\mbox{,}}\quad Pr=Sc=1{\mbox{,}}\quad Nt=}$$0.5{\mbox{,}}\quad Nb=0.3{\mbox{,}}\quad He=0.3{\mbox{,}}\quad Ec=$$0.3{\mbox{,}}\quad \alpha =0.2$ and ${\textstyle \delta =0.1}$ for different values of ${\textstyle \beta {\mbox{,}}M{\mbox{,}}Df{\mbox{,}}Sr}$ and ${\textstyle N_{R}}$.

${\textstyle \beta }$	M	Df	Sr	${\textstyle N_{R}}$	${\textstyle \left(1+{\frac {1}{\beta }})f^{''}(0\right)}$	${\textstyle -{\theta }^{'}(0)}$	${\textstyle -{\phi }^{'}(0)}$
0.5					−3.23231	−0.31768	0.52947
1.0	5.0	0.5	0.4	0.2	−2.56075	−0.33313	0.55522
2.0					−2.16359	−0.34371	0.57284
	0.5				−1.44319	−0.40475	0.67458
2.0	1.0	0.5	0.4	0.2	−1.54818	−0.39609	0.66014
	2.0				−1.73352	−0.38055	0.63425
		0.0			−2.16359	−0.31031	0.51718
2.0	5.0	0.1	0.4	0.2	−2.16359	−0.31658	0.52763
		0.3			−2.16359	−0.33020	0.55034
			0.1		−2.16359	−0.34587	0.57644
2.0	5.0	0.5	0.5	0.2	−2.16359	−0.34227	0.57044
			0.7		−2.16359	−0.33490	0.55817
				0.5	−2.16359	−0.33718	0.56197
2.0	5.0	0.5	0.4	1.0	−2.16359	−0.32389	0.53982
				3.0	−2.16359	−0.28473	0.47456

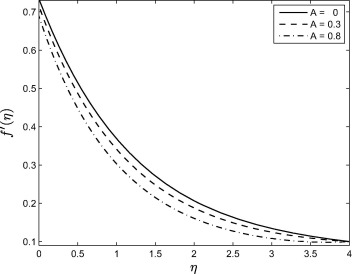
Fig. 1 shows the effect of the unsteadiness parameter on the velocity profiles. Here, it is shown that increasing the unsteadiness parameter reduces the velocity profiles. The velocity along the sheet decreases with an increase in the unsteadiness parameter due to the accompanying reduction in the thickness of the momentum boundary layer. Similar flow patterns for Casson fluid can be found in the literature, for instance, see [14] and [21].

Figure 1. Effect of the unsteadiness parameter A   on the velocity profile ${\textstyle f^{'}(\eta )}$ when ${\textstyle \delta =Bi=0.5{\mbox{,}}Ec=0.1{\mbox{,}}\alpha =0.1{\mbox{,}}N_{R}=}$$Nb=Nt=0.5{\mbox{,}}He=0.3{\mbox{,}}Df=0.5{\mbox{,}}\beta =$$1.0{\mbox{,}}M=0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sr=1.0$ and ${\textstyle Sc=1.0}$.

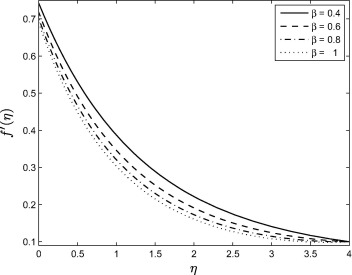
Fig. 2 shows the effect of the Casson parameter ${\textstyle \beta }$ on the velocity profiles. We note that as ${\textstyle \beta }$ increases, the velocity and the boundary layer thickness decrease. Hence, the magnitude of the velocity is greater in Casson fluid when compared with viscous fluids. Nandy [11], [18] and [21] investigated similar patterns of fluid flow.

Figure 2. Effect of the Casson parameter ${\textstyle \beta }$ on the velocity profile ${\textstyle f^{'}(\eta )}$ when ${\textstyle \delta =Bi=0.5{\mbox{,}}\alpha =0.1{\mbox{,}}N_{R}=Nb=Nt=}$$0.5{\mbox{,}}He=0.3{\mbox{,}}Df=0.5{\mbox{,}}Sr=1.0$, ${\textstyle M=0.5{\mbox{,}}Sc=1.0{\mbox{,}}Ec=1.0{\mbox{,}}Pr=1.0}$ and ${\textstyle A=0.8}$.

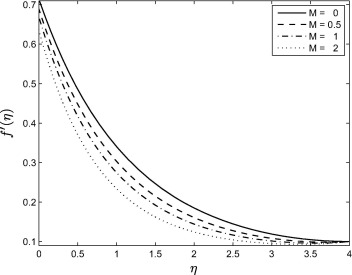
Fig. 3 shows the effect of the magnetic parameter M   on velocity profiles ${\textstyle f^{'}}$. The velocity profiles decrease with increasing magnetic field parameter values leading to a reduction in the velocity boundary layer thickness. The Lorentz force which opposes the motion occurs due to the applied transverse magnetic field, and is responsible for reducing the fluid velocity. Similar type of fluid flow patterns have been observed in [11] and [18].

Figure 3. Effect of the magnetic parameter M   on the velocity profile ${\textstyle f^{'}(\eta )}$ when ${\textstyle \delta =Bi=0.5{\mbox{,}}\alpha =0.1{\mbox{,}}N_{R}=Nb=Nt=}$$0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=$$1{\mbox{,}}Pr=1{\mbox{,}}Sc=\beta =1.0$ and ${\textstyle A=0.8}$.

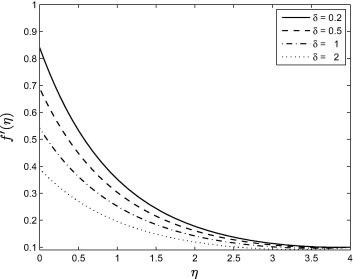
Fig. 4 shows that the velocity profiles are decreasing function of the slip parameter ${\textstyle \delta }$. This implies that when slip occurs (for non-zero values of ${\textstyle \delta }$) the fluid velocity near the sheet is no longer equal to the stretching sheet velocity. Increasing ${\textstyle \delta }$ decreases the velocity because under the slip condition, the pulling of the stretching sheet can be only partly transmitted to the fluid. The boundary layer thickness also decreases as the slip parameter ${\textstyle \delta }$ increases.

Figure 4. Effect of the velocity slip parameter ${\textstyle \delta }$ on the velocity profile ${\textstyle f^{'}(\eta )}$ when ${\textstyle Bi=0.5{\mbox{,}}\alpha =0.1{\mbox{,}}N_{R}=0.5{\mbox{,}}Nb=}$$Nt=0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=$$1.0{\mbox{,}}M=0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sc=1.0{\mbox{,}}\beta =$$1.0$ and ${\textstyle A=0.8}$

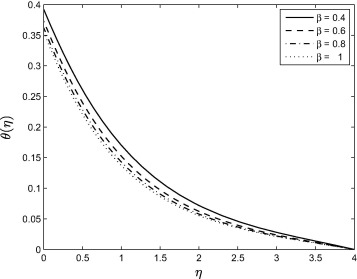
Fig. 5 shows that the temperature profiles decrease with increasing the value of the Casson parameters ${\textstyle \beta }$. Increasing the Casson parameter, i.e., reducing the yield stress suppresses the fluid velocity. The temperature curves in Fig. 5 show that the rate of transport is considerably reduced by an increase in ${\textstyle \beta }$.

Figure 5. Effect of the Casson parameter ${\textstyle \beta }$ on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =Bi=0.5{\mbox{,}}N_{R}=Nb=Nt=}$$0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=1.0{\mbox{,}}Df=0.5{\mbox{,}}Sr=$$1.0{\mbox{,}}M=0.5{\mbox{,}}Pr=Sc=1.0$ and ${\textstyle A=0.8}$.

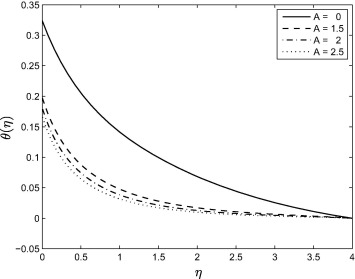
Fig. 6 shows that the temperature profiles decrease significantly as the unsteadiness parameter increases. The rate of heat transfer (from the sheet to the fluid) decreases with increasing values of A  . Less heat is transferred from the sheet to the fluid when the unsteadiness parameter increases. For this reason the temperature profiles ${\textstyle \theta (\eta )}$ decrease. Since the fluid flow is caused solely by the stretching sheet and the sheet surface temperature is higher than the free stream temperature, the fluid velocity and temperature decrease as A increases. It is important to note that the rate of cooling is much faster for higher values of unsteadiness parameter. In the studies [14] and [21] similar temperature profiles patterns were obtained.

Figure 6. Effect of the unsteadiness parameter A   on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \delta =Bi=0.5{\mbox{,}}N_{R}=Nb=Nt=0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=}$$0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=1.0{\mbox{,}}M=0.5{\mbox{,}}Pr=$$1.0{\mbox{,}}Sc=1.0{\mbox{,}}\beta =1.0$ and ${\textstyle \alpha =0.1}$.

Fig. 7 shows that the temperature profiles increase as thermal radiation increases, and because the effect of ${\textstyle N_{R}}$ is to enhance heat transfer, the thermal boundary layer thickness increases with thermal radiation.

Figure 7. Effect of the thermal radiation parameter ${\textstyle N_{R}}$ on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \delta =0.5{\mbox{,}}Bi=0.5{\mbox{,}}Nb=Nt=0.5{\mbox{,}}He=}$$0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=1.0{\mbox{,}}M=$$0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sc=1.0{\mbox{,}}\alpha =0.1{\mbox{,}}\beta =$$1.0$ and ${\textstyle A=0.8}$.

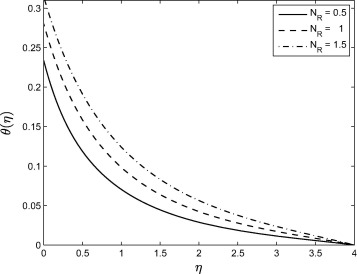
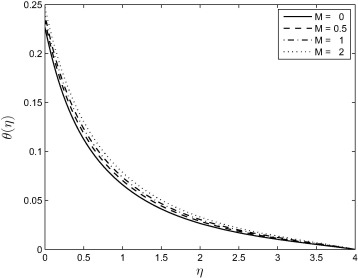
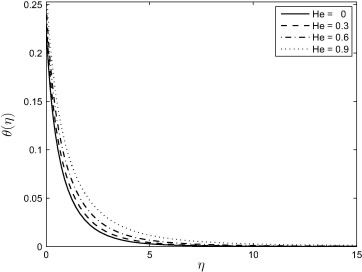
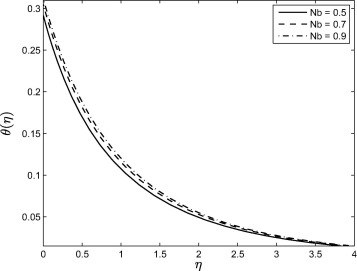
Fig. 8 shows that magnetic field increases the temperature profiles. Because of the application of transverse magnetic field in an electrically conducting fluid. It is also noticed that the thermal boundary layer thickness increases in the presence of a magnetic field. Fig. 9 shows that increasing heat generation parameter enhances the temperature profiles thereby increasing the thermal boundary layer thickness. Fig. 10 shows that temperature profiles increase with increasing the Brownian motion parameter. Because of this increase in the temperature profiles, there is also an enhancement in the thermal boundary layer thickness.

Figure 8. Effect of the magnetic parameter M   on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \delta =0.5{\mbox{,}}Bi=0.5{\mbox{,}}N_{R}=Nb=Nt=0.5{\mbox{,}}He=}$$0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=1.0{\mbox{,}}Pr=$$1.0{\mbox{,}}Sc=1.0{\mbox{,}}\alpha =0.1{\mbox{,}}\beta =$$1.0$ and ${\textstyle A=0.8}$.

Figure 9. Effect of the heat generation parameter He   on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =0.5{\mbox{,}}Bi=0.5{\mbox{,}}N_{R}=}$$Nb=Nt=0.5{\mbox{,}}Sr=1.0{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}M=$$0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sc=1.0{\mbox{,}}\beta =1.0$ and ${\textstyle A=0.8}$.

Figure 10. Effect of the Brownian motion parameter Nb   on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =Bi=0.5{\mbox{,}}N_{R}=0.5{\mbox{,}}Nt=}$$0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=$$1.0{\mbox{,}}M=0.5{\mbox{,}}Pr=0.7{\mbox{,}}Sc=1.0{\mbox{,}}\beta =$$1.0$ and ${\textstyle A=0.8}$.

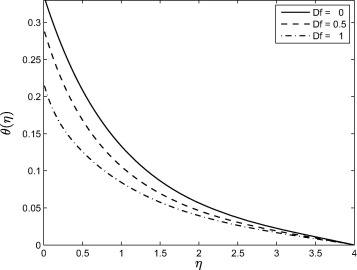
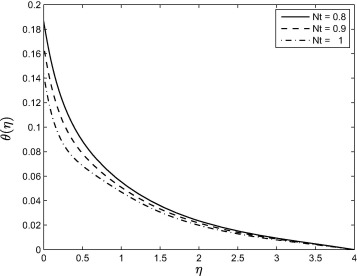
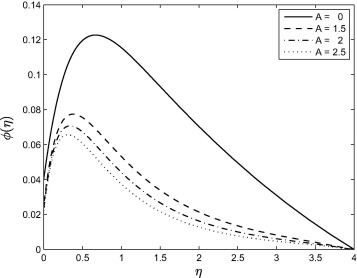
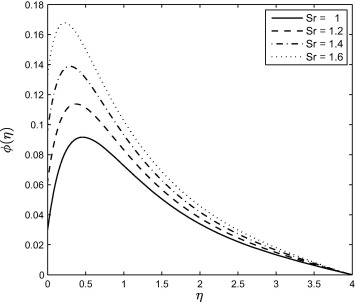
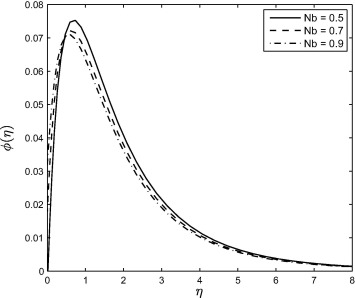
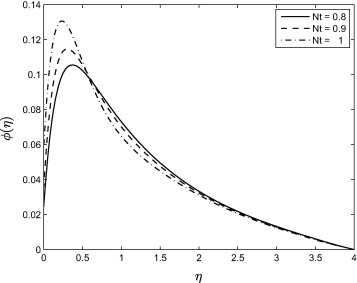
Fig. 11 shows the effect of the Dufour number on the temperature profiles. Increasing Df parameter leads to a decrease in the temperature profiles. Dufour effect is the heat transfer induced by volume fraction gradients and significant because of the density difference in the flow regime. Thus the figure shows the effect of the concentration gradient on the thermal energy flux in the flow region. Since it is decreasing, it implies that the effect of the composition gradient on temperature is reduced and this leads to a cooling of the boundary layer region, as explained in [33]. Effect of the thermophoresis is given in Fig. 12. From the figure, it is observed that the temperature profiles are decreased as the thermophoresis parameter is increasing and due to this effect, the thermal boundary layer thickness is also decreased. Fig. 13 shows that the concentration profiles decrease with increasing values of A. As can be observed in Figure 1, Figure 6 and Figure 13, increasing value of the unsteadiness parameter A reduces the flow properties such as velocity, temperature and concentration. When A values are increased in the system, the boundary layer thicknesses are reduced and this inhibits the development of transition from laminar to turbulent flow. This shows that stretching of surfaces can be used as a flow stabilizing mechanism. Fig. 14 shows that the concentration boundary layer thickness increases with Sr and consequently, leads to an increase in the concentration profiles due to enhancement of the profiles by the mass flux created by the temperature gradient. This similar trend is observed with some other fluid types like micropolar fluids as pointed out in [33] and [34]. Fig. 15 shows that increasing the values of the Brownian motion parameter first causes a sharp decrease in the concentration profiles followed by a slight increase. The concentration profiles decrease with increasing Nb   near the stretching sheet wall up to a certain value of ${\textstyle \eta }$ but beyond this point, the opposite trend is observed. Near the wall the concentration boundary layer decreases with increasing Nb but away from the wall, we observe the opposite trend. Fig. 16 shows the influence of the thermophoresis parameter on the concentration profiles. It is seen from this figure that the concentration profiles increase with increasing Nt   near the stretching sheet wall up-to a certain value of ${\textstyle \eta }$ but beyond this point, the opposite trend is observed. It means that concentration boundary layer thickness increases up-to a certain value of ${\textstyle \eta }$ but beyond this point it decreases. This is due to the revised nanoparticle concentration boundary condition.

Figure 11. Effect of the Dufour number Df   on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =Bi=0.5{\mbox{,}}N_{R}=0.5{\mbox{,}}Nt=}$$0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Nb=0.5{\mbox{,}}Sr=$$1.0{\mbox{,}}M=0.5{\mbox{,}}Pr=0.7{\mbox{,}}Sc=1.0{\mbox{,}}\beta =$$1.0$ and ${\textstyle A=0.8}$.

Figure 12. Effect of the thermophoresis parameter Nt   on the temperature profile ${\textstyle \theta (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =0.5{\mbox{,}}Bi=0.5{\mbox{,}}N_{R}=}$$Nb=0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}M=$$0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sc=Sr=1.0{\mbox{,}}\beta =1.0$ and ${\textstyle A=0.8}$.

Figure 13. Effect of the unsteadiness parameter A   on the concentration profile ${\textstyle \phi (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =0.5{\mbox{,}}Bi=0.5{\mbox{,}}N_{R}=}$$Nb=Nt=0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}M=$$0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sc=Sr=1.0$ and ${\textstyle \beta =1.0}$.

Figure 14. Effect of the Soret number Sr   on the concentration profile ${\textstyle \phi (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =0.5{\mbox{,}}Bi=0.5{\mbox{,}}N_{R}=}$$Nb=Nt=0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}M=$$0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sc=1.0{\mbox{,}}\beta =1.0$ and ${\textstyle A=0.8}$.

Figure 15. Effect of the Brownian motion parameter Nb   on the concentration profile ${\textstyle \phi (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =Bi=0.5{\mbox{,}}N_{R}=0.5{\mbox{,}}Nt=}$$0.5{\mbox{,}}He=0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=$$1.0{\mbox{,}}M=0.5{\mbox{,}}Pr=0.7{\mbox{,}}Sc=1.0{\mbox{,}}\beta =$$1.0$ and ${\textstyle A=0.8}$.

Figure 16. Effect of the thermophoresis parameter Nt   on the concentration profile ${\textstyle \phi (\eta )}$ when ${\textstyle \alpha =0.1{\mbox{,}}\delta =Bi=0.5{\mbox{,}}N_{R}=Nb=0.5{\mbox{,}}He=}$$0.3{\mbox{,}}Ec=0.1{\mbox{,}}Df=0.5{\mbox{,}}Sr=1.0{\mbox{,}}M=$$0.5{\mbox{,}}Pr=1.0{\mbox{,}}Sc=1.0{\mbox{,}}\beta =1.0$ and ${\textstyle A=0.8}$.

5. Conclusion

In this paper, we have studied the combined effects of Soret and Dufour numbers on the fluid flow, heat and mass transfer of a Casson nanofluid over an unsteady stretching sheet in the presence of thermal radiation and heat generation. The effects of partial slip on the velocity boundary condition, convective thermal boundary condition, Brownian and thermophoresis diffusion coefficients on the concentration boundary condition are also analyzed here. The governing equations were solved using the Spectral Relaxation Method. The study has shown, inter alia, that by increasing the Casson, Dufour and unsteadiness parameters, we reduce the fluid velocity, temperature and concentration profiles. As would be expected, increasing thermal radiation increases the temperature profiles and also the Soret parameter increases the concentration profiles. As has been shown previously in the literature for Newtonian fluids, our findings are that for a Casson nanofluid as discussed in this paper, increasing the intensity of the magnetic field has the effect of reducing the fluid flow while enhancing the fluid temperature. Additional conclusions that can be drawn from this study are that;

• Increasing the velocity slip parameter reduces the velocity profile.
• Increasing the heat generation parameter reduces the temperature profile.

Acknowledgement

The authors are thankful to the University of KwaZulu-Natal and Claude Leon Foundation, South Africa for the necessary support.

References

1. [1] S. Choi; Enhancing thermal conductivity of fluids with nanoparticles; ASME-Publ. Fed., 231 (1995), pp. 99–106
2. [2] J. Buongiorno; Convective transport in nanofluids; J. Heat Trans., 128 (2006), pp. 240–250
3. [3] A. Noghrehabadi, R. Pourrajab, M. Ghalambaz; Effect of partial slip boundary condition on the flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature; Int. J. Ther. Sci., 54 (2012), pp. 253–261
4. [4] W.A. Khan, I. Pop; Boundary layer flow of a nanofluid past a stretching sheet; Int. J. Heat Mass Trans, 53 (2010), pp. 2477–2483
5. [5] S. Nadeem, R.U. Haq, N.S. Akbar, C. Lee, Z.H. Khan; Numerical study of boundary layer flow and heat transfer of Oldroyd-B nanofluid towards a stretching sheet; PLoS One, 8 (2013), p. e6981 http://dx.doi.org/10.1371/journal.pone.0069811
6. [6] O.D. Makinde, W.A. Khan, Z.H. Khan; Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet; Int. J. Heat Mass Trans., 62 (2013), pp. 526–533
7. [7] N.A. Haroun, P. Sibanda, S. Mondal, S.S. Motsa; On unsteady MHD mixed convection in a nanofluid due to a stretching/shrinking surface with suction/injection using the spectral relaxation method; Bound. Val. Probl., 1 (2015), pp. 1–17 http://dx.doi.org/10.1186/s13661-015-0289-5
8. [8] N.A. Haroun, P. Sibanda, S. Mondal, S.S. Motsa, M.M. Rashidi; Heat and mass transfer of nanofluid through an impulsively vertical stretching surface using the spectral relaxation method; Bound. Value Problems, 161 (2015), pp. 1–16 http://dx.doi.org/10.1186/s13661-015-0424-3
9. [9] M. Mustafa, T. Hayat, I. Pop, A. Hendi; Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet; Z. Naturforsch., 67a (2011), pp. 70–76
10. [10] M. Mustafa, T. Hayat, I. Pop, A. Aziz; Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate; Heat Trans.-As. Res., 40 (2011), pp. 563–576
11. [11] S.K. Nandy; Analytical solution of MHD stagnation-point flow and heat transfer of Casson fluid over a stretching sheet with partial slip; ISRN Therm. (2013) http://dx.doi.org/10.1155/2013/108264 Article ID 108264
12. [12] G. Makanda, S. Shaw, P. Sibanda; Diffusion of chemically reactive species in Casson fluid flow over an Unsteady Stretching surface in porous medium in the presence of a magnetic field; Math. Probl. Eng., 2015 (2015), Article Article ID 724596 http://dx.doi.org/10.1155/2015/724596 10 pages
13. [13] K. Bhattacharyya; MHD stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation; J. Therm. (2013) http://dx.doi.org/10.1155/2013/169674 Article ID 169674
14. [14] S. Mukhopadhyay, P.R. De, K. Bhattacharyya, G.C. Layek; Casson fluid flow over an unsteady stretching surface; Ain Shams Eng. J., 4 (2013), pp. 933–938
15. [15] H.I. Andersson, J.B. Aarseth, B.S. Dandapat; Heat transfer in a liquid film on an unsteady stretching surface; Int. J. Heat Mass Trans., 43 (2000), pp. 69–74
16. [16] T. Hayat, S.A. Shehzad, A. Alsaedi; Soret and Dufour effects on magnetohydrodynamic(MHD) flow of Casson fluid; Appl. Math. Mech. – Engl Ed., 33 (2012), pp. 1301–1312
17. [17] S. Nadeem, R.U. Haq, N.S. Akbar, Z.H. Khan; MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet; Alexan. Eng. J., 52 (2012), pp. 577–582
18. [18] K. Bhattacharyya, T. Hayat, A. Alsaedi; Analytic solution for magnetohydrodynamic boundary layer flow of Casson fluid over a stretching/shrinking sheet with wall mass transfer; Chin. Phys. B, 22 (2013), pp. 0247021–0247026
19. [19] S. Nadeem, R.U. Haq, C. Lee; MHD flow of a Casson fluid over an exponentially shrinking sheet; Sci. Iranic., 19 (2012), pp. 1550–1553
20. [20] S. Nadeem, R.U. Haq, N.S. Akbar; MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition; IEEE Trans. Nanotech., 13 (2014), pp. 109–115
21. [21] S. Mukhopadhyay; Effects of thermal radiation on Casson fluid flow and heat transfer over an unsteady stretching surface subjected to suction/blowing; Chin. Phys. B, 22 (2013), p. 114702
22. [22] C.S.K. Raju, N. Sandeep, V. Sugunamma, M.B. Jayachandra, R.J.V. Ramana, Heat and mass transfer in magnetohydrodynamic Casson fluid over an exponentially permeable stretching surface, Eng. Sci. Technol. Int. J., in press. doi: http://dx.doi.org/10.1016/j.jestch.2015.05.010.
23. [23] A.V. Kunetsov, D.A. Nield; Natural convective boundary layer flow of a nanofluid past a vertical plate: a revised model; Int. J. Ther. Sci., 77 (2014), pp. 126–129
24. [24] S.S. Motsa; A new spectral relaxation method for similarity variable nonlinear boundary layer flow systems; Chem. Eng. Commun., 201 (2014), pp. 241–256
25. [25] S.S. Motsa, P.G. Dlamini, M. Khumalo; Spectral relaxation method and spectral quasilinearization method for solving unsteady boundary layer flow problems; Adv. Math. Phys., 2014 (2014) http://dx.doi.org/10.1155/2014/341964 Article ID 341964
26. [26] S.S. Motsa, Z.G. Makukula; On spectral relaxation method approach for steady von Karman flow of a Reiner–Rivlin fluid with Joule heating and viscous dissipation; Cen. Eur. J. Phys., 11 (2013), pp. 363–374
27. [27] M. Nakamura, T. Sawada; Numerical Study on the flow of a non-Newtonian fluid through an axisymmetric stenosis; J. Biomech. Eng., 110 (1988), pp. 137–143
28. [28] S. Sharidan, T. Mahmood, I. Pop; Similarity solutions for the unsteady boundary layer flow and heat transfer due to a stretching sheet; Int. J. Appl. Mech. Eng., 11 (2006), pp. 647–654
29. [29] A.J. Chamkha, A.M. Aly, M.A. Mansour; Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects; Chem. Eng. Commun., 197 (2010), pp. 846–858
30. [30] T.R. Mahapatra, A.S. Gupta; Heat transfer in stagnation-point flow towards a stretching sheet; Heat Mass Trans., 38 (2002), pp. 517–521
31. [31] A. Ishak, R. Nazar, N.M. Arifin, I. Pop; Mixed convection of the stagnation-point flow towards a stretching vertical permeable sheet; Malay. J. Math. Sci., 1 (2007), pp. 217–226
32. [32] B. Sahoo, Y. Do; Effects of slip on sheet-driven flow and heat transfer of a third grade fluid past a stretching sheet; Int. Commun. Heat Mass Trans., 37 (2010), pp. 1064–1071
33. [33] O.A. Beg, V.R. Prasad, B. Vasu, N.B. Reddy, Q. Li, R. Bhargava; Free convection heat and mass transfer from an isothermal sphere to a micropolar regime with Soret/Dufour effects; Int. J. Heat Mass Trans., 54 (2011), pp. 9–18
34. [34] F. Mabood, S.M. Ibrahim, M.M. Rashidi, M.S. Shadloo, Giulio Lorenzini; Non-uniform heat source/sink and Soret effects on MHD non-Darcian convective flow past a stretching sheet in a Micropolar fluid with radiation; Int. J. Heat Mass Trans., 93 (2016), pp. 674–682