Evaluation of three different approximations for the solution of the direct problem on electrical impedance tomography

Resumo

Neste trabalho foram comparadas 3 diferentes soluções para o problema direto da tomografia de impedância elétrica utilizando o método das diferenças finitas. Nesta técnica são posicionados elétrodos no contorno/fronteira de um volume a ser estudado e, em 2 deles, são injetados padrões de correntes e, nos elétrodos restantes, realizadas medidas do potencial elétrico. A inversão numérica dos dados permite a reconstrução do domínio analisado. Duas novas aproximações são propostas para o problema direto e comparações são realizadas a partir de resultados disponíveis na literatura. Com o estudo aqui realizado, para uma das aproximações propostas foi observada uma melhora significativa da acurácia comparada aos resultados obtidos com a aproximação da literatura.

Abstract

The present study compares three different solutions for the direct problem of Electrical Impedance Tomography using the finite difference method. In this technique, electrodes are positioned on the boundary of a volume to be studied, and in two of them current patterns are injected and measurements of electrical potential are made in the remaining electrodes. The numerical inversion of the data allows reconstruction of the analyzed domain. Two new approximations are proposed for the direct problem and comparisons are performed based on results available in the literature. In the study performed here, in one of the proposed approximations it was observed a significant improvement in accuracy compared to results obtained with the approximations in the literature.

Palavras‐chave

Tomografia por impedância elétrica ; Métodos numéricos ; Imageamento não invasivo

Keywords

Electrical impedance tomography ; Numerical methods ; Non‐invasive imaging

1. Introdução

A técnica de tomografia por impedância elétrica (TIE) é um método de imageamento não invasivo, onde são utilizadas informações das propriedades elétricas de um objeto para obtenção de imagens de uma seção transversal do seu interior. Por propriedades elétricas se entendem especificamente a condutividade e a permissividade elétrica. No processo de obtenção de imagens por TIE é necessário alocar elétrodos no contorno de uma determinada região do objeto em conjunto com uma fonte de corrente. A fonte de corrente utiliza 2 dos elétrodos alocados para injetar corrente no interior do domínio e medidas dos potenciais elétricos são realizadas nos demais elétrodos. Um algoritmo matemático reconstrói numericamente imagens de um plano transversal do corpo, a partir dos valores de impedância, condutividade ou permissividade elétrica estimados no plano analisado.

Foram desenvolvidos estudos numéricos aplicados à solução do problema direto da TIE, utilizando para isso o método das diferenças finitas (MDF). Valendo‐se desse método foram desenvolvidas 2 novas aproximações e testadas 3 para a equação generalizada de Laplace. Por sua vez, o objetivo desse trabalho é avaliar as 2 aproximações propostas em relação a uma terceira aproximação comumente utilizada na literatura e definir aquela que apresenta melhor equilíbrio entre acurácia, tempo e estabilidade, pensando no emprego dessa aproximação para solução do problema inverso da TIE, o qual é mal condicionado e, para sua solução, necessita o emprego de técnicas numéricas precisas, velozes^b e estáveis.

2. Modelagem matemática do problema direto

O problema direto da TIE envolve a determinação da distribuição dos potenciais no interior de uma região Ω e a resposta no contorno ∂Ω , supondo conhecida a distribuição de condutividade. A modelagem matemática desse problema, considerando uma distribuição quase estática de cargas [1]  and [2]^c , permite obter uma equação diferencial parcial capaz de modelar o potencial em Ω, a qual é exibida a seguir [1] , [2]  and [3] :

${\overset {\rightharpoonup }{\nabla }}.(\sigma {\mbox{ }}{\overset {\rightarrow }{\nabla }}u)=0{\mbox{ }}em{\mbox{ }}\Omega$

( 1)

onde u é o potencial e σ é a condutividade elétrica em um ponto qualquer no interior da região.

Propriedades elétricas, tais como a condutividade elétrica e a permissividade elétrica, determinam o comportamento de materiais quando submetidos a campos elétricos externos. Teoricamente seria possível construir um modelo matemático de distribuição de condutividades em Ω ou, de outro modo, também poderia ser construído um modelo levando em consideração apenas a permissividade [4] desta região. Esses 2 modelos podem ser utilizados separados ou conjuntamente para produzir imagens de Ω [5] . No entanto, como pode ser observado na equação (1), um modelo teórico tipicamente utilizado na literatura e utilizado neste artigo considera somente a condutividade do domínio avaliado, ou seja, considera somente o termo real da impedância elétrica.

As condições de contorno (CC) para o problema direto da TIE correspondem aos valores de correntes/potenciais aplicados e medidos no contorno, e satisfazem a seguinte expressão:

$J_{n}=-\sigma {\frac {\partial u}{\partial n}}{\mbox{ }}em{\mbox{ }}\partial \Omega$

( 2)

onde n é um versor normal à superfície do objeto e J_n é a densidade de corrente na direção do versor n .

O problema direto pode ser definido matematicamente como a solução da equação (1) para a condição de contorno (2).

3. O método das diferenças finitas

No MDF o domínio é discretizado na forma de retângulos ou quadrados. Sendo assim, a malha pode ser representada por intervalos definidos por ${\textstyle \Delta x={\frac {x_{m}}{N}}}$ e ${\textstyle \Delta y={\frac {y_{n}}{M}}}$ , onde N e M são números inteiros positivos que representam o número de divisões do domínio nas coordenadas x e y , respectivamente [6] . O ponto nodal (i , j ) possui as coordenadas (x_i , y_j ), dadas por x_i  = x₀  + Δxi e y_j  = y₀  + Δyj . O número máximo de linhas em x é denotado por i_max  = N e o número total de linhas em y é denotado por j_max  = M .

Quanto às derivadas na direção normal à ∂Ω , a sua discretização pode ser realizada de diversas maneiras, dependendo do grau de acurácia desejado. No entanto, isso foi realizado utilizando 4 expressões; 2 delas são apresentadas a seguir [7] :

${\begin{array}{l}\displaystyle {\frac {\partial u}{\partial n}}\approx {\overset {\rightarrow }{n}}.\left({\frac {3u_{i,j}-4u_{i-1,j}+u_{i-2,j}}{2\Delta x}}{\overset {\rightarrow }{i}}+\right.\\\left.\displaystyle +{\frac {3u_{i,j}-4u_{i,j-1}+u_{i,j-2}}{2\Delta y}}{\overset {\rightarrow }{j}}\right)\end{array}}$

( 3)

${\begin{array}{l}\displaystyle {\frac {\partial u}{\partial n}}\approx {\overset {\rightarrow }{n}}\cdot \left({\frac {3u_{i,j}-4u_{i+1,j}+u_{i+2,j}}{2\Delta x}}{\overset {\rightarrow }{i}}+\right.\\\left.\displaystyle +{\frac {3u_{i,j}-4u_{i,j+1}+u_{i,j+2}}{2\Delta y}}{\overset {\rightarrow }{j}}\right)\end{array}}$

( 4)

Duas outras são apresentadas a seguir [8] :

${\frac {\partial u}{\partial n}}\approx {\overset {\rightarrow }{n}}\cdot \left({\begin{array}{c}{\frac {(147u_{i,j}-360u_{i-1,j}+450u_{i-2,j}-400u_{i-3,j}+225u_{i-4,j}-72u_{i-5,j}+10u_{i-6,j})}{60\Delta x}}{\overset {\rightarrow }{i}}+\\{\frac {(147u_{i,j}-360u_{i,j-1}+450u_{i,j-2}-400u_{i,j-3}+225u_{i,j-4}-72u_{i,j-5}+10u_{i,j-6})}{60\Delta y}}{\overset {\rightarrow }{j}}\end{array}}\right)$

( 5)

${\frac {\partial u}{\partial n}}\approx {\overset {\rightarrow }{n}}\cdot \left({\begin{array}{c}{\frac {(147u_{i,j}-360u_{i+1,j}+450u_{i+2,j}-400u_{i+3,j}+225u_{i+4,j}-72u_{i+5,j}+10u_{i+6,j})}{60\Delta x}}{\overset {\rightarrow }{i}}+\\{\frac {(147u_{i,j}-360u_{i,j+1}+450u_{i,j+2}-400u_{i,j+3}+225u_{i,j+4}-72u_{i,j+5}+10u_{i,j+6})}{60\Delta y}}{\overset {\rightarrow }{j}}\end{array}}\right)$

( 6)

O vetor unitário ${\textstyle {\overset {\rightarrow }{n}}}$ em coordenadas cartesianas é definido como ${\textstyle {\overset {\rightarrow }{n}}=\left[cos(\theta ){\overset {\rightarrow }{i}}+sen(\theta ){\overset {\rightarrow }{j}}\right]}$ , onde θ   é o ângulo entre o vetor ${\textstyle {\overset {\rightarrow }{n}}}$ e o eixo da coordenada x no plano.

Para a solução do problema direto da TIE é necessário discretizar a equação (1). Isso pode ser realizado utilizando a equação a seguir, deduzida nesse trabalho a partir de aproximações por diferenças finitas centradas para a derivada de primeira e de segunda ordem:

${\begin{array}{l}\displaystyle u_{i,j}={\frac {u_{i-1,j}+u_{i+1,j}+u_{i,j+1}+u_{i,j-1}}{4}}+{\frac {1}{16.\sigma _{i,j}}}\cdot [(\sigma _{i+1,j}-\\\displaystyle -\sigma _{i-1,j})(u_{i+1,j}-u_{i-1,j})+(\sigma _{i,j+1}-\\\displaystyle -\sigma _{i,j-1})(u_{i,j+1}-u_{i,j-1})]\end{array}}$

( 7)

Foram testadas ainda 2 outras aproximações para o potencial elétrico em Ω. Uma dessas aproximações é tipicamente encontrada na literatura e foi extraída do trabalho [3] .

${\begin{array}{l}\displaystyle u_{i,j}=\\\displaystyle =\left[{\frac {(\sigma _{i+{\frac {1}{2}},j}u_{i+1,j})+(\sigma _{i-{\frac {1}{2}},j}u_{i-1,j})+(\sigma _{i,j+{\frac {1}{2}}}u_{i,j+1})+(\sigma _{i,j-{\frac {1}{2}}}u_{i,j-1})}{(\sigma _{i+{\frac {1}{2}},j}+\sigma _{i-{\frac {1}{2}},j}+\sigma _{i,j+{\frac {1}{2}}}+\sigma _{i,j-{\frac {1}{2}}})}}\right]\end{array}}$

( 8)

onde, σ_{i +1/2,j} , σ_{i −1/2,j} , σ_{i ,j +1/2} e σ_{i ,j −1/2} , são os valores da condutividade em pontos localizados centralmente entre os pontos (i , j ) e (i  + 1, j ), (i , j ) e (i  − 1, j ), (i , j ) e (i , j  + 1) e (i , j ) e (i , j  − 1), respectivamente. A condutividade nesses pontos pode ser obtida através do cálculo da média harmônica da condutividade entre as regiões adjacentes avaliadas. Portanto, a condutividade no ponto médio entre os pontos (i  + a , j  + b ) e o ponto (i , j ), sendo a e b números inteiros quaisquer, é dada por:

$\sigma _{i+{\frac {a}{2}},j+{\frac {b}{2}}}={\frac {\left(\sigma _{i+a,j+b}\sigma _{i,j}\right)}{\left({\frac {\sigma _{i+a,j+b}+\sigma _{i,j}}{2}}\right)}}$

( 9)

Além das equações (7) e (8), foi proposta uma terceira equação para aproximar o potencial numa região com condutividade heterogênea. As equações (7) e (8) aproximam o potencial em um ponto ${\textstyle \left(i,j\right)}$ , utilizando os 4 pontos adjacentes mais próximos a ele (estêncil de 5 pontos). No entanto, é possível fazer essa mesma aproximação utilizando os 8 pontos adjacentes ao ponto ${\textstyle \left(i,j\right)}$ (estêncil de 9 pontos). Como uma alternativa para as aproximações (7) e (8), o potencial em Ω pode ser aproximado utilizando a expressão mostrada a seguir:

${\begin{array}{c}u_{i,j}={\frac {4}{5}}\left[{\frac {\left(\sigma _{i+{\frac {1}{2}},j}u_{i+1,j}\right)+\left(\sigma _{i-{\frac {1}{2}},j}u_{i-1,j}\right)}{\left(\sigma _{i+{\frac {1}{2}},j}+\sigma _{i-{\frac {1}{2}},j}+\sigma _{i,j+{\frac {1}{2}}}+\sigma _{i,j-{\frac {1}{2}}}\right)}}+\right.\\\left.\displaystyle +{\frac {\left(\sigma _{i,j+{\frac {1}{2}}}u_{i,j+1}\right)+\left(\sigma _{i,j-{\frac {1}{2}}}u_{i,j-1}\right)}{\left(\sigma _{i+{\frac {1}{2}},j}+\sigma _{i-{\frac {1}{2}},j}+\sigma _{i,j+{\frac {1}{2}}}+\sigma _{i,j-{\frac {1}{2}}}\right)}}\right]+\\{\frac {1}{5}}\left[{\frac {\left(\sigma _{i+{\frac {1}{2}},j+{\frac {1}{2}}}\cdot u_{i+1,j+1}\right)+\left(\sigma _{i+{\frac {1}{2}},j-{\frac {1}{2}}}u_{i+1,j-1}\right)}{\left(\sigma _{i+{\frac {1}{2}},j+{\frac {1}{2}}}+\sigma _{i+{\frac {1}{2}},j-{\frac {1}{2}}}+\sigma _{i-{\frac {1}{2}},j+{\frac {1}{2}}}+\sigma _{i-{\frac {1}{2}},j-{\frac {1}{2}}}\right)}}+\right.\\\left.\displaystyle +{\frac {\left(\sigma _{i-{\frac {1}{2}},j+{\frac {1}{2}}}u_{i-1,j+1}\right)+\left(\sigma _{i-{\frac {1}{2}},j-{\frac {1}{2}}}u_{i-1,j-1}\right)}{\left(\sigma _{i+{\frac {1}{2}},j+{\frac {1}{2}}}+\sigma _{i+{\frac {1}{2}},j-{\frac {1}{2}}}+\sigma _{i-{\frac {1}{2}},j+{\frac {1}{2}}}+\sigma _{i-{\frac {1}{2}},j-{\frac {1}{2}}}\right)}}\right]\end{array}}$

( 10)

Esta nova equação é proposta com base na equação (8) e na equação apresentada por Adams et al. [9] .

4. Materiais e métodos

Utilizando o ambiente virtual Matlab®, foram implementados algoritmos capazes de solucionar problemas de valor de contorno (PVC) que envolvam a equação (1). Primeiramente, as aproximações foram utilizadas para a solução de um PVC com as seguintes condições de contorno: ${\textstyle u\left(0,y\right)=0}$ , ${\textstyle u\left(1,y\right)=cos\left(\pi y\right)}$ , ${\textstyle {\frac {\partial u}{\partial n}}\left(x,0\right)=0}$ e ${\textstyle {\frac {\partial u}{\partial n}}\left(x,1\right)=0}$ . Considerando um domínio com condutividade homogênea, este PVC possui a seguinte solução analítica

$u(x,y)={\frac {senh(\pi x)cos(\pi y)}{senh(\pi )}}$

( 11)

Para a solução numérica, a aproximação do valor da variável de interesse em Ω foi realizada utilizando as equações (10) e (8). A aproximação (7) não foi empregada porque se reduz à aproximação (8) para um domínio com condutividade homogênea. Para os valores das derivadas em ∂Ω, foram utilizadas as equações (3), (4), (5) e (6), e a definição de vetor unitário em coordenadas cartesianas. As equações obtidas são mostradas a seguir: Para a equação (3) com y  = 1, ângulo de 90° e isolando u_{i ,j} .

$u_{i,j}\approx {\frac {4u_{i,j-1}-u_{i,j2}}{3}}$

( 12)

Para a equação (4) com y  = 0, ângulo de 270° e isolando u_{i ,j} .

$u_{i,j}\approx {\frac {4u_{i,j+1}-u_{i,j+2}}{3}}$

( 13)

Para a equação (5) com y  = 1, ângulo de 90° e isolando u_{i ,j} .

$u_{i,j}\approx {\frac {\left(360u_{i,j-1}-450u_{i,j-2}+400u_{i,j-3}-225u_{i,j-4}+72u_{i,j-5}-10u_{i,j-6}\right)}{147}}$

( 14)

Para a equação (6) com y  = 0, ângulo de 270° e isolando u_{i ,j} .

$u_{i,j}\approx {\frac {\left(360u_{i,j+1}-450u_{i,j+2}+400u_{i,j+3}-225u_{i,j+4}+72u_{i,j+5}-10u_{i,j+6}\right)}{147}}$

( 15)

As equações (12) e (13) foram utilizadas associadas à equação (8), enquanto as equações (14) e (15) foram empregadas conjuntamente à equação (10), para a aproximação da solução do PVC.

A solução das equações foi realizada utilizando 3 diferentes malhas regulares com matrizes de 25 × 25, 49 × 49 e 97 × 97. Para a solução do sistema linear foi utilizado um algoritmo iterativo de sobre relaxação sucessiva [10] .

O erro associado a cada aproximação foi o fator principal a ser considerado para a escolha do conjunto de equações utilizadas durante a solução numérica. No caso das equações (12) e (13), elas possuem erro da ordem de h² , sendo que h  = Δx  = Δy , de acordo com a referência [8] , da mesma ordem de grandeza da equação (8). Enquanto, de acordo com a mesma referência, o erro associado às equações (14) e (15) é aproximadamente igual a h⁶ , exatamente a mesma ordem de grandeza do erro associado à equação (10) [11] .

Após a introdução das CC e a obtenção do valor da variável de interesse em cada nó, foi calculado o erro relativo para as soluções aproximadas em relação à solução analítica. O erro relativo foi calculado em cada um dos nós da malha, sendo assim obtida uma distribuição para o erro no domínio.

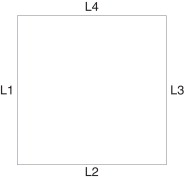
Em uma segunda etapa do trabalho foi resolvido o problema direto da TIE para geometria retangular. Quanto à discretização do contorno, nos pontos onde não havia presença de elétrodos, a derivada do potencial na direção normal à superfície foi considerada como possuindo valor 0. Assim, foram obtidas 4 discretizações para a derivada no contorno, dependendo do lado do retângulo considerado. Para facilitar a compreensão das quantizações realizadas, a cada lado foi atribuído um rótulo L1, L2, L3 e L4, como mostra a figura 1 apresentada a seguir.

Figura 1. Rótulos atribuídos a cada um dos lados da região avaliada.

Nos elétrodos foi considerado o valor da densidade linear de corrente J , definida como a razão entre o valor nominal da corrente e a dimensão linear de contato do elétrodo com o domínio. Utilizando essa definição para a densidade superficial de corrente, foram obtidas as aproximações para o contorno, as quais estão reunidas nas Tabela 1  and Tabela 2 .

Tabela 1. Aproximações por diferenças finitas da equação (2), utilizadas em conjunto com as discretizações de 5 pontos para a equação (1)

Lado	Região com elétrodo	Região sem elétrodo
L1	${\textstyle u_{i,j}={\frac {4u_{i+1,j}-u_{i+2,j}}{3}}-{\frac {2\Delta xi}{3\sigma _{0}L}}}$	${\textstyle u_{i,j}={\frac {4u_{i+1,j}-u_{i+2,j}}{3}}}$
L2	${\textstyle u_{i,j}={\frac {4u_{i,j+1}-u_{i,j+2}}{3}}-{\frac {2\Delta yi}{3\sigma _{0}L}}}$	${\textstyle u_{i,j}={\frac {4u_{i,j+1}-u_{i,j+2}}{3}}}$
L3	${\textstyle u_{i,j}={\frac {4u_{i-1,j}-u_{i-2,j}}{3}}-{\frac {2\Delta xi}{3\sigma _{0}L}}}$	${\textstyle u_{i,j}={\frac {4u_{i-1,j}-u_{i-2,j}}{3}}}$
L4	${\textstyle u_{i,j}={\frac {4u_{i,j-1}-u_{i,j-2}}{3}}-{\frac {2\Delta yi}{3\sigma _{0}L}}}$	${\textstyle u_{i,j}={\frac {4u_{i,j-1}-u_{i,j-2}}{3}}}$

Tabela 2.

Aproximações por diferenças finitas da equação (2), utilizadas em conjunto com a discretização de 9 pontos para a equação (1)

Lado	Região com elétrodo	Região sem elétrodo
L1	${\textstyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i+1,j}-450.u_{i+2,j}+400.u_{i+3,j}\\-225.u_{i+4,j}+72.u_{i+5,j}-10.u_{i+6,j}\end{array}}\right)}{147}}-{\frac {60\Delta xi}{147\sigma _{0}L}}}$	${\textstyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i+1,j}-450.u_{i+2,j}+400.u_{i+3,j}\\-225.u_{i+4,j}+72.u_{i+5,j}-10.u_{i+6,j}\end{array}}\right)}{147}}}$
L2	${\textstyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i,j+1}-450.u_{i,j+2}+400.u_{i,j+3}\\360.u_{i,j+1}-450.u_{i,j+2}+400.u_{i,j+3}\end{array}}\right)}{147}}-{\frac {60\Delta xi}{147\sigma _{0}L}}}$	${\textstyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i,j+1}-450.u_{i,j+2}+400.u_{i,j+3}\\-225.u_{i,j+4}+72.u_{i,j+5}-10.u_{i,j+6}\end{array}}\right)}{147}}}$
L3	${\textstyle {\begin{array}{l}\displaystyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i-1,j}-450.u_{i-2,j}+400.u_{i-3,j}\\-225.u_{i-4,j}+72.u_{i-5,j}-10.u_{i-6,j}\end{array}}\right)}{147}}-\\\displaystyle -{\frac {60\Delta x.i}{147\sigma _{0}L}}\end{array}}}$	${\textstyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i-1,j}-450.u_{i-2,j}+400.u_{i-3,j}\\360.u_{i-1,j}-450.u_{i-2,j}+400.u_{i-3,j}\end{array}}\right)}{147}}}$
L4	${\textstyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i,j-1}-450.u_{i,j-2}+400.u_{i,j-3}\\360.u_{i,j-1}-450.u_{i,j-2}+400.u_{i,j-3}\end{array}}\right)}{147}}-{\frac {60\Delta xi}{147\sigma _{0}L}}}$	${\textstyle u_{i,j}={\frac {\left({\begin{array}{c}360.u_{i,j-1}-450.u_{i,j-2}+400.u_{i,j-3}\\-225.u_{i,j-4}+72.u_{i,j-5}-10.u_{i,j-6}\end{array}}\right)}{147}}}$

O domínio analisado conta com 16 elétrodos dispostos em um quadrado com dimensões 1 × 1 unidades de medida de área (u. m. a.), sendo que em cada face do domínio foram arranjados 4 elétrodos. Cada um dos elétrodos possui dimensão linear 0,12 unidades de medida de comprimento (u. m. cp.). O valor de Δx é numericamente igual ao valor de Δy , valor que irá depender do tamanho da matriz. Basicamente, foram utilizados 3 distintos tamanhos de matriz para os testes: 25 × 25, 49 × 49 e 97 × 97 elementos de matriz.

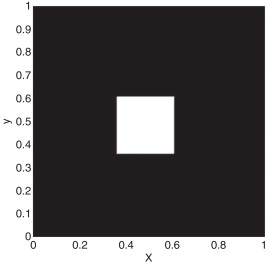
Em relação às distribuições de condutividade utilizadas para os testes, para um domínio homogêneo foi utilizado o valor de 20 unidades de medida de condutividade (u. m. c.); para um domínio heterogêneo a distribuição de condutividade utilizada possui 2 distintos valores, 20 u. m. c. e 110 u. m. c., respectivamente, para regiões da figura 2 , apresentada a seguir.

Figura 2. Forma da distribuição de condutividade utilizada durante os testes. Para a região escura foi utilizado o valor para condutividade de 20 u. m. c., enquanto para a região branca o valor utilizado foi de 110 u. m. c.

Para a corrente, foi empregado o valor de 3,00 unidades de medida de corrente (u. m. cr.), e esta foi injetada em pares de elétrodos adjacentes. Por sua vez, os elétrodos de injeção de corrente estão localizados entre as posições 0,0833 ‐ 0,1667 u. m. cp. e 0,3333 – 0,4167 u. m. cp. em todos os testes realizados.O sistema linear foi resolvido utilizando o algoritmo iterativo de Gauss‐Seidel [12] .

Após fazer a aproximação do potencial, foram realizadas comparações entre diferentes tamanhos de matriz. Isso foi realizado mediante a construção de gráficos do potencial em função de x ou y , para um valor de y ou x específico. As regiões escolhidas para traçar os gráficos foram as regiões do contorno, ou seja, aquelas regiões onde estavam localizados os elétrodos de injeção. O principal objetivo desse teste é observar a diferença entre os potenciais calculados por uma mesma aproximação, para diferentes tamanhos de matriz.

Foi realizado apenas um teste para analisar a estabilidade das aproximações. Resumidamente, esse teste utilizou domínios semelhantes aos apresentados na figura 2 , variando a condutividade da região em branco e verificando para determinada distribuição de condutividade se a solução numérica convergia ou não.

Quanto ao tempo computacional, não foram realizados procedimentos específicos para analisá‐lo. No entanto, por meio do emprego de um computador (2 Gb de memória RAM, processador Intel, modelo core 2 duo ) e considerando o método iterativo de Gauss‐Seidel para as matrizes 25 × 25, as soluções numéricas foram obtidas em poucos segundos (cerca de 3‐4 s). Em relação às matrizes maiores, como 49 × 49 e 97 × 97, o tempo necessário para obtenção das soluções foi maior. Por exemplo, considerando matrizes 49 × 49, as soluções foram obtidas em cerca de 30‐40 segundos, enquanto para matrizes 97 × 97, de 3‐4 minutos foram necessários para a visualização da solução numérica. Quanto às soluções produzidas utilizando o método de sobre relaxação sucessiva, para todos os tamanhos de matriz empregados as soluções foram obtidas em poucos segundos, no máximo 10 segundos para matrizes 97 × 97.

5. Resultados

Os resultados para a aproximação da solução do PVC estão reunidos na figura 3 apresentada a seguir:

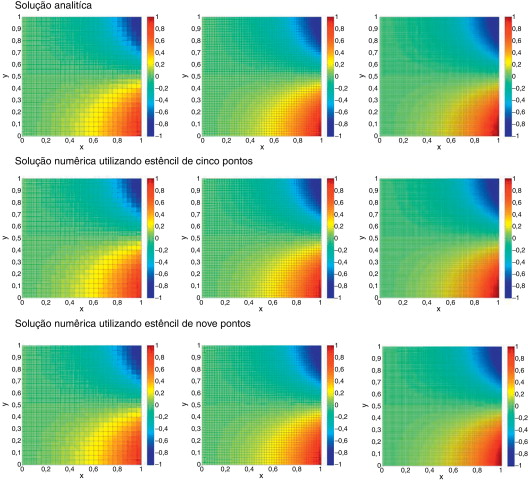
Figura 3. Solução analítica e numérica do PVC abordada para as matrizes 25 × 25, 49 × 49 e 97 × 97.

Cada uma das cores presentes nos gráficos dispostos na figura 3 representa o valor numérico de uma variável qualquer u , em um ponto qualquer do domínio discretizado. Os gráficos arranjados na parte superior da figura foram construídos utilizando os valores calculados para u , empregando a solução analítica do PVC, representada pela expressão (11). Para a construção dos outros gráficos, os valores de u foram obtidos valendo‐se das aproximações (8) e (10). Esse teste teve por objetivo analisar a acurácia das aproximações numéricas apresentadas. Por sua vez, a partir da visualização das soluções presentes na figura 4 , devido à precisão das soluções numéricas não é possível observar diferenças entre elas e a solução analítica. No entanto, foi realizado um teste onde, para cada ponto do domínio, o erro relativo das soluções numéricas em relação à solução analítica foi calculado. Avaliando os dados obtidos com estêncil de 5 pontos (equação [8]), para uma matriz de 25 × 25, o erro relativo máximo apresentado por esta aproximação foi cerca de 10⁴ vezes maior comparado ao erro relativo observado para aproximação de 9 pontos (equação [10]). Diferenças semelhantes foram observadas para as matrizes 49 × 49 e 97 × 97. A figura 4 apresentada a seguir é uma representação do erro relativo entre as soluções numéricas e a solução analítica, para cada ponto do domínio analisado, considerando uma matriz de 25 × 25, para solução do PVC utilizando (8) e (10).

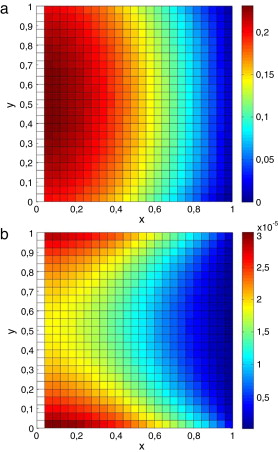
Figura 4. Erro relativo percentual calculado em cada ponto da matriz 25 × 25, utilizando as soluções numéricas e solução analítica do PVC. A) erro da solução numérica utilizando a aproximação com estêncil de 5 pontos; B) erro da solução numérica utilizando a aproximação com estêncil de 9 pontos.

O erro percentual máximo apresentado pela aproximação com estêncil de 5 pontos na figura 4 , foi cerca de 2 x 10^‐1 %, enquanto o erro máximo apresentado, para o mesmo tamanho de matriz, para a aproximação de 9 pontos foi cerca de 3 x 10^‐5 %. Em cada um dos gráficos, as regiões em vermelho são aquelas onde o erro percentual é aproximadamente igual ao erro máximo apresentado considerando todo o domínio.

Para a solução do problema direto em um domínio com distribuição de condutividade homogênea foram obtidos os seguintes resultados, exibidos na figura 5 .

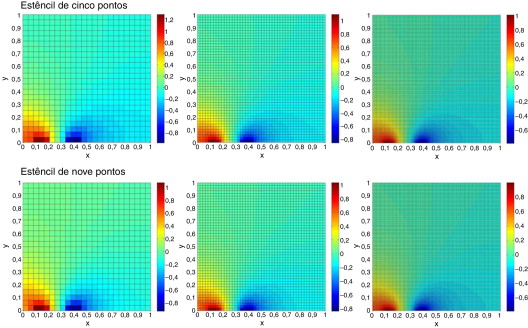
Figura 5. Solução do problema direto utilizando o padrão adjacente de injeção de correntes e o estêncil de 5 e 9 pontos para as matrizes 25 × 25, 49 × 49 e 97 × 97.

A figura 5 apresenta a solução do problema direto para um domínio com distribuição de condutividade constante igual 20 u. m. c. Esperava‐se um comportamento do potencial semelhante àquele apresentado pelo potencial de um dipolo elétrico. Essa expectativa foi confirmada pelos dados, para as 2 aproximações. Novamente, apenas utilizando os gráficos do potencial elétrico u em função de x e y , é difícil avaliar as diferenças dos resultados obtidos para 2 soluções numéricas e para os diferentes tamanhos de matriz. Por isso, na região dos elétrodos, onde o gradiente de potencial é maior, foram traçados gráficos de u em função de x com y = 0. Os gráficos do perfil do potencial, exibidos a seguir na figura 6 , representam os dados obtidos para soluções do problema direto apresentadas na figura 6 .

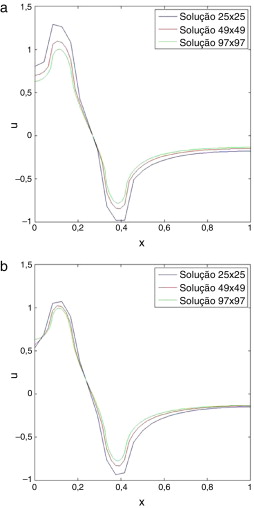
Figura 6. Gráficos do perfil do potencial traçado na região onde estão posicionados os elétrodos de injeção para a matriz 25 × 25, 49 × 49 e 97 × 97. A) gráfico traçado utilizando a aproximação com estêncil a aproximação (8); B) gráfico traçado utilizando a aproximação (10).

Os gráficos da figura 6 representam a solução do problema direto para todos os tamanhos de matriz e, de forma individual, aproximações (estêncil de 5 e 9 pontos) testadas na região dos elétrodos de injeção de corrente. Nessa região, como o potencial varia de forma mais intensa, supostamente seria mais facilmente observável a diferença entre os potenciais calculados utilizando diferentes tamanhos de matriz. Como a expressão (10) é mais precisa se comparada à expressão (8), era esperado que ela apresentasse menor variação entre as curvas traçadas. Observando a figura 6 , o gráfico A é aquele aonde há maior discrepância entre as curvas do potencial. Como ele foi traçado utilizando os dados da solução numérica do problema direto, obtidos por meio do emprego da expressão (8), a expectativa em relação aos resultados desse teste se confirmou, conforme pode ser observado na figura 6 .

A seguir são apresentados os resultados da solução do problema direto para uma distribuição de condutividade heterogênea, utilizando as aproximações (7), (8) e (10).

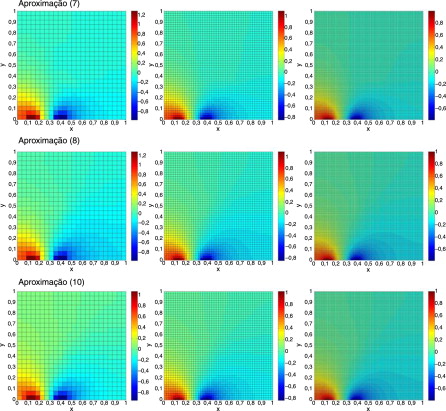
A distribuição de condutividade, sobre a qual as soluções apresentadas na figura 7 foram produzidas, é aquela representada na figura 2 . Quanto às aproximações, as equações testadas apresentaram, qualitativamente, bons resultados para essa distribuição de condutividade. No entanto, para melhor avaliação das aproximações, gráficos do perfil do potencial em y = 0 foram traçados. Para esses gráficos era esperado que a equação (10), caso pudesse aproximar o potencial em um domínio com distribuição de condutividade heterogênea, apresentasse resultados similares aos resultados obtidos com o emprego da aproximação (8). No entanto, as soluções produzidas através do emprego da aproximação (10) para diferentes tamanhos de matriz deveriam apresentar menor diferença entre si, como foi observado nos gráficos do perfil do potencial para uma distribuição de condutividade homogênea. Quanto à aproximação (7), como ela possui acurácia semelhante à equação (8), os resultados obtidos através do seu emprego deveriam ser idênticos ou muito próximos aos resultados apresentados por (8).

Figura 7. Solução numérica do problema direto utilizando matrizes 25 × 25, 49 × 49 e 97 × 97, para as aproximações (07), (08) e (10).

Os gráficos do perfil do potencial, para cada uma das aproximações abordadas, são apresentados na figura 8 .

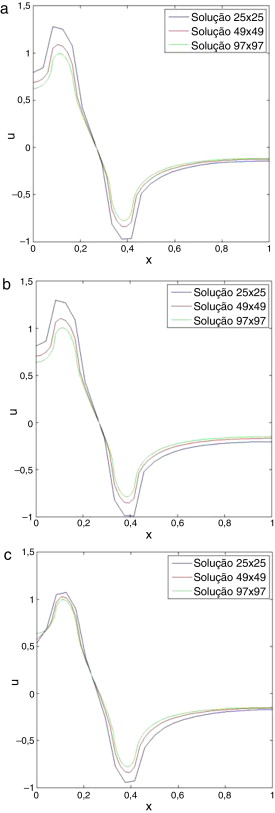
Figura 8. Gráficos do perfil do potencial traçado na região onde estão posicionados os elétrodos de injeção para a matriz 25 × 25, 49 × 49 e 97 × 97. A) gráfico traçado utilizando a aproximação (7); B) gráfico traçado utilizando a aproximação (8); gráfico traçado utilizando a aproximação (10).

Considerando os gráficos B e C dispostos na figura 8 , eles apresentaram diferenças entre as curvas traçadas e entre si, análogas às diferenças observadas nos gráficos dispostos na figura 6 . Isso indica que a aproximação (10) pode ser aplicada para domínios com distribuição de condutividade heterogênea. Quanto à equação (7), como esperado, os resultados obtidos para essa distribuição de condutividade são equivalentes aos resultados obtidos utilizando (8).

Os resultados dos testes de estabilidade indicam que a aproximação (7) não converge quando aplicada a domínios com grandes gradientes de condutividade. Por sua vez, as aproximações (8) e (10) convergiram para todas as distribuições de condutividade utilizadas durante os testes.

Não foram realizados testes para avaliar o tempo de convergência para as soluções. No entanto, de forma qualitativa, não foram observadas diferenças significativas para o tempo de convergência entre as soluções avaliadas para um mesmo tamanho de matriz.

6. Considerações finais

Este trabalho testou diferentes aproximações para o problema direto da TIE, pensando em sua aplicação para a solução do problema inverso. A solução do problema inverso, por sua vez, costuma necessitar diversas soluções do problema direto. Por isso, a definição de uma aproximação mais precisa e ao mesmo tempo veloz para o problema direto, pode em muito contribuir para um ganho de velocidade e/ou precisão das soluções do problema inverso.

Das aproximações testadas, a aproximação (7) foi aquela com resultados menos promissores. Em relação à precisão, ela é equivalente à aproximação (8). Por outro lado, apresentou diversos problemas de convergência, diferentemente das outras 2 aproximações.

A aproximação (8) exibiu bons resultados em relação à convergência e razoáveis em relação à precisão.

A aproximação (10) mostrou ótimos resultados para precisão e convergência, sendo, dentre as aproximações testadas, aquela que proporcionou melhores resultados.

Os dados obtidos permitem concluir que, utilizando uma das aproximações que propomos (10), é possível resolver o problema direto com malhas menores mantendo ou melhorando a precisão e a velocidade de convergência das soluções, quando estas soluções são comparadas às soluções produzidas empregando as demais equações testadas neste trabalho. Sendo assim, a equação (10) é a mais indicada para aproximar a solução do problema da TIE aplicando o MDF em malhas retangulares.

A solução tridimensional do problema direto da TIE pode ser uma alternativa para melhorar a acurácia das soluções produzidas, tendo em vista que soluções bidimensionais do problema direto não consideram a propagação tridimensional da corrente elétrica através do objeto analisado. Por isso, os autores deste trabalho estão estudando uma extensão tridimensional do método descrito, por meio da modificação para domínios não homogêneos das aproximações estudadas na referência [13] .

Agradecimentos

Os autores agradecem ao apoio financeiro da Petrobras ‐ Petróleo Brasileiro e ao Dr. Adriano Roessler Viana pela criteriosa análise do manuscrito e permissão para a publicação.

Bibliografia

1. [1] O.H. MENIN, Método dos Elementos de Contorno para Tomografia de Impedância Elétrica. Ribeirão Preto: USP, 2009. 71 pág. Dissertação (Mestrado), Programa de Pós‐Graduação em Física Aplicada à Medicina, Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto da Universidade de São Paulo, Brasil.
2. [2] M. Denai, M. Mahfouf, S. Mohamad-Samuri, G. Panoutsos, B. Brown e, G. Mills; Absolute electrical impedance tomography (aEIT) guided ventilation therapy in critical care patients: Simulations and future trends; IEEE Trans. Inf. Technol. Biomed, 14 (2010), pp. 641–649
3. [3] Y.J. Kim, M.G. Lee, Electrical impedance tomography on a resistive network with internal currents, [consultado 09 Jan 2012]. Disponível em: http://amath.kaist.ac.kr/papers/Kim/18.pdf
4. [4] T.P. Figueroa, P.P. Seleghim Jr.; Sensitivity analysis of different sensing strategies for electrical impedance imaging of two‐phase flows; J. Electron. Imaging., 10 (2001), pp. 641–645
5. [5] G.J. Saulnier, R.S. Blue, J.C. Newell, D. Isaacson, P.M. Edic; Electrical impedance tomography; Signal Processing Magazine, IEEE, 18 (2001), pp. 31–43 doi: 10.1109/79.962276
6. [6] B. Carnahan, H.A. Luther, J.O. Wilkes; Applied numerical methods; Wiley, N.Y (1969)
7. [7] D. Greenspan; Discrete numerical methods in physics and engineering; Academic Press, Inc, NY (1974)
8. [8] Numerical Solution of Partial Differential Equations ‐ Wolfram Mathematica 8 Documentation, [consultado 29 Nov 2011]. Disponível em: http://reference.wolfram.com/mathematica/tutorial/NDSolvePDE.html
9. [9] L.M. Adams, R.J. LeVeque, D.M. Young; Analysis of the SOR iteration for the 9‐point Laplacian; SIAM J. Numer. Anal., 25 (1988), pp. 1156–1180
10. [10] R.W. Hornbeck; Numerical methods; Prentice Hall (1975)
11. [11] C.J. Kuo, B.C. Levy; Mode‐dependent finite‐difference discretization of linear homogeneous differential equations; SIAM J. Sci. and Stat. Comput., 9 (1987), pp. 992–1015
12. [12] R.L. Burden, J.D. Faires; Análise numérica; Thomson Learning, São Paulo (2003)
13. [13] R.C. O’Reilly, J.M. Beck; A family of large‐stencil discrete Laplacian approximations in three‐dimensions; Int. J. Numer. Methods Eng., 1–16 (2006) [consultado 29 Nov2012]. Disponível em: http://psych.colorado.edu/∼oreilly/papers/OReillyBeckIP_lapl.pdf

Notes

b. Nesse artigo a «velocidade» de uma determinada aproximação numérica é sinônima do custo computacional de processamento da mesma.

c. Ler páginas 28 e 29 da referência [1] .