The fractional Rosenau–Hyman model and its approximate solution

Abstract

A relatively new method called q-Homotopy Analysis Method (q-HAM) is adopted in this paper to obtain an analytical solution of the time fractional Rosenau–Hyman equation in series form. Our analysis shows the simplicity nature of the application of q-HAM to nonlinear fractional differential equations. The convergence rate of the method used is faster in the sense that just very few terms of the series solution are needed for a good approximation due to the presence of the auxiliary parameter h comparable to exact solutions. Numerical solution obtained by this method is compared with the exact solution and solutions obtained by other analytical methods of the equation under various conditions. The numerical results are obtained using Mathematica 9 and MATLAB R2012b.

Keywords

Rosenau–Hyman equation; Fractional derivative; q-Homotopy Analysis Method

1. Introduction

The frequent use of analytical methods in solving nonlinear differential equations has the restriction that the variables involved in such methods are discretized and therefore the numerical techniques are always rounded off, see [1]. For some other analytical methods for solving nonlinear differential equations see [2] and [3].

The Rosenau–Hyman equation was found as a simplified model for the study of the role which nonlinear dispersion plays in pattern formation in liquid drops and it has found diverse applications in modelling of various problems in physics and engineering.

Modern advances in fractional differential equations are motivated by new examples of its applications in visco-elasticity, fluid mechanics, electro-chemistry, mathematical biology, and physics. Examples of such applications include the use of fractional derivatives in the model of nonlinear oscillation of earthquake [4] and in fluid-dynamic traffic model to eliminate the deficiency arising from the assumption of continuum traffic flow [5]. Experimental data obtained for seepage flow in porous media suggest that the differential equations associated with them are fractional and in recent times fractional differential equations have proven to be valuable tools for the modelling of many physical phenomena [6].

Many analytical methods have been successfully put to use to obtain solutions of the Rosenau–Hyman equation, such as the semi-analytical methods, Dissipative perturbation methods, Variational Iteration Method and Homotopy Perturbation Method, see [7], [8] and [9]. In recent, a modified HAM called q-Homotopy Analysis Method was introduced in [10], see also [11], [12], [13], [14], [15], [16] and [17]. The reliability of this method in terms of the rate of convergence was proven from the fact that the algorithm contains fraction factor which aids the convergence. The conclusion was reached that the method is better than the usual HAM in terms of fast convergence.

No attempt has been made regarding analytical solutions of the time-fractional Rosenau–Hyman equation using q-Homotopy Analysis Method to the best of our knowledge. In this paper, we consider this equation subject to some appropriate initial condition. Comparative analysis of our results is carried out with exact solution and with other analytical results for this problem. The effects of the auxiliary parameter h   and the fractional order ${\textstyle \alpha }$ on the solution are also shown. The numerical results of the problems are presented graphically.

2. Preliminaries

We give some definitions and some known results in this section. Caputo’s fractional derivative is adopted in this work.

Definition 2.1.

The Riemann–Liouville’s (RL) fractional integral operator of order ${\textstyle \alpha \geqslant 0}$, of a function ${\textstyle f\in L^{1}(a{\mbox{,}}b)}$ is given as

$I^{\alpha }f(t)={\frac {1}{\Gamma (\alpha )}}{\int }_{0}^{t}{\left(t-\tau \right)}^{\alpha -1}f(\tau )d\tau {\mbox{,}}\quad t>0{\mbox{,}}\quad \alpha >0{\mbox{,}}$

(1)

where ${\textstyle \Gamma }$ is the Gamma function and ${\textstyle I^{0}f(t)=f(t)}$.

Definition 2.2.

The fractional derivative in the Caputo’s sense is defined as [6],

$D^{\alpha }f(t)=I^{n-\alpha }D^{n}f(t)={\frac {1}{\Gamma (n-\alpha )}}{\int }_{0}^{t}{\left(t-\tau \right)}^{n-\alpha -1}f^{\left(n\right)}(\tau )d\tau {\mbox{,}}$

(2)

where ${\textstyle n-1<\alpha \leqslant n{\mbox{,}}\quad n\in N{\mbox{,}}\quad t>0}$.

Lemma 2.1.

Let  ${\textstyle t\in (a{\mbox{,}}b]}$. Then

$\left[I^{\alpha }{\left(t-a\right)}^{\beta }\right](t)=$${\frac {\Gamma (\beta +1)}{\Gamma (\beta +\alpha +1)}}{\left(t-a\right)}^{\beta +\alpha }{\mbox{,}}\quad \alpha \geqslant 0{\mbox{,}}\quad \beta >0{\mbox{.}}$

(3)

3. q-Homotopy Analysis Method (q-HAM)

Differential equation of the form

$N\left[D_{t}^{\alpha }u(x{\mbox{,}}t)\right]-f(x{\mbox{,}}t)=$$0$

(4)

is considered, where N   is a nonlinear operator, ${\textstyle D_{t}^{\alpha }}$ denote the Caputo fractional derivative, ${\textstyle \left(x{\mbox{,}}t\right)}$ are independent variables, f is a known function and u is an unknown function. To generalize the original homotopy method, the zeroth-order deformation equation is constructed as

$(1-nq)L\left(\phi (x{\mbox{,}}t{\mbox{;}}q)-u_{0}(x{\mbox{,}}t)\right)=$$qhH(x{\mbox{,}}t)\left(N\left[D_{t}^{\alpha }\phi (x{\mbox{,}}t{\mbox{;}}q)\right]-\right.$$\left.f(x{\mbox{,}}t)\right){\mbox{,}}$

(5)

where ${\textstyle n\geqslant 1{\mbox{,}}q\in \left[0{\mbox{,}}{\frac {1}{n}}\right]}$ denotes the so-called embedded parameter, L   is an auxiliary linear operator, ${\textstyle h\quad \not =\quad 0}$ is an auxiliary parameter, and ${\textstyle H(x{\mbox{,}}t)}$ is a non-zero auxiliary function.

It is clearly seen that when ${\textstyle q=0}$ and ${\textstyle q={\frac {1}{n}}}$, Eq. (5) becomes

$\phi (x{\mbox{,}}t{\mbox{;}}0)=u_{0}(x{\mbox{,}}t)\quad {\mbox{and}}\quad \phi \left(x{\mbox{,}}t{\mbox{;}}{\frac {1}{n}}\right)=$$u(x{\mbox{,}}t)$

(6)

respectively. So, as q   increases from 0 to ${\textstyle {\frac {1}{n}}}$, the solution ${\textstyle \phi (x{\mbox{,}}t{\mbox{;}}q)}$ varies from the initial guess ${\textstyle u_{0}(x{\mbox{,}}t)}$ to the solution ${\textstyle u(x{\mbox{,}}t)}$.

If ${\textstyle u_{0}(x{\mbox{,}}t){\mbox{,}}L{\mbox{,}}h{\mbox{,}}H(x{\mbox{,}}t)}$ are chosen appropriately, solution ${\textstyle \phi (x{\mbox{,}}t{\mbox{;}}q)}$ of Eq. (5) exists for ${\textstyle q\in \left[0{\mbox{,}}{\frac {1}{n}}\right]}$.

Expansion of ${\textstyle \phi (x{\mbox{,}}t{\mbox{;}}q)}$ in Taylor series gives

$\phi (x{\mbox{,}}t{\mbox{;}}r)=u_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }u_{m}(x{\mbox{,}}t)q^{m}{\mbox{.}}$

(7)

where

$u_{m}(x{\mbox{,}}t)={{\frac {1}{m!}}{\frac {{\partial }^{m}\phi (x{\mbox{,}}t{\mbox{;}}q)}{\partial q^{m}}}}_{q=0}{\mbox{.}}$

(8)

Assume that the auxiliary linear operator L  , the initial guess ${\textstyle u_{0}}$, the auxiliary parameter h   and ${\textstyle H(x{\mbox{,}}t)}$ are properly chosen such that the series (7) converges at ${\textstyle q={\frac {1}{n}}}$, then we have

$u(x{\mbox{,}}t)=u_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }u_{m}(x{\mbox{,}}t){\left({\frac {1}{n}}\right)}^{m}{\mbox{.}}$

(9)

Let the vector ${\textstyle u_{n}}$ be defined as follows:

${\overset {\rightarrow }{u}}_{n}=\left\{u_{0}(x{\mbox{,}}t){\mbox{,}}u_{1}(x{\mbox{,}}t){\mbox{,}}\ldots {\mbox{,}}u_{n}(x{\mbox{,}}t)\right\}{\mbox{.}}$

(10)

Differentiating Eq. (5)m-times with respect to the (embedding) parameter q  , then evaluating at ${\textstyle q=0}$ and finally dividing them by ${\textstyle m!}$, we have what is known as the ${\textstyle m}$th-order deformation equation [18] as

$L\left[u_{m}(x{\mbox{,}}t)-{\chi }_{m}^{_{\ast }}u_{m-1}(x{\mbox{,}}t)\right]=$$hH(x{\mbox{,}}t)R_{m}\left({\overset {\rightarrow }{u}}_{m-1}\right){\mbox{.}}$

(11)

with initial conditions

$u_{m}^{\left(k\right)}(x{\mbox{,}}0)=0{\mbox{,}}\quad k=$$0{\mbox{,}}1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}m-1{\mbox{.}}$

(12)

where

$R_{m}\left({\overset {\rightarrow }{u}}_{m-1}\right)={{\frac {1}{(m-1)!}}{\frac {{\partial }^{m-1}\left(N[D_{t}^{\alpha }\phi (x{\mbox{,}}t{\mbox{;}}q)]-f(x{\mbox{,}}t)\right)}{\partial q^{m-1}}}}_{q=0}$

(13)

and

${\chi }_{m}^{_{\ast }}={\begin{array}{ll}0&m\leqslant 1\\n&{\mbox{otherwise,}}\end{array}}$

(14)

4. Fractional Rosenau–Hyman equation

We consider the time-fractional Rosenau–Hyman equation.

Let

${\frac {{\partial }^{\alpha }u}{\partial t^{\alpha }}}=$$u{\frac {{\partial }^{3}u}{\partial x^{3}}}+u{\frac {\partial u}{\partial x}}+$$3{\frac {\partial u}{\partial x}}{\frac {{\partial }^{2}u}{\partial x^{2}}}{\mbox{,}}\quad t>0{\mbox{,}}\quad 0<\alpha \leqslant 1$

(15)

subject to the initial condition

$u(x{\mbox{,}}0)=-{\frac {8c}{3}}{cos}^{2}\left({\frac {x}{4}}\right){\mbox{.}}$

(16)

The exact solution to this problem for ${\textstyle \alpha =1}$ and c arbitrary constant, is given [19] as follows:

$u(x{\mbox{,}}t)=-{\frac {8c}{3}}{cos}^{2}\left({\frac {x-ct}{4}}\right){\mbox{.}}$

(17)

Analytical solution of this problem is considered in [7] using VIM and HPM.

4.1. Application of q-HAM

To solve the problem given in (15) by q-HAM, we choose the linear operator

$L[\phi (x{\mbox{,}}t{\mbox{;}}q)]=D_{t}^{\alpha }\phi (x{\mbox{,}}t{\mbox{;}}q)$

(18)

with property that ${\textstyle L[d_{1}]=0{\mbox{,}}d_{1}}$ is constant.

Using ${\textstyle u_{0}(x{\mbox{,}}t)=-{\frac {8c}{3}}{cos}^{2}\left({\frac {x}{4}}\right)}$ as initial approximation, we define the non-linear operator as

$N[\phi (x{\mbox{,}}t{\mbox{;}}q)]=D_{t}^{\alpha }\phi (x{\mbox{,}}t{\mbox{;}}q)-$$\phi (x{\mbox{,}}t{\mbox{;}}q){\phi }_{xxx}(x{\mbox{,}}t{\mbox{;}}q)-$$\phi (x{\mbox{,}}t{\mbox{;}}q){\phi }_{x}(x{\mbox{,}}t{\mbox{;}}q)-$$3{\phi }_{x}(x{\mbox{,}}t{\mbox{;}}q){\phi }_{xx}(x{\mbox{,}}t{\mbox{;}}q){\mbox{.}}$

We construct the zeroth order deformation equation

$(1-nq)L\left[\phi (x{\mbox{,}}t{\mbox{;}}q)-u_{0}(x{\mbox{,}}t)\right]=$$qhH(x{\mbox{,}}t)N\left[D_{t}^{\alpha }\phi (x{\mbox{,}}t{\mbox{;}}q)\right]{\mbox{.}}$

(19)

Choosing ${\textstyle H(x{\mbox{,}}t)=1}$, the mth-order deformation equation is

$L\left[u_{m}(x{\mbox{,}}t)-{\chi }_{m}^{_{\ast }}u_{m-1}(x{\mbox{,}}t)\right]=$$hR_{m}\left({\overset {\rightarrow }{u}}_{m-1}\right){\mbox{,}}$

(20)

with initial condition for ${\textstyle m\geqslant 1{\mbox{,}}u_{m}(x{\mbox{,}}0)=0{\mbox{,}}{\chi }_{m}^{_{\ast }}}$ is as defined in (14) and

$R_{m}\left({\overset {\rightarrow }{u}}_{m-1}\right)=D_{t}^{\alpha }u_{m-1}-$$\sum _{k=0}^{m-1}u_{k}{\left(u_{m-1-k}\right)}_{xxx}-$$\sum _{k=0}^{m-1}u_{k}{\left(u_{m-1-k}\right)}_{x}-3\sum _{k=0}^{m-1}{\left(u_{k}\right)}_{x}{\left(u_{m-1-k}\right)}_{xx}{\mbox{.}}$

(21)

So, the solution to Eq. (15) for ${\textstyle m\geqslant 1}$ becomes

$u_{m}(x{\mbox{,}}t)={\chi }_{m}^{_{\ast }}u_{m-1}+{hI}_{t}^{\alpha }\left[R_{m}\left({\overset {\rightarrow }{u}}_{m-1}\right)\right]{\mbox{.}}$

(22)

Therefore, we obtain components of the solution using q-HAM successively as follows:

$u_{1}(x{\mbox{,}}t)={\chi }_{1}^{_{\ast }}u_{0}+{hI}_{t}^{\alpha }\left[D_{t}^{\alpha }u_{0}-\right.$$\left.u_{0}{\left(u_{0}\right)}_{xxx}-3{\left(u_{0}\right)}_{x}{\left(u_{0}\right)}_{xx}-\right.$$\left.u_{0}{\left(u_{0}\right)}_{x}\right]$ $={\frac {2{hc}^{2}}{3}}sin\left({\frac {x}{2}}\right){\frac {t^{\alpha }}{\Gamma (1+\alpha )}}$ $u_{2}(x{\mbox{,}}t)={\chi }_{2}^{_{\ast }}u_{1}+{hI}_{t}^{\alpha }\left[D_{t}^{\alpha }u_{1}-\right.$$\left.u_{0}{\left(u_{1}\right)}_{xxx}-u_{1}{\left(u_{0}\right)}_{xxx}-\right.$$\left.3\left({\left(u_{0}\right)}_{x}{\left(u_{1}\right)}_{xx}+\right.\right.$$\left.\left.{\left(u_{1}\right)}_{x}{\left(u_{0}\right)}_{xx}\right)\right]$ $-{hI}_{t}^{\alpha }\left[u_{0}{\left(u_{1}\right)}_{x}+u_{1}{\left(u_{0}\right)}_{x}\right]$ $={\frac {2(n+h){hc}^{2}}{3}}sin\left({\frac {x}{2}}\right){\frac {t^{\alpha }}{\Gamma (1+\alpha )}}+$${\frac {h^{2}c^{3}}{3}}cos\left({\frac {x}{2}}\right){\frac {t^{2\alpha }}{\Gamma (1+2\alpha )}}$ $+{\frac {4h^{2}c^{3}}{9}}(cos(x)-1){\frac {t^{2\alpha }}{\Gamma (1+2\alpha )}}{\mbox{.}}$

(23)

Following the same approach, ${\textstyle u_{m}(x{\mbox{,}}t)}$ for ${\textstyle m=3{\mbox{,}}4{\mbox{,}}5{\mbox{,}}\ldots }$ can be obtained using Mathematica.

Then the series solution expression by q-HAM can be written in the form of

$u(x{\mbox{,}}t{\mbox{;}}n{\mbox{;}}h)=-{\frac {8c}{3}}{cos}^{2}\left({\frac {x}{4}}\right)+$$\sum _{i=1}^{\infty }u_{i}(x{\mbox{,}}t{\mbox{;}}n{\mbox{;}}h){\left({\frac {1}{n}}\right)}^{i}{\mbox{.}}$

(24)

Eq. (24) is an appropriate solution to the problem (15) in terms of convergence parameter h and n.

5. Numerical results

In this section, we give some numerical results using series solution obtained above. Comparison is made with exact solution for a special case using the 2-term series solution. We also show the graph displaying the best choice of h for fast convergence and the effects of different fractional order ${\textstyle \alpha }$ on the solution obtained.

5.1. Approximate solution vs exact solution

Exact solution is known in the case of ${\textstyle \alpha =1}$ and so we present the numerical result (2-term series solution) obtained by the q-Homotopy Analysis Method and the exact solution of Eq. (15) under some conditions.

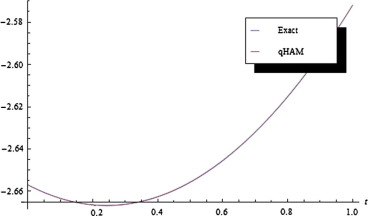
Remark 5.1.

It should be noted that we have used only 2-term of the series solution obtained by our method to make Fig. 1 as against 5-term series solution obtained by the variational iterative method and homotopy perturbation method used in [7]. Fig. 1 shows a perfect match with exact solution. This shows the effectiveness of the homotopy analysis method over other analytical methods due to the ability to control or choose appropriately the auxiliary parameter h.

Figure 1. q-HAM solution plot of u   for ${\textstyle h=-1.02{\mbox{,}}n=1{\mbox{,}}c=1}$ and ${\textstyle \alpha =1}$ against exact solution.

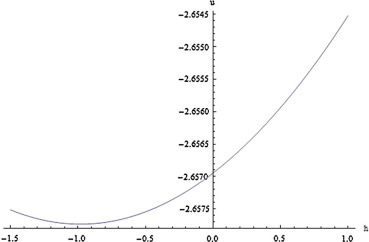
5.2. The h-curve

The question that comes to mind when following this method of solution is how does one choose the auxiliary parameter h to get a good approximate solution. The answer is in the h-curve. Apparently, our choice in the plots can be seen directly from the graph, the range of which is by drawing a horizontal line on the curve parallel to x-axis. Fig. 2 is made with ${\textstyle c=1{\mbox{,}}n=1}$ and ${\textstyle \alpha =1}$.

Figure 2. q-HAM solution plot against h   with fixed ${\textstyle x={\frac {\pi }{13}}}$ and ${\textstyle t=0.01}$.

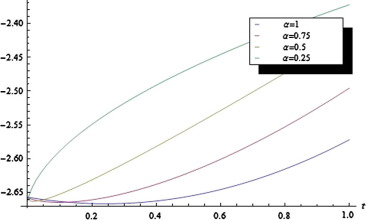
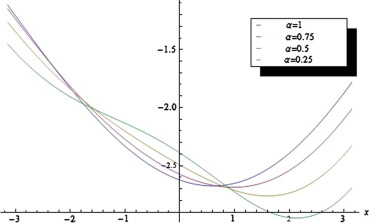
5.3. Solution plots with different values of ${\textstyle \alpha }$5.3. Solution plots with different values of α {\textstyle \alpha }

Here, we give the solution plots of the 2-term series solution given by our method. This shows the effect of the fractional order ${\textstyle \alpha }$ on the obtained solution (see Figure 3 and Figure 4).

Figure 3. q-HAM solution plot of Eq. (15) for different values of ${\textstyle \alpha }$ with fixed ${\textstyle x=\pi /13{\mbox{,}}c=1{\mbox{,}}h=-1.02}$ and ${\textstyle n=1}$.

Figure 4. q-HAM solution plot of Eq. (15) for different values of ${\textstyle \alpha }$ with fixed ${\textstyle t=0.5{\mbox{,}}c=1{\mbox{,}}h=-1.02}$ and ${\textstyle n=1}$.

6. Conclusion

The main achievement of this paper is the demonstration of the successful application of the q-Homotopy Analysis Method (q-HAM) in obtaining an analytical solution of the time fractional Rosenau–Hyman equation. Our results confirm that the method is very effective for handling solutions of a class of non-linear partial differential equations of fractional order system.

The comparisons made with the exact solution and other analytical methods such as a variational iterative method (VIM) and homotopy perturbation method (HPM), see [7], expose the accuracy nature of q-HAM in the sense that just two terms of the series solution are needed to obtain better approximation using the auxiliary parameter h. This method is a potential analytical method for further works in strongly nonlinear fractional differential equations.

References

1. [1] H.-K. Pang, H.-W. Sun; Multigrid method for fractional diffusion equations; J. Comput. Phys. (2011) http://dx.doi.org/10.1016/j.jcp.2011.10.005
2. [2] Md. N. Alam, M.G. Hafez, M.A. Akbar; H-Or- Roshid; exact traveling wave solutions to the ${\textstyle \left(3+1\right)}$-dimensional mKdV–ZK and the ${\textstyle \left(2+1\right)}$-dimensional Burgers equations via exp${\textstyle \left(-\Phi (\eta )\right)}$-expansion method; Alexandria Eng. J., 54 (2015), pp. 635–644
3. [3] S. Gupta, D. Kumar, J. Singh; Analytical solutions of convection-diffusion problems by combining Laplace transform method and homotopy perturbation method; Alexandria Eng. J., 54 (2015), pp. 645–651
4. [4] J.H. He; Semi-inverse method of establishing generalized variational principles for fluid mechanics with emphasis on turbomachinery aerodynamics; Int. J. Turbo Jet Engines, 14 (1) (1997), pp. 23–28
5. [5] J.-H. He; Some applications of nonlinear fractional differential equations and their approximations; Bull. Sci. Technol. Soc., 15 (2) (1999), pp. 86–90
6. [6] I. Podlubny; Fractional differential equations; Mathematics in Science and Engineering, vol. 198, Academic Press, San Diego, Calif, USA (1999)
7. [7] R. Yulita, M.S.M. Nooorani; Solving the fractional Rosenau–Hyman equation via variational iteration method and homotopy perturbation method; Int. J. Diff. Eq. (2012), p. 14
8. [8] J. Garralón, F.R. Villatoro; Dissipative perturbations for the K(n,n) Rosenau–Hyman equation; Commun. Nonlinear Sci. Numer. Simulat., 17 (2012), pp. 4642–4648
9. [9] M. Dehghan, J. Manafian, A. Saadatmandi; Application of semi-analytical methods for solving the Rosenau–Hyman equation arising in the pattern formation in liquid drops; Int. J. Numer. Meth. Heat Fluid Flow, 22 (6) (2012), pp. 777–790
10. [10] M.A. El-Tawil, S.N. Huseen; The Q-homotopy analysis method (Q-HAM); Int. J. Appl. Math. Mech., 8 (15) (2012), pp. 51–75
11. [11] O.S. Iyiola, F.D. Zaman; A fractional diffusion equation model for cancer tumor; AIP Adv., 4 (2014), p. 107121
12. [12] O.S. Iyiola, G.O. Ojo; Analytical solutions of time-fractional models for homogeneous gadner equation and non-homogeneous differential equations; Ain Shams Eng. J., 5 (2014), pp. 999–1004
13. [13] O.S. Iyiola, M.E. Soh, C.D. Enyi; Generalised homotopy analysis method (q-HAM) for solving foam drainage equation of time fractional type; Math. Eng. Sci. Aerospace, 4 (4) (2013), pp. 105–116
14. [14] O.S. Iyiola, G.O. Ojo; On the analytical solution of Fornberg–Whitham equation with the new fractional derivative; Pramana J. Phys., 85 (4) (2015), pp. 567–575
15. [15] M.S. Mohamed, Y.S. Hamed; Solving the convection-diffusion equation by means of the optimal q-homotopy analysis method (Oq-HAM); Results Phys., 6 (2016), pp. 20–25
16. [16] O.S. Iyiola; On the solutions of non-linear time-fractional gas dynamic equations: an analytical approach; Int. J. Pure Appl. Math., 98 (4) (2015), pp. 491–502
17. [17] O.S. Iyiola; Exact and approximate solutions of fractional diffusion equations with fractional reaction terms; Prog. Fract. Diff. Appl., 2 (1) (2016), pp. 21–30
18. [18] S.-J. Liao; An approximate solution technique not depending on small parameters: a special example; Int. J. Non-linear Mech., 30 (3) (1995), pp. 371–380
19. [19] P.A. Clarkson, E.L. Mansfield, T.J. Priestley; Symmetries of a class of nonlinear third-order partial differential equations; Math. Comput. Modell., 25 (8–9) (1997), pp. 195–212