Design of optimal input–output scaling factors based fuzzy PSS using bat algorithm

Abstract

In this article, a fuzzy logic based power system stabilizer (FPSS) is designed by tuning its input–output scaling factors. Two input signals to FPSS are considered as change of speed and change in power, and the output signal is considered as a correcting voltage signal. The normalizing factors of these signals are considered as the optimization problem with minimization of integral of square error in single-machine and multi-machine power systems. These factors are optimally determined with bat algorithm (BA) and considered as scaling factors of FPSS. The performance of power system with such a designed BA based FPSS (BA-FPSS) is compared to that of response with FPSS, Harmony Search Algorithm based FPSS (HSA-FPSS) and Particle Swarm Optimization based FPSS (PSO-FPSS). The systems considered are single-machine connected to infinite-bus, two-area 4-machine 10-bus and IEEE New England 10-machine 39-bus power systems for evaluating the performance of BA-FPSS. The comparison is carried out in terms of the integral of time-weighted absolute error (ITAE), integral of absolute error (IAE) and integral of square error (ISE) of speed response for systems with FPSS, HSA-FPSS and BA-FPSS. The superior performance of systems with BA-FPSS is established considering eight plant conditions of each system, which represents the wide range of operating conditions.

Keywords

Bat algorithm (BA) ; Fuzzy logic controller (FLC) ; Fuzzy logic based power system stabilizer (FPSS) ; Harmony search algorithm (HSA) ; Input–output scaling factors ; Particle swarm optimization (PSO) ; Performance indices (PIs) ; Power system stabilizer (PSS)

Nomenclature

A⁰- Loudness of sound

A- System matrix

B- Input matrix

D_i- Damping coefficient for the ${\textstyle i^{th}}$ generator

ε- Elite percentage

${\textstyle E_{fdi}}$- Equivalent excitation voltage of the ${\textstyle i^{th}}$ generator

${\textstyle {E^{'}}_{qi}}$- Internal voltage behind the d-axis transient reactance

${\textstyle f_{max}}$- Maximum frequency

${\textstyle f_{min}}$- Minimum frequency

i- ${\textstyle i^{th}}$ generator

${\textstyle K_{Ai}}$- AVR gain of the ${\textstyle i^{th}}$ generator

${\textstyle K_{1ij}-K_{6ij}}$- Heffron-Phillip constants

K_p- Scaling factor for Δp signal

K_u- Scaling factor for Δu signal

K_ω- Scaling factor for Δω signal

M_i- Machine inertia coefficient for the ${\textstyle i^{th}}$ generator

N- Number of generators

${\textstyle N_{pss}}$- Number of PSS

${\textstyle P_{g0}}$- Active power

Δp- Change in power

r- Pulse rate

${\textstyle T_{Ai}}$- AVR time-constant of the ${\textstyle i^{th}}$ generator

${\textstyle {T^{'}}_{d0i}}$- d-axis open-circuit transient time-constant of the ${\textstyle i^{th}}$ gen

${\textstyle T_{mi}}$- Mechanical torque of the ${\textstyle i^{th}}$ generator

U- Input variable vector

Δu- Change in PSS output signal

Δω- Change in speed

Δω_i- Change in speed for the ${\textstyle i^{th}}$ generator

ω₀- Synchronous speed of the generator

X- State variable vector

X_l- Transmission line reactance

U_i- PSS output signal of the ${\textstyle i^{th}}$ generator

1. Introduction

Modern electric power systems (EPSs) are complex, interconnected and susceptible to low frequency oscillations (LFOs) in the frequency range of 0.2 Hz–3.0 Hz. Power system stabilizers (PSSs) have been commonly used to damp out these LFOs. The changes in loading conditions, operating conditions and some sort of disturbance are main causes to develop LFOs in EPSs. Conventional power system stabilizers (CPSSs) consisting of lead-lag networks are generally used PSS for damping out these oscillations because of simple structure and easy installation. The design of CPSS is based on linear control theory and involves the linearized dynamic model with a specific operatic condition of EPS. These controllers give degraded performance with varying operating conditions and sometime unable to maintain stability of EPS on a higher degree of loading conditions [1]  and [2] .

The wide range of operating conditions for real EPS has motivated researchers to develop different methods to design PSS with improved performances and this resulted to the application of adaptive and robust control to design PSS. The basic idea behind the adaptive technique is to estimate the dynamic model with resting uncertainties in the system online based on measured signals. The erroneous estimation of states and the uncertainty may lead to design of PSS with degraded performance. In online transient stability assessment, some selected contingencies need to be evaluated as fast as possible before occurrence of a fault or a disturbance in the system. Therefore, the computational time is very critical. H∞ optimization technique is used to design robust PSS, but it gives the PSS order as high as that of the plant, which increases the complexity to the system and reduces its applicability [3] .

In early phase of optimization, CPSS parameters have been tuned using gradient based optimization technique. It requires the computation of sensitivity and eigenvectors at the end iteration, which resulted with heavy computational burden and slow convergence rate. The heuristic based optimization techniques are employed to tune the parameters of CPSS and proportional integral derivative (PID) based PSS. Among these are Tabu search algorithm [1] , real coded genetic algorithm (RCGA) [4] , genetic algorithm [3] , particle swarm optimization (PSO) [4]  and [5] , and breeder genetic algorithm [6] . Bacteria foraging algorithm [3] , simulated annealing [7] , differential evolution [1] and strength pareto evolutionary algorithms [8] have been used successfully to tune the CPSS parameters. However, genetic and simulated annealing algorithms have the tendency of revisiting the sub-optimal solutions and thus the designed CPSS may give deteriorated performance. These optimization techniques fail with an epistatic objective function, which have closely related to multi-model problems and the higher number of variables [9] .

To mitigate these limitations, an artificial intelligence based methods of PSS design, such as artificial neural networks (ANNs) [10] , fuzzy logic [11] , [12] , [13]  and [14] , adaptive fuzzy [15] , neuro-fuzzy [16]  and [17] , and interval type-2 [18]  and [19] , have been reported in literature. In the case of ANN, the gradient algorithm is being used to learn its parameters using either input/output [20] parameters or online data from different operating points in a power system network.

Fuzzy logic controllers (FLCs) can cope with those that naturally have lots of vagueness or uncertainty in their behavior. These do not require a mathematical model of the controlled process. These have rigidity and robustness as their profound and interesting characteristics in comparison to other methods. The properly designed fuzzy logic based PSS works similar to PD or PID based PSS [21] . Development of an equivalence between the scaling factor of a fuzzy controller and linear PID controller coefficients is reported in [22] . The selection of scaling factors, appropriate membership function, number of linguistic variables and the corresponding rule table are the major requirement in designing PSS based on FLC. The detail on linguistic variables and selection of membership function is well reported in [23] . Based on an organized approach, a standardized rule table is proposed in [24] . The optimization of scaling factors using particle swarm optimization is reported in [5] . The harmony search algorithm (HSA) is proposed by Geem et al in 2001 [25] , and is inspired by the process of the improvisation used by musicians to achieve harmony. The HS algorithm [26] is a meta-heuristic optimization algorithm that is similar to the PSO [27] and GA [28] . It has been implemented extensively in the fields of engineering optimization in [26] . It became an alternative to other heuristic algorithms like PSO [27] and simulated annealing (SA) [7] . It is a derivative free, meta-heuristic optimization (which does not use trial-and-error), inspired by the way musicians improvise new harmonies [29] , and it uses higher-level techniques to solve problems efficiently [2] .

In the field of optimization, much of algorithms are floating with unique properties. Some are useful to one application, while others are not so. The bat algorithm reported by Yang (2010) is meta-heuristic in nature [30] . It is based on the echolocation based behavior of micro bats [31] . It was established by considering benchmark functions that the behavior is superior to PSO and GA [32] . It has also reported that the application of GA and PSO is inappropriate with multi-model problems. The frequency-tuning and automatic zooming are out of the main features of the bat algorithm.

Particle swarm optimization (PSO) and Firefly algorithm (FA) generate an efficient codebook, but undergo instability in convergence when particle velocity is high and with the non-availability of brighter fireflies in the search space, respectively. The application of Bat Algorithm (BA) on the initial solution of LindeBuzoGray (LBG) is presented in [33] . It produces an efficient codebook with less computational time and results due to its automatic zooming feature using adjustable pulse emission rate and loudness of bats [33] . The design of fuzzy proportional derivative controller and fuzzy proportional derivative integral controller for speed control of brushless direct current drive has been presented in [34] . The problem of controller design is considered as an optimization using nature inspired optimization algorithms such as particle swarm, cuckoo search, and bat algorithms [34] . A Firefly Algorithm (FA) optimized fuzzy PID controller is proposed for Automatic Generation Control (AGC) of multi-area multi-source power system in [35] .

In [5] , the scaling factors associated with two inputs and one output are optimized by PSO for single-machine infinite-bus (SMIB) and two-area 4-machine 10-bus power system. These scaling factors (input–output) have been further optimized using harmony search algorithm in [2] . The performance of the HSA-FPSS has been compared and was found better as compared to PSO-FPSS for both power systems. In this paper, bat algorithm (BA) has been used to optimize scaling factors of FPSSs for SMIB, 4-machine and IEEE New England 10-machine 39-bus power systems. The performance of the proposed BA-FPSS is to be compared to the PSO-FPSS [5] and HSA-FPSS [2] for the three-power systems. The performance evaluation is carried out in terms of ITAE, IAE and ISE in each case of a controller as well as a power system under study.

In the organization of this paper, the problem formulation is considered by introducing test power systems, and an objective function used for optimization of scaling factors in Section 2.2 . The bat algorithm used to determine optimal set of input–output scaling factors is mentioned in Section 3 . Optimization of scaling factors of FPSSs for all three-power systems using bat algorithm is carried out in Section 4 . The optimal set of scaling factors for SMIB power system using bat algorithm and performance comparison with BA-FPSS, with HSA-FPSS, PSO-FPSS [5] and with FPSS (without scaling factors) is discussed in Section 4.1 . It is repeated for 4-machine power system in Section 4.2 . The process of optimal parameters for 10-machine power system is determined using harmony search, as well as bat algorithm in Section 4.3 . The detail on harmony search is not given and considered as in [2] with same initializing parameters. The nonlinear time-domain simulation is carried out on this power system using BA-FPSS and HSA-FPSS and compared with FPSS (without scaling factors) in this section. Lastly, Section 5 concludes.

2. Problem formulation

The aim of this paper is to utilize the superior performance of Bat algorithm for tuning input and output scaling factors of FPSS in connection with power systems; therefore, the EPS elements such as generators, excitation system and PSS must be modeled. To complete the tuning process, an objective function to obtain satisfactory results is necessary and should be defined. Accordingly, the system model and an objective function used in PSS parameter tuning process for SMIB, and multi-machine power systems, should be elaborated.

2.1. Test power systems

2.1.1. SMIB power system

The power system is a multi-component system. The equivalent of system can be represented by using differential equations. Assuming that the vector of states and the vector of inputs are represented by X and U , respectively, then the power system may be represented as in Eqn. (1) .

${\dot {X}}=f\left(X,{\mbox{ }}U\right)$

( 1)

A nonlinear power system can be linearized by considering small perturbation around an operating point. It is easy to design PSS to such linearized model of power system [9]  and [36] . The EPS represented by Eqn. (1) may be shown by state equations as in Eqn. (2) .

$\Delta {\dot {X}}=A\Delta X+BU$

( 2)

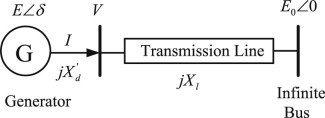
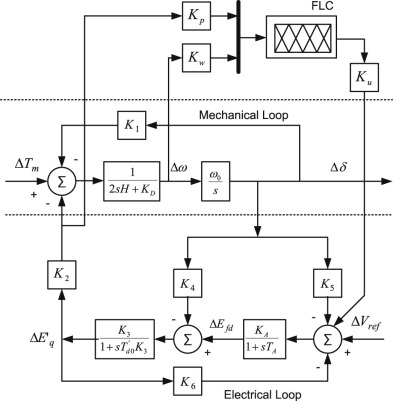
The infinite-bus of the SMIB power system can be considered by Thevenins equavalent of the large and complex power system. The components and inter-connections of the SMIB power system are shown in Fig. 1 . The inadequate damping of the generator is the main cause of small signal oscillations. The PSS may be connected to excitation system to add extra-damping of the generator as elaborated in [9] . The pioneer work on the design of appropriate PSS is presented in [37] .

Fig. 1. Line diagram of single-machine infinite-bus power system.

In system representation by Eqn. (2) , A is the system matrix of an order as 4 × 4 and is given by δf /δX , while B is the input matrix with order 4 × 1 and is given by δf /δU . The order of state vector is 4 × 1; the order is 1 × 1. Here, the well-known Heffron-Phillip linearized model is considered for fabricating the model in MATLAB 2011b as in [2]  and [9] . The SMIB power system dynamics in terms of differential equations are considered as in [38] .

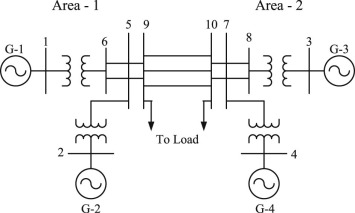
2.1.2. Two-area 4-machine 10-bus power system

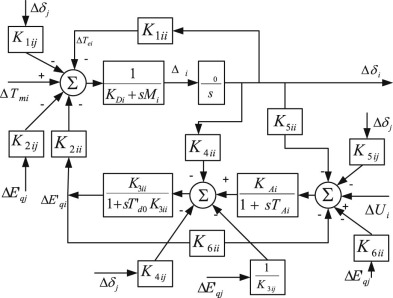
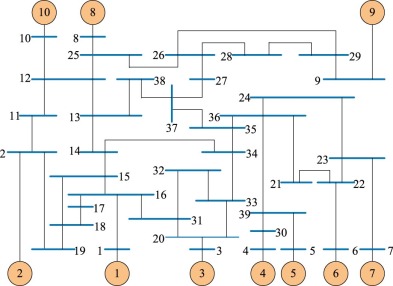
The 2nd system considered is two-area 4-machine 10-bus power system [2] . The line-diagram of the system is shown in Fig. 2 . The development of the small-signal model of multi-machine power system is well explained in [38] . It can be represented by a large number of differential and algebraic equations. The general representation of Heffron-Philip model for multi-machine power systems is shown in Fig. 3 . Consider N   as the number of generators of multi-machine power system, with ${\textstyle N_{pss}}$ the number of power system stabilizer connected in decentralized manner to the generators. The state model can be represented as in Eqn. (2) , where A is the system matrix with order 4N  × 4N (16 × 16) and is given by δf /δX , while B   is the input matrix with order ${\textstyle 4N\times N_{pss}}$ (16 × 4) and is given by δf δU . The order of state vector ΔX is 4N  × 1 (16 × 1), and the order of ΔU   is ${\textstyle N_{pss}\times 1}$ (4 × 1). Here, the well-known Heffron-Phillip linearized model is used to represent the large multimachine power system as in [2]  and [39] and the system dynamics is given in [38]  and [40] .

Fig. 2. Line diagram of two-area 4-machine 10-bus power system.

Fig. 3. General representation of Heffron-Philip model for multi-machine power systems.

2.1.3. IEEE New England 10-machine 39-bus power system

The state equations to the power system, consisting of N   , the number of generators, and ${\textstyle N_{pss}}$ , the number of power system stabilizers, can be written as in Eqn. (2) . In this case, A is the system matrix of the order 4N  × 4N (40 × 40) and B   is the input matrix with the order ${\textstyle 4N\times N_{pss}}$ (40 × 10). The order of state vector ΔX is 4N  × 1 (40 × 1), and the order of ΔU   is ${\textstyle N_{pss}\times 1}$ (10 × 1). Here, the well-known Heffron-Phillip linearized model is used to represent the large multi-machine power system, as in Fig. 3 , and the single-line diagram of IEEE 39-bus power system is shown in Fig. 4 .

Fig. 4. Line diagram of IEEE New England 10-machine 39-bus power systems.

2.2. Objective function

The scheme of input–output scaling factors of FPSS is considered as presented in [2] . The input signals to the FPSS are considered as change in speed (Δω ) and change in power (Δp ) with associated scaling factors as K_ω and K_p , respectively. The output signal of FPSS is considered as change in correction voltage (Δu ) and the scaling factor as K_u[2] . In this paper, these scaling factors are determined using bat algorithm. The problem of tuning scaling factors is considered as an optimization with minimization of integral squared error (ISE) of change in speed signal as a fitness function.

As an objective function, the ISE based cost function is represented for SMIB, four-machine and ten-machine power system by Eqns. (3) , (4)  and (5) , respectively. The connections of scaling factors of FPSS are shown in Fig. 5 , where the change in speed is subjected to minimize using the bat algorithm to obtain optimal set of input–output scaling factors.

$J=\int _{0}^{T_{sim}}{\vert \Delta \omega \left(t\right)\vert }^{2}\cdot dt$

( 3)

$J=\sum _{i=1}^{4}\int _{0}^{T_{sim}}{\vert \Delta {\omega }_{i}{\mbox{ }}\left(t\right)\vert }^{2}\cdot dt$

( 4)

$J=\sum _{i=1}^{9}\int _{0}^{T_{sim}}{\vert \Delta {\omega }_{i}{\mbox{ }}\left(t\right)\vert }^{2}\cdot dt$

( 5)

Fig. 5. Representation of Heffron-Philip model for SMIB power system with input–output scaling factors of FPSS.

The parameter bounds for SMIB power system are as in Eqn. (6)[2] .

${\begin{array}{l}K_{p}^{min}\leq K_{p}\leq K_{p}^{max}\\K_{\omega }^{min}\leq K_{\omega }\leq K_{\omega }^{max}\\K_{u}^{min}\leq K_{u}\leq K_{u}^{max}\end{array}}$

( 6)

${\begin{array}{l}K_{pi}^{min}\leq K_{pi}\leq K_{pi}^{max}\\K_{\omega i}^{min}\leq K_{\omega i}\leq K_{\omega i}^{max}\\K_{ui}^{min}\leq K_{ui}\leq K_{ui}^{max}\end{array}}$

( 7)

Eqn. (7) includes parameter bounds for both multi-machine power systems [2] . The i   stands for ${\textstyle i^{th}}$ generator in the multi-machine power system and ${\textstyle T_{sim}}$ refers to simulation time during optimization process and specified as 100 seconds. In the case of IEEE 10-machine power system, the value of i   is 09, because ${\textstyle {10}^{th}}$ generator is considered as slack without controller at this generator. Considering one of the above objectives corresponding to the system under investigation, the proposed approach employs the bat algorithm with parameter bounds to solve this optimization problem for an optimal set of input–output scaling factors of FPSS.

3. Review on bat algorithm

This algorithm is based on the echolocation behavior produced by natural bats in locating their prey. The pulse generated by microbats lasts for 8–10 seconds, with frequency range of 25–150 kHz and with associated wave length of 2–14 mm. Necessary assumptions are required to be considered during development of the echolocation characteristics of microbats [9]  and [41] .

• The bats are able to differentiate/detect the prey and background barriers in the search path using echolocation behavior.
• Assuming that ${\textstyle r^{th}}$ bat is randomly moving with velocity, location, frequency, wavelength and intensity represented by v_r , x_r   , ${\textstyle f_{min}}$ , λ_r and A⁰ , respectively, the pulse frequency is regulated and the pulse rate is adjusted in the range pr  = [0,1] on the basis of the distance of the prey.
• The loudness of the pulse is adjusted according to the distance of the prey as A⁰ (maximum for large distance) to ${\textstyle A_{min}}$ (minimum for lower distance) [42] .

In optimization problems, an objective function is represented by minimization of F (r ) and subjected to x_r  ∈ X_r   , ${\textstyle r=1,{\mbox{ }}2,{\mbox{ }}\ldots {\mbox{ }},{\mbox{ }}n}$ . In initialization step of the bat algorithm, the bat population is generated with velocity v_r and position x_r   for ${\textstyle r=1,{\mbox{ }}2,{\mbox{ }}\ldots {\mbox{ }},{\mbox{ }}n}$ . The pulse frequency is selected in the range ${\textstyle f_{r}\in \left[f_{min}{\mbox{​}},{\mbox{ }}f_{max}\right]}$ . Pulse rate and the loudness are set as above, while the search loop is set to maximum iteration counts as ${\textstyle t\leq T_{max}}$[31]  and [42] .

In step 2, the new solutions are generated by considering the following equations of frequency, velocity and position. For ${\textstyle r^{th}}$ bat, the new position and velocity at time step t   are represented by ${\textstyle x_{r}^{t}}$ and ${\textstyle v_{r}^{t}}$ , respectively [43] .

$f_{r}=f_{min}+\left(f_{max}-f_{min}\right)\beta$

( 8)

$v_{r}^{t}=v_{r}^{t-1}+\left(x_{r}^{t-1}-x^{'}\right)f_{r}$

( 9)

$x_{r}^{t}=x_{r}^{t-1}+v_{r}^{t}$

( 10)

where β represents the uniform distribution in the range β  ∈ [0, 1]. The value represents the best location in the search step for n bats.

In step 3, the local search is applied for the generation of the new solutions using local random walk behavior as described by the following Eqn. (11) . The ε is selected in the range of [−1, 1] with average value of loudness A^t at time t .

$x_{new}=x_{old}+\epsilon A^{t}$

( 11)

In step 4, the loop operation for generation of the new solutions is considered. On advancement of iterations, the loudness and the rate of pulse emission have to be updated by Eqns. (9)  and (10) . The rate of pulse emission is increased when shortening the path to prey.

$A_{r}^{t+1}=x_{old}+\alpha A_{r}^{t}$

( 12)

$pr_{r}^{t+1}=pr_{r}^{0}{\mbox{ }}\left[1-e^{-\gamma t}\right]$

( 13)

where α and γ represent the constant values in the range of 0 ≤ α  ≤ 1 and 0 < γ . The process behaves like the cooling factor of a cooling schedule in the simulated annealing [44] . The generally selected value of these constants is 0.9 in the literature [45] .

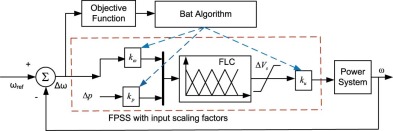
In the last step 5, the stopping criterion is checked as the maximum count of iterations is reached and termination of computation is executed. Otherwise, go to steps 3–4 to repeat the process. The tuning scheme of input–output scaling factors is shown in Fig. 6 , where the speed deviation is minimized using bat algorithm to decide optimal set of parameters. As the connection of scaling factors is already shown in Fig. 5 , Δp is left open intentionally to save space.

Fig. 6. Representation of tuning scheme for input–output scaling factors of FPSS using bat algorithm.

4. Results and discussion

4.1. SMIB power system

4.1.1. Plant creation for simulation

The line diagram and the small signal model of SMIB power system are represented in Figs. 1 and 5 , respectively. The operating conditions of SMIB power system are represented by different sets of active power ${\textstyle P_{g0}}$ and transmission line reactance X_l as mentioned in Table 1 . The plants are designed to represent operating conditions and weak conditions through heavy loading conditions. Plant-6 represents the nominal operating conditions as in [40] .

Table 1. Plant configuration of SMIB power system [38] .

PS model	$P_{g0}$	$Q_{g0}$	Xl
Plant-1	0.50	0.0251	0.20
Plant-2	0.50	0.0505	0.40
Plant-3	0.75	0.0566	0.20
Plant-4	0.75	0.1152	0.40
Plant-5	1.00	0.1010	0.20
Plant-6	1.00	0.2087	0.40
Plant-7	1.10	0.2550	0.40
Plant-8	1.20	0.3068	0.40

4.1.2. Optimal set of scaling factors

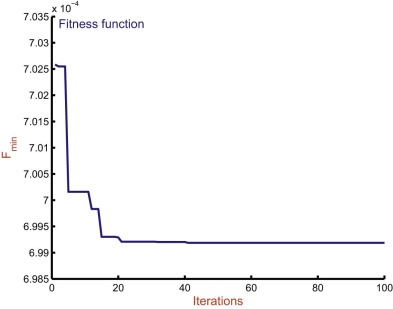
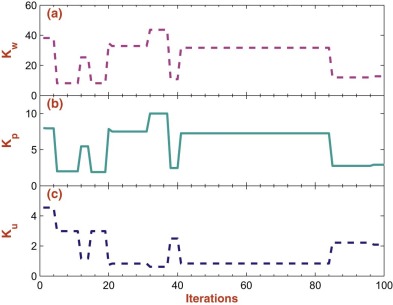
The problem is formulated in MATLAB environment and executed on Intel (R) Core (TM) – 2 Duo CPU T6400 @ 2.00 GHz with 3 GB RAM, 32-bit operating system. The SMIB system is equipped with FPSS along with input–output scaling factors. The scheme of optimization is shown in Fig. 6 . The problem of optimization of scaling factors is considered with an ISE based objective function as in Eqn. (3) . The steps of the bat algorithm are shown in Section 3 . In [32]  and [42] , the generally opted values of initializing parameters, such as intensity (A ) and pulse rate (r ) are 0.5 and 0.5, respectively. However, the proper initializing parameters for bat algorithm are considered after long efforts and found as A  = 0.9 and r  = 0.1. The other constraint such as initializing population is selected as n    = 25 and the bandwidth are considered as ${\textstyle f_{min}=0}$ and ${\textstyle f_{max}=2.0}$ . The plant (SMIB power system) operating at nominal operating condition (where in X_l  = 0.4pu   and ${\textstyle P_{g0}=1.0pu}$ ) is considered for optimal tuning of input–output scaling factors of FPSS. The scaling factors are considered with lower and upper bounds as ${\textstyle 0.001\leq K_{\omega }\leq 50.0}$ , ${\textstyle 0.001\leq K_{p}\leq 10.0}$ , and ${\textstyle 0.001\leq K_{u}\leq 5.0}$ . The optimization process with bat algorithms is set to terminate with maximum iteration counts as 100. The behavior of bat algorithm in terms of fitness function with iterations is shown in Fig. 7 . The variation of the PID parameters with iteration count is shown in Fig. 8 . The optimal set of parameters obtained using the bat algorithm is enlisted in Table 2 . The scaling factors using PSO in [5] and HSA in [2] for SMIB system are also included in the table for the purpose of comparison.

Fig. 7. Plot of fitness function using bat algorithm in tuning of input–output scaling factor for SMIB power system with nominal operating condition.

Fig. 8. Plot of input–output scaling factors with iteration count for SMIB power system.

Table 2. Optimal values of input–output scaling factors of FPSS with PSO [5] , HSA [2] and proposed BA on SMIB power system.

Controller	Parameters		Bounds
	Symbol	Values	Lower	Upper
BA-FPSS (Prop.)	Kω	13.2238	0.001	50.0
	Kp	3.0358	0.001	10.0
	Ku	2.0128	0.001	5.00
HSA-FPSS [2]	Kω	26.3928	0.001	50.0
	Kp	5.3353	0.001	10.0
	Ku	2.4531	0.001	5.00
PSO-FPSS [5]	Kω	59.80	0.0	70.0
	Kp	4.0	0.0	10.0
	Ku	1.0	0.0	10.0

4.1.3. Speed response analysis

A SIMULINK based block diagram, including all the nonlinear blocks, is generated in MATLAB software. The SMIB power system performance under nonlinear mode is carried out by creating self-clearing fault at time 5 seconds and persistent for 0.1 second with the wide range of operating conditions. The system with unlike combinations of different active power and transmission line reactance as in Table 1 (eight different plants) and system data as in [9]  and [38] is considered for nonlinear simulations. Such obtained eight-plants (covering wide range of operating conditions) are examined for the speed response with FPSS, HSA-FPSS and BA-FPSS in this section.

The fuzzy logic based PSS (FPSS) reported in [14]  and [46] is considered for comparison purpose. The numbers of linguistic variables are five as LN (large negative), MN (medium negative), Z (zero), MP (medium positive) and LP (large positive). The input signals to FLC have been considered as change in speed (Δw ) and change in power (Δp   ), while that of the output signal is considered as correction voltage (${\textstyle \Delta V_{pss}}$ ). The corresponding 25 rules of the rule-base are considered as presented in [46] . The triangular type membership function is considered for both input and output signals. The crisp value is obtained using centroid type defuzzification method.

The SIMULINK model of SMIB system is prepared in the MATLAB software equipped with FPSS, BA-FPSS and HSA-FPSS controllers. These systems are simulated for all eight plants as created in Table 1 . The comparison of speed response of SMIB system with FPSS, with PSO-FPSS [5] , with HSA-FPSS [2] and with BA-FPSS is carried out for each plant configuration. The comparative response is carried out for 8-plant conditions but shown only for plant-3, plant-6 and plant-7 in Fig. 9 , Fig. 10  and Fig. 11 , respectively. However, the response with other plants are not shown because of space limitation. Clearly, the settling time with BA-FPSS is better as compared to HSA-FPSS [2] , PSO-FPSS [5] and greatly improved with respect to FPSS [14]  and [46] . The response with HSA-FPSS [2] and BA-FPSS is comparable but the response with FPSS [46] settles in more than 25 seconds. The closely related responses with HSA-FPSS [2] and BA-FPSS are to be differentiated by recording performance indices.

Fig. 9. Speed response for Plant-3 with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and proposed BA-FPSS for SMIB power system.

Fig. 10. Speed response for Plant-6 with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and proposed BA-FPSS for SMIB power system.

Fig. 11. Speed response for Plant-7 with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and proposed BA-FPSS for SMIB power system.

To carry out the analysis with clear perceptiveness and completeness about the system response for all the system conditions, three performance indices that reflect the settling time and overshoot are introduced and evaluated as in [2]  and [9] . These indices are defined as folowing in Eqns. (14) , (15)  and (16) .

• Integral of the Time-Weighted Absolute Error (ITAE)

$ITAE={\int }_{t=0}^{T=t_{sim}}t\vert \Delta \omega \left(t\right)\vert dt$

( 14)

• Integral Square Error (ISE)

$ISE={\int }_{t=0}^{T=t_{sim}}{\vert \Delta \omega \left(t\right)\vert }^{2}dt$

( 15)

• Integral of the Absolute Error (IAE)

$IAE={\int }_{t=0}^{T=t_{sim}}\vert \Delta \omega \left(t\right)\vert dt$

( 16)

where ${\textstyle t_{sim}}$ is the simulation time of the system and Δω (t ) represents the instantaneous speed change. To prove superiority of the BA-FPSS, the SMIB system is simulated one by one with all four controllers (FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS) and the performance indices (ITAE, IAE and ISE) of speed response are recorded for the simulation time as 40 seconds and enlisted in Table 3 . The closely related responses with HSA-FPSS and BA-FPSS are well differentiated by distinct values of performance indices. The lower value of performance index (PI) represents the comparatively better performance of the system with reduced settling time and overshoot. In Table 3 , the value of performance indices (PIs) with BA-FPSS is lesser as compared to others, resulting to good performance. The value of PIs of system response with PSO-FPSS [5] or plant-7 and plant-8 are higher as compared to that of with BA-FPSS. Therefore, the performance of system with PSO-FPSS is degraded against the proposed BA-FPSS.

Table 3. Performance comparison of speed response with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and proposed BA-FPSS for SMIB power system.

PS model	Controllers	ITAE	IAE	ISE
Plant-1	FPSS [46]	0.0140	0.0025	5.1939E-06
	PSO-FPSS [5]	0.0072	0.0013	3.0359E-06
	HSA-FPSS [2]	0.0073	0.0013	3.0437E-06
	BA-FPSS (Prop.)	0.0073	0.0013	2.9941E-06
Plant-2	FPSS [46]	0.0221	0.0036	7.0078E-06
	PSO-FPSS [5]	0.0119	0.0021	3.9812E-06
	HSA-FPSS [2]	0.0117	0.0039	3.9599E-06
	BA-FPSS (Prop.)	0.0115	0.0020	3.8997E-06
Plant-3	FPSS [46]	0.0259	0.0044	1.4628E-06
	PSO-FPSS [5]	0.0159	0.0029	9.5283E-06
	HSA-FPSS [2]	0.0131	0.0024	8.6405E-06
	BA-FPSS (Prop.)	0.0110	0.0020	6.7405E-06
Plant-4	FPSS [46]	0.0453	0.0071	2.2915E-05
	PSO-FPSS [5]	0.0162	0.0029	1.0369E-05
	HSA-FPSS [2]	0.0181	0.0032	1.0954E-05
	BA-FPSS (Prop.)	0.0177	0.0032	1.0785E-05
Plant-5	FPSS [46]	0.0529	0.0086	3.9531E-05
	PSO-FPSS [5]	0.0229	0.0041	1.6368E-05
	HSA-FPSS [2]	0.0245	0.0044	2.1180E-05
	BA-FPSS (Prop.)	0.0150	0.0028	1.1477E-05
Plant-6	FPSS [46]	0.1364	0.0182	8.1390E-05
	PSO-FPSS [5]	0.0411	0.0070	3.1181E-05
	HSA-FPSS [2]	0.0328	0.0057	2.6481E-05
	BA-FPSS (Prop.)	0.0247	0.0044	1.9924E-05
Plant-7	FPSS [46]	0.2791	0.0313	1.5210E-04
	PSO-FPSS [5]	0.0821	0.0129	6.7567E-05
	HSA-FPSS [2]	0.0448	0.0077	4.0846E-05
	BA-FPSS (Prop.)	0.0398	0.0069	3.4579E-05
Plant-8	FPSS [46]	0.97088	0.07295	3.7782E-04
	PSO-FPSS [5]	124.26	7.7840	6.6780
	HSA-FPSS [2]	0.0733	0.0120	7.6007E-05
	BA-FPSS (Prop.)	0.0644	0.0107	6.7486E-05

4.2. Two-area 4-machine 10-bus power system

4.2.1. Plant creation for simulation

The single-line diagram of the two-area four-machine ten-bus power system is shown in Fig. 2 , which is a benchmark power system to study small signal oscillations [40] . The line data, load flow and machine data are considered as in [38]  and [40] . The above multimachine system is modeled using SIMULINK Toolbox with machine model 1.0. The test system (four-machine system) is considered with the wide range of operating conditions of power system and system connection configuration. Here, the different test models are created by changing the active power of generation, distributed load, line outage and fault at different bus location as mentioned in Table 4 .

Table 4. Plant configuration with different operating conditions for two-area 4-machine 10-bus power system [38] .

PS model	Active power	Active load	F/Ba	L/Ob
Plant-1	7, 7, 7.2172, 7	11.59; 15.75	B/No. 3	As in Fig. 2
Plant-2	7, 7, 7.2172, 7	11.59; 15.75	B/No. 4	B/No. 9–10
Plant-3	7.2, 7.1, 7.0, 6.9	11.59; 15.75	B/No. 5	As in Fig. 2
Plant-4	7.2, 7.1, 7.0, 6.9	11.59; 15.75	B/No. 6	B/No. 7–10
Plant-5	7.2, 7.1, 7.0, 6.9	11.99; 15.45	B/No. 7	As in Fig. 2
Plant-6	7.1, 6.9, 7.5, 6.5	11.19; 15.95	B/No. 8	As in Fig. 2
Plant-7	7.1, 6.9, 7.5, 6.5	11.19; 15.95	B/No. 9	B/No. 5–9
Plant-8	5, 8, 6.2172, 8	11.59; 15.75	B/No. 10	As in Fig. 2

a. Fault location at a particular bus for non-linear study.

b. System as in in Fig. 2 or with line outage between two buses.

In Table 4 , the configuration of the 4-machine power system is considered by varying active power, active load, bus structure and fault at a particular bus of Fig. 2 . In plant-1, the bus structure is as in Fig. 2 but a line between bus no. 9 and bus no. 10 is disconnected in plant-2 configuration of the system. It can be observed that the nonlinear simulation is considered by creating self-clearing fault at bus no. 3 and bus no. 4 in plant-1 and pant-2 configuration, respectively. The active power plant-1 associated to 4-generators is [7, 7, 7.2172] and changed to [7.2, 7.1, 7.0, 6.9] in plant-3. The load connected to system are 2 as [11.59 + j2.12; 15.75 + j2.88] in plant-1 configuration but only real parts are enlisted in Table 4 because imaginary part remains the same for all plant conditions. In this way, the eight different plants of the system are considered as shown in Table 4 .

4.2.2. Optimal set of scaling factors

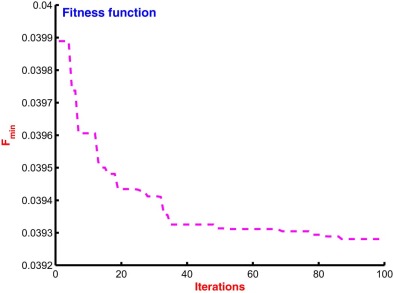
The system model referring to plant-1 configuration as in Table 4 is equipped with FPSS to all four-machines (named as Gen-1 to Gen-4) and subjected to design using the bat algorithm (as described in Section 3 ), with a simple time domain based minimization of ISE as an objective function as in Eqn. (4) with bounds as defined in Eqn. (7) . The speed signal from each generator is sensed and the minimum value of sum of ISE of the error signal is minimized to tune input–output scaling factors of four FPSSs with parameter bounds as 40 ≤ K_ω    ≤ 70, ${\textstyle 1.0\leq K_{p}\leq 10}$ , and ${\textstyle 1.0\leq K_{u}\leq 5.0}$ . The initializing parameters for BA are considered the same as in the previous section. The termination criterion of the tuning process is considered as the maximum number of iterations and set as 100. The parameter bounds are selected by using the trial-and-error method; therefore, several attempts are required. The optimized scaling factors are shown in Table 5 . The behavior of BA during optimization in terms of fitness function is plotted in Fig. 12 .

Table 5. Comparison of input–output scaling factors of FPSS using PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS for two-area 4-machine 10-bus power system.

Controllers	Generators	$K_{\omega i}$	$K_{pi}$	$K_{ui}$
PSO-FPSS [5]	Gen-1	59.8000	4.0000	1.0000
	Gen-2	59.8000	4.0000	1.0000
	Gen-3	59.8000	4.0000	1.0000
	Gen-4	59.8000	4.0000	1.0000
HSA-FPSS [2]	Gen-1	61.1017	3.9703	0.7327
	Gen-2	60.8977	4.7107	0.5536
	Gen-3	57.0917	3.8375	0.6540
	Gen-4	60.3711	3.6118	0.5258
BA-FPSS (Prop.)	Gen-1	58.6538	4.0109	1.8991
	Gen-2	56.0157	4.0016	1.0021
	Gen-3	59.3950	6.4531	4.0501
	Gen-4	40.0012	7.997	3.9996

Fig. 12. Fitness function plot for simultaneous tuning of input–output scaling factors of FPSSs for 4-machine 10-bus power system using bat algorithm.

4.2.3. Speed response analysis

The two-area four-machine ten-bus power system is described and the creations of system models based on operating conditions are elaborated in the previous section. The FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and proposed BA-FPSS are connected to the system and simulations are carried out for the speed response. In each plant condition as listed in Table 4 is considered with fault location. The disturbance is considered as self-clearing at different buses at 1.0 second and cleared after 0.05 second. As a sample, the speed response of Gen-1 to Gen-4 for plant-3 is compared with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS in Fig. 13 , Fig. 14 , Fig. 15  and Fig. 16 . These graphical representations of the simulation results reveal that the performance of the system with PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS is greatly improved as compared to FPSS [46] . The responses of the system with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS are closely related, therefore differentiating the associated performance indices was to be carried out in the next section.

Fig. 13. Speed response for Gen-1 of Plant-3 with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS.

Fig. 14. Speed response for Gen-2 of Plant-3 with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS.

Fig. 15. Speed response for Gen-3 of Plant-3 with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS.

Fig. 16. Speed response for Gen-4 of Plant-3 with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS.

To evaluate the robustness of the proposed BA-FPSS, simulation is carried out for all eight plant configurations, which represent the wide range of operating conditions and system configurations. The system is simulated FPSS [46] , PSO-FPSS [5] , HAS-FPSS [2] and BA-FPSS for comparison purpose with eight plant conditions. Each time the performance indices (ITAE, IAE and ISE) are recorded and enlisted in Table 6 . Since the system possesses four generators, the PI values in Table 6 are the sum of PIs of four generators. Comparatively lower value of PI refers to better performance. It is clear from this table that the performance of the system is enhanced by using proposed BA-FPSS as compared to other controllers.

Table 6. Performance comparison of speed response with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and BA-FPSS for 4-machine 10-bus power system.

PS model	Controllers	ITAE	IAE	ISE
Plant-1	FPSS [46]	0.0763	0.0231	4.5996E-05
	PSO-FPSS [5]	0.0308	0.0128	4.0754E-05
	HSA-FPSS [2]	0.0356	0.0135	4.2913E-05
	BA-FPSS (Prop.)	0.0285	0.0133	3.9055E-05
Plant-2	FPSS [46]	0.1823	0.0473	1.4331E-04
	PSO-FPSS [5]	0.0828	0.0322	1.6105E-04
	HSA-FPSS [2]	0.0846	0.0354	1.8268E-04
	BA-FPSS (Prop.)	0.0775	0.0302	1.4252E-04
Plant-3	FPSS [46]	0.0596	0.0169	1.4331E-04
	PSO-FPSS [5]	0.0191	0.0053	8.3550E-06
	HSA-FPSS [2]	0.0169	0.0050	7.4998E-06
	BA-FPSS (Prop.)	0.0155	0.0046	6.4506E-06
Plant-4	FPSS [46]	0.0497	0.0132	1.1295E-05
	PSO-FPSS [5]	0.0301	0.0062	9.0234E-06
	HSA-FPSS [2]	0.0262	0.0059	8.2087E-06
	BA-FPSS (Prop.)	0.0183	0.0055	7.6245E-06
Plant-5	FPSS [46]	0.0625	0.0167	1.7306E-05
	PSO-FPSS [5]	0.0224	0.0052	6.5374E-06
	HSA-FPSS [2]	0.0280	0.0064	7.6419E-06
	BA-FPSS (Prop.)	0.0171	0.0048	5.7325E-06
Plant-6	FPSS [46]	0.0362	0.0111	1.0156E-05
	PSO-FPSS [5]	0.0206	0.0050	6.1350E-06
	HSA-FPSS [2]	0.0270	0.0058	6.7488E-06
	BA-FPSS (Prop.)	0.0132	0.0046	5.8600E-06
Plant-7	FPSS [46]	0.0613	0.0149	9.2326E-06
	PSO-FPSS [5]	0.0320	0.0038	1.7054E-06
	HSA-FPSS [2]	0.0309	0.0037	1.7049E-06
	BA-FPSS (Prop.)	0.0195	0.0036	1.6846E-06
Plant-8	FPSS [46]	0.0428	0.0111	6.8407E-06
	PSO-FPSS [5]	0.0082	0.0021	1.2035E-06
	HSA-FPSS [2]	0.0168	0.0037	2.0258E-06
	BA-FPSS (Prop.)	0.0094	0.0027	1.5931E-06

4.3. IEEE New England 10-machine 39-bus power system

4.3.1. Plant creation for simulation

The IEEE 39-bus power system is configured with different sets of active power and active load connected to the system shown in Fig. 4 . It has 10 generators and 19 loads connected as in [38] . The active power assigned to plant-1 (base case) are as [5.519816, 10.0, 6.5, 5.08, 6.32, 6.5, 5.6, 5.4, 8.3, 2.5]. The load assigned to plant-1 (base-case) for bus nos. [1, 2, 13, 14, 17, 18, 21, 23, 24, 25, 26, 27, 28, 29, 30, 32, 35, 36, 38] = [(0.092 + j0.046), (11.04 + j2.5), (3.22 + j0.024), (5.0 + j1.84), (2.3380 + j0.8400), (5.22 + j1.76), (2.74 + j1.15), (2.745 + j0.8466), (3.086 + j0.922), (2.24 + j0.472), (1.39 + j0.17), (2.81 + j0.755), (2.06 + j0.276), (2.835 + j0.269), (6.28 + j1.030), (.075 + j0.88), (3.20 + j1.53), (3.294 + j0.323), (1.58 + j0.30)]. To generate 8-plant configurations, the different sets of active power of generators and active load are considered. These system plants are shown in Table 7 . The last column of Table 7 refers to the self-clearing fault at a bus for nonlinear behavior of system.

Table 7. Plant configuration with different operating conditions for IEEE New England 10-machine 39-bus power system [38] .

Power system model	Active powera	Active loadb	Fault at bus
Plant-1	Base case	Base case	Bus-16
Plant-2	3,5	2,13,27,28	Bus-13
Plant-3	1,2,3,4	17,24	Bus-11
Plant-4	7,8	27,28,30,32	Bus-9
Plant-5	2,7	30,35,36,38	Bus-7
Plant-6	1,3,9,10	24–27,30,35,36	Bus-17
Plant-7	1,4,5,6	13,25,30,35	Bus-19
Plant-8	4,5,6,7	18,21,27,28,36,38	Bus-21

a. Active power of the generators is changed w.r.t. base case.

b. The connected load to the buses is changed w.r.t. base case.

4.3.2. Optimal set of scaling factors

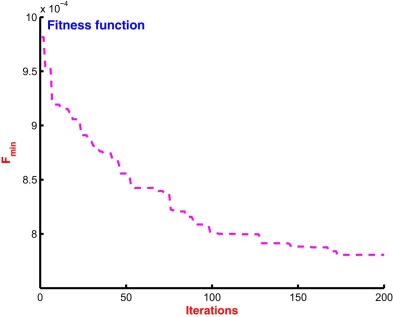
The creation of experimental plants for IEEE New England ten-machine thirty nine-bus power system is well explained in the previous section. The required machine data, load flow data, transformer data and line data for the system configuration are considered as presented in [38]  and [40] . The system model referring to plant-1 configuration as in Table 7 is equipped with FPSS at all nine-machines (named as Gen-1 to Gen-9) except Gen-10, which is considered as the slack and subjected to controller design using harmony search algorithm (as described in [2] ) and the bat algorithm in Section 3 , with parameter bounds as ${\textstyle 0.001\leq K_{\omega }\leq 60}$ , ${\textstyle 0.001\leq K_{p}\leq 8.0}$ , and ${\textstyle 0.001\leq K_{u}\leq 5.0}$ . With the initializing parameters as above for BA and as in [2] for HSA; the systems are simulated for an iteration count as 200. The fitness function variation for 200 iterations with HSA and BA is shown in Fig. 17 . The optimal values of scaling factors with bat and harmony search algorithm are mentioned in Table 8 .

Fig. 17. Fitness function plot for simultaneous tuning of input–output scaling factors of FPSSs for 10-machine 39-bus power system using bat algorithm.

Table 8. Comparison of input–output scaling factors of FPSS using HSA-FPSS and BA-FPSS for IEEE 10-machine 39-bus power system.

Controllers	Generators	$K_{\omega i}$	$K_{pi}$	$K_{ui}$
HSA-FPSS	Gen-1	10.0000	9.7770	9.9991
	Gen-2	56.8062	6.8892	9.9382
	Gen-3	10.0899	9.9099	10.000
	Gen-4	59.8892	5.8811	10.000
	Gen-5	55.5804	8.9766	9.7362
	Gen-6	59.5663	9.8928	10.000
	Gen-7	60.0000	6.5596	8.9733
	Gen-8	52.9681	9.0131	8.7615
	Gen-9	56.4434	7.9649	6.4976
BA-FPSS	Gen-1	19.6546	4.7485	3.0247
	Gen-2	59.7079	8.4225	4.8785
	Gen-3	13.1155	8.4256	3.9920
	Gen-4	59.4908	7.1621	3.1274
	Gen-5	25.9536	2.9191	4.6584
	Gen-6	17.4769	4.2649	4.8460
	Gen-7	44.3857	9.0319	3.6861
	Gen-8	45.5560	4.6530	3.9345
	Gen-9	27.4008	7.8812	4.7202

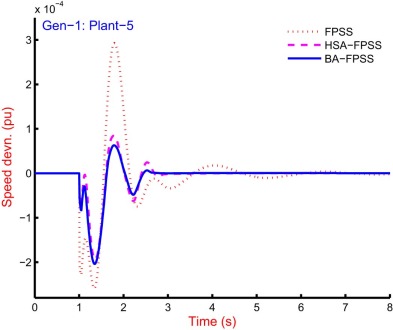
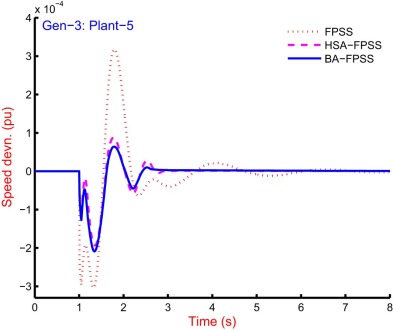
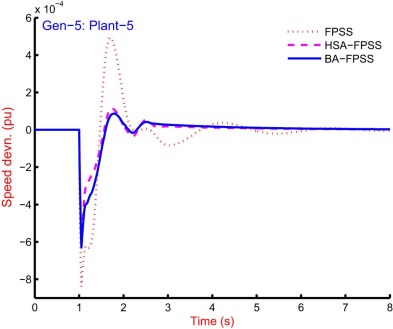
4.3.3. Speed response analysis

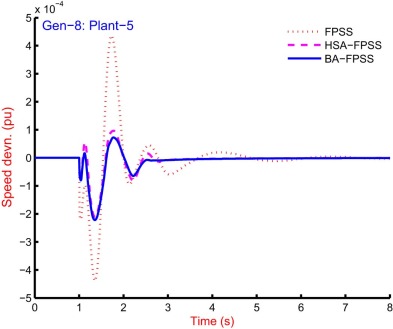
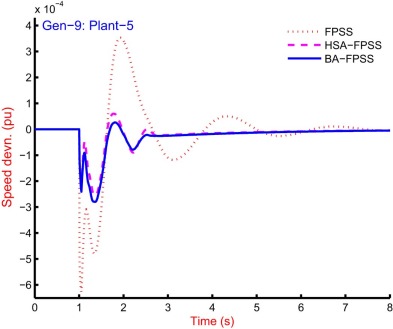
The 9-generators of the system are equipped controllers, and simulation is carried out for the speed response from the system. The system is equipped with FPSS [47]  and [48] , HSA-FPSS and BA-FPSS and graphical comparison is recorded. The response from the system with all controllers and for all generators is impossible because of space constraint. The response of plant-5 for Gen-1, Gen-3, Gen-5, Gen-8 and Gen-9 is shown in Fig. 18 , Fig. 19 , Fig. 20 , Fig. 21  and Fig. 22 . The improved performance from the system with the bat algorithm can be observed with reduced settling time and overshoot as compared to others. The graphical representation of the response due to these controllers is quite clear to interpret best performance with BA-FPSS and worst as with FPSS [47]  and [48] . It can be seen that the overshoot as well as the settling time with BA-FPSS is greatly improved as compared to that of FPSS [47]  and [48] . However, the response with BA-FPSS is closely related to that of HSA-FPSS; therefore, the performance indices based analysis is needed to differentiate the degree of performance.

Fig. 18. Speed response of Gen-1 for plant-5 of 10-machine 39-bus power system with FPSS [47]  and [48] , HSA-FPSS and BA-FPSS.

Fig. 19. Speed response of Gen-3 for plant-5 of 10-machine 39-bus power system with FPSS [47]  and [48] , HSA-FPSS and BA-FPSS.

Fig. 20. Speed response of Gen-5 for plant-5 of 10-machine 39-bus power system with FPSS [47]  and [48] , HSA-FPSS and BA-FPSS.

Fig. 21. Speed response of Gen-8 for plant-5 with of 10-machine 39-bus power system FPSS [47]  and [48] , HSA-FPSS and BA-FPSS.

Fig. 22. Speed response of Gen-9 for plant-5 with of 10-machine 39-bus power system FPSS [47]  and [48] , HSA-FPSS and BA-FPSS.

To evaluate the robustness of the proposed BA-FPSS, simulation is carried out for all eight plant configurations, which represent the wide range of operating conditions and system configurations. The system is simulated with FPSS and with HSA-FPSS for comparison purpose with eight plant conditions. Each time the performance indices (ITAE, IAE and ISE) are recorded and enlisted in Table 9 . Since the system possesses ten generators, the PI values in Table 9 are the sum of PIs of ten generators. Comparatively lower value of PI refers to better performance. It is clear from this table that the performance of the system is enhanced by using proposed BA-FPSS as compared to performance with FPSS and with HAS-FPSS.

Table 9. Performance comparison of speed response with FPSS [47]  and [48] , HSA-FPSS and BA-FPSS for IEEE New England 10-machine 39-bus power system.

PS model	Controllers	ITAE	IAE	ISE
Plant-1	FPSS [47]  and [48]	0.0236	0.0122	8.3233E-06
	HSA-FPSS	0.0104	0.0064	5.8288E-06
	BA-FPSS	0.0099	0.0063	5.3339E-06
Plant-2	FPSS [47]  and [48]	0.0339	0.0149	8.4324E-06
	HSA-FPSS	0.0097	0.0056	3.1842E-06
	BA-FPSS	0.0080	0.0051	3.0877E-06
Plant-3	FPSS [47]  and [48]	0.0115	0.0063	1.5598E-06
	HSA-FPSS	0.0021	0.0022	5.5395E-07
	BA-FPSS	0.0017	0.0019	5.0791E-07
Plant-4	FPSS [47]  and [48]	0.0185	0.0104	1.0332E-05
	HSA-FPSS	0.0066	0.0048	6.3518E-06
	BA-FPSS	0.0063	0.0048	5.6729E-06
Plant-5	FPSS [47]  and [48]	0.0132	0.0086	7.0048E-06
	HSA-FPSS	0.0082	0.0056	6.3767E-06
	BA-FPSS	0.0079	0.0054	5.7404E-06
Plant-6	FPSS [47]  and [48]	0.0204	0.0107	5.8676E-06
	HSA-FPSS	0.0081	0.0052	3.4451E-06
	BA-FPSS	0.0076	0.0049	3.6366E-06
Plant-7	FPSS [47]  and [48]	0.0120	0.0066	1.9293E-06
	HSA-FPSS	0.0030	0.0025	8.0286E-07
	BA-FPSS	0.0027	0.0023	7.7544E-07
Plant-8	FPSS [47]  and [48]	0.0291	0.0135	8.2817E-06
	HSA-FPSS	0.0084	0.0056	4.3251E-06
	BA-FPSS	0.0075	0.0052	4.3215E-06

5. Conclusion

In this paper, the application of the bat algorithm is used to tune the input–output scaling factors of fuzzy logic based power system stabilizer for three systems such as single-machine infinite-bus power system (SMIB), two-area four-machine ten-bus power system and IEEE New England ten-machine thirty nine-bus power systems.

The SMIB power system is equipped with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and proposed BA-FPSS. The system is simulated for eight plant conditions, and consequently the speed response from the system for different plants is compared. The performance indices with BA-FPSS are greatly improved as compared to others.

The two-area four-machine ten-bus power system is simulated for speed response comparison with FPSS [46] , PSO-FPSS [5] , HSA-FPSS [2] and proposed BA-FPSS. The simulation study is revealed that speed response with BA-FPSS is much better as compared to others. The superiority of the proposed controller (BA-FPSS) proved in terms of performance indices.

In case of IEEE ten-machine power system only FPSS [47]  and [48] is available; therefore, the harmony search and bat algorithms are considered to optimize the input–output scaling factors. The system responses with FPSS [47]  and [48] , with HSA-FPSS and with BA-FPSS are compared and found that the BA-FPSS appeared with superior performance. The speed response is compared graphically as a sample for plant-5 and superior performance with BA-FPSS is validated over eight plant conditions using performance indices.

The strong aspect of the bat algorithm is its quick start property and the strength to optimize in global space. The harmony search is able to optimize system globally but after a prolonged number of iterations.

Acknowledgments

This research was supported by All India Council for Technical Education , New Delhi, India in the name of D. K. Sambariya. The author is grateful to the University College of Engineering, Rajasthan Technical University, Kota, for sponsoring him under Quality Improvement Programme. He also thanks his colleagues for sharing the responsibility at the parent institute during the stay at Roorkee.

References

1. [1] M. Abido; Robust Design of Power System Stabilizers for Multimachine Power Systems Using Differential Evolution, Vol. 302 of Studies in Computational Intelligence; Springer, Berlin and Heidelberg (2010), pp. 1–18 http://dx.doi.org/10.1007/978-3-642-14013-6_1
2. [2] D.K. Sambariya, R. Prasad; Optimal tuning of fuzzy logic power system stabilizer using harmony search algorithm; Int. J. Fuzzy Syst, 17 (3) (2015), pp. 457–470 http://dx.doi.org/10.1007/s40815-015-0041-4
3. [3] S. Abd-Elazim, E. Ali; Power system stability enhancement via bacteria foraging optimization algorithm; Arabian J. Sci. Eng, 38 (3) (2013), pp. 599–611 http://dx.doi.org/10.1007/s13369-012-0423-y
4. [4] A.D. Falehi; Design and scrutiny of maiden PSS for alleviation of power system oscillations using RCGA and PSO techniques; J. Electr. Eng. Technol, 8 (3) (2013), pp. 402–410
5. [5] A.M. El-Zonkoly, A.A. Khalil, N.M. Ahmied; Optimal tuning of lead-lag and fuzzy logic power system stabilizers using particle swarm optimization; Expert Syst. Appl, 36 (2) (2009), pp. 2097–2106 http://dx.doi.org/10.1016/j.eswa.2007.12.069
6. [6] M. Linda, N. Nair; A new-fangled adaptive mutation breeder genetic optimization of global multi-machine power system stabilizer; Int. J. Electr. Power Energy Syst, 44 (1) (2013), pp. 249–258 http://dx.doi.org/10.1016/j.ijepes.2012.06.005
7. [7] M. Abido; Simulated annealing based approach to PSS and FACTS based stabilizer tuning; Int. J. Electr. Power Energy Syst, 22 (4) (2000), pp. 247–258 http://dx.doi.org/10.1016/S0142-0615(99)00055-1
8. [8] H. Yassami, A. Darabi, S. Rafiei; Power system stabilizer design using strength Pareto multi-objective optimization approach; Electr. Power Syst. Res, 80 (7) (2010), pp. 838–846 http://dx.doi.org/10.1016/j.epsr.2009.12.011
9. [9] D.K. Sambariya, R. Prasad; Robust tuning of power system stabilizer for small signal stability enhancement using metaheuristic bat algorithm; Int. J. Electr. Power Energy Syst, 61 (0) (2014), pp. 229–238 http://dx.doi.org/10.1016/j.ijepes.2014.03.050
10. [10] H.N. Al-Duwaish, Z.M. Al-Hamouz; A neural network based adaptive sliding mode controller: application to a power system stabilizer; Energy Convers. Manag, 52 (2) (2011), pp. 1533–1538 http://dx.doi.org/10.1016/j.enconman.2010.06.060
11. [11] D.K. Sambariya; Power system stabilizer design using compressed rule base of fuzzy logic controller; J. Electr. Electron. Eng, 3 (3) (2015), pp. 52–64 http://dx.doi.org/10.11648/j.jeee.20150303.16
12. [12] D.K. Sambariya, R. Prasad; Design of PSS for SMIB system using robust fast output sampling feedback technique; in: 7th International Conference on Intelligent Systems and Control (ISCO-13)  (2013), pp. 166–171 http://dx.doi.org/10.1109/ISCO.2013.6481142
13. [13] R. Gupta, D.K. Sambariya, R. Gunjan; Fuzzy logic based robust power system stabilizer for multi-machine power system; in: IEEE International Conference on Industrial Technology, ICIT-06  (2006), pp. 1037–1042 http://dx.doi.org/10.1109/ICIT.2006.372299
14. [14] D.K. Sambariya, R. Gupta, A. Sharma; Fuzzy applications to single machine power system stabilizers; J. Theor. Appl. Inf. Technol, 5 (3) (2009), pp. 317–324
15. [15] T. Hussein, M. Saad, A. Elshafei, A. Bahgat; Damping inter-area modes of oscillation using an adaptive fuzzy power system stabilizer; Electr. Power Syst. Res, 80 (12) (2010), pp. 1428–1436 http://dx.doi.org/10.1016/j.epsr.2010.06.004
16. [16] D.K. Chaturvedi, O.P. Malik; Neurofuzzy power system stabilizer; IEEE Trans. Energy Conv, 23 (3) (2008), pp. 887–894 http://dx.doi.org/10.1109/TEC.2008.918633
17. [17] A. Albakkar, O. Malik; Adaptive neuro-fuzzy controller based on simplified ANFIS network; (2012), pp. 1–6 http://dx.doi.org/10.1109/PESGM.2012.6344842
18. [18] D.K. Sambariya, R. Prasad; Evaluation of interval type-2 fuzzy membership function & robust design of power system stabilizer for SMIB power system; Sylwan J., 158 (5) (2014), pp. 289–307
19. [19] D.K. Sambariya, R. Prasad; Power system stabilizer design for multimachine power system using interval type-2 fuzzy logic controller; Int. Rev. Electr. Eng, 8 (5) (2013), pp. 1556–1565 http://dx.doi.org/10.15866/iree.v8i5.2113
20. [20] E. Abu-Al-Feilat, M. Bettayeb, H. Al-Duwaish, M. Abido, A. Mantawy; A neural network-based approach for on-line dynamic stability assessment using synchronizing and damping torque coefficients; Electr. Power Syst. Res, 39 (2) (1996), pp. 103–110 http://dx.doi.org/10.1016/S0378-7796(96)01099-1
21. [21] D.K. Sambariya, R. Prasad; Design of robust PID power system stabilizer for multimachine power system using HS algorithm; Am. J. Electr. Electron. Eng, 3 (3) (2015), pp. 75–82 http://dx.doi.org/10.12691/ajeee-3-3-3
22. [22] T. Hiyama; Real time control of micro-machine system using micro-computer based fuzzy logic power system stabilizer; IEEE Trans. Energy Conv, 9 (4) (1994), pp. 724–731 http://dx.doi.org/10.1109/60.368335
23. [23] D.K. Sambariya, R. Prasad; Robust power system stabilizer design for single machine infinite bus system with different membership functions for fuzzy logic controller; in: Intelligent Systems and Control (ISCO), 2013 7th International Conference on  (2013), pp. 13–19 http://dx.doi.org/10.1109/ISCO.2013.6481115
24. [24] M. Sanaye-Pasand, O.P. Malik; A fuzzy logic based PSS using a standardized rule table; Electr. Mach. Power Syst, 27 (3) (1999), pp. 295–310 http://dx.doi.org/10.1080/073135699269316
25. [25] Z.W. Geem, J.H. Kim, G. Loganathan; A new heuristic optimization algorithm: harmony search; SIMULATION, 76 (2) (2001), pp. 60–68 http://dx.doi.org/10.1177/003754970107600201
26. [26] Z. Geem; Harmony search applications in industry; B. Prasad (Ed.), Soft Computing Applications in Industry, Vol. 226 of Studies in Fuzziness and Soft Computing, Springer, Berlin and Heidelberg (2008), pp. 117–134 http://dx.doi.org/10.1007/978-3-540-77465-5_6
27. [27] J. Yu, P. Guo; Improved PSO algorithm with harmony search for complicated function optimization problems; (2012) http://dx.doi.org/10.1007/978-3-642-31346-2_70
28. [28] Y. Abdel-magid, M. Abido; Optimal multiobjective design of robust power system stabilizers using genetic algorithms; IEEE Trans. Power Syst, 18 (3) (2003), pp. 1125–1132 http://dx.doi.org/10.1109/TPWRS.2003.814848
29. [29] D.K. Sambariya, R. Prasad; Design of harmony search algorithm based tuned fuzzy logic power system stabilizer; Int. Rev. Electr. Eng, 8 (5) (2013), pp. 1594–1607 http://dx.doi.org/10.15866/iree.v8i5.2117
30. [30] X.S. Yang; A New Metaheuristic Bat-Inspired Algorithm, vol. 284, Springer, Berlin and Heidelberg (2010), pp. 65–74 http://dx.doi.org/10.1007/978-3-642-12538-6_6
31. [31] S.K. Saha, R. Kar, D. Mandal, S.P. Ghoshal, V. Mukherjee; A new design method using opposition-based bat algorithm for IIR system identification problem; Int. J. Bio-Inspired Comput, 5 (2) (2013), pp. 99–132
32. [32] X.S. Yang, A.H. Gandomi; Bat algorithm: a novel approach for global engineering optimization; Engng. Comp, 29 (5) (2012), pp. 464–483 http://dx.doi.org/10.1108/02644401211235834
33. [33] C. Karri, U. Jena; Fast vector quantization using a bat algorithm for image compression; Eng. Sci. Technol. Int. J. (2015) http://dx.doi.org/10.1016/j.jestch.2015.11.003
34. [34] K. Premkumar, B. Manikandan; Bat algorithm optimized fuzzy PD based speed controller for brushless direct current motor; Eng. Sci. Technol. Int. J. (2015) http://dx.doi.org/10.1016/j.jestch.2015.11.004
35. [35] P.C. Pradhan, R.K. Sahu, S. Panda; Firefly algorithm optimized fuzzy PID controller for AGC of multi-area multi-source power systems with UPFC and SMES; Eng. Sci. Technol. Int. J. (2015) http://dx.doi.org/10.1016/j.jestch.2015.08.007
36. [36] H. Alkhatib, J. Duveau; Dynamic genetic algorithms for robust design of multimachine power system stabilizers; Int. J. Electr. Power Energy Syst, 45 (1) (2013), pp. 242–251 http://dx.doi.org/10.1016/j.ijepes.2012.08.080
37. [37] F. Demello, C. Concordia; Concepts of synchronous machine stability as affected by excitation control; IEEE Trans. Power Appar. Syst, 88 (4) (1969), pp. 316–329 http://dx.doi.org/10.1109/TPAS.1969.292452
38. [38] D.K. Sambariya; Small signal stability enhancement using power system stabilizer; Ph.D. Thesis),; Department of Electrical Engineering, Indian Institute of Technology Roorkee, Roorkee  (2015), pp. 1–287
39. [39] R. Gupta, B. Bandyopadhyay, A. Kulkarni, T. Manjunath; Design of decentralized power system stabilizer for multi-machine power system using periodic output feedback technique; in: 7th International Conference on Control, Automation, Robotics and Vision, ICARCV-02, Vol. 3  (2002), pp. 1676–1681 http://dx.doi.org/10.1109/ICARCV.2002.1235027
40. [40] K.R. Padiyar; Power System Dynamics Stability and Control; (second ed.)B. S. Publications, Hyderabad, India (2008)
41. [41] E. Ali; Optimization of power system stabilizers using BAT search algorithm; Int. J. Electr. Power Energy Syst, 61 (2014), pp. 683–690 http://dx.doi.org/10.1016/j.ijepes.2014.04.007
42. [42] X.S. Yang; Bat algorithm for multi-objective optimisation; Int. J. Bio-Inspired Comput, 3 (5) (2011), pp. 267–274 http://dx.doi.org/10.1504/ijbic.2011.042259
43. [43] D.K. Sambariya, H. Manohar; Model order reduction by integral squared error minimization using bat algorithm; in: Proceedings of 2015 RAECS UIET Panjab University Chandigarh, 21–22nd December 2015  (2015), pp. 1–7
44. [44] S. Kirkpatrick, C. Gelatt, M. Vecchi; Optimization by simulated annealing; Science, 220 (4598) (1983), pp. 671–680 http://dx.doi.org/10.1126/science.220.4598.671
45. [45] Z. Yang, A. Bose; Design of wide-area damping controllers for interarea oscillations; IEEE Trans. Power Syst, 23 (3) (2008), pp. 1136–1143 http://dx.doi.org/10.1109/tpwrs.2008.926718
46. [46] D.K. Sambariya, R. Gupta; Fuzzy applications in a multi-machine power system stabilizer; J. Electr. Eng. Technol, 5 (3) (2010), pp. 503–510
47. [47] M. Ramirez-Gonzalez, O.P. Malik; Self-tuned power system stabilizer based on a simple fuzzy logic controller; Electr. Power Comp. Syst, 38 (4) (2010), pp. 407–423 http://dx.doi.org/10.1080/15325000903330591
48. [48] M. Ramirez-Gonzalez, O. Malik; Simplified fuzzy logic controller and its application as a power system stabilizer; in: 15th International Conference on Intelligent System Applications to Power Systems (ISAP '09)  (2009), pp. 1–6 http://dx.doi.org/10.1109/ISAP.2009.5352817