Resumen
La Asociación Colombiana de Ingeniería Sísmica (AIS) ha realizado una actualización del Código Colombiano de Diseño Sismorresistente para Puentes (CCP-14). Entre las diferentes tareas realizadas, ha establecido el valor de los coeficientes de diseño sismorresistente compatibles con la forma funcional del espectro elástico de diseño seleccionado. Para ello, se ha actualizado la evaluación probabilista de la amenaza sísmica a escala nacional y, a partir de ella, se han calculado dichos coeficientes para todo el territorio nacional. Con respecto al último estudio general de amenaza sísmica de Colombia, se dispone de cinco años más de registros de sismicidad y, por consiguiente, de un mejor entendimiento del entorno sísmico colombiano, lo cual ha permitido realizar actualizaciones relacionadas con los parámetros de sismicidad de las fuentes sismogénicas y utilizar relaciones de atenuación de movimiento fuerte calibradas a partir de registros locales. Se presentan los mapas de zonificación sísmica para los tres coeficientes de diseño incluidos en el CCP-14 así como la herramienta gratuita de visualización en línea de los resultados.
Abstract
A recent update of the Colombian earthquake resistant building code for bridges (CCP-14) was developed by the Colombian Association for Earthquake Engineering (AIS). Among the different tasks developed, the values for the seismic design coefficients, compatible with the functional form of the selected elastic design spectra were established. For that reason an update of the probabilistic seismic hazard assessment was performed from which the seismic design coefficients have been estimated for Colombia. With respect to the latest national seismic hazard assessment, 5 more years of earthquake records and the consequent better understanding of the Colombian seismic environment are included in the analysis by updating the seismicity parameters of the seismogenetic sources and using ground motion prediction equations calibrated with local strong ground motion records. The seismic zonation maps for the three seismic design coefficients included in the CCP-14 are presented as well as the free online results visualization tool
Palabras clave
Evaluación probabilista de amenaza sísmica ; Coeficientes sísmicos de diseño ; Reglamentos de construcción ; Cálculo y diseño en ingeniería
Keywords
Probabilistic seismic hazard assessment ; Seismic design coefficients ; Building codes ; Calculation and design in engineering
1. Introducción
El cálculo de los coeficientes de diseño sismorresistente incluidos en los códigos de construcción es una tarea que requiere evaluar la amenaza sísmica en la zona objeto de estudio. Debido a las incertidumbres inherentes a los procesos de ocurrencia de terremotos, es preciso utilizar metodologías probabilistas que no solamente las incluyan, sino que además las propaguen a lo largo del análisis. Durante el proceso de actualización del Código Colombiano de Diseño Sismorresistente para Puentes (CCP-14) [1] , se establecieron unos coeficientes sísmicos de diseño que fuesen compatibles con la forma funcional del espectro elástico de diseño. Para ello, basándose en la mejor información existente del entorno local, se evaluó la amenaza sísmica en roca utilizando una metodología probabilista.
Anteriormente, se habían realizado diferentes estudios generales de amenaza sísmica en Colombia, que siempre estaban asociados con actualizaciones de los reglamentos de construcción sismorresistente para edificaciones [2] , [3] and [4] . El más reciente, fechado en 2009, sirvió para establecer el valor de los coeficientes incluidos en el Reglamento NSR-10 [5] , que constituyó un primer paso para la utilización de métodos numéricos totalmente probabilistas [6] para el cálculo de la amenaza sísmica en Colombia. Aunque la amenaza sísmica se considera estacionaria y los órdenes de magnitud no han presentado históricamente grandes cambios, la disponibilidad de un mayor número de registros de movimiento fuerte y los consiguientes avances que estos permiten en el desarrollo de relaciones de atenuación de movimiento fuerte constituyen la razón principal por la cual estos estudios se deben actualizar de manera periódica.
Este estudio utiliza el mismo modelo tectónico que el de 2009 [4] and [6] , pero presenta cambios tanto en los parámetros de sismicidad como en las relaciones de atenuación del movimiento fuerte asociadas a las fuentes sismogénicas, obtenidas mediante algoritmos genéticos calibrados con registros locales [7] .
Para el CCP-14, se ha seleccionado la forma funcional del espectro elástico de diseño establecida en la 6 ª edición de las AASHTO LRFD Bridge Design Specifications[8] , que depende de tres coeficientes sísmicos denotados como PGA, SS y S1 . PGA corresponde a la aceleración máxima del terreno; SS , a la aceleración espectral a 0,2 s, y S1 , a la aceleración espectral a 1,0 s. Suponiendo una vida útil de 75 años para cada puente, dichos coeficientes tienen una probabilidad de excedencia del 7% en dicho tiempo, lo cual corresponde a un período medio de retorno del orden de 975 años. Tanto SS como S1 se establecen para una amortiguación con respecto al crítico (ξ) del 5%.
Siguiendo el enfoque propuesto por Esteva [9] , se divide el territorio colombiano en distintas zonas tectónicas, representadas mediante fuentes sismogénicas, y para cada una de ellas se calculan una serie de parámetros de sismicidad que dan cuenta del proceso de ocurrencia de terremotos; a cada fuente se le asigna una relación de atenuación de movimiento fuerte para finalmente establecer las tasas anuales de excedencia para diferentes medidas de intensidad, en este caso aceleraciones espectrales.
La evaluación de la amenaza sísmica se ha realizado utilizando el programa CRISIS2014 [10] , un módulo de amenaza de la Plataforma CAPRA [11] , [12] and [13] y, sobre la base de los resultados obtenidos, se ha realizado la zonificación sísmica a escala nacional de los tres coeficientes sísmicos de diseño. Este artículo presenta la descripción de la metodología utilizada, el proceso de cálculo de los coeficientes y los mapas de zonificación para cada uno de ellos.
Este trabajo representa un paso más para incrementar la seguridad de la infraestructura frente a terremotos, especialmente para un sector que resulta fundamental, de acuerdo con las directrices de desarrollo económico de Colombia, dada la importancia que van a tener los puentes en las denominadas autopistas de cuarta generación (4 G). Además, es la aplicación puntual de una serie de métodos numéricos a un problema de diseño en ingeniería.
2. Metodología de evaluación de la amenaza sísmica
Debido a las incertidumbres existentes en aspectos tales como la localización, la magnitud y las aceleraciones esperadas del terreno relacionadas con la ocurrencia de futuros terremotos, se requiere utilizar metodologías probabilistas para evaluar la amenaza sísmica mediante simulaciones numéricas de futuros eventos. A pesar de que existe un marco conceptual común para dichas evaluaciones, pueden seleccionarse diferentes opciones relacionadas con los modelos geométricos y de sismicidad, dependiendo no solo de la razón de ser del análisis, sino también de la información disponible para realizarlo. En general, se pueden identificar cuatro etapas en la evaluación probabilista de la amenaza sísmica: 1) selección del modelo geométrico y zonificación tectónica, 2) selección del modelo de sismicidad y estimación de sus parámetros, 3) selección de las relaciones de atenuación de movimiento fuerte y asignación a las fuentes sismogénicas y 4) cálculo de la amenaza sísmica. A continuación, se presentan en detalle cada una de estas etapas del presente estudio.
2.1. Modelo geométrico seleccionado y zonificación tectónica
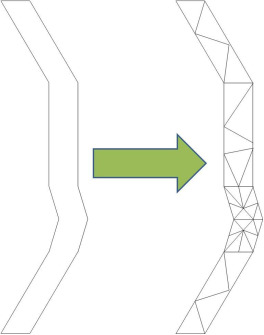
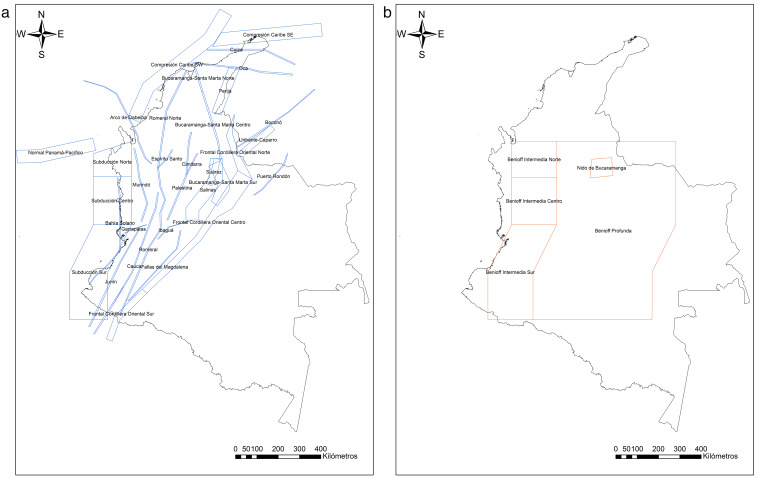
Sobre la base de los estudios existentes del entorno tectónico del norte de los Andes [14] , [15] , [16] , [17] and [18] , se han identificado diferentes fallas que han sido agrupadas en familias, dado el carácter nacional que tiene la evaluación. Dichas familias, 38 en total, se consideran fuentes sismogénicas y se representan a partir de un modelo geométrico de áreas. Cada una de ellas queda descrita mediante un plano construido a partir de varios vértices, que da cuenta no solamente de su localización en planta, sino de su profundidad y ángulo de buzamiento. Cada una de estas fuentes se subdivide de manera recursiva en geometrías triangulares, como se muestra en la figura 1 . Dado que los triángulos se construyen a partir de los vértices que definen la fuente sismogénica, no todos ellos tienen la misma área, aunque si la misma sismicidad por unidad de área. Esto representa un cambio significativo con respecto a los mapas de amenaza sísmica utilizados en el anterior código colombiano de puentes, en que se utilizó el modelo geométrico de línea fuente.
|
|
|
Figura 1. Subdivisión de las fuentes sismogénicas en geometrías sencillas. |
En el presente análisis, las fuentes sismogénicas se clasifican en superficiales y profundas, de acuerdo con los rangos de profundidad de los eventos que puedan generar. Para ello, se ha seleccionado un límite de profundidad de 60 km y se han definido 33 fuentes superficiales y 5 fuentes profundas, como se ilustra en la figura 2 .
|
|
|
Figura 2. Fuentes sismogénicas modeladas: superficiales (a la izquierda) y profundas (a la derecha). |
2.2. Selección del modelo de sismicidad y estimación de los parámetros requeridos
En esta segunda etapa, se debe realizar la selección del modelo que describa el proceso de ocurrencia de terremotos asociados a las fuentes sismogénicas modeladas. En el presente trabajo, se ha seleccionado el modelo propuesto por Cornell y Van Marke [19] para la ocurrencia de terremotos en cada fuente sismogénica, el cual es una versión modificada del modelo de Gutenberg-Richter [20]
|
|
( 1) |
donde λ(M) es la tasa anual de recurrencia de eventos con magnitud igual o superior a la umbral seleccionada, M0 (4.0 en este caso); λ0 , β y MU son los parámetros de sismicidad calculados para cada fuente sismogénica, y M es la variable aleatoria que representa la magnitud. λ0 describe la tasa anual de ocurrencia con magnitud igual o superior a la umbral; β representa la pendiente inicial de la regresión logarítmica, equivalente a la relación entre sismos grandes y pequeños, y MU es la magnitud última asociada a cada fuente sismogénica. Los parámetros λ0 y β pueden calcularse mediante métodos estadísticos basados en el catálogo de eventos sísmicos, que para este caso corresponde al utilizado en el estudio general de amenaza sísmica más reciente para Colombia [4] y que, a su vez, ha sido complementado con información del NEIC del U.S. Geological Survey [21] y del ISC-GEM [22] hasta el 31 de diciembre de 2013. Estos dos últimos parámetros son considerados, en el algoritmo de cálculo de la amenaza sísmica del programa CRISIS2014 [10] como variables aleatorias independientes donde además, para β se asume que la incertidumbre queda descrita mediante una distribución de probabilidad Gamma.
Haciendo uso del método de máxima verosimilitud [23] , λ0 se ha calculado como
|
|
( 2) |
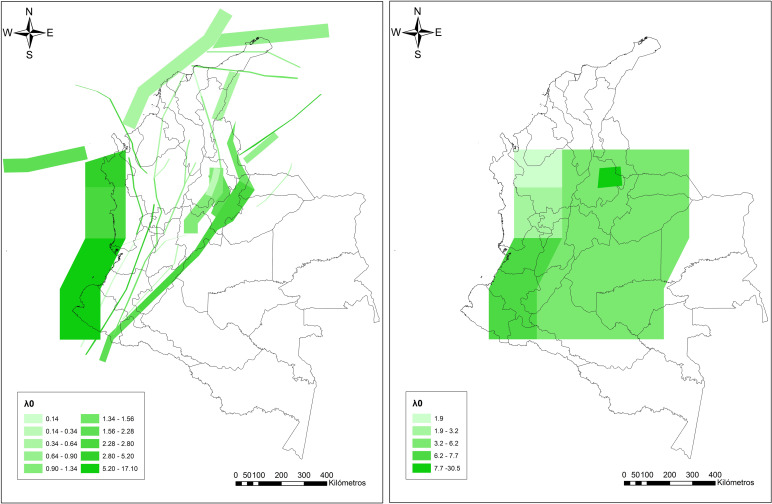
donde N corresponde al número de eventos asociados a la fuente sismogénica y t es la ventana de observación del catálogo sísmico, que en este caso se establece en 50 años mediante un cálculo de completitud para M0 igual a 4.0, utilizando la metodología propuesta por Tinti y Mulargia [24] . La figura 3 muestra los valores de λ0 para las fuentes modeladas.
|
|
|
Figura 3. Valores λ0 calculados para las fuentes sismogénicas: superficiales (a la izquierda) y profundas (a la derecha). |
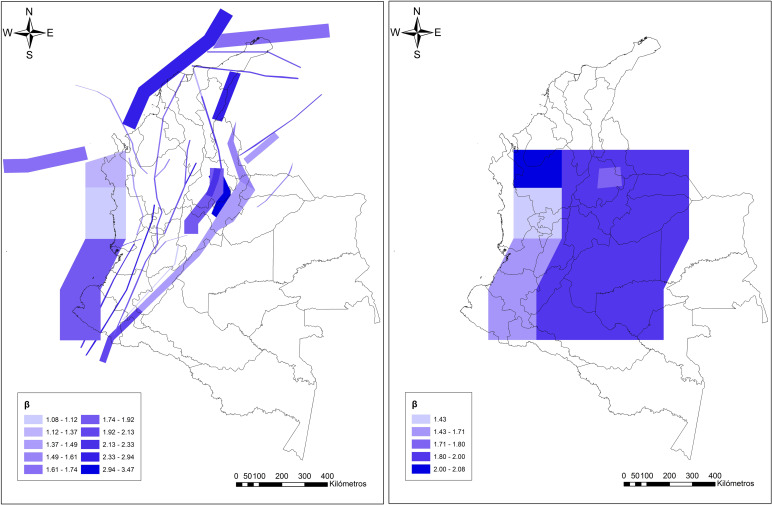
Por otro lado, el parámetro β se calcula a partir de la ecuación 3 y los valores estimados para cada fuente son los que se presentan en la figura 4
|
|
( 3) |
|
|
|
Figura 4. Valores β calculados para las fuentes sismogénicas: superficiales (a la izquierda) y profundas (a la derecha). |
Los parámetros MU se fijan igual que los establecidos en el estudio general de amenaza sísmica de Colombia 2010 [4] , pero además se considera la incertidumbre asociada a cada parámetro a partir de una variable aleatoria que sigue una distribución normal truncada, que se calcula a partir de su valor esperado y de su desviación estándar.
2.3. Relaciones de atenuación de movimiento fuerte
Dentro de todos los insumos necesarios para el cálculo de la amenaza sísmica, el que ha incorporado más mejoras en este estudio en comparación con los anteriores [2] , [3] and [4] es el relacionado con las relaciones de atenuación de movimiento fuerte. En el estudio de 2009, tras una serie de chequeos de sesgos y desviaciones estándar usando registros locales, se seleccionaron las relaciones de atenuación propuestas por Campbell [25] y García et al . [26] , todas desarrolladas a partir de terremotos registrados fuera del entorno sísmico colombiano. Dado el papel fundamental que tienen las relaciones de atenuación de movimiento fuerte a la hora de evaluar la amenaza sísmica, dado que son estas las que cuantifican los niveles de movimiento del terreno ante la ocurrencia de un terremoto, resulta de interés desarrollarlas tomando como base información local. Para el presente estudio, se han desarrollado relaciones de atenuación calibradas con registros locales [27] siguiendo la metodología propuesta por Bernal [7] y considerando 206 acelerogramas de sismos intraplaca y de subducción.
Los parámetros asociados a la fuente, la trayectoria y la atenuación local, que son relevantes en la atenuación del movimiento fuerte, pueden ser modelados mediante el uso de un modelo de espectro de fuente que combina el escalamiento de la fuente, la propagación geométrica, la atenuación del medio de tránsito y la atenuación local, para proporcionar una solución teórica de las amplitudes espectrales del movimiento fuerte. Los modelos de espectro de fuente se han utilizado ampliamente durante décadas en todo el mundo para desarrollar modelos de atenuación [28] , [29] , [30] , [31] and [32] .
En la formulación del espectro de fuente, las fuentes sísmicas son consideradas discontinuidades en un medio homogéneo e isotrópico y los terremotos se modelan como dislocaciones de cortante puro. Utilizando estas suposiciones básicas, la forma del espectro de amplitudes de Fourier (EAF) en roca firme puede calcularse para cualquier ubicación. En este estudio, se emplea como modelo base el propuesto por Singh et al . [33] , el cual considera un espectro de fuente específico para el campo cercano y otro para el lejano. Para el campo lejano, se define un modelo de fuente puntual dado por las siguientes relaciones. Para R≤Rx , es decir, donde existe predominancia de ondas de cuerpo:
|
|
( 4) |
y, para R > Rx , donde hay predominancia de ondas de superficie:
|
|
( 5) |
La constante C se define como
|
|
( 6) |
mientras que
|
|
( 7) |
donde f es la frecuencia; R , la distancia hipocentral; M0 , el momento sísmico; Rθϕ es el patrón de radiación; F es un factor de amplificación por superficie libre; P es un factor de partición de la energía en dos componentes ortogonales; ρ es la densidad del medio; β es su velocidad de onda de cortante; Aup es un factor de corrección por la amplificación inducida en las ondas S por su propagación hacia arriba a través de capas de material con velocidad de onda de cortante progresivamente menor [34] ; Δσ es la caída de esfuerzos; fc es la frecuencia de esquina; Rx es la distancia en la cual se espera que cambie el tipo de ondas predominantes; Q0 es el coeficiente del factor de calidad de las rocas Q[35] ; ɛ , su exponente, y κ es el término asociado al filtro de alta frecuencia en la atenuación local. En Bernal [7] , se dan más detalles sobre los parámetros mencionados.
Para el campo cercano, donde la ruptura no puede considerarse puntual, Singh et al . [33] proponen un modelo de fuente finita que está basado en la definición de una geometría circular, formada a partir de múltiples diferenciales de área donde cada uno de ellos puede modelarse como una fuente puntual. El espectro de campo cercano resultante, calculado en un punto localizado sobre el eje del círculo de ruptura, es, entonces:
|
|
( 8) |
donde α = 2π /β Q0 , r0 es el radio del área de ruptura y E 1 es la integral exponencial [36] . El modelo de fuente finita es válido únicamente para f ≥ fc . Para frecuencias menores, el modelo indica amplitudes espectrales casi constantes, lo que hace imposible aplicar solamente el modelo de fuente finita. La banda de baja frecuencia del espectro radiado (f < fc ) queda definida por medio del modelo de fuente puntual, una suposición adecuada dado que el espectro es de tipo ω-2 incluso para el campo cercano. Por otra parte, el modelo de fuente puntual predice amplitudes espectrales muy grandes para la banda de frecuencias centrales (fc < f < fmáx ) cuando se trata de sismos de grandes magnitudes. Esta situación se corrige en el modelo de fuente finita dado que este modelo se satura debido a la naturaleza finita del rompimiento. En este modelo, todos los diferenciales de área que componen la zona de ruptura aportan amplitud al espectro radiado, pero aquellos ubicados cerca del perímetro de la zona aportan menos que los localizados cerca de su centro. Por esta razón, se define el espectro radiado como el mínimo entre los espectros calculados con los modelos de fuente finita y puntual.
Una vez se ha calculado el EAF, la esperanza matemática de los valores máximos del movimiento fuerte, en el dominio del tiempo, se calcula aplicando las herramientas dadas por la teoría de vibraciones aleatorias. A partir de los trabajos de Cartwright y Longuett-Higgins [37] y Davenport [38] , se puede establecer:
|
|
( 9) |
donde Td es la duración de la fase intensa, γ es la constante de Euler (γ = 0,57…) y mn son los momentos de orden n del EAF
|
|
( 10) |
De acuerdo con Hermann [39] , la duración de la fase intensa puede obtenerse como:
|
|
( 11) |
El enfoque mencionado permite calcular la esperanza matemática de parámetros máximos del movimiento fuerte, como PGA, para cualquier ubicación, dados un momento sísmico (el cual está asociado a la magnitud) y una distancia hipocentral. Cuando se repite el cálculo para diferentes magnitudes y distancias hipocentrales, se obtiene la relación de atenuación de movimiento fuerte. E {PGA } puede expresarse entonces como una función de todos los parámetros involucrados en su formulación
|
|
( 12) |
Los parámetros de la función presentada en la ecuación 12 son las variables de calibración; sin embargo, no en todas ellas se puede realizar dicha tarea. Puesto que la magnitud y la distancia son conocidas, M0 y R son suprimidos del conjunto de variables. M0 es función de la magnitud de momento (Mw ), como se indica en Hanks y Kanamori [40] . Por otro lado, se asumen valores para ρ = 2,5 Ton/m3 y β = 3,5 km/s, mientras que Rx ha sido previamente definido por Gallego y Ordaz [41] como 100 km para el territorio colombiano. El conjunto final de parámetros sismológicos que hay que calibrar es, pues: Δσ, ɛ , Q0 , κ , y Rθϕ . La cantidad E {PGA } es definida, entonces, mediante una función no lineal en un espacio de 6 dimensiones, por lo cual la aplicación de métodos estadísticos clásicos de ajuste no resulta práctica. Por este motivo, se utiliza el algoritmo genético propuesto por Bernal [7] con el fin de buscar el conjunto óptimo de parámetros sismológicos que se ajusten mejor a los valores de PGA observados en los registros acelerográficos.
Mediante la implementación del algoritmo genético, se cuenta con una serie de individuos donde cada uno de ellos representa diferentes modelos de atenuación de movimiento fuerte para ser calibrados y cuyo genotipo se encuentra definido por valores asignados a los seis parámetros sismológicos de calibración. Partiendo de una población de cientos de individuos con genotipos definidos por valores de parámetros sismológicos generados aleatoriamente, se sigue un proceso iterativo en el cual son cruzados y mutados con lo cual se origina una nueva generación. Para cada generación, se evalúa el sesgo que presenta cada individuo frente a los acelerogramas en términos de PGA a partir del cálculo de sus residuales (Re) como:
|
|
( 13) |
donde E {PGA } es la esperanza matemática de PGA establecida mediante el modelo y arec es la aceleración nominal de cada registro acelerográfico calculada mediante:
|
|
( 14) |
donde ax y ay son las componentes horizontales del movimiento. El sesgo (S ) se calcula finalmente como:
|
|
( 15) |
donde N corresponde al número de acelerogramas. Una vez se minimiza el sesgo, el algoritmo finaliza y, de esta manera, se encuentra al individuo que contiene la combinación óptima de parámetros sismológicos que definen el modelo de espectro fuente.
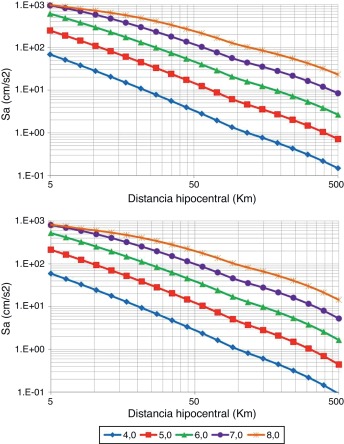
Dado que se han utilizado registros acelerográficos de sismos con diferentes orígenes (intraplaca y subducción), se han desarrollado dos modelos de atenuación de movimiento fuerte diferentes, que se presentan en la figura 5 .
|
|
|
Figura 5. Relaciones de atenuación de movimiento fuerte utilizadas para PGA: zona intraplaca (a la izquierda) y zona de subducción (a la derecha). Magnitudes en MW . |
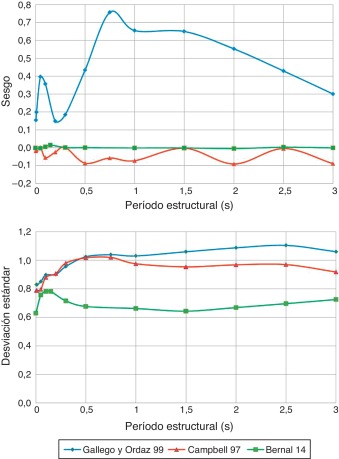
Por otro lado, la figura 6 compara los sesgos y la desviación estándar del modelo de atenuación de movimiento fuerte propuesto con los utilizados en evaluaciones previas de la amenaza sísmica en Colombia para sismos intraplaca.
|
|
|
Figura 6. Comparación de sesgos (a la izquierda) y desviaciones estándar (a la derecha) entre diferentes modelos de atenuación de movimiento fuerte para sismos intraplaca. |
En este campo, también existe una variación significativa con respecto a la metodología utilizada en la definición del coeficiente sísmico de diseño en el anterior Código colombiano de diseño de puentes, donde no solo se utilizaba una relación de atenuación de movimiento fuerte desarrollada con registros de otra región del mundo, sino que se describía la amenaza sísmica en términos de únicamente la aceleración máxima del terreno.
2.4. Cálculo de la amenaza sísmica
Para el cálculo de la amenaza sísmica, se asume que la medida de intensidad, en este caso la aceleración espectral (Sa ), es una variable aleatoria que sigue una distribución log-normal. Así pues, la probabilidad de que se exceda cierto nivel de intensidad, conocidas la magnitud y la distancia de un evento, Pr(A > a |M, Ri) , puede calcularse como:
|
|
( 16) |
donde Φ(·) es la distribución normal estándar, MED(A |M, Ri) es la mediana de la aceleración, dada por la relación de atenuación de movimiento fuerte asociada para un par magnitud-distancia conocido, y σLna es la desviación estándar del logaritmo natural de la aceleración, que da cuenta de su incertidumbre.
Dado que se ha seleccionado el modelo geométrico de áreas, se requiere utilizar un procedimiento de integración espacial que considere las diferentes localizaciones de los terremotos simulados, determinados por el centro de gravedad de los triángulos en que ha sido subdividida cada fuente. La probabilidad espacial de ocurrencia de los futuros terremotos se asume uniforme a lo largo de cada fuente, lo cual significa, en otras palabras, que todos tienen la misma probabilidad de ser un epicentro y, por tanto, el cálculo de las tasas de excedencia de las aceleraciones para cada fuente sismogénica, νi(a) , se calcula como [42] :
|
|
( 17) |
donde j corresponde al número de elementos en que ha sido dividida la fuente sismogénica; wij es el peso asignado a cada elemento, el cual es proporcional a su tamaño; Rij es la distancia entre el sitio de ocurrencia y el elemento j de la fuente i , y Pr(A > a|M,Ri) es la probabilidad de que la aceleración sea excedida, dada la ocurrencia de un sismo de magnitud M en la distancia Rij .
Puesto que hay más de una fuente sismogénica que puede contribuir a la tasa de excedencia de aceleraciones en cada punto de cálculo, la contribución de cada una de ellas se suma mediante:
|
|
( 18) |
Dado que se han utilizado relaciones de atenuación de movimiento fuerte espectrales, el proceso anterior se realiza para cada uno de los períodos de vibración de interés, en este caso: 0,0, 0,2 y 1,0 segundos. Para las tres ordenadas espectrales, la tasa anual de excedencia de interés es igual a 1,0256E-03, que corresponde aproximadamente a un período medio de retorno de 975 años.
2.5. Coeficientes de diseño sismorresistente para puentes en Colombia
A continuación, se presentan los mapas de zonificación para los coeficientes sísmicos requeridos, de acuerdo con la forma funcional seleccionada para el espectro elástico de diseño del CCP-14. Los resultados de la amenaza sísmica, expresados en fracciones de gravedad (g), se redondean al 0,05 más cercano con el fin de facilitar su uso y control, tanto a los usuarios como a las autoridades competentes para la verificación de los diseños. Dicho lo anterior, la figura 7 presenta la zonificación sísmica para el coeficiente de diseño PGA, que toma valores de entre 0,05 y 0,55 g y se encuentra distribuido en 11 regiones. Por otro lado, la figura 8 muestra la zonificación sísmica para el coeficiente de diseño SS , el cual toma valores de entre 0,10 y 1,30 g y se halla distribuido en 13 regiones. Finalmente, la figura 9 muestra la zonificación sísmica para el coeficiente de diseño S1 , el cual toma valores de entre 0,05 y 0,75 g y se encuentra distribuido en 15 regiones.
|
|
|
Figura 7. Zonificación sísmica para el coeficiente de diseño PGA. Datos extraídos de [1] . |
|
|
|
Figura 8. Zonificación sísmica para el coeficiente de diseño SS . Datos extraídos de [1] . |
|
|
|
Figura 9. Zonificación sísmica para el coeficiente de diseño S1 . Datos extraídos de [1] . |
2.6. Visualizador en línea de los resultados
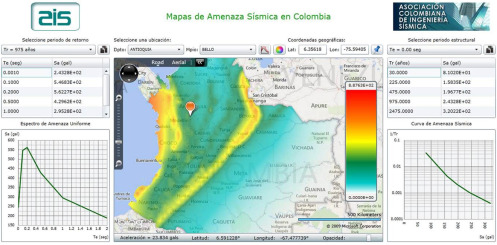
Con el objetivo de poner a disposición de los especialistas una herramienta que permita realizar consultas acerca de los valores de la amenaza sísmica para el cálculo de los espectros elásticos de diseño, se ha desarrollado una aplicación web [43] en la cual, mediante la introducción de las coordenadas geográficas sobre las cuales se ubicará el puente, se muestran informaciones tales como el espectro de amenaza uniforme y las curvas de amenaza sísmica para diferentes ordenadas espectrales, tal como se muestra en la figura 10 .
|
|
|
Figura 10. Visualización en línea de los resultados de la amenaza sísmica para Colombia. |
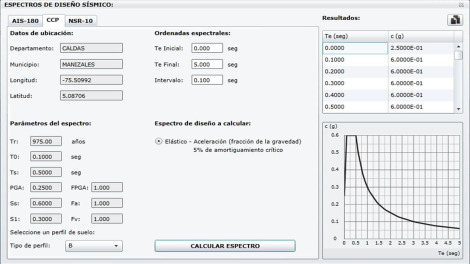
Si además, el usuario desea calcular el espectro elástico de diseño, este proceso se realiza de manera automática para las coordenadas geográficas especificadas mediante una herramienta que permite establecer diferentes tipos de suelo y rango de ordenadas espectrales, entre otros datos, como se muestra en la figura 11 para la ciudad de Manizales. La herramienta es gratuita y se encuentra disponible en la siguiente dirección web de la Asociación Colombiana de Ingeniería Sísmica: <http://201.244.179.21:8000/AIS-2014/AIS.html >
|
|
|
Figura 11. Herramienta online para el cálculo de espectros elásticos de diseño. |
3. Conclusiones
Se ha realizado una evaluación probabilista de la amenaza sísmica de Colombia utilizando no solo metodologías analíticas modernas, sino también la mejor información disponible del entorno con relación al catálogo de sismos y las relaciones de atenuación de movimiento fuerte. Además, los resultados del estudio se han incorporado en la reciente actualización del Código Colombiano de Diseño de Puentes (CCP-14) mediante la determinación de los coeficientes sísmicos de diseño denotados como PGA, SS y S1 . Para ello, se han incorporado nuevos avances, tanto de la sismología como de la ingeniería sísmica y estructural, teniendo en cuenta las particularidades de este tipo de estructuras.
La metodología probabilista para la estimación de la amenaza sísmica resulta obligatoria en este tipo de trabajos, dado que se requiere la consideración formal, explícita y rigurosa de las incertidumbres asociadas a los diferentes aspectos de la ocurrencia de terremotos. Aunque existen variaciones en los modelos geométricos y de sismicidad que pueden utilizarse, se considera que, para los fines del presente estudio, las seleccionadas y explicadas anteriormente son las más adecuadas. Por otro lado, la herramienta de cálculo utilizada es reconocida mundialmente como robusta e incluso ha sido utilizada, con variaciones en el modelo geométrico, para la estimación global de la amenaza sísmica [44] .
La utilización de dichos valores es obligatoria a escala nacional para el diseño de puentes, un tipo de estructuras que no solo tienen interés urbano, sino que, debido a la compleja topografía del país y al modelo de desarrollo económico basado en la construcción de las denominadas autopistas de cuarta generación (4 G), son fundamentales para la infraestructura de transporte del país.
Los mapas de zonificación de la amenaza sísmica presentados en ningún caso resultan obsoletos o incompatibles a los incluidos en el reglamento NSR-10 [5] o en el documento AIS 180-13 [45] , puesto que dan cuenta de unos coeficientes sísmicos diferentes, asociados a otras ordenadas espectrales y a otros períodos medios de retorno. Para evitar confusiones, con vistas al futuro se plantea unificar la forma funcional del espectro elástico de diseño para diferentes construcciones en Colombia, como edificios, puentes, tanques de almacenamiento de agua y silos, entre otras.
Los resultados de la presente evaluación de la amenaza sísmica también pueden utilizarse como insumos para evaluaciones probabilistas de riesgo sísmico en el país, ya sea de puentes o de otro tipo de infraestructura expuesta, como las edificaciones urbanas [46] , [47] , [48] , [49] and [50] .
Finalmente, en cuanto a los mapas de amenaza sísmica que deben incluirse en los reglamentos de diseño y construcción sismorresistente, se sugiere explorar los enfoques basados en los niveles de desempeño (en que el riesgo de colapso es un caso especial) o en el establecimiento de aceleraciones que conduzcan a diseños óptimos, tal como sucede hoy en día en México [51] .
Agradecimientos
Este trabajo se ha realizado en el marco de un proyecto en virtud del cual la Asociación Colombiana de Ingeniería Sísmica llevó a cabo la actualización del Código Colombiano de Diseño de Puentes con el apoyo financiero del Instituto Nacional de Vías (INVIAS) y el Ministerio de Transporte de Colombia. Además, los autores agradecen la colaboración del Dr. Mario Ordaz, Daniela Zuloaga y Miguel Leonardo-Suárez en el desarrollo de algunas tareas a lo largo de diferentes etapas de la evaluación de la amenaza sísmica y su visualización. Finalmente, también han colaborado el Ministerio de Educación y Ciencia de España con el «Enfoque integral y probabilista para la evaluación del riesgo sísmico en España»–CoPASRE (CGL2011-29063), y el Ministerio de Economía y Competitividad, en el marco del programa de formación de investigadores (FPI).
Referencias
- [1] Asociación Colombiana de Ingeniería Sísmica–AIS, Norma Colombiana de Diseño de Puentes. Comité AIS-200, 2014.
- [2] Asociación Colombiana de Ingeniería Sísmica–AIS, Estudio General de Amenaza Sísmica de Colombia 1984. Comité AIS-300, 1984.
- [3] Asociación Colombiana de Ingeniería Sísmica–AIS, Estudio General de Amenaza Sísmica de Colombia 1996. Comité AIS-300, 1996.
- [4] Asociación Colombiana de Ingeniería Sísmica–AIS, Estudio General de Amenaza Sísmica de Colombia 2009. Comité AIS-300, 2010.
- [5] Ministerio de Ambiente Vivienda y Desarrollo Territorial de Colombia–MAVDT, Reglamento Colombiano de Construcción Sismo Resistente NSR-10, 2010.
- [6] M.A. Salgado-Gálvez, G., Bernal, L. Yamín, Cardona O, Evaluación de la amenaza sísmica de Colombia. Actualización y uso en las nuevas normas colombianas de diseño sismo resistente NSR-10, Revista de Ingeniería 32 (2010) 28-37. Universidad de Los Andes, Bogotá, Colombia.
- [7] G. Bernal, Metodología para la modelación, cálculo y calibración de parámetros de la amenaza sísmica para la evaluación probabilista del riesgo [tesis doctoral], Universidad Politécnica de Cataluña, Barcelona, España, 2014.
- [8] American; Association of State Highway and Transportation Officials–AASHTO; LRFD Bridge Design Specifications, Washington (2012)
- [9] L. Esteva; Regionalización sísmica de México para fines de ingeniería; Universidad Nacional Autónoma de México (2010)
- [10] M. Ordaz, F. Martinelli, A. Aguilar, J. Arboleda, C. Meletti, V. D’Amico; CRISIS2014 Program for computing seismic hazard; Instituto de Ingeniería, Universidad Nacional Autónoma de México (2014)
- [11] O.D. Cardona, M. Ordaz, E. Reinoso, L. Yamín, A.H. Barbat; Comprehensive Approach to Probabilistic Risk Assessment (CAPRA). International initiative for disaster risk management effectiveness; Proceedings of the 14th European conference on earthquake engineering, Ohrid, Macedonia (2010)
- [12] O.D. Cardona, M., Ordaz, E., Reinoso, L. Yamín, A.H., Barbat, CAPRA — Comprehensive Approach to Probabilistic Risk Assessment: International Initiative for Risk Management Effectiveness, en: Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 2012.
- [13] C.A. Velásquez, O.D. Cardona, M.G. Mora, L.E. Yamín, M.L. Carreño, A.H. Barbat; Hybrid loss exceedance curve (HLEC) for disaster risk assessment; Nat. Haz., 72 (2014), pp. 455–479
- [14] J.N. Kellogg, V. Vega, Tectonic development of Panama, Costa Rica and the Colombian Andes: Constraints from global positioning system geodetic studies and gravity. Geol. soc. of am. Special Paper 295 (1995) 75-90.
- [15] A. Taboada, L.A. Rivera, A. Fuenzalida, A. Cisternas, H. Philip, H. Bijwaard, J. Olaya, C. Rivera; Geodynamics of the northern Andes: Subductions and intracontinental deformation (Colombia); Tecton., 19 (2000), pp. 787–813
- [16] G. Paris, M., Machette, R., Dart, K. Haller, Map and database of quaternary faults and folds in Colombia and its offshore regions, United States Geological Survey Open File Report: 00-0284. 2000.
- [17] N. Pulido; Seismotectonics of the Northern Andes (Colombia) and the development of seismic networks; Bull. Int. Inst. Seismol. Earthq. Eng., Special edition (2003), pp. 69–76
- [18] Proyecto Multinacional Andino–PMA. Atlas de deformaciones cuaternarias de Los Andes. No. 7, Canadá. 2009.
- [19] C.A. Cornell, E.H. Van Marke; The major influence on seismic risk; Proceedings of the third world conference on earthquake engineering, Santiago, Chile (1969)
- [20] R. Guttenberg, C.F. Richter; Frequency of earthquakes in California; Bull. of the seismol. soc. of am., 34 (1944), pp. 185–188
- [21] National Earthquake Information Center - NEIC, Earthquake catalogue search. United States Geological Survey. 2014. Disponible en: http://earthquake.usgs.gov/earthquakes/search/ .
- [22] D.A. Storchak, D. Di Giacomo, I. Bondár, E. R., Engdahl, J., Harris, W.H.K., Lee, A. Villaseñor, P. Bormann Public Release of the ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009). Seismol. res. lett., 84 (2013) 810-815.
- [23] R. McGuire; Seismic hazard and risk analysis; Earthquake Engineering Research Institute, Oakland, California, United States of America (2004)
- [24] S. Tinti, F. Mulargia; An improved method for the analysis of the completeness of a seismic catalogue; Lett. Al nuovo cim., Series 2, 42 (1985), pp. 21–27
- [25] K. Campbell; Empirical near-source attenuation relationships for horizontal and vertical components of peak ground acceleration, peak ground velocity and pseudo-absolute response spectra; Seismol. res. lett., 68 (1997), pp. 154–179
- [26] D. García, S.K. Singh, M. Herráiz, M. Ordaz, J.F. Pacheco; Inslab earthquakes of Central Mexico: peak ground-motion parameters and response spectra; Bull. of the seismol. soc. of am., 95 (2005), pp. 2272–2282
- [27] G. Bernal, O. Cardona, A. Barbat, M.A. Salgado-Gálvez; Strong ground motion attenuation relationships for Colombia; Proceedings of the Second European Conference on Earthquake Engineering and Seismology, Istambul, Turkey (2014)
- [28] M. Ordaz, S.K. Singh; Source spectra and spectral attenuation of seismic waves from Mexican earthquakes, and evidence of amplification in the hill zone of Mexico City; Bull. of the seismol. soc. of am., 82 (1992), pp. 24–43
- [29] G.M. Atkinson; Attenuation and Source Parameters of Earthquakes in the Cascadia Region; Bull. of the seismol. soc. of am., 85 (1995), pp. 1327–1342
- [30] M. Gallego, Estimación del riesgo sísmico en la República de Colombia [tesis de maestría], Universidad Nacional Autónoma de México, Distrito Federal, México, 1999.
- [31] B. Tavakoli, S. Pezeshk; S., Empirical-Stochastic Ground-Motion Prediction for Eastern North America; Bull. of the seismol. soc. of am., 95 (2005), pp. 2283–2296
- [32] H. Zafarani, M. Soghrat; Simulation of Ground Motion in the Zagros Region of Iran Using the Specific Barrier Model and the Stochastic Method; Bull. of the seismol. soc. of am., 102 (2012), pp. 2031–2045
- [33] S.K. Singh, M. Ordaz, J.G. Anderson, M. Rodríguez, R. Quaas, E. Mena, M. Ottaviani, D. Almora; Analysis of near source strong ground motion recordings along the Mexican subduction zone; Bull. of the seismol. soc. of am., 70 (1989), pp. 903–914
- [34] D. Boore; The effect of finite bandwidth on seismic scaling relationships; S. Das, J. Boatwright, C.H. Scholz (Eds.), Earthquake Source Mechanics, 37, American Geophysical Union Monograph (1986), pp. 275–283
- [35] L. Knopoff, Q. Review of Geophysics, 2 (1964) 625-660.
- [36] M. Abramowitz, I.A. Stegun; Handbook of mathematical functions. National Bureau of Standards. Applied Mathematics Series; Dover Publications. (1965)
- [37] D.E. Cartwright, M.S. Longuett-Higgins; The statistical distribution of a maxima of a random function; Proc. Roy. Soc. London., 237 (1956), pp. 212–232
- [38] A.G. Davenport; Note on the distribution of the largest value of a random function with application to gust loading; Proc. Inst. Civ. Eng., 28 (1964), pp. 187–196
- [39] R.B. Hermann; An extension of random vibration theory estimates of strong ground motion to large distances; Bull. of the seismol. soc. of am., 73 (1985), pp. 157–171
- [40] T.C. Hanks, H. Kanamori; Moment magnitude scale; J. Geophys. Res., 84 (1979), pp. 2348–2350
- [41] M. Gallego, M. Ordaz; Construcción de leyes de atenuación para Colombia a partir de espectros fuente y teoría de vibraciones aleatorias; Rev. Interam. de Planif., 4 (1999), pp. 45–66
- [42] L. Esteva; Criterios para la construcción de espectros para diseño sísmico, en Memorias del tercer simposio panamericano de estructuras; Venezuela, Caracas (1967)
- [43] M. Leonardo-Suárez, Universidad Nacional Autónoma de México, Asociación Colombiana de Ingeniería Sísmica, Aplicación web para consulta y diseminación de datos de amenaza sísmica y el cálculo de espectros de diseño sísmico en Colombia. 2014. Disponible en: http://201.244.179.21:8000/AIS-2014/AIS.html .
- [44] M. Ordaz, O.D. Cardona, M.A. Salgado-Gálvez, G.A. Bernal-Granados, S.K. Singh, D. Zuloaga-Romero; Probabilistic seismic hazard assessment at global level; Int. J. of Disaster Risk Reduction., 10 (2014), pp. 419–427
- [45] Asociación Colombiana de Ingeniería Sísmica–AIS, Recomendaciones para requisitos sísmicos de estructuras diferentes de edificaciones. Comité AIS-180. 2013.
- [46] M.A. Salgado-Gálvez, D. Zuloaga, G. Bernal, M. Mora, O. Cardona; Fully probabilistic seismic risk assessment considering local site effects for the portfolio of buildings in Medellín, Colombia; Bull. Earthquake Eng, 12 (2014), pp. 671–695
- [47] M.A. Salgado-Gálvez, D. Zuloaga, C.A. Velásquez, M.L. Carreño, O.D. Cardona, A.H. Barbat, Urban Seismic Risk Index for Medellín, Colombia, based on probabilistic loss and casualties estimations, Nat. Haz. In press.
- [48] M.A. Salgado-Gálvez, M.L. Carreño, A.H. Barbat, O.D. Cardona; Evaluación probabilista del riesgo sísmico en Lorca mediante simulaciones de escenarios; Rev. Int. Metodos Numer. Calc. Diseño Ing. (2014) http://dx.doi.org/10.1016/j.rimni.2014.12.001 In press
- [49] M.L. Carreño, A.H. Barbat, O.D. Cardona; Método numérico para la evaluación holística del riesgo sísmico utilizando la teoría de conjuntos difusos; Rev. Int. Metodos Numer. Calc. Diseño Ing., 30 (2014), pp. 25–34
- [50] A.H. Barbat, M.L. Carreño, O.D. Cardona, M.C. Marulanda; Evaluación holística del riesgo sísmico en zonas urbanas; Rev. Int. Metodos Numer. Calc. Diseño Ing., 27 (2011), pp. 3–27
- [51] L.E. Pérez-Rocha, M. Ordaz; Maxima earthquakes for seismic design of structures; Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China (2008)
Document information
Published on 01/12/16
Accepted on 06/07/15
Submitted on 22/04/15
Volume 32, Issue 4, 2016
DOI: 10.1016/j.rimni.2015.07.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?
![Zonificación sísmica para el coeficiente de diseño PGA. Datos extraídos de [1].](/wd/images/9/96/Draft_Content_611651835-1-s2.0-S0213131515000528-gr7.jpg)
![Zonificación sísmica para el coeficiente de diseño SS. Datos extraídos de [1].](/wd/images/8/80/Draft_Content_611651835-1-s2.0-S0213131515000528-gr8.jpg)
![Zonificación sísmica para el coeficiente de diseño S1. Datos extraídos de [1].](/wd/images/4/4e/Draft_Content_611651835-1-s2.0-S0213131515000528-gr9.jpg)