Resumen
En este trabajo se aplica un procedimiento basado en el concepto de Acción Repartida Equivalente (ARE) al análisis, por el Método de Elementos Finitos (MEF) formulado en desplazamientos y solución nodal exacta, de pilares con deformación por cortante de acuerdo con la teoría de Timoshenko. Los resultados obtenidos con la metodología ARE-MEF, en los casos analizados, ponen de manifiesto que con un número muy reducido de elementos (uno y dos en los ejemplos desarrollados) se alcanza gran exactitud en desplazamientos, giros y esfuerzos. Sin embargo con otras metodologías formuladas en desplazamientos, como por ejemplo la de integración reducida, se requiere del orden de 40 elementos para alcanzar resultados similares. Asimismo en el presente trabajo, a partir del MEF con solución nodal exacta se determinan de una forma directa y sistemática las funciones de estabilidad y la carga de pandeo para el pilar de Timoshenko.
Abstract
This paper describes a procedure based on the concept of Equivalent Distributed Loads (EDL) applied to the Finite Elements Method (FEM) based on displacements and exact nodal solution of columns subject to shear deformation in accordance with the Timoshenko beam theory. The results obtained using this “EDL-FEM” methodology, in the cases studied, show that a high level of exactness in displacements, rotations as well as shear force and bending moment is obtained with a very small number of elements (one or two in the examples developed). Other methodologies based on displacements, such as reduced integration, require on the order of 40 elements to achieve similar results. The stability functions and buckling load for the Timoshenko beam are also determined in a direct and systematic way from the FEM with exact nodal solution.
Palabras clave
Método de elementos finitos;Solución nodal exacta;Acción repartida equivalente;Viga-columna de Timoshenko;Viga-columna de Bernoulli-Euler;Carga de pandeo
Keywords
Finite element method;Exact nodal solution;Equivalent distributed load;Timoshenko beam-column;Bernoulli-Euler beam-column;Buckling load
1. Introducción
En la metodología de los elementos finitos formulados en desplazamientos, algunos autores emplean como funciones de forma soluciones del sistema de ecuaciones diferenciales homogéneo relativo al problema, que se quiere resolver, debido a la propiedad de conseguirse soluciones nodalmente exactas, tal y como demostró P. Tong [1] de forma general. Siguiendo la idea de este autor en Romero et. al [2] se expone una metodología aplicable a problemas de elementos finitos que incluye los casos de operadores no autoadjuntos para la ecuación diferencial. Resultando la propiedad de exactitud nodal con la condición de emplear como funciones de ponderación en el método de Petrov-Galerkin, soluciones de la ecuación diferencial homogénea del operador adjunto de la ecuación. Esto sucede independientemente de cuál sea la función empleada para aproximar los desplazamientos. Posteriormente otro autores [3] ; [4] realizan también estudios en conexión con esta idea de la exactitud nodal.
En el campo de las estructuras, otros autores han realizado diversas aplicaciones de dicho tipo de aproximación a diferentes modelos de vigas. Entre las distintas referencias puede destacarse la de Reddy [5] donde dicho autor realiza aplicaciones al modelo de viga de Timoshenko y justifica que los elementos están libres del fenómeno de bloqueo al emplear funciones de forma que son soluciones del sistema homogéneo de ecuaciones diferenciales. También otros autores [6] ; [7] recientemente han empleado elementos finitos con solución nodal exacta en la misma línea de la referencia anterior.
En Romero et. al [8] se emplea por primera vez la metodología de elementos finitos con solución nodal exacta y el concepto de acción repartida equivalente (ARE) aplicado al modelo de viga de Bernoulli-Euler. En dicho trabajo se destaca la ventaja del procedimiento al permitir mejorar la aproximación de la solución en el interior de los elementos. Posteriormente en [9]; [10] ; [11] se aplican ambas ideas al modelo de viga de Timoshenko. En [12] ; [13] se aplica ya el concepto de ARE al análisis del pandeo de pilares en el modelo de Bernoulli-Euler.
El objetivo del presente trabajo es aplicar por primera vez la metodología ARE-MEF en el estudio del pilar de Timoshenko. El planteamiento seguido ha sido el siguiente. Tras ésta introducción se realiza el desarrollo de la teoría de los elementos finitos con solución nodal exacta para el pilar de Timoshenko. Con dicho desarrollo se puede considerar el pilar de Bernoulli-Euler como un caso particular del de Timoshenko. Este planteamiento permite también obtener de una manera directa y sistemática la carga de pandeo y las funciones de estabilidad para los dos tipos de pilares. En relación con estas funciones se indica que la deducción de las mismas fue ya realizada por Absi en 1967 [14], siguiendo una línea diferente a la que aquí se expone. En el trabajo se continúa después exponiendo el concepto de ARE para el problema considerado, destacando las propiedades de interpolación y ortogonalidad, que son la base del buen comportamiento del método expuesto, para la aproximación de los esfuerzos y también para los desplazamientos y giros, en el interior de cada elemento finito. Además en el trabajo se han realizado dos ejemplos numéricos, que ponen de manifiesto las excelentes ventajas de la metodología empleada, al poder aproximar los desplazamientos, giros y esfuerzos de manera óptima con un número muy reducido de elementos, uno y dos, en los casos desarrollados.
Finalmente se quiere indicar que estas metodologías de elementos finitos aplicadas al modelo Timoshenko siguen muy vigentes, de ahí el interés de los autores por dicho modelo para el estudio de los pilares con deformación por cortante. No obstante en la literatura se van introduciendo también otras formas de análisis basadas en teorías no locales de la elasticidad y modelos de alto orden [15]; [16]; [17]; [18] ; [19]. En relación con estos últimos, se indica que aunque aproximan mejor la distribución de tensiones en las secciones presentan mayor complejidad computacional y sus aplicaciones están dirigidas, por ahora, esencialmente hacia problemas de tipo académico.
2. Elementos finitos con solución nodal exacta para el pilar de timoshenko
El sistema de ecuaciones diferenciales que rige el modelo de Timoshenko para el pilar es L(U) = F[20], donde
|
|
(1) |
siendo w el desplazamiento, ψ el giro, P el axil y k, A y G, el factor de corrección para el esfuerzo cortante, el área de la sección y el módulo de rigidez de cortante, respectivamente. Llamando H a la rigidez EI y K al producto kAG, el sistema puede expresarse en la forma:
|
|
(2) |
y también como:
|
|
(3) |
La formulación variacional de manera análoga a la expuesta en [8]; [11] ; [20] se obtiene, realizando la ponderación usual en el sistema original, con y tras el correspondiente proceso de integración por partes en el subintervalo genérico , resulta:
|
|
(4) |
donde las formas, bilineales y lineales, son respectivamente:
|
|
(5a) |
|
|
(5b) |
|
|
(5c) |
El problema variacional para el caso, por ejemplo, de una pieza empotrada en el extremo x = a y libre en x = b, sometida a un axil P constante y con cargas FH y M en el extremo libre consiste en obtener:
|
|
tal que
|
|
(6) |
donde es el espacio de Sobolev de las funciones g tales que g, g′ ∈ L2(Ω) junto con g(a) = 0. La solución única de este problema, como es conocido, es la que hace estacionario el siguiente funcional de energía:
|
|
(7) |
La simetría de la forma bilineal b(· , ·) permite expresar, en cualquier subintervalo, o en el intervalo total:
|
|
(8) |
y tomando las funciones de ponderación, de modo que sean soluciones del sistema homogéneo del pilar de Timoshenko, se tiene , no dependiendo la forma bilineal de los valores que toma U en el interior del subintervalo. La ecuación variacional a nivel de elemento
|
|
se puede expresar, de acuerdo con lo anterior, en la forma:
|
|
(9) |
La construcción ahora de las ecuaciones de equilibrio de elementos finitos, es decir las ecuaciones locales y la global, se realizan del mismo modo que se indica en las referencias [8]; [11] ; [20]. En las mismas se demuestra que la solución obtenida empleando funciones de forma:
|
|
que verifican las ecuaciones homogéneas del modelo correspondiente, son nodalmente exactas. Dichas funciones constituyen una base de Lagrange para la interpolación, o sea, li(Nj) = δij, i, j = 1, .., 4.
Estas funciones de forma se determinan en el Apéndice, para P, H y K constantes en cada elemento finito . En este caso el sistema de ecuaciones diferenciales es:
|
|
(10) |
con H1 = H(1 − P/K) y m = H/K.
La ecuación de equilibrio en es Keue = fe + qe, donde los desplazamientos nodales, las cargas nodales equivalentes y las nodales de equilibrio son:
|
|
(11) |
|
|
(12) |
|
|
(13) |
Los elementos de la matriz de rigidez local son los cuales pueden calcularse mediante integración en la forma:
|
|
(14) |
y también por derivación de las funciones de forma mediante la expresión [8]; [11] ; [20]:
|
|
(15) |
Las matrices de rigidez exactas del elemento para el pilar de Timoshenko, , y el de Bernoulli-Euler, , que resultan son respectivamente (16) y (17):
|
|
(16) |
donde:
|
|
Cuando m = 0, es:
|
|
(17) |
donde:
|
|
3. Cargas de pandeo y funciones de estabilidad
Cuando se considera la deformación por cortante, el valor de la carga de pandeo disminuye, por ello es importante conocer cuáles son dichas cargas para las diferentes condiciones en los extremos del pilar. Esta carga es el valor positivo más pequeño de P que anula el determinante de la matriz , ya reducida, es decir una vez considerada las condiciones de contorno esenciales del correspondiente problema de autovalores.
Para el caso de un pilar de longitud L , que está articulado en ambos extremos, es decir en los nodos 1 y 2, la matriz se reduce a la formada por los cuatro elementos ubicados en las filas y columnas segunda y cuarta de la matriz de rigidez (16). Anulando el correspondiente determinante, o sea:
|
|
(18) |
y operando se obtiene:
|
|
resultando s1 = sen(r1L) = 0. Tomando la raíz positiva más pequeña, r1L = π, y teniendo en cuenta la relación:
|
|
(19) |
que se deduce de , la carga de pandeo es:
|
|
(20) |
Para el caso de una viga-columna de longitud L , empotrada en un extremo (nodo 1) y libre en el otro (nodo 2), la matriz se reduce a la formada por los cuatro elementos ubicados en las filas y columnas tercera y cuarta de la matriz de rigidez (16). Anulando el correspondiente determinante, o sea:
|
|
(21) |
y operando se obtiene:
|
|
resultando c1 = cos(r1L) = 0 y tomando la raíz positiva más pequeña r1 = π/(2L), y empleando la expresión (19), la carga de pandeo en este caso es:
|
|
(22) |
En [20] se han obtenido los valores de la carga de pandeo para el pilar empotrado-empotrado y empotrado-articulado, siguiendo el mismo procedimiento anterior, obteniéndose las mismas de manera exacta, ya que se sigue el procedimiento de anular el determinante de la matriz .
Por otra parte, si se tiene en cuenta la carga de pandeo para la pieza de Bernoulli-Euler, PcrE, la carga crítica de pandeo para el pilar de Timoshenko se puede poner de la siguiente manera [21]:
|
|
(23) |
cuando la configuración del pilar es empotrado-libre, articulado-articulado y empotrado-empotrado.
Cuando el pilar está empotrado-articulado la expresión (23) no es aplicable. Para este caso se tiene la aproximación siguiente [22]:
|
|
(24) |
Hay que destacar que la expresión (23) es aplicable también para un pilar con empotramientos elásticos de igual rigidez en ambos extremos [23].
Por otra parte, las denominadas funciones de estabilidad se obtienen de manera directa a partir de la matriz de rigidez exacta (16). Para el caso de un pilar de longitud L, que está articulado en ambos extremos se tiene la siguiente relación entre momentos y giros:
|
|
(25) |
Llamando x = r1L (adimensional) en (25) la expresión anterior se puede poner:
|
|
(26) |
siendo ρ y , en función de x, las siguientes expresiones:
|
|
Asimismo, la expresión (19) se puede poner en términos de x en la forma:
|
|
(27) |
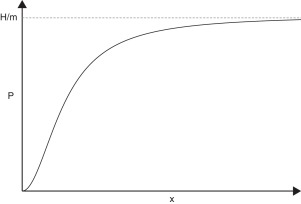
La relación entre P y x se representa en la figura 1.
|
|
|
Figura 1. Relación biunívoca de P y x. |
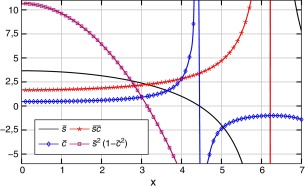
Por otra parte, la expresión (26) puede ponerse en la siguiente forma clásica, con las funciones y de estabilidad representadas en la figura 2:
|
|
(28) |
donde:
|
|
|
|
|
Figura 2. Funciones de estabilidad para una sección rectangular y de L=5m, con un valor de m=0.26. |
Dichas funciones de estabilidad se recogen en la literatura habitualmente por separado para Bernoulli-Euler y Timoshenko [14] ; [24], y han sido empleadas por otros autores para encontrar el valor de la carga crítica en pórticos [25]; [26] ; [27]. Sin embargo, el proceso seguido en este trabajo ha permitido su construcción de forma directa y sistemática a partir de la matriz de rigidez, englobando a ambos modelos de viga-columna.
En la figura 2, además de de las funciones de estabilidad, y , se ha representado y . Esta última función es el determinante de la matriz de la expresión (26), que se anula en x = π, valor que se corresponde con PcrT, de acuerdo con (20) y (27).
4. Método de acciones repartidas equivalentes
Considerando la descomposición del dominio en la forma , y teniendo en cuenta el concepto de acción repartida equivalente [2]; [8]; [11] ; [20], donde dos acciones f y se definen como equivalentes respecto de dicha descomposición, si en cada [α, β] de la descomposición, se verifica la igualdad de los siguientes productos escalares que representan las cargas nodales equivalentes:
|
|
con dada mediante una combinación lineal de las componentes N1i, i = 1, .., 4 soluciones de la homogénea. Obsérvese que es la proyección ortogonal de f sobre el espacio de funciones engendrado por las N1i, i = 1, .., 4.
Del sistema (2) se deduce para f y las ecuaciones diferenciales siguientes:
|
|
(29) |
y considerando ahora la equivalencia de las acciones se puede poner:
|
|
(30) |
resultando:
|
|
(31) |
donde como es sabido, la función de ponderación v pertenece al espacio de soluciones del sistema homogéneo, es decir al engendrado por N1i, i = 1, .., 4.
Integrando por partes (31) se tiene:
|
|
(32) |
donde el primer sumando es nulo debido a la igualdad de desplazamientos y giros en los nodos para dos acciones equivalentes, teniéndose por tanto:
|
|
(33) |
Integrando de nuevo por partes:
|
|
(34) |
siendo también el primer sumando nulo por la razón indicada anteriormente. Y en consecuencia se tiene:
|
|
(35) |
De acuerdo con las consideraciones anteriores, las expresiones (33) y (35) y llamando:
|
|
(36) |
se reducen a:
|
|
(37) |
|
|
(38) |
El esfuerzo cortante en cada sección x viene dado por la expresión , por lo tanto la función V(x ) de la expresión (33) representa un nuevo esfuerzo que puede denominarse pseudo-cortante o cortante corregido (proyección en la dirección del desplazamiento de las acciones que quedan a la derecha de la sección, incluyendo la contribución de [20]). La función M(x) representa el momento flector en la citada sección.
La expresión (37) nos indica que la función diferencia de cortantes corregidos, , que es nula en los extremos del intervalo, ya que interpola los mismos valores, es además ortogonal al espacio de funciones engendrado por las .
Y del mismo modo que en el caso de la viga [2] ; [8], se puede demostrar que engendran un espacio de dimensión tres. Asimismo la expresión (38) indica que la función:
|
|
que representa la diferencia de momentos más la carga P por la diferencia de desplazamientos, es nula y con derivada nula en los extremos del intervalo (pues interpolan los mismos valores), es además ortogonal al espacio de funciones engendrado por las . Estas últimas engendran un espacio de dimensión dos.
Estas propiedades de ortogonalidad e interpolación, en cada elemento, para y , son la base del buen comportamiento del método expuesto, para la aproximación de los esfuerzos y también para los desplazamientos y giros, en el interior de cada elemento finito.
Tal y como se ha demostrado en [8] ; [11], se puede calcular también de manera análoga la solución y los esfuerzos derivados de ella, y , relativos a , sin necesidad de calcular previamente , para el caso del pilar de Timoshenko.
A continuación se desarrolla, para el caso particular de H y K constantes, la determinación mediante interpolación, de la solución aproximada correspondiente a la acción repartida equivalente .
A partir de se deduce que la solución equivalente es:
|
|
(39) |
donde:
|
|
siendo la matriz C:
|
|
(40) |
donde:
|
|
Las leyes de desplazamientos y giros vienen dados por la expresión (39) mientras que las leyes de momentos flectores, esfuerzos cortantes equivalentes y asimismo la acción repartida equivalente, , en cada intervalo [α, β], se puede ver en [20,ec. 3.89]. Las mismas se deducen considerando que:
|
|
(41) |
Obsérvese que la acción repartida equivalente, en el desarrollo anterior se ha obtenido a partir de la derivación correspondiente de la función de desplazamientos y no a partir de la proyección ortogonal (que es otra posibilidad) de la función que define la carga f del intervalo [α, β] sobre el espacio definido por las funciones de forma N1i, i = 1, .., 4.
Destacamos finalmente que si la acción f(x) viene dada en cada intervalo o elemento por una expresión que sea combinación lineal de las cuatro funciones 1, z, sen(r1z), y cos(r1z), el procedimiento indicado proporcionará la solución exacta para los desplazamientos, giros y leyes de esfuerzos, no solo en los nodos (lo que se consigue para cualquier tipo de carga f(x) utilizando elementos finitos con solución nodal exacta) sino también en el interior de cada elemento (véase la Propiedad de solución exacta I en [8]; [11] ; [20])
5. Aplicaciones numéricas
A continuación se desarrollan dos ejemplos, en los que se aborda el cálculo en régimen lineal de la deformada y de las leyes de esfuerzos de una viga-columna, empleando el modelo de Timoshenko.
5.1. Ejemplo 1
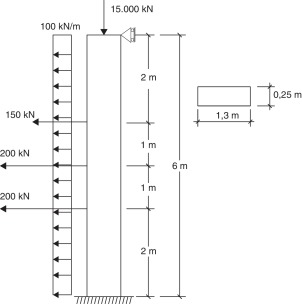
Se analiza una viga-columna de 6 m de largo y sección rectangular constante en toda su longitud (ver fig. 3). Se considera una material ideal cuyas características son: módulo de elasticidad, E = 2, 1 × 107kN/m2, coeficiente de Poisson, υ = 30 × 10−2, y factor de corrección por cortante, k = 5/6.
|
|
|
Figura 3. Pilar empotrado-articulado. |
La solución aproximada para este caso, de pieza empotrada-articulada, se ha obtenido considerando un solo elemento de longitud l = 6m. Dicha solución puede compararse con la exacta, que a su vez puede determinarse también con el procedimiento desarrollado, tal y como se ha indicado en el último párrafo del apartado anterior. Para la determinación de la solución exacta se discretiza la viga-columna en 4 elementos finitos, acordes con la definición de la carga en el dominio:
|
|
También, con la finalidad de comparación, se ha realizado un cálculo con elementos finitos lineales e integración reducida (Int. Red.) [5]; [28] ; [29]. Se han requerido al menos 20 elementos para los desplazamientos, giros y esfuerzos cortantes y 40 elementos para los momentos flectores, para obtener resultados similares a los calculados con la metodología propuesta ARE-MEF con un solo elemento.
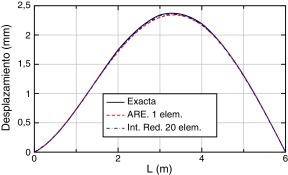
Los resultados obtenidos, exacto (ARE con 4 elementos) y aproximados (ARE con 1 elemento, Int. Red. con 20 y 40 elementos), en términos de desplazamientos, giros, momentos, esfuerzos cortantes y acciones, son los que se muestran respectivamente en las Figura 4, Figura 5, Figura 6, Figura 7 ; Figura 8.
|
|
|
Figura 4. Comparación de desplazamientos. |
|
|
|
Figura 5. Comparación de giros. |
|
|
|
Figura 6. Comparación de momentos flectores. |
|
|
|
Figura 7. Comparación de esfuerzos cortantes. |
|
|
|
Figura 8. Representación de las acciones originales y las repartidas equivalentes. |
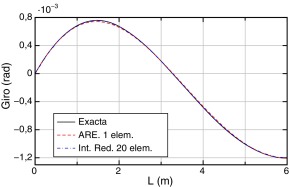
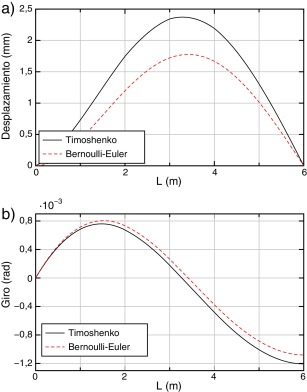
Para los desplazamientos (fig. 4) se puede ver que las soluciones aproximadas prácticamente coinciden con la solución exacta del problema. Ocurre lo mismo con los giros (fig. 5).
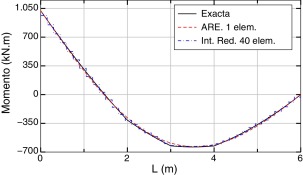
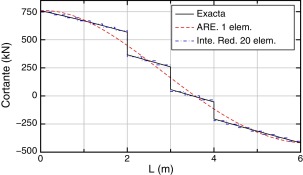
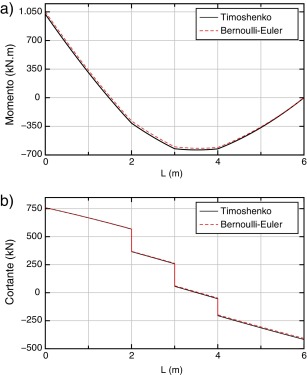
En las Figura 6 ; Figura 7 se dan, respectivamente, las gráficas de momentos y esfuerzos cortantes. El máximo error del momento flector, empleando ARE y un elemento, se produce en la abscisa 3 m, siendo el mismo inferior al 5% respecto al valor exacto. Empleando la integración reducida y 40 elementos, el error es del orden del 6% y se produce en el extremo inferior de la pieza.
Por otra parte en el esfuerzo cortante el máximo error se produce en los puntos donde están aplicadas las cargas puntuales, ya que el método regulariza la ley eliminando las discontinuidades, pues promedia en cierto modo los valores del cortante a la izquierda y derecha de dichos puntos. De modo que el error es por tanto el menor posible considerando que la ley del esfuerzo cortante aproximado viene dada en el procedimiento por una función continua.
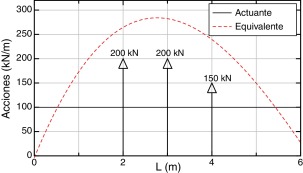
Asimismo, en la figura 8 se puede apreciar la distribución de las acciones repartidas equivalentes y cómo éstas aproximan la carga original.
Adicionalmente, en las Figura 9 ; Figura 10 se puede observar la diferencia entre los resultados exactos obtenidos en la forma ya indicada con ARE y 4 elementos, para los modelos de Timoshenko y Bernoulli-Euler, en los desplazamientos, giros y esfuerzos. Como se puede ver existen diferencias apreciables entre los valores exactos de ambos modelos.
|
|
|
Figura 9. Comparación de resultados entre Timoshenko y Bernoulli-Euler: a) desplazamientos y b) giros. |
|
|
|
Figura 10. Comparación de resultados entre Timoshenko y Bernoulli-Euler: a) momentos flectores y b) esfuerzos cortantes. |
En el caso de los desplazamientos la diferencia relativa máxima se produce en el punto de abscisa 3 m y es del orden del 26,5% y para los giros la diferencia máxima se produce en el extremo superior y es del orden del 10,5%.
Para los momentos flectores la diferencia máxima se produce en el punto de abscisa 2,5 m y es del orden del 5,5% y para los esfuerzos cortantes, la diferencia máxima se produce en el extremo superior y es menor del 5%.
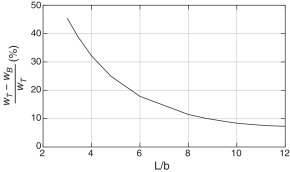
A continuación se muestra la influencia de la esbeltez (L/b) en los modelos de Timoshenko y Bernoulli-Euler en lo relativo a desplazamientos. Para ello se mantienen las mismas condiciones de carga, longitud y espesor de la pieza ( fig. 3), variando el canto b. En la figura 11 se observa que cuando disminuye la esbeltez, la diferencia entre ambos modelos es mayor. Para una esbeltez de 12 la diferencia relativa es del orden del 7%, sin embargo para una esbeltez de 3 la diferencia es ya notable, alcanzando el 45%. Para los giros y esfuerzos se tiene un comportamiento similar.
|
|
|
Figura 11. Variación de la diferencia de desplazamientos entre Timoshenko y Bernoulli-Euler en función de la esbeltez (L/b). |
5.2. Ejemplo 2
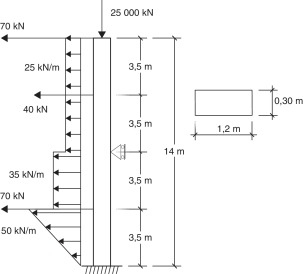
Se analiza una viga-columna de 14m de largo y sección rectangular constante en toda su longitud (ver fig. 12). Se considera una material ideal cuyas características son: coeficiente de Poisson, υ = 30 × 10−2, módulo de elasticidad, E = 3 × 107kN/m2 y factor de corrección por cortante, k = 5/6.
|
|
|
Figura 12. Pilar empotrado en la base y apoyado en el centro. |
Las condiciones de vínculo y estado de carga se muestran en la figura 12, el valor de la carga axial P = 25000kN representa aproximadamente el 60%PcrT de Timoshenko. Se ha empleado una distribución poco frecuente de las cargas transversales: combinación de una triangular como la indicada junto con otras distribuidas constantes además de las puntuales, con el fin de mostrar las posibilidades de la metodología. Obsérvese que el procedimiento daría valores exactos incluso si en el elemento la carga distribuida viniera dada por una función con parte polinómica de grado uno y parte trigonométrica.
Del mismo modo que en el ejemplo anterior, se obtiene tanto la solución exacta como las aproximadas. La solución aproximada, empleando ARE-MEF, se ha obtenido discretizando la pieza en el menor número de elementos posible dadas las condiciones de vínculo, es decir, en dos elementos definidos por:
|
|
Por otra parte la solución aproximada empleando elementos finitos lineales e integración reducida, se ha obtenido discretizando la pieza en 20 elementos para los desplazamientos, giros y esfuerzos cortantes, y 40 elementos para los momentos flectores.
Sin embargo, la solución exacta en este caso, con el procedimiento propuesto, requiere la discretización de la viga-columna en 4 elementos finitos, acordes con la definición de la carga en el dominio:
|
|
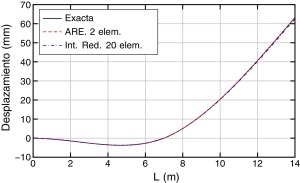
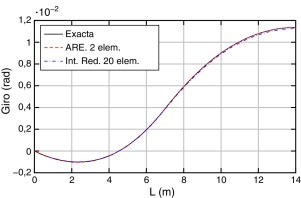
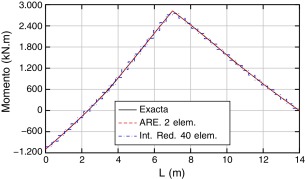
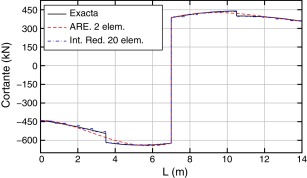
Los resultados obtenidos, exacto y aproximados (ARE e Int. Red.), en términos de desplazamientos, giros, momentos y esfuerzos cortantes, son los que se muestran en las Figura 13, Figura 14, Figura 15 ; Figura 16, respectivamente.
|
|
|
Figura 13. Comparación de desplazamientos. |
|
|
|
Figura 14. Comparación de giros. |
|
|
|
Figura 15. Comparación de momentos flectores. |
|
|
|
Figura 16. Comparación de esfuerzos cortantes. |
Para los desplazamientos (fig. 13) y los giros (fig. 14) se puede ver que la solución exacta y las aproximadas son prácticamente iguales.
En las Figura 15 ; Figura 16 se dan, respectivamente, las gráficas de momentos y esfuerzos cortantes. El máximo error del momento flector (fig. 15), empleando ARE y 2 elementos, se produce en la abscisa 3,5 m donde el error es inferior al 1,2% respecto al valor exacto. Empleando interpolación lineal e integración reducida y 40 elementos finitos, el error es 2,5% aproximadamente y se produce en la abscisa 5 m.
Por otra parte, para el esfuerzo cortante el máximo error se produce en los puntos donde están aplicadas las cargas puntuales. Adicionalmente se puede comprobar que se cumplen las propiedades de interpolación en el sentido de Lagrange (para el cortante) y en el sentido de Hermite (para el momento). Es decir los valores del cortante y momentos obtenidos a través de la acción repartida equivalente en los extremos coinciden con los correspondientes a la solución exacta y para el momento ocurre lo mismo con la primera derivada de dicho esfuerzo, ya que toma el valor opuesto del cortante [20].
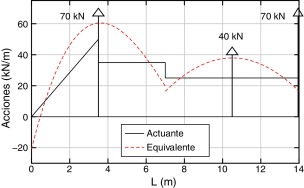
En la figura 17 se puede apreciar la distribución de las acciones equivalentes y cómo éstas aproximan a la carga original en cada uno de los elementos. Se observa asimismo la tendencia de la acción repartida equivalente de recoger también la información de las cargas puntuales.
|
|
|
Figura 17. Representación de las acciones originales y las repartidas equivalentes. |
6. Conclusiones
En este trabajo se ha aplicado por primera vez el método de elementos finitos formulado en desplazamientos con solución nodal exacta y acción repartida equivalente a pilares con deformación por cortante empleando el modelo de Timoshenko.
Los resultados obtenidos en los ejemplos desarrollados ponen de manifiesto las excelentes ventajas de ésta metodología ya observadas en aplicaciones previas a otros problemas. En particular en los dos ejemplos expuestos ha sido suficiente con emplear uno y dos elementos, respectivamente, para alcanzar una gran aproximación en desplazamientos, giros y esfuerzos, con respecto a la solución exacta del problema. Sin embargo con otras metodologías formuladas también en desplazamientos, como por ejemplo la integración reducida, se requiere del orden de 40 elementos para alcanzar resultados de aproximación similares.
También otro aspecto destacable de la metodología seguida ha sido la determinación de cargas de pandeo y funciones de estabilidad para la pieza con distintas condiciones de vínculo, siguiendo una vía diferente y más directa que las desarrolladas en los trabajos que han sido mencionados.
Agradecimientos
Los autores expresan su agradecimiento a los revisores por las modificaciones sugeridas, lo que ha permitido mejorar la configuración final del artículo. Asimismo, reconocen el apoyo recibido mediante la beca JAE-Predoc otorgada a Elvira M. López (JAEPre098), correspondiente al Programa Junta para la Ampliación de Estudios del CSIC y cofinanciada por el Fondo Social Europeo.
Apéndice.
La solución del sistema homogéneo asociado a (10) en cada en cada elemento finito se puede expresar mediante las funciones de forma, Ni, i = 1, ..., 4, en términos de los valores de w y ψ en los extremos:
|
|
donde:
|
|
con q = ρ/r1, y siendo C1 la matriz
|
|
Para el pilar de Bernoulli-Euler m = 0, y los desplazamientos en el elemento son:
|
|
donde la matriz es
|
|
Bibliografía
- [1] P. Tong; Exact solution of certain problems by finite-element method; AIAA Journal., 7 (1) (1969), pp. 178–180
- [2] J.L. Romero, M.A. Ortega; Splines generalizados y solución nodal exacta en el método de elementos finitos; Informes de la Construcción, 51 (464) (1999), pp. 41–85
- [3] I. Hlavacek, M. Krizek; On exact results in the finite element method; Applications of Mathematics, 46 (6) (2001), pp. 467–478
- [4] C.A. Felippa, E. Oñate; Nodally exact Ritz discretizations of 1 D diffusion–absorption and Helmholtz equations by variational FIC and modified equation methods; Computational Mechanics, 39 (2) (2007), pp. 91–111
- [5] J.N. Reddy; On locking-free shear deformable beam finite elements; Comput. Methods Appl. Mech. Engrg., 149 (1997), pp. 113–132
- [6] S.P. Triantafyllou, V.K. Koumousis; An inelastic Timoshenko beam element with axial-shear-flexural interaction; Computational Mechanics, 48 (6) (2011), pp. 713–727
- [7] N. Li, Z. Li, L. Xie; A fiber-section model based Timoshenko beam element using shear-bending interdependent shape function; Earthquake Engineering and Engineering Vibration, 12 (3) (2013), pp. 421–432
- [8] J.L. Romero, M.A. Ortega; Acciones equivalentes y solución en desplazamientos interpolada en la viga de Bernoulli-Euler; Informes de la Construcción, 49 (454) (1998), pp. 5–27
- [9] J.L. Romero, M.A. Ortega, J.M. Corrales; Estudio y resolución del modelo de viga de Timoshenko. Algoritmo de acciones equivalentes; V Congreso de Métodos Numéricos en Ingeniería, 3-6 de Junio de 2002, SEMNI, Madrid, España (2002)
- [10] E.M. López, J.L. Romero, M.A. Ortega, O. Río; Simplified finite element assessment of beams with and without shear deformation; Proceedings of the Fourteenth International Conference on Civil, Structural and Environmental Engineering Computing, 3-6 de Septiembre de 2013, Civil-Comp Press, Cagliari, Sardinia, Italia (2013)
- [11] J.L. Romero, M.A. Ortega, E.M. López, O. Río; Elementos finitos con acciones repartidas equivalentes de cualquier orden. Aplicación a los modelos de vigas de Timoshenko y Bernoulli-Euler; Informes de la Construcción., 66 (535) (2014), p. e029
- [12] M.A. Ortega; Análisis del pandeo de pilares en régimen no lineal mediante splines generalizados; Universidad Politécnica de Madrid, Madrid (2004) Tesis doctoral
- [13] J.L. Romero, M.A. Ortega, F.J. Navarro; Método de acciones equivalentes en el análisis del pandeo de pilares con comportamiento lineal o no lineal del material; VI Congreso de Métodos Numéricos en Ingeniería, 4-7 de Julio de 2005, SEMNI, Granada, España (2005)
- [14] Z.P. Bažant, L. Cedolin; Stability of structures. elastic, inelastic, fracture, and damage theories; Dover Publications, INC (1991)
- [15] J.N. Reddy; Nonlocal theories for bending, buckling and vibration of beams; International Journal of Engineering Science, 45 (2) (2007), pp. 288–307
- [16] N. Challamel; Higher-order shear beam theories and enriched continuum; Mechanics Research Communications, 38 (5) (2011), pp. 388–392
- [17] N. Challamel, I. Mechab, N. Elmeiche, M. Sid, A. Houari, H.A. Atmane; Buckling of generic higher-order shear beam/columns with elastic connections: local and nonlocal formulation; Journal of Engineering Mechanics, 139 (8) (2013), pp. 1091–1109
- [18] S. Monleón, C. Lázaro; El concepto de hiperviga como generalización de los modelos unidimensionales en la estática de piezas alargadas; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 27 (4) (2011), pp. 294–303
- [19] S. Monleón, C. Lázaro, J. Casanova, A. Domingo; Pseudoesfuerzos y evaluación de tensiones en modelos hiperviga; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 31 (2) (2015), pp. 71–80
- [20] E.M. López; Análisis de elementos viga-columna en régimen no lineal con deformación por cortante; Universidad Politécnica de Madrid, Madrid (2015) Tesis doctoral
- [21] C.M. Wang, C.Y. Wang, J.N. Reddy; Exact solutions for buckling of structural members; CRC press (2005)
- [22] H.Z. Ziegler; Arguments for and against Engessers buckling formulas; Ingeniur-Archiv, 52 (1982), pp. 105–113
- [23] J.R. Banerjee, F.W. Williams; The effect of shear deformation on the critical buckling columns; Journal of Sound and Vibration, 174 (5) (1994), pp. 607–616
- [24] R.K. Livesly; Métodos matriciales para cálculo de estructuras; Editorial BLUME (1970)
- [25] Z.P. Bažant, M. Christensen; Long-wave extensional buckling of large regular frames; Journal of Structural Division, 98 (10) (1972), pp. 2269–2289
- [26] S.Z. Al-Sarraf; Shear effect on the elastic stability frames; The Structural Engineer, 64B (2) (1986), pp. 43–47
- [27] S.Z. Al-Sadder; Exact expressions for stability functions of a general non-prismatic beam–column member; Journal of Constructional Steel Research, 60 (11) (2004), pp. 1561–1584
- [28] E. Oñate; Cálculo de estructuras por el método de los elementos finitos; (2a ed.)Editorial UPC (2004)
- [29] J.N. Reddy; An introduction to the finite element method; (third ed.)Editorial McGraw-Hill (2006)
Document information
Published on 20/12/17
Accepted on 24/05/17
Submitted on 24/05/17
Volume 33, Issue 4, 2017
DOI: 10.1016/j.rimni.2016.06.002
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?