Resumen
En este artículo se estudia la influencia de la interacción dinámica vehículo-vía-estructura-suelo en el comportamiento de viaductos. Dicho análisis se lleva a cabo usando un modelo acoplado, formulado en el dominio del tiempo, para predecir las vibraciones producidas por el paso de trenes. El vehículo se modeliza usando un sistema multicuerpo, la vía y el viaducto se representan mediante elementos finitos, y el suelo es considerado como un semiespacio homogéneo modelizado con elementos de contorno. Para predecir la respuesta de viaductos, normalmente, se han empleado modelos de fuerzas móviles y masas móviles. En este trabajo, el sistema multicuerpo usado considera los mecanismos de excitación cuasi-estático y dinámico. Los resultados obtenidos muestran la influencia de la interacción suelo-estructura tanto en la caracterización dinámica de un viaducto corto de un solo vano, como en su respuesta en régimen resonante y no resonante.
Abstract
The dynamic vehicle-track-bridge-soil interaction is studied on high speed lines. The analysis is carried out using a general and fully three dimensional multi-body-finite element-boundary element model, formulated in the time domain to predict vibrations due to the train passage over the bridge. The vehicle is modelled as a multi-body system, the track and the bridge are modelled using finite elements and the soil is considered as a homogeneous half-space by the boundary element method. Usually, moving force model and moving mass model are employed to study the dynamic response of bridges. In this work, the multi-body system allows one to consider the quasi-static and dynamic excitation mechanisms. Soil-structure interaction is taken into account on the dynamic structure behaviour on simply-supported short span bridges. The influence of soil-structure interaction is analysed in both resonant and non-resonant regimes.
Palabras clave
Tren de alta velocidad ; Interacción suelo-estructura ; Puente de ferrocarril ; Resonancia
Keywords
High-speed train ; Soil-structure interaction ; Railway bridge ; Resonant vibration
1. Introducción
Los fenómenos de resonancia en puentes destinados al tráfico ferroviario aparecen cuando la velocidad de paso del tren es tal que la frecuencia de excitación coincide con alguna de las frecuencias naturales del puente, o sub-múltiplos de estas, produciéndose un nivel de vibraciones elevado. En viaductos cortos, las velocidades a las que se pueden producir estos efectos son ampliamente superadas por las velocidades actuales de explotación de las líneas de alta velocidad. Los niveles de vibraciones alcanzados en régimen de resonancia afectan, principalmente, a la seguridad y estabilidad del tren, al confort de los pasajeros y a la integridad de la vía. Por tanto, la respuesta dinámica de viaductos se ha convertido en uno de los estudios fundamentales a tener en cuenta durante las etapas de diseño de este tipo de estructura. Las normativas de diseño establecen que el comportamiento dinámico de un puente está determinado por la propia naturaleza móvil de la carga, por la aplicación sucesiva de cargas móviles y por las irregularidades de la vía. La normativa actualmente en vigor para el cálculo de puentes de ferrocarril evalúa los efectos dinámicos mediante coeficientes de impacto, que representan la amplificación de la respuesta dinámica respecto a una única carga móvil [1] . Sin embargo, los coeficientes de impacto no tiene en cuenta los efectos de resonancia, estando restringida la evaluación de los efectos dinámicos mediante este método a trenes circulando a una velocidad inferior a 220 km/h.
Existen numerosos trabajos acerca de la caracterización y evaluación de los efectos dinámicos que se producen en puentes destinados al tráfico ferroviario. Frýba [2] presentó un modelo teórico basado en transformaciones integrales proporcionando una estimación de las velocidades de resonancia y de la amplitud de la vibración debida a la aplicación sucesiva de cargas móviles equiespaciadas. Li et al. [3] emplearon un modelo de viga simplemente apoyada para analizar la influencia de la interacción vehículo-vía en los efectos de resonancia, estableciendo que la respuesta máxima en régimen resonante de un puente se produce para la primera velocidad resonante asociada al modo de vibración excitado. Ju et al. [4] propusieron un modelo tridimensional de elementos finitos para estudiar los efectos de resonancia en puentes de uno y de varios vanos, concluyendo que la diferencia entre la frecuencia de paso de la carga transmitida al puente y las frecuencias resonantes del puente deben ser lo mayor posible. Xia et al. [5] investigaron los mecanismos de resonancia del sistema vehículo-puente y los efectos de resonancia en el vehículo debidos a la deformación del tablero, obteniendo regímenes resonantes para varios mecanismos de excitación.
Por otra parte, el estudio del comportamiento dinámico de puentes destinados al paso de trenes de alta velocidad (TAV) pasa por el análisis de la influencia de los diferentes factores que conforman el sistema vehículo-vía-puente. En el modelo más simple de interacción se considera despreciable la inercia de las masas del vehículo comparadas con el peso propio de este, representándose la carga transmitida como un conjunto de cargas móviles. Diversos autores han usado satisfactoriamente modelos de cargas móviles [6] , [7] , [8] and [9] . Un modelo algo más preciso es el modelo de masas móviles en el que se desprecia el efecto de las suspensiones primarias y secundarias del vehículo. Otros autores han usado modelos de osciladores móviles [3] , [4] , [5] , [10] , [11] , [12] and [13] . Pesterev et al. [12] han presentado un análisis riguroso de la equivalencia entre los modelos de carga móvil, masa móvil y de osciladores móviles en las vibraciones producidas en vigas, concluyendo que para reproducir con exactitud la fuerza transmitida es necesario usar modelos multicuerpos. Liu et al. [13] establecieron las condiciones bajo las cuales debe considerarse la interacción vehículo-puente, concluyendo que el grado de interacción dinámica entre ambos es más importante cuanto mayor sea la relación entre la masa del vehículo y la masa del puente. Li y Su [3] concluyeron que la respuesta en régimen resonante considerando la interacción dinámica vehículo-puente es menor que la obtenida empleando modelos de cargas móviles.
El número de trabajos que consideran la influencia de la interacción suelo-estructura en el comportamiento dinámico de puentes destinados al tráfico ferroviario es reducido. Takemiya et al. [14] and [15] han presentado un modelo de interacción suelo-puente empleando una formulación desacoplada mediante la cual analizan la interacción entre el suelo y la cimentación y la interacción pila-puente. Recientemente, Ülker-Kaustell et al. [16] han realizado un análisis simplificado de la influencia de la interacción suelo-estructura en viaductos de líneas de alta velocidad empleando un modelo basado en los trabajos de Takemiya y colaboradores, anteriormente citados. En este trabajo, los autores analizan la influencia de la interacción suelo-estructura en el amortiguamiento modal del sistema puente-suelo y en la respuesta dinámica producida por el paso de sucesivas cargas móviles.
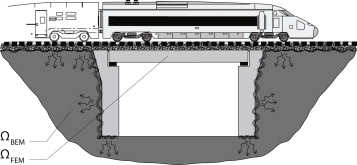
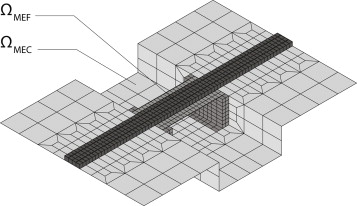
En el presente trabajo se desarrolla un modelo tridimensional acoplado de interacción vehículo-vía-puente-suelo (fig. 1 ). El modelo está basado en la formulación tridimensional en el dominio del tiempo de los métodos de elementos finitos y de elementos de contorno para modelizar la vía, el puente y el suelo. Se considera una configuración de tren articulado, representado mediante un sistema multicuerpo. Este sistema permite reproducir adecuadamente el efecto de los diferentes mecanismos de excitación presentes en la respuesta de la estructura: la contribución cuasi-estática de la carga, las excitación paramétrica producida por el paso por traviesa, los efectos transitorios producidos por las uniones de los carriles y las irregularidades de las ruedas y del carril.
|
|
|
Figura 1. Interacción vehículo-vía-estructura-suelo. |
Los contenidos del artículo se organizan del siguiente modo. En primer lugar se presenta el modelo numérico, incluyendo una breve descripción de la formulación tridimensional en el dominio del tiempo del método de elementos de contorno, del método de elementos finitos y del modelo multicuerpo usado para el vehículo. En segundo lugar, se realiza una caracterización dinámica de la estructura considerando su interacción con el suelo, analizándose las diferencias existentes con los modelos que no la consideran. Posteriormente, se estudia la influencia de los mecanismos de excitación cuasi-estático y dinámico en las vibraciones producidas por el paso de trenes de alta velocidad. Finalmente, se analiza la respuesta de puente cortos para distintas velocidades de circulación, analizándose la influencia de la interacción suelo-estructura en regímenes resonantes y no resonantes de la estructura.
2. Interacción suelo-estructura
El modelo numérico empleado se basa en la formulación tridimensional en el dominio del tiempo del método de los elementos finitos [17] y del método de elementos de los contorno [18] .
El sistema de ecuaciones del método de elementos de contorno se resuelve paso a paso para obtener la evolución temporal de los desplazamientos y de las tracciones nodales. Se emplean funciones de interpolación temporal constantes para las tracciones y lineales para los desplazamientos. La discretización espacial se realiza mediante elementos rectangulares cuadráticos de nueve nodos. La solución fundamental corresponde a un espacio tridimensional solicitado por una carga puntual y se evalúa analíticamente. Las expresiones explícitas de los desplazamientos y de las tracciones pueden encontrarse en [19] .
Una vez realizada la discretización espacial y temporal, el siguiente sistema de ecuaciones permite describir el comportamiento del suelo.
|
|
( 1) |
donde, un y pn son los vectores de desplazamientos y de tracciones al final del paso de tiempo n , respectivamente. Hnn y Gnn son las matrices llenas no simétricas del método de los elementos de contorno en el intervalo de tiempo n y Δt es el paso de tiempo. Para describir el amortiguamiento interno del suelo se usa una aproximación basada en la expresión clásica de Barkan [20] ; el término de la derecha del sistema de ecuaciones (1) que tiene en cuenta la influencia de los pasos de tiempo anteriores al intervalo n , se amortigua exponencialmente con un exponente α que se incrementa linealmente a medida que transcurre el tiempo.
El sistema de ecuaciones que se obtiene del método de elementos finitos puede expresarse mediante la siguiente expresión:
|
|
( 2) |
donde Mn , Cn y Kn son las matrices de masa, amortiguamiento y rigidez del sistema, respectivamente, un el vector de desplazamientos y fn es el vector de fuerzas, en el instante de tiempo n .
En este artículo se ha supuesto la matriz de amortiguamiento Cn proporcional a las matrices de masa, Mn , y rigidez, Kn .
|
|
( 3) |
Las constantes α0 y α1 se obtienen a partir de los coeficientes de amortiguamiento ζi y ζj para los modos i y j del sistema, respectivamente, teniendo en cuenta que el coeficiente de amortiguamiento para el modo n -ésimo es [21] :
|
|
( 4) |
Los modos i y j se eligen de forma que proporcionen coeficientes de amortiguamiento aceptables para todos los modos que contribuyen significativamente a la respuesta del sistema. Si se supone que ambos modos tienen el mismo coeficiente de amortiguamiento ζ , se obtiene:
|
|
( 5) |
El acoplamiento entre las partes del modelo representadas con elementos de contorno y con elementos finitos se realiza imponiendo las condiciones de compatibilidad y de equilibrio en la interfase suelo-estructura, obteniéndose un único sistema de ecuaciones [22] .
3. Modelo del vehículo
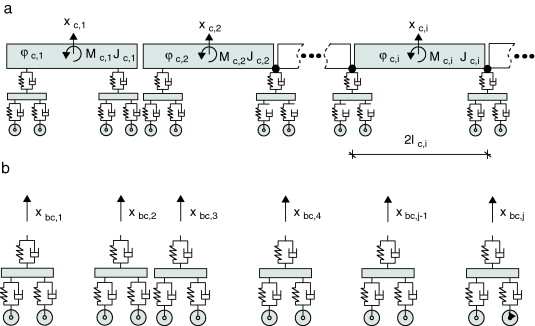
Para representar la interacción vehículo-estructura-suelo se emplea el sistema multicuerpo mostrado en la fig. 2 a. En dicho modelo, los ejes y las cajas de los vehículos se consideran sólidos rígidos y las suspensiones primarias y secundarias se representan mediante elementos muelle-amortiguador [23] .
|
|
|
Figura 2. (a) Modelo multicuerpo del tren articulado. (b) Bogies desacoplados. |
Las ecuaciones de movimiento del sistema multicuerpo de la figura 2 b pueden expresarse como:
|
|
( 6) |
donde, , y son las matrices de masa, amortiguamiento y rigidez del sistema multicuerpo, respectivamente. Los grados de libertad de cada vagón se corresponden con el desplazamiento vertical xc y la rotación φc de la caja, el desplazamiento vertical xb y la rotación φb de cada bogie, y el desplazamiento vertical de la rueda trasera xwr y de la rueda delantera xwf de los bogies (figs. 2 y 3 ).
|
|
|
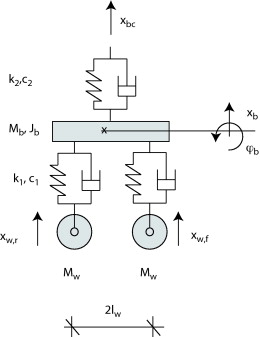
Figura 3. Modelo multicuerpo de un bogie. |
La matriz de masa de cada bogie (ec. (7) ) está relacionada con la masa Mb del bogie, la inercia al giro de éste Jb y las masas de las ruedas, :
|
|
( 7) |
Las matrices de rigidez y amortiguamiento de los bogies son las siguientes:
|
|
( 8) |
|
|
( 9) |
donde, k1 y c1 son la rigidez y el amortiguamiento vertical de la suspensión primaria, k2 y c2 la rigidez y el amortiguamiento vertical de la suspensión secundaria, y es la distancia entre las ruedas de un mismo bogie.
Las matrices del tren articulado completo se obtienen imponiendo las relaciones entre los desplazamientos de las cajas y los desplazamientos de los bogies. Para la locomotora delantera, imponiendo las relaciones indicadas en la ec. (10) se obtienen las matrices para un vehículo [23] .
|
|
( 10) |
En la ec. (10) , xc ,1 y φc ,1 son el desplazamiento vertical y el giro de la caja, respectivamente, y 2lc la distancia entre los bogies que soportan la caja. Del mismo modo, se imponen relaciones análogas para el primer vagón de pasajero (vehículo 2 en la figura 2 ). De este modo, para el vehículo m el desplazamiento xbc ,n resulta:
|
|
( 11) |
Así, las relaciones para el tren completo pueden expresarse de forma compacta como:
|
|
( 12) |
Si se introduce la ec. (12) en la ec. (6) , se obtiene:
|
|
( 13) |
siendo, , y las matrices de masa, amortiguamiento y rigidez del tren articulado representado en la figura 2 a. La matriz de masa estaría formada por las submatrices de masa de los bogies y por las submatrices de masa de las cajas de los vehículos, , donde Mc es la masa y Jc la inercia al giro de la caja de cada vehículo. La consideración de los grados de libertad asociados a las rotaciones de las cajas de los vehículos permite introducir en el modelo la inercia al giro de estas.
La ecuación de movimiento del vehículo se acopla al modelo de interacción suelo-estructura imponiendo las condiciones de compatibilidad y equilibrio en cada punto de contacto entre las ruedas de los diferentes bogies y la vía, considerándose un contacto hertziano entre ambos [24] . Para tener en cuenta en cada instante de tiempo la posición del tren, se crea un nodo móvil en sendos carriles por cada punto de contacto para acoplar el vehículo y la vía. Este punto de contacto cambia de acuerdo a la velocidad del tren. Por lo tanto, la discretización de la vía varía en cada paso de tiempo y se obtienen unas matrices de elementos finitos dependientes de la variable tiempo.
La integración temporal del sistema no-lineal descrito por la ec. (2) se realiza paso a paso empleando la metodología presentada en la ref. [25] . El procedimiento de resolución se basa en el método de Newmark [26] . En este método se resuelve la ec. (2) en el intervalo Δt asumiéndose que:
|
|
( 14) |
|
|
( 15) |
donde, α y δ son los parámetros de integración. Si α = 1/4 y δ = 1/2 el método resulta incodicionalmente estable [17] . El desplazamiento en el paso de tiempo n + 1 puede obtenerse a partir de la siguiente expresión:
|
|
( 16) |
Una vez se ha obtenido el desplazamiento un +1 se actualizan las matrices del sistema. Finalmente, y se obtienen a partir de las ecs. (2) y (15) .
La formulación indicada en la ref. [25] requiere emplear las matrices del sistema en el paso de tiempo n para determinar un +1 , según la ec. (16) . Para calcular y se usan las matrices del sistema correspondientes al paso de tiempo n + 1, de acuerdo a la ec. (2) . La metodología descrita permite extender el análisis a problemas no lineales. Sin embargo, requiere un coste computacional adicional debido a que en cada paso de tiempo es necesario actualizar las matrices del método de los elementos finitos.
4. Análisis dinámico de puentes cortos
En esta sección se estudia el comportamiento de un puente corto al paso de un TAV. En primer lugar se analiza la interacción suelo-estructura en la caracterización dinámica del puente. Posteriormente, se examina la influencia de los mecanismos de excitación en la respuesta de la estructura. Finalmente, se presenta la respuesta dinámica del puente producida por el paso de un TAV a diferentes velocidades y se analiza la influencia de la interacción suelo-estructura en la respuesta.
4.1. Interacción dinámica suelo-estructura
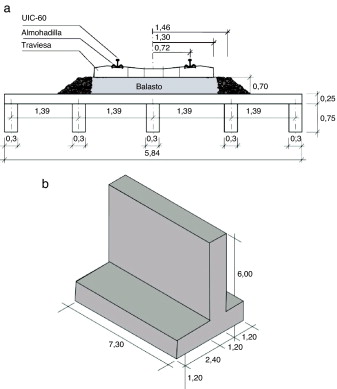
El puente estudiado en este trabajo se corresponde con una estructura de un solo vano con una luz de 12 m y es viaje nulo. El tablero (fig. 4 a) está constituido por una losa de hormigón de 0,25 m de espesor y 5,84 m de ancho. La losa se encuentra sobre cinco vigas de hormigón de 0,75 m de canto y 0,3 m de ancho. Las vigas se disponen equiespaciadas con una distancia entre ejes de las vigas de 1,39 m. El hormigón considerado tiene una densidad ρ = 2.500 kg/m3 , un coeficiente de Poisson ν = 0,3, y un módulo de Young igual a E = 31 × 109 N/m2 .
|
|
|
Figura 4. (a) Sección transversal del tablero. (b) Geometría de los estribos. |
Los apoyos extremos se encuentran sobre estribos de hormigón (fig. 4 b) de densidad ρ = 2.500 kg/m3 , coeficiente de Poisson ν = 0,3, y módulo de Young igual a E = 20 × 109 N/m2 . Las vigas del tablero descansan sobre los estribos a través de neoprenos de 20 mm de espesor y rigidez kN = 560 × 106 N/m.
Sobre el tablero se sitúa una vía balasto compuesta por dos carriles UIC60 con rigidez a flexión EI = 6,45 × 106 Nm2 y masa por unidad de longitud m = 60,3 kg/m, por cada carril. Las almohadillas bajo carril tienen un espesor de 10 mm y sus valores de rigidez y amortiguamiento son krp = 150 × 106 N/m y crp = 13,5 × 103 Ns/m, respectivamente. Las traviesas monobloques de hormigón pretensado tienen longitud l = 2,60 m, ancho ,235 m, altura h = 0,205 m (bajo carril) y masa m = 300 kg. Se considera una distancia entre traviesas d = 0,6 m. La capa de balasto tiene una densidad ρ = 1.500 kg/m3 , un coeficiente de Poisson ν = 0,2, y un módulo de Young igual a E = 209 × 106 N/m2 . El ancho de la capa de balasto es 2,92 m y el espesor h = 0,7 m.
El sistema vía-estructura (fig. 5 ) se encuentra sobre un semiespacio homogéneo que representa un suelo duro, con velocidad de propagación de ondas S, Cs = 400,0 m/s, velocidad de propagación de ondas P, Cp = 799,4 m/s, y velocidad de propagación de ondas de Rayleigh, CR = 372,6 m/s.
|
|
|
Figura 5. Discretización del sistema vía-puente-suelo. |
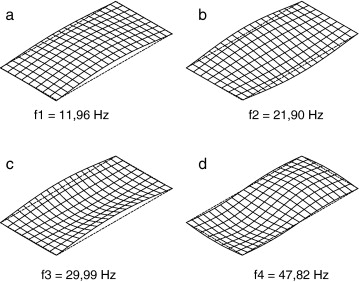
En la figura 6 se muestran los cuatro primeros modos de vibración del sistema formado por la vía y el puente. Los modos de vibración se corresponden con los modos fundamentales del tablero: primer modo simétrico de flexión, primer modo de torsión, primer modo de flexión transversal del puente y el segundo modo de flexión longitudinal, respectivamente.
|
|
|
Figura 6. Cuatro primeros modos de vibración del sistema vía-estructura. |
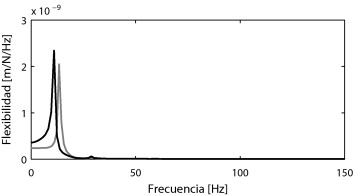
En la figura 7 se muestra la respuesta de la sección central del tablero ante una carga impulso, modelizada por la siguiente función de carga P (t ) = − 1 N [H (t ) − H (t − 0,045 s)], aplicada en ambos carriles. La respuesta del sistema está gobernada por el primer modo de flexión del tablero y por el primer modo de flexión de la sección transversal del puente. Se ha considerado un valor de amortiguamiento de la estructura ζ = 2% para todos los modos que intervienen en la respuesta. Para obtener la matriz de amortiguamiento se ha seleccionado ωi = ω1 y ωj = ω4 , resultando α0 = 2,3 y α1 = 1,24 × 10−4 . En la figura 7 puede observarse como el efecto de la interacción suelo-estructura produce una reducción de las frecuencias resonantes y un incremento de la amplitud de la respuesta debido al nivel de flexibilidad adicional aportado por los estribos y el suelo. La primera frecuencia resonante adquiere un valor ,06 Hz y el amortiguamiento estructural, calculado a partir de la evolución de los desplazamientos en vibración libre, incrementa su valor a ,9%.
|
|
|
Figura 7. Flexibilidad del sistema vía-estructura-suelo (línea negra) y del sistema vía-estructura (línea gris). |
4.2. Mecanismos de excitación
Las vibraciones ocasionadas durante el paso de TAV están producidas por diferentes mecanismos de excitación: la carga cuasi-estática transmitida a la vía debida al paso del vehículo, la excitación paramétrica producida por el paso del vehículo sobre las traviesas y la carga dinámica producida por las irregularidades de las ruedas y del carril.
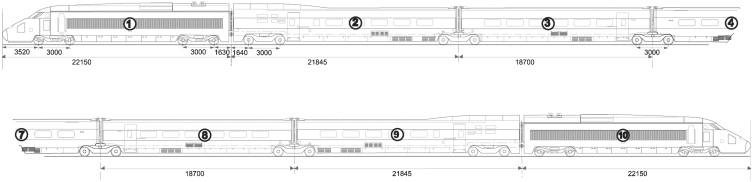
La contribución cuasi-estática de la carga se ha modelizado tradicionalmente mediante fuerzas móviles despreciándose la inercia del vehículo. El modelo multicuerpo propuesto permite considerar la influencia de la masa y el efecto de la suspensión de los diferentes vagones en la contribución cuasi-estática. En la figura 8 se presenta la configuración de TAV estudiada en este trabajo, compuesta por dos locomotoras y ocho vagones de pasajeros. Los valores de la distancia entre bogies, lb , y entre ejes, la , se muestran en dicha figura. Los dos vagones de pasajeros adyacentes a las locomotoras comparten un bogie con el vagón de pasajeros vecino, mientras que el resto de vagones comparten ambos bogies. En la tabla 1 se recogen los valores de las propiedades másicas y mecánicas de los diferentes vehículos del convoy considerado.
|
|
|
Figura 8. Configuración TAV. |
| Descripción | Notación | Unidad | Locomotora | Vagón pasajeros |
|---|---|---|---|---|
| Masa caja vehículo | M_c | kg | 55.790 | 24.000 |
| Masa bogie | Mb | kg | 2.380 | 3.040 |
| Masa eje-rueda | kg | 2.048 | 2.003 | |
| Inercia caja vehículo | Jc | kg m2 | 1,15 × 103 | 1,48 × 103 |
| Inercia bogie | Jb | kg m2 | 1,48 × 106 | 2,68 × 103 |
| Rigidez suspensión primaria | k1 | N/m | 2,45 × 106 | 1,4 × 106 |
| Rigidez suspensión secundaria | k2 | N/m | 2,45 × 106 | 0,82 × 106 |
| Amortiguamiento suspensión primaria | c1 | Ns/m | 20 × 103 | 10 × 103 |
| Amortiguamiento suspensión secundaria | c2 | Ns/m | 40 × 103 | 48 × 103 |
La carga trasmitida al carril por cada eje se puede obtener como la fuerza de interacción FH entre la rueda y el carril a partir de la siguiente expresión [12] :
|
|
( 17) |
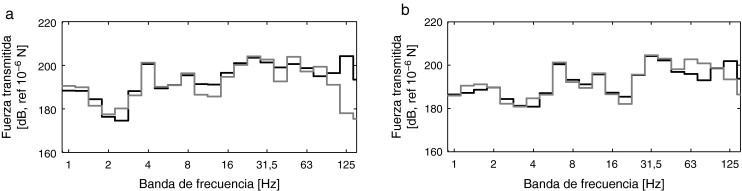
donde, uc es el desplazamiento del carril en cada punto de contacto, es el desplazamiento de la rueda y kH = 1,4 × 109 N/m es la rigidez del contacto hertziano entre la rueda y el carril [24] . En la figura 9 se muestra el contenido en frecuencia de la fuerza transmitida al carril por un TAV circulando a m/s y a una velocidad V1,2 = 110,14 m/s que posteriormente se verá resulta resonante (sección 4.3 ). Los resultados obtenidos se comparan con la carga aplicada usando un modelo de fuerza móvil. Ambos modelos presentan niveles similares en las bandas asociadas a las frecuencias de paso por bogie, (26,6 y 36,7 Hz, respectivamente), y de paso por eje, (4,3 y 5,9 Hz, respectivamente). Sin embargo, la fuerza transmitida al puente obtenida considerando el efecto de la masa y de la amortiguación del vehículo presenta un contenido a alta frecuencia que no reproduce el modelo de fuerza móvil.
|
|
|
Figura 9. Fuerza transmitida a la vía considerando un modelo de carga móvil (línea gris) y un modelo multicuerpo (línea negra) para (a) m/s y (b) V1,2 = 110,14 m/s. |
Las irregularidades del carril y de las ruedas son una de las causas principales de las vibraciones resultantes del tráfico ferroviario. Para considerar su efecto, el desplazamiento del carril en cada punto de contacto uc se descompone en la deflexión del carril producida por la componente cuasi-estática de la carga ur y en las irregularidades del carril [27] and [28] :
|
|
( 18) |
En este artículo, se considera un perfil de irregularidades modelado por un proceso aleatorio gaussiano estacionario caracterizado por la función de densidad espectral (PSD) . A partir de esta función, se puede generar un perfil de irregularidades mediante una superposición de funciones armónicas con desfase aleatorio [27] and [28] :
|
|
( 19) |
donde kym = m Δky es la frecuencia de muestreo en el dominio del número de onda, Δky es el incremento en el número de onda y θm corresponde al desfase aleatorio de las funciones armónicas que se encuentra distribuido uniformemente en el intervalo [0, 2π ]. La función PSD se obtiene de acuerdo a la norma ISO 8608 [29] según la ecuación:
|
|
( 20) |
En este artículo se ha seleccionado ky 0 = 1 rad/m y un valor m3 . Normalmente se supone ,5 para las irregularidades de las ruedas y el carril existentes en líneas de alta velocidad.
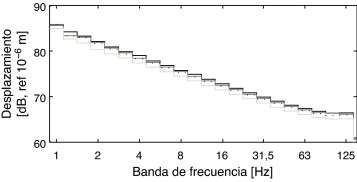
En la figura 10 se muestra el contenido en frecuencia del desplazamiento vertical de la rueda, del bogie y de la caja representado en tercios de octava, debido a la excitación producida por el perfil de irregularidades representado también en dicha figura. La respuesta de la caja muestra como los sistemas de suspensión primario y secundario atenúan las vibraciones con contenido en frecuencia superior a las frecuencias naturales de la caja y el bogie, 1,2 y 5,5 Hz, respectivamente. También se observa una reducción de los desplazamientos del bogie respecto al perfil de irregularidades debido a la suspensión primaria del vehículo.
|
|
|
Figura 10. Desplazamiento vertical de la rueda (línea gris oscura), del bogie (línea negra a puntos) y de la caja del vehículo (línea gris clara) representado en tercios de octava producido por las irregularidades de la vía (línea negra). |
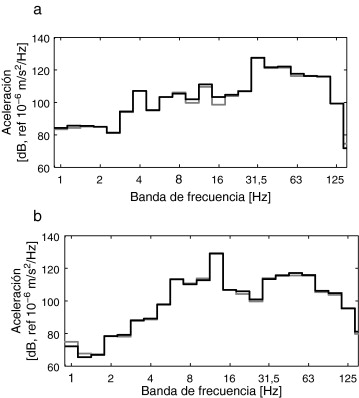
En la figura 11 se muestra la aceleración vertical del punto central de la sección central del tablero producida por el paso de un TAV circulando a m/s y a la velocidad resonante V1,2 = 110,14 m/s (sección 4.3 ). En la figura se representa la repuesta debida a la contribución cuasi-estática de la carga y la producida por la carga total. La componente de la respuesta debida a la contribución cuasi-estática es dominante y la respuesta obtenida no depende del efecto de las irregularidades. Se observa que la respuesta en la vía y en sus proximidades está producida principalmente por el mecanismo de excitación cuasi-estático [22] and [28] .
|
|
|
Figura 11. Aceleración vertical del punto central de la sección central del tablero representado en tercios de octava debida al paso de un TAV circulando a (a) m/s y (b) V1,2 = 110 m/s. Contribución total de la carga (línea negra) y por la excitación cuasi-estática (línea gris). |
4.3. Vibraciones producidas por el paso de TAV
A continuación, se estudia la influencia de la interacción suelo-estructura en las vibraciones ocasionadas en el tablero en régimen resonante y no resonante de la estructura. Las propiedades de la estructura son las descritas anteriormente.
La condición necesaria para que un puente excitado por un conjunto de cargas móviles entre en régimen resonante puede expresarse como [2] :
|
|
( 21) |
donde, Vn ,i es la velocidad resonante del tren, fn es la n -ésima frecuencia resonante de la estructura y d es la distancia característica entre cargas.
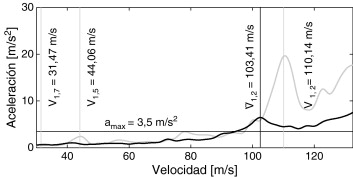
En la figura 12 se muestra la evolución de la máxima aceleración vertical del centro de la sección central del tablero frente a la velocidad de paso. En la respuesta se observa un incremento de las aceleraciones del tablero con la velocidad de paso del tren. Se alcanzan niveles máximos a las velocidades de resonancia asociadas al primer modo de flexión (f1 = 11,96 Hz) para i = 2, 5, 7, considerando d = 18,7 m la distancia entre bogies: V1,2 = 110,14 m/s, V1,5 = 44,06 m/s y V1,7 = 31,47 m/s. En la figura 12 se ha marcado el valor límite de aceleraciones admisibles del tablero, amax = 3,5 m/s2 , en puentes de vía con balasto [1] . La aceleración máxima del tablero se encuentra por debajo de este límite en el rango de velocidades de explotación de las líneas de alta velocidad. La respuesta de la estructura varía sustancialmente cuando se considera el efecto de su interacción con el suelo. Las velocidades de resonancia disminuyen debido a la variación del comportamiento dinámico de la estructura. Considerando el valor ,06 Hz de la primera frecuencia de resonancia (fig. 7 ) se obtiene la velocidad resonante ,41 m/s. Se observa como el nivel máximo de aceleraciones alcanzado en régimen resonante es significativamente menor al considerar la interacción suelo-estructura debido al incremento del amortiguamiento.
|
|
|
Figura 12. Aceleración vertical máxima en la sección central del tablero con interacción suelo-estructura (línea negra) y sin interacción (línea gris). |
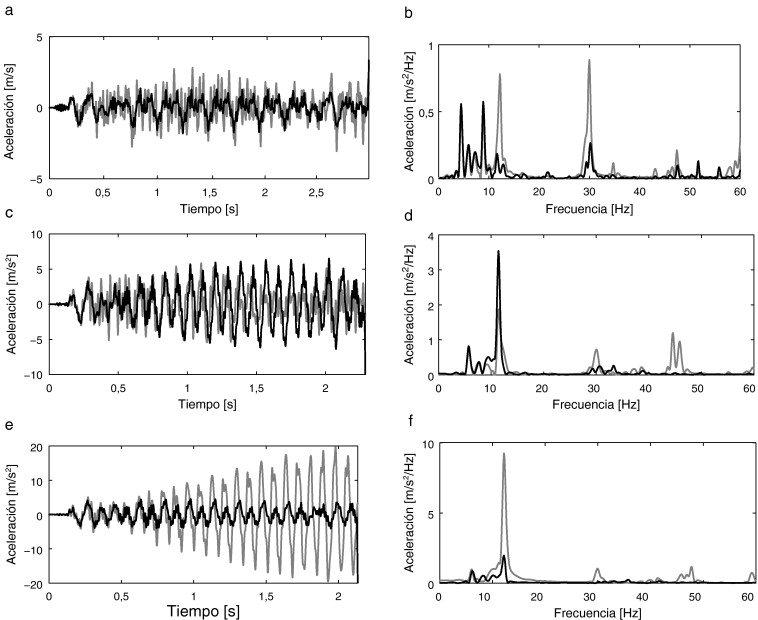
En la figura 13 se representa la evolución temporal y el contenido en frecuencia de la aceleración vertical en el punto central de la sección media del tablero para tres velocidades de paso: m/s, ,41 m/s y V1,2 = 110,14 m/s. La respuesta en régimen no resonante está gobernada por la frecuencia de paso por bogie fb = 4,28 Hz, por el primer modo de vibración de flexión simétrico y por el primer modo de flexión de la sección transversal del puente. En la figura 13 b se observa que el efecto de la interacción suelo-estructura produce un incremento del nivel de las vibraciones a la frecuencia de paso por bogie y una reducción de la respuesta asociada a las frecuencias resonantes de la estructura. Para la velocidad de paso ,41 m/s (figs. 13 c,d) la respuesta de la estructura se encuentra en régimen resonante si se considera la interacción suelo-estructura (línea negra), produciéndose un incremento gradual de las vibraciones con la entrada sucesiva de los ejes del tren hasta alcanzar un nivel máximo a la salida del último eje. La frecuencia predominante de la respuesta se corresponde con la frecuencia del primer modo de flexión simétrico. El modelo sin interacción no predice el comportamiento resonante de la estructura, subestimando los niveles de vibración producidos. Para la velocidad de paso V1,2 = 110,14 m/s se predice un comportamiento resonante de la estructura cuando no se considera la interacción suelo-estructura (línea gris), siendo los niveles de vibración obtenidos muy superiores a los que se producen en régimen resonante cuando se considera el efecto del suelo.
|
|
|
Figura 13. Respuesta temporal y contenido en frecuencia de la aceleración vertical del centro de la sección central del tablero debida al paso de un TAV para (a,b) m/s, (c,d) ,41 m/s y (e,f) V1,2 = 110,14 m/s, considerando la interacción suelo-estructura (línea negra) y sin considerarla (línea gris). |
5. Conclusiones
En este artículo se ha desarrollado un modelo numérico que permite analizar las vibraciones producidas en puentes por el paso de TAV. El modelo presentado se basa en la formulación tridimensional acoplada del método de elementos finitos y del método de elementos de contorno en el dominio del tiempo. La interacción vehículo-vía permite considerar los distintos mecanismos de excitación. Las principales conclusiones que pueden obtenerse de los resultados presentados en este artículo son las siguientes:
- La fuerza transmitida al puente considerando el efecto de la masa y de la amortiguación del vehículo presenta un contenido a alta frecuencia debido a la interacción vehículo-estructura que no reproduce el modelo de fuerza móvil.
- La interacción suelo-estructura produce una reducción de las frecuencias de resonancia y un incremento del amortiguamiento del puente.
- Las velocidades de resonancia disminuyen cuando se considera la interacción dinámica suelo-estructura debido a la variación de las frecuencias naturales del puente.
- La respuesta resonante de una estructura está condicionada por el amortiguamiento estructural y por el tiempo en el que se excita a la frecuencia de resonancia. La amplitud de las vibraciones en régimen resonante en puentes es inversamente proporcional al amortiguamiento de la estructura [2] , por lo que el nivel de amortiguamiento adicional que introduce el suelo produce un cambio sustancial en la respuesta de la estructura. En el caso estudiado, la amplitud de la respuesta en régimen resonante es significativamente menor cuando se considera la interacción suelo-estructura.
Agradecimientos
El contenido de este artículo se encuentra enmarcado en los trabajos de investigación asociado al proyecto BIA2010-14843. Los autores de este artículo agradecen el apoyo del Ministerio de Ciencia e Innovación y del Centro Informático Científico de Andalucía (CICA).
References
- [1] Ministerio de Fomento, Instrucción sobre las acciones a considerar en el proyecto de puentes de ferrocarril IAPF07, Ministerio de Fomento 2007.
- [2] L. Frýba; A rough assessment of railway bridges for high speed trains; Engineering Structures, 23 (2001), pp. 548–556
- [3] J. Li, M. Su; The resonant vibration for a simply supported girder bridge under high-speed trains; Journal of Sound and Vibration, 224 (1999), pp. 897–915
- [4] S.H. Ju, H.T. Lin; Resonance characteristics of high-speed trains passing simply supported bridges; Journal of Sound and Vibration, 267 (2003), pp. 1127–1141
- [5] H. Xia, N. Zhang, W.W. Guo; Analysis of resonance mechanism and conditions of train-bridge system; Journal of Sound and Vibration, 297 (2006), pp. 812–822
- [6] P. Museros, E. Alarcón; Influence of the second bending mode on the response of high-speed bridges at resonance; Journal of Structural Engineering, 131 (2005), pp. 405–415
- [7] P. Museros, M.D. Martinez-Rodrigo; Vibration control of simply supported beams under moving loads using fluid viscous dampers; Journal of Sound and Vibration, 300 (2007), pp. 292–315
- [8] M.D. Martínez-Rodrigo, J. Lavado, P. Museros; Transverse vibrations in existing railway bridges under resonant conditions: Single-track versus double-track configurations; Engineering Structures, 32 (2010), pp. 1861–1875
- [9] M.D. Martínez-Rodrigo, P. Museros; Optimal design of passive viscous dampers for controlling the resonant response of orthotropic plates under high-speed moving loads; Journal of Sound and Vibration (2010) http://dx.doi.org/10.1016/j.jsv.2010.10.017
- [10] J.M. Goicolea, J. Domínguez, J.A. Navarro, F. Gabaldón; Modelos numéricos para el cálculo dinámico de puentes de ferrocarril de alta velocidad; Métodos Numéricos en Ingeniería V, España (2002)
- [11] J.M. Goicolea, F. Gabaldón, F. Riquelme; Design Issues for Dynamics of High Speed Railway Bridges; International Association for Bridge Maintenance and Safety, Porto (2006)
- [12] A.V. Pesterev, L.A. Bergman, C.A. Tan, T.-C. Tsao, B. Yang; On the asymptotics of the solution of the moving oscillator problem; Journal of Sound and Vibration, 260 (2003), pp. 519–536
- [13] K. Liu, G. De Roeck, G. Lombaert; The effect of dynamic train-bridge interaction on the bridge response during a train passage; Journal of Sound and Vibration, 325 (2009), pp. 240–251
- [14] H. Takemiya, X.C. Bia; Shinkansen high-speed train induced ground vibratios in view of víaduct-ground interaction; Soil Dynamics and Earthquake Engineering, 27 (2007), pp. 506–520
- [15] H. Takemiya; Analyses of wave field from high-speed train on víaduct at shallow/deep soft grounds; Journal of Sound and Vibration, 310 (2008), pp. 631–649
- [16] M. Ülker-Kaustell, R. Karoumi, C. Pacoste; Simplified analysis of the dynamic soil-structure interaction of a portal frame railway bridge; Engineering Structures, 32 (2010), pp. 3692–3698
- [17] O.C. Zienkiewicz; The Finite Element Method; McGraw-Hill Company, Londres (1977)
- [18] J. Domínguez; Boundary elements in dynamics; Computational Mechanics Publications and Elsevier Applied Science, Southampton (1993)
- [19] P. Galvín, J. Domínguez; Analysis of ground motion due to moving surface loads induced by high-speed trains; Engineering analysis with boundary elements, 30 (2007), pp. 931–941
- [20] D.D. Barkan; Dynamics of Bases and Foundations; McGraw-Hill, New York (1962)
- [21] R.W. Clough, J. Penzien; Dynamic of Structures; McGraw-Hill, New York (1975)
- [22] P. Galvín, A. Romero, J. Domínguez; Fully three-dimensional analysis of high-speed train-track-soil-structure dynamic interaction; Journal of Sound and Vibration, 329 (2010), pp. 5147–5163
- [23] X. Sheng, C.J.C. Jones, D.J. Thompson; A theoretical model for ground vibration from trains generated by vertical track irregularities; Journal of Sound and Vibration, 272 (2004), pp. 937–965
- [24] C. Esveld; Modern Railway Track; MRT Productions, Zaltbommel (2001)
- [25] S.Y. Chang; Nonlinear error propagation analysis for explicit pseudodynamics algorithm; Journal of engineering mechanics ASCE, 123 (2003), pp. 841–850
- [26] N.M. Newmark; A method of computation for structural dynamics; ASCE Journal of the Engineering Mechanics Division, 85 (1959), pp. 67–94
- [27] G. Lombaert, G. Degrande, J. Kogut, S. François; The experimental validation of a numerical model for the prediction of railway induced vibrations; Journal of Sound and Vibration, 297 (2006), pp. 512–535
- [28] G. Lombaert, G. Degrande; Ground-borne vibration due to static and dynamic axle loads of InterCity and high-speed trains; Journal of Sound and Vibration, 319 (2009), pp. 1036–1066
- [29] International Organization for Standardization ISO 8608:1995, Mechanical vibration road surface profiles-reporting of measured data, 1995.
Document information
Published on 01/03/12
Accepted on 15/03/11
Submitted on 15/12/10
Volume 28, Issue 1, 2012
DOI: 10.1016/j.rimni.2011.11.004
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?