Resumen
La fundición nodular es una aleación metálica de Fe-C-Si cuya microestructura está formada por una matriz, en general compuesta por ferrita y perlita, en la cual se encuentran embebidos nódulos de grafito. Al ser este un material microscópicamente heterogéneo, su comportamiento está definido por las propiedades, la morfología y la topología de las fases que lo componen. En este trabajo se plantea como objetivo hallar el valor de las constantes elásticas, el módulo de Young y el coeficiente de Poisson, de un material homogéneo equivalente que caracteriza el comportamiento macroscópico de una fundición nodular. Para la estimación del comportamiento elástico se utiliza el método de homogeneización asintótica. Este método se aplica a celdas multipartículas tridimensionales y bidimensionales que se analizan mediante el método de los elementos finitos (MEF). Para la determinación del elemento de volumen representativo (RVE [representative volume element] ) del comportamiento del material se utilizan 2 criterios, uno físico y otro geométrico, encontrándose que el tamaño del RVE es sensible al criterio utilizado para su definición. Las principales características microestructurales son extraídas de una simulación computacional de la solidificación del material. Se comparan los resultados obtenidos de la aplicación de los modelos tridimensionales y bidimensionales y se analiza la influencia del modelo utilizado en las propiedades analizadas. Del análisis de los resultados obtenidos se observa que los modelos que emplean celdas multipartícula tridimensionales requieren tamaños menores de la misma para ser representativos de la fundición nodular, es decir, los tamaños de los RVE tridimensionales son menores que los correspondientes bidimensionales. Se observa también que estos últimos presentan una respuesta elástica menos rígida en relación con los primeros.
Abstract
Nodular cast iron is a Fe-C-Si metallic alloy whose microstructure consists of a matrix, composed in general of ferrite and pearlite, with graphite nodules embedded in it. Owing to its microscopical heterogeneity, the material response is governed by the properties, morphology and typology of the phases involved. This work reports on the evaluation of the elastic properties, i.e., Youngs modulus and Poissons ratio, of an equivalent homogeneous material that characterizes the macroscopic response of a nodular cast iron. Asymptotic homogenization is used to this end. This approach is applied to both 3D and 2D multiparticle cells simulated via the finite element method. Two different physically and geometrically-based criteria are considered to estimate the representative volume element (RVE), where the size of the RVE is found to be sensitive to the chosen criterion. The main microstructural features are obtained from a computational simulation of the solidification process of the material. The numerical predictions computed for the 3D and 2D cases are compared and discussed in terms of the resulting elastic properties. It is observed that the models employing 3D multiparticle cells require lower RVE sizes than the corresponding 2D models, where the latter present a stiffer elastic response.
Palabras clave
Fundición nodular ; Propiedades elásticas ; Elemento de volumen representativo ; Homogeneización asintótica
Keywords
Nodular cast iron ; Elastic properties ; Representative volume element ; Asymptotic homogenization
1. Introducción
Entre los materiales metálicos utilizados en la industria destaca el conjunto de aleaciones férreas formado por aceros y fundiciones que, conjuntamente, representan el 90% en peso del total de materiales metálicos empleados industrialmente [1] .
Las fundiciones son aleaciones de Fe-C-Si con entre 3-4,3% de carbono y 1,3-3% de silicio, en las cuales el silicio promueve la precipitación del carbono en forma de grafito. Con estas aleaciones se puede obtener un amplio espectro de propiedades mecánicas, definidas por su microestructura, y bajos niveles de defectos propios de piezas coladas debido a la elevada fluidez que le confieren el alto contenido de carbono y el bajo punto de fusión. Estas características hacen que actualmente las fundiciones de hierro sean las aleaciones fundidas de mayor producción mundial [2] .
El amplio espectro de microestructuras, y por lo tanto de propiedades mecánicas, que es posible obtener en las fundiciones hace necesario clasificarlas en base a su microestructura. Dentro de esta clasificación se encuentra la fundición nodular, también conocida como dúctil o de grafito esferoidal (SGI [spheroidal graphite iron] ), cuya microestructura está caracterizada por la presencia de carbono en forma de grafito con morfología esférica. La geometría nodular del grafito confiere al material elevados valores de elongación y de resistencia mecánica al impacto y a la fractura. Estas propiedades mecánicas han hecho que la producción de fundición nodular haya experimentado en los últimos años un importante crecimiento, alcanzando valores que representan el 33% del tonelaje de aleaciones ferrosas producidas mundialmente.
Se puede considerar que la fundición nodular está formada por una matriz metálica en la cual se encuentran embebidos los nódulos de grafito. La matriz metálica puede estar formada por ferrita, perlita o una combinación de ambas. Tomando en consideración esta característica microestructural, se clasifica a la fundición dúctil en estado de colada, es decir, sin tratamiento térmico, en ferrítica, semiferrítica, ferrítica-perlítica, semiperlítica y martensítica. De acuerdo al tipo de matriz obtenida, las propiedades que exhibe la fundición varían ampliamente. Una mayor fracción volumétrica de perlita brinda al material mayor valor de tensión última, de tensión de fluencia y de dureza pero con una reducción en la ductilidad. En cambio, la resistencia a la fractura y las propiedades dinámicas son mejoradas al aumentar la fracción volumétrica de ferrita, aunque en detrimento de la tensión última, la de fluencia y la dureza.
Lo indicado anteriormente permite incluir a la fundición nodular dentro de los materiales heterogéneos, también llamados microestructurados [3] , pues está formada por diferentes fases y microconstituyentes que pueden ser identificados a determinada escala. A su vez, la topología de la microestructura permite incluir a la fundición nodular en el grupo de materiales heterogéneos con un arreglo de matriz-inclusión [3] .
Al ser la fundición nodular un material heterogéneo, su comportamiento está definido por las propiedades de sus microconstituyentes, así como por su geometría y su topología. Específicamente para la fundición nodular, sus propiedades están controladas principalmente por el tipo de matriz, por la presencia de defectos en la misma y por el tamaño, la forma y la distribución de los nódulos de grafito. Por lo tanto, para obtener piezas con propiedades mecánicas especificadas es de gran importancia conocer las relaciones entre la microestructura y las propiedades mecánicas.
Uno de los enfoques empleados para el estudio de la relación entre la microestructura y las propiedades mecánicas se basa en modelos fenomenológicos fundamentados en información experimental. Guo et al. [4] estudian la relación de las características de la matriz y del grafito con diferentes propiedades mecánicas de la fundición, y proponen expresiones para determinar la dureza Brinell, la tensión última, la tensión de fluencia y el alargamiento en función de las características microestructurales analizadas. Wenzhen y Baicheng [5] desarrollan un modelo de solidificación con el cual determinan microestructuras cuyas propiedades mecánicas son computadas usando expresiones experimentales desarrolladas por Lundback et al. [6] .
Otro enfoque es el basado en el modelado multiescala y en la micromecánica del continuo. Pundale et al. [7] investigan la influencia que tiene la fracción volumétrica, la forma, el tamaño y la distribución del grafito en el módulo de Young efectivo analizando celdas unitarias. La celda unitaria constituye un volumen de estudio conteniendo un nódulo, que se asume como vacío, y una porción de matriz que lo rodea. En estas celdas unitarias emplean 2 formulaciones: una de tensión plana y otra axilsimétrica. Para investigar la influencia de la distribución del grafito en el módulo de elasticidad efectivo, utilizan celdas constituidas por un número constante de nódulos, también considerados como vacíos. La distribución que se da a estos nódulos tiene una media constante, coincidente con el centro de la celda, pero una dispersión variable. Collini y Nicoletto [8] proponen un modelo de celda unitaria para predecir la ley constitutiva y la falla de una fundición nodular. Consideran una celda unitaria con una matriz mixta de ferrita y perlita que les permite analizar la influencia de la fracción volumétrica de estas fases en las propiedades mecánicas. Collini [9] implementa diferentes modelos de micromecánica computacional para determinar el comportamiento en el campo elastoplástico e identificar el mecanismo de iniciación de falla. Este autor compara los resultados obtenidos con diferentes modelos y realiza una validación con resultados experimentales. Todos los trabajos mencionados son realizados en el marco del MEF.
El segundo enfoque requiere una adecuada representación del material a través de un elemento de volumen representativo (RVE [representative volume element] ). La obtención de los RVE se puede realizar principalmente siguiendo 2 metodologías [3] : a) la que emplea microestructuras «sintéticas» generadas mediante algoritmos de computadora, y b) la que se basa en micrografías obtenidas experimentalmente para generar microgeometrías adecuadas para el tratamiento numérico, valiéndose para esto de la adquisición y del procesamiento de imágenes.
El objetivo final del metalurgista es diseñar un proceso de producción que permita obtener un producto que cumpla un conjunto de especificaciones, es decir, con determinadas propiedades mecánicas. Las propiedades de la fundición están definidas por su microestructura, que está determinada por los cambios de fase que ocurren durante el enfriamiento del material en el molde. Por este motivo, el objetivo primario que se debe cumplir para lograr una pieza con las características deseadas es diseñar un proceso que produzca una microestructura acorde a las mismas. Actualmente es habitual el uso de modelos metalúrgicos que simulan los cambios de fase microscópicos, aplicando leyes de nucleación y de crecimiento, capaces de aportar información sobre las características microestructurales del material. Estos modelos metalúrgicos microestructurales se acoplan a modelos macroscópicos de transporte y mecánicos.
Algunos investigadores clasifican las principales teorías que explican el proceso de solidificación de la fundición nodular [10] en uninodular y plurinodular. La teoría uninodular sostiene que la unidad de solidificación está formada por un nódulo de grafito y su envoltura de austenita [11] and [12] . La teoría plurinodular, en cambio, propone la nucleación independiente de la austenita y de los nódulos de grafito y considera que la unidad de solidificación cuenta con numerosas esferas de grafito [13] and [14] .
El objetivo principal de este trabajo es obtener numéricamente, mediante homogeneización asintótica [15] , el módulo de Young y el coeficiente de Poisson de una SGI. Para alcanzar este objetivo se emplea un modelo de celda multipartícula [16] and [17] tridimensional, generada computacionalmente de forma tal que represente la microestructura resultante de la simulación de la solidificación del material.
En la sección 2 se describe brevemente el modelo de solidificación con cuyos resultados se generan las microgeometrías. En la sección 3 se reportan aspectos generales del modelado micromecánico, el cual permite obtener las constantes elásticas considerando la influencia de los nódulos de grafito. La metodología utilizada en el análisis del comportamiento elástico de la SGI se detalla en la sección 4. La implementación computacional de modelos de celda multipartícula, mediante el MEF, se expone en la sección 5. Finalmente se presentan los resultados y las conclusiones.
2. Modelado de la solidificación
La solidificación de la fundición dúctil involucra fenómenos térmicos, metalúrgicos y mecánicos fuertemente acoplados entre sí. El modelo utilizado en el presente trabajo aborda los 2 primeros. El problema térmico se trata a nivel macroscópico resolviendo la ecuación del calor por el MEF; y el problema metalúrgico de cambio de fase se analiza con un modelo metalúrgico desarrollado por Boeri [13] que responde a la teoría de solidificación plurinodular. Si bien los fenómenos mecánicos no son modelados, algunos de sus efectos se incluyen en el modelo implícitamente en los coeficientes utilizados. Para considerar la convección de la fundición líquida se modifica el coeficiente de conductividad térmica a elevadas temperaturas. También se incorporan al modelo los efectos de contracción durante el enfriamiento utilizando un coeficiente de transferencia de calor total pieza-molde dependiente de la temperatura de la fundición.
A continuación se presentan brevemente los aspectos generales del modelo de solidificación empleado. La implementación del mismo y la simulación se realizan utilizando el programa para propósitos generales ABAQUS. Para mayor profundidad en los conceptos y métodos de implementación, véase Rodriguez et al. [18] .
2.1. Modelo de transferencia de calor
La ecuación que gobierna el problema térmico analizado es la ecuación de balance de energía de Green and Naghdi [19] :
|
|
( 1) |
donde V es el volumen del cuerpo, S es la superficie que lo encierra, ρ es la densidad del material, es la derivada temporal de la energía interna, q es el flujo de calor por unidad de área del cuerpo y r es el calor generado por unidad de volumen.
Debido a que en este modelo no se consideran los fenómenos mecánicos de la solidificación, se asume que la energía interna depende únicamente de la temperatura del material:
|
|
( 2) |
donde c es el calor específico, es la velocidad de enfriamiento; L es el calor latente de solidificación y es la derivada temporal de la fracción sólida. El acoplamiento entre los modelos térmico y metalúrgico se realiza a través del método del calor latente. La tasa de liberación del calor latente se determina con la fracción volumétrica solidificada que se obtiene del modelo metalúrgico.
La solidificación del metal fundido se da dentro de un molde, por lo cual es preciso modelar el contacto entre pieza y molde. Debido al contacto se produce una transferencia de calor desde la pieza hacia el molde, la cual se modela definiendo un coeficiente de transferencia de calor, variable con la temperatura, en la interfaz.
2.2. Modelo metalúrgico
El modelo microestructural utilizado es el propuesto originalmente por Boeri [13] . Este modelo simula la solidificación equiaxial estable de una fundición nodular de composición eutéctica según la teoría plurinodular.
El modelo propuesto por Boeri utiliza una ley de nucleación exponencial continua para el grafito:
|
|
( 3) |
donde es la derivada temporal de la densidad volumétrica de nódulos; b y c son parámetros del modelo que dependen del tratamiento del líquido; fs es la fracción volumétrica de sólido, y ΔT = TE–T es el sobreenfriamiento del líquido con respecto a la temperatura eutéctica TE .
La nucleación comienza cuando la temperatura desciende por debajo de la temperatura eutéctica, y el final se define según el criterio de temperatura mínima [18] . Debido a que la nucleación del grafito se considera continua, una cierta cantidad de nódulos por unidad de volumen nuclea en cada paso de tiempo. El conjunto de nódulos que nuclea en un mismo paso de tiempo constituye una «familia» de nódulos.
Boeri propone que el crecimiento de los nódulos se produce en 2 etapas: una inicial, en la que el crecimiento se da en contacto con el líquido, y una segunda cuando ya han sido rodeados por la austenita. En la primera etapa, que dura hasta que los nódulos alcanzan un radio de 6 μm, el radio de los nódulos se calcula según la siguiente expresión que se basa en la ecuación de Zener:
|
|
( 4) |
donde Rgr es el radio de la esfera de grafito; t y Δt son el tiempo y su incremento, respectivamente; es el coeficiente de difusión del carbono en el líquido; ρl y ρgr son las densidades del líquido y del grafito, respectivamente; Cl/gr es la concentración de equilibrio de carbono en el líquido en la interfaz líquido-grafito; Cl/γ es la concentración de equilibrio de carbono en el líquido en la interfaz líquido-austenita, y Cgr es la concentración de carbono en el grafito, es decir, el 100%.
Durante la segunda etapa, el mecanismo de crecimiento es la difusión del carbono desde el líquido hacia el grafito a través de la austenita, según la ecuación utilizada por Su et al. [12] y Wetterfall et al. [20] . Esta ecuación se modifica con un factor de corrección para considerar que la envoltura de austenita no es esférica [13] :
|
|
( 5) |
donde Rγ es el radio de la cápsula de austenita; Cγ/gr es la concentración de equilibrio de carbono en la austenita en la interfaz austenita-grafito; Cγ/l es la concentración de equilibrio de carbono en la austenita en la interfaz austenita-líquido, y ργ es la densidad de la austenita. Se supone que la relación entre los radios de austenita y de grafito, Rγ/Rgr , es 2,4.
Empleando el radio y la densidad de los nódulos de grafito de cada familia se calcula la fracción volumétrica fgr de la fundición con la siguiente expresión:
|
|
( 6) |
donde nfam es el número de familias de nódulos que existen en el elemento de volumen debido a la nucleación continua; kfam es el número identificador de cada familia, y Nkfam es el número de nódulos por unidad de volumen con que cuenta cada una de estas.
Utilizando el valor de fgr , la fracción volumétrica de austenita fγ se calcula mediante la regla de la palanca, según la cual la relación entre la cantidad de austenita y de grafito REAG es:
|
|
( 7) |
en la cual CE representa la concentración de carbono eutéctica y CTE la máxima concentración de carbono que puede disolver la austenita a temperatura eutéctica. Aplicando la regla de la palanca, la fracción de austenita se calcula como:
|
|
( 8) |
Y la fracción sólida resulta:
|
|
( 9) |
2.3. Aplicación del modelo
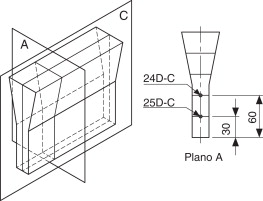
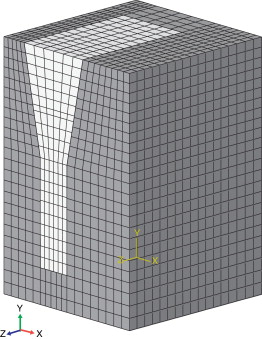
El modelo de solidificación se aplica a 2 bloques de ensayo tipo Y de 1” (fig. 1 ), cuya geometría se especifica en la norma ASTM A536-84 [21] . Los bloques tipo Y se utilizan para obtener probetas de tracción y dureza, con las cuales se efectúan ensayos que permiten caracterizar a la fundición mecánicamente y definir su conformidad. En la figura 2 se muestra la malla de elementos finitos (elementos hexaedros de 8 nodos, DC3D8 en ABAQUS) utilizada en la simulación de la solidificación.
|
|
|
Figura 1. Bloque Y normalizado de 1” de espesor y ubicación de los puntos analizados. |
|
|
|
Figura 2. Malla del modelo. |
La simulación mediante este modelo da como resultado, en cada punto de integración, la fracción volumétrica de grafito y austenita, así como la densidad volumétrica de nódulos para las diferentes familias.
En el modelado micromecánico se utilizan los resultados de los puntos 25D-C y 24D-C (fig. 1 ), que se encuentran en la zona del bloque tipo Y destinada a la obtención de las probetas. En la tabla 1 se informan los valores de fracciones calculados para los puntos mencionados.
| Punto | Fracción de grafito [%] | Fracción de austenita [%] |
|---|---|---|
| 25D-C | 7,5989 | 92,4011 |
| 24D-C | 7,5984 | 92,4016 |
3. Modelado micromecánico
Mediante el modelado micromecánico se trata de establecer las variables continuas en la vecindad de un punto material, considerando la microestructura del entorno y las propiedades de las fases constituyentes. Este tipo de modelo se apoya en la resolución numérica de un problema, en este trabajo elástico, en un dominio con unas condiciones de contorno definidas.
La aplicación de los modelos micromecánicos considera que cualquier punto de un medio continuo a escala macroscópica está asociado a un RVE (fig. 3 ). Este, de dominio ΩS , está formado, en general, por una matriz en la cual se encuentran embebidas inclusiones de diferente material. El RVE posee una longitud característica lS , la cual es mucho menor que la dimensión característica l de la escala macroscópica.
|
|
|
Figura 3. Continuo macroscópico con un RVE local [22] . |
Si esta relación de escalas se cumple, los campos que describen el comportamiento de un material heterogéneo, es decir, los microcampos de deformación ɛ(x) y tensión σ(x) , se pueden descomponer aditivamente considerando la contribución que a estos realiza cada escala de análisis [3] . La descomposición de los campos en cada escala se puede escribir como:
|
|
( 10) |
donde 〈(·) 〉 representan los campos homogéneos, dentro del RVE, coincidentes con los macroscópicos, y (·)’ representa las fluctuaciones de los microscópicos respecto a este valor homogeneizado.
La cuestión principal de la micromecánica es efectuar la vinculación entre estas escalas de análisis. Esta vinculación involucra 2 aspectos: el primero es la homogeneización que realiza la determinación del comportamiento a una escala macroscópica empleando información proveniente de la escala micro; el segundo implica encontrar la respuesta local en la escala microscópica en función de las condiciones de carga en la escala macro.
Para un RVE de un material heterogéneo cuyas dimensiones son representativas del componente de la microestructura del material, que no contienen gradientes de composición significativos ni variaciones significativas en la carga aplicada, entonces la homogeneización para una determinada variable f(x)[3] es:
|
|
( 11) |
Los resultados de aplicar esta expresión a los tensores de deformación y tensión permiten obtener los llamados teoremas de deformación y tensión promedio válidos para el comportamiento lineal elástico del material,
|
|
( 12) |
|
|
( 13) |
donde ΓS representa la superficie del elemento de volumen; u(x) es el vector de desplazamiento; t(x) = σ(x)nΓ(x) es el vector de fuerza de superficie, y nΓ(x) es el vector normal a la superficie.
Las ecuaciones anteriores implican que, en la homogeneización, los promedios volumétricos de las fluctuaciones de los campos microscópicos se anulan para volúmenes de integración suficientemente grandes.
La homogeneización requiere que el RVE tenga una relación suficiente entre escalas y que las condiciones de contorno impuestas al mismo sean tales que la condición de Hill-Mandel
|
|
( 14) |
sea válida para cualquier campo de tensión y de desplazamiento. La condición de Hill-Mandel establece que la densidad de energía de deformación de los microcampos es igual a la de los macrocampos, haciendo energéticamente equivalente las descripciones macroscópicas y microscópicas.
3.1. Elemento de volumen representativo
La microgeometría empleada para la homogeneización debe ser un subdominio de Ω con un tamaño suficiente como para contar con toda la información necesaria para describir el comportamiento del material heterogéneo [23] . Tal como fue mencionado anteriormente, este subdominio se llama RVE.
La respuesta macroscópica obtenida con estos modelos muestra una marcada dependencia del tamaño del elemento de volumen. Por tanto, es de gran importancia encontrar un tamaño óptimo para el elemento de volumen que sea suficientemente grande como para capturar adecuadamente el comportamiento físico del material estudiado pero que implique el menor costo computacional posible.
Se pueden adoptar 2 criterios [3] and [24] para definir el RVE: el geométrico y el físico. En el geométrico el RVE debe ser estadísticamente representativo de la microestructura del material, siendo por lo tanto independiente de la propiedad física estudiada. El criterio físico define el RVE basado en el requerimiento de que su respuesta global, en relación con un determinado comportamiento físico, no dependa de las condiciones de borde aplicadas.
Empleando una definición geométrica del RVE, las estimaciones del tamaño apropiado se obtienen en base a características de la microgeometría sin considerar la propiedad física. El tamaño adecuado del RVE será aquel con características geométricas equivalentes a las del material analizado. Este criterio para la elección del tamaño del RVE, según algunos investigadores [3] , ha probado ser adecuado para modelos micromecánicos utilizados para estimar el comportamiento elástico de materiales heterogéneos, como la fundición nodular. Drugan y Willis [25] demostraron que, para materiales heterogéneos isótropos constituidos por una matriz con partículas esféricas, con celdas de tamaño entre 2 y 5 veces el diámetro de las partículas, se logran resultados representativos de rigidez macroscópica elástica con errores menores al 5 y al 1%, respectivamente. Como puede notarse, según estos autores, el tamaño del RVE es independiente de la fracción volumétrica de partículas.
Según el enfoque del RVE físico, el tamaño de la microgeometría es adecuado cuando un aumento en el tamaño de la misma no produce modificación en la propiedad física estudiada. Adicionalmente, este tamaño del RVE debe ser capaz de capturar las simetrías macroscópicas del material.
En algunos casos, el costo computacional impone limitaciones en el tamaño de las microgeometrías que pueden utilizarse, impidiendo el uso de un RVE apropiado. En estos casos se utilizan elementos de volumen, con un tamaño insuficiente como para ser un RVE, llamados estadísticos (SVE [statistical volume element] ) [3] . El promedio de un número de resultados obtenidos de un conjunto de SVE se utiliza para lograr una mejor estimación de las propiedades del material heterogéneo. El número de SVE requeridos para alcanzar una determinada precisión se reduce cuando su tamaño se aproxima al del RVE. Para propiedades lineales, el número de muestras necesarias se puede determinar como aquel a partir del cual incorporar un nuevo SVE no modifica significativamente el valor de la propiedad analizada.
3.2. Modelos micromecánicos
Las condiciones de borde a aplicar al elemento de volumen deben cumplir la condición de Hill-Mandel. Esta condición se puede escribir como una integral de superficie:
|
|
( 15) |
Existen 4 tipos de condiciones de borde, y por lo tanto 4 modelos, a aplicar aplicarse a un elemento de volumen de tamaño finito [3] que verifican esta condición.
La primera de estas hace nula la integral especificando una condición de borde de Neumann para t(x) de forma que el primer término se anule. Este modelo de tensión de contorno uniforme, o mínimamente restringido, consiste en prescribir un tensor de tensiones macroscópico homogéneo σ0 en todas las caras del elemento de volumen:
|
|
( 16) |
El modelo de Taylor o de deformación homogénea cumple la condición de Hill-Mandel anulando el segundo término de la integral e imponiendo condiciones de borde de desplazamiento uniforme en todo el contorno del elemento mediante un tensor de deformación macroscópico homogéneo ɛ0 :
|
|
( 17) |
La condición también puede verificarse si el producto escalar en la integral de la ecuación (15) se anula para cada una de las caras Γk que conforman el contorno del elemento de volumen. Estos modelos de desplazamiento lineal del contorno utilizan una condición de borde uniforme mixta imponiendo combinaciones de componentes de tensiones y de deformaciones apropiadas.
Por último, el modelo de homogeneización periódico cumple la condición de Hill-Mandel haciendo que las fluctuaciones de los campos no uniformes del contorno se anulen asegurando que en las caras simétricas del elemento de volumen periódico se tengan idénticas fluctuaciones pero con normales opuestas. Para la utilización de este modelo, el elemento de volumen debe tener periodicidad geométrica.
3.3. Homogeneización asintótica
La técnica de homogeneización asintótica permite la sustitución de un medio heterogéneo por uno homogéneo equivalente, permitiendo el uso de leyes de comportamiento macroscópicas obtenidas en base a información microestructural. Algunos investigadores [26] and [27] han aplicado esta técnica al modelado de materiales con una microestructura no exactamente periódica. Tomando esto en consideración y dadas las características microestructurales de la fundición nodular, esta se puede modelar aproximadamente mediante una repetición periódica de una celda.
Utilizando una aproximación asintótica del campo de desplazamiento y operando sobre la misma [15] se obtiene una expresión que, si es satisfecha, garantiza las condiciones de periodicidad de la celda:
|
|
( 18) |
siendo el tensor de deformaciones macroscópico; uk , el desplazamiento del nodo k , y , el desplazamiento de su nodo periódico.
3.4. Propiedades homogeneizadas
La homogeneización tiene como objetivo encontrar un material homogéneo cuyo comportamiento sea equivalente al del material heterogéneo estudiado. Para problemas elásticos esto consiste en evaluar el tensor constitutivo efectivo.
En los modelos de celda multipartícula se impone a esta un conjunto de casos de carga o de deformación. Luego se calcula el campo de desplazamiento microscópico, en este trabajo por el método de los elementos finitos (MEF), asociado a cada solicitación mecánica. Las deformaciones y tensiones microscópicas correspondientes se obtienen en los puntos de integración de Gauss.
A partir de los campos de deformación y de tensión determinados numéricamente se evalúan los tensores de tensión y de deformación macroscópicos, correspondientes a un estado de solicitación mecánica particular. La determinación de estas medidas macroscópicas puede efectuarse mediante dos metodologías [17] : a través del promedio volumétrico de los campos de tensión y de deformación microscópicos en el interior del dominio de cálculo, o bien mediante las fuerzas externas actuantes en las caras de la celda.
La primera metodología se denomina medida interior de la tensión y de la deformación macroscópica. Los tensores de tensión y de deformación promedio se calculan como:
|
|
( 19) |
|
|
( 20) |
donde 〈σij 〉 y 〈ɛij 〉 representan los tensores macroscópicos de tensión y de deformación. En el marco de los elementos finitos estas expresiones quedan de la siguiente manera:
|
|
( 21) |
|
|
( 22) |
donde σk , ɛk y Ωk son el valor de tensión, de deformación y la función de peso (en términos del volumen del punto de integración), respectivamente, asociados con el punto k de integración dentro de un volumen de integración Ωs con N puntos de integración.
La segunda metodología, denominada exterior, se vale para el cálculo de los valores de las componentes de fuerza y de desplazamiento de un conjunto de nodos de control. Estos nodos de control se utilizan dentro del modelo de elementos finitos para imponer las solicitaciones mecánicas macroscópicas. Entonces, las componentes de la tensión macroscópica se calculan como el cociente entre la fuerza de reacción y el área actual:
|
|
( 23) |
donde L0 es la arista del volumen en la configuración inicial indeformada y ckk es la k-ésima componente de desplazamiento del nodo de control k-ésimo . A su vez, las componentes ɛij del tensor de deformaciones macroscópicas se obtienen como:
|
|
( 24) |
Si el domino de integración ΩS corresponde al RVE completo, entonces ambas metodologías dan como resultados medidas macroscópicas equivalentes entre sí, y pueden considerarse representativas del estado tensodeformacional del material heterogéneo.
4. Metodología
La fundición nodular es un material heterogéneo formado por una matriz, que a su vez puede estar formada por diferentes microconstituyentes, con nódulos de grafito embebidos en ella. En este trabajo, con el objetivo de reducir el número de grados de libertad del problema estudiado, la fundición se modela como un material poroso ya que los nódulos no constituyen un refuerzo a la matriz a causa de su bajo módulo de Young [7] and [8] . La matriz se considera formada por un material homogéneo, lineal e isótropo. En las simulaciones se supone una matriz ferrítica y se adoptan los valores de E = 209 GPa y ν = 0,3 utilizados por Pundale et al. [7].
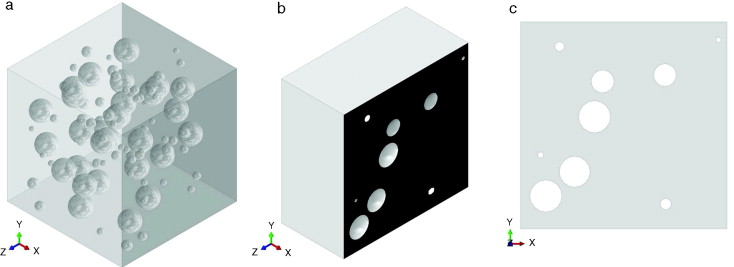
Para encontrar la relación entre los comportamientos macroscópico y microscópico se consideran modelos de celda multipartícula. Se utilizan 2 modelos de celda: el tridimensional de forma cúbica y el bidimensional de forma cuadrada considerando una formulación en tensión plana [7] , según se detalla en la sección 5.1. En la figura 4 se ilustra una de las celdas tridimensionales y el seccionamiento de esta mediante el cual se genera su correspondiente celda bidimensional.
|
|
|
Figura 4. Celda multipartícula tridimensional (a), corte de la misma (b) y su correspondiente celda bidimensional (c). |
La implementación, incluyendo el pre y el posproceso, se realiza en el programa de elementos finitos de propósito general ABAQUS. La construcción del modelo se ejecuta a través de un script desarrollado en lenguaje Python.
Para el cálculo del módulo de Young E y del coeficiente de Poisson ν , se procede mediante el método de homogeneización asintótico [15] , resolviendo el campo de desplazamiento dentro de la celda mediante el MEF. Para la determinación de las propiedades elásticas se imponen a la celda 2 deformaciones prescriptas linealmente independientes.
Con el fin de tener un valor comparativo, se determina el módulo de Young mediante el modelo de regla de mezclas, que es una cota superior para esta propiedad. Este simple modelo, utilizado en la determinación de propiedades de materiales heterogéneos, toma como entradas solamente las fracciones volumétricas y el valor de la propiedad analizada para cada fase. En el caso analizado en este trabajo, en el que una de las fases es considerada como un vacío, el valor de módulo de elasticidad ERM calculado según la regla de mezclas es:
|
|
( 25) |
donde Ef es el módulo de Young para la ferrita y fv es la fracción volumétrica de matriz.
Se determina el tamaño del RVE según los criterios geométricos y físico en ambos modelos. Al aumentar sucesivamente el tamaño de la celda se obtiene una secuencia de respuestas. La definición del RVE se hace imponiendo la condición de que un error relativo, entre tamaños de celda consecutivos, sea inferior a una tolerancia de convergencia definida en un 2%. Este error relativo ξr% , empleado en el criterio físico, se expresa como:
|
|
( 26) |
donde Ai y Ai+1 son los valores de la propiedad analizada para un determinado tamaño i y la obtenida con un tamaño de celda inmediato superior i + 1 . En la definición geométrica del RVE también se utiliza la ecuación (26), pero Ai+1 es el valor de la fracción volumétrica para el tamaño de celda analizado y Ai es el valor obtenido de la simulación numérica (tabla 1 ).
Para los puntos 24D-C y 25D-C (fig. 1 ) se generan RVE tridimensionales y bidimensionales. Se comparan los resultados obtenidos con ambos modelos considerados y con el modelo de mezclas, para los 2 puntos analizados.
5. Modelos de celda multipartícula
5.1. Generación de la celda
En este trabajo se emplean celdas multipartículas sintéticas, en 2 y 3 dimensiones, para representar un elemento de volumen de fundición nodular. Las celdas se modelan asumiendo que la matriz es homogénea y los nódulos son vacíos de forma perfectamente esférica, o circular para las celdas bidimensionales. Los nódulos poseen diferentes tamaños y se encuentran embebidos en la matriz según una distribución aleatoria. El tamaño absoluto de la celda L —en adelante tamaño de la celda— se define como la longitud del lado de la celda en los modelos bidimensionales y la longitud de la arista para los tridimensionales. Se define, además, un tamaño relativo de celda dado por el cociente entre L y el radio de los nódulos de mayor tamaño, que son los pertenecientes a la familia de nódulos que nuclea primeramente.
Para la celda tridimensional, los nódulos de grafito se representan mediante vacíos esféricos de diferentes radios, según los resultados obtenidos de la simulación numérica de la solidificación. En cada celda se incluye un número de nódulos, para cada familia, que se determina a partir de su densidad volumétrica y del volumen total de la celda considerada:
|
|
( 27) |
donde N es el conteo de nódulos de una familia incluidos en la celda, Nvol es la densidad volumétrica de nódulos obtenida de la simulación de la solidificación y ΩC es el volumen de la celda utilizada. El valor obtenido de este cálculo se redondea, debido a que la cantidad de nódulos debe ser un número natural.
La celda multipartícula tridimensional se genera por el método de adición aleatoria secuencial (RSA [random sequential addition] ). Este método genera de manera secuencial y aleatoria las coordenadas de los centros de las esferas, permitiendo obtener distribuciones aleatorias de partículas. Se impone la condición de que las partículas no deben interpenetrarse y deben estar contenidas completamente dentro de la celda, sin cortar los bordes de la misma ( fig. 4 a).
La celda bidimensional se obtiene en base a la tridimensional seccionándola con un plano de corte paralelo a una de sus caras y con posición aleatoria. Para esto, una vez elegido el plano con el cual se seccionará, se identifican los nódulos que lo cortan y se determina el radio de la circunferencia que resulta de la intersección entre el plano y cada una de estas esferas (fig. 4 c).
5.2. Elección del tamaño del elemento de volumen representativo
El tamaño de un RVE que permita calcular las constantes elásticas de la fundición nodular requiere considerar 2 aspectos: la precisión deseada y el número de elementos finitos de la malla utilizada; ambos aumentan al incrementarse el tamaño del volumen.
Tomando como base los resultados de Drugan y Willis [25] y Drugan [28] , se realiza un análisis para determinar el tamaño del RVE según los criterios geométrico y físico. Para efectuar este estudio se emplea la definición de tamaño relativo de celda, empleando celdas de tamaño relativo creciente entre 8 y 70.
Para la generación de las celdas tridimensionales se determina el número de nódulos de cada familia a incluir en el volumen, según se detalla en la sección 5.1. En celdas de pequeñas dimensiones solo se incluyen, dentro de la misma, nódulos pertenecientes a las familias con una elevada densidad volumétrica. Esto es así puesto que, según la ecuación (27), dado un volumen de la celda, las familias con baja densidad volumétrica tienen conteo volumétrico nulo.
Debido a que la densidad volumétrica de nódulos es un valor constante determinado en la simulación de la solidificación, el aumento del tamaño de celda da lugar a un incremento del conteo volumétrico para cada una de las familias. Este aumento origina un conteo volumétrico no nulo para algunas familias de baja densidad volumétrica de nódulos. El aumento del tamaño de celda hace que un mayor número de familias tengan nódulos incluidos en la misma, haciéndola más representativa de la fundición analizada. Para tamaños suficientemente grandes de celda todos los grupos cuentan con al menos un nódulo contenido en ella.
La característica que se evalúa para definir el tamaño del RVE según el criterio geométrico es la fracción volumétrica de matriz. Se considera principalmente su evolución con el aumento del tamaño de celda, contemplando también las distribuciones de tamaño de nódulos en cada una.
Para seleccionar el tamaño del RVE según el criterio físico se analiza la evolución de las constantes que definen el comportamiento elástico de la fundición, a saber, el módulo de Young y el coeficiente de Poisson. Se aplica el método de homogeneización asintótica a celdas de tamaño creciente, con tamaño relativo inicial 8, para determinar el valor de estas constantes elásticas. El mallado se realiza con elementos tetraédricos cuadráticos con formulación estándar y modificada.
En 3 dimensiones se tienen valores únicos que caracterizan geométricamente a cada tamaño de celda; por ejemplo, el conteo y la fracción volumétrica de vacíos es igual para todas las celdas tridimensionales de dimensiones iguales. Sin embargo, la forma propuesta de obtención de celdas bidimensionales hace que las características geométricas sean particulares de cada una, es decir, no características del tamaño. Esto se debe a que tanto el número de vacíos intersectados por el plano como la posición por la cual se cortan los mismos son variables.
La variabilidad de las características geométricas de la celda bidimensional conduce a una elevada dispersión de los resultados. Esta dispersión origina que, con el aumento del tamaño de la celda, no se evidencie una convergencia de resultados para ninguno de los criterios utilizados.
Para reducir esta dispersión en los resultados se utiliza el concepto de promedio de una muestra o ensamble averaging[24] . La generación de celdas tridimensionales se realiza con el algoritmo RSA, que al ser aleatorio genera geometrías de celda diferentes en cada ejecución. Entonces, es posible generar M celdas tridimensionales diferentes y, para cada una de estas, obtener su correspondiente celda bidimensional; cada una de las celdas bidimensionales es un miembro de lo que, en conjunto, se denomina muestra.
La respuesta de cada unidad de la muestra Q(K ) es, en general, diferente, pudiéndose entonces definir una respuesta promedio 〈〈 Q 〉〉 de la muestra considerada con la siguiente expresión:
|
|
( 28) |
Incorporar un miembro extra a la muestra, aumentando el tamaño de esta, da lugar a una respuesta promedio 〈〈 Q 〉〉 k . El incremento de sucesivo tamaño de muestra da origen a una secuencia de 〈〈 Q 〉〉 k . Esta secuencia pone de manifiesto una convergencia con el aumento del número de miembros de la misma, permitiendo aliviar los efectos de la aleatoriedad en las respuestas.
Entonces, para definir un valor característico de respuesta para cada tamaño de celda bidimensional, se incrementa sucesivamente el tamaño de la muestra hasta que el valor marginal de la propiedad estudiada es despreciable. Cuando esto ocurre, se asume que esta respuesta promedio constituye un valor característico de este tamaño de celda.
5.3. Mallado
Dada la complejidad de la geometría generada, el mallado se realiza mediante elementos tetraédricos. Se utiliza un mallador automático no estructurado debido a que la geometría de la celda no es regular. El mallado se realiza con elementos cuadráticos, ya que los de interpolación lineal exhiben una excesiva rigidez. ABAQUS cuenta con 2 formulaciones diferentes, y sus respectivas versiones híbridas, para los elementos tetraédricos cuadráticos, a saber, el C3D10 y el C3D10M. El primero de estos es el elemento cuadrático estándar, mientras que el segundo tiene una formulación que es propia de ABAQUS. El elemento C3D10M cuenta con 3 grados de libertad internos más asociados al desplazamiento de un nodo auxiliar interno.
Según Segurado [16] , el elemento C3D10 exhibe una respuesta más rígida en relación con el elemento modificado. Él atribuye este comportamiento a que el nodo auxiliar permite una mejor representación de los fuertes gradientes de tensión en las zonas próximas a los vacíos. Estos 3 grados de libertad extra mejoran sensiblemente la interpolación del desplazamiento donde los gradientes son elevados, como por ejemplo en la zona entre partículas. El mallado de las microgeometrías se realiza con ambos tipos de elementos y se comparan los resultados obtenidos en cada caso.
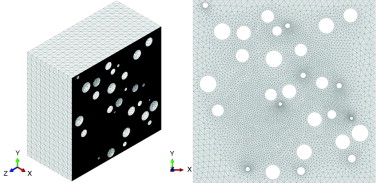
Los modelos 2D se mallan utilizando un mallador automático no estructurado empleando elementos triangulares cuadráticos de tensión plana, CPS6. En la figura 5 se muestra la malla obtenida para las celdas tri y bidimensionales representadas.
|
|
|
Figura 5. Malla para los modelos 3D y 2D. |
La implementación de condiciones de borde periódicas, en el marco del método de los elementos finitos, requiere que la discretización de los contornos opuestos del RVE, el cual inicialmente es periódico, se realice de igual forma. Esto se lleva a cabo para asegurar que cada nodo en uno de los contornos tenga su nodo periódico correspondiente, en el contorno opuesto, ubicado en exactamente la misma posición.
La densidad de malla se controla mediante el «sembrado» sobre las aristas o las caras de la celda y sobre el contorno de los nódulos. Se realiza un análisis de convergencia para cada tamaño de celda considerado modificando el sembrado de la celda. Como se puede observar en la figura 5 , la malla ha sido densificada en las proximidades de los nódulos, ya que estas son las zonas en las cuales se presentan los mayores gradientes en los campos de deformación y de tensión.
5.4. Condiciones de borde
En este trabajo, para describir el comportamiento macromecánico de la fundición nodular se utilizan modelos de celda multipartícula. Estos realizan el análisis de un material modelo con microestructura y condiciones de contorno periódicas. Tanto en la configuración inicial como en la deformada, la geometría de las celdas, así como las condiciones de contorno impuestas a la misma, deben asegurar que todo el espacio sea cubierto por las celdas.
La aplicación de la homogeneización asintótica a celdas multipartículas hace necesario imponer condiciones de contorno periódicas. Debido a que las mismas requieren relacionar los desplazamientos en las 3 direcciones del espacio de cada par de nodos ubicados en posiciones simétricas, su costo computacional es elevado.
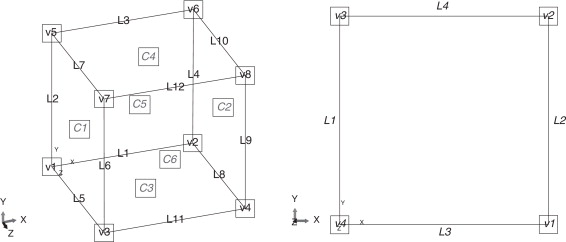
Utilizando la técnica de homogeneización asintótica, las condiciones de periodicidad de la celda utilizada se garantizan si se cumple la ecuación (18). Dado que en esta expresión es desconocido, para la implementación numérica de estas condiciones se deben obtener expresiones adecuadas que relacionen los desplazamientos de un par de puntos ubicados sobre caras opuestas. Siguiendo el procedimiento indicado en [27] se determinan las siguientes condiciones de contorno a imponer a las caras, las aristas y los vértices de la celda tridimensional. En la figura 6 se identifican estos elementos utilizando la nomenclatura empleada en adelante.
|
|
|
Figura 6. Identificación de caras, aristas y vértices de la celda tridimensional y de lados y vértices para la celda bidimensional. |
Las ecuaciones a utilizar en un modelo 3D de celda cúbica de tamaño L , para sus vértices, son:
|
|
( 29) |
para las aristas, excluyendo los vértices:
|
|
( 30) |
y finalmente en las caras:
|
|
( 31) |
Siguiendo un procedimiento similar para el modelo plano, las condiciones para los lados de la celda, sin incluir vértices, son:
|
|
( 32) |
y para los vértices:
|
|
( 33) |
Esta implementación requiere agregar 3 nodos de control, cada uno de ellos con 3 grados de libertad adicional, a los cuales se les imponen los diferentes casos de solicitación mecánica. Es necesario, además, restringir el movimiento de cuerpo rígido de la celda anulando el desplazamiento de un punto cualquiera perteneciente a la misma [29] .
5.5. Casos de deformación macroscópica
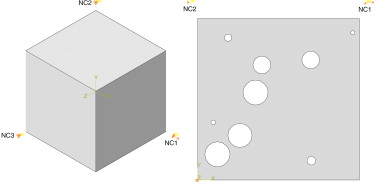
Para computar las propiedades elásticas efectivas es preciso obtener la solución de un solo problema de valor de contorno. Para esto se somete la celda a un conjunto de deformaciones macroscópicas prescriptas empleando, en este trabajo, el método de grados de libertad macroscópicos [30] . Este consiste en imponer desplazamientos en nodos de control NC (fig. 7 ), a efectos de obtener las deformaciones prescritas.
|
|
|
Figura 7. Nodos de control para las celdas en 3 (a) y 2 (b) dimensiones, con las condiciones de contorno prescritas para el caso de carga . |
Los desplazamientos a imponer a los nodos de control se obtienen del producto entre la deformación macroscópica y el tamaño absoluto de la celda. En general, para obtener el tensor constitutivo elástico se deben evaluar los resultados para 6 solicitaciones mecánicas linealmente independiente [28] . Sin embargo, asumiendo un comportamiento isótropo para el material homogéneo equivalente, solo una, con componentes volumétrica y desviadora no nulas, es necesaria [31] , pues las propiedades elásticas quedan definidas con 2 constantes. La evidencia experimental muestra que la fundición nodular exhibe una respuesta isótropa, por lo cual se realiza esta consideración para la determinación de las constantes elásticas. En este trabajo, en lugar de utilizar una única deformación macroscópica acoplada se imponen 2 deformaciones macroscópicas linealmente independientes:
|
|
( 34) |
5.6. Determinación de constantes elásticas
Existen varios pares de constantes, equivalentes entre sí, que permiten describir el comportamiento elástico de un material isótropo. En este trabajo se emplea el módulo de Young y el coeficiente de Poisson. Utilizando la notación de Nye, la relación entre tensiones y deformaciones para materiales isótropos se puede escribir en términos de estas 2 constantes como:
|
|
( 35) |
Entonces, conocidas las deformaciones macroscópicas impuestas y con las tensiones homogeneizadas calculadas para ambos casos de deformación macroscópica impuesta:
|
|
( 36) |
|
|
( 37) |
el módulo de Young E y el coeficiente de Poisson ν se obtienen de la solución del siguiente sistema de ecuaciones:
|
|
( 38) |
6. Resultados y discusión
La elección del tamaño del RVE se realiza según los criterios geométrico y físico, empleando para la generación de la microgeometría los resultados de la simulación de la solidificación correspondientes al punto 25D-C. Mediante una serie de análisis independientes, se define en primer lugar el tamaño del RVE tridimensional según ambos criterios y en segundo término se hace lo propio para el modelo plano. Se analizan celdas con un tamaño relativo creciente de entre 8 y 70.
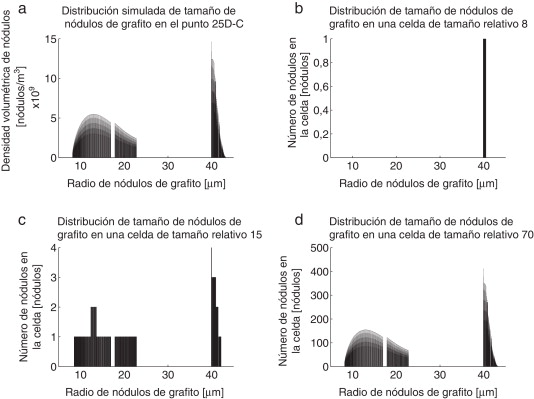
En la definición del tamaño del RVE tridimensional se analizan celdas con tamaño relativo creciente entre 8 y 70. La figura 8 muestra la distribución de tamaño de nódulos de grafito obtenida a través del modelo de solidificación, así como las distribuciones para los nódulos incluidos dentro de una celda de tamaño relativo de 8, 15 y 70. Se observa que el aumento del tamaño de la celda analizada produce que las distribuciones de radio de nódulos se asemejen a la distribución resultante de la simulación.
|
|
|
Figura 8. Distribución de tamaño de nódulos simulada y para celdas de tamaño 8, 15 y 70. |
Analizando la figura 8 b se puede notar que, tal como se indica en la sección 5.2, en celdas de pequeñas dimensiones solo se incluyen nódulos pertenecientes a las familias con una elevada densidad volumétrica (fig. 8 a), dando lugar a familias con conteos nodulares nulos.
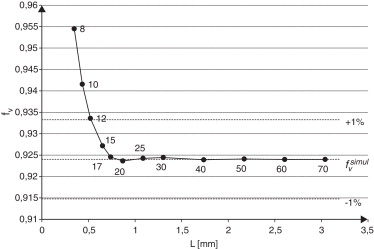
En la figura 9 se muestra la evolución de la fracción volumétrica de la matriz del modelo tridimensional en función del tamaño absoluto de la celda L. Las etiquetas que se muestran para cada punto del gráfico indican el tamaño relativo de celda. Se nota una rápida convergencia al valor de fracción volumétrica obtenido de la simulación de la solidificación, fvsimul = 0,924011, alcanzando ξr% menores al 1% para tamaños relativos superiores a 12.
|
|
|
Figura 9. Fracción volumétrica de matriz, en el modelo tridimensional, en función del tamaño de celda. |
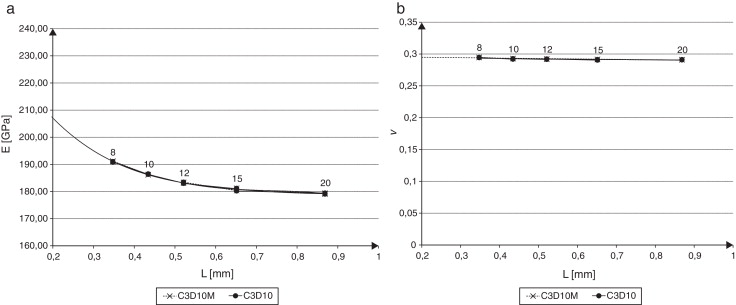
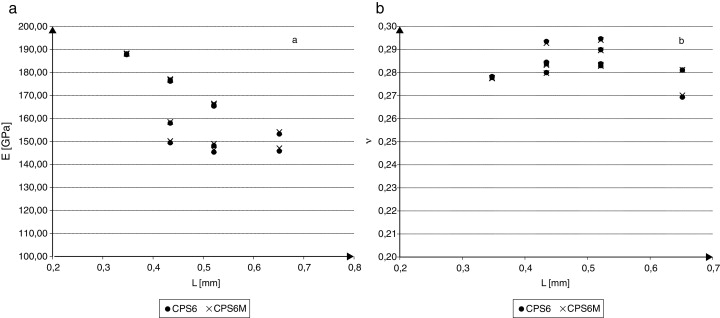
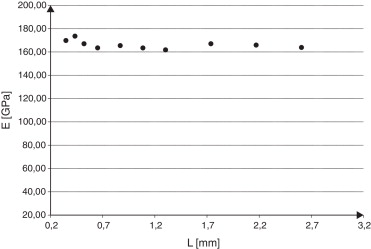
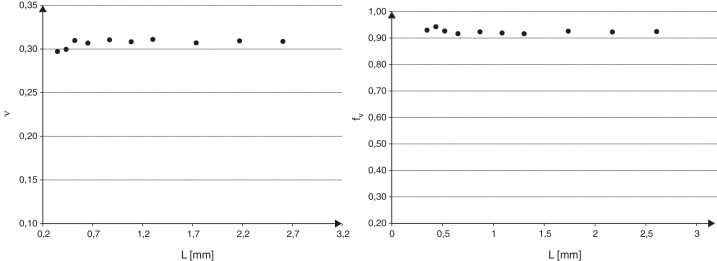
La figura 10 muestra la evolución de las constantes elásticas en función del tamaño absoluto de celda, para los 2 tipos de elementos empleados. El valor de E muestra una convergencia a partir de tamaños relativos de celda de 15, mostrando un ξr% de 1,13% y de 0,90% para una celda cuyo tamaño relativo es 20. En cambio, el valor del coeficiente ν se mantiene prácticamente insensible al cambio de tamaño de celda utilizado, experimentando una leve reducción.
|
|
|
Figura 10. a) Módulo de Young E ; b) coeficiente de Poisson ν en función del tamaño de celda. |
Observando los resultados no se pueden encontrar diferencias significativas entre las respuestas homogeneizadas calculadas utilizando elementos C3D10 y C3D10M. Esto se puede deber a que, por la baja densidad de nódulos de grafito, no se originan elevados gradientes de desplazamiento dentro de la celda, por lo cual la respuesta para ambos elementos es similar.
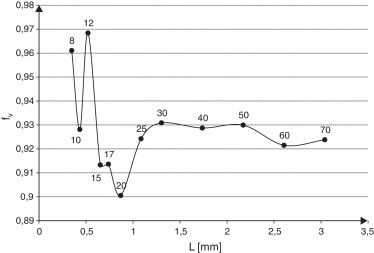
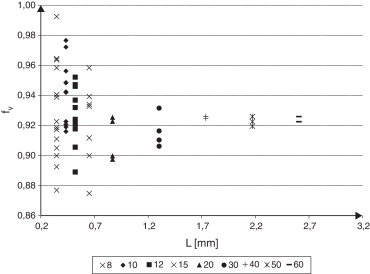
En la definición del tamaño del RVE plano se analizan celdas con tamaño relativo creciente entre 8 y 70. Tanto para la definición geométrica (fig. 11 ) como física (fig. 12 ) del tamaño del RVE se observa la dispersión en los resultados indicada en la sección 5.2. Se aplica el procedimiento descrito en esta sección para determinar las respuestas características de cada tamaño de celda. En la figura 13 se muestran los resultados obtenidos con este procedimiento para una celda de tamaño relativo 8.
|
|
|
Figura 11. Fracción volumétrica de matriz fv para diferentes tamaños de celda bidimensional. |
|
|
|
Figura 12. Valores obtenidos con el modelo bidimensional para: a) módulo de Young E , y b) coeficiente de Poisson ν en función del tamaño de celda considerando una única celda. |
|
|
|
Figura 13. a) Módulo de Young E , b) coeficiente de Poisson ν y fracción volumétrica fv con el aumento del tamaño de la muestra. |
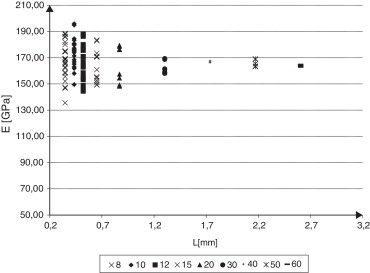
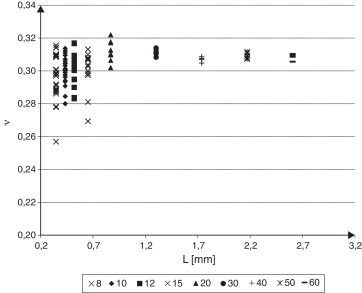
En las Figura 14 , Figura 15 and Figura 16 se puede notar la dispersión de los resultados determinados con cada tamaño de celda analizado y cómo la dispersión se reduce con el aumento de tamaño de la celda.
|
|
|
Figura 14. Módulo de Young para las diferentes celdas que constituyen la muestra de cada tamaño de celda considerado. |
|
|
|
Figura 15. Coeficiente de Poisson ν para las diferentes celdas que constituyen la muestra de cada tamaño de celda considerado. |
|
|
|
Figura 16. Fracción volumétrica para las diferentes celdas que constituyen la muestra de cada tamaño de celda considerado. |
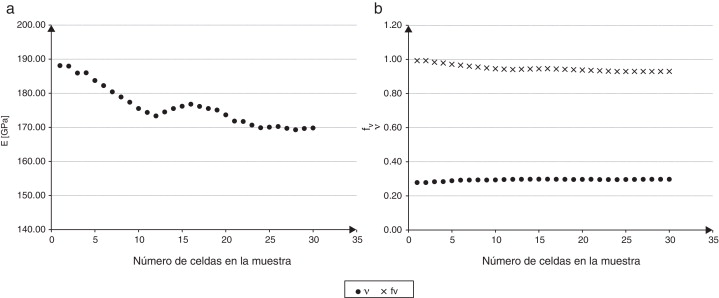
Los resultados característicos para cada tamaño de celda plana se grafican en las Figura 17 and Figura 18 . Los valores de fracción volumétrica, módulo de Young y coeficiente de Poisson característicos exhiben convergencia con el aumento del tamaño de celda considerado. Los valores promediados de fracción volumétrica de matriz, que permiten definir el tamaño del RVE según el criterio geométrico, muestran una convergencia más rápida que las propiedades físicas que se utilizan en la definición física del tamaño del RVE.
|
|
|
Figura 17. Valor promedio del módulo de Young para cada tamaño de celda analizado. |
|
|
|
Figura 18. Coeficiente de Poisson y fracción volumétrica de matriz característicos para cada tamaño de celda. |
Con tamaño relativo de celda 15, el ξr% en la fracción volumétrica es de 1,08%. De las propiedades elásticas analizadas, el módulo de Young es la que muestra una mayor variabilidad. Para que los valores converjan se requieren tamaños relativos de celda superiores a 30.
Se adopta como tamaño de celda representativo (RVE) aquel con el cual se tenga una respuesta con un ξr% menor al 2% y que para tamaños mayores el ξr% se mantenga dentro de estos límites. Con este criterio, y en base a los resultados determinados, se decide adoptar un tamaño relativo del RVE, para el modelo tridimensional, de 12 según el criterio geométrico (ξr% = 1,62%) y 15 para el criterio físico, para el cual el error relativo en el módulo de Young es de 1,08%.
Para el RVE bidimensional se adopta, según el criterio geométrico, un tamaño relativo de 15 cuyo ξr% es de 1,08%. Según el criterio físico, se toma como RVE la celda con tamaño relativo de 40 que exhibe un error relativo de 1%.
En la tabla 2 se muestran los resultados obtenidos de la simulación, en los puntos 24D-C y 25D-C (fig. 1 ) y el valor de módulo de Young determinado mediante el modelo de mezclas. Se utilizan los tamaños del RVE definidos con el criterio físico, ya que especifica tamaños de celda mayores que incluyen los geométricos. Se generan 3 RVE para los modelos en 3 y 2 dimensiones.
| Punto | Muestra | Módulo de Young [GPa] | Coeficiente de Poisson | |||
|---|---|---|---|---|---|---|
| Regla de mezclas | Modelo 2D | Modelo 3D | Modelo 2D | Modelo 3D | ||
| 24D-C | 1 | 193,118 | 166,474 | 179,312 | 0,3102 | 0,2909 |
| 2 | 164,952 | 179,958 | 0,3142 | 0,2908 | ||
| 3 | 168,583 | 179,158 | 0,3104 | 0,2914 | ||
| 25D-C | 1 | 193,119 | 167,501 | 181,025 | 0,3075 | 0,2903 |
| 2 | 166,784 | 181,149 | 0,3086 | 0,2904 | ||
De estos resultados se puede ver, como se esperaba, que la regla de mezclas da la respuesta elástica más rígida, siendo el modelo bidimensional el que predice el comportamiento menos rígido.
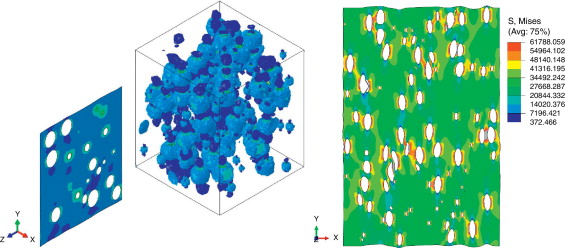
En la figura 19 se muestran los campos de tensiones equivalentes de Von Mises calculados de la muestra 1 del punto 25D-C para los RVE tridimensional y bidimensional.
|
|
|
Figura 19. Tensión de Von Mises para un RVE tridimensional y uno bidimensional del punto 25D-C. |
7. Conclusiones
En el presente trabajo se obtienen las propiedades elásticas macroscópicas de la fundición nodular empleando el método de homogeneización asintótica con modelos de celda multipartícula.
Empleando los resultados de la simulación de la solidificación de la fundición nodular, según el modelo propuesto por Boeri [13] , se generan microgeometrías que se consideran formadas por una matriz homogénea con nódulos embebidos en ella. Los nódulos se representan mediante vacíos. La distribución de los nódulos se realiza mediante el método RSA, que permite obtener distribuciones aleatorias de partículas.
La construcción del modelo de elementos finitos, incluyendo la generación de las celdas multipartícula, la asignación de propiedades a la misma, la imposición de condiciones de borde y periodicidad, así como la simulación y el posproceso, se realizaron utilizando el programa ABAQUS.
El módulo de Young y el coeficiente de Poisson se obtienen mediante el método de homogeneización asintótica, imponiendo a la celda 2 casos de solicitación mecánica linealmente independientes. Se analizaron diferentes celdas, en 2 y 3 dimensiones, con tamaño creciente, con el objetivo de definir el tamaño del RVE.
En el caso estudiado se puede notar que los criterios para definir el RVE arrojan resultados diferentes, siendo en general el criterio geométrico el que da los tamaños menores. La elección de la respuesta mecánica a utilizar en el criterio físico permite determinar tamaños disímiles para el RVE, aunque la diferencia entre ambos parece ser menor.
Respecto a las celdas en 2 y 3 dimensiones, se observa que se obtienen valores representativos para las últimas menores que para el caso bidimensional. Esto puede atribuirse a que los modelos en 3 dimensiones proveen una descripción más completa de la estructura del material, siendo necesarios RVE de menores dimensiones. Sin embargo, el uso de modelos tridimensionales tiene un costo computacional mucho mayor aún si se compara con RVE bidimensionales de tamaños relativos mayores.
Del análisis de la respuesta con los 2 modelos se observa un comportamiento más rígido en el tridimensional respecto al bidimensional. Estas diferencias se atribuyen a las hipótesis que se adoptan al considerar el problema como de tensión plana.
Agradecimientos
Esta investigación fue apoyada por el Ministerio de Ciencia, Tecnología e Innovación Productiva de Argentina; Universidad Tecnológica Nacional — Facultad Regional Córdoba y CONICET. F. J. Rodríguez posee beca de doctorado CONICET tipo I.
Bibliografía
- [1] A. Spada, C. Rajan, P. Gil; U.S. ductile iron metalcasting: Competing globally; Proceedings of the Keith Millis Symposium on Ductile Cast Iron, Las Vegas, Nevada, EE. UU. (2008)
- [2] S. Panchal; Indian Foundry Industry; International Foundry Forum, Barcelona, España (2010)
- [3] H.J. Böhm; A short introduction to basic aspects of continuum micromechanics. ILSB Report, Institute of Lightweight Design and Structural Biomechanics; Vienna University of Technology, Viena, Austria (2012)
- [4] X. Guo, D.M. Stefanescu, L. Chuzhoy, M.A. Pershing, G.L. Biltgen; A mechanical properties model for ductile iron; AFS Transactions, 105 (1997), pp. 47–54
- [5] L. Wenzhen, L. Baicheng; Microstructure simulation and properties prediction of spheroidal graphite iron castings; International Proceedings of 62nd World Foundry Congress, Philadelphia, Pennsylvania (1996), pp. 2–10
- [6] E. Lundback, I.L. Svensson, P. Person; Modelling of structure formation and relation to mechanical properties of nodular cast iron; J.L. Chenot, E. Oñate (Eds.), Modelling of Metal Forming Processes. Proceedings of the Euromech 233 Colloquium, Springer Netherlands, Sophia Antipolis, France (1988), pp. 37–46
- [7] S.H. Pundale, R.J. Rogers, G.R. Nadkarni; Finite element modeling of elastic modulus in ductile irons: Effect of graphite morphology; AFS Transactions, 102 (98) (2000), pp. 99–105
- [8] L. Collini, G. Nicoletto; Determination of the relationship between microstructure and constitutive behaviour of nodular cast iron with a unit cell model; J. Strain Anal. Eng. Des., 40 (2) (2005), pp. 95–106
- [9] L. Collini; Micromechanical modeling of the elasto-plastic behavior of heterogeneous nodular cast iron [tesis doctoral]; Università degli Studi di Parma, Italia (2004)
- [10] J. Sikora, R. Boeri, G. Rivera; Characteristics of austenite in ductile iron: Its influence on the microstructure and properties; Proceedings of the International Conference on the Science of Casting and Solidification, Rumania (2001), pp. 28–31
- [11] E. Fras; A Computer-aided Simulation of the Kinetics of Solidification of the Eutectic Ductile Cast Iron; Proceedings of the 3rd International Symposium on the Metallurgy of Cast Iron, Estocolmo, Suecia (1984), pp. 191–199
- [12] K. Su, I. Ohnaka, I. Yamauchi, T. Fukusako; Computer Simulation of Solidification of nodular Cast Iron; Proceedings of the 3rd International Symposium on the Metallurgy of Cast Iron, Estocolmo, Suecia (1984), pp. 181–189
- [13] E.R. Boeri; The Solidification of Ductile Cast Iron [tesis doctoral]; University of British Columbia, Canadá (1989)
- [14] P.M. Dardati; Simulación micromecánica de la solidificación de la fundición dúctil [tesis doctoral]; Universidad Nacional de Córdoba, Argentina (2005)
- [15] E. Sánchez-Palencia; Homogenization in mechanics. A survey of solved and open problems; Rend. Sem. Mat. Univ. Politec. Torino, 44 (1) (1986), pp. 1–45
- [16] J. Segurado; Micromecánica computacional de materiales compuestos reforzados con partículas [tesis doctoral]; Universidad Politécnica de Madrid, España (2004)
- [17] J.A. Zahr Viñuela; Comportamiento mecánico de materiales compuestos de matriz metálica y refuerzo de partículas. Un enfoque basado en celdas multipartícula [tesis doctoral]; Universidad Carlos III de Madrid, España (2010)
- [18] F.J. Rodriguez, A.D. Boccardo, P.M. Dardati, F.D. Carazo, D.J. Celentano, L.A. Godoy; Implementación de un modelo de solidificación de fundición nodular en un programa de elementos finitos para propósitos generales; Mec. Comput., XXXI (12) (2012), pp. 2093–2118
- [19] Simulia; Abaqus Theory Manual 6.7; Dassault Systèmes (2007)
- [20] S. Wetterfall, H. Fredriksson, M. Hillert; Solidification process of nodular iron; J. Iron Steel Inst., 210 (Part I) (1972), pp. 323–333
- [21] ASTM., A536; Standard Specification for Ductile Iron Castings (2009)
- [22] F.D. Carazo, S.M. Giusti, A.D. Boccardo, P.M. Dardati, L.A. Godoy; Characterization of nodular cast-iron using multi-scale constitutive modeling; Mec. Comput., XXX (8) (2011), pp. 611–629
- [23] L.A. Godoy; Modelos y enfoques para problemas con acoplamiento de micro y macro estructuras; Mec. Comput., XXII (22) (2003), pp. 1964–1984
- [24] I. Temizer; Micromechonics: Analysis of heterogeneous materials. Lecture Notes; Department of Mechanical Engineering. Bilkent University, Ankara, Turquía (2012)
- [25] W.J. Drugan, J.R. Willis; A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites; J. Mech. Phys. Solids, 44 (1996), pp. 497–524
- [26] J. Pinho-da-Cruz, J.A. Oliveira, F. Texeira-Dias; Asymptotic homogeneisation in linear elasticity. Part I: Mathematical formulation and finite element modelling; Comput. Mater. Sci., 45 (2009), pp. 1073–1080
- [27] A.A. Ibarra Pino, A.P. Cisilino; Estimación del comportamiento elástico aparente del hueso trabecular mediante métodos de homogenización; Mec. Comput., XXX (44) (2011), pp. 3413–3430
- [28] W. Drugan; Micromechanics based variational estimates for a higher non-local constitutive equation and optimal choice of effective moduli of elastic composites; J. Mech. Phys. Solids, 48 (2000), pp. 1359–1387
- [29] A. Caporale, R. Luciano, E. Sacco; Micromechanical analysis of interfacial debonding in unidirectional fiber-reinforced composites; Comput. Struct., 84 (31-32) (2006), pp. 2201–2210
- [30] C. Miehe, J. Schotte, J. Schröder; Computational micro-macro transitions and overall moduli in the analysis of polycrystals at large strains; Comput. Mater. Sci., 16 (1-4) (1999), pp. 372–382
- [31] T.I. Zohdi, P. Wriggers; Introduction to Computational Micromechanics; LNACM 20, Springer-Verlag, Berlín-Heidelberg (2005)
Document information
Published on 01/06/15
Accepted on 13/01/14
Submitted on 16/09/13
Volume 31, Issue 2, 2015
DOI: 10.1016/j.rimni.2014.01.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?
![Continuo macroscópico con un RVE local [22].](/wd/images/7/72/Draft_Content_562447694-1-s2.0-S0213131514000285-gr3.jpg)