Abstract
This paper describes a new weather generator – the 10-state empirical model – that combines a 10-state, first-order Markov chain with a non-parametric precipitation amounts model. Using a doubly-stochastic transition-matrix results in a weather generator for which the overall precipitation distribution (including both wet and dry days) and the temporal-correlation can be modified independently for climate change studies. This paper assesses the ability of the 10-state empirical model to simulate daily area-average precipitation in the Torne River catchment in northern Sweden/western Finland in the context of 3 other models: a 10-state model with a parametric (Gamma) amounts model; a wet/dry chain with the empirical amounts model; and a wet/dry chain with the parametric amounts model. The ability to accurately simulate the distribution of multi-day precipitation in the catchment is the primary consideration.
Results showed that the 10-state empirical model represented accumulated 2- to 14-day precipitation most realistically. Further, the distribution of precipitation on wet days in the catchment is related to the placement of a wet day within a wet-spell, and the 10-state models represented this realistically, while the wet/dry models did not. Although all four models accurately reproduced the annual and monthly averages in the training data, all models underestimated inter-annual and inter-seasonal variance. Even so, the 10-state empirical model performed best. We conclude that the multi-state model is a promising candidate for hydrological applications, as it simulates multi-day precipitation well, but that further development is required to improve the simulation of interannual variation.
Keywords
Weather generator ; Multi-state ; Torne River ; Precipitation
1. Introduction
A weather generator (WG) is a stochastic model that is designed to generate synthetic weather time-series with the same statistical properties as observed data. WGs can provide additional data when the observed climate record is insufficient with respect to completeness, spatial coverage or length to reliably estimate of the probability of extreme events (Jones et al., 2011 ; Kilsby et al., 2007 ; e.g. Wilks and Wilby, 1999 ). WGs can be used to simulate short-term weather (e.g. at daily or sub-daily scales) for the past or future, and have become a common tool for studying impacts of climate change on ecosystems and human settlements (Jones et al., 2011 ; e.g. Wilks, 2010 ). One particular advantage of using WGs is that they can generate time-series for an extended period without significant computational investment.
Within the broad family of WGs that have been developed for simulating daily precipitation, two categories of models dominate the literature, which we call the “Richardson” (Richardson and Wright, 1984 ; Richardson, 1981 ) and the “serial” (Racsko et al., 1991;Semenov et al., 1998 ) types. The Richardson-type WG – applied in this study – simulates daily precipitation in two separate steps, the first to simulate rainfall occurrence and the second to estimate the rainfall amount on wet days. With the classical Richardson model, the first step is accomplished using a first-order, two-state Markov chain, which describes the probability of a wet day following a dry day, a wet day following a wet day, etc. The transition probabilities can be estimated from the observed data.
Once a certain day is modeled as wet, an “amounts model” simulates the precipitation amount for that day. Parametric approaches (e.g. Chen et al., 2015 ; Chen and Brissette, 2014 ) use pre-specified functions to approximate the observed precipitation distribution. With non-parametric approaches, the observed precipitation distribution itself is used as the basis for the amounts model. The simplest non-parametric approach is to resample directly from the observed sequence, or from a sub-set of the sequence which represents the “nearest neighbors” with-respect-to weather conditions (e.g. Sharma and Lall, 1999 ). Kernel-density smoothing the observed distribution allows non-parametric methods to generate a continuous distribution of precipitation, and also to generate values higher than observed historically (e.g. Harrold et al., 2003 ; Mehrotra and Sharma, 2007a ). Non-parametric methods allow a WG to generate precipitation sequences that match the observed distribution with arbitrary-high precision, at the cost of introducing arbitrarily-many parameters. Non-parametric methods allow more flexibility for including new forms of conditional dependence; they have the ability to reproduce features such as non-linearity, asymmetry, or multi-modality in observed records (Mehrotra et al., 2006 ); and they do not make any strong assumptions about the precipitation distribution (Mehrotra and Sharma, 2007a ).
Many WGs using Markov-approaches have been found to have 3 partially-related deficiencies: they underestimate the frequency of extended drought periods (Mehrotra and Sharma, 2007a ), they often ignore temporal correlations within wet-spells (Harrold et al., 2003 ), and they underestimate low-frequency (usually described by inter-annual) variability (e.g. Gregory et al., 1993 ; Katz and Zheng, 1999 ; Srikanthan et al., 2005 ). These issues appear to be partially related, as a proportion of low-frequency variability in precipitation can be accounted for by the short-lag correlation (Gregory et al., 1993 ) or by the rainfall occurrence process (Mehrotra and Sharma, 2007a ).
The tendency of purely Markov-based WGs to underestimate inter-annual variability has been attributed to climatic non-stationarities, for example the influence of the El Niño Southern Oscillation (Harrold et al., 2003 ). One way to increase the simulated inter-annual variability is to condition the WG parameters on a physical, slowly-varying index representing atmospheric circulation or SST (Katz and Parlange, 1993 ; Wilby et al., 2002 ). Another method is to use longer-period, aggregated precipitation as the conditioning index, either explicitly (Harrold et al., 2003 ; Mehrotra and Sharma, 2007a ; Mehrotra and Sharma, 2007b ) or via wavelet decomposition (Steinschneider and Brown, 2013 ). Finally, the low-frequency signal can be increased by postulating dependence on a “hidden” index, whose variation must be estimated using iterative methods (Katz and Zheng, 1999 ).
Consecutive days with similar rainfall amounts are often clustered in time, a property which is not represented by two-state Markov chains that distinguish only between dry and wet. This property can be represented using a multi-state Markov chain model that models transitions between different precipitation bands (e.g. Boughton, 1999 ; Gregory et al., 1993 ; Haan et al., 1976 ; Srikanthan and McMahon, 2001 ). The state boundaries can be defined using geometric progression, resulting in increasing class widths (e.g. Haan et al., 1976 ; Srikanthan et al., 2005 ) and a relatively even number observations in each state.
Simulation of catchment runoff often requires multiple precipitation time-series, each representing a different sub-catchment or gauge, with realistic spatial correlations. There are many approaches to generating such series. One is to drive a collection of individual models (representing different locations) with a common “random” number series, which is in-turn derived from an index of larger-scale atmospheric circulation. Another is to feed independent models with serially-independent but spatially correlated random series (Wilks, 1998 ). Finally, it is possible to simulate the catchment-average precipitation as a single time-series (Chen et al., 2012 ), which is the approach used in this study.
This paper introduces a new WG that combines a 10-state, first-order Markov chain and a non-parametric precipitation amounts model. Our innovation is to adopt a doubly-stochastic transition-matrix, rather than manually defining transition thresholds, which gives the model the property that the overall precipitation distribution (defined as including both wet and dry days) is independent of the transition-matrix. The paper first describes the new WG and its implementation for the Torne River catchment in northern Sweden/western Finland. The paper then quantitatively-assesses whether the models performance is an improvement over simpler two-state approaches. The properties assessed are those that are important for hydrological modeling: inter-annual, inter-seasonal and multi-day precipitation distributions; lengths of wet and dry spells; and the variations of precipitation within multi-day events.
2. Site description and data
2.1. The Torne River catchment
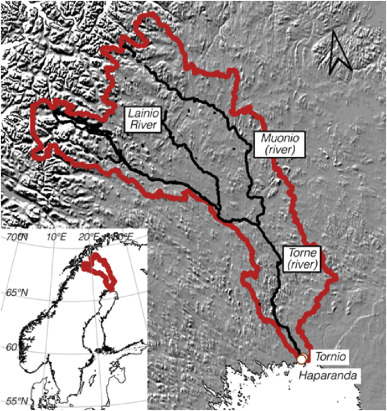
The Torne River catchment (Fig. 1 ) straddles the border of Sweden and Finland and covers 40,157 km2 . The catchment extends from the northern mountains of Sweden and north-western Finnish Lapland, south-east down through marshes and lowlands to the Gulf of Bothnia in the Baltic Sea. The lower reaches of the Torne River comprises the border between Sweden and Finland, with the closely-connected towns of Haparanda (Sweden) and Tornio (Finland) near the river mouth together having around 23,000 inhabitants. The Torne River is essentially unregulated and the catchment is sparely populated. Around half of the catchment area is covered by forest, a fifth is mountains and a tenth is marshland, with some agriculture in the lowlands. For a comprehensive description of the catchment geography, see Bowling et al. (2003) .
|
|
|
Fig. 1. Location and topography of the Torne River catchment (red outline), showing major rivers and settlements. |
Annual average precipitation is 550–600 mm in the lowland areas of the catchment, increasing to 800 mm closer to the Scandinavian mountains and to over 1000 mm in the western highland areas (Asp, 2011 ). The catchment is typically snow-covered October to May, and peak river discharge occurs in May–June (Carlsson, 1999 ).
Beginning in the mid-1980s, the social-disruption and damage caused by spring floods began to receive increasing attention. Flood-levels were particularly high in 1990, but large floods have also occurred in 1615, 1677 and in 1968 (MSB, 2011 ). The most critical situation occurs when thick ice builds in the river mouth, and the ice behaves as a dam behind which water-levels can rise rapidly. A system for forecasts and warnings has now been implemented for Haparanda and Tornio. Haparanda is one of the 18 towns in Sweden designated as having a “significant flood risk” (MSB, 2012 ).
2.2. Precipitation time-series
The preparation of precipitation data for the Torne River basin is described in Asp (2011) . The daily precipitation data used in this paper were provided by the Swedish Meteorological and Hydrological Institute as 49 sub-catchment time-series covering the years 1961–2010. Daily catchment-average precipitation was then calculated as the area-weighted average over the sub-catchments. Annual-mean catchment precipitation is 627 mm (1.7 mm d−1 ), with a standard deviation of 85 mm, with the highest precipitation in summer and the lowest in spring. Although the dry-day fraction (defined as precipitation < 0.1 mm, which is the minimum non-zero value in the provided data) for individual sub-catchments is typically 0.35, the fraction of days for which all 49 sub-catchments have < 0.1 mm is only 0.06.
There is significant temporal auto-correlation within the daily catchment-average time-series, with lag-1 Spearman rank correlation coefficients (after removing the seasonal cycle) of 0.46 for all days and 0.32 for wet-days (precipitation ≥ 0.1 mm). For wet-days, lag-1 and lag-2 autocorrelations are statistically-significant for all months except October; in summer, lag-3 autocorrelations are also statistically-significant. Winter precipitation is closely correlated with the North Atlantic Oscillation (Spearman rank correlation coefficient of 0.56; see also Bartolini et al., 2009 ).
3. Methods
3.1. Development of the WG
3.1.1. Primary considerations
The WG was developed within the framework of the project “Future rainfall and flooding in Sweden: a framework to support climate adaptation actions”. The aim was to develop a compliment to the bias-corrected regional climate model outputs (Yang et al., 2010 ) that are usually used for studies of future runoff in Sweden. The WG model will be also be used to assess uncertainties related to downscaling methods.
We chose to simulate catchment-average precipitation as a single time-series, with a view to subsequent spatial disaggregation to sub-catchment scale. Spatial disaggregation is not covered in this paper. Our choice was partially motivated by a preference for a downscaling framework that was based on GCM outputs: by avoiding regional climate model outputs, we hope to obtain a more holistic assessment of uncertainties in the downscaling process when comparing against methods based on regional model outputs. Given this preference, modeling catchment-averages was a natural choice, because the resolution of GCM outputs is more representative of catchment-scales than sub-catchment scales, and thus modeling catchment-averages avoids a large scale-mismatch. In addition, it is simpler to parameterize the effects of climate change on a single time-series than on multiple, spatially-correlated time-series.
Initial experimentation with two-state WGs for catchment-average precipitation in the Torne River catchment revealed, however, that the models were unable to realistically-simulate multi-day precipitation totals (the two-state models are introduced below, and their performance is documented in Section 4 ). Thus, we decided to explore whether we could develop a multi-state precipitation model that could generate realistic multi-day precipitation totals whilst still being straightforward to modify to represent a changed climate.
3.1.2. Precipitation state model
All of the Richardson-type Markov models for daily occurrence of which we are aware – both two- and multi-state models – have been constructed with “user-defined” states. That is, for a two-state matrix, a threshold state for a wet day is chosen (e.g. 0.1 mm), and then the transition matrix P – defined such that the chance of transitioning from state i to state j is pij – is estimated empirically. That is, suppose that the chance of transitioning from state 1 (dry) to state 2 (wet) was 0.1, and the chance of transitioning from state 2 to state 1 was 0.4, then the matrix would be defined by p11 = 0.9, p12 = 0.1, p21 = 0.4 and p22 = 0.6. The matrix P is then said to be singly (or row) stochastic: the sum of the elements in each row is 1, but the sums of the columns are not 1.
The transition matrix P also defines the overall fraction of wet and dry days. This follows from the general result (e.g. Ching et al., 2013 ) that the steady-state distribution π of an irreducible and aperiodic Markov chain can be calculated as the solution to the equation sets:
|
|
( 1) |
and
|
|
( 2) |
For the two-states example given above, the solution to the above equations is π = [0.8, 0.2]. That is, the fraction of dry days π1 = 0.8 and the fraction of wet days π2 = 0.2.
An alternative strategy is to first specify the length-n vector π. If π is defined such that all elements are equal (πi = πj = 1/n ), then all states will be equally likely in the steady-state distribution. The transition matrix P for such a Markov chain must be doubly-stochastic, i.e., both the rows and the columns of P sum to 1 ( Sinkhorn and Knopp, 1967 ).
To estimate the P for such a system, the observed data must be first classified into groups of equal size, and then the transition matrix can be estimated empirically. An obvious method for defining the groups is to split the data into quantiles, so then P defines the transition probabilities between quantiles. For example, with n = 10, P defines transitions between precipitation deciles.
However, an issue arises immediately when attempting to estimate P using real precipitation data: how to treat transitions to/from days of zero precipitation? For the example above the dry day fraction is 0.8. If we choose n = 10, we cannot say if a dry day belongs to decile 1 or decile 8, and so we are unable to say if transition from a dry day to a highest-decile wet day (j = 10) should be classified as p1,10 , p2,10 , …, or p8,10 .
The solution is to realize that we do not actually need to know the quantile of each dry day; all that is required to create matrix P is to divide the data into groups of equal size. We are free to select any appropriate algorithm for classifying days into particular states. In this study we model area-average precipitation, and the highest monthly dry-day fraction is only 0.16. Thus, we employed the simple expedient of adding a tiny random amount (from 0 to 10−5 mm) to all precipitation values to ensure unique rankings across both wet and dry days. This process allocates dry days randomly and uniformly amongst the lowest deciles; in the example above, with a dry-day fraction is 0.8, the dry days would be distributed evenly between deciles 1 to 8. More elaborate possibilities exist; for example dry days could be ranked according to how long before or after a wet-spell they occurred.
The advantage of using a Markov chain with a doubly-stochastic transition-matrix is that the overall precipitation distribution (defined as including both wet and dry days) is independent of the transition-matrix. This follows because all states are – by definition – equally likely. This property is advantageous when modifying a WG to represent the effects of climate change: changes to the transition matrix will not change the precipitation distribution, provided that the modified matrix remains doubly-stochastic. In contrast, modifying a classical two-state wet/dry transition matrix implicitly changes the overall precipitation distribution, which may then necessitate further correction factors. In addition, there are also (n − 1)2 parameters in a doubly-stochastic matrix, slightly-less than the n (n − 1) parameters in a row-stochastic matrix of the same size.
In practice, transition matrices estimated from empirical data will not be doubly-stochastic to within machine-precision because real data sets have finite length.1 However, it is simple to rescale the matrix to be double-stochastic using the Sinkhorn–Knopp algorithm (Sinkhorn and Knopp, 1967 ; see Knight (2008) for a code fragment).
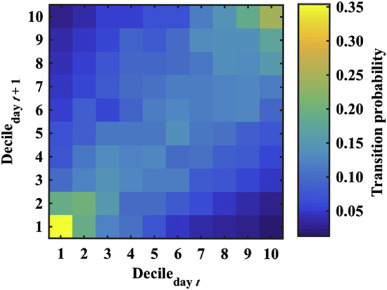
An n = 10 transition matrix was used in this paper, a size selected so that most dry days were allocated to one state. This setup is referred to as the 10-state model. Although transition matrices were calculated independently for each month, they were all quite similar, and the annual-average of the monthly transition matrices (shown in Fig. 2 ) accounted for 71% of the variance in the monthly matrices, with no identifiable patterns in the residuals.
|
|
|
Fig. 2. Annual-average of the monthly catchment-average precipitation transition matrices. The distribution of precipitation amounts is shown in Fig. 3 . |
The serial correlation in the precipitation time-series noted in Section 2.2 is evident in the transition matrix average shown in Fig. 2 . The transition probabilities are not uniform; days with low (first-decile) precipitation are most likely to be followed by first-decile precipitation days, and the same for high (tenth-decile) precipitation days. In general, the probability of transition to a similar decile is larger than for transitions to “more distant” deciles.
3.1.3. Empirical precipitation amounts function
Conversion from precipitation-state to precipitation-amount is straightforward with the double-stochastic matrix. States are converted to a continuous cumulative-frequency value F by adding a uniform random value. Thus, for the 10-state model, state 1 covers the interval [0, 0.1), state 2 covers [0.1, 0.2), etc.
The F values were then converted into precipitation amounts using a “mostly non-parametric” function. A non-parametric approach was chosen as it provides a simple way to obtain a good fit to the observed data. The disadvantages of our non-parametric approach, as compared to a parametric approach, are that the model is over-parameterized and it is difficult to estimate parameter uncertainty. However, these disadvantages are not detrimental to the aims of the current paper.
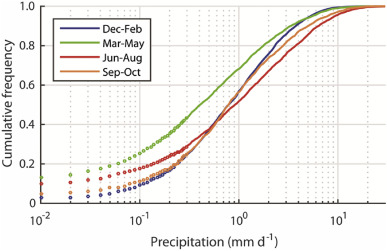
The amounts-function is based on the observed cumulative frequency distribution for 0 < F ≤ 0.995, and an exponential fit to the high-tail of the observations for 0.995 < F < 1. The later provides a convenient extrapolation of the observed cumulative frequency distribution to high F values, and allows extreme precipitation to be represented as a continuous distribution. We do not claim that the underlying distribution for the upper-tail actually follows an exponential distribution rather than, for example, a Pareto distribution ( Lennartsson et al., 2008 ). Rather, it is simply an admission that 50 years of data does not permit determining the shape of the tail of the distribution with any certainty. The choice of tail distribution is not critical for the purposes of this paper, which focuses on how well the new WG represents multi-day precipitation event statistics.
For computational expediency, the precipitation amounts model was implemented by sampling the cumulative frequency distribution as 200 (F , prcp ) pairs. This represents a compromise between a precise representation the observed cumulative frequency distribution and computational efficiency. The sampling covered both the observed and fitted sections of the cumulative frequency distribution. The sampling-intervals were non-linear in both F and prcp . The sampling was initially conducted with fixed intervals in prcp (0.01 mm, 0.02 mm, 0.03 mm, …, 0.19 mm), and thereafter with logarithmic intervals up to 10 times the maximum observed precipitation. In practice, the WG generates F values that are continuous on the interval [0, 1), and these were converted to continuous values of prcp by linearly-interpolating between the two enclosing (F , prcp ) pairs. F values less than F0.01mm were set to give prcp = 0 mm.
This precipitation amounts model, shown graphically in Fig. 3 , is referred to as the “empirical model” in the remainder of this paper.
|
|
|
Fig. 3. The “empirical” precipitation amounts model for the Torne River catchment. The model consists of 200 (F , prcp ) pairs for each month, but here months with similar values have been averaged into seasonal curves for clarity. The first 30 individual (F , prcp ) points are shown for each season, after which the data are plotted as continuous curves. |
3.2. Experimental setup
3.2.1. Alternative models: wet/dry and parametric amounts
In this paper we investigate how well the new 10-state empirical model simulated precipitation for the Torne River catchment, and also investigated whether it had advantages over simpler models.
For the later purposes, a WG with a two-state (wet/dry) Markov chain with a parametric (Gamma distribution) precipitation amounts model was developed. Treating all non-zero precipitation values as “wet” gave a very poor fit to the observed cumulative frequency distribution, and a wet-day threshold of prcp = 0.1 mm (corresponding to F ∼0.15, dependent on month) was found to be appropriate by trial-and-error.
The experimental setup was designed to identify which component of the new WG – the transition model or amounts model – was most important for accurately simulating multi-day precipitation events. Thus, both of the precipitation state models (two-state and 10-state) were paired with both of the precipitation amounts models, as shown in Table 1 . The wet/dry parametric model closely resembles the classical Richardson weather generator, and does not generate precipitation values between 0 mm and 0.1 mm. Despite the name, the wet/dry empirical model can actually generate precipitation values between 0 mm and 0.1 mm, as the F for dry days was selected from the interval [0, F0.1mm ), and precipitation determined from cumulative frequency distribution resampling. For the 10-state parametric model, a day is determined to be dry if F < F0.1mm , and precipitation is set to zero, whereas for wet days, F from the Markov chain is scaled to the cumulative frequency within the wet day fraction, and then the precipitation calculated using the inverse-cumulative-frequency Gamma function.
| Model name | States | Precipitation amounts function |
|---|---|---|
| 10-state empirical | Ten equally-likely | Cfd resampling, 0 ≤ F ≤ 0.995 Exponential, 0.995 < F < 1 |
| Wet/dry empirical | Dry (prcp ≤ 0.1 mm), wet (prcp > 0.1 mm) | Cfd resampling, 0 ≤ F ≤ 0.995 Exponential, 0.995 < F < 1 |
| 10-state parametric | Ten equally-likely | Gamma for prcp > F0.1mm , zero otherwise. |
| Wet/dry parametric | Dry (prcp ≤ 0.1 mm), wet (prcp > 0.1 mm) | Gamma for prcp > 0.1 mm, zero otherwise. |
Note: Cfd represents cumulative frequency distribution.
3.2.2. Calibration and validation
The 50-year observed data record was divided into interleaved calibration (1961, 1963, 1965, …, 2009) and validation (1962, 1964, 1966, …, 2010) datasets to provide a consistency-check on the model formulation and calibration. The WGs' parameters were determined using the calibration dataset, and the tables and figures presented in this paper generally show both calibration and validation datasets and the model results. Note that, with interleaved calibration/validation data, the validation results cannot be interpreted as an estimate of how accurately the model might represent an independent (future) period. This is especially so for the Torne River catchment, because the observed dataset contains statistically-significant precipitation trends. The issue of deriving a method to calibrate the model that incorporates such trends is inseparable from the issue of incorporating the effects of global climate change into the model. We defer this issue to a future study. Note also that the observed annual precipitation time-series do not show serial correlation.
The WG models each ran 200 times to quantify the range of random variability, with each run simulating the entire 50-year record.
3.3. Statistical measures
The two-sample Kolmogorov–Smirnov test statistic was used to quantify differences between observed and simulated precipitation distributions, both for single and multi-day distributions. The test statistic is calculated following Conover (1999) :
|
|
( 3) |
where n is the sample size, F1,n and F2,n are the empirical cumulative frequency functions for the observed and simulated samples, respectively, over all values of precipitation x . ks = 0 would indicate a perfect match between the cumulative frequency curve of a model and the observations; ks = 1 would indicate that the ranges of modeled and observed distributions do not overlap. Note that the ks statistic is always positive, so the median ks for the model runs indicates the typical maximum differences between the distributions; it does not indicate whether the models “over-estimate” or “under-estimate” the distribution. When calculating the ks test statistics for the parametric models (which cannot simulate daily precipitation between 0 mm and 0.1 mm, by definition), observed precipitation values < 0.1 mm were also set to zero.
Throughout this paper, the 95% confidence intervals displayed for model simulations were estimated from the 95th-percentile-range of the 200 model runs. The 95% confidence intervals for the annual and seasonal means and standard deviations of the calibration and validation datasets in Table 2 and Table 3 were obtained by fitting normal distributions to the data.
| Precipitation | Mean (mm per year) | Standard deviation (mm per year) |
|---|---|---|
| Observations, calibration | 643 ± 31 | 76 ± 23 |
| Observations, validation | 611 ± 38 | 92 ± 28 |
| 10-state empirical | 646 ± 19 | 71 ± 13 |
| Wet/dry empirical | 645 ± 14 | 54 ± 10 |
| 10-state parametric | 642 ± 17 | 64 ± 12 |
| Wet/dry parametric | 641 ± 14 | 48 ± 10 |
| Observation/model | Precipitation mean (mm) | Precipitation standard-deviation (mm) | ||||||
|---|---|---|---|---|---|---|---|---|
| Winter | Spring | Summer | Fall | Winter | Spring | Summer | Fall | |
| Observations (1961–2012) | 109 ± 8 | 219 ± 16 | 170 ± 9 | 129 ± 9 | 32 ± 7 | 28 ± 6 | 58 ± 12 | 32 ± 7 |
| 10-state empirical | 117 ± 8 | 223 ± 11 | 174 ± 10 | 131 ± 6 | 23 ± 5 | 28 ± 5 | 50 ± 9 | 34 ± 8 |
| Wet/dry empirical | 117 ± 6 | 222 ± 10 | 174 ± 7 | 131 ± 5 | 18 ± 4 | 22 ± 5 | 37 ± 7 | 27 ± 5 |
| 10-state parametric | 116 ± 6 | 222 ± 13 | 173 ± 8 | 130 ± 5 | 21 ± 5 | 25 ± 6 | 45 ± 9 | 30 ± 5 |
| Wet/dry parametric | 117 ± 6 | 221 ± 10 | 174 ± 6 | 131 ± 4 | 16 ± 3 | 19 ± 4 | 33 ± 6 | 23 ± 4 |
4. Results
4.1. Annual averages and annual cycle
All models reproduced the observed annual-average precipitation from the calibration dataset almost exactly (Table 2 ). The differences between the calibration and modeled means were much less than between the calibration and validation means, and can therefore be considered insignificant.
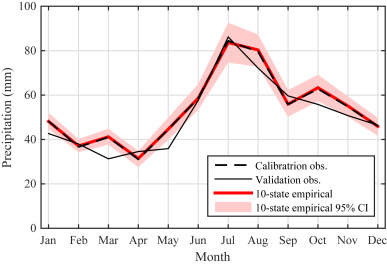
All the models also accurately-reproduced the annual cycle in precipitation of the calibration dataset (Fig. 4 ). The results for the 10-state empirical model are shown in Fig. 4 , but results for the other models were very similar.
|
|
|
Fig. 4. Annual cycle for precipitation simulated by the 10-state empirical model. Note the calibration observations (dashed black line) and the mean of the 200 model runs (solid red line) are essentially identical. Shading indicates 95th percentile range of 200 model runs. |
4.2. Interannual variability
The interannual variability in the annual precipitation – as characterized by the standard deviation in annual totals – is under-estimated by all the models (Table 2 ). The best-performing model is the 10-state empirical model, for which the standard deviation is 71 mm per year, which compares reasonably with (76 ± 23) mm per year for the calibration dataset. However, the standard deviation in the validation dataset is (92 ± 28) mm per year. A test in which the models were calibrated with the validation years gave modeled standard deviations very similar to Table 2 , suggesting that the underestimation of interannual variability is an inherent property of the model, rather than a calibration effect. Further tests in which daily extreme precipitation (defined as F values exceeding 0.9 to 0.999, depending on the test) were removed prior to model calibration reduced the standard deviation for observed and modeled datasets by similar fractions, demonstrating that this deficiency is not caused by approximating the tail of the observed precipitation distribution with an exponential function.
The average seasonal totals and their interannual variability are shown in Table 3 . Note that the values for the observations were calculated over the entire (1961–2012) dataset, as otherwise the calibration/validation scheme splits the winter season. The 10-state empirical model underestimates the standard deviation in winter and summer precipitation, but values for spring and fall seasons are reasonable. Again, interannual variation in the other models is too low, and the wet/dry models' performance is worst.
4.3. Cumulative multi-day precipitation distributions
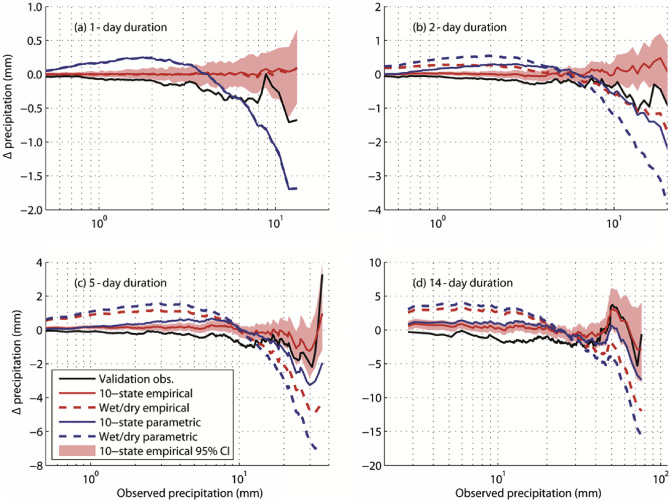
The most important aspect of the current study was to determine whether the new WG generated realistic multi-day (2- to 14-day) accumulated precipitation. Quantile–quantile residual plots (see Cox, 2007 ) for block-sum 1-, 2-, 5- and 14-day precipitation are shown in Fig. 5 . Quantile–quantile residual plots show residuals after subtracting the 1:1 line from a regular quantile–quantile plot: for two perfectly-matched distributions, the residuals would be a horizontal line at 0 mm. The results are further summarized as Kolmogorov–Smirnov (ks ) statistics in Table 4 .
|
|
|
Fig. 5. Quantile–quantile residuals for (a) 1-day, (b) block-sum 2-day, (c) 5-day, and (d) 14-day precipitation. The horizontal axes describe quantiles 0.01–0.99 of the calibration observations, and the vertical axis the difference with the matching quantile from the model simulations or validation observations. Shading shows the 95th percentile range from the 10-state empirical model runs; the ranges for the other models are similar, and are omitted for clarity. Note the changes in vertical and horizontal scales from (a) to (d). |
| Observation/model | Duration | |||
|---|---|---|---|---|
| 1-day | 2-day | 5-day | 14-day | |
| Validation observations | 0.02 | 0.03 | 0.04 | 0.07 |
| 10-state empirical model | 0.01 | 0.01 | 0.02 | 0.03 |
| Wet-dry empirical model | 0.01 | 0.06 | 0.10 | 0.10 |
| 10-state parametric model | 0.04 | 0.04 | 0.05 | 0.05 |
| Wet-dry parametric model | 0.04 | 0.10 | 0.13 | 0.12 |
Fig. 5 shows that the residuals for the 10-state empirical model do not deviate significantly from zero, and this is clearly the best-performing model in the experiment. Similarly, the ks statistics ( Table 4 ) show the 10-state empirical model has the lowest value for all precipitation durations. All other models generally overestimate low-precipitation totals (positive anomalies in Fig. 5 ) and underestimate high totals (negative anomalies), with two exceptions. Of these, the wet-dry empirical model simulates 1-day precipitation precisely, which occurs almost by definition. More surprisingly, the 10-state parametric model simulates of the 14-day precipitation distribution relatively accurately.
Curiously, the 10-state model matches the validation observations more closely than the calibration observations for higher-quantile 5-day and 14-day duration precipitation. A test in which the model was calibrated using the validation observations yielded much smaller residuals for higher-quantile accumulated precipitation, suggesting that this pattern is a feature of the model construction, rather than of calibration.
4.4. Average lengths of wet and dry spells
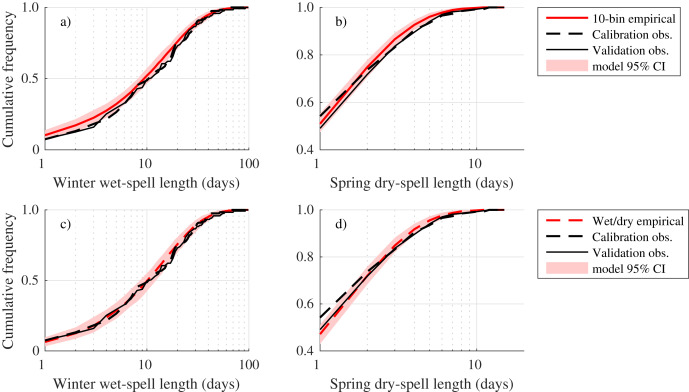
The average lengths of wet and dry spells vary over the course of the year, with the longest wet spells occurring in winter while the longest dry spells are in spring. The distributions of winter wet-spell lengths and spring dry-spell lengths are shown in Fig. 6 . Note that the average durations of wet-spells (defined as catchment-average prcp > 0.1 mm) are longer for the catchment as a whole than for individual stations within the catchment.
|
|
|
Fig. 6. Cumulative probability that a winter wet-spell (a, c) or a spring dry-spell (b, d) has a given duration. Top row (a, b) the 10-bin empirical model, and bottom row (c, d) the wet/dry empirical model. Shading indicates 95th-percentile-ranges calculated from 200 model runs. |
The observed distributions of wet- and dry-spells lay generally-within the 95% confidence bands of the models. The 10-state models slightly overestimate the number of shorter wet-spells, and both models slightly overestimate the number of longer dry-spells, but neither model performs remarkably better than the other. The results for the 10-state empirical and 10-state parametric models were indistinguishable, as were the results for the wet/dry empirical and wet/dry parametric models.
4.5. Distribution of precipitation amounts for isolated wet days and during wet spells
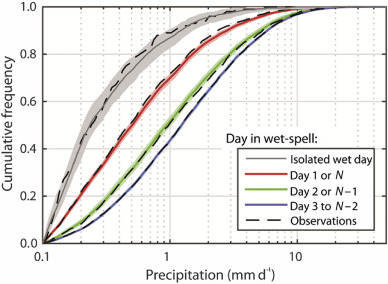
The distribution of observed precipitation on wet (prep > 0.1 mm) days in the catchment depends on the placing of a wet day within a wet-spell. This is shown graphically in Fig. 7 . Isolated wet days (grey line) have lower precipitation than the first or last day of a multi-day wet-spell (red line), which in-turn have lower precipitation than the second or second-last days of wet-spells (green line) or the remaining days in the middle of 5-day-or-longer wet-spells (blue line). This result holds for both the observations and the 10-state empirical model simulations. Note that further subdivision of the day 3 to day N ‒2 (blue curve) data did not yield a further distinct distribution. Although Fig. 7 contains data from all seasons, similar results were obtained for each season separately. The results from the 10-state parametric model (not shown) were similar to the 10-state empirical model, although the model curves were further from the calibration data curves. The wet/dry models cannot (by definition) generate different precipitation distributions for different placements within a wet-spell, and so are unable to replicate this feature of the precipitation time-series.
|
|
|
Fig. 7. Cumulative frequency distributions for days classed according to their position in a wet-spell of length N . Days are classed as: (grey) isolated wet days; (red) the first (day 1) or last (day N ) day of a wet-spell; (green) second (day 2) or second-last (N –1) day; (blue) all other days (day 3 to N –2). Solid lines show median of the 10-state empirical model runs; shading indicates the 95th percentile range; calibration observations shown as dashed lines. |
5. Discussion
Our results showed that the new multi-state empirical WG could realistically represent both accumulated 2- to 14-day precipitation distributions and the way that the distribution of daily precipitation changes according to the placement of a wet day within a wet-spell in the Torne River catchment. However, the model underestimated inter-annual and inter-seasonal variance. This suggests that the multi-state model is a promising candidate for hydrological applications in the Torne River catchment, but that further development will be required.
5.1. Simulation of multi-day precipitation and wet-spells
For the purposes of flood-simulation, the ability to accurately simulate the distribution of accumulated, multi-day precipitation is a primary consideration. The empirical amounts-model (paired with either a 10-state or wet/dry transition matrix) represents the observed 1-day precipitation distribution better than the parametric amounts-model. This is not surprising, however, as the empirical amounts-model uses 200 parameters and is intended as a proxy for “perfect knowledge” of the 1-day precipitation distribution.
For multi-day precipitation, however, it is the transition model, rather than the amounts model, which most affects the models' performances. The precipitation distributions simulated by wet/dry models increasingly deviate from the observed distribution as accumulation period increases, such that they overestimate low-precipitation totals and underestimating high totals. In contrast, the 10-state parametric model simulates 14-day totals almost as well as the 10-state empirical model. That is, for accumulated precipitation, the 10-state transition model paired with a very simple amounts model (a Gamma distribution) performed better than a wet/dry transition model paired with an empirical amounts model, even though the latter represents “perfect knowledge” of the daily precipitation distribution.
5.2. Distribution of wet- and dry-spell lengths
The analysis of wet- and dry-spell lengths found that neither the 10-state nor the wet–dry transition model gave obviously-better simulations. This is perhaps surprising, given that the wet/dry model was calibrated using a threshold of 0.1 mm to define the transition matrix, and the same threshold was used for calculating wet- and dry-spell lengths. In contrast, 0.1 mm does not correspond to any specific transition-threshold in the 10-state model.
5.3. Precipitation distribution during wet-spells
That the distribution of precipitation is different for isolated wet-days, and differs within wet-spells, has been observed before (see Section 1 ). Reproducing this behavior is certainly desirable for hydrological modeling, and our results show that a multi-state model offers a method for representing this phenomenon. What is surprising in this study is that model matches the observations so well, given that this phenomenon was not explicitly included in the model calibration.
The differences between precipitation on isolated wet-days, days at the beginning or end of wet-spells, and days in the middle of wet-spells, have previously been attributed to observational procedures (Harrold et al. (2003) and references therein); because precipitation is measured over fixed 24-hour periods, first/last days should be thought of as only “partially wet”. But we also found differences between the second and third days of 5-day-or-longer wet-spells. A physical explanation for these differences is less obvious. A direct causal relationship (i.e. heavy precipitation on a given day physically contributes to heavy precipitation on a subsequent day, presumably via enhanced evaporation) seems unlikely in northern Sweden, especially during winter. A 5-day wet-spell usually represents the passage of a series of frontal or convective systems, so the enhanced precipitation towards the middle of the wet-spells is presumably related to larger-scale circulation features such as atmospheric blocking systems.
5.4. Interannual variability
High flows in the Torne River occur when heavy precipitation accompanies a rapid melt of the winter snow-pack. Thus, the ability to simulate interannual variability (i.e. the accumulation of above-average snow depth) is an important consideration. The 10-state empirical model underestimates interannual variability, with the worst statistics for summer and winter seasons.
The winter interannual variance in the observed data (32 ± 7) mm vs. (22 ± 4) mm in the 10-state empirical model, is associated with the influence of the NAO (Bartolini et al., 2009 ). A rough-estimate of the contribution of the NAO to interannual winter precipitation in the catchment can be obtained using simple linear regression; after subtracting the influence of the NAO, the standard-deviation of the residuals reduces to (26 ± 11) mm in winter, which is within the 95% confidence interval of the models winter standard-deviation. We note, however, that some of the interannual variability associated with the NAO has already been implicitly subsumed into the models transition matrices; a fair comparison would require subtracting the influence of the NAO from both the observations and from the model. For the latter, of course, this is not possible.
The drivers of inter-annual summer precipitation variability in Europe are not as well-understood as for winter (Zveryaev and Allan, 2010 ). However, the Scandinavian (“Eurasia-1”) index of Barnston and Livezey (1987) and the Summer NAO (e.g. Folland et al., 2009 ) index have statistically-significant correlations with summer precipitation. The Scandinavian teleconnection pattern, defined using 500 hPa heights, has one action center over Scandinavia, and action-centers with opposite sign over the northeastern Atlantic and Siberia (see Bueh and Nakamura, 2007 ). Both these indices are associated with changes in storm-track density and blocking frequency (Dong et al., 2013 ). A statistically-significant correlation was found between summer precipitation in the Torne River catchment and the Scandinavian index (Spearman correlation coefficient = −0.32), but not with Summer NAO (correlation coefficient = −0.23). Removing the influence of the Scandinavian index on summer precipitation by linear regression, as above, yielded a series with standard deviation of (54 ± 11) mm. This is still higher than the 10-state empirical models standard deviation of (49 ± 10) mm in summer, but is within the 95% confidence interval.
6. Further work
We identify 3 lines of work that we believe need to be undertaken to confirm that the 10-state model is suitable for hydrological simulations, and two important extensions.
6.1. Improve interannual variance
The multi-state empirical WG model clearly needs to be further developed so it can reproduce observed interannual variability. As discussed in the Introduction, many methods have been proposed in the literature for conditioning WGs to show realistic low-frequency variability. However, these might not be suitable. The most attractive feature of the multi-state empirical model, for climate change impact studies, is that the daily precipitation distribution and transition behaviors can be modeled and modified independently. Thus, the challenge is to introduce low-frequency variability in such a way that it, too, can be modeled and modified independently. This is not merely a desire for computational elegance: Steinschneider and Brown (2013) found, in their study of the Connecticut River catchment, that GCMs simulated an increase in annual mean precipitation with very little change in interannual standard deviation.
Within the current modeling framework, a pragmatic approach could be to modulate the random sequence used to convert precipitation state (i.e. decile) into a cumulative-frequency value F . We have conducted a simple test to demonstrate that this technique can inflate the modeled interannual variability sufficiently to match the observed. In the test, the WG algorithm was modified so that F values for odd years were selected from the lower half of each decile, and F values for even years were selected from the upper half. The result doubled the standard-deviation in modeled annual-average precipitation. Even so, the overall precipitation distribution and transition matrices in the WG output match those of the original dataset.
6.2. Reducing the number of model parameters
Another line of future work would be to reduce number of model parameters. Thus far, we have not made any systematic study of how many states a transition matrix needs in order to give an acceptable simulation of multi-day precipitation. But there are other options for reducing the number of model parameters, too.
The results from this study suggest that even a simple Gamma distribution, when paired with the 10-state transition model, can represent multi-day accumulated precipitation well. This suggests a simple way to reduce the number of model parameters would be to adopt a parametric amounts-model, presumably a mixed-model so that extremes are accurately represented. Alternatively, the non-parametric amounts-model could be retained, but the 200-point sampling scheme used to represent the daily precipitation distribution replaced with a series of splines.
In the present study, the transition matrices were derived completely-independently for each month, but the inter-monthly differences were relatively small. Thus, another option for reducing the number of model parameters would be to use the average annual transition matrix, or at least to approximate the monthly transition matrices as linear combinations of the annual matrix and a small set of modifier matrices. We note that some scheme for allowing seasonal variation should be retained to facilitate incorporating seasonally-distinct climate-change signals into the transition probabilities in future studies.
6.3. Compare with dynamical downscaling approaches
Global climate models provide information about how the future climate will evolve under enhanced-greenhouse conditions. Because GCM-outputs typically have a horizontal resolution of 100–200 km, their outputs are downscaled in regional climate models (RCMs) to produce climate time-series with higher spatial-resolution (12–50 km) over a limited area. Even the outputs from RCMs, however, show biases compared to present-day local climate conditions (Kotlarski et al., 2005 ). The Swedish Meteorological and Hydrological Institute has developed bias-correction techniques that adjust RCM outputs so that they have a similar statistical distribution to observed climate time-series (Yang et al., 2010 ). Such adjustments are then applied to RCM outputs for future periods, using climate change simulations from the ENSEMBLES project (van der Linden and Mitchell, 2009 ). These methods will be used to generate local climate time-series that can be compared with the stochastic model results presented in this paper.
6.4. Evaluate the model using other river basins
This study is exclusively concerned with the Torne River catchment in northern Sweden/western Finland. In order to be useful to the wider community, the model will need to be calibrated and evaluated for other river basins.
6.5. Generation of complimentary temperature time-series
Hydrological models usually require more meteorological inputs than simply precipitation. Temperature is particularly important, both for simulating snow-accumulation in high-latitude or alpine catchments, and as a component of simulating evapotranspiration during the growing season. Thus, the model will need to be extended to simulate temperature time-series that are consistent with the precipitation time-series before it can be useful for hydrological purposes.
7. Conclusions
Modeling catchment-average precipitation is a reasonable choice for studies that will characterize the effect of climate change using global climate model outputs, as it avoids the large scale-mismatch between global climate model and sub-catchment scale. However, modeling catchment-average precipitation in the Torne River catchment using a two-state (wet/dry) Markov chain did not simulate the multi-day precipitation distribution well, nor the variation in the distribution of daily precipitation within wet-spells.
In this paper, we introduced a new multi-state WG for catchment-average daily precipitation. The new WG uses a doubly-stochastic transition-matrix, which has the property that the overall precipitation distribution (including both wet and dry days) and the temporal-correlation can be modified independently in climate change studies.
The new WG successfully simulated the distribution of accumulated, multi-day precipitation in the catchment, which is a primary consideration for the purposes of flood-simulation. However, the ability to simulate interannual and seasonal variability is also an important consideration, and the model does not perform well in this regard.
Thus, we conclude that the multi-state model is a promising candidate for hydrological applications. However, further development is required to improve the simulation of interannual variation, and evaluation using other river basins is also required.
Acknowledgments
Financial support for this study by the Swedish Civil Contingencies Agency (2011-3778 ), though the project “Future rainfall and flooding in Sweden: a framework to support climate adaptation actions”, is gratefully acknowledged.
References
- Asp, 2011 S.-S. Asp; Sammanställning kalibrering och dimensionering av Torneälven samt Tärendöälven 2009–2011; (2011) Norrköping (in Swedish)
- Barnston and Livezey, 1987 A. Barnston, R. Livezey; Classification, seasonality and persistence of low-frequency atmospheric circulation patterns; Mon. Weather Rev., 115 (1987), pp. 1083–1126
- Bartolini et al., 2009 E. Bartolini, P. Claps, P. D'Odorico; Interannual variability of winter precipitation in the European Alps: relations with the North Atlantic oscillation; Hydrol. Earth Syst. Sci., 13 (2009), pp. 17–25
- Boughton, 1999 W.C. Boughton; A Daily Rainfall Generating Model for Water Yield and Flood Studies 99/9; Cooperative Research Centre for Catchment Hydrology, Canberra (1999)
- Bowling et al., 2003 L.C. Bowling, D.P. Lettenmaier, B. Nijssen, et al.; Simulation of high-latitude hydrological processes in the Torne–Kalix basin: PILPS Phase 2(e); Glob. Planet. Change, 38 (2003), pp. 1–30
- Bueh and Nakamura, 2007 C. Bueh, H. Nakamura; Scandinavian pattern and its climatic impact; Q. J. R. Meteorol. Soc., 133 (2007), pp. 2117–2131
- Carlsson, 1999 B. Carlsson; Some facts about the Torne and Kalix River basins: a contribution to the NEWBALTIC II workshop in Abisko, June 1999; SMHI Hydrol., 80 (1999)
- Chen et al., 2015 D. Chen, C. Achberger, T. Ou, et al.; Projecting future local precipitation and its extremes for Sweden; Geogr. Ann. Ser. A, Phys. Geogr., 97 (2015), pp. 25–39
- Chen and Brissette, 2014 J. Chen, F. Brissette; Stochastic generation of daily precipitation amounts: review and evaluation of different models; Clim. Res., 59 (2014), pp. 189–206
- Chen et al., 2012 J. Chen, F. Brissette, R. Leconte; Downscaling of weather generator parameters to quantify hydrological impacts of climate change; Clim. Res., 51 (2012), pp. 185–200
- Ching et al., 2013 W.-K. Ching, X. Huang, M.K. Ng, et al.; Markov Chains; International Series in Operations Research & Management ScienceSpringer US, Boston, MA (2013) http://dx.doi.org/10.1007/978-1-4614-6312-2
- Conover, 1999 W.J. Conover; Practical Nonparametric Statistics; (third ed.)Wiley, New York (1999)
- Cox, 2007 N.J. Cox; Stata tip 47: quantile-quantile plots without programming; Stata J., 7 (2007), pp. 275–279
- Dong et al., 2013 B. Dong, R.T. Sutton, T. Woollings, et al.; Variability of the North Atlantic summer storm track: mechanisms and impacts on European climate; Environ. Res. Lett., 8 (2013), Article 034037
- Folland et al., 2009 C.K. Folland, J. Knight, H.W. Linderholm, et al.; The summer North Atlantic Oscillation: past, present, and future; J. Clim., 22 (2009), pp. 1082–1103
- Gregory et al., 1993 J. Gregory, T. Wigley, P. Jones; Application of Markov models to area-average daily precipitation series and interannual variability in seasonal totals; Clim. Dyn., 8 (1993), pp. 299–310
- Haan et al., 1976 C. Haan, D. Allen, J. Street; A Markov chain model of daily rainfall; Water Resour. Res., 12 (1976), pp. 443–449
- Harrold et al., 2003 T.I. Harrold, A. Sharma, S.J. Sheather; A nonparametric model for stochastic generation of daily rainfall amounts; Water Resour. Res., 39 (2003) SWC 8-1–8–12
- Jones et al., 2011 P.D. Jones, C. Harpham, Goodess, et al.; Perturbing a weather generator using change factors derived from regional climate model simulations; Nonlinear Process. Geophys., 18 (2011), pp. 503–511
- Katz and Parlange, 1993 R.W. Katz, M.B. Parlange; Effects of an index of atmospheric circulation on stochastic properties of precipitation; Water Resour. Res., 29 (1993), pp. 2335–2344
- Katz and Zheng, 1999 R.W. Katz, X. Zheng; Mixture model for overdispersion of precipitation; J. Clim., 12 (1999), pp. 2528–2537
- Kilsby et al., 2007 C.G. Kilsby, P.D. Jones, A. Burton, et al.; A daily weather generator for use in climate change studies; Environ. Model. Softw., 22 (2007), pp. 1705–1719
- Knight, 2008 P.A. Knight; The Sinkhorn–Knopp algorithm: convergence and applications; SIAM J. Matrix Anal. Appl., 30 (2008), pp. 261–275
- Kotlarski et al., 2005 S. Kotlarski, A. Block, U. Böhm, et al.; Regional climate model simulations as input for hydrological applications: evaluation of uncertainties; Adv. Geosci., 5 (2005), pp. 119–125
- Lennartsson et al., 2008 J. Lennartsson, A. Baxevani, D. Chen; Modelling precipitation in Sweden using multiple step markov chains and a composite model; J. Hydrol., 363 (2008), pp. 42–59
- Mehrotra and Sharma, 2007a R. Mehrotra, A. Sharma; A semi-parametric model for stochastic generation of multi-site daily rainfall exhibiting low-frequency variability; J. Hydrol., 335 (2007), pp. 180–193
- Mehrotra and Sharma, 2007b R. Mehrotra, A. Sharma; Preserving low-frequency variability in generated daily rainfall sequences; J. Hydrol., 345 (2007), pp. 102–120
- Mehrotra et al., 2006 R. Mehrotra, R. Srikanthan, A. Sharma; A comparison of three stochastic multi-site precipitation occurrence generators; J. Hydrol., 331 (2006), pp. 280–292
- MSB, 2011 MSB; Seminarium och beredskapsövning Torne älv: Utvärderingsrapport; (2011) (in Swedish)
- MSB, 2012 MSB; Översvämningsförordningen – Sveriges genomförande av översvämningsdirektivet; (2012) Karlstad (in Swedish)
- Racsko et al., 1991 P. Racsko, L. Szeidl, M. Semenov; A serial approach to local stochastic weather models; Ecol. Modell., 57 (1991), pp. 27–41
- Richardson, 1981 C.W. Richardson; Stochastic simulation of daily precipitation, temperature, and solar radiation; Water Resour. Res., 17 (1981), pp. 182–190
- Richardson and Wright, 1984 C.W. Richardson, D.A. Wright; WGEN: A Model for Generating Daily Weather Variables; United States Department of Agriculture ARS-8 (1984)
- Semenov et al., 1998 M.A. Semenov, R.J. Brooks, E.M. Barrow, et al.; Comparison of the WGEN and LARS-WG stochastic weather generators for diverse climates; Clim. Res., 10 (2) (1998), pp. 95–107
- Sharma and Lall, 1999 A. Sharma, U. Lall; A nonparametric approach for daily rainfall simulation; Math. Comput. Simul., 48 (1999), pp. 361–371
- Sinkhorn and Knopp, 1967 R. Sinkhorn, P. Knopp; Concerning nonnegative matrices and doubly stochastic matrices; Pac. J. Math., 21 (1967), pp. 343–348
- Srikanthan and McMahon, 2001 R. Srikanthan, T.A. McMahon; Stochastic generation of annual, monthly and daily climate data: a review; Hydrol. Earth Syst. Sci., 5 (2001), pp. 653–670
- Srikanthan et al., 2005 R. Srikanthan, T.I. Harrold, A. Sharma, et al.; Comparison of two approaches for generation of daily rainfall data; Stoch. Environ. Res. Risk Assess., 19 (2005), pp. 215–226
- Steinschneider and Brown, 2013 S. Steinschneider, C. Brown; A semiparametric multivariate, multisite weather generator with low-frequency variability for use in climate risk assessments; Water Resour. Res., 49 (2013), pp. 7205–7220
- van der Linden and Mitchell, 2009 P. van der Linden, J.F.B. Mitchell; ENSEMBLES: Climate Change and its Impacts: Summary of Research and Results from the ENSEMBLES Project; Met Office Hadley Centre, Exeter, UK (2009)
- Wilby et al., 2002 R.L. Wilby, D. Conway, P.D. Jones; Prospects for downscaling seasonal precipitation variability using conditioned weather generator parameters; Hydrol. Process., 16 (2002), pp. 1215–1234
- Wilks, 1998 D.S. Wilks; Multisite generalization of a daily stochastic precipitation generation model; J. Hydrol., 210 (1998), pp. 178–191
- Wilks, 2010 D.S. Wilks; Use of stochastic weather generators for precipitation downscaling; Wiley Interdiscip. Rev. Clim. Chang., 1 (2010), pp. 898–907 http://dx.doi.org/10.1002/wcc.85
- Wilks and Wilby, 1999 D.S. Wilks, R.L. Wilby; The weather generation game: a review of stochastic weather models; Prog. Phys. Geogr., 23 (1999), pp. 329–357
- Yang et al., 2010 W. Yang, J. Andréasson, L. Phil Graham, et al.; Distribution-based scaling to improve usability of regional climate model projections for hydrological climate change impacts studies; Hydrol. Res., 41 (2010), pp. 211–229
- Zveryaev and Allan, 2010 I.I. Zveryaev, R.P. Allan; Summertime precipitation variability over Europe and its links to atmospheric dynamics and evaporation; J. Geophys. Res., 115 (2010), p. D12102
Notes
1. Dividing a dataset into n states, each with m observations, yields only (n × m –1) transitions.
Document information
Published on 15/05/17
Submitted on 15/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?