Implementation of fractional order integrator/differentiator on field programmable gate array

Abstract

Concept of fractional order calculus is as old as the regular calculus. With the advent of high speed and cost effective computing power, now it is possible to model the real world control and signal processing problems using fractional order calculus. For the past two decades, applications of fractional order calculus, in system modeling, control and signal processing, have grown rapidly. This paper presents a systematic procedure for hardware implementation of the basic operators of fractional calculus i.e. fractional integrator and derivative, using Grünwald–Letnikov definition, on field programmable gate array (FPGA) in LabVIEW environment. The simulation and hardware implementation results for fractional order integrator and derivative of sinusoid and square waveform signals for some selected fractional orders have been presented. A close agreement between the simulated and the experimental results demonstrated the suitability of FPGA device in fractional order control and signal processing applications. LabVIEW being one of the finest tools for measurement and control, and signal processing applications the fractional order operator implementation is expected to further enhance the capability of the tool to cater to the needs of advanced experimental research employing fractional order operators.

Keywords

Fractional order integrator; Fractional order differentiator; FPGA; Virtual instrumentation

1. Introduction

In recent years, fixed-point operations have been used for hardware implementations to save costs at the enhanced computational speed. Field programmable gate array (FPGA) is one such device. Because of their enormous advantages, there is an increasing trend in the use of FPGA devices as real time hardware targets in industry. FPGA finds potential applications in various domains such as real time measurement and control, signal processing and digital communication. These are reconfigurable real time devices available at relatively low costs. On a FPGA device, all of the logic gets implemented in digital hardware alone thus yielding very high processing speed. Modern day FPGAs have clock rates in the range of several MHz and also allow the user to set precise bit settings for accurate computations in addition to the effective memory usage. Additionally, each independent task can utilize a different set of logic on the same FPGA hardware allowing multiple tasks to run simultaneously in contrast to microprocessors. Overall, FPGAs are perfectly suitable for applications in time-critical systems. On the other hand, the disadvantage of FPGAs is that the hardware resources are limited and design requires lots of careful considerations of the precisions required, with specific planning for each individual application. An excellent review of FPGA technologies and their contribution to industrial control applications has been presented in [1]. Various potential application areas were addressed which can exploit the advantages of FPGAs. Benefits of using FPGAs in the case of control applications are then exhibited and supported with case studies of artificial neural networks based control system designs targeting FPGAs.

Fractional calculus has been a topic of theoretical research for scientists and engineers for a very long time. In the past two decades, several potential applications of fractional order calculus have been developed. One of the areas where fractional calculus has been found to be very useful is system modeling. As real objects are generally fractional, system modeling using fractional calculus is much more accurate as compared to the integer order modeling. In a recent work on fractional order modeling, a fractional derivative model was selected to describe the arterial wall mechanics in vivo. The fractional derivative model proved to naturally mimic the elastic modulus spectrum with only four parameters and a reasonable small computational effort [2]. In another work, a nonlinear fractional order model for steer by wire system was presented. Validation of the proposed approach was done in simulation. As reported, this method is very useful in design of a robust controller for steer by wire systems [3]. Fractional order model of Permanent Magnet Synchronous Motor (PMSM) has been proposed in [4]. Simulation and experimental comparisons between the fractional order and the integer order model of PMSM were presented to show the existence of fractional order model on the PMSM speed servo system.

Process control is another area where fractional order control is being sought as an improvement over conventional control. In the conventional PID controller, integral term eliminates the steady-state error but decreases the relative stability of the system and makes it sluggish as well. Derivative term increases the relative stability and makes the system much faster while compromising the sensitivity to noise. Fractional order control, which involves the use of fractional integrals and derivatives instead of classical integer order integral and derivative terms, is able to achieve satisfactory compromises between the above stated positive and negative effects of conventional PID control. Thus, instead of pure integral ${\textstyle \left({\frac {1}{s}}\right)}$ or pure derivative (s) term, fractional integral/derivative term was used i.e., s^γ (γ ∈ R+). [5]. In [6], a fractional order PID controller was investigated in simulation for a position servomechanism control system considering actuator saturation and the shaft tensional flexibility. This work claimed that if fractional order PID controller is properly designed and implemented, it will outperform the conventional integer order PID controller. Another such work presents a strategy to tune a fractional order integral and derivative controller satisfying gain and phase margins. This work aimed to apply the tuning procedure proposed to temperature control at selected points in M/S Quanser’s heat flow experimental platform. The effectiveness and validity of the technique was experimentally illustrated by comparison with the traditional PI/PID controller based on Ziegler Nichol’s tuning method [7]. In [8], explicit analytical expressions for step and impulse responses of a linear fractional-order system with fractional-order controller for open and closed loop were presented. Superiority of the fractional order control over the convention one was demonstrated with the help of an example. A fractional order controller was proposed for a class of fractional order system and a tuning procedure was developed [9]. In the same direction, an intelligent robust fractional surface sliding mode control is proposed for a nonlinear system [10]. A recent research on intelligent fractional order control proposed a novel fractional order fuzzy PID controller. Closed loop performances and controller efforts in the presented cases were compared with conventional PID, fuzzy PID and PI^λD^μ controller subjected to different performance indices in simulation. As reported, the fractional order fuzzy PID controller outperformed the others in most cases [11]. Several other recent interesting works on the applications of fractional order control are automatic voltage regulator [12], oscillatory fractional order processes with dead time [13], robotic manipulator [14], binary distillation column [15] and hybrid electric vehicle [16].

Fractional order signal processing and digital filters are also promising application areas of fractional order phenomena. In an early stage work, the behavior of passive RC low pass filters when the capacitive element acquires a fractional order was numerically investigated. The effect of the fractional capacitor on time and frequency-domain responses was numerically studied. The research claimed that speed of the response increases with fractional order and that by allowing the capacitor to acquire a fractional order greater than unity; one can achieve the advantages of fast response and linear phase shift over few decades of frequency [17]. Another research presents a general procedure to obtain Butterworth filter of required specifications in the fractional-order domain. The necessary and sufficient conditions for achieving fractional-order Butterworth filter with a specific cutoff frequency were derived as a function of the orders in addition to the transfer function parameters. The effect of equal-orders on the filter bandwidth was discussed showing how the integer-order case is considered as a special case from the proposed procedure. Several passive and active filters were studied to validate the concept such as Kerwin–Huelsman–Newcomb and Sallen–Key filters through numerical simulations. These circuits were tested experimentally using discrete components to model the fractional order capacitor showing good match with the numerical simulations [18].

The mathematics involved in fractional integrator/differentiator is much more complex as compared to integer order integrator/differentiator. Therefore, hardware implementation of fractional operators is also relatively complex. Some techniques for hardware implementation of fractional operators have been proposed and reported in the literature. Several hardware platforms have been used in various applications. In [19], an experimental study of the fractional order controller, implemented on a desktop computer, was presented. The LabVIEW based experimental results validated the advantages of the proposed fractional order controller. An experimental study of the fractional order proportional and derivative controller to control a fractional horsepower dynamometer system is presented in [20]. The controller was implemented on a desktop computer. In [21], realization of fractional order controller, to control a DC motor – generator plant, was presented in LabVIEW environment on a real time platform. The fractional order controller transfer function was realized using continuous fraction expansion scheme. A differentiator using Richardson extrapolation and fractional delay was proposed and implemented on Field Programmable Gate Array (FPGA). This work resolves the problems caused by the high order interpolator used to implement fractional delay by implementing a higher sampling rate system on FPGA, which acts like a system using fractional delay [22]. In another such work, the fractional order integrative operator s^−m, where m is a real positive number, is approximated via a mathematical formula and then, hardware implementation of fractional integral operator is proposed using FPGA. The paper claims that FPGA-based implementation is up to one hundred times faster than implementations based on microprocessor and this extra speed is exploited to allow higher performance in terms of digital approximations of fractional order systems [23]. The proposed method was validated in simulation. In a recent research, an improved particle swarm optimization (PSO) algorithm was adopted to optimize fractional order PID controller parameters. This paper adopted FPGA combined with external circuit to implement fractional order PID controller because of high complexity of PSO and long tuning time. Validation of the technique was done in simulation. The research claimed that fractional PID controller implemented with FPGA has some advantages such as flexible design, self-tuning on line, high reliability, low development cycle and high speed [24]. A new hardware architecture for implementing a Discrete Fractional Fourier Transform which requires hardware complexity of O(4N), where N is transform order was proposed in [25]. This proposed architecture was simulated and synthesized using Verilog HDL, targeting a FPGA device (XLV5LX110T).

The literature survey conducted above clearly indicates that the use of FPGA in LabVIEW environment for hardware implementation of fractional order integrator/differentiator has not been explored. Bridging this technical gap is the key motivation of this research. This paper presents a step-by-step procedure for the hardware implementation of basic operators of fractional calculus i.e. fractional integrator and differentiator on a FPGA device by M/S National Instruments (NI-PXI 7833R) in LabVIEW environment. Using the well-known Grünwald–Letnikov (G–L) equation for fractional order integrator/differentiator with a good approximation, the operator was first applied on several standard waveform signals in simulation mode. Once satisfactory results were obtained in simulation, the logic was deployed onto the FPGA hardware using the FPGA toolkit of LabVIEW. This toolkit converted the graphical LabVIEW code into very high speed integrated circuits hardware description language (VHDL) and deployed it onto the FPGA hardware target. In a way, the LabVIEW user is freed from learning the intricacies of VHDL. The results for fractional integration/differentiation of standard waveforms such as sinusoid and square for some selected fractional orders have been presented in this work.

The rest of the paper is organized as follows. In Section 2, the basic mathematics for fractional integrator/differentiator has been described. Section 3 presents the algorithm developed for the implementation of G–L fractional order operator algorithm in LabVIEW environment. The constraints involved in the implementation of the proposed algorithm on FPGA device in LabVIEW environment and their remedies are also presented. Simulation results for some standard waveforms along with the validation are also presented in this section. Then, the experimental results obtained on the FPGA target for sine and square waveforms along with the resources consumed on the hardware target are presented in the section. Section 4 concludes the work.

2. Fractional order operator

The G–L definition for fractional order operator is defined as follows:

$D^{\gamma }x(t)={\underset {h\rightarrow 0}{lim}}h^{-\gamma }\sum _{j=0}^{\infty }{\left(-1\right)}^{j}\left({\frac {\gamma }{j}}\right)x(t-$$jh)$

(1)

where D   is the differintegral operator, ${\textstyle \left({\frac {\gamma }{j}}\right)={\frac {\left(\gamma )(\gamma -1)(\gamma -2)\ldots (\gamma -j+1\right)}{\Gamma (j-1)}}}$ and h being the step size.

FPGA being a discrete time implementation device requires a discrete time version of G–L definition. This could be arrived at by expanding binomially the backward difference equation for the derivative operator i.e. ${\textstyle s={\frac {1-z^{-1}}{T}}}$; T being the sampling interval (assumed to be very small).

Hence, the fundamental fractional operator s^γ, where γ is a real number, can also be approximated using the binomial expansion of the backward difference [26].

Therefore,

$s^{\gamma }={\left({\frac {1-z^{-1}}{T}}\right)}^{\gamma }$

On applying binomial expansion for ${\textstyle {\left({\frac {1-z^{-1}}{T}}\right)}^{\gamma }}$

$s^{\gamma }=T^{-\gamma }\sum _{j=0}^{\infty }{\left(-1\right)}^{j}{\frac {\left(\gamma )(\gamma -1)(\gamma -2)\ldots (\gamma -j+1\right)}{\Gamma (j-1)}}z^{-j}$

Hence, in discrete time differintegral operator, D can be written as follows:

$D^{\gamma }=T^{-\gamma }\sum _{j=0}^{\infty }{\left(-1\right)}^{j}\left({\frac {\gamma }{j}}\right)z^{-j}$

(2)

$D^{\gamma }=T^{-\gamma }\sum _{j=0}^{\infty }b_{j}z^{-j}$

where ${\textstyle b_{j}={\left(-1\right)}^{j}\left({\frac {\gamma }{j}}\right)}$.

Furthermore, coefficient ‘b’ can be simplified to the following recursive algorithm:

$b_{j}=\left(1-{\frac {1+\gamma }{j}}\right)b_{j-1}{\mbox{;}}j=$$1{\mbox{,}}2{\mbox{,}}\ldots$

(3)

with b₀ = 1.

So, the fractional integrator/differentiator of a sequence x[n] is as follows:

$D^{\gamma }(x[n])=T^{-\gamma }\sum _{j=0}^{\infty }b_{j}x[n-$$j]$

(4)

As shown in Eq. (4), an infinite series of coefficients needs to be calculated and stored for implementation of the differintegral operator. FPGA, as any other hardware device, has limited memory and storing very large number of coefficients would require longer processing thereby leading to the larger sampling intervals. Therefore, instead of calculating and storing all previous values, only the last few sample values are stored in memory in the form of an array. Keeping the window size of L, a short memory of L, Eq. (4) can be further simplified as follows:

$D^{\gamma }(x[n])=T^{-\gamma }\sum _{j=0}^{L}b_{j}x[n-j]$

(5)

This equation matches with the G–L equation with short memory of L. This is a well implementable logic on the FPGA as it only requires delays, multipliers and the set of adders.

3. FPGA implementation: Issues and results

FPGA being a hardware device needs to be programmed using some hardware description language. But in this study, LabVIEW was used for the purpose because it has a well-developed state-of-the-art toolkit for programming and deployment of FPGA device. So, FPGA hardware can be programmed without the need of learning any hardware description language. The software automatically converts the graphical code into an equivalent VHDL code. The user is required to take care of the timing and hardware constraints of the hardware device, if reported by the tool. Once the LabVIEW code is deployed onto the FPGA, it can be executed any number of times independent of the host computer.

The digital hardware implementation of a fractional order differintegral operator requires a careful consideration of certain issues including hardware resources and computational speed. FPGA based implementations are generally faster than implementations based on microprocessors; this extra speed can be exploited to allow a higher performance in terms of digital approximations of fractional order systems and higher throughput. Though a FPGA promises speed and reliability, it lacks in resolution. The NI-7833R FPGA device also works on fixed-point mathematics and hence, the resolution gets affected. If word sizes are not correctly assigned to the variables, then timing violations may occur and the code will not get deployed onto the FPGA. Another issue to be kept in mind is the availability of the hardware resources. It may so happen that the code may be too complex and may run out of resources. Therefore, a concise code with optimum use of resources must be conceived. Another constraint is that the NI-7833R FPGA device allows only fixed size arrays to be allocated as dynamic arrays cannot be created and handled in this device. Hence, an efficient approach to apply the differintegral algorithm is required.

As can be seen from the G–L equation, pre-computed binomial coefficients are required to be multiplied successively with previous values of sampled input and the multiplication needs to be accumulated and scaled by T^−γ to yield the result. This process needs to be continued for every new sample acquisition. Since a long memory (large window) would take more time for multiplication and accumulation of large number set, one would be left with a lower sampling rate and there may be issues to represent the signal correctly on account of the poor sampling rate alone. On the other hand, a long memory will enhance the implementation accuracy. So, a trade-off needs to be set between the memory length and the required sampling rate.

In the present study a memory length L of 100 was kept for the investigation at 20 Hz waveforms and a memory length L of 400 was kept for the measurement of frequency responses of the developed differentiators and integrators. This reduces the accuracy to some extent but the hardware resources were plausibly utilized while maintaining a good approximation and required sampling rates. In order to implement the effect of delay, before every new acquisition the array set is right shifted and the new acquisition is inserted at the beginning. It may be noted that initially the entire array is initialized to zero. Therefore, in this study the samples are stored one by one in an array having a fixed size of L elements. When the number of input samples reaches L, the oldest value is exited from the array, the array elements are right shifted and the new sample is inserted in the beginning. Thus only a fixed number of calculations were required to be performed at each acquisition. For example, if the array size is fixed to 100, then only 100 past samples need to be multiplied with the corresponding binomial coefficients and accumulated to realize the operated output for the present iteration. Furthermore, it may be noted that there will be a transient state of 100 samples in the output waveforms.

FPGA implementation of the differintegral operator is not a very straight forward operation and needs some special mention. The real world voltage signal of few volts (say 1 V) acquired using FPGA board formed a large numeric value (i.e. 3276.7) on the FPGA and hence, it needed to be treated appropriately. Also, a large numeric value (say 3276.7) on the FPGA board formed a voltage signal of 1 V to the real world. Computation of the factor T^−γ present in Eq. (5) on the FPGA target also requires a special mention. As there is no inbuilt mathematical library present in the FPGA toolkit of LabVIEW to perform x^y operation, instead of implementing T^−γ directly, the same was implemented as in Eq. (6).

$T^{-\gamma }=e^{-\gamma ln(T)}$

(6)

Another consideration has been the supported exponential function on FPGA board which is designed to take input in the range of ±1 only. For the same, the actual input value, that is, −γ ln(T) was scaled down by 10 as in this study, this value was never greater than 10 and then, the exponential operation was performed. Now, to obtain the actual applicable values, the computed exponential function was further raised to the power of 10 as given in Eq. (7). This obtained exponential value is the required value.

$e^{-\gamma ln(T)}={\left(e^{\frac {-\gamma ln(T)}{10}}\right)}^{10}$

(7)

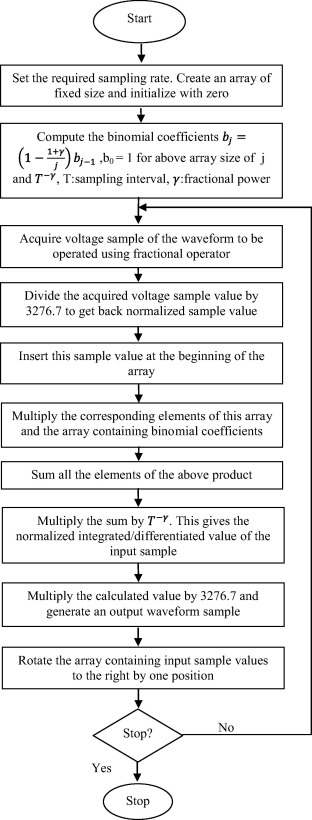
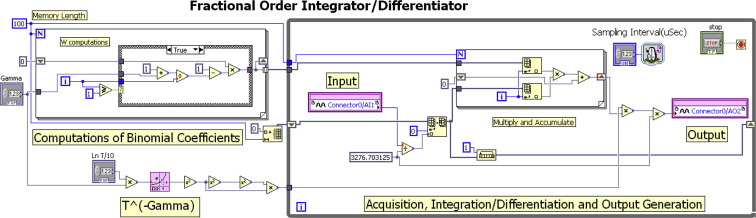
Finally, the algorithm for differintegral operator was implemented as shown in the flowchart of Fig. 1. A LabVIEW code which used the FPGA resources effectively was developed. The G-code shown in Fig. 2 is the code for implementation of fractional order integration/differentiation on FPGA. The part of the code present inside the while loop is recursive. It was found by means of various experiments on the hardware that an iteration of this recursive part takes approximately 20 μs. So, the delay in the data acquisition loop of two successive samples was always kept at a value greater than 20 μs. This means that the sampling interval for the input waveform to the fractional operator deployed on the FPGA is required to be set greater than 20 μs.

Figure 1. Flowchart for FPGA implementation of differintegral operator.

Figure 2. LabVIEW code for implementation of differintegral operator on FPGA for a window size of 100.

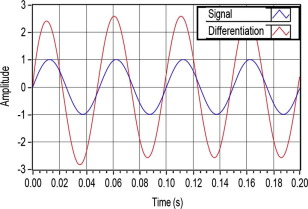
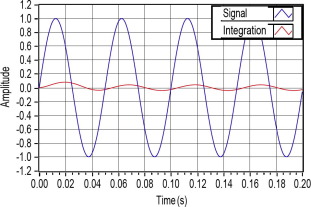
The code in Fig. 2 was first validated in simulation. The results obtained in simulation for sine and square waveforms for different values of γ are presented in Figure 3, Figure 4, Figure 5 and Figure 6.

Figure 3. Fractional derivative of sine waveform for ${\textstyle \gamma =0.2}$.

Figure 4. Fractional integral of sine waveform for ${\textstyle \gamma =-0.6}$.

Figure 5. Fractional derivative of square waveform for ${\textstyle \gamma =0.2}$.

Figure 6. Fractional integral of square waveform for ${\textstyle \gamma =-0.6}$.

In this implementation, the fixed-point coding is used to process the data. The data is converted to a signed bit stream of 24 bits, wherein the first 7 bits are used to represent the integer part of the data, while the remaining 17 bits are used for the fractional value of the data. This word length allowed defining a maximum signed value of ±64 having an accuracy of about 7.6294E−06.

Theoretically, 1 V sinusoid waveform of 20 Hz sampled at 0.5 ms, and for the differential operator of fractional order 0.2, the output signal is amplified by a factor of s^γ = (2·π·20)^0.2 = 2.63 i.e. for an input signal of amplitude 1 V, an output of 2.63 V is produced. The output signal is also advanced of a phase equal to γ·90° = 18°, equal to 2.5 ms. In simulation using 100 binomial coefficients, these results were obtained as 2.59 V and 2.5 ms. Furthermore, for a window size of 400 results are further improved to 2.68 V and 2.5 ms. Similarly, for the same signal, for the integral operator of fractional order 0.6, the output signal is attenuated by a factor of s^γ = (2·π·20)^0.6 = 18.18 i.e. an input signal of amplitude 1 V produced an output of 0.055 V. The output signal is also delayed of a phase equal to γ·90° = 54°, equal to 7.5 ms. On the fixed-point mathematics, the results are obtained as 0.042 V and 5.5 ms. For a window size of 400, results are little improved to 0.050 V and 5.5 ms. The result, for both the operations, closely matches with the theoretical ones.

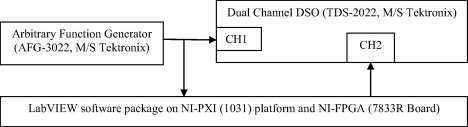
After satisfactory results were obtained in simulation, the code was deployed onto the FPGA device for a window size of 100. Inputs to the FPGA device were waveforms generated by an arbitrary waveform generator (AFG-3022, M/S Tektronix) and the generated integrated/differentiated waveforms were displayed on a digital storage oscilloscope (TDS-2022, M/S Tektronix). Fig. 7 shows the schematic of the experimental setup and Fig. 8 shows the snap shot of the actual experimental setup. The inputs used were sinusoid and square waveforms of 20 Hz. The results for these waveforms for different values of gamma have been given in Figure 9, Figure 10, Figure 11 and Figure 12.

Figure 7. Experimental setup block diagram.

Figure 8. Experimental setup.

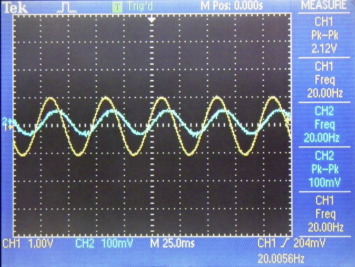
Figure 9. Fractional derivative of sine waveform for ${\textstyle \gamma =0.2}$ (input – yellow, output – cyan). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

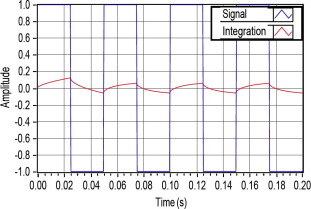
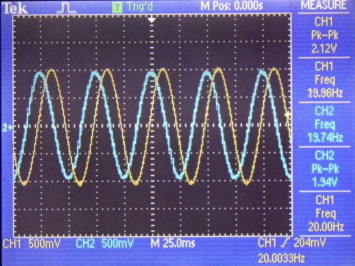
Figure 10. Fractional integral of sine waveform for ${\textstyle \gamma =-0.6}$ (input – yellow, output – cyan). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

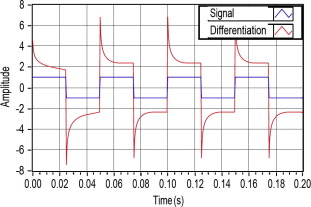
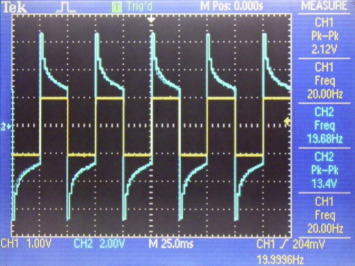
Figure 11. Fractional derivative of square waveform for ${\textstyle \gamma =0.2}$ (input – yellow, output – cyan). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

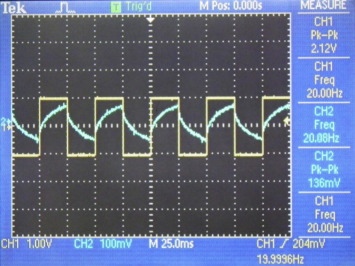
Figure 12. Fractional integral of square waveform for ${\textstyle \gamma =-0.6}$ (input – yellow, output – cyan). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

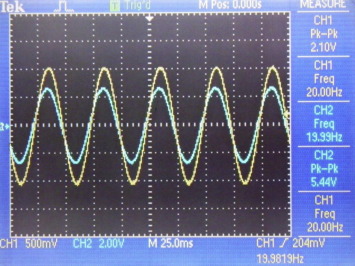
As can be seen, the hardware implementation results closely conform to the simulation results. In case of differentiation of γ = 0.2, for an input of 2.10 V_p–p the oscilloscope recorded an output of 5.44 V_p–p i.e. an amplification of 2.69 against the 2.63. In case of integration of γ = 0.6, for an input of 2.10 V_p–p the oscilloscope recorded an output of 100 mV_p–p i.e. an attenuation of 21 against the 18. It may also be noted that the signal in second case being very small also picks up the noise yielding more uncertainty. Also, the results for the square waveform are also in agreement with the simulation.

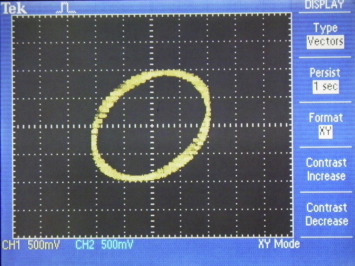
For further validation of the technique, fractional derivative of sine waveform was performed for γ = 0.99 which resulted in approximate complete derivative of sine waveform as shown in Fig. 13. In this particular case, the output signal was appropriately attenuated to yield a 1.0 V physical signal on the oscilloscope. This was done because in normal case the resulting amplitude was much higher (>122 V) and would have forced the device to saturate. It can be clearly seen that the input and the output waveforms on a digital storage oscilloscope show a phase difference of near 90°. To validate this, the differentiated waveform was given as external trigger to the oscilloscope and sine waveform was given as input. This resulted in the formation of an elliptical Lissajous pattern as shown in Fig. 14 which authenticated that the waveforms were 90° apart in phase. In this way, complete differentiation of sine waveform was achieved using the same technique as was used for fractional order derivative thus showing the effectiveness of the proposed implementation technique.

Figure 13. Fractional derivative of sine waveform for ${\textstyle \gamma =0.99}$ (input – yellow, output – cyan). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Figure 14. Lissajous pattern.

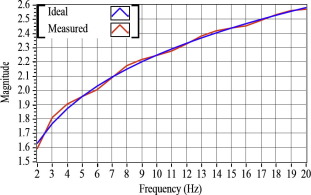
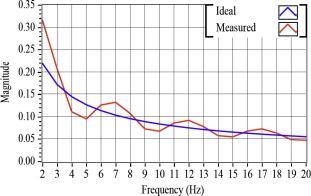
To further investigate the implemented fractional order operators, on the used FPGA target, frequency responses of the fractional derivative of γ = 0.2 and fractional integral of γ = −0.6 were recorded for a window size of 400 in the frequency range of 2–20 Hz. Since arrays of this size were not supported by the used FPGA device, first-in-first-out (FIFO) memory was used to implement the same for storing of input signal and the coefficients. Fig. 15 shows the comparison between the implemented fractional derivative of γ = 0.2 for the frequency range of 2–20 Hz with the ideal one. Good match between the theoretical and the measured responses can be clearly observed in the considered frequency range. Similarly, Fig. 16 compares the implemented fractional integral of γ = −0.6 for the frequency range of 2–20 Hz with the ideal one.

Figure 15. Frequency response comparison for fractional derivative (γ = 0.2, memory = 400).

Figure 16. Frequency response comparison for fractional integrator (γ = −0.6, memory = 400).

An important aspect while working on a hardware device is the resources utilized by the developed code. This aspect becomes even more important while working on a real time hardware device. As the amount of logic used for implementation of a code increases, propagation delay also increases which adversely influences the performance of a real time device and the device deviates from the expected performance. Even power dissipation also increases with the increase in logic influencing the device’s performance. So, it becomes crucial to present the resources employed by a code on FPGA. The resources utilized by the code using FIFO memory for input and coefficient for a window size of 400 are given in Table 1.

Table 1. Design summary.

Resource	Utilization	Utilization (%)
Sliced flip flops	2538 out of 28,672	8
4 Input LUTs	3854 out of 28,672	13
BUFGMUXs	2 out of 16	12
LOCed BUFGMUXs	1 out of 2	50
External IOBs	113 out of 484	23
LOCed IOBs	113 out of 113	100
MULT18X18s	25 out of 96	26
RAMB16s	14 out of 96	14
Slices	2852 out of 14,336	19
Design information
Target device	xc2v3000-4-fg676
Input format	VHDL

4. Conclusion

In this paper, a step by step procedure for hardware implementation of fractional integrators and derivatives on field programmable gate arrays (FPGA), using Grünwald–Letnikov algorithm, was presented. Various FPGA implementation aspects including the fixed point operations, supported mathematical functions and programming constraints on the used FPGA target were addressed for the LabVIEW implementation environment. Detailed hardware implementation results, verifying the theoretical simulations, for fractional integrations and derivatives of sine and square waveforms for fractional powers of −0.6 and 0.2 have been presented in addition to the frequency responses of the developed operators. Developed fractional integrations and derivatives demonstrated a very close agreement with the expected ideal theoretical results and thereby validated the procedure used in this work. As a future scope of this work, the developed fractional operators can be integrated with the hardware processes for fractional order control or signal processing applications and enhanced performances may be utilized for a particular case.

Acknowledgment

The authors would like to thank anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper.

References

1. [1] E. Monmasson, L. Idkhajine, M.N. Cirstea, I. Bahri, A. Tisan, M.W. Naouar; FPGAs in industrial control applications; IEEE Trans. Ind. Inf., 7 (2) (2011), pp. 224–243
2. [2] Damian O. Craiem, Ricardo L. Armentano, Arterial viscoelasticity: a fractional derivative model, in: Proceedings of the 28th IEEE EMBS Annual International Conference, New York City, USA, Aug 30–Sept 3, 2006, pp. 1098–1101.
3. [3] F. Tahami, H. Afshang, A fractional order model for steer-by-wire systems, in: Proceedings of the 35th IEEE conference, IECON Industrial Electronics, 3–5th November, 2009, pp. 4161–4166.
4. [4] Wei Yu, Youguo Pi, Fractional order modeling and simulation experiment of permanent magnet synchronous motor, in: Proceedings of the 28th IEEE/ASME Conference on Mechatronics and Embodied Systems and Applications (MESA), 8–10 July, 2012, pp. 114–118.
5. [5] J. Sabatier, A. Oustaloup, A.G. Iturricha, P. Lanusse; CRONE control: principles and extension to time-variant plants with asymptotically constant coefficients; Nonlinear Dyn., 29 (2002), pp. 363–385
6. [6] Dingyu Xue, Chunna Zhao, YangQuan Chen, Fractional order PID control of a DC-motor with elastic shaft: a case study, in: Proceedings of the 2006 American Control Conference, Minneapolis, Minnesota, USA, June 14–16, 2006, pp. 3182–4187.
7. [7] Hyo-Sung Ahn, Varsha Bhambhani, YangQuan Chen, Fractional-order integral and derivative controller design for temperature profile control, in: Proceedings of the Control and Decision Conference (CCDC 2008), 2–4 July, 2008, pp. 4766–4771.
8. [8] Igor Podlubny; Fractional-order systems and controllers; IEEE Trans. Autom. Control, 44 (1) (1999), pp. 208–213
9. [9] Ying Luo, Yang Quan Chen; Fractional order [proportional derivative] controller for a class of fractional order systems; Automatica, 45 (2009), pp. 2446–2450
10. [10] H. Delavari, R. Ghaderi, N.A. Ranjbar, S. Momani; Fuzzy fractional order sliding mode controller for nonlinear systems; Commun. Nonlinear Sci. Numer. Simul., 15 (4) (2010), pp. 963–978
11. [11] Saptarshi Das, Indranil Pan, Shantanu Das, Amitava Gupta; A novel fractional order fuzzy PID controller and its optimal time domain tuning based on integral performance indices; Eng. Appl. Artif. Intell., Elsevier, 25 (2) (2012), pp. 430–442
12. [12] I. Pan, S. Das; Chaotic multi-objective optimization based design of fractional order PI^λD^μ controller in AVR system; Electr. Power Energy Syst., 43 (1) (2012), pp. 393–407
13. [13] S. Das, I. Pan, S. Das; Performance comparison of optimal fractional order hybrid fuzzy PID controllers for handling oscillatory fractional order processes with dead time; ISA Trans., 52 (4) (2013), pp. 550–566
14. [14] R. Sharma, K.P.S. Rana, V. Kumar; Performance analysis of fractional order fuzzy PID controllers applied to a robotic manipulator; Expert Syst. Appl., 41 (9) (2014), pp. 4274–4289
15. [15] P. Mishra, V. Kumar, K.P.S. Rana; A fractional order fuzzy PID controller for binary distillation column control; Expert Syst. Appl., 42 (22) (2015), pp. 8533–8549
16. [16] V. Kumar, K.P.S. Rana, P. Mishra, Robust speed control of hybrid electric vehicle using fractional order fuzzy PD & PI controllers in cascade control loop, J Franklin Inst, Elsevier, 2016 (in press), http://dx.doi.org/10.1016/j.jfranklin.2016.02.018.
17. [17] Wajdi Ahmad, Reyad El-Khazali, Fractional-order passive low-pass filters, in: Proceedings of the 10th IEEE International Conference on Electronics, Circuits and Systems (ICECS 2003), 14–17 Dec, 2003, pp. 160–163.
18. [18] A. Soltan Ali, A.G. Radwan, Ahmed M. Soliman; Fractional order Butterworth filter: active and passive realizations; IEEE J. Emerg. Sel. Top. Circ. Syst., 3 (3) (2013), pp. 346–354
19. [19] Yongshun Jin, Ying Luo, Chunyang Wang, YangQuan Chen, LabVIEW based experimental validation of fractional order motion controllers, Chinese Control and Decision Conference (CCDC 2009), 2009, pp. 323–328.
20. [20] Ying Luo, Yang Quan Chen, Youguo Pi; Experimental study of fractional order proportional derivative controller synthesis for fractional order systems; Mechatronics, 21 (2011), pp. 204–214
21. [21] A. Ruszewski, A. Sobolewski; Comparative studies of control systems with fractional controllers; Przegląd Elektrotechniczny (Electr. Rev.) (2012), pp. 204–208
22. [22] Yasuaki Kaneda, Teruyoshi Sadahiro, MasakiYamakita, FPGA Implementation of digital differentiator using richardson extrapolation and high sampling rate acting like fractional delay, SICE Annual Conference, Waseda University, Tokyo, Japan, September 13–18, 2011, pp. 2378–2383.
23. [23] R. Caponetto, G. Dongola, A. Gallo, Fractional integrative operator and its FPGA implementation, in: Proceedings of the ASME 2009 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE 2009), San Diego, California, USA, August 30–September 2, 2009, pp. 1–7.
24. [24] Liguo Qu, Haibo Hu, Yourui Huang, Fractional order PID controller based on particle swarm optimization implemented with FPGA, in: Proceedings of the International Conference on Artificial Intelligence and Computational Intelligence (AICI-2010), IEEE Computer Society, 23–24 Oct, 2010, pp. 165–169.
25. [25] M.V.N.V. Prasad, K. C. Ray, A. S. Dhar, FPGA implementation of discrete fractional Fourier transform, International Conference on Signal Processing and Communications (SPCOM-2010), 18–21 July, 2010, pp. 1–5.
26. [26] R. Caponetto, G. Dongola, L. Fortuna, I. Petras; Fractional Order Systems: Modeling and Control Applications; World Scientific Publishing Co. Pte. Ltd., Singapore (2010)