Stagnation point flow of Maxwell fluid towards a permeable surface in the presence of nanoparticles

Abstract

Analysis has been carried out to study the stagnation point flow of Maxwell fluid towards a permeable stretching sheet in the presence of nanoparticles. Using suitable transformations, the governing partial differential equations are first converted to ordinary one and then solved numerically by fourth–fifth order Runge–Kutta–Fehlberg method with MAPLE. The flow and heat transfer characteristics are analyzed and discussed for different values of the parameters. Present work reveals that the velocity increases whereas the temperature and concentration decrease with the increase of Maxwell parameter. The thermal and concentration boundary layer thickness decreases with velocity ratio, Lewis number, Prandtl number suction, Brownian motion and thermophoresis parameters. Comparison with known results for Newtonian fluid flow is found an excellent agreement.

Keywords

Stagnation point flow; Maxwell fluid; Permeable surface; Nanoparticles; Numerical solution

Nomenclature

${\textstyle A}$- velocity ratio

${\textstyle c}$- stretching rate

${\textstyle C_{f}}$- skin friction

${\textstyle c_{p}}$- specific heat

${\textstyle C}$- nanoparticle volume fraction

${\textstyle D_{B}}$- Brownian diffusion coefficient

${\textstyle D_{T}}$- thermophoresis diffusion coefficient

${\textstyle Nb}$- Brownian motion parameter

${\textstyle Nt}$- thermophoresis parameter

${\textstyle {Nu}_{x}}$- local Nusselt number

${\textstyle Le}$- Lewis number

${\textstyle Pr}$- Prandtl number

${\textstyle {Sh}_{x}}$- local Sherwood number

${\textstyle T}$- temperature of the fluid

${\textstyle T_{w}}$- temperature at the wall

${\textstyle T_{\infty }}$- ambient fluid temperature

${\textstyle u{\mbox{,}}v}$- velocity components along ${\textstyle x}$ and ${\textstyle y}$ directions

${\textstyle U_{w}}$- stretching sheet velocity

${\textstyle U}$- free stream velocity

${\textstyle x}$- coordinate along the stretching sheet

${\textstyle y}$- distance normal to the stretching sheet

Greek symbols

${\textstyle \nu }$- kinematic viscosity

${\textstyle \phi }$- rescaled nanoparticle volume fraction

${\textstyle {\rho }_{f}}$- density of the base fluid

${\textstyle {\rho }_{p}}$- density of the particles

${\textstyle \lambda }$- suction parameter

${\textstyle \beta }$- Maxwell parameter

${\textstyle \theta }$- dimensionless temperature

${\textstyle \eta }$- similarity variable

${\textstyle \alpha }$- thermal diffusivity

${\textstyle {\tau }_{w}}$- wall shearing stress

1. Introduction

There is no doubt that human society development greatly depends upon energy. However the rapid development of human society during the past few years leads to the shortage of global energy and the serious environmental protection. Sustainable energy generation in recent time is thus a challenging issue globally. Solar energy in which circumstances has been regarded one of the best sources of renewable energy via least environmental impact. Solar power in fact is a natural way of obtaining water, heat and electricity. Power tower solar collectors could benefit from the potential efficiency improvements that arise from using a nanofluid as a working fluid. Particle size of nanomaterial is similar or smaller than the wavelength of de Broglie and coherent waves. It is now recognized that solar thermal system with nanofluids becomes the new study hotspot.

On the other hand several industrial fluids are non-Newtonian in their flow characteristics. In a Newtonian fluid, the shear stress is directly proportional to the rate of shear strain, whereas in a non-Newtonian fluid, the relationship between the shear stress and the rate of shear strain is nonlinear. Most of the particulate slurries such as china clay and coal in water, multiphase mixtures such as oil–water emulsions, paints, synthetic lubricants, and biological fluids including blood at low shear rate, synovial fluid, and saliva and foodstuffs such as jams, jellies, soups, and marmalades are examples of non-Newtonian fluids. Because of the large variety of the non-Newtonian fluids, many models of non-Newtonian fluids exist. Maxwell model is one subclass of rate type fluids. This fluid model predicts the relaxation time effects. Such effects cannot be predicted by differential-type fluids. This fluid model is especially useful for polymers of low molecular weight. A review of non-Newtonian fluid flow problems may be found in [1], [2] and [3].

Initially, Sakiadis [4] introduced the concept of boundary layer flow over a moving surface. Crane [5] modified the idea introduced by Sakiadis and extended this concept linear stretching sheet. Flow in the neighborhood of stagnation point in a plane was first studied by Hiemenz [6]. Mahapatra and Gupta [7], [8] and [9] investigated the magnetohydrodynamic stagnation point flow towards a stretching sheet. They shown that the velocity at a point decreases/increases with increase in the magnetic field when the free stream velocity is less/greater than the stretching velocity. Also they have studied the temperature distribution when the surface has constant temperature and constant heat flux. Further they have extended their work on power law fluid and discussed the uniqueness of solutions of stagnation-point flow towards a stretching surface. Accordingly, researchers in the [10], [11], [12] and [13] studied the stagnation point flow over a surface.

Aforementioned studies were primarily concerned with the laminar flow of a clear fluid. Nanotechnology is an emerging research topic having extensive use in industry due to the unique chemical and physical properties which the nano-sized materials possess. These fluids are colloidal suspensions, typically metals, oxides, carbides or carbon nanotubes in a base fluid. The term nanofluid was coined by Choi [14] in his seminal paper presented in 1995 at the ASME Winter Annual Meeting. It refers to fluids containing a dispersion of submicronic solid particles (nanoparticles) with typical length of the order of 1–50 nm. Kuznetsov and Nield [15] analytically studied the natural convective boundary layer flow of nanofluid past a vertical plate. Khan and Pop [16] first time studied the problem of laminar fluid flow resulting from the stretching of a flat surface in a nanofluid. Mustafa et al. [17] investigated the stagnation point flow of viscous nanofluid towards a stretching surface using homotopy analysis method. Alsaedi et al. [18] examined the influence of heat generation/absorption on the stagnation point flow of nanofluid towards a linear stretching surface. Rahman et al. [19] examined the dynamics of natural convection boundary layer flow of water based nanofluids over a wedge. They discussed the analysis in the presence of a transverse magnetic field with internal heat generation or absorption. Nandy and Mahapatra [20] analyzed the effects of velocity slip and heat generation/absorption on magnetohydrodynamic stagnation-point flow and heat transfer over a stretching/shrinking surface and then obtained the solution numerically using fourth order Runga–Kutta method with the help of shooting technique. Different from a stretching sheet, it was found that the solutions for a shrinking sheet are non-unique. Makinde et al. [21] studied the combined effects of buoyancy force, convective heating, Brownian motion and thermophoresis on the stagnation point flow and heat transfer of an electrically conducting nanofluid towards a stretching sheet. Effect of magnetic field on stagnation point flow and heat transfer due to nanofluid towards a stretching sheet has been investigated by Ibrahim et al. [22]. Nadeem et al. [23] and [24] reported the numerical solutions of non-Newtonian nanofluid flow over a stretching sheet using the Maxwell fluid model. Further they obtained the analytic solution for non-orthogonal stagnation point flow of a nanosecond grade fluid toward a stretching surface with heat transfer. Hady et al. [25] studied the natural convection boundary-layer flow over a downward-pointing vertical cone in a porous medium saturated with a power-law nanofluid in the presence of heat generation or absorption. Unsteady boundary layer flow of viscous nanofluid with thermal radiation has been discussed by Khan et al. [26]. Sheikholeslami et al. [27] examined the natural convection flow of nanofluid in the presence of magnetic field. MHD flow of viscous nanofluid due to rotating disk is addressed by Rashidi et al. [28]. Turkyilmazoglu and Pop [29] discussed thermal radiation effect in unsteady natural convection flow of nanofluids past a vertical infinite plate. Mohamad et al. [30] examined Hiemenz flow of nanofluid due to porous wedge. Turkyilmazoglu [31] and [32] explores slip and convection effects in the flow of nanofluids. Nadeem et al. [33] analyzed the flow of three-dimensional water-based nanofluid over an exponentially stretching sheet. Very recently Ramesh and Gireesha [34] and [35] studied the heat source/sink effects on Maxwell fluid over a stretching surface with convective boundary condition in the presence of nanoparticles, and also obtained the numerical solution of the influence of heat source on stagnation point flow towards a stretching surface of a Jeffrey nanoliquid.

In this paper, we study the behavior of the stagnation point flow of Maxwell fluid towards a stretching sheet in the presence of nanoparticles. The sheet is taken permeable. Similarity transforms are used for this problem, and non-dimensionalized equations are solved numerically. Graphical results for various values of the parameters are presented to gain thorough insight towards the physics of the problem. To the best of our knowledge, this problem has not been studied before.

2. Mathematical analysis

Consider the flow of an incompressible non-Newtonian Maxwell fluid in the region ${\textstyle y>0}$ driven by a stretching surface located at ${\textstyle y=0}$ with a fixed stagnation point at ${\textstyle x=0}$. The ${\textstyle x}$ and ${\textstyle y}$ axes are chosen along and perpendicular to the sheet. The stretching velocity ${\textstyle U_{w}(x)}$ and the ambient fluid velocity ${\textstyle U(x)}$ are assumed to vary linearly from the stagnation point, i.e., ${\textstyle U_{w}(x)=cx}$ and ${\textstyle U(x)=bx}$ where ${\textstyle c}$ and ${\textstyle b}$ are rate constant.

We assume that flow is laminar, steady and two-dimensional. The sheet is flat and permeable, and the temperature ${\textstyle T}$ and the nanoparticle fraction ${\textstyle C}$ take constant values ${\textstyle T_{w}}$ and ${\textstyle C_{w}}$ respectively. The ambient values attained as ${\textstyle y}$ tend to infinity of ${\textstyle T}$ and ${\textstyle C}$ denoted by ${\textstyle T_{\infty }}$ and ${\textstyle C_{\infty }}$ respectively. All the thermo-physical properties are taken constant.

The flow problem under consideration is governed by the following boundary layer equations:

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0{\mbox{,}}$

(1)

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$$\nu {\frac {{\partial }^{2}u}{\partial y^{2}}}-{\frac {1}{\rho }}{\frac {dp}{dx}}-$$k_{0}\left(u^{2}{\frac {{\partial }^{2}u}{\partial x^{2}}}+v^{2}{\frac {{\partial }^{2}u}{\partial y^{2}}}+\right.$$\left.2uv{\frac {{\partial }^{2}u}{\partial x\partial y}}\right){\mbox{,}}$

(2)

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$$\alpha {\frac {{\partial }^{2}T}{\partial y^{2}}}+\tau \left\{D_{B}\left({\frac {\partial C}{\partial y}}{\frac {\partial T}{\partial y}}\right)+\right.$$\left.\left({\frac {D_{T}}{T_{\infty }}}\right){\left({\frac {\partial T}{\partial y}}\right)}^{2}\right\}{\mbox{,}}$

(3)

$u{\frac {\partial C}{\partial x}}+v{\frac {\partial C}{\partial y}}=$$D_{B}{\frac {{\partial }^{2}C}{\partial y^{2}}}+\left({\frac {D_{T}}{T_{\infty }}}\right)\left({\frac {{\partial }^{2}T}{\partial y^{2}}}\right){\mbox{,}}$

(4)

where ${\textstyle u}$ and ${\textstyle v}$ are the velocity components along the ${\textstyle x}$ and ${\textstyle y}$ axes, respectively. Further, ${\textstyle \alpha {\mbox{,}}\quad {\rho }_{f}{\mbox{,}}\quad {\rho }_{p}{\mbox{,}}\quad \nu {\mbox{,}}\quad T}$ and ${\textstyle T_{\infty }}$ are respectively the thermal diffusivity, density of the base fluid, density of the particles, kinematic viscosity of the fluid, fluid temperature and ambient fluid temperature. ${\textstyle k_{0}}$ is the relaxation time of the UCM fluid, ${\textstyle D_{B}}$ is the Brownian diffusion coefficient, ${\textstyle D_{T}}$ is the thermophoresis diffusion coefficient and ${\textstyle c_{p}}$ is the specific heat at constant pressure. Here ${\textstyle \tau }$ is the ratio of the effective heat capacity of the nanoparticle material and the heat capacity of the ordinary fluid and ${\textstyle C}$ is the nanoparticle volume fraction.

The associated boundary conditions for the present problem are

${\begin{array}{rl}&u=U_{w}(x){\mbox{,}}\quad v=-V_{w}(x){\mbox{,}}\quad T=T_{w}{\mbox{,}}\quad C=C_{w}\quad {\mbox{at}}\quad y=0{\mbox{,}}\\&u\rightarrow U(x){\mbox{,}}\quad v\rightarrow 0{\mbox{,}}\quad T\rightarrow T_{\infty }{\mbox{,}}\quad C\rightarrow C_{\infty }\quad {\mbox{as}}\quad y\rightarrow \infty \end{array}}$

(5)

where ${\textstyle U_{w}(x)=cx}$ is the stretching sheet velocity, ${\textstyle c>0}$ this is known as stretching rate. ${\textstyle T_{w}}$ and ${\textstyle C_{w}}$ are the temperature of fluid and nanoparticles fraction at wall, and ${\textstyle C_{\infty }}$ is ambient nanoparticle volume fraction.

To employing the generalized Bernoulli’s equation, in the free stream ${\textstyle U(x)=bx}$ Eq. (2) reduces to

$U{\frac {dU}{dx}}=-{\frac {1}{\rho }}{\frac {dp}{dx}}$

(6)

Using (6) into (2) one can obtain

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$$\nu {\frac {{\partial }^{2}u}{\partial y^{2}}}+U{\frac {dU}{dx}}-$$k_{0}\left(u^{2}{\frac {{\partial }^{2}u}{\partial x^{2}}}+v^{2}{\frac {{\partial }^{2}u}{\partial y^{2}}}+\right.$$\left.2uv{\frac {{\partial }^{2}u}{\partial x\partial y}}\right)$

(7)

The specific forms of the stretching velocity and the surface temperature and concentration are chosen to allow the coupled nonlinear partial differential Eqs. (1), (2), (3) and (4) to be converted to a set of coupled, nonlinear ordinary differential equations by the similarity transformation

$\eta ={\left({\frac {U_{w}}{vx}}\right)}^{1/2}y{\mbox{,}}\quad f(\eta )=$${\frac {\psi }{{\left({xvU}_{w}\right)}^{1/2}}}{\mbox{,}}\quad \theta (\eta )=$${\frac {T-T_{\infty }}{T_{w}-T_{\infty }}}{\mbox{,}}\quad \varphi (\eta )=$${\frac {C-C_{\infty }}{C_{w}-C_{\infty }}}{\mbox{,}}$

(8)

where ${\textstyle \eta }$ is the similarity variable, ${\textstyle f{\mbox{,}}\quad \theta }$ and ${\textstyle \phi }$ are the dimensionless stream function, temperature and concentration respectively. The velocity components ${\textstyle u}$ and ${\textstyle v}$ in Eq. (8) automatically satisfy the continuity Eq. (1). In terms of ${\textstyle f(\eta ){\mbox{,}}\quad \theta (\eta )}$ and ${\textstyle \phi (\eta )}$ the momentum Eq. (2), energy Eq. (3) and concentration Eq. (4) can be written as

$f^{{'}2}-f\quad f^{''}=f^{'''}+A^{2}-\beta f^{2}f^{'''}+$$2\beta \quad f\quad f^{'}\quad f^{''}{\mbox{,}}$

(9)

${\frac {1}{Pr}}{\theta }^{''}+f{\theta }^{'}+Nb{\theta }^{'}{\phi }^{'}+$$Nt{\theta }^{{'}2}=0$

(10)

${\phi }^{''}+Le\quad Prf{\phi }^{'}+{\frac {Nt}{Nb}}{\theta }^{''}=$$0$

(11)

Here ${\textstyle f^{'}}$ represents an ordinary derivative with respect to ${\textstyle \eta }$ and the corresponding boundary conditions in the non-dimensional form are

${\begin{array}{rl}&f=\lambda {\mbox{,}}\quad f^{'}=1{\mbox{,}}\quad \theta =1{\mbox{,}}\quad \phi =1\quad at\quad \eta =0\\&f^{'}\rightarrow A{\mbox{,}}\quad \theta \rightarrow 0{\mbox{,}}\quad \phi \rightarrow 0\quad as\quad \eta \rightarrow \infty \end{array}}$

(12)

The dimensionless parameters in Eqs. (9), (10) and (11) are ${\textstyle A={\frac {c}{b}}}$ is the ratio of rates of velocities, ${\textstyle \beta =k_{0}c}$ is the Maxwell parameter, ${\textstyle \lambda ={\frac {V_{w}}{{\left(\nu c\right)}^{1/2}}}}$ is suction parameter, ${\textstyle Nb={\frac {\tau D_{B}(C_{w}-C_{\infty })}{\nu }}}$ is the Brownian motion, ${\textstyle Nt={\frac {\tau D_{T}(T_{w}-T_{\infty })}{\nu T_{\infty }}}}$ is the thermophoresis parameter, ${\textstyle Le={\frac {\alpha }{D_{B}}}}$ is the Lewis number and ${\textstyle Pr={\frac {\nu }{\alpha }}}$ is the Prandtl number.

For practical purposes, the functions ${\textstyle f(\eta ){\mbox{,}}\quad \theta (\eta )}$ and ${\textstyle \phi (\eta )}$ allow us to determine the skin friction coefficient, Nusselt number and Sherwood number respectively.

$C_{f}={\frac {\left(1+\beta )f^{''}(0\right)}{{Re}_{x}^{1/2}}}{\mbox{,}}\quad {Nu}_{x}=$$-{Re}_{x}^{1/2}{\theta }^{'}(0){\mbox{,}}\quad {Sh}_{x}=$$-{Re}_{x}^{1/2}{\phi }^{'}(0)$

(13)

where ${\textstyle {Re}_{x}={\frac {{xU}_{w}(x)}{\nu }}}$ is the local Reynolds number.

3. Numerical solutions

Numerical solutions to the governing ordinary differential Eqs. (9), (10) and (11) with the boundary conditions (12) are obtained using a fourth–fifth order Runge–Kutta–Fehlberg method with the help of MAPLE to obtain the missing values of ${\textstyle f^{''}(0){\mbox{,}}\quad {\theta }^{'}(0)}$ and ${\textstyle {\phi }^{'}(0)}$. The problem for a regular (non-Newtonian) fluid involves four parameters, namely Maxwell parameter, Prandtl number, suction parameter, and velocity ratio parameters. The present extension involves three more parameters ${\textstyle Nb{\mbox{,}}\quad Le}$ and ${\textstyle Nt}$. Therefore, we need to be very selective in the choice of the values of the parameters. Since most nanofluids examined to date have large values of the Lewis number ${\textstyle Le}$, we are interested mainly in the case ${\textstyle Le\geqslant 1}$. Because the physical domain in this problem is unbounded, whereas the computational domain has to be finite, we apply the far field boundary conditions for the similarity variable g at a finite value denoted here by ${\textstyle {\eta }_{\mbox{max}}{\mbox{.}}}$ We run our bulk computations with the value ${\textstyle {\eta }_{\mbox{max}}=5}$, which was sufficient to achieve the far field boundary conditions asymptotically for all values of the parameters considered. Researchers can solve the above nonlinear differential equations analytically see [36] and [37].

4. Result and discussion

In order to validate the method used in this study and to judge the accuracy of the present analysis, a comparison with available results corresponding to the skin-friction coefficient ${\textstyle f^{''}(0)}$ and Nusselt number ${\textstyle -{\theta }^{'}(0)}$ for ${\textstyle Nt=Nb=Le=0}$ (in the absence of nanoparticles), ${\textstyle \beta =0}$ (in the absence of Maxwell parameter) and ${\textstyle \lambda =0}$ (i.e. for stretching impermeable plate) with the available published results of Mahapatra and Gupta [8], Ibrahim et al. [22], and Hayat et al. [40] for various values of ${\textstyle A}$ is made and presented in Table 1 and Table 2. A comparison is also made with Nusselt number ${\textstyle -{\theta }^{'}(0)}$ in the presence of nanoparticles (${\textstyle \beta =A=\lambda =0{\mbox{,}}}$ the absence of Maxwell parameter, velocity rates ratio and suction) for various values of ${\textstyle Nt}$, which can be seen in Table 3. These show a favorable agreement and thus give confidence that the numerical results obtained are accurate.

Table 1. Comparison of the values of skin friction coefficient ${\textstyle f^{''}(0)}$ for various values of velocity ratio ${\textstyle A}$.

${\textstyle A}$	Mahapatra and Gupta [8]	Hayat et al. [40]	Ibrahim et al. [22]	Present study
0.01	–	−0.9982	−0.9980	−0.9991
0.1	−0.9694	−0.9695	−0.9694	−0.9696
0.2	−0.9181	−0.9181	−0.9181	−0.9181
0.5	−0.6673	−0.6673	−0.6673	−0.6672
2.0	2.0175	2.0176	2.0175	2.0175
3.0	4.7293	4.7296	4.7292	4.7292

Table 2. Comparison of the values of Nusselt number ${\textstyle -{\theta }^{'}(0)}$ for various values of velocity ratio ${\textstyle A}$.

${\textstyle Pr}$	${\textstyle A}$	Mahapatra and Gupta [8]	Hayat et al. [40]	Ibrahim et al. [22]	Present study
1	0.1	0.603	0.6021	0.6022	0.6048
	0.2	0.625	0.6244	0.6245	0.6256
	0.5	0.692	0.6924	0.6924	0.6925
1.5	0.1	0.777	0.7768	0.7768	0.7769
	0.2	0.797	0.7971	0.7971	0.7971
	0.5	0.863	0.8647	0.8648	0.8647

Table 3. Comparison results for the local Nusselt number ${\textstyle -{\theta }^{'}(0)}$ in the absence of Maxwell parameter, velocity ratio and suction parameter.

${\textstyle Nt}$	Khan and Pop [12]	Present study ${\textstyle -{\theta }^{''}(0)}$	Errors
	${\textstyle Nb=0.1}$	${\textstyle Nb=0.1}$
0.1	0.9524	0.9523	0.0001
0.3	0.5201	0.5200	0.0001
0.5	0.3211	0.3210	0.0001

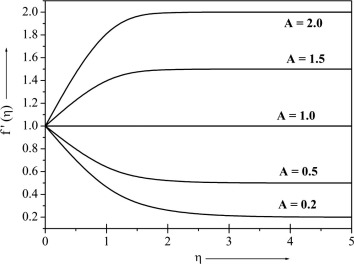
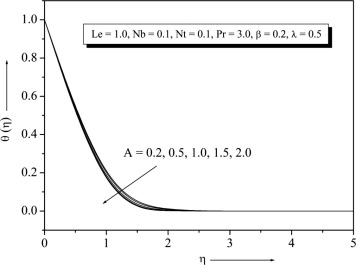
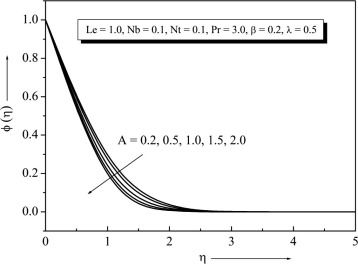
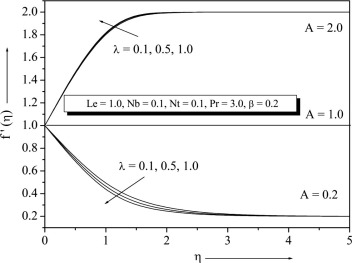
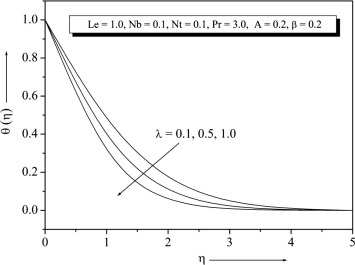
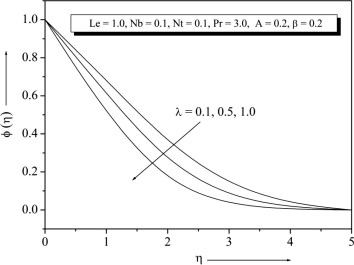
Fig. 1 exhibits the velocity profiles for several values of ${\textstyle A}$. It is found that when the stretching velocity is less than the free stream velocity ${\textstyle \left(A>1\right)}$, the flow has a boundary layer structure, physically saying that the straining motion near the stagnation region increases so the acceleration of the external stream increases which leads to decrease in the thickness of the boundary layer with increase in ${\textstyle A}$. When the stretching velocity ${\textstyle cx}$ of the surface exceeds the free stream velocity ${\textstyle bx}$${\textstyle \left(A<1\right)}$ inverted boundary layer structure is formed and for ${\textstyle A=1}$ there is no boundary layer formation because the stretching velocity is equal to the free stream velocity. The temperature and concentration profiles for different values of ${\textstyle A}$ with other fixed parameter are presented in Figure 2 and Figure 3 respectively. It can be seen from these figures that both ${\textstyle \theta (\eta )}$ and ${\textstyle \phi (\eta )}$ decrease with increase in ${\textstyle A}$.

Figure 1. Velocity profile for different values of ${\textstyle A}$.

Figure 2. Temperature profile for different values of ${\textstyle A}$.

Figure 3. Concentration profile for different values of ${\textstyle A}$.

Fig. 4, shows plots for velocity distribution for different values of ${\textstyle \beta }$. When ${\textstyle A<1}$ the velocity increases with the increase of ${\textstyle \beta }$, and hence the boundary layer thickness decreases. Similar effect can be found when ${\textstyle A>1}$. Converse part can be seen when increase of ${\textstyle \beta }$, shows decrease in temperature ${\textstyle \theta }$ and concentration ${\textstyle \phi }$ profiles see the Figure 5 and Figure 6. This is exactly opposite effects for regular Maxwell fluid in the absence of nanoparticles.

Figure 4. Velocity profile for different values of ${\textstyle \beta }$.

Figure 5. Temperature profile for different values of ${\textstyle \beta }$.

Figure 6. Concentration profile for different values of ${\textstyle \beta }$.

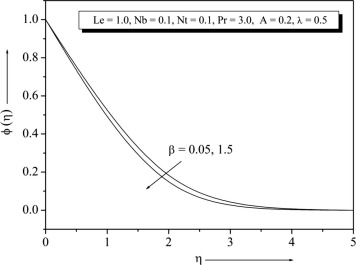
The graph of velocity profile ${\textstyle f^{'}}$ versus ${\textstyle \eta }$ for different values of ${\textstyle \lambda }$ is plotted in Fig. 7. It is found that for a fixed value of ${\textstyle A<1}$ the velocity decreases with the increase of ${\textstyle \lambda }$. The velocity profiles tends asymptotically to the horizontal axis, and the non-dimensional velocities absorbs maximum at the wall. It is fact that suction stabilizes the boundary layer growth. At ${\textstyle A>1}$ the velocity increases with the increase of ${\textstyle \lambda }$. It is also interesting to note that there is a significant enhancement of temperature and concentration at the wall, when it is porous. The temperature and concentration profiles start to decrease monotonically from the very beginning which can be seen from Figure 8 and Figure 9.

Figure 7. Velocity profile for different values of ${\textstyle \lambda }$.

Figure 8. Temperature profile for different values of ${\textstyle \lambda }$.

Figure 9. Concentration profile for different values of ${\textstyle \lambda }$.

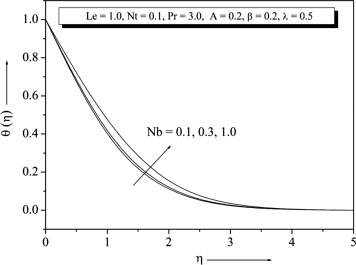
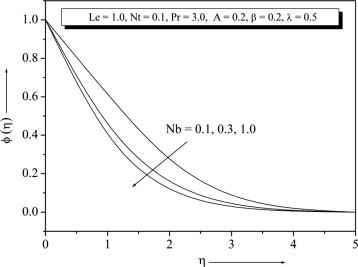
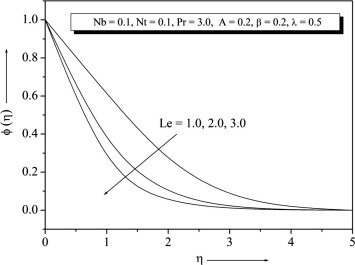
Figure 10 and Figure 11, illustrate the variations of ${\textstyle \theta }$ and ${\textstyle \phi }$ with ${\textstyle \eta }$ for various values of ${\textstyle Nb}$. It is found that the increase in the value of ${\textstyle Nb}$ is to increase ${\textstyle \theta (\eta )}$ in the boundary layer, whereas concentration boundary layer reduces as ${\textstyle Nb}$ increases which thereby enhances the nanoparticles concentration at the sheet. The graph of ${\textstyle Nt}$ on the ${\textstyle \theta }$ and ${\textstyle \phi }$ profiles is depicted in Figure 12 and Figure 13. From these plots, it is observed that the effect of increasing values of ${\textstyle Nt}$ is to increase the temperature and concentration profiles. Fig. 14, displays the effect of ${\textstyle Le}$ on concentration profiles. It is noted that the concentration of fluid decreases with increase of ${\textstyle Le}$. Physically this is due to the fact that mass transfer rate increases as ${\textstyle Le}$ increases. It also reveals that the concentration gradient at surface of the plate increases.

Figure 10. Temperature profile for different values of ${\textstyle Nb}$.

Figure 11. Concentration profile for different values of ${\textstyle Nb}$.

Figure 12. Temperature profile for different values of ${\textstyle Nt}$.

Figure 13. Concentration profile for different values of ${\textstyle Nt}$ .

Figure 14. Concentration profile for different values of ${\textstyle Le}$.

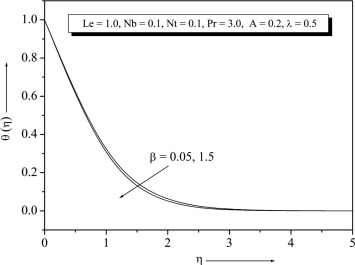
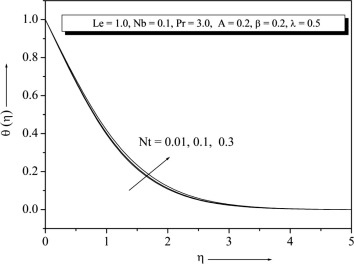
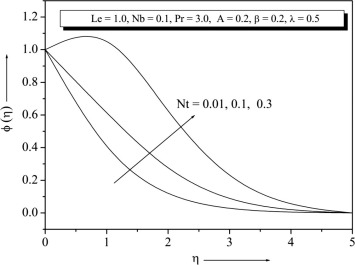
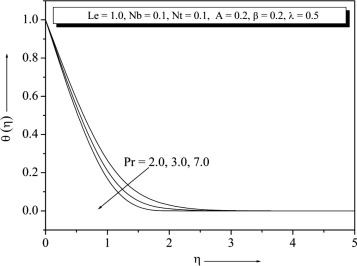
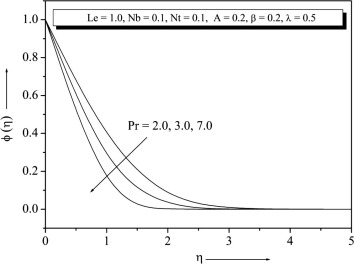
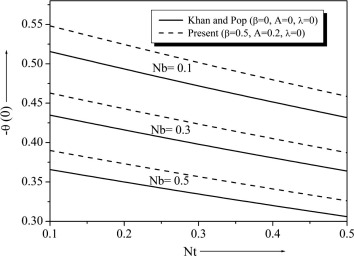
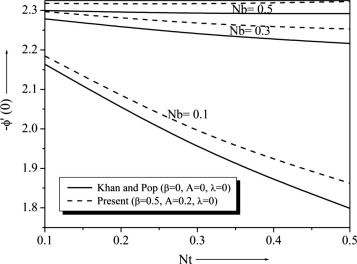
Temperature and concentration profiles for the selected values of ${\textstyle Pr}$ are plotted in Figure 15 and Figure 16. The graph depicts that the temperature decreases when the values of ${\textstyle Pr}$ increase. This is due to the fact that a higher ${\textstyle Pr}$ fluid has relatively low thermal conductivity, which reduces conduction and thereby the thermal boundary layer thickness, and as a result, temperature decreases. We note that the ${\textstyle Nb{\mbox{,}}\quad Nt{\mbox{,}}\quad Le}$ and ${\textstyle Pr}$ have no influence on the flow field, which is clear from Eq. (9). Figure 17 and Figure 18 show that the variations ${\textstyle -{\theta }^{'}(0)}$ and ${\textstyle -{\phi }^{'}(0)}$. From these graph we observe that ${\textstyle -{\theta }^{'}(0)}$ decreases with the increase of Nt  ${\textstyle -{\phi }^{'}(0)}$ increases with the increase of ${\textstyle Nt}$. It is also noted that in the absence of ${\textstyle \beta {\mbox{,}}\quad A}$ and ${\textstyle \lambda }$ our results are similar to those by Khan and Pop (Newtonian fluid). From Figure 17 and Figure 18 one can see Nusselt and Sherwood number for that non-Newtonian fluid is higher than the Newtonian fluid.

Figure 15. Temperature profile for different values of ${\textstyle Pr}$.

Figure 16. Concentration profile for different values of ${\textstyle Pr}$.

Figure 17. Variation of ${\textstyle -{\theta }^{'}(0)}$ with ${\textstyle Nt}$ for different values of ${\textstyle Nb}$.

Figure 18. Variation of ${\textstyle -{\phi }^{'}(0)}$ with ${\textstyle Nt}$ for different values of ${\textstyle Nb}$.

From Table 4 one can see that the skin friction coefficient ${\textstyle f^{''}(0)}$ is negative at ${\textstyle A<1}$. Physically, negative value of ${\textstyle f^{''}(0)}$ means the surface exerts a drag force on the fluid, and positive value means the opposite. This is not surprising since in the present problem, we consider the case of a stretching sheet, which induces the flow. Negative value of ${\textstyle {\theta }^{'}(0)}$ means that the heat flows from the fluid to the solid surface. This is not surprising since the fluid is hotter than the solid surface. In the future, the same problem can be extended to power law fluid see [38] and [39].

Table 4. Values of skin friction coefficient ${\textstyle -f^{''}(0)}$, Nusselt number ${\textstyle -{\theta }^{'}(0)}$ and Sherwood number ${\textstyle -{\phi }^{'}(0)}$ for different values of the physical parameters with ${\textstyle A=0.2}$.

${\textstyle \beta }$	${\textstyle \lambda }$	${\textstyle Le}$	${\textstyle Nb}$	${\textstyle Nt}$	${\textstyle Pr}$	${\textstyle -f^{''}(0)}$	${\textstyle -{\phi }^{''}(0)}$	${\textstyle -{\theta }^{''}(0)}$
0	0. 2	1	0.1	0.1	3	1.1465	0.9255	1.8027
0.1						1.1605	0.9264	1.8025
0.2						1.1745	0.9274	1.8024
0.2	0	1	0.1	0.1	3	0.9333	0.7313	0.9265
	0.1					0.9814	0.7730	1.0848
	0.5					1.1745	0.9274	1.8024
0.2	0.5	1	0.1	0.1	3	1.1745	0.9274	1.8024
		2				1.1745	2.8591	1.6933
		3				1.1745	4.6009	1.6406
0.2	0.5	1	0.1	0.1	3	1.1745	0.9274	1.8024
			0.3			1.1745	2.0012	1.2903
			1.0			1.1745	2.2960	0.3260
0.2	0.5	1	0.1	0.01	3	1.1745	2.1467	1.9526
				0.1		1.1745	0.9274	1.8024
				0.3		1.1745	-1.0223	1.5126
0.2	0.5	1	0.1	0.1	2	1.1745	0.5903	1.4193
					3	1.1745	2.1467	1.9526
					7	1.1745	2.6723	2.5741

5. Conclusions

In the present investigation, the influence of different parameters on the velocity, temperature and concentration profiles is illustrated and discussed. The numerical results give a view toward understanding the response characteristics of the stagnation point flow of a Maxwell fluid in the presence of nanoparticles and suction. It is found that boundary layer is formed when ${\textstyle A>1}$ on the other hand inverted boundary layer is formed when ${\textstyle A<1}$. Some results of thermal characteristics at the wall are usually analyzed from the numerical results and the same are documented in Table 4 and Table 5. Analyzing this table, it reveals that the effects of increasing the values of ${\textstyle \beta }$ are to increase ${\textstyle -f^{''}(0)}$ and decrease the ${\textstyle -{\phi }^{'}(0){\mbox{,}}}$ whereas for ${\textstyle A<1}$${\textstyle -\theta (0)}$ increases but decreases at ${\textstyle A>1}$. Also one can observe that there is no change in ${\textstyle -f^{''}(0)}$, when ${\textstyle Le{\mbox{,}}\quad Nb{\mbox{,}}\quad Nt}$ and ${\textstyle Pr}$ vary.

Table 5. Values of skin friction coefficient ${\textstyle f^{''}(0)}$, Nusselt number ${\textstyle -{\theta }^{'}(0)}$ and Sherwood number ${\textstyle -{\phi }^{'}(0)}$ for different values of the physical parameters with ${\textstyle A=2.0}$.

${\textstyle \beta }$	${\textstyle \lambda }$	${\textstyle Le}$	${\textstyle Nb}$	${\textstyle Nt}$	${\textstyle Pr}$	${\textstyle f^{''}(0)}$	${\textstyle -{\phi }^{''}(0)}$	${\textstyle -{\theta }^{''}(0)}$
0	0.2	1	0.1	0.1	3	2.3101	1.3887	2.0733
0.1						2.4135	1.3946	2.0783
0.2						2.5208	1.4005	2.0833
0.2	0	1	0.1	0.1	3	2.1145	1.1966	1.2519
	0.1					2.1961	1.2425	1.4047
	0.5					2.5208	1.4005	2.0833
0.2	0.5	1	0.1	0.1	3	2.5208	1.4005	2.0833
		2				2.5208	3.3331	1.9733
		3				2.5208	5.0605	1.9174
0.2	0.5	1	0.1	0.1	3	2.5208	1.4005	2.0833
			0.3			2.5208	2.4373	1.4901
			1.0			2.5208	2.7057	0.3756
0.2	0.5	1	0.1	0.01	3	2.5208	2.5340	2.2752
				0.1		2.5208	1.4005	2.0833
				0.3		2.5208	-0.1647	1.7155
0.2	0.5	1	0.1	0.1	2	2.5208	1.0058	1.7290
					3	2.5208	1.4005	2.0833
					7	2.5208	3.2781	2.7331

References

1. [1] T. Hayat, Z. Abbas, M. Sajid; MHD stagnation-point flow of an upper-convected Maxwell fluid over a stretching surface; Chaos, Solitons Fractals, 39 (2009), pp. 840–848
2. [2] V. Aliakbar, A.A. Pahlavan, K. Sadeghy; The influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets; Commun. Nonl. Sci. Numer. Simul., 14 (2009), pp. 779–794
3. [3] T. Hayat, M. Qasim; Influence of thermal radiation and joule heating on MHD flow of a Maxwell fluid in the presence of thermophoresis; Int. J. Heat Mass Trans., 53 (2010), pp. 4780–4788
4. [4] B.C. Sakiadis; Boundary layer behaviour on continuous solid surface; J. Am. Inst. Chem. Eng., 7 (1961), pp. 26–28
5. [5] L.J. Crane; Flow past a stretching sheet; Zeit. Angew. Math. Phys., 21 (1970), pp. 645–647
6. [6] K. Hiemenz; Die grenzschicht an einem in dengleich formigen flussigkeitsstrom eingetauchten geraden kreiszlinder; Dingl. Polytec. J., 326 (1911), pp. 321–328
7. [7] T.R. Mahapatra, A.S. Gupta; Magnetohydrodynamics stagnation point flow towards a stretching sheet; Acta Mech., 152 (2001), pp. 191–196
8. [8] T.R. Mahapatra, A.S. Gupta; Heat transfer in stagnation point flow towards a stretching sheet; Heat Mass Transfer, 38 (2002), pp. 517–521
9. [9] T.R. Mahapatra, S.K. Nandy, A.S. Gupta; Magnetohydrodynamic stagnation point flow of a power-law fluid towards a stretching surface; Int. J. Nonl. Mech., 44 (2009), pp. 124–129
10. [10] T. Hayat, M. Qasim, S.A. Shehzad, A. Alsaedi; Unsteady stagnation point flow of second grade fluid with variable free stream; Alex. Eng. J., 53 (2) (2014), pp. 455–461
11. [11] Z. Abbas, Y. Wang, T. Hayat, M. Oberlack; Mixed convection in the stagnation-point flow of a Maxwell fluid towards a vertical stretching surface; Nonl. Anal.: Real World Appl., 11 (4) (2010), pp. 3218–3228
12. [12] K. Sadeghy, H. Hajibeygi, S.M. Taghavi; Stagnation-point flow of upper-convected Maxwell fluids; Int. J. Non-Linear Mech., 41 (10) (2006), pp. 1242–1247
13. [13] N.S. Akbar, S. Nadeem, R. Ul Haq, S. Ye; MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: Dual solutions; Ain Shams Eng. J., 5 (2014), pp. 1233–1239
14. [14] S.U.S. Choi, Enhancing thermal conductivity of fluids with nanoparticles; Int. Mech. Eng. Cong. Exp., ASME, FED 231/MD, 66 (1995), pp. 99–105
15. [15] A.V. Kuznetsov, D.A. Nield; Natural convective boundary-layer flow of a nanofluid past a vertical plate; Int. J. Therm. Sci., 49 (2010), pp. 243–247
16. [16] W.A. Khan, I. Pop; Boundary-layer flow of a nanofluid past a stretching sheet; Int. J. Heat Mass Trans., 53 (2010), pp. 2477–2483
17. [17] M. Mustafa, T. Hayat, I. Pop, S. Asghar, S. Obaidat; Stagnation-point flow of a nanofluid towards a stretching sheet; Int. J. Heat Mass Trans., 54 (2011), pp. 5588–5594
18. [18] A. Alsaedi, M. Awais, T. Hayat; Effects of heat generation/absorption on stagnation point flow of nanofluid over a surface with convective boundary conditions; Commun. Nonl. Sci. Numer. Simul., 17 (2012), pp. 4210–4223
19. [19] M.M. Rahman, M.A. Al-Lawatia, I.A. Eltayeb, N. Al-Salti; Hydromagnetic slip flow of water based nanofluids past a wedge with convective surface in the presence of heat generation (or) absorption; Int J. Therm. Sci., 57 (2012), pp. 172–182
20. [20] S.K. Nandy, T.R. Mahapatra; Effects of slip and heat generation/absorption on MHD stagnation flow of nanofluid past a stretching/shrinking surface with convective boundary conditions; Int. J. Heat Mass Trans., 64 (2013), pp. 1091–1100
21. [21] O.D. Makinde, W.A. Khan, Z.H. Khan; Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet; Int. J. Heat Mass Trans., 62 (2013), pp. 526–533
22. [22] W. Ibrahim, B. Shankar, M.M. Nandeppanavar; MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet; Int. J. Heat Mass Trans., 56 (2013), pp. 1–9
23. [23] S. Nadeem, R.U. Haq, Z.H. Khan; Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles; J. Taiwan Inst. Chem. Eng. (2013) http://dx.doi.org/10.1016/j.jtice.2013.04.006
24. [24] S. Nadeem, R. Mehmood, N.S. Akbar; Non-orthogonal stagnation point flow of a nano non-Newtonian fluid towards a stretching surface with heat transfer; Int. J. Heat Mass Trans., 57 (2013), pp. 679–689
25. [25] F.M. Hady, F.S. Ibrahim, S.M. Abdel-Gaied, M.R. Eid; Effect of heat generation/absorption on natural convective boundary-layer flow from a vertical cone embedded in a porous medium filled with a non-Newtonian nanofluid; Int. Commun. Heat Mass Transfer, 38 (2011), pp. 1414–1420
26. [26] M.S. Khan, I. Karim, L.E. Ali, A. Islam; Unsteady MHD free convection boundary layer flow of a nanofluid along a stretching sheet with thermal and viscous dissipation effects; Int. Nano Lett., 24 (2012), pp. 1–9
27. [27] M. Sheikholeslami, M.G. Bandpy, D.D. Ganji, S. Soleimani; Natural convection heat transfer in a cavity with sinusoidal wall filled with Cuo-water nanofluid in presence of magnetic field; J. Taiwan Inst. Chem. Eng., 45 (1) (2014), pp. 40–49
28. [28] M.M. Rashidi, S. Abelman, N.F. Mehr; Entropy generation in steady MHD flow due to rotating disk in a nanofluid; Int. J. Heat Mass Trans., 62 (2013), pp. 515–525
29. [29] M. Turkyilmazoglu, I. Pop; Heat and mass transfer of unsteady natural convection flow of some nanofluids past a vertical infinite flat plate with radiation effects; Int. J. Heat Mass Trans., 59 (2013), pp. 167–171
30. [30] R.B. Mohamad, R. Kandasamy, I. Muhaimin; Enhance of heat transfer on unsteady Hiemenz flow of nanofluid over a porous wedge with heat source/sink due to solar energy radiation with variable stream condition; Heat Mass Transfer, 49 (2013), pp. 1261–1269
31. [31] M. Turkyilmazoglu; Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids; Chem. Eng. Sci., 84 (2012), pp. 182–187
32. [32] M. Turkyilmazoglu; Unsteady convection flow of some nanofluids past a moving vertical flat plate with heat transfer; ASME J. Heat Transfer, 136 (3) (2013) 7 pages
33. [33] S. Nadeem, R. Ul Haq, Z.H. Khan; Heat transfer analysis of water-based nanofluid over an exponentially stretching sheet; Alex. Eng. J., 53 (1) (2014), pp. 219–224
34. [34] G.K. Ramesh, B.J. Gireesha; Influence of heat source/sink on a Maxwell fluid over a stretching surface with convective boundary condition in the presence of nanoparticles; Ain Shams Eng. J., 5 (2014), pp. 991–998
35. [35] G.K. Ramesh; Numerical study of the influence of heat source on stagnation point flow towards a stretching surface of a Jeffrey nanoliquid; J. Eng., 2015 (2015), p. 10
36. [36] M.R. Hajmohammadi, S.S. Nourazar, A.H. Manesh; Semi-analytical treatments of conjugate heat transfer; J. Mech. Eng. Sci., 227 (2012), pp. 492–503
37. [37] M.R. Hajmohammadi, S.S. Nourazar; On the solution of characteristic value problems arising in linear stability analysis; Semi Anal. Approach, Appl. Math. Comput., 239 (2014), pp. 126–132
38. [38] M.R. Hajmohammadi, S.S. Nourazar; On the insertion of a thin gas layer in micro cylindrical Couette flows involving power-law liquids; Int. J. Heat Mass Transfer, 75 (2014), pp. 97–108
39. [39] M.R. Hajmohammadi, S.S. Nourazar, A. Campo; Analytical solution for two-phase flow between two rotating cylinders filled with power law liquid and a micro layer of gas; J. Mech. Sci. Technol., 28 (5) (2014), pp. 1849–1854
40. [40] T. Hayat, T. Javed, Z. Abbas; MHD flow of a micropolar fluid near a stagnation point towards a non-linear stretching surface; Non-Linear Anal.: Real World Appl., 10 (2009), pp. 1514–1526