Effects of induced magnetic field and homogeneous–heterogeneous reactions on stagnation flow of a Casson fluid

Abstract

In this study, we analyzed the induced magnetic field effect on the stagnation-point flow of a non-Newtonian fluid over a stretching sheet with homogeneous–heterogeneous reactions and non-uniform heat source or sink. The transformed ordinary differential equations are solved numerically using Runge–Kutta and Newtons method. For physical relevance we analyzed the behavior of homogeneous and heterogeneous profiles individually in the presence of induced magnetic field. The effects of different non-dimensional governing parameters on velocity, induced magnetic field, temperature and concentration profiles, along with the skin friction coefficient and local Nusselt number, are discussed and presented through graphs. The results of the present study are validated by comparing with the existed literature. Results indicate that induced magnetic field parameter and stretching ratio parameter have the tendency to enhance the heat transfer rate.

Keywords

Induced magnetic field ; Homogeneous–heterogeneous reactions ; Non-uniform heat source/sink ; Casson fluid ; Stagnation flow

Nomenclature

${\textstyle u,{\mbox{ }}v}$- Velocity components in ${\textstyle x{\mbox{ }}{\mbox{and}}{\mbox{ }}y}$ directions

${\textstyle I_{1}{\mbox{​}},{\mbox{ }}I_{2}}$- Magnetic components in ${\textstyle x{\mbox{ }}{\mbox{and}}{\mbox{ }}y}$ directions

${\textstyle I_{0}}$- Magnetic component in free stream flow

${\textstyle x}$- Distance along the surface

${\textstyle y}$- Distance normal to the surface

${\textstyle c_{p}}$- Specific heat capacity at constant pressure

${\textstyle f}$- Dimensionless velocity

${\textstyle u_{e}}$- Free stream velocity

${\textstyle T}$- Temperature of the fluid

${\textstyle q^{'''}}$- Dimensionless non-uniform heat source/sink

${\textstyle A\ast }$ ,${\textstyle B\ast }$- Non-uniform heat source/sink

${\textstyle C_{f}}$- Skin friction coefficient

${\textstyle Nu}$- Local Nusselt number

${\textstyle {Re}_{x}}$- Local Reynolds number

${\textstyle Pr}$- Prandtl number

${\textstyle a,{\mbox{ }}d}$- Positive constants

${\textstyle k}$- Thermal conductivity

${\textstyle K}$- Homogeneous reaction

${\textstyle K_{s}}$- Heterogeneous reaction

Greek symbols

${\textstyle a,{\mbox{ }}b}$- Rate constants

${\textstyle \eta }$- Similarity variable

${\textstyle \sigma }$- Electrical conductivity

${\textstyle \theta }$- Dimensionless temperature

${\textstyle \rho }$- Density

${\textstyle \beta }$- Casson parameter

${\textstyle \lambda }$- Reciprocal magnetic Prandtl number

${\textstyle \Lambda }$- Magnetic parameter

${\textstyle {\mu }_{e}}$- Magnetic permeability

${\textstyle \mu }$- Dynamic viscosity

${\textstyle \upsilon }$- Kinematic viscosity

${\textstyle D_{A}{\mbox{​}},{\mbox{ }}D_{B}}$- Diffusion coefficients

${\textstyle \alpha }$- Thermal diffusivity

${\textstyle \delta }$- ${\textstyle a/c}$ stretching ratio parameter

Subscripts

${\textstyle f}$- Fluid

${\textstyle w}$- Condition at the wall

${\textstyle \infty }$- Condition at the free stream

1. Introduction

The study of convection flows over stretching sheet has extensive applications in the field of manufacturing production of plastic, polythene, paper, polymer extrusion, cooling of elastic sheets, and fiber technology, science and engineering technology. The applications of stretching surface were broadly discussed by Chaim [1] . The flow of a non-Newtonian fluid over a stretching sheet has potential applications in the biosciences, blood flows, jelly and engineering. Casson is a shear thinning liquid. It can exhibit yield stress. If applied yield stress is greater than the shear stress, then it acts as solid, whereas if yield stress is lesser than the applied shear stress then it starts to move. The application of Casson fluid was discussed by Hayat et al. [2] . The homogeneous–heterogeneous reactions on stagnation-point flow past a stretching surface was discussed by Bachok et al. [3] . Peristaltic flow of a Carreau fluid flow with convective boundary conditions was analyzed by Hayat et al. [4] , and concluded that brinkman number and hall parameters help to enhance the thermal boundary layer thickness. Khan and Pop [5] investigated the viscoelastic fluid flow through a stretching surface with homogeneous–heterogeneous effects. Hayat et al. [6] illustrated the three-dimensional MHD bidirectional flow of a nanofluid past a permeable stretching sheet in the presence of slip condition and homogeneous–heterogeneous reactions.

Heat transfer analysis of magneto hydrodynamic stagnation-point flow toward a stretching surface in the presence of induced magnetic field was done by Ali et al. [7] . Abbas et al. [8] considered the slip conditions and homogeneous–heterogeneous effects on MHD stagnation-point flow of viscous fluid past a stretching or shrinking surface. Sandeep and Sulochana [9] discussed the mixed convection flow of an unsteady micropolar fluid flow over a stretching or shrinking sheet in the presence of magnetic and non-uniform heat source/sink. Raju et al. [10] analyzed the non-uniform heat source or sink effects on ferrofluid flow through a flat plate with thermal radiation and aligned magnetic field effects. The stagnation-point flow toward a vertical stretching surface was explained by Ishak et al. [11] . Mallikarjuna et al. [12] investigated the variable porosity regime on convection flow over a vertical cone with chemical reaction and magnetic field effect. An unsteady MHD nanofluid flow through a stretching surface in the presence of non-uniform heat source/sink and magnetic field effect was studied by Sandeep et al. [13] . Pal and Mandal [14] analyzed the induced magnetic field effect on stagnation point flow of a nanofluid past a non-isothermal stretching surface.

Heat transfer analysis of a stagnation point viscoelastic fluid flow toward a stretching sheet was investigated by Mahapatra and Gupta [15] . Gorla [16] depicted the stagnation point flow of non-Newtonian fluid flow in the presence of transverse magnetic field. Heat transfer characteristics of MHD Casson fluid flow past a permeable an exponentially stretching sheet was considered by Raju et al. [17] . Hayat et al. [18] analyzed the two-dimensional flow of Eyring–Powell fluid flow toward a stretching sheet with homogeneous–heterogeneous reactions and concluded that the Eyring–Powell fluid material parameter enhances the boundary layer thickness. Heat transfer characteristics of Casson fluid flow past a permeable exponentially stretching sheet in the presence of thermal radiation was discussed by Pramanik [19] and concluded that an increasing value of Casson parameter suppresses the velocity profiles. Animasaun [20] discussed the MHD Casson fluid flow in the presence of viscous dissipation. Stagnation point flow of optimized exact solution for oblique flow of Casson-nanofluid with convective boundary conditions was discussed by Nadeem et al. [21] . Makinde and Aziz [22]  and [23] examined the boundary layer analysis of a nanofluid flow through a stretching surface in the presence of convective boundary conditions and buoyancy effects. MHD heat transfer characteristics of an electrically conducting nanofluid flow through nonlinearly stretching surface in the presence of viscous dissipation was examined numerically by Mabood et al. [24] . Nadeem and Saleem [25] proposed an analytical solution for an unsteady mixed convection MHD flow on a rotating cone. Dissipation and magnetic field effects on the boundary layer flow of a power-law nanofluid induced by a permeable stretching/shrinking sheet were investigated numerically by Dhanai et al. [26] . Chaudhary and Merkin [27] proposed a simple isothermal model for homogeneous–heterogeneous reactions for boundary layer flow. Very recently, Hayat et al. [28] and Mahanta and Shaw [29] investigated the heat transfer characteristics of Casson fluid through different channels. Hayat et al. [30] studied the homogeneous and heterogeneous reactions on the flow over a nanotube with homogeneous heating. Further, Farooq et al. [31] discussed the homogeneous–heterogeneous characteristics on the flow of Jeffrey fluid.

In this study, we investigated the induced magnetic field and non-uniform heat source or sink effects on the stagnation-point flow of a non-Newtonian fluid toward a stretching sheet in the presence of homogeneous–heterogeneous reactions. The emerging set of governing nonlinear partial differential equations is transformed into a set of ordinary differential equations using similarity transformation, which are then solved numerically using Runge–Kutta and Newtons method. The effects of different non-dimensional governing parameters on velocity, induced magnetic field, temperature and concentration profiles, along with the friction factor and local Nusselt number, are discussed and presented through graphs and tables.

2. Flow analysis

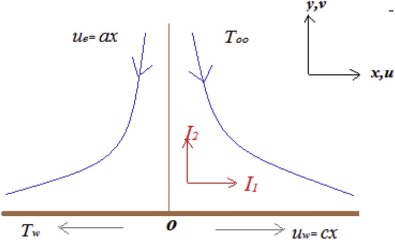
Consider a steady, incompressible, electrically conducting stagnation point flow of a Casson fluid toward a stretching sheet in the presence of induced magnetic field, non-uniform heat source/sink and homogeneous–heterogeneous reactions. The stretching sheet is considered along the ${\textstyle x-}$ axis and ${\textstyle y-}$ axis is normal to it as displayed in Fig. 1 .

Fig. 1. Physical model and coordinate system.

The governing boundary layer equations for the flow and induced magnetic field profiles are given by [7] .

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0,$

( 1)

${\frac {\partial I_{1}}{\partial x}}+{\frac {\partial I_{2}}{\partial y}}=$$0,$

( 2)

$\rho \left(u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}\right)=$$u_{e}{\mbox{ }}\left(x\right){\frac {\partial u_{e}{\mbox{ }}\left(x\right)}{\partial x}}+$$\nu \left(1+{\frac {1}{\beta }}\right){\frac {{\partial }^{2}u}{\partial y^{2}}}$ ${\mbox{ }}+{\mbox{ }}{\frac {\mu }{4\pi }}\left(I_{1}{\frac {\partial I_{1}}{\partial x}}+\right.$$\left.I_{2}{\frac {\partial I_{1}}{\partial y}}-I_{e}{\frac {\partial I_{e}}{\partial x}}\right),$

( 3)

$u{\frac {\partial I_{1}}{\partial x}}+v{\frac {\partial I_{1}}{\partial y}}=$$I_{1}{\frac {\partial u}{\partial x}}+I_{2}{\frac {\partial u}{\partial y}}+$${\mu }_{e}{\frac {{\partial }^{2}I_{1}}{\partial y^{2}}},$

( 4)

Subjected to the boundary conditions

${\begin{array}{c}u=u_{w}{\mbox{ }}\left(x\right)=cx,{\mbox{ }}v=0,{\mbox{ }}{\frac {\partial I_{1}}{\partial y}}=I_{2}=0,{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{at}}{\mbox{ }}y=0,\\u=u_{e}{\mbox{ }}\left(x\right)=ax,{\mbox{ }}{\frac {\partial u}{\partial y}}\rightarrow 0,{\mbox{ }}{\frac {\partial v}{\partial y}}\rightarrow 0,{\mbox{ }}I_{1}=I_{e}{\mbox{ }}\left(x\right)=I_{0}x,{\mbox{ }}{\mbox{as}}{\mbox{ }}y\rightarrow \infty ,\end{array}}\rbrace$

( 5)

where ${\textstyle {\mu }_{e}}$ is the magnetic diffusivity of the fluid, which is given by ${\textstyle {\mu }_{e}=1/4\pi \sigma }$ , ${\textstyle u}$ and ${\textstyle v}$ are the velocity components along the ${\textstyle x}$ and ${\textstyle y}$ directions, respectively, ${\textstyle \rho }$ is the density, and ${\textstyle \nu }$ is the viscosity.

To convert the governing equations of the flow into a set of nonlinear ordinary differential equations, we now introduce the following similarity transformation:

${\begin{array}{c}u=cxf^{'}\left(\eta \right),{\mbox{ }}v=-{\upsilon }_{f}{}^{1/2}c^{1/2}f\left(\eta \right),{\mbox{ }}\eta ={\upsilon }_{f}{}^{-1/2}c^{1/2}y,\\I_{1}=I_{0}xg^{'}\left(\eta \right),{\mbox{ }}I_{2}=-I_{0}{\upsilon }_{f}^{1/2}c^{-1/2}g\left(\eta \right),\end{array}}\rbrace$

( 6)

Equation (6) identically satisfies the continuity equations (1) and (2) , and equations (3) and (4) become

$\left(1+{\frac {1}{\beta }}\right)f^{'''}-\left({f^{'}}^{2}-\right.$$\left.ff^{''}\right)+\Lambda \left({g^{'}}^{2}-\right.$$\left.gg^{''}-1\right)+{\left({\frac {a}{c}}\right)}^{2}=$$0,$

( 7)

$\lambda g^{'''}+fg^{''}-f^{''}g=0,$

( 8)

Subjected to the transformed boundary conditions

${\begin{array}{c}f=g=0,{\mbox{ }}f^{'}=1,{\mbox{ }}g^{''}=0,{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{at}}{\mbox{ }}\eta =0,\\f^{'}=a/c,{\mbox{ }}g^{'}=1,{\mbox{ }}g^{''}=f^{''}=0,{\mbox{ }}{\mbox{as}}{\mbox{ }}\eta \rightarrow \infty ,\end{array}}\rbrace$

( 9)

where ${\textstyle \beta }$ is the Casson parameter, ${\textstyle \Lambda }$ is the magnetic parameter, and ${\textstyle \lambda }$ is the reciprocal magnetic Prandtl number, which are given by ${\textstyle \Lambda ={\frac {\mu H_{0}^{2}}{4\pi \rho c^{2}}},{\mbox{ }}\lambda =}$${\frac {1}{4\pi \sigma \upsilon }}$ .

3. Heat transfer analysis

The governing equation for energy in the presence of no-uniform heat source/sink is given by

$\left(u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}\right)=$$\alpha {\frac {{\partial }^{2}T}{\partial y^{2}}}+{\frac {1}{\rho c_{p}}}q^{'''},$

( 10)

With the boundary conditions

$T=T_{w}{\mbox{​}},{\mbox{ }}{\mbox{at}}{\mbox{ }}y=0,{\mbox{ }}T=$$T_{\infty }{\mbox{​}},{\mbox{ }}{\mbox{as}}{\mbox{ }}y\rightarrow \infty ,$

( 11)

The space and temperature-dependent heat generation/absorption (non-uniform heat source/sink) ${\textstyle q^{'''}}$ is defined by Sandeep and Sulochana [9] :

$q^{'''}=\left({\frac {ku_{w}{\mbox{ }}\left(x\right)}{x\upsilon }}\right)\left(A\ast \left(T_{w}-\right.\right.$$\left.\left.T_{\infty }\right)f^{'}+B\ast \left(T-\right.\right.$$\left.\left.T_{\infty }\right)\right),$

( 12)

where T   is the fluid temperature, ${\textstyle \alpha }$ is the thermal diffusivity coefficient, ${\textstyle \upsilon }$ is the kinematic viscosity of the base fluid, and ${\textstyle A\ast }$ and ${\textstyle B\ast }$ are parameters of the space and temperature-dependent internal heat generation/absorption. The positive and negative values of ${\textstyle A\ast }$ and ${\textstyle B\ast }$ represent heat generation and absorption parameters respectively. Now introducing the similarity transformation

$\eta ={\upsilon }_{f}{}^{-1/2}c^{1/2}y,{\mbox{ }}\theta \left(\eta \right)=$$\left(T-T_{\infty }\right)/\left(T_{w}-T_{\infty }\right),$

( 13)

By using equation (13) , equations (10) , (11)  and (12) transformed to

${\theta }^{''}+\left(A\ast f^{'}+B\ast \theta \right)+$$Prf{\theta }^{'}=0,$

( 14)

With the transformed boundary conditions

$\theta =1,{\mbox{ }}{\mbox{at}}{\mbox{ }}\eta =0,{\mbox{ }}\theta =$$0,{\mbox{ }}{\mbox{as}}{\mbox{ }}\eta \rightarrow \infty ,$

( 15)

where ${\textstyle Pr={\frac {v}{\alpha }}}$ is the Prandtl number.

4. Mass transfer analysis

We considered a simple homogeneous–heterogeneous reaction model that exists as proposed by Chaudhary and Merkin [27] in the following form:

$\left(u{\frac {\partial a}{\partial x}}+v{\frac {\partial a}{\partial y}}\right)=$$D_{A}{\frac {{\partial }^{2}a}{\partial y^{2}}}-k_{c}ab^{2}{\mbox{​}},$

( 16)

$\left(u{\frac {\partial b}{\partial x}}+v{\frac {\partial b}{\partial y}}\right)=$$D_{B}{\frac {{\partial }^{2}b}{\partial y^{2}}}+k_{c}ab^{2}{\mbox{​}},$

( 17)

Subject to the boundary conditions

${\begin{array}{c}D_{A}{\frac {\partial a}{\partial y}}=k_{s}a\left(y\right),{\mbox{ }}D_{B}{\frac {\partial b}{\partial y}}=-k_{s}a\left(y\right){\mbox{ }}{\mbox{at}}{\mbox{ }}y=0,\\a\left(y\right)=a_{0}{\mbox{​}},{\mbox{ }}b\left(y\right)=0{\mbox{ }}{\mbox{as}}{\mbox{ }}y\rightarrow \infty ,\end{array}}\rbrace$

( 18)

where${\textstyle D_{A}{\mbox{ }}{\mbox{and}}{\mbox{ }}D_{B}}$ are the diffusion coefficients. We now introduced the similarity transformations as

$G\left(\eta \right)=a/a_{0}{\mbox{​}},{\mbox{ }}H\left(\eta \right)=$$b/a_{0}{\mbox{​}},$

( 19)

Using equation (19) , equations (16) , (17)  and (18) transformed to

$G^{''}+Sc\left(fG^{'}-KGH^{2}\right)=0,$

( 20)

$\delta H^{''}+Sc\left(fH^{'}+KGH^{2}\right)=0,$

( 21)

With the transformed boundary conditions

${\begin{array}{c}G^{'}=K_{s}G,{\mbox{ }}\delta H^{'}=-K_{s}G{\mbox{ }}{\mbox{at}}{\mbox{ }}\eta =0,\\G=1,{\mbox{ }}H=0{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{as}}{\mbox{ }}\eta \rightarrow \infty ,\end{array}}\rbrace$

( 22)

${\textstyle Sc}$ is the Schmidt number, ${\textstyle K}$ is the measure of strength of homogeneous reaction, ${\textstyle K_{s}}$ is the strength of heterogeneous reaction, ${\textstyle Re=c/\nu }$ is the Reynolds number and ${\textstyle \delta }$ is the ratio of diffusion coefficient, which are represented below.

$\delta ={\frac {D_{B}}{D_{A}}},{\mbox{ }}Sc={\frac {\nu }{D_{A}}},{\mbox{ }}K=$${\frac {k_{c}a_{0}{}^{2}}{c}},{\mbox{ }}K_{s}={\frac {k_{s}}{D_{A}{\sqrt {Re}}}}\rbrace$

( 23)

In most of the applications, we expect the diffusion coefficient of chemical species A and B to be of comparable size. This leads us to make an assumption that the diffusion coefficients D_A and D_B are equal. That is the case to ${\textstyle \delta =1}$ .

For engineering interest, the shear stress coefficient ${\textstyle C_{f}}$ (friction factor) and the local Nusselt number ${\textstyle Nu_{x}}$ are given by

$C_{f}={\frac {{\tau }_{w}}{{\rho }_{f}U_{w}^{2}}},{\mbox{ }}{\mbox{ }}Nu_{x}=$${\frac {xq_{w}}{k_{f}{\mbox{ }}\left(T_{w}-T_{\infty }\right)}},\rbrace$

( 24)

Here, ${\textstyle {\tau }_{w}}$ is the wall shear stress and ${\textstyle q_{w}}$ is the wall heat flux, which are given by

${\tau }_{w}=\mu {\left({\frac {\partial u}{\partial y}}\right)}_{y=0}{\mbox{​}},{\mbox{ }}q_{w}=$$-k{\left({\frac {\partial T}{\partial y}}\right)}_{y=0}{\mbox{​}},\rbrace$

( 25)

Using (6) and (13) we get

${Re}_{x}^{1/2}C_{f}=\left(1+{\frac {1}{\beta }}\right)f^{''}\left(0\right),$

( 26)

${Re}_{x}^{-1/2}Nu_{x}=-{\theta }^{'}\left(0\right),$

( 27)

where ${\textstyle {Re}_{x}=u_{w}x/v_{f}}$ is the local Reynolds number.

5. Results and discussion

The set of nonlinear ordinary differential equations (7) , (8) , (10) , (20) and (21) subjected to the boundary conditions (9), (11) and (22) are solved numerically using Runge–Kutta and Newtons method (Mallikarjuna et al. [12] ). The influence of non-dimensional governing parameters on velocity, induced magnetic field, temperature and concentration profiles, along with the friction factor coefficient and local Nusselt number, are discussed and presented through graphs and tables. For numerical calculations, we considered ${\textstyle K=K_{S}=1,{\mbox{ }}a/c=0.5,{\mbox{ }}\delta =3,{\mbox{ }}\lambda =}$$0.2,{\mbox{ }}Pr=1$ , ${\textstyle \Lambda =A\ast =B\ast =0.1,{\mbox{ }}Sc=0.6}$ . In the entire study we kept these values as common except the variations in the corresponding graphs and tables. In this paper green color indicates the Newtonian fluid case and red color indicates the non-Newtonian fluid case.

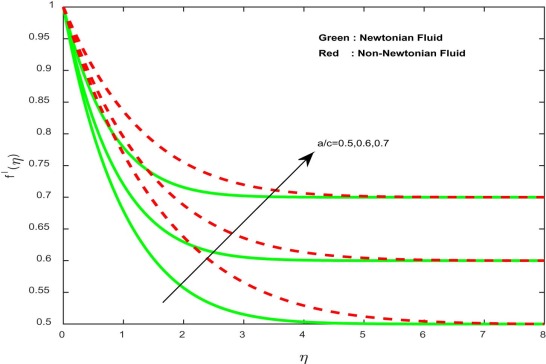
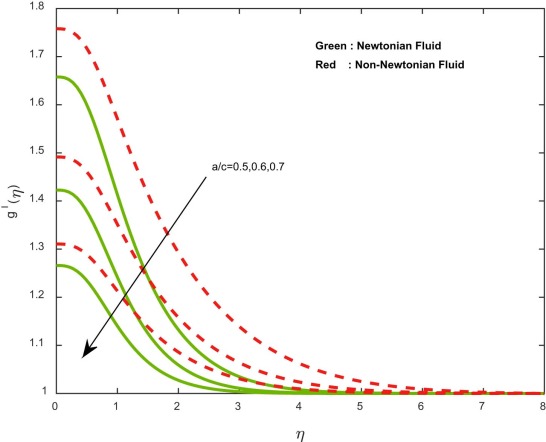
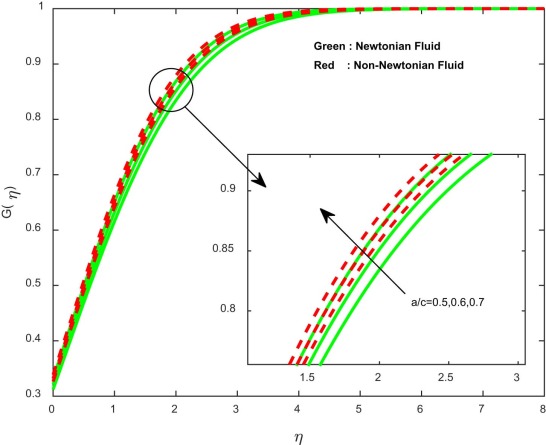
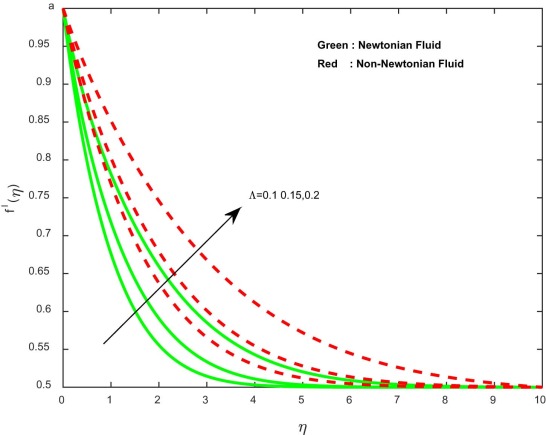
Fig. 2 , Fig. 3 , Fig. 4  and Fig. 5 depict the influence of stretching ratio parameter on velocity, induced magnetic field and concentration profiles for both Newtonian and non-Newtonian fluid cases. It is evident that the velocity and homogeneous concentration profiles are encouraged with increasing values of stretching ratio parameter, and reverse profiles are observed in induced magnetic field and heterogeneous concentration profiles. Basically, an increase in the stretching ratio parameter initially develops the more pressure on the flow; due to this reason, we have seen an enhancement in the velocity profiles.

Fig. 2. Velocity profiles for different values of stretching ratio parameter.

Fig. 3. Induced magnetic field profiles for different values of stretching ratio parameter.

Fig. 4. Concentration profiles for different values of stretching ratio parameter.

Fig. 5. Concentration profiles for different values of stretching ratio parameter.

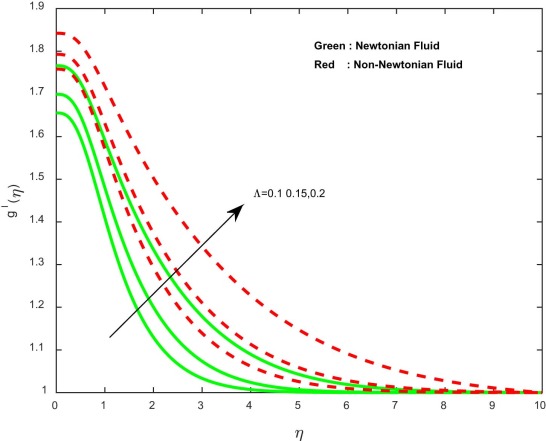
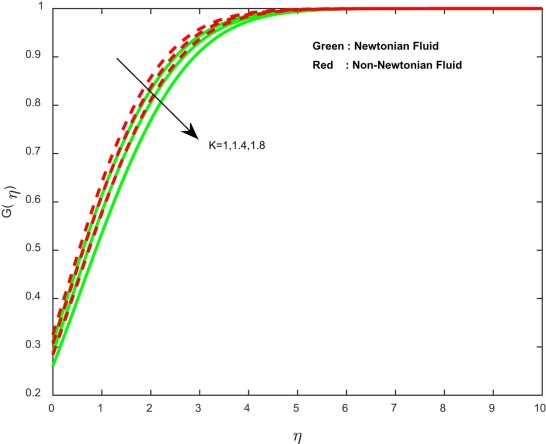
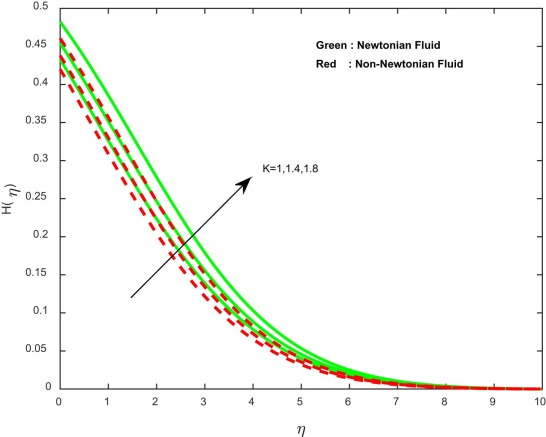
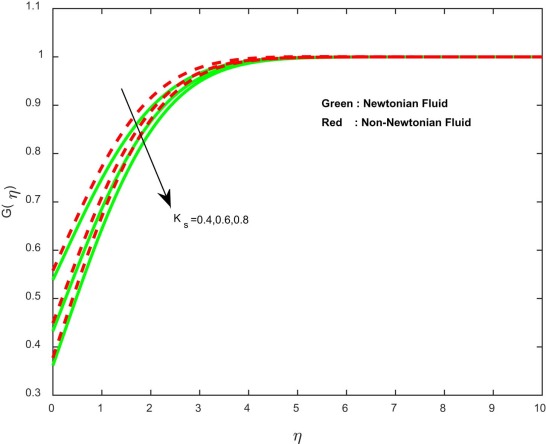
The effects of induced magnetic field parameter on velocity, induced magnetic field and concentration profiles for both Newtonian and non-Newtonian cases are plotted in Fig. 6 , Fig. 7 , Fig. 8  and Fig. 9 . It is noticed that the momentum, thermal and concentration boundary layer thicknesses are enhanced with an increase in the induced magnetic field parameter. Usually an increase in the induced magnetic field develops the electric current. This electric force can help to enhance the momentum and thermal boundary layer thickness. This leads to an increase in the momentum and thermal boundary layer thickness.

Fig. 6. Velocity profiles for different values of induced magnetic field parameter.

Fig. 7. Induced velocity profiles for different values of induced magnetic field parameter.

Fig. 8. Concentration profiles for different values of induced magnetic field parameter.

Fig. 9. Concentration profiles for different values of induced magnetic field parameter.

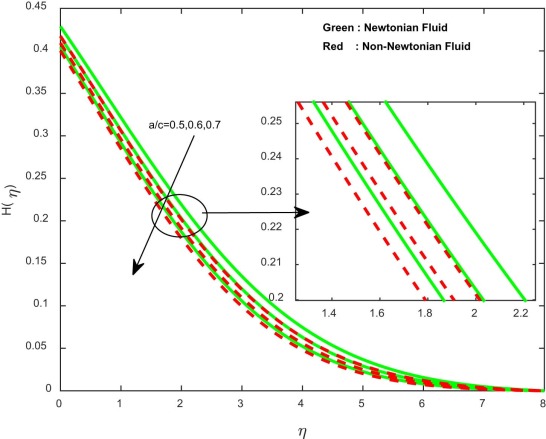
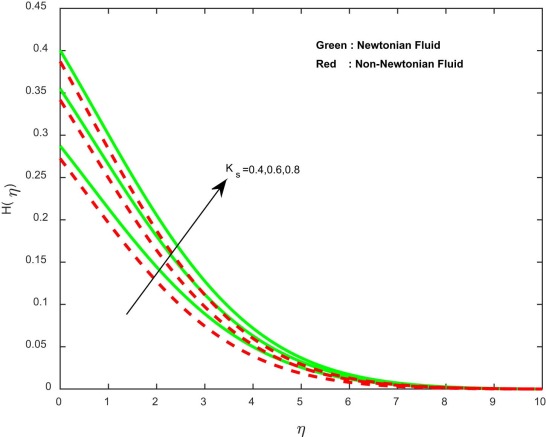
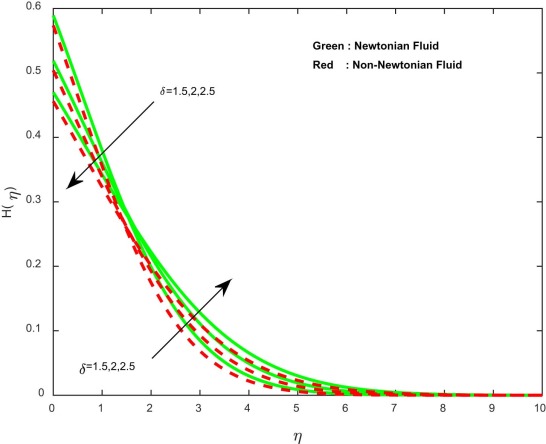
The influence of homogeneous reaction parameter on concentration profiles for both Newtonian and non-Newtonian cases is depicted in Fig. 10  and Fig. 11 . It displays that an increasing value of ${\textstyle K}$ enhances the ${\textstyle H}$ concentration profiles and depreciates the${\textstyle G}$ concentration profiles. It may be due to the fact that the reaction rates dominate diffusion coefficients. Quite similar results are displayed in Fig. 12  and Fig. 13 , with an increase in the heterogeneous parameter. This agrees with the general physical behavior of homogeneous and heterogeneous reactions.

Fig. 10. Concentration profiles for different values of strength of homogeneous reaction parameter.

Fig. 11. Concentration profiles for different values of strength of homogeneous reaction parameter.

Fig. 12. Concentration profiles for different values of heterogeneous reaction parameter.

Fig. 13. Concentration profiles for different values of strength of heterogeneous reaction parameter.

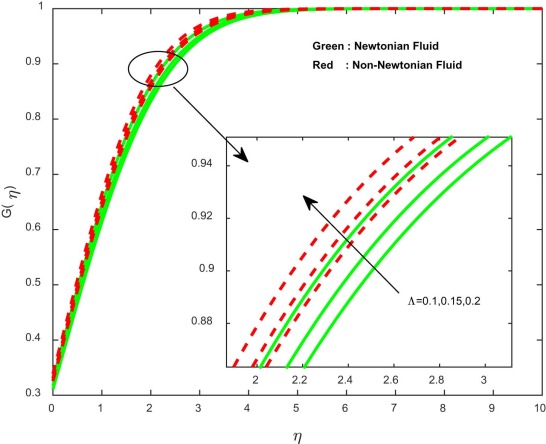
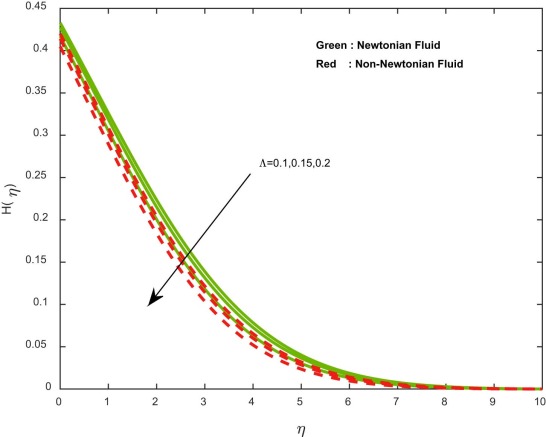
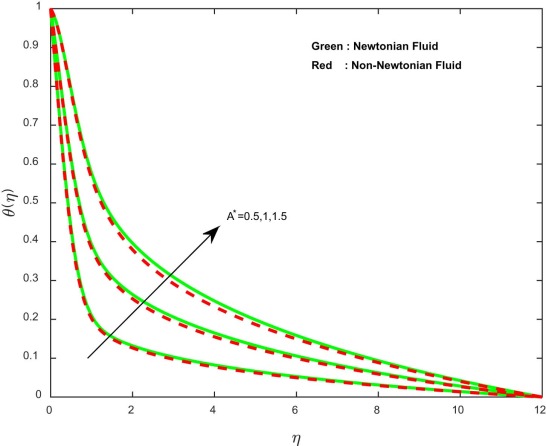
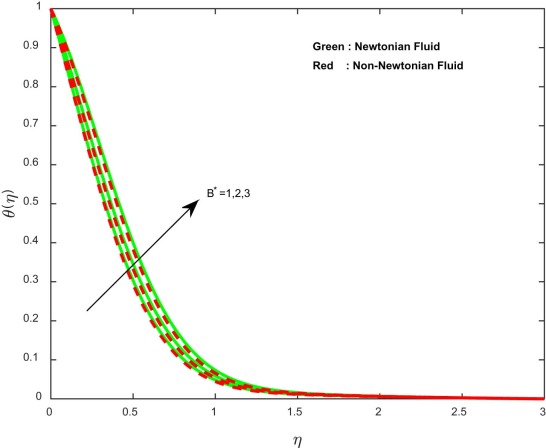
The effect of the ratio of the diffusion coefficient on the concentration profiles is depicted in Fig. 14 . Mixed profiles in the concentration are observed; initially, less diffused particles are developed in the concentration. Due to this reason, initially we have noticed depreciation in the concentration profiles. Fig. 15  and Fig. 16 illustrate the effect of non-uniform heat source or sink parameter on temperature profiles. Generally, higher values of non-uniform heat source or sink parameter enhance temperature profiles. Because it generates an internal energy in the flow, we have seen an improvement in temperature profiles.

Fig. 14. Concentration profiles for different values of ratio of diffusion parameter.

Fig. 15. Temperature profiles for different values of non-uniform heat source/sink parameter.

Fig. 16. Temperature profiles for different values of non-uniform heat source/sink parameter.

Table 1  and Table 2 depict the comparison of the present results with previously published work under some special limited cases. We found an excellent agreement of the present results with existing results. This proves the validity of the present results along with the accuracy of the numerical technique we used in this study. Table 3  and Table 4 presented the effect of various emerging thermo physical parameters for skin friction coefficients and local Nusselt number for both Newtonian and non-Newtonian fluid cases. It is evident that the friction factor coefficients and heat transfer rate are enhanced with an increase in the induced magnetic field parameter. The quite similar types of results are displayed in stretching ratio parameter. It is also observed that an increase in the non-uniform heat source or sink parameter declines the rate of heat transfer.

Table 1. Comparison of the skin friction coefficient when ${\textstyle K_{s}=K=\Lambda =K=A\ast =B\ast =Sc=0{\mbox{ }}and{\mbox{ }}\beta \rightarrow \infty }$ .

$a/c$	Ishak et al. [11]	Mahapatra and Gupta [15]	Ali et al. [7]	Present
0.1	−0.9694	−0.9694	−0.9694	−0.96941
0.2	−0.9181	−0.9181	−0.9181	−0.91810
0.5	−0.6673	−0.6673	−0.6673	−0.66731
2	2.0175	2.0175	2.0175	2.01750
3	4.7294	4.7293	4.7293	4.72931

Table 2. Comparison of local Nusselt number when ${\textstyle K=K_{s}=Sc=\Lambda =K=A\ast =B\ast =0,{\mbox{ }}\beta \rightarrow \infty }$ .

$a/c$	$Pr$
	Mahapatra and Gupta [15]				Present results
	0.05	0.5	1	1.5	0.05	0.5	1	1.5
0.1	−0.081	−0.383	−0.603	−0.777	−0.0811	−0.3833	−0.6031	−0.7772
0.2	−0.099	−0.408	−0.625	−0.797	−0.0991	−0.4082	−0.6252	−0.7971
0.5	−0.136	−0.473	−0.692	−0.863	−0.1360	−0.4731	−0.6921	−0.8632
1	−0.178	−0.563	−0.796	−0.974	−0.1782	−0.5632	−0.7962	−0.9741
2	−0.241	−0.709	−0.974	−1.171	−0.2413	−0.7094	−0.9743	−1.1713
3	−0.289	−0.829	−1.124	−1.341	−0.2891	−0.8290	−1.1241	−1.3411

Table 3. The physical parameter values for Newtonian fluid case.

$a/c$	$\Lambda$	$K$	$K_{s}$	$A\ast$	$B\ast$	$\delta$	$f^{''}\left(0\right)$	${\theta }^{'}\left(0\right)$
0.5							−0.510405	1.731575
0.6							−0.458589	1.739244
0.7							−0.371571	1.753433
	0.1						−0.516500	1.723825
	0.15						−0.435305	1.739196
	0.2						−0.321719	1.760058
		1					−0.516500	1.723825
		1.4					−0.516500	1.723825
		1.8					−0.516500	1.723825
			0.4				−0.516500	1.723825
			0.6				−0.516500	1.723825
			0.8				−0.516500	1.723825
				0.5			−0.520685	1.268812
				1			−0.520685	0.707954
				1.5			−0.520685	0.147097
					1		−0.475514	1.521289
					2		−0.475514	1.216227
					3		−0.475514	0.860203
						1.5	−0.516500	1.723825
						2	−0.516500	1.723825
						2.5	−0.516500	1.723825

Table 4. The physical parameter values in non-Newtonian fluid case.

$a/c$	$\Lambda$	$K$	$K_{s}$	$A\ast$	$B\ast$	$\delta$	$f^{''}\left(0\right)$	$-{\theta }^{'}\left(0\right)$
0.5							−0.305742	1.766651
0.6							−0.277062	1.769630
0.7							−0.225497	1.777041
	0.1						−0.305683	1.760185
	0.15						−0.253464	1.769873
	0.2						−0.183574	1.782195
		1					−0.305683	1.760185
		1.4					−0.305683	1.760185
		1.8					−0.305683	1.760185
			0.4				−0.305683	1.760186
			0.6				−0.305683	1.760185
			0.8				−0.305683	1.760185
				0.5			−0.305679	1.297576
				1			−0.305679	0.726128
				1.5			−0.305679	0.154680
					1		−0.328580	1.551278
					2		−0.328580	1.255117
					3		−0.328580	0.913042
						1.5	−0.305683	1.760185
						2	−0.305683	1.760185
						2.5	−0.305683	1.760185

6. Conclusions

This study deals with the stagnation-point flow of a Casson fluid past a stretching sheet in the presence of induced magnetic field and homogeneous–heterogeneous reactions. The non-uniform heat source/sink is also taken into account. The arising sets of governing nonlinear coupled partial differential equations are transformed into a set of nonlinear coupled ordinary differential equations using self-similarity transformations, which are then solved numerically. The conclusions are as follows:

• Heat transfer performance of Newtonian fluids was comparatively high when compared with the transfer performance of non-Newtonian fluids.
• The non-uniform heat source/sink parameter enhances the temperature profiles for both Newtonian and non-Newtonian fluid cases.
• Stretching ratio parameter improves the local Nusselt number and friction factor coefficients.
• An increase in the induced magnetic field parameter enhances the heat transfer rate.
• A homogeneous–heterogeneous reaction does not show significant variations in the heat transfer rate.

References

1. [1] T.C. Chiam; Micropolar fluid flow over a stretching sheet; Zeitschrift für Angewandte Mathematik und Mechanik, 62 (1982), pp. 565–568
2. [2] T. Hayat, M. Awais, M. Sajid; Mass transfer effects on the unsteady flow of UCM fluid over a stretching sheet; Int. J. Mod. Phys. B, 25 (2011), pp. 2863–2878
3. [3] N. Bachok, A. Ishak, I. Pop; On the stagnation-point flow towards a stretching sheet with homogeneous-heterogeneous reactions effects; Commun. Nonlinear Sci. Numer. Simul, 16 (2011), pp. 4296–4302
4. [4] T. Hayat, A. Tanveer, H. Yasmin, A. Alsaedi; Homogeneous-heterogeneous reactions in peristaltic flow with convective conditions; PLoS ONE, 9 (12) (2014), p. e113851
5. [5] W.A. Khan, I.M. Pop; Effects of homogeneous-heterogeneous reactions on the viscoelastic fluid towards a stretching sheet; J. Heat Transfer, 134 (2012), pp. 1–5
6. [6] T. Hayat, M. Imtiaz, A. Alsaedi; Impact of magneto hydrodynamics in bidirectional flow of nanofluid subject to second order slip velocity and heterogeneous-homogeneous reactions; J. Magn. Mater, 395 (2015), pp. 294–302
7. [7] F.M. Ali, R. Nazar, N.M. Arfin, I. Pop; MHD stagnation-point flow and heat transfer towards stretching sheet with induced magnetic field; Appl. Math. Mech. Engl. Ed, 32 (4) (2011), pp. 409–418
8. [8] Z. Abbas, M. Shekh, I. Pop; Stagnation-point flow of hydromagnetic viscous fluid over stretching/shrinking sheet with generalized slip condition in the presence of homogeneous-heterogeneous reactions; J. Taiwan Inst. Chem. Eng, 55 (2015), pp. 69–75
9. [9] N. Sandeep, C. Sulochana; Dual solutions for unsteady mixed flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink; Eng. Sci. Technol. Int. J., 8 (2015), pp. 1–8
10. [10] C.S.K. Raju, N. Sandeep, C. Sulochana, V. Sugunamma; Effects of aligned magnetic field and radiation on the flow of ferrofluids over a flat plate with non-uniform heat source/sink; Int. J. Sci. Eng, 8 (2) (2015), pp. 151–158
11. [11] A. Ishak, R. Nazar, I. Pop; Mixed convection boundary layers in the stagnation-point flow towards a vertical stretching sheet; Meccanica, 41 (2006), pp. 509–518
12. [12] B. Mallikarjuna, A.M. Rashad, A.J. Chamka, S. Hariprasad Raju; Chemical reaction effects on MHD convective heat and mass transfer flow past a rotating vertical cone embedded in a variable porosity regime; Afr. Math (2015) http://dx.doi.org/10.1007/s13370-015-0372-1
13. [13] N. Sandeep, C. Sulochana, C.S.K. Raju, M. Jayachandra Babu, V. Sugunamma; Unsteady boundary layer flow of thermophoretic MHD nanofluid past a stretching sheet with space and time dependent internal heat source/sink; Appl. Appl. Math, 10 (1) (2015), pp. 312–327
14. [14] D. Pal, G. Mandal; MHD convective stagnation-point flow of nanofluids over a non-isothermal stretching sheet with induced magnetic field; Meccanica, 50 (8) (2015), pp. 2023–2035
15. [15] T.R. Mahapatra, A.S. Gupta; Stagnation-point flow of a viscoelastic fluid towards a stretching surface; Int. J. Non-Linear Mech, 39 (2004), pp. 811–820
16. [16] R.S.R. Gorla; Non-Newtonian fluid at a stagnation point in presence of a transverse magnetic field; Mech. Res. Commun, 3 (1976), pp. 1–6
17. [17] C.S.K. Raju, N. Sandeep, V. Sugunamma, M. Jayachandrababu, J.V. Ramanareddy; Heat and mass transfer in magneto hydrodynamic Casson fluid over an exponentially permeable stretching surface; Eng. Sci. Technol. Int. J. (2015) http://dx.doi.org/10.1016/j.jestch.2015.05.010
18. [18] T. Hayat, M. Imtiaz, A. Alsaedi; Effects of homogeneous-heterogeneous reactions in flow of Powell-Eyring fluid; J. Cent. South Univ, 22 (2015), pp. 3211–3216
19. [19] S. Pramanik; Casson fluid flow and Heat transfer past an exponentially porous stretching sheet in presence of thermal radiation; Ain Shams Eng. J., 5 (2014), pp. 205–212
20. [20] I.L. Animasaun; Effects of thermophoresis, variable viscosity and thermal conductivity on free convective heat and mass transfer of non-Darcian MHD dissipative Casson fluid flow with suction and nth order of chemical reaction; J. Niger. Math. Soc, 34 (2015), pp. 11–31
21. [21] S. Nadeem, R. Mehmood, N.S. Akbar; Optimized analytical solution for oblique flow of a Casson-nanofluid with convective boundary conditions; Int. J. Therm. Sci, 78 (2014), pp. 90–100
22. [22] O.D. Makinde, A. Aziz; Boundary layer flow of a nanofluid past a stretching sheet with convective boundary condition; Int. J. Therm. Sci, 50 (2011), pp. 1326–1332
23. [23] O.D. Makinde, W.A. Khan, Z.H. Khan; Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet; Int. J. Heat Mass Transfer, 62 (2013), pp. 526–533
24. [24] F. Mabood, W.A. Khan, A.I.M. Ismail; MHD boundary layer flow and heat transfer of nanofluids over a non-linear stretching sheet: a numerical study; J. Magn. Magn. Mater, 374 (2015), pp. 569–576
25. [25] S. Nadeem, S. Saleem; Analytical treatment of unsteady mixed convection MHD flow on a rotating cone in a rotating frame; J. Taiwan Inst. Chem. Eng, 44 (2013), pp. 596–604
26. [26] R. Dhanai, P. Rana, L. Kumar; Multiple solutions of MHD boundary layer flow and heat transfer behavior of nanofluids induced by a power-law stretching/shrinking permeable sheet with viscous dissipation; Power Technol, 273 (2015), pp. 62–70
27. [27] M.A. Chaudhary, J.H. Merkin; A simple isothermal model for homogeneous-heterogeneous reactions in boundary layer flow: I. Equal diffusivities; Fluid Dyn. Res, 16 (1995), pp. 311–333
28. [28] T. Hayat, M. Farooq, A. Alsaedi; Thermally stratified stagnation point flow of Casson fluid with slip conditions; Int. J. Numer. Methods Heat Fluid Flow, 25 (4) (2015), pp. 724–748
29. [29] G. Mahanta, S. Shaw; 3D Casson fluid flow past a porous linearly stretching sheet with convective boundary condition; Alex. Eng. J., 54 (3) (2015), pp. 653–659
30. [30] T. Hayat, M. Farooq, A. Alsaedi; Homogeneous-heterogeneous reactions in the stagnation point flow of carbon nano tubes with Newtonian heating; AIP Adv, 5 (2015), p. 027130 http://dx.doi.org/10.1063/1.4908602
31. [31] M. Farooq, A. Alsaedi, T. Hayat; Note on characteristics of homogeneous-heterogeneous reaction in flow of Jeffrey fluid; Appl. Math. Mech. Engl. Ed, 36 (10) (2015), pp. 1319–1328