Resumen
En este artículo se desarrollan dos aproximaciones distintas para la resolución de problemas de alto orden mediante métodos de descomposición propia generalizada (PGD, del inglés Proper Generalized Decomposition ). La primera está basada en el uso de técnicas de colocación y polinomios de Chebyshev, mientras que la segunda se basa en el uso de polinomios de Hermite en el marco de una formulación de Galerkin. Ambas poseen ventajas e inconvenientes, que se analizan en detalle con la ayuda de distintos problemas clásicos de validación.
Abstract
In this paper two different approximations for the solution of high-order problems by proper generalized decompositions (PGD) are developed. The first one is based upon the use of collocation techniques, along with Chebyshev polynomials, while the second employs Hermite polynomials in a Galerkin framework. Both approaches having pros and cons, they are studied with the help of some classical benchmark tests.
Palabras clave
Reducción de modelos ; Descomposición propia generalizada ; Hermite ; Chebyshev
Keywords
Model order reduction ; Proper generalized decompositions ; Hermite ; Chebyshev
1. Introducción
Los ingenieros han acudido tradicionalmente a la reducción de los modelos como única metodología disponible para solucionar problemas complejos en épocas en las que la capacidad de cálculo disponible no era mucha. Así, por ejemplo, el modelo de viga de Euler, Bernoulli y Navier desarrolla unas ecuaciones monodimensionales para la resolución práctica del campo de desplazamientos, deformaciones y tensiones en piezas que son realmente tridimensionales. De la misma manera, el método de los modos normales para resolver problemas elastodinámicos lineales supone que la solución del problema puede escribirse como una combinación lineal de unos pocos modos que son realmente las frecuencias propias de vibración de la estructura a analizar.
Más recientemente (ya en el siglo XX , de hecho), esta metodología de reducción de la complejidad de los modelos ha sido sistematizada y aplicada con éxito en multitud de campos de las ciencias aplicadas y la ingeniería, tanto para problemas lineales [1] , [2] , [3] and [4] como no lineales [5] and [6] . En general, estas técnicas, que reciben nombres distintos en distintos campos de la ciencia, y que han sido redescubiertas en multitud de ocasiones, como Principal Component Analysis (PCA), Proper Orthogonal Decomposition (POD), empirical eigenvectors , o muchos otros nombres similares, buscan funciones que permitan una buena aproximación de la solución empleando un número mínimo de ellas, es decir, de grados de libertad. Para ello, generalmente se han de resolver ciertos problemas similares al dado, de los cuales se extraen, mediante un proceso de minimización estadística, las funciones que contienen más información (energía) de la solución, en la esperanza de que constituyan, de la misma manera, una buena elección para el problema dado, que solo difiere ligeramente de aquellos de los cuales se conoce la solución completa.
En problemas definidos en coordenadas espacio-temporales, se trataría, en suma, de encontrar aproximaciones del tipo:
|
|
donde λi (t ) representa una colección de coeficientes temporales y ϕi (x ) una serie de funciones dependientes únicamente de variables espaciales y que son las que mejor representan, desde un punto de vista estadístico, la solución del problema. Si consideramos los resultados de una simulación de elementos finitos, de la que dispondríamos de los valores nodales para cada incremento de tiempo, y los agrupáramos todos en una matriz A cuyas columnas fueran los valores nodales u (xj , tk ), j = 1, …, M , k = 1, …, T , entonces los N vectores ϕi (x ) se corresponderían con los autovectores asociados a los N mayores valores singulares de la matriz A .
En general, este tipo de técnicas ha gozado de un amplio predicamento en muchas ramas de la ciencia, pero posee severas limitaciones. La primera, el hecho de que sean necesarias las soluciones de ciertos problemas completos similares para determinar la base ϕi con la que resolver el problema dado, en la esperanza de que ésta sea también óptima para él. La segunda, que su complejidad aumenta exponencialmente si el problema a considerar es paramétrico, es decir, del tipo:
|
|
donde los distintos pm , m = 1, …, P , representan parámetros del problema. Intentar obtener soluciones completas mallando el hiperdominio que resultaría es simplemente imposible, por el crecimiento exponencial del número de grados de libertad de la malla resultante con el número de dimensiones del espacio de fase. Es lo que se ha dado en llamar la maldición de la dimensionalidad[7] .
Para intentar solucionar la primera de las dificultades antes mencionadas, P. Ladeveze desarrolló un método a priori, es decir, que no requería la solución de problemas similares a posteriori, obteniendo así una aproximación espacio-tiempo que denominó radial loading approximation dentro de su método de LArge Time INcrements (LATIN) [8] and [9] .
Más recientemente, F. Chinesta generalizó de manera independiente esta aproximación, orientándola hacia el problema multidimensional, dando así lugar a la PGD, por oposición a la descomposición propia ortogonal (POD, por sus siglas en inglés) [10] , [11] , [12] , [13] , [14] and [15] . Desde entonces la PGD ha tenido un tremendo desarrollo en multitud de aplicaciones, como lo prueba la larga lista de referencias posibles que, sin ánimo de ser exhaustivos, se incluyen: [9] , [16] , [17] , [18] , [19] , [20] , [21] , [22] and [23] . Las «reduced bases» [24] han tratado de obtener la base reducida haciendo un muestreo óptimo del espacio paramétrico. Sin embargo, este muestreo requiere conocer estimadores de error a priori cuya obtención resulta delicada en muchas circunstancias. Por ello, en lo que sigue el trabajo se centra en la PGD que resulta ser una técnica mas sistemática.
En la sección 2 se realiza un breve resumen de las características más importantes de la técnica PGD en su versión más estándar, aquella basada en la aproximación por polinomios a trozos lineales en un método de Galerkin.
2. Un repaso a la descomposición propia generalizada
La descomposición propia generalizada (PGD) es una metodología de reduccion de modelos a priori basada en el uso de representaciones separadas. Como se ha comentado anteriormente, inicialmente se desarrolló para la resolución de problemas estructurales no lineales en espacio-tiempo [8] , pero pronto evolucionó hacia su aplicación en modelos definidos en espacios con un alto número de dimensiones y, posteriormente, se extendió a modelos generales en mecánica computacional.
La característica principal de la PGD es que aproxima la solución exacta del problema imponiendo separación de variables. Así, si , es la solución del problema, esta se aproxima en la PGD como:
|
|
( 1) |
donde d es el número de dimensiones del problema. A diferencia de otras metodologías (como la POD), las funciones son funciones desconocidas a priori. Nótese que no es estrictamente necesario realizar una descomposición completa del espacio de fase , pudiéndose agrupar ciertas dimensiones y otras no. Por ejemplo, en [25] se utiliza de manera especialmente eficiente la PGD para obtener soluciones tridimensionales en geometrías degeneradas como placas y láminas mediante una descomposición del tipo:
|
|
donde la complejidad resultante del método es esencialmente la de la determinación de las funciones y, por tanto, aproximadamente la de un problema bidimensional, siendo la determinación de las funciones de coste despreciable, al ser problemas unidimensionales.
La estrategia de determinación de las funciones incógnita sigue un algoritmo voraz (greedy) , por lo que en cada determinación de cada sumando se selecciona un óptimo local con la perspectiva de encontrar el óptimo global. Pero cada sumando está compuesto por un producto de funciones desconocidas, que se aproximan en general mediante elementos finitos, cuyos valores nodales deben determinarse. Esto da lugar, como puede comprenderse fácilmente, a un problema no lineal. El método con el que se calculan los nuevos términos de la suma puede ser cualquiera de los muchos existentes (Newton, cuasi-Newton...), pero los autores prefieren el de punto fijo, siempre que se pueda, por su sencillez conceptual y de programación. En cada paso del algoritmo se obtiene una de las funciones separadas, que se actualizan sucesivamente para minimizar el residuo.
En este artículo se desarrolla la aplicación de la PGD a la resolución de problemas de alto orden, n > 2. Se presentan y comparan 2 estrategias alternativas para resolver el problema biarmónico (n = 4): la primera hace uso del método espectral de colocación mediante polinomios de Chebyshev, mientras que la segunda combina el método de Galerkin con polinomios de Hermite para las funciones de forma. Por supuesto, no son las únicas posibles. Otras, como el uso de funciones de aproximación suaves como MLS [26] , máxima entropía local [27] , etc., serían igualmente posibles.
3. PGD para problemas de alto orden
El problema biarmónico, además de ser un problema de referencia para métodos numéricos y analíticos, aparece en muchas aplicaciones prácticas. Por ejemplo, modela la flexión de placas delgadas o el flujo de un fluido viscoso en 2D cuando se utiliza la llamada función de corriente, por ejemplo. Por ello, se ha tomado como problema de referencia sobre el que estudiar el comportamiento de las soluciones desarrolladas en este trabajo: la flexión de placas delgadas y el problema del flujo en una cavidad forzado «por la tapa»(lid-driven cavity flow) .
El problema biarmónico bidimensional se describe mediante la siguiente ecuación:
|
|
( 2) |
y se suponen las siguientes condiciones de contorno:
|
|
( 3) |
para el problema con condiciones de contorno homogéneas, donde
|
|
En el caso de la PGD, a diferencia de las técnicas de elementos finitos tradicionales, la imposición de condiciones de contorno no homogéneas juega un papel preponderante en el desarrollo del método [12] . En el siguiente epígrafe se desarrollan estos aspectos en detalle.
3.1. Un método PGD basado en la colocación de polinomios de Chebyshev
El método de colocación espectral mediante polinomios de Chebyshev se puede describir de la siguiente manera. Por un lado, se aproxima cada una de las funciones de la ecuación (1) mediante el uso de polinomios de Chebyshev. Por otro, se fuerza la anulación del residuo de las ecuaciones que las gobiernan en los nodos de la discretización. Las condiciones de contorno, en este caso asociadas a u y , se deben satisfacer también en los puntos de colocación del contorno.
En este contexto, el objetivo del método consiste en hallar N parejas de funciones {Xi (x ), Yi (y )}, i = 1, …, N tales que la solución bidimensional para el problema dado por la ecuación (2) tendrá la forma:
|
|
A pesar de que posteriormente se trabajará en forma fuerte, como corresponde a un método de colocación, el desarrollo de la PGD parte de la forma débil del problema dado por la ecuación (2) , que se obtiene a partir de:
|
|
ecuación que, como es sabido, debe cumplirse para todas las funciones test u* (x , y ) seleccionadas en un espacio funcional adecuado.
A continuación se calculan las funciones que forman parte de la representación separada. Se supone conocido, porque se ha calculado previamente, el conjunto de parejas funcionales {Xi (x ), Yi (y )}, i = 1, …, n con 1 ≤ n < N . En la iteración actual se busca la pareja de enriquecimiento {R (x ), S (y )} mediante la aplicación de un algoritmo de punto fijo en direcciones alternadas que, tras la convergencia, constituirá la siguiente pareja funcional {Xn +1 , Yn +1 }. Por lo tanto, en la iteración n + 1 suponemos la representación separada como:
|
|
La función test u* (x , y ) se supone entonces como:
|
|
( 4) |
Introduciendo las funciones de prueba y ponderación en la formulación débil se obtiene:
|
|
( 5) |
Primero, se supone que R (x ) es conocida, lo que implica que R* (x ) = 0. De esta forma, la ecuación (5) resulta:
|
|
donde
|
|
Puesto que la formulación débil se satisface para todo S* (y ), es posible regresar a su forma fuerte asociada:
|
|
Es esta ecuación diferencial de cuarto orden la que se resolverá usando el método de colocación de Chebyshev.
Una vez obtenida la función S (y ), se busca R (x ). En este caso, la función conocida es S (y ) (y por lo tanto, S* (y ) es nula), por lo que la ecuación (5) se expresará como:
|
|
donde
|
|
cuya forma fuerte se expresa como:
|
|
que, de nuevo, se calculará mediante el método de colocación de Chebyshev.
Estos 2 pasos se repetirán hasta alcanzar el punto fijo. Si se denota la función R (x ) en las iteraciones actual y previa como Rp (x ) y Rp −1 (x ), respectivamente, y de la misma forma para la función S (y ), Sp (y ) y Sp −1 (y ), se puede definir el error en la iteración actual como:
|
|
donde ɛ es un valor suficientemente pequeño. Tras la convergencia, se puede dar por calculada la siguiente pareja funcional, haciendo la identificación Xn +1 = R y Yn +1 = S .
El procedimiento de enriquecimiento debe continuar hasta que se alcance la convergencia, que se puede evaluar a partir del error E :
|
|
( 6) |
siendo otro parámetro lo suficientemente pequeño.
Para la resolución de los problemas unidimensionales de cuarto orden que aparecen en la formulación anterior se supone en primer lugar una ecuación diferencial ordinaria (ODE) de cuarto orden de tipo general:
|
|
( 7) |
La función incógnita u (x ) se aproxima en el dominio Ωx = (−1, 1) mediante la expresión:
|
|
donde M denota el número de nodos considerados en Ωx . Las coordenadas de estos nodos vienen determinadas por:
|
|
Los interpolantes Ti (x ) basados sobre los polinomios de Chebyshev verifican la propiedad de la delta de Kroenecker, es decir, Ti (xk ) = δik . Para cada nodo k , con 3 ≤ k ≤ M − 2 (los cuatro nodos restantes se utilizarán para la imposición de las condiciones de contorno), la ecuación discreta (7) se puede reescribir como:
|
|
Las funciones R (x ) y S (y ) están sujetas a las condiciones de contorno de Dirichlet y Neumann. Se debe cumplir entonces que u (x1 ) = u (xM ) = 0 y . La imposición de las condiciones da como resultado:
|
|
3.2. Método de Galerkin con polinomios de Hermite
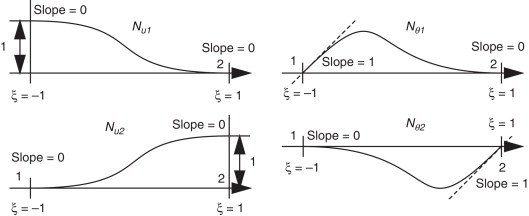
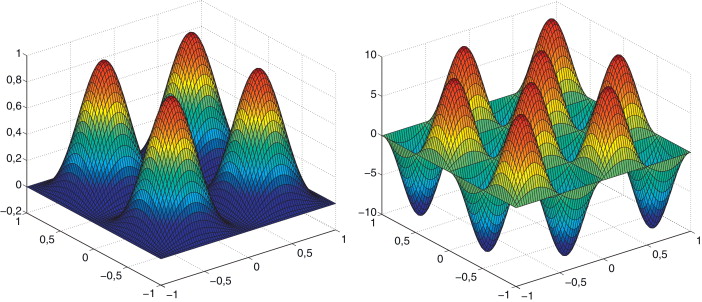
En esta sección se utilizará otra estrategia para hallar una solución aproximada al problema biarmónico. Se empleará el método de Galerkin para la discretización del problema y se usarán los polinomios de Hermite como funciones de forma (fig. 1 ). Los polinomios de Hermite permiten obtener de manera sencilla una solución con continuidad , al precio de tener que introducir los giros nodales (primera derivada de la variable esencial) como incógnitas del problema.
|
|
|
Figura 1. Polinomios de Hermite |
El procedimiento parte nuevamente de la forma débil del problema, ecuación (2) , resultante de la aplicación de integración por partes y de aplicar las condiciones de contorno:
|
|
La función de ponderación u* (x , y ) tiene la misma expresión que la ecuación (4) , de tal forma que, al introducirla junto a la función de aproximación en la formulación débil, se obtiene:
|
|
En la etapa de enriquecimiento de la PGD, se utilizará el método iterativo del punto fijo para despejar S (y ), suponiendo que R (x ) es conocida (y por lo tanto, R* (x ) = 0). Una vez obtenido S (y ), se seguirá el mismo procedimiento para obtener R (x ). Estos 2 pasos se repetirán hasta que el error en la iteración actual sea menor que un determinado valor de tolerancia.
La etapa de enriquecimiento continuará hasta que se alcance la convergencia, evaluada a partir del error E , como en la ecuación (6) .
Desde este punto de vista, la formulación PGD del problema biarmónico empleando polinomios de Hermite parecería no introducir ninguna dificultad adicional sobre la formulación estándar con operadores de orden 2. Sin embargo, la imposición de condiciones de contorno esenciales no homogéneas, definidas ahora tanto en la variable esencial como en su primera derivada, merece un comentario especial.
3.3. Imposición de condiciones de contorno esenciales no homogéneas
Como es fácil comprobar, el método PGD proporciona siempre soluciones al problema homogéneo. Para la resolución, como es el caso, de problemas con condiciones de contorno Dirichlet no homogéneas, habitualmente se acude a una técnica de cambio de variable. Así, se supone que es posible encontrar una función ψ , continua en Ω, que satisface las condiciones de contorno no homogéneas. Entonces, la solución al problema se puede obtener como:
|
|
de forma que el problema se traslada a uno homogéneo en la variable z :
|
|
( 8) |
|
|
( 9) |
Se puede encontrar información más detallada sobre cómo cambiar la condición de contorno inhomogénea a la homogénea en el contexto de la PGD en [12] .
En lo que sigue se proponen 2 alternativas:
- Empleo de R -funciones
La determinación eficiente de esta función ψ se vuelve entonces un ingrediente fundamental de la técnica desarrollada. En algunos trabajos previos de los autores [12] , la función ψ se determina mediante el uso de R -funciones [28] and [29] . Es importante hacer notar que, en el caso de problemas de alto orden, las condiciones de contorno están impuestas tanto en la variable del problema como en sus derivadas. Por tanto, obtener una función ψ que las verifique todas y hacerlo de manera eficiente se convierte en un problema de primera magnitud. Sin embargo, la técnica de R -funciones permite una solución especialmente eficiente para este problema.
En efecto, en [29] se propone una construcción de la función φ como sigue. Supóngase en primer lugar que el contorno se define como un Planar Straight Line Graph (PSLG), es decir, un conjunto de líneas rectas ∂Ωi que lo discretizan. Sea entonces ω una función normalizada , es decir, que se comporta como una pseudo-distancia:
|
|
k = 2, …, m , con n la normal al contorno esencial. Entonces, se denomina normalizador de una función f (x ) a la función
|
|
Entonces, por construcción, f* verifica que
|
|
es decir, f* se comporta esencialmente como una constante en la dirección normal al contorno.
Supóngase entonces que cada segmento ∂Ωi , i = 1, …, s , del PSLG se define mediante una ecuación implícita ωi = 0. De esta forma, si las condiciones de contorno definidas sobre ∂Ω son del tipo
|
|
k = 1, 2, …, m , entonces, si se han definido en el contorno condiciones de orden mi − 1, se puede construir la función buscada ψ de la forma
|
|
donde cada Pi se corresponde con los polinomios de Taylor generalizados
|
|
Nótese que hay un polinomio Pi para cada uno de los s segmentos del contorno sobre los que se define una condición esencial no homogénea. Se recomienda al lector interesado en la técnica de R -funciones acudir a la referencia [29] para una explicación más detallada.
En la figura 2 se muestra un ejemplo de construcción de una R -función para un contorno esencial arbitrario con condiciones esenciales no homogéneas de primer orden. En la sección 4 se incluyen ejemplos de R -funciones con condiciones en la primera derivada de la variable esencial.
|
|
|
Figura 2. Ejemplo de aplicación del método de las R -funciones a la imposición de condiciones de contorno esenciales no homogéneas. Arriba, PSLG que define el contorno esencial. Abajo, R -función resultante que, como se puede observar, se anula en el contorno esencial. |
- Formulación penalizada
Otra posibilidad, si no se quiere obtener la función ψ verificando las 2 condiciones sobre la variable esencial y su primera derivada, es obtener una que solo verifique la condición u (x ∈ Γ) = f0 e introducir la condición en la primera derivada en la formulación diferencial con un coeficiente de penalización, es decir
|
|
En lo que sigue se aplicará la formulación penalizada combinada con la colocación espectral y el uso de las R -funciones junto con una discretización Hermite.
4. Resultados numéricos
En esta sección se comparan los resultados obtenidos con las 2 estrategias anteriormente presentadas para 2 problemas que se pueden modelar con la ecuación biarmónica: la flexión de una placa de Kirchhoff rectangular y la cavidad forzada (lid-driven cavity , en inglés).
4.1. Flexión de una placa de Kirchhoff rectangular
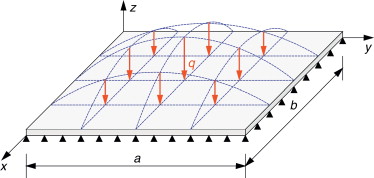
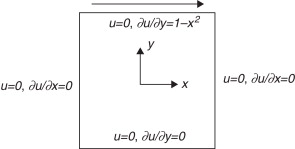
El problema propuesto en las ecuaciones (2) y (3) es equivalente al cálculo de la deformación en una placa de Kirchhoff a la que se le aplica una carga distribuida definida por la función f (x , y ) (véase la fig. 3 ). En este caso, sin embargo, se considera una placa simplemente apoyada, de forma que las condiciones de contorno esenciales en la primera derivada del desplazamiento no están fijadas, pasando a estarlo las segundas derivadas (condiciones de Neumann, proporcionales al momento flector en el borde que, al considerarse ahora libre el giro, serán nulas).
|
|
|
Figura 3. Definición del problema de una placa de Kirchhoff en flexión, solicitada por una carga distribuida f (x , y ). |
Se ha tomado para este caso,
|
|
de forma que la solución analítica del problema es
|
|
( 10) |
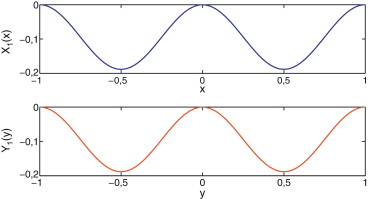
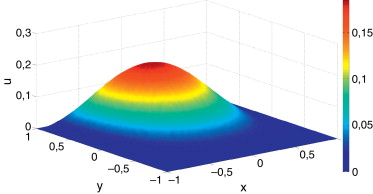
En la figura 4 se representan los modos de la solución (un solo producto X1 (x ) · Y1 (y )) en el enfoque colocación-Chebyshev. Como corresponde a la solución analítica del problema, ecuación (10) , la solución numérica debe obtenerse con un único producto funcional. Lo mismo sucede con el enfoque Galerkin-Hermite, que proporciona un único modo. La solución así construida se muestra en la figura 5 .
|
|
|
Figura 4. Modos obtenidos con el enfoque colocación-Chebyshev para la placa de Kirchhoff rectangular. |
|
|
|
Figura 5. Solución en desplazamientos (izquierda) y giros (derecha) para el problema de flexión de placas se la Sección 4.1 . Las solución está compuesta por un único modo. |
4.2. Problema con condiciones de contorno no homogéneas: la cavidad forzada
Se considera ahora el problema clásico de la cavidad forzada o lid-driven cavity flow . En este problema, un fluido se encuentra contenido en un depósito generalmente cuadrado, con condiciones de contorno de velocidad conocida en todo el contorno (velocidad nula en 3 de sus lados y forzada en el cuarto). Este último es precisamente el que fuerza el movimiento del fluido en el seno del depósito. En este caso, la solución de la ecuación biarmónica representa la función de la corriente, a partir de la cual puede calcularse la velocidad del fluido como:
|
|
La geometría y las condiciones de contorno del problema de la cavidad forzada se muestran en la figura 6 .
|
|
|
Figura 6. Condiciones de contorno en el problema de la cavidad forzada. |
El problema se considera como biarmónico bidimensional, en el dominio Ω = (− 1, 1)2 y sujeto a las condiciones de contorno:
|
|
( 11a) |
|
|
( 11b) |
donde f0 y f1 son funciones dadas. La forma de f1 para este problema se muestra en la figura 6 .
4.2.1. Enfoque colocación-Chebyshev
Se ha obtenido la función ψ (x , y ) que verifica en u (x ∈ Γ) = f0 , a la que se le ha aplicado la técnica de descomposición en valores singulares (SVD) para obtener los modos previos para el método PGD. En este caso, esta operación es trivial, al ser f0 = 0. A continuación se aplica el método de Chebyshev combinado con la PGD anteriormente expuesto, sobre la formulación penalizada, para resolver el problema con condiciones de contorno homogéneas.
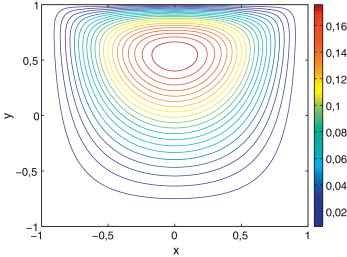
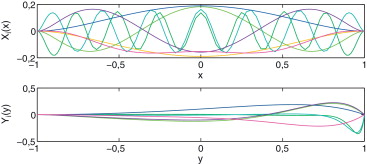
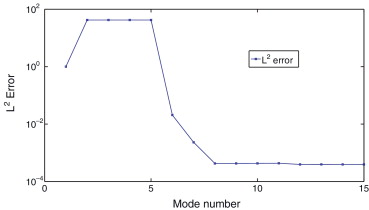
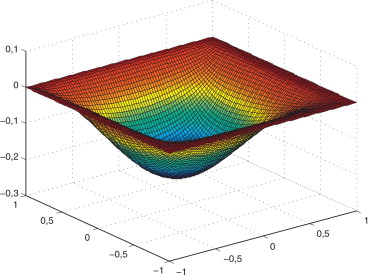
La solución numérica que se obtiene aplicando el método de Chebyshev se muestra en la figura 7 . Las líneas de corriente se muestran en la figura 8 y los modos necesarios en la figura 9 . La evolución del error se muestra en la figura 10 . La solución en este caso se ha obtenido con un número total de 8 modos.
|
|
|
Figura 7. Solución del problema de la cavidad forzada obtenida mediante colocación-Chebyshev. |
|
|
|
Figura 8. Solución del problema de la cavidad forzada obtenida mediante colocación-Chebyshev. Líneas de corriente. |
|
|
|
Figura 9. Solución del problema de la cavidad forzada obtenida mediante colocación-Chebyshev. Modos obtenidos. |
|
|
|
Figura 10. Solución del problema de la cavidad forzada obtenida mediante colocación-Chebyshev. Convergencia del error con el número de funciones empleadas en la aproximación. |
4.2.2. Enfoque Galerkin-Hermite
En este enfoque, como se ha comentado anteriormente, la solución del problema biarmónico se redefine, mediante un simple cambio de variable para la imposición de condiciones de contorno, como u = z + ψ , donde ψ es una función cuya traza es igual a las condiciones de contorno esenciales (definidas para el operador bilaplaciano sobre la función y su primera derivada) no homogéneas impuestas al problema.
Una vez obtenida la función ψ mediante la aplicación de la técnica de R -funciones mencionada anteriormente, la forma débil para el nuevo problema en z pasa a ser, para la i -ésima iteración de la etapa de enriquecimiento y supuesto conocido R (R* = 0):
|
|
Por su parte, cuando la variable conocida es S (S* = 0):
|
|
donde .
La función bidimensional representada por la matriz que se obtiene al multiplicar debe cumplir las condiciones de contorno. Para obtenerla, se ha recurrido al método de R -funciones detallado anteriormente. Una vez obtenida la superficie, se le ha aplicado descomposición en valores singulares (SVD) para la obtención de las funciones y .
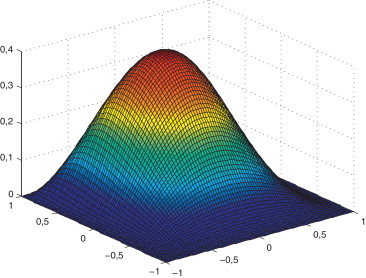
En la figura 11 se muestra la solución obtenida para la variable homogénea z . Por el contrario, en la figura 12 se muestra la función ψ que permite la imposición de las condiciones esenciales, es decir, la R -función obtenida. La forma de la solución obtenida se muestran en la figura 13 .
|
|
|
Figura 11. Solución en la variable z para el problema de la cavidad forzada de la Secćion 4.2 . |
|
|
|
Figura 12. R -función ψ para el problema de la cavidad forzada de la Secćion 4.2 . |
|
|
|
Figura 13. Solución para el problema de la cavidad forzada de la Secćion 4.2 . |
5. Conclusiones
En este trabajo se ha presentado una discusión referente a la aplicación del método de la descomposición propia generalizada a problemas de alto orden, con un énfasis especial en problema de tipo bilaplaciano. Se han estudiado, de entre la pléyade de posibles formulaciones, 2 que se han considerado como representativas. La primera, basada en el uso de polinomios de Chebyshev y métodos de colocación. La segunda, basada en un método de Galerkin y polinomios de Hermite.
Mientras que puede afirmarse con rotundidad que ambas aproximaciones al problema proporcionan resultados satisfactorios, la principal diferencia práctica que se ha encontrado entre ambas es la relativa a la imposición de condiciones de contorno esenciales. En el método de colocación se ha hecho uso de la penalización para imponer condiciones de contorno esenciales, mientras que en el caso de Galerkin se ha visto que la técnica de R -funciones, aunque formalmente compleja, proporciona una forma muy práctica de imponer tales condiciones. La penalización, sin embargo, actúa en todos los modos que se calculan, sumando los errores de cada modo en la solución final. Sin embargo, la imposición mediante R -funciones elimina esos problemas y proporciona formulaciones robustas, aunque para ello sea necesario calcular la descomposición en valores singulares de la R -función (que, por otra parte, tiene un coste computacional muy reducido).
Agradecimientos
El trabajo recogido en el presente artículo ha sido financiado parcialmente por el Ministerio de Economía e Innovación de España, a través del proyecto CICYT-DPI2011-27778-C02-01.
References
- [1] K. Karhunen; Uber lineare methoden in der wahrscheinlichkeitsrechnung; Ann. Acad. Sci. Fennicae, ser. Al. Math. Phys. (1946), p. 37
- [2] E.N. Lorenz, Empirical Orthogonal Functions and Statistical Weather Prediction. MIT, Department of Meteorology, Scientific Report Number 1, Statistical Forecasting Project, 1956.
- [3] M.M. Loève; Probability theory; The University Series in Higher Mathematics (3rd ed.), Van Nostrand, Princeton, NJ (1963)
- [4] D. Ryckelynck, F. Chinesta, E. Cueto, A. Ammar; On the a priori Model Reduction: Overview and recent developments; Archives of Computational Methods in Engineering, 12 (1) (2006), pp. 91–128
- [5] J.B. Tenenbaum, V. de Silva, J.C. Langford; A global framework for nonlinear dimensionality reduction; Science, 290 (2000), pp. 2319–2323
- [6] S. Chaturantabut, D.C. Sorensen; Nonlinear model reduction via discrete empirical interpolation; SIAM J. Sci. Comput., 32 (2010 Sep.), pp. 2737–2764
- [7] R.B. Laughlin, D. Pines; The theory of everything; Proceedings of the National Academy of Sciences, 97 (1) (2000), pp. 28–31
- [8] P. Ladeveze; Nonlinear Computational Structural Mechanics; Springer, N. Y. (1999)
- [9] P. Ladeveze, L. Chamoin; On the verification of model reduction methods based on the proper generalized decomposition; Computer Methods in Applied Mechanics and Engineering, 200 (23-24) (2011), pp. 2032–2047
- [10] A. Ammar, B. Mokdad, F. Chinesta, R. Keunings; A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids; J. Non-Newtonian Fluid Mech, 139 (2006), pp. 153–176
- [11] A. Ammar, B. Mokdad, F. Chinesta, R. Keunings; A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids. part II: transient simulation using space-time separated representations; J. Non-Newtonian Fluid Mech, 144 (2007), pp. 98–121
- [12] D. Gonzalez, A. Ammar, F. Chinesta, E. Cueto; Recent advances on the use of separated representations; International Journal for Numerical Methods in Engineering, 81 (5) (2010)
- [13] F. Chinesta, A. Ammar, E. Cueto; Recent advances in the use of the Proper Generalized Decomposition for solving multidimensional models; Archives of Computational Methods in Engineering, 17 (4) (2010), pp. 327–350
- [14] F. Chinesta, P. Ladeveze, E. Cueto; A short review on model order reduction based on proper generalized decomposition; Archives of Computational Methods in Engineering, 18 (2011), pp. 395–404
- [15] F. Chinesta, A. Leygue, F. Bordeu, J. Aguado, E. Cueto, D. Gonzalez, I. Alfaro, A. Ammar, A. Huerta; PGD-Based Computational Vademecum for Efficient Design, Optimization and Control; Archives of Computational Methods in Engineering, 20 (1) (2013), pp. 31–59
- [16] A. Ammar, E. Cueto, F. Chinesta; Reduction of the chemical master equation for gene regulatory networks using proper generalized decompositions; International Journal for Numerical Methods in Biomedical Engineering, in press (2012)
- [17] L. Boucinha, A. Gravouil, A. Ammar; Space-time proper generalized decompositions for the resolution of transient elastodynamic models; Computer Methods in Applied Mechanics and Engineering, 255 (0) (2013), pp. 67–88
- [18] C. Ghnatios, F. Masson, A. Huerta, A. Leygue, E. Cueto, F. Chinesta; Proper generalized decomposition based dynamic data-driven control of thermal processes; Computer Methods in Applied Mechanics and Engineering, 213-216 (0) (2012), pp. 29–41
- [19] D. Gonzalez, F. Masson, F. Poulhaon, E. Cueto, F. Chinesta; Proper generalized decomposition based dynamic data driven inverse identification; Mathematics and Computers in Simulation, 82 (2012), pp. 1677–1695
- [20] P. Ladeveze, J.-C. Passieux, D. Neron; The latin multiscale computational method and the proper generalized decomposition; Computer Methods in Applied Mechanics and Engineering, 199 (21-22) (2010), pp. 1287–1296
- [21] A. Nouy; A priori model reduction through Proper Generalized Decomposition for solving time-dependent partial differential equations; Computer Methods in Applied Mechanics and Engineering, 199 (23-24) (2010), pp. 1603–1626
- [22] E. Pruliere, F. Chinesta, A. Ammar; On the deterministic solution of multidimensional parametric models using the Proper Generalized Decomposition; Mathematics and Computers in Simulation, 81 (4) (2010 DEC), pp. 791–810
- [23] A. Ammar, F. Chinesta, P. Diez, A. Huerta; An error estimator for separated representations of highly multidimensional models; Computer Methods in Applied Mechanics and Engineering, 199 (25-28) (2010), pp. 1872–1880
- [24] Y. Maday, A.T. Patera, G. Turinici; Global a priori convergence theory for reduced-basis approximations of single-parameter symmetric coercive elliptic partial differential equations, 335 (3) (2002 AUG 1), pp. 289–294
- [25] B. Bognet, F. Bordeu, F. Chinesta, A. Leygue, A. Poitou; Advanced simulation of models defined in plate geometries: 3d solutions with 2d computational complexity; Computer Methods in Applied Mechanics and Engineering, 201-204 (0) (2012), pp. 1–12
- [26] T. Belytschko, Y.Y. Lu, L. Gu; Element-Free Galerkin Methods; International Journal for Numerical Methods in Engineering, 37 (1994), pp. 229–256
- [27] D. González, E. Cueto, M. Doblaré; A higher order method based on local maximum entropy approximation; International Journal for Numerical Methods in Enginnering, 84 (2010), pp. 741–764
- [28] V.L. Rvachev, T.I. Sheiko, V. Shapiro, I. Tsukanov; Transfinite interpolation over implicitly defined sets; Computer Aided Geometric Design, 18 (2001), pp. 195–220
- [29] V.L. Rvachev, T.I. Sheiko, V. Shapiro, I. Tsukanov; On completeness of rfm solution structures; Computational Mechanics, 25 (2000), pp. 305–316
Document information
Published on 01/09/15
Accepted on 16/09/14
Submitted on 12/05/14
Volume 31, Issue 3, 2015
DOI: 10.1016/j.rimni.2014.09.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?