Greens function for time-harmonic elastodynamics in a half-space with hysteretic damping

Resumen

Se presenta una solución analítica para la respuesta de un semiespacio tridimensional homogéneo con una carga puntual armónica en el tiempo. Esta expresión es de gran importancia debido a que se puede emplear como solución fundamental en el Método de los Elementos de Contorno para la resolución de problemas elastodinámicos tridimensionales de semiespacios. Las expresiones se han validado comparando los resultados con otros empleados en el Método de Elementos de Contorno en los que es necesaria la discretización de la superficie del semiespacio. También se ha comparado con otras soluciones para el semiespacio en 2.5D y con resultados experimentales obtenidos de referencias bibliográficas.

Por último, se estudia el comportamiento asintótico de la solución para diferentes estados comparando los resultados con soluciones fundamentales existentes.

Abstract

This paper presents an analytical solution for the steady-state response of a homogeneous three-dimensional half-space subject to a time-harmonic point load. This expresion is of great importance in the formulation of three-dimensional elastodynamic problems in a half-space by means of boundary element methods which can be employed as a Fundamental Solution. The expressions are validated comparing the results with those obtained with the boundary element method solution, where the free surface is discretized. The solution is further compared to that of a 2.5D half-space, and with experimental results available in the literature.

The asymptotic behaviour of the solution is explored for different limits of the distance, frequency and wave number, and the ensuing limits are compared to existing fundamental solutions.

Palabras clave

Función de Green ; Transformada de Fourier ; Semiespacio tridimensional ; Elasticidad armónica

Keywords

Greens function ; Fourier transform ; Three-dimensional half space ; Time-harmonic elasticity

1. Introducción

La aplicación de métodos numéricos para la propagación de ondas requiere el empleo de soluciones fundamentales (SF, a partir de ahora) para obtener resultados válidos compatibles con un tiempo de cálculo óptimo. El Método de los Elementos de Contorno precisa de la definición de SF. Las principales aplicaciones de la propagación de ondas en semiespacios son el estudio de vibraciones provocadas por el paso de trenes, la ingeniería sísmica, la interacción dinámica suelo-estructura, etc. En problemas en los que sea necesaria la definición de la superficie de un semiespacio, el uso de SF específicas reduce el coste computacional al no tener que discretizar la superficie.

Los principales avances en el cálculo de SF elastodinámicas se muestran en una reciente revisión [1] .

Muchos investigadores han estudiado la generación de movimientos de superficie [2] ; [3] ; [4] ; [5]  ;  [6] pero el número de ellos que desarrolla el caso de movimientos bajo la superficie es limitado. Eason [7] , Gakenheimer [8] y Johnson [9] analizaron los desplazamientos producidos en un semiespacio elástico por una carga aplicada en la superficie.

Años después, Pilant [10] obtuvo la SF para una carga lineal aplicada en la superficie de un semiplano elástico obteniendo los desplazamientos en un punto interior y viceversa. El estudio se realizó en el dominio del tiempo y empleando el método Cagniard-De Hoop. Ese mismo año, Bouchon [11] desarrolló un método para estudiar el campo de desplazamientos provocado por una carga en el interior de un espacio estratificado tridimensional. El campo de ondas elástico se representaba mediante la superposición de ondas planas en direcciones discretas.

El problema de una carga concentrada que actúa en el interior de un semiespacio elástico homogéneo tridimensional fue estudiado en primer lugar por Mindlin [12] bajo condiciones estáticas. Obtuvo la solución analítica para un medio isótropo empleando el principio de superposición a partir de la solución de Kelvin.

Sin embargo, el cálculo del núcleo de esta SF es tedioso. En [13] se realiza una solución diferente al mismo problema empleando el método de las imágenes. Posteriormente, en [14] se reconsidera el problema y se resuelve empleando los potenciales de Papkovitch [15] .

Garvin [16] desarrolla la solución para una fuerza lineal que actúa en una cavidad infinitesimal localizada bajo la superficie libre. Emplea la transformada de Laplace para obtener la solución en dominios bidimensionales. Kontoni et al. [17] desarrollan una SF aproximada mediante el uso del método de las imágenes para semiplanos elastodinámicos en el dominio de la frecuencia, en el caso de cargas armónicas, o empleando la transformada de Laplace para alteraciones transitorias.

Kobayashi [18] obtiene la SF para un semiespacio basada en la del espacio completo en el dominio de la frecuencia, para lo que emplea la transformada de Laplace en el tiempo y la de Fourier en la frecuencia. Pak [19] estudió analíticamente la SF para un semiespacio axisimétrico e isótropo sometido a una fuerza interna armónica en el tiempo empleando el método de los potenciales de desplazamiento.

Banerjee y Mamoon [20] obtienen la solución para un semiespacio sometido a una fuerza periódica empleando la técnica desarrollada en [21] para obtener la SF transitoria a una carga aplicada. En los 2 estudios se emplean los métodos de síntesis y superposición en el espacio transformado de Laplace y en el dominio de la frecuencia.

Tadeu [22] formula la solución analítica para la respuesta de un espacio homogéneo tridimensional sujeto a una carga armónica senoidal. Una extensión de este modelo para semiespacios se obtiene en [23] . La SF del semiespacio se escribe como suma de la SF para el espacio completo más términos de superficie que, a su vez, se descomponen en 2 partes: una correspondiente a la solución del método de las imágenes más otra obtenida de la metodología propuesta en [24] .

Park [25] presenta una solución mixta en el dominio del tiempo trasformada en el espacio para un semiplano sujeto a una carga armónica antiplana en la superficie.

En este documento se presenta la solución analítica para la respuesta de semiespacio tridimensional sometido a una carga armónica puntual incluyendo el amortiguamiento. Esta expresión tiene gran importancia en formulación de problemas elastodinámicos tridimensionales en un semiespacio, empleada como SF en la aplicación del Método de los Elementos de Contorno. Las expresiones se obtienen empleando los potenciales de desplazamientos [6] .

La SF para el semiespacio se obtiene asumiendo condiciones de tensiones libres en el contorno de la superficie, equilibrio de tensiones y continuidad de desplazamientos en el punto de aplicación de la carga y condiciones de radiación.

Las expresiones se validan comparando la obtenida con el Método de los Elementos de Contorno empleando la solución para el espacio completo, donde la superficie es discretizada. Asimismo, se compara con resultados experimentales obtenidos en la literatura.

Por último, se estudia el comportamiento asintótico de la solución, estudiando límites en distancia, en frecuencia y en número de onda y comparándola con SF existentes.

2. Planteamiento del problema

La respuesta elástica lineal de un espacio isótropo tridimensional se puede obtener a partir de las ecuaciones de Navier:

$\mu {\boldsymbol {\nabla }}^{2}{\boldsymbol {\mbox{u}}}\left({\boldsymbol {\mbox{x}}},t\right)+$$\left(\lambda +\mu \right){\boldsymbol {\nabla }}{\boldsymbol {\nabla }}\cdot {\boldsymbol {\mbox{u}}}\left({\boldsymbol {\mbox{x}}},t\right)+$${\boldsymbol {\mbox{f}}}\left({\boldsymbol {\mbox{x}}},t\right)=$$\rho {\frac {{\partial }^{2}{\boldsymbol {\mbox{u}}}\left({\boldsymbol {\mbox{x}}},t\right)}{\partial t^{2}}}$

( 1)

donde ρ es la densidad del material, μ y λ   son las constantes de Lamé, ${\textstyle {\boldsymbol {\mbox{u}}}\left({\boldsymbol {\mbox{x}}},t\right)}$ es el campo de desplazamientos, ${\textstyle {\boldsymbol {\mbox{f}}}\left({\boldsymbol {\mbox{x}}},t\right)}$ son las fuerzas de volumen y ${\textstyle {\boldsymbol {\mbox{x}}}=\left(x,y,z\right)}$ son las coordenadas cartesianas.

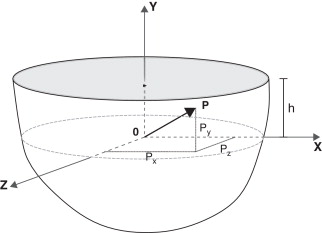
La figura 1 representa ${\textstyle \Omega =\left(x,y,z\right){}_{-\infty <y<h}}$ , un semiespacio limitado por una superficie superior ${\textstyle S={\left(x,y,z\right)}_{y=h}}$ en el sistema de referencia cartesiano {0  ; x , y , z }. El dominio tiene aplicada una carga puntual unitaria en el punto 0 :

Figura 1. Semiespacio bajo carga puntual.

$f_{i}\left({\boldsymbol {\mbox{x}}},t\right)={\delta }_{il}\delta \left({\boldsymbol {\mbox{x}}}\right)\delta (t)$

( 2)

donde δ_il es la delta de Kronecker y δ (·) es la delta de Dirac en el tiempo o el espacio.

Para resolver la ecuación (1) , se define la siguiente transformada de Fourier en el tiempo y en el espacio:

$G\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$${\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }g\left({\boldsymbol {\mbox{x}}},t;{\boldsymbol {0}}\right)e^{-i\left(\omega t-k_{x}x-k_{z}z\right)}dxdzdt$

( 3)

donde ${\textstyle {\boldsymbol {\mbox{X}}}=\left(k_{x},y,k_{z}\right)}$ son las coordenadas en el dominio transformado, k_x y k_z son los números de onda en las direcciones x y z , respectivamente, y ω es la frecuencia.

La transformada inversa correspondiente está determinada por la expresión:

$g\left({\boldsymbol {\mbox{x}}},t;{\boldsymbol {0}}\right)=$${\frac {1}{{\left(2\pi \right)}^{3}}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }G\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)e^{i\left(\omega t-k_{x}x-k_{z}z\right)}{dk}_{x}{dk}_{z}d\omega$

( 4)

Aplicando la transformada de Fourier definida a la expresión (1 ) se obtiene la ecuación por resolver.

$\mu {\boldsymbol {\nabla }}_{k}^{2}{\boldsymbol {\mbox{U}}}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)+$$\left(\lambda +\mu \right){\boldsymbol {\nabla }}_{k}{\boldsymbol {\nabla }}_{k}\cdot {\boldsymbol {\mbox{U}}}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)+$${\boldsymbol {\mbox{F}}}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$$-\rho {\omega }^{2}{\boldsymbol {\mbox{U}}}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)$

( 5)

donde el superíndice se refiere a una carga puntual en la dirección l . La carga puntual en el dominio transformado es de la forma:

${\boldsymbol {\mbox{F}}}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$${\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\delta }_{il}\delta (x)\delta (y)\delta (z)\delta (t)e^{-i\left(\omega t-k_{x}x-k_{z}z\right)}dxdzdt=$${\delta }_{il}\delta (y)$

( 6)

y ${\textstyle {\boldsymbol {\nabla }}_{k}}$ es el operador ∇ en el dominio transformado, que viene dado por:

${\boldsymbol {\nabla }}_{k}=\left(-ik_{x},{\frac {d}{dy}},-\right.$$\left.ik_{z}\right)$

Para considerar un comportamiento del material viscoelástico se ha adoptado el modelo de Kelvin-Voigt, definiendo en la ecuación (5) las propiedades del material de tipo complejo [26] . Así, las constantes elásticas μ y λ están definidas mediante las siguientes expresiones:

$\mu ={\mu }_{R}\left(1+2i\zeta sign\left(\omega \right)\right)\quad \lambda =$${\lambda }_{R}\left(1+2i\zeta sign\left(\omega \right)\right)$

( 7)

donde ${\textstyle {\mu }_{R}}$ y ${\textstyle {\lambda }_{R}}$ son las constantes de Lamé y ζ el coeficiente de amortiguamiento histerético.

Para resolver la ecuación (5) , el vector de desplazamientos ${\textstyle {\boldsymbol {\mbox{U}}}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)}$ se descompone en la suma de potenciales escalar y vectorial [27] :

${\boldsymbol {\mbox{U}}}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$${\boldsymbol {\nabla }}_{k}{\Phi }^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)+$${\boldsymbol {\nabla }}_{k}\times {\boldsymbol {\Psi }}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)$

( 8)

Aplicando la divergencia y rotacional a (5) , se obtienen las siguientes ecuaciones para cada potencial:

${\frac {d^{2}{\Phi }^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)}{dy^{2}}}+$$\left(k_{p}^{2}-k_{r}^{2}\right){\Phi }^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$$0$ ${\frac {d^{2}{\boldsymbol {\Psi }}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)}{dy^{2}}}+$$\left(k_{s}^{2}-k_{r}^{2}\right){\boldsymbol {\Psi }}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$$0$

( 9)

donde ${\textstyle k_{r}^{2}=k_{x}^{2}+k_{z}^{2}}$ ; ${\textstyle k_{p}={\frac {\omega }{c_{p}}}}$ y ${\textstyle k_{s}={\frac {\omega }{c_{s}}}}$ son los números de onda para las ondas P y S, respectivamente, y ${\textstyle c_{p}={\sqrt {\frac {\lambda +2\mu }{\rho }}}}$ y ${\textstyle c_{s}={\sqrt {\frac {\mu }{\rho }}}}$ son las velocidades de onda P y S del material.

La solución general a estas 4 ecuaciones diferenciales se puede escribir de la siguiente forma:

$\Phi \left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$$c_{1\alpha }e^{k_{\alpha }y}+c_{2\alpha }e^{-k_{\alpha }y}$ ${\boldsymbol {\Psi }}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$${\boldsymbol {\mbox{c}}}_{1\beta }e^{k_{\beta }y}+{\boldsymbol {\mbox{c}}}_{2\beta }e^{-k_{\beta }y}$

( 10)

donde ${\textstyle k_{\alpha }={\sqrt {k_{r}^{2}-k_{p}^{2}}}}$ y ${\textstyle k_{\beta }={\sqrt {k_{r}^{2}-k_{s}^{2}}}}$ . La solución depende de 8 constantes de integración que se obtienen aplicando las condiciones de contorno, radiación y continuidad, que se describen a continuación.

2.1. Cálculo de las constantes de integración

Los potenciales de desplazamientos (10 ) dependen de 8 constantes de integración c_ij , donde i  = 1, 2 y j  = α , β¹ . Al considerar la carga puntual aplicada en y  = 0 que provoca discontinuidad en las tensiones, las constantes difieren en la parte superior (y  > 0) y la parte inferior de la región (y  < 0). En consecuencia, existen 16 constantes de integración, 8 para y  > 0 (que se denotan por ${\textstyle c_{ij}^{+}}$ ) y otras 8 para y  < 0 (${\textstyle c_{ij}^{-}}$ ). Todas estas constantes se calculan considerando las siguientes condiciones:

• Condición de tensión libre en la superficie (y  = h ).
• Condición de radiación en y → − ∞.
• Continuidad de desplazamientos en y  → 0^±
• Equilibrio de tensiones en y  → 0^±

Se obtienen restricciones adicionales a partir de la condición de Miklovitz [28] , ∇  · Ψ  = 0 que se define:

$-ik_{x}{\Psi }_{x}+{\frac {d{\Psi }_{y}}{dy}}-ik_{z}{\Psi }_{z}=$$0$

( 11)

en el dominio transformado.

Todas estas condiciones se describen detalladamente a continuación.

Condición de tensiones libre en la superficie y  = h . Considerando el sistema de referencia cartesiano dado en la figura 1 , las condiciones de contorno en la superficie vienen determinadas por:

${{\Sigma }_{xy}^{l}}_{y=h}=0\quad {{\Sigma }_{yy}^{l}}_{y=h}=$$0\quad {{\Sigma }_{yz}^{l}}_{y=h}=0$

( 12)

donde ${\textstyle {\Sigma }_{ij}^{l}}$ es el tensor de tensiones de la solución fundamental. Este es un conjunto de 3 ecuaciones para las 8 icógnitas ${\textstyle c_{ij}^{+}}$ , por lo que es necesario establecer 13 condiciones más.

Condición de radiación en y → − ∞. Las condiciones de radiación implican que no existen ondas que se generen en el infinito. Los téminos e^−yA que aparecen para y  < 0 representan este tipo de ondas y, por tanto, las 4 constantes correspondientes ${\textstyle c_{2\alpha }^{-}}$ y ${\textstyle {\boldsymbol {\mbox{c}}}_{2\beta }^{-}}$ desaparecen. Tras establecer estas condiciones, quedan 9 ecuaciones para resolver el problema.

Continuidad de desplazamientos en y  → 0^± . En el punto de aplicación de la carga (y  = 0) debe haber continuidad de desplazamientos. Esta condición permite definir 3 ecuaciones:

${\underset {y\rightarrow 0^{+}}{l{\acute {\imath }}m}}U_{x}^{l}=$${\underset {y\rightarrow 0^{-}}{l{\acute {\imath }}m}}U_{x}^{l}$ ${\underset {y\rightarrow 0^{+}}{l{\acute {\imath }}m}}U_{y}^{l}=$${\underset {y\rightarrow 0^{-}}{l{\acute {\imath }}m}}U_{y}^{l}$ ${\underset {y\rightarrow 0^{+}}{l{\acute {\imath }}m}}U_{z}^{l}=$${\underset {y\rightarrow 0^{-}}{l{\acute {\imath }}m}}U_{z}^{l}$

( 13)

Quedan 6 ecuaciones por definir.

Equilibrio de tensiones en y  → 0^± . El equilibrio de tensiones en el punto de aplicación de la carga implica un salto en el tensor de tensiones en y  = 0 debido a la carga puntual aplicada.

${{\Sigma }_{xy}^{l}}_{y=0^{+}}-{{\Sigma }_{xy}^{l}}_{y=0^{-}}=$$-{\delta }_{lx}$ ${{\Sigma }_{yy}^{l}}_{y=0^{+}}-{{\Sigma }_{yy}^{l}}_{y=0^{-}}=$$-{\delta }_{ly}$ ${{\Sigma }_{yz}^{l}}_{y=0^{+}}-{{\Sigma }_{yz}^{l}}_{y=0^{-}}=$$-{\delta }_{lz}$

( 14)

Condición de Miklovitz . La condición de Miklovitz (11) se aplica tanto para las ecuaciones superiores (y  > 0) como para las inferiores (y  < 0). Para la parte superior, se obtienen 2 ecuaciones, quedando despreciados los coeficientes de e^−k_βy y e^k_βy . Para la parte inferior, solo una ecuación es necesaria, mientras que el coeficiente que multiplica e^k_βy ha sido despreciado por las condiciones de radiación.

2.2. Solución fundamental para el campo de desplazamientos

Resolviendo las 16 ecuaciones consideradas por las condiciones anteriores se obtienen las constantes de integración. Sustituyendo estas en las expresiones de los potenciales definidos en la descomposición dada por la ecuación (8) , se obtiene la función de Green en desplazamientos para el semiespacio considerado.

${\boldsymbol {\mbox{U}}}_{i}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$ $\quad {\frac {1}{2\rho {\omega }^{2}}}k_{i}k_{l}{\frac {1}{k_{\alpha }}}\left(e^{-k_{\alpha }\vert y\vert }-\right.$$\left.e^{k_{\alpha }y}\left(k_{\alpha }\varphi +e^{-2hk_{\alpha }}\chi \right)\right)$ $\quad -{\frac {1}{k_{\beta }}}\left(e^{-k_{\beta }\vert y\vert }+\right.$$\left.e^{k_{\beta }y}\left(k_{\beta }\varphi +e^{-2hk_{\beta }}\left(\chi -\right.\right.\right.$$\left.\left.\left.\eta \right)\right)\right)$ $\quad +{\delta }_{il}{\frac {k_{s}^{2}}{k_{\beta }}}\left(e^{-k_{\beta }\vert y\vert }+\right.$$\left.e^{k_{\beta }\left(-2h+y\right)}\right)$

( 15)

donde los índices i y l toman los valores x y/o z .

${\boldsymbol {\mbox{U}}}_{y}^{i}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$ $\quad {\frac {ik_{i}}{2\rho {\omega }^{2}}}-sign\left(y\right)e^{-k_{\alpha }\vert y\vert }-$$e^{k_{\alpha }y}\left(k_{\alpha }\varphi +e^{-2hk_{\alpha }}\chi \right)+$ $\quad sign\left(y\right)e^{-k_{\beta }\vert y\vert }-$$e^{k_{\beta }y}\left({\frac {k_{r}^{2}}{k_{\beta }}}\varphi +\right.$$\left.e^{-2hk_{\beta }}\chi \right)$

( 16)

donde i  = x , z .

${\boldsymbol {\mbox{U}}}_{i}^{y}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$ $\quad {\frac {ik_{i}}{2\rho {\omega }^{2}}}-sign\left(y\right)e^{-k_{\alpha }\vert y\vert }+$$e^{k_{\alpha }y}\left({\frac {k_{r}^{2}}{k_{\beta }}}\varphi +\right.$$\left.e^{-2hk_{\alpha }}\chi \right)+$ $\quad sign\left(y\right)e^{-k_{\beta }\vert y\vert }+$$e^{k_{\beta }y}\left(k_{\alpha }\varphi +e^{-2hk_{\beta }}\chi \right)$

( 17)

siendo i  = x , z . Por último:

${\boldsymbol {\mbox{U}}}_{y}^{y}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$ $\quad {\frac {1}{2\rho {\omega }^{2}}}-k_{\alpha }\left(e^{-k_{\alpha }\vert y\vert }+\right.$$\left.e^{k_{\alpha }y}\left({\frac {k_{r}^{2}}{k_{\beta }}}\varphi +\right.\right.$$\left.\left.e^{-2hk_{\alpha }}\chi \right)\right)+$ $\quad {\frac {k_{r}^{2}}{k_{\beta }}}\left(e^{-k_{\beta }\vert y\vert }-\right.$$\left.e^{k_{\beta }y}\left(k_{\alpha }\varphi +e^{-2hk_{\beta }}\chi \right)\right)$

( 18)

En estas ecuaciones se han definido los siguientes parámetros:

$\varphi ={\frac {4k_{\beta }\left(-2k_{r}^{2}+k_{s}^{2}\right)}{{\left(-2k_{r}^{2}+k_{s}^{2}\right)}^{2}-4k_{r}^{2}k_{\alpha }k_{\beta }}}e^{-h\left(k_{\alpha }+k_{\beta }\right)}$ $\chi ={\frac {{\left(-2k_{r}^{2}+k_{s}^{2}\right)}^{2}+4k_{r}^{2}k_{\alpha }k_{\beta }}{{\left(-2k_{r}^{2}+k_{s}^{2}\right)}^{2}-4k_{r}^{2}k_{\alpha }k_{\beta }}}$ $\eta ={\frac {8k_{\alpha }k_{\beta }k_{s}^{2}}{{\left(-2k_{r}^{2}+k_{s}^{2}\right)}^{2}-4k_{r}^{2}k_{\alpha }k_{\beta }}}$

2.3. Solución fundamental para el campo de tensiones

La función de Green para las tensiones ${\textstyle {\Sigma }_{ij}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)}$ se obtiene sustituyendo la función de Green obtenida para el campo de desplazamientos definida por las ecuaciones (15 -18 ) en la ley de Hooke formulada en el espacio transformado. El tensor de tensiones puede expresarse en función de la dilatación Δ = E_kk y del tensor de deformaciones E_ij :

${\Sigma }_{ij}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)=$$\lambda {\Delta }^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right){\delta }_{ij}+$$2\mu E_{ij}^{l}\left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)$

( 19)

donde δ_ij es la delta de Kronecker y las expresiones para las deformaciones son:

${\Delta }^{l}=-ik_{x}U_{x}^{l}+{\frac {dU_{y}^{l}}{dy}}-ik_{z}U_{z}^{l}$ $E_{xx}^{l}=-ik_{x}U_{x}^{l}$ $E_{yy}^{l}={\frac {dU_{y}^{l}}{dy}}$ $E_{zz}^{l}=-ik_{z}U_{z}^{l}$

( 20)

$E_{xy}^{l}={\frac {1}{2}}\left({\frac {dU_{x}^{l}}{dy}}-ik_{x}U_{y}^{l}\right)$ $E_{xz}^{l}=-{\frac {i}{2}}\left(k_{z}U_{x}^{l}+k_{x}U_{z}^{l}\right)$ $E_{yz}^{l}={\frac {1}{2}}\left(-ik_{z}U_{y}^{l}+{\frac {dU_{z}^{l}}{dy}}\right)$

( 21)

Se han suprimido las coordenadas ${\textstyle \left({\boldsymbol {\mbox{X}}},\omega ;{\boldsymbol {0}}\right)}$ para una mayor claridad de la formulación.

3. Evaluación de las integrales para la transformada inversa de Fourier

Para obtener la SF dinámica en un semiespacio 2.5D (x , y , k_z , ω ) es necesario realizar la transformada inversa de Fourier para el número de onda k_x ,

${\tilde {f}}(x,y,k_{z},\omega )={\frac {1}{2\pi }}{\int }_{-\infty }^{\infty }F\left(k_{x},y,k_{z},\omega \right)e^{-ik_{x}x}dk_{x}$

( 22)

Esta integral no se puede obtener de forma analítica para todos los términos de la SF y es necesaria una aproximación numérica:

${\tilde {f}}\left(s\Delta x,y,k_{z},\omega \right)={\frac {\Delta k_{x}}{2\pi }}\sum _{r=0}^{N_{x}-1}F\left(r\Delta k_{x},y,k_{z},\omega \right)e^{-2\pi i{\frac {r\quad s}{N_{x}}}}$

( 23)

donde s  = 1, …, N_x ; Δk_x es el incremento en el número de onda k_x ; N_x es el número total de puntos necesarios para poder realizar eficientemente la transformada inversa y ${\textstyle \Delta x={\frac {2\pi }{(N_{x}-1)\Delta k_{x}}}}$ . Para acelerar el tiempo de cálulo se emplea el algoritmo correspondiente a la transformada rápida de Fourier.

De modo análogo, es necesario realizar la doble transformada inversa de Fourier para las variables k_x y k_z para obtener la SF en el semiespacio 3D. Su expresión analítica viene dada por:

$f(x,y,z,\omega )={\frac {1}{{\left(2\pi \right)}^{2}}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }F(k_{x},y,k_{z},\omega )e^{-i(k_{x}x+k_{z}z)}dk_{x}dk_{z}$

( 24)

donde es necesaria una aproximación discreta para su cálculo mediante la expresión:

${\tilde {f}}_{s_{x}s_{z}}\left(x_{s_{x}},y,z_{s_{z}},\omega \right)=$${\frac {\Delta k_{x}\Delta k_{z}}{{\left(2\pi \right)}^{2}}}\sum _{r_{x}=1}^{N_{x}}\sum _{r_{z}=1}^{N_{z}}\left[F_{r_{x}r_{z}}\left({k_{x}}_{r_{x}},y,{k_{z}}_{r_{z}},\omega \right)\quad e^{-2\pi i{\frac {\left(r_{x}-1)(s_{x}-1\right)}{N_{x}}}}e^{-2\pi i{\frac {\left(r_{z}-1)(s_{z}-1\right)}{N_{x}}}}\right]$

( 25)

siendo Δk_x y Δk_z los incrementos de números de onda para k_x y k_z , y N_x y N_z son los números totales de puntos en los dominios k_x y k_z , respectivamente.

Para aplicar estas funciones de Green transformadas en formulaciones de elementos de contorno, es necesario calcularlas exactamente en todos los casos. La función de Green es singular en los dominios (x , y , z , ω ) y (x , y , k_z , ω ) pero es regular en el dominio (k_x , y , k_z , ω ).

4. Validación de la función de Green

La solución obtenida se ha validado mediante los siguientes procedimientos:

• Ejemplos basados en el teorema de reciprocidad para los desplazamientos. Se validan las propiedades básicas de la SF empleando únicamente la teoría desarrollada en este procedimiento.
• Validación numérica empleando el programa de elementos de contorno con la solución fundamental para el espacio completo, siendo necesaria la dicretización de la superficie.
• La solución se compara con resultados experimentales.

4.1. Teorema de reciprocidad

El campo de desplazamientos elastodinámico correspondiente a cualquier SF debe satisfacer la siguiente identidad:

$u_{i}^{j}\left({\boldsymbol {\mbox{x}}},{\boldsymbol {\mbox{y}}}\right)=$$u_{j}^{i}\left({\boldsymbol {\mbox{y}}},{\boldsymbol {\mbox{x}}}\right)$

( 26)

denominada Teorema de Maxwell de los desplazamientos recíprocos, donde x e y son las posiciones de los puntos receptor y emisor, respectivamente. El superíndice denota la dirección de la fuerza y el subíndice indica la componente cartesiana del desplazamiento.

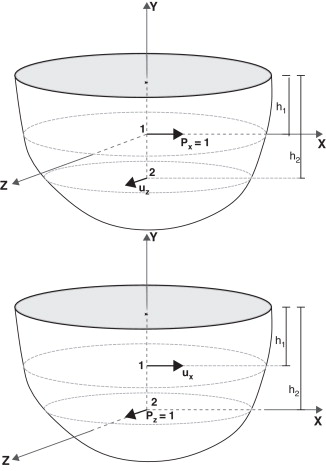
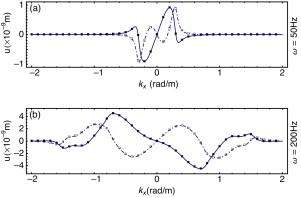
La figura 2 representa la comparación de reciprocidad ${\textstyle u_{z}^{x}=u_{x}^{z}}$ . Se considera un semiespacio con coeficiente de Poisson ν  = 0,3, densidad ρ  = 2.242 kg/m³ , módulo de rigidez μ  = 1,43488 10⁹ N/m² y coeficiente de amortiguamiento ζ  = 0,005. La figura 3 representa las partes real e imaginaria para 2 soluciones recíprocas. Las soluciones se han calculado para 2 frecuencias (ω  = 50 Hz en fig. 3 a y ω  = 200 Hz en fig. 3 b) en un intervalo de número de onda k_x  = (−2, 2) y k_z  = 0,25. La partes real e imaginaria de ${\textstyle u_{z}^{x}}$ están representadas en línea continua y discontinua, respectivamente. En este caso, la carga está situada a una profundidad h₁  = 6 m y se calculan los desplazamientos en h₂  = 2 m. Los desplazamientos ${\textstyle u_{x}^{z}}$ se calculan en h₁  = 2 m para las mismas frecuencias y números de onda para una carga situada en h₂  = 6 m, y se muestran en el mismo gráfico: el símbolo ▪ corresponde a la parte real y □ a la parte imaginaria. Puede observarse que el ajuste entre ambas es perfecto.

Figura 2. Comparación de reciprocidad.

Figura 3. Validación del teorema de reciprocidad. Parte real (línea continua) e imaginaria (línea discontinua) de ${\textstyle u_{z}^{x}}$ ; parte real (cuadrado sombreado) e imaginaria (cuadrado) de ${\textstyle u_{z}^{x}}$ (líneas de puntos).

4.2. Comparación con la solución para el espacio completo 2.5D

El objeto principal de este ejemplo de validación es comparar la solución obtenida con otros resultados publicados previamente. Las expresiones se han validado mediante el cálculo de la solución 2.5D generada por una carga armónica en la dirección z en un semiespacio. Los resultados se han obtenido a partir de un código generado empleando la SF del espacio completo descrita en [22] e implementada utilizando el Método de los Elementos de Contorno.

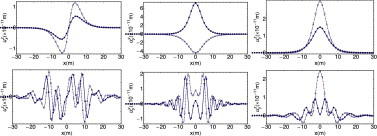
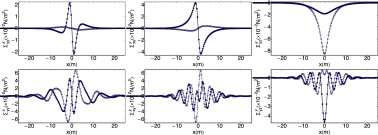
Se considera un semiespacio con coeficiente de Poisson ν  = 0,3, densidad ρ  = 2.242 kg/m³ , módulo de rigidez μ  = 1,43488 10⁹ N/m² y coeficiente de amortiguamiento ζ  = 0,005. Las figuras 4 y 5 representan las componentes real e imaginaria para el desplazamiento y las tensiones, respectivamente, en la superficie del semiespacio 2.5D para un número de onda k_z  = 0,50 y frecuencias 50 Hz y 200 Hz, calculadas mediante el programa de elementos de contorno y la SF propuesta es este trabajo.

Figura 4. Partes real (línea continua o cuadrado sombreado) e imaginaria (línea discontinua o cuadrado) para los desplazamientos sobre la línea (y  = 5) debido a una carga unitaria y armónica de 50 Hz (arriba) y 200 Hz (abajo) aplicada en el origen, obtenida mediante el Método de Elementos de Contorno (líneas) y calculada mediante la transformada inversa de Fourier en kx de la solución fundamental (punteada); número de onda kz  = 0,5 en todos los casos.

Figura 5. Partes real (línea continua o cuadrado sombreado) e imaginaria (línea discontinua o cuadrado) para las tensiones sobre la línea (y  = 2) debido a una carga unitaria y armónica de 50 Hz (arriba) y 200 Hz (abajo) aplicada en el origen, obtenida mediante el Método de Elementos de Contorno (líneas) y calculada mediante la transformada inversa de Fourier en kx de la solución fundamental (punteada); número de onda kz  = 0,5 en todos los casos.

La solución calculada mediante el programa de elementos de contorno se representa con líneas, siendo la parte real continua y la componente imaginaria discontinua. Ha sido necesaria una discretización de la superficie de 200 elementos cuadráticos en un contorno de longitud 300 m. Para obtener la SF para el semiespacio 2.5D se ha realizado la transformada inversa para el número de onda k_x en las expresiones dadas en las ecuaciones (15 -18 ) y las tensiones obtenidas por la ecuación (eq-hooke-law) . Para calcular esta transformada inversa han sido necesarios N_x  = 256 puntos y el incremento en el número de onda Δk_x  = 0,078125 rad/m.

4.3. Comparación con resultados experimentales

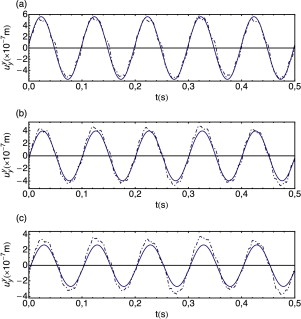
Por último, se ha validado experimentalmente la SF obtenida mediante los datos registrados en el ensayo desarrollado en [29] , consistente en medir las aceleraciones de vibración ocasionadas en la superficie de un suelo oscilado armónicamente con una frecuencia de ω  = 10 Hz por un excitador electromagnético con una amplitud de fuerza aplicada de 402 N, obtenida a partir de la masa y de la aceleración del excitador. El suelo tiene una densidad de ρ  = 1.850 kg/m³ , el coeficiente de Poisson es ν  = 0,2 y la velocidad de las ondas de superficie c_R  = 166,7 m/s, proporcionando así las velocidades de onda P y S, c_s  = 183,47 m/s y c_p  = 299,62 m/s, respectivamente.

La figura 6 muestra el desplazamiento medido en la superficie del suelo por 3 acelerómetros a 1,0 m, 1,5 m y 2,0 m y calculado mediante la triple transformada inversa de Fourier (ecuación 4 de la SF). Se puede observar que la SF reproduce con bastante exactitud la respuesta en la superficie del sólido para diferentes puntos, si bien cabe destacar que la discrepancia en los resultados con la distancia puede deberse al ajuste del amortiguamiento, de ahí que aumenten las diferencias al ser mayor la distancia al punto de aplicación. Por otra parte, la forma de la curva experimental contiene posibles reflexiones debido a que el terreno puede presentar heterogeneidades.

Figura 6. Desplazamiento vertical debido a una carga armónica de 402 N y 10 Hz aplicada en la superficie de un semiespacio, obtenida mediante datos experimentales (línea discontinua) y calculada mediante la transformada inversa de Fourier de la SF (línea continua): (a) 1,0 m, (b) 1,5 m, (c) 2,0 m.

5. Comportamiento asintótico de la Solución Fundamental

Es muy útil obtener el comportamiento de la función de Green para 2 casos particulares: (i) el límite cuando la profundidad de la carga es grande y (ii) el límite cuando la frecuencia de excitación es cero. El primer límite proporciona la SF para el espacio completo en el dominio transformado ${\textstyle \left(k_{x},y,k_{z},\omega \right)}$ , mientras que el segundo límite conduce a la SF elastostática del semiespacio en el dominio transformado.

Otras SF pueden obtenerse fácilmente, como:

• Considerando h → ∞ y ω  → 0 se obtiene la SF armónica del espacio completo.
• El límite k_z  → 0 proporciona la SF dinámica armónica para el espacio bidimensional en el dominio transformado (k_x , y ).
• La combinación de superposiciones diferentes de estos límites permite obtener otras SF útiles.

En las siguientes secciones se muestran las expresiones más útiles.

5.1. Solución Fundamental para el espacio completo en el dominio transformado

Considerando h → ∞, las expresiones de las ecuaciones (15 -18 ) conducen a las siguientes:

${\boldsymbol {\mbox{U}}}_{i}^{l}={\frac {1}{2\rho {\omega }^{2}}}k_{i}k_{l}\left({\frac {1}{k_{\alpha }}}e^{-k_{\alpha }y}-\right.$$\left.{\frac {1}{k_{\beta }}}e^{-k_{\beta }y}\right)$ $+{\delta }_{il}{\frac {k_{s}^{2}}{k_{\beta }}}e^{-k_{\beta }y}\quad \lbrace i,l\rbrace =$$x,z$ ${\boldsymbol {\mbox{U}}}_{y}^{i}={\boldsymbol {\mbox{U}}}_{i}^{y}=$${\frac {ik_{i}}{2\rho {\omega }^{2}}}\left[-e^{-k_{\alpha }y}+\right.$$\left.e^{-k_{\beta }y}\right]\quad i=x,z$ ${\boldsymbol {\mbox{U}}}_{y}^{y}={\frac {1}{2\rho {\omega }^{2}}}\left[-\right.$$\left.k_{\alpha }e^{-k_{\alpha }y}+{\frac {k_{r}^{2}}{k_{\beta }}}e^{-k_{\beta }y}\right]$

( 27)

que se corresponden con la SF del espacio 3D en el dominio transformado (k_x , y , k_z , ω ).

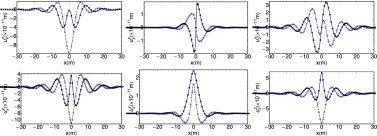
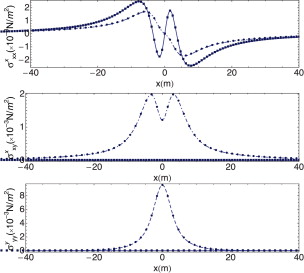
A partir de estas ecuaciones se puede obtener fácilmente la SF para espacio 2.5D realizando la transformada inversa para el número de onda k_x . En la figura 7 se presentan algunos resultados calculando la transformada inversa de la SF en k_x (línea de puntos) comparada con la expresión de la SF (línea continua) obtenida directamente de las ecuaciones de la elastodinámica 2.5D [22] . Las propiedades del medio en el que se realiza este ejemplo son: ν  = 0,3, ρ  = 2.242 kg/m³ , μ  = 1,43488 10⁹ N/m² y ζ  = 0,005. Para realizar la transformada inversa se han empleado N_x  = 256 puntos.

Figura 7. Componentes real (línea continua y puntos sombreados) e imaginaria (línea discontinua o puntos) del desplazamiento sobre la línea y  = 1 debido a una carga armónica unitaria ω  = 100 Hz aplicada en el origen obtenida a partir de la SF 2,5D para el espacio completo (líneas) [22] y calculada mediante la transformada inversa de Fourier en kx de la SF transformada (cuadrados); en todos los casos kz  = 0,5).

5.2. Solución Fundamental para el semiespacio elastostático en el dominio transformado

Considerando el límite ω  → 0 en las expresiones de los desplazamientos dados por las ecuaciones (15 -18 ) se obtienen las siguientes expresiones:

${\boldsymbol {\mbox{U}}}_{i}^{l}={\frac {1}{8\mu k_{r}\left(1-\nu \right)}}\left[k_{i}k_{l}\chi +\right.$$\left.{\delta }_{il}4\left(1-\nu \right)\left(e^{-k_{r}\vert y\vert }+\right.\right.$$\left.\left.e^{k_{r}\left(-2h+y\right)}\right)\right]\lbrace i,l\rbrace =$$x,z{\boldsymbol {\mbox{U}}}_{y}^{i}={\frac {ik_{i}}{8\mu k_{r}\left(1-\nu \right)}}\left[e^{-k_{r}\vert y\vert }y+\right.$$\left.e^{k_{r}\left(-2h+y\right)}\left(-{\frac {4\left(1-\nu \right)\left(1-2\nu \right)}{k_{r}}}+\right.\right.$$\left.\left.y\left(3-4\nu \right)+2hk_{r}\left(h-y\right)\right)\right]i=$$x,z{\boldsymbol {\mbox{U}}}_{i}^{y}={\frac {ik_{i}}{8\mu k_{r}\left(1-\nu \right)}}\left[e^{-k_{r}\vert y\vert }y+\right.$$\left.e^{k_{r}\left(-2h+y\right)}\left({\frac {4\left(1-\nu \right)\left(1-2\nu \right)}{k_{r}}}+\right.\right.$$\left.\left.y\left(3-4\nu \right)-2hk_{r}\left(h-y\right)\right)\right]i=$$x,z{\boldsymbol {\mbox{U}}}_{y}^{y}={\frac {1}{8\mu k_{r}\left(1-\nu \right)}}\left[e^{-k_{r}\vert y\vert }\left(3-\right.\right.$$\left.\left.4\nu +sign\left(y\right)k_{r}y\right)+\right.$$\left.e^{k_{r}\left(-2h+y\right)}\left(5-4\nu \left(3-\right.\right.\right.$$\left.\left.\left.2\nu \right)-k_{r}\left(-2h+y\right)\left(3-\right.\right.\right.$$\left.\left.\left.4\nu \right)+2hk_{r}^{2}\left(h-y\right)\right)\right]$

( 28)

donde

$\chi =-{\frac {e^{-k_{r}\vert y\vert }}{k_{r}^{2}}}\left(1+\right.$$\left.k_{r}\vert y\vert \right)$ $\quad +{\frac {e^{k_{r}\left(-2h+y\right)}}{k_{r}^{2}}}1-8\nu \left(1-\right.$$\left.\nu \right)$ $\quad +\left(y-2h\right)\left(3-4\nu \right)k_{r}+2h\left(h-\right.$$\left.y\right)k_{r}^{2}$

que corresponden a la SF de Midlin en el dominio transformado (k_x , y , k_z ) [12] .

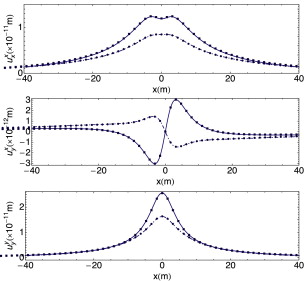
Ambas soluciones se comparan en las figuras 8 y 9 para un espacio elástico con las propiedades siguientes: ν  = 0,3, densidad ρ  = 2.242 kg/m³ y módulo de rigidez transversal μ  = 1,43488 10⁹ N/m² . La doble transformada inversa se ha realizado con una malla de N_x  × N_z  = 256 × 256 puntos.

Figura 8. Desplazamientos en la superficie (línea continua y puntos) y sobre la línea y  = − h (línea discontinua y puntos) debido a una carga unitaria aplicada en el origen obtenida con la SF de Mindlin (líneas) [12] y calculada mediante la transformada de la SF (puntos).

Figura 9. Tensiones en la superficie (línea continua y puntos) y sobre la línea y  = − h (línea discontinua y puntos) debido a una carga unitaria aplicada en el origen obtenida con la SF de Mindlin (líneas) [12] y calculada mediante la transformada de la SF (puntos).

6. Integración espacial de la Solución Fundamental

Para aplicar esta SF en el código del Método de los Elementos de Contorno es importante determinar el tipo de integración por abordar y, particularmente, el caso singular, como es el caso en el que el punto de aplicación de la carga o el punto de colocación esté sobre el elemento de integración. En estos casos, los desplazamientos y tensiones de la SF son singulares en coordenadas físicas (x , y , z ), (r⁻¹ ) y (r⁻² ), respectivamente, donde ${\textstyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}$ es la distancia entre el punto de colocación y observación. Si solo se realiza una transformada en las coordenadas físicas, (x , y , k_z ) o (k_x , y , z ), la SF en desplazamientos y tensiones sigue siendo singular, (log r ) y (r⁻¹ ), respectivamente, donde ${\textstyle r={\sqrt {x^{2}+y^{2}}}}$ o ${\textstyle r={\sqrt {y^{2}+z^{2}}}}$ . Sin embargo, la SF en el dominio (k_x , y , k_z ) no es singular cuando y  → 0.

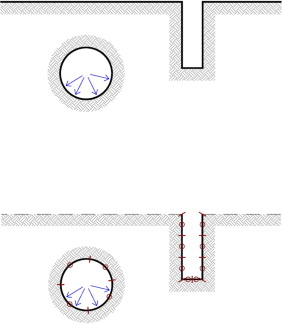
Supongamos que queremos integrar la SF para resolver un problema dinámico 2.5D en un semiespacio como el mostrado en la figura 10 . Es evidente que el esfuerzo en la discretización se reduce empleando la SF del semiespacio, o lo que es lo mismo, el cálculo de la SF es computacionalmente más costoso para la SF en el espacio completo. Así, considerando la siguiente integral elemental singular,

Figura 10. Problema dinámico 2.5D en un semiespacio.

$I={\int }_{{\Gamma }_{e}}F^{H-S}(k_{x},y,z,\omega ){\phi }_{e}(y,z)d{\Gamma }_{e}$

( 29)

donde F^H−S (k_x , y , z ) es alguna de las componentes de la SF para el semiespacio en desplazamientos o tensiones y ϕ (y , z ) es una función de forma regular. Existen 2 técnicas para resolver las integrales singulares:

• Regularización mediante la sustracción de una SF más simple.
• Cambio en el orden de integración.

6.1. Regularización mediante la sustracción de una SF más simple

Para regularizar la SF del semiespacio se pueden emplear diferentes SF dependiendo de las integrales singulares programadas. Por ejemplo, si se ha implementado la SF para un código dinámico 2.5D que emplea la SF para el espacio completo, se pueden usar las siguientes expresiones:

$I={\int }_{{\Gamma }_{e}}F^{H-S}(k_{x},y,z,\omega ){\phi }_{e}(y,z)d{\Gamma }_{e}$ $={\int }_{{\Gamma }_{e}}F^{F-S}(k_{x},y,z,\omega ){\phi }_{e}(y,z)d{\Gamma }_{e}$ $+{\int }_{{\Gamma }_{e}}\Delta F(k_{x},y,z,\omega ){\phi }_{e}(y,z)d{\Gamma }_{e}$

( 30)

donde

ΔF (k_x , y , z , ω ) = F^H−S (k_x , y , z , ω ) − F^F−S (k_x , y , z , ω ) es regular cuando r  → 0 y puede calcularse:

$\Delta F(k_{x},y,z,\omega )=$ $\quad {\frac {\Delta k_{z}}{2\pi }}\sum _{n_{z}=1}^{N_{z}}F^{H-S}(k_{x},y,n_{z}\Delta k_{z},\omega )$ $\quad -F^{F-S}(k_{x},y,n_{z}\Delta k_{z},\omega )e^{2\pi i(z-1)\Delta k_{z}{\frac {n_{z}-1}{N_{z}}}}$

( 31)

Las expresiones de F ^H−S (k_x , y , n_z Δk_z , ω ) y

F ^F−S (k_x , y , n_z Δk_z , ω ) vienen dadas en las ecuaciones ( 15 -18 ) y (27) , respectivamente, en el caso de los desplazamientos de la SF.

Otra forma de regularizar se obtiene partiendo de un código 2.5D elastostático que emplea la SF del semiespacio (Mindlin) y en el que se utilizarían las siguientes expresiones:

$I={\int }_{{\Gamma }_{e}}F^{H-S}(k_{x},y,z,\omega ){\phi }_{e}(y,z)d{\Gamma }_{e}$ $={\int }_{{\Gamma }_{e}}F^{Midlin}(k_{x},y,z){\phi }_{e}(y,z)d{\Gamma }_{e}$ $+{\int }_{{\Gamma }_{e}}\Delta F(k_{x},y,z,\omega ){\phi }_{e}(y,z)d{\Gamma }_{e}$

( 32)

donde

$\Delta F(k_{x},y,z,\omega )=F^{H-S}(k_{x},y,z,\omega )-$$F^{Midlin}(k_{x},y,z)$

es regular para r  → 0. Se puede calcular entonces:

$\Delta F(k_{x},y,z,\omega )=$ $\quad {\frac {\Delta k_{z}}{2\pi }}\sum _{n_{z}=1}^{N_{z}}F^{H-S}(k_{x},y,n_{z}\Delta k_{z},\omega )$ $\quad -F^{Midlin}(k_{x},y,n_{z}\Delta k_{z},\omega )e^{2\pi i(z-1)\Delta k_{z}{\frac {n_{z}-1}{N_{z}}}}$

( 33)

Las expresiones F ^H−S (k_x , y , n_z Δk_z , ω ) vienen determinadas por las ecuaciones ( 15 -18 ), mientras que

F ^Midlin (k_x , y , n_z Δk_z , ω ) están determinadas por las ecuaciones (28) .

6.2. Cambio en el orden de integración

Dependiendo del tipo de problema considerado pueden ser necesarias la realización de una o 2 integraciones para la transformada inversa en el cálculo de la SF. Considerando el caso de un problema dinámico armónico 2,5D, F ^H−S (k_x , y , z , ω ) viene dada por:

$F^{H-S}(k_{x},y,z,\omega )={\frac {1}{2\pi }}{\int }_{-\infty }^{\infty }F(k_{x},y,k_{z},\omega )e^{ik_{z}z}dk_{z}$

( 34)

y por tanto:

$I={\int }_{{\Gamma }_{e}}F^{H-S}(k_{x},y,z,\omega ){\phi }_{e}(y,z)d{\Gamma }_{e}(y,z)\quad =$${\int }_{{\Gamma }_{e}}\left\{{\frac {1}{2\pi }}{\int }_{-\infty }^{\infty }F(k_{x},y,k_{z},\omega )e^{ik_{z}z}dk_{z}\right\}d{\Gamma }_{e}(y,z)$

( 35)

Se puede cambiar el orden de integración entre Γ_e y k_z :

$I={\frac {1}{2\pi }}{\int }_{-\infty }^{\infty }\left\{{\int }_{{\Gamma }_{e}}F(k_{x},y,k_{z},\omega )e^{ik_{z}z}d{\Gamma }_{e}(y,z)\right\}dk_{z}$

( 36)

La ventaja de esta aproximación es que mientras F ^H−S (k_x , y , z , ω   ) es singular, ${\textstyle F(k_{x},y,k_{z},\omega )e^{ik_{z}z}}$ es regular y su integral puede calcularse directamente mediante la cuadratura de Gauss.

Discretizando la transformada inversa de Fourier, el valor de I viene determinado por:

$I={\frac {\Delta k_{z}}{2\pi }}$ $\sum _{n_{z}=1}^{N_{z}}\left\{{\int }_{{\Gamma }_{e}}F(k_{x},y,n_{z}\Delta k_{z},\omega )e^{2\pi i(z-1)\Delta k_{z}{\frac {n_{z}-1}{N_{z}}}}d{\Gamma }_{e}(y,z)\right\}$

( 37)

7. Conclusiones

Se ha presentado la respuesta de un semiespacio viscoelástico para una carga armónica empleando el método de los potenciales de desplazamiento y transformadas de Fourier. Las componentes del campo de desplazamientos y tensiones se obtienen de forma analítica. Esta solución no tiene singularidades y se puede calcular tanto para cargas en superficie como en el interior del semiespacio.

El procedimiento es útil en problemas de propagación de ondas. Se muestra, asimismo, que la SF converge analíticamente a otras soluciones conocidas, tales como la SF para el espacio completo y la SF del semiespacio elastostático, entre otras.

Las expresiones se han validado comparando los resultados con otros numéricos generados mediante el Método de los Elementos de Contorno y resultados experimentales.

La SF presentada en este estudio tiene un gran valor en la formulación de semiespacios elastodinámicos tridimensionales empleando el Método de los Elementos de Contorno. Se pueden incorporar en un código de dicho método evitando la discretización de la superficie del semiespacio.

Se presentan alternativas diferentes de regularización para el desarrollo de la integración singular dependiendo del código de Método de los Elementos de Contorno empleado por el investigador.

Este procedimiento empleado para el desarrollo de las SF del semiespacio puede generalizarse para obtener la SF dinámica armónica de placas 3D o en medios estratificados.

Agradecimientos

Este trabajo es parte de una investigación financiada por el Ministerio de Fomento de España bajo el título Evaluación de efectos dinámicos del ferrocarril .

Los autores expresan su agradecimiento a los profesores Pedro Galvín y José Domínguez por proporcionar el material mostrado procedente de resultados experimentales en la sección de validación.

References

1. [1] E. Kausel; Fundamental Solutions in Elastodynamic. A Compendium; Cambridge University Press (2006)
2. [2] H. Lamb; On the propagation of tremors over the surface of an elastic solid; Philos. Trans. R. Soc. London, 203 (1904), pp. 1–42
3. [3] L. Cagniard; Reflexion et Refraction des Ondes Seismiques Progressive; Gauthier-Villard, Paris (1939)
4. [4] C.C. Chao, H.H. Bleich, J. Sackman; Surface waves in an elastic half space; J. Appl. Mech., 28 (1961), pp. 300–302
5. [5] A.C. Eringen, S.S. Suhubi; Elastodynamics, volume II; Academic Press (1975)
6. [6] J.D. Achenbach; Wave Propagation in Elastic Solids; Elsevier Science Publishers, Amsterdam (1973)
7. [7] G. Eason; The displacements produced in an elastic halfspace by a suddenly applied surface force; IMA J. Appl. Math., 2 (4) (1966), pp. 299–326
8. [8] D.C. Gakenheimer; Numerical results for lambs point load problem; J. Appl. Mech., 37 (1970), pp. 522–524
9. [9] L.R. Johnson; Greens function for lambs problem; Geophys. J. R. Astron. Soc., 37 (1) (1974), pp. 99–131
10. [10] W.L. Pilant; Elastic waves in the earth, volume 11 of Developments in Solid Earth Geophysics; Elsevier, Amsterdam (1979)
11. [11] M. Bouchon; Discrete wave number representation of elastic wave fields in three-space dimensions; J. Geophys. Res., 84 (B7) (1979), pp. 3609–3614
12. [12] R.D. Mindlin; Force at a point in the interior of a semi-infinite solid; J. Appl. Phys., 7 (1936), pp. 195–202
13. [13] W.R. Dean, H.W. Parsons, I.N. Sneddon; A type of stress distribution on the surface of a semi-infinite elastic solid; Proc. Cambridge Phil. Soc., 40 (1944), pp. 5–18
14. [14] R. D. Mindlin, Force at a point in the interior of a semi-infinite solid. Technical Report 8, Columbia University, New York, May 1953.
15. [15] S. Timoshenko, J.N. Goodier; Theory of elasticity; McGraw Hill Company, Inc (1951)
16. [16] W. W. Garvin, Exact transient solution of the buried line source problem. Proc. R. Soc. London, Ser. A, Mathematical and Physical Sciences, 234(1199):528-541, March 1956.
17. [17] D.-P.N. Kontoni, D.E. Beskos, G.D. Manolis; Uniform half-plane elastodynamic problems by an approximate boundary element method; Soil Dyn. Earthquake Eng., 6 (4) (1987), pp. 227–238
18. [18] T. Kobayashi, Some problems of the boundary integral equation method in elastodynamics. En: C. A. Brebbia, editor, Boundary Elements V, pages 775-784, Berlin, 1983. Springer.
19. [19] R.Y.S. Pak; Asymmetric wave propagation in an elastic half-space by a method of potentials; J. Appl. Mech., 54 (1) (1987), pp. 121–126
20. [20] P.K. Banerjee, S.M. Mamoon; A fundamental solution due to a periodic point force in the interior of an elastic halfspace; Earthquake Eng. Struct. Dyn., 19 (1990), pp. 91–105
21. [21] F. Guan, I.D. Moore, C.C. Spyrakos; Two dimensional transient fundamental solution due to suddenly applied load in a half-space; Soil Dyn. Earthquake Eng., 17 (1998), pp. 269–277
22. [22] A. Tadeu, E. Kausel; Greens functions for two-and-a-half-dimensional elastodynamic problems; J. Eng. Mech., 126 (10) (2000 October), pp. 1093–1097
23. [23] A. Tadeu, J. António, L. Godinho; Greens functions for two-and-a-half-dimensional elastodynamic problems in a half space; Comput. Mech., 27 (2001), pp. 484–491
24. [24] H. Kawase, K. Aki; A study on the response of a soft basin for incident s, p and rayleigh waves with special reference to the long duratin observed in mexico city; Bull. Seismol. Soc. Am., 79 (5) (1989), pp. 1361–1382
25. [25] J. Park, E. Kausel; Impulse response of elastic half-space in the wave number-time domain; J. Eng. Mech., 130 (10) (2004), pp. 1211–1222
26. [26] R. Christensen; Theroy of Viscoelasticity. An Introduction; Academic Press, New York (1971)
27. [27] J. Domínguez; Boundary Elements in Dynamics; Elsevier, CMP, Southampton, Boston (1993)
28. [28] J. Miklovitz; The Theory of Elastic Waves and Waveguides; North-Holland (1978)
29. [29] P. Galvín, J. Domínguez; Analysis of ground motion due to moving surface loads induced by high-speed trains; Eng. Anal. Boundary Elem., 31 (2007), pp. 931–941

Notes

1. Hay que tener en cuenta que para j  = β , c_iβ es un vector con 3 componentes.