Resumen
Los desagües de fondo juegan un papel fundamental en la seguridad de las presas, ya que permiten controlar el caudal liberado en cada momento, y por tanto el nivel de embalse por debajo del nivel máximo normal. Desde principios del siglo xx se ha observado que para el correcto funcionamiento del desagüe y para evitar daños durante su operación, es conveniente disponer un sistema de aducción de aire aguas abajo de las compuertas, donde pueden aparecer presiones negativas. De otro modo, es frecuente que se produzcan daños por cavitación y vibraciones.
Debido a la dificultad para tomar datos o hacer estudios del fenómeno in situ y a escala real, el diseño de los sistemas de aireación se ha realizado tradicionalmente a partir de ensayos en laboratorio con modelos físicos a escala reducida, con cuyos resultados se han obtenido diferentes fórmulas empíricas que estiman el caudal de aire necesario para diseñar el sistema de aducción.
En el presente trabajo el problema se estudia mediante modelación numérica, incluyendo la interacción agua-aire. Para ello se utiliza el método de partículas y elementos finitos (PFEM), que había sido previamente aplicado y validado para el análisis del comportamiento de otras estructuras hidráulicas. De este modo se pretenden evitar los efectos de escala inherentes a los ensayos en modelo físico y analizar con más detalle los parámetros fundamentales. Los resultados permiten obtener conclusiones acerca de la influencia de las variables que intervienen.
Abstract
Dam bottom are key elements to control the water surface elevation below the spillway crest level. As a consequence, they are essential in reservoir management, and play a vital role in dam safety.
The convenience of installing an aeration system in dam bottom outlets is well known nowadays. Otherwise, damages due to cavitation and vibration are frequently serious, as could be observed in several dams built in the beginning of the 20th century.
The intrinsic features of the phenomenon make it hard to analyze either in situ or in full scaled experimental facilities. As a consequence, most of the previous studies have been carried out in small-scale physical models. The results of these works have been used to develop empirical formulas which provide an estimation of the maximum air demand of the aeration system.
The progress in the development of numerical methods allows addressing this problem using numerical modeling. The Particle Finite Element Method (PFEM) had been previously applied and validated for the analysis of the performance of other hydraulic structures. In this work, it has been used to simulate air-water interaction in free-flowing gated conduits. The objective is to avoid the scale effects of physical modeling and to study in detail the key parameters. The results clarify the behaviour of the involved fluids (air and water) and provide information about the influence of the main variables that affect their circulation.
Palabras clave
Aireación ; Desagües de fondo ; Modelación numérica ; Método de partículas y elementos finitos
Keywords
Aeration ; Bottom outlets ; Numerical modeling ; Particle Finite Element Method
1. Introducción y objetivos
1.1. Dispositivos de aireación en desagües de fondo de presas
En los desagües de fondo de presas que no descargan directamente a la atmósfera se produce una corriente de agua que se mueve a gran velocidad, lo cual causa el arrastre del aire que inicialmente se encontraba en el conducto, con la posible aparición de presiones negativas tras la compuerta. Esta caída de presión, que depende del caudal circulante de agua, del grado de apertura de compuerta y de la geometría de la instalación, puede provocar interferencias en la operación de las compuertas, debido a la aparición de vibraciones y cavitación [1] .
En los primeros diseños de desagües con compuertas sometidas a grandes presiones de agua no se tomaron precauciones frente a la cavitación o las vibraciones. Poco después de la construcción de la presa de Roosevelt (Estados Unidos) en 1908, con 67 m de carga de agua en el embalse, aparecieron problemas de erosión en el hormigón, pérdida de remaches y daños en el metal. Se hicieron reparaciones, pero al cabo de poco tiempo los problemas volvieron a aparecer. En la presa de Pathfinder, durante la operación del desagüe de fondo se escuchaban golpes y ruidos que aumentaban con el caudal de agua. Tras cerrar el conducto se encontraron grandes pérdidas de masa de metal y trozos de hormigón. El recubrimiento de acero se había doblado como si fuera papel. Posteriormente, se instaló un conducto de aducción de aire en el techo inmediatamente aguas abajo de las compuertas y se reparó el túnel. La solución resultó ser bastante efectiva [1] .
Desde entonces, se ha provisto a las compuertas sometidas a gran presión de sistemas de aireación diseñados para introducir aire en grandes cantidades en los desagües, muy cerca de la cara de aguas abajo de la compuerta. Estos dispositivos permiten mantener la presión cerca de la atmosférica en esa zona y evitar los daños a la estructura. Durante el desagüe con aperturas parciales de la compuerta el agua arrastra el aire a lo largo del túnel y el sistema de aireación entra en funcionamiento.
Las características principales de la aireación en desagües de fondo son las siguientes [2] :
- Grandes velocidades de la corriente de agua con pequeñas pendientes en la conducción.
- Depende en gran medida de las condiciones aguas arriba de la compuerta y de la existencia de aireadores en la solera y en las caras laterales del conducto.
- Existen diferentes tipos de flujos y la demanda de aire es sustancialmente distinta para cada uno de ellos.
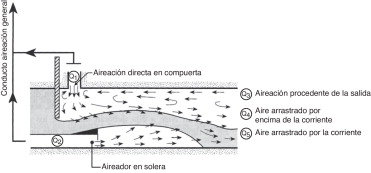
Pueden aparecer 5 tipos de corrientes de aire en el sistema [3] , dependiendo de la geometría de la instalación, del grado de apertura, de la existencia o no de aireación en la solera, y de las condiciones de aguas abajo (fig. 1 ).
|
|
|
Figura 1. Corrientes de aire habituales en desagües de fondo y campo de velocidades. Fuente: CNEGP [3] . |
La demanda de aire que debe suministrar el dispositivo de aducción para la aireación directa (Q1 ) viene determinada por el arrastre de aire que provoca el flujo básicamente a través del contorno superior (Q4 ), descontando el caudal proveniente de la salida del desagüe (Q3 ). En la práctica es frecuente dimensionar sin tener en cuenta ese caudal (Q3 ), de modo que el dispositivo pueda suministrar todo el caudal de aire necesario por sí mismo. De esta forma el diseño queda del lado de la seguridad.
A pesar de que el fenómeno ha sido objeto de numerosos estudios en el pasado, el comportamiento hidráulico de los flujos de aire y agua en los desagües de fondo no está adecuadamente comprendido y depende mucho de cada caso particular, por lo que los investigadores recomiendan su estudio mediante modelos a escalas suficientemente grandes [4] .
1.2. Antecedentes
El diseño del sistema de aireación en desagües de fondo de presas se realiza a partir del caudal de aire máximo que es necesario aportar para mantener la presión lejos de valores compatibles con la aparición de cavitación. Por tanto, el interés se centra en el cálculo de dicha demanda máxima de aire. Diversos grupos de investigación llevaron a cabo campañas de ensayos en prototipo para recolectar datos, con los que elaboraron fórmulas empíricas de aplicación general. Los resultados se expresan en función del coeficiente de aireación (β), que se calcula como:
|
|
( 1) |
donde Qa es el caudal de aire en el dispositivo de aireación y Qw el caudal de agua circulante bajo la compuerta. Los trabajos más destacados en este campo fueron los de Kalinske y Robertson [5] , Campbell y Guyton [6] , U.S. Army Corps of Engineers [7] , Levin [8] y Sharma [9] . La mayor parte de ellos dieron como resultado expresiones para el cálculo de β de la forma:
|
|
( 2) |
Donde A y b son constantes que varían dependiendo del autor y del tipo de régimen aguas abajo y Fc el número de Froude en el punto de contracción de la lámina de agua.
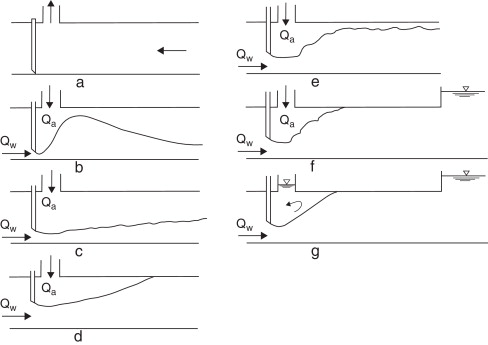
Finalmente, los estudios de Sharma [9] sobre la aireación en desagües de fondo han perdurado en el tiempo como un punto de referencia importante, porque obtuvo expresiones para cualquier tipo de condición de aguas abajo en base a una información muy completa, y porque los resultados son similares o ligeramente más conservadores que otras expresiones [3] . Sharma sostiene que se pueden dar 7 tipos de flujos diferentes de la mezcla entre agua y aire (fig. 2 ).
|
|
|
Figura 2. Tipos de flujos en desagües de fondo. a) Flujo de aire solo. b) Flujo pulverizado. c) Flujo en lámina libre. d) Flujo espumoso. e) Resalto hidráulico 1. f) Resalto hidráulico 2. g) Flujo de agua solo. Fuente: Sharma [9] . |
Las expresiones propuestas por Sharma para el cálculo de β son:
- Para flujos del tipo con resalto:
|
|
( 3) |
- Para flujos del tipo pulverizado:
|
|
( 4) |
- Para flujos del tipo en lámina libre:
|
|
( 5) |
Las expresiones anteriores han sido utilizadas con frecuencia para el diseño de sistemas de aireación. Sin embargo, siendo el fenómeno tan sensible al diseño particular del conducto y sus condiciones, es frecuente la elaboración de modelos físicos específicos de cada caso. Algunos de los modelos más relevantes de este tipo han sido desarrollados por Safavi et al. [10] para estudiar la entrada de aire desde la salida del conducto o desde el sistema aireador, por Tullis y Larchar [11] para reparar sistemas de aireación y por Frizell [12] para diseñar mejoras en el sistema de aireación de la presa de Folsom.
1.3. Objetivos
El presente trabajo se centra en la modelación numérica del funcionamiento de desagües de fondo regulados con compuertas de asiento plano y paso circular, cuyo diseño ha sido desarrollado por Ingeniería Hidráulica, S.A. (INHISA). La determinación precisa de la demanda de aire en este tipo de instalaciones no puede realizarse directamente a partir de las fórmulas descritas ya que las válvulas de INHISA, además de un diseño novedoso, tienen un obturador con geometría especial en la zona de cierre, lo que hace conveniente un estudio específico de sus necesidades de aireación. La campaña de modelación numérica tiene como objetivos determinar los siguientes aspectos:
- La diferencia existente entre modelos 2D y modelos 3D para la medición del caudal de aire circulante en desagües de fondo para diferentes aperturas de compuerta consideradas.
- La influencia de la longitud del conducto de desagüe en relación con el origen de las entradas de aire al sistema.
- La evolución de la demanda de aire en el sistema de aireación al variar la apertura de la compuerta de operación del desagüe.
- La evolución de la demanda de aire en el sistema de aireación al considerar diferentes niveles de agua en el embalse.
- La influencia del diámetro del conducto aireador en el caudal de aire y en el grado de apertura de compuerta que produce la máxima demanda de aire.
2. Metodología
2.1. Planteamiento general
Con objeto de determinar la influencia de los diversos parámetros en el comportamiento del flujo de aire y agua se utilizó para la modelación del fenómeno el método de partículas y elementos finitos (PFEM).
En primer lugar se realizó la validación del método de forma cualitativa y cuantitativa, a partir de estudios teóricos y experimentales de otros autores. Tras las comprobaciones, se elaboraron modelos bidimensionales y tridimensionales para comparar los resultados obtenidos con ambas opciones.
A continuación se realizó una campaña de experimentación numérica tomando un modelo de base y haciendo variar los principales parámetros que pueden influir en un desagüe de fondo. Este modelo es tridimensional y está basado en la geometría de compuerta de asiento plano y paso circular de INHISA, instalada en un conducto de desagüe de 1,5 m de diámetro. Los parámetros a variar en el modelo fueron: la longitud del conducto de desagüe, la carga de agua sobre la compuerta, el grado de apertura de la compuerta y el diámetro del conducto aireador.
Los resultados obtenidos permiten establecer conclusiones sobre el comportamiento de los desagües de fondo y su sistema de aducción de aire cuando se producen variaciones de los principales parámetros, además de comprobar la utilidad del PFEM para este tipo de estudios.
2.2. Sobre el método de partículas y elementos finitos
La resolución de problemas de dinámica de fluidos mediante métodos numéricos tiene una gran complejidad, por la propia dificultad de las ecuaciones de Navier-Stokes, que son las que gobiernan el fenómeno. La dificultad es mayor cuando además es necesario calcular la posición de la superficie libre del fluido, como ocurre por ejemplo en aliviaderos de presas. Esto ha hecho que en el campo de la hidráulica de presas hasta ahora los métodos numéricos tengan una importancia pequeña en comparación con los experimentales.
Sin embargo, en los últimos años está creciendo la frecuencia con la que se utilizan herramientas de cálculo numérico para el diseño de estructuras hidráulicas, gracias al avance en el desarrollo de los métodos numéricos y en el rendimiento de los ordenadores.
Las mayores dificultades del análisis de problemas de dinámica de fluidos con superficie libre utilizando el método de elementos finitos (MEF), bien con la formulación euleriana o con la arbitraria lagrangiana euleriana (ALE), son el tratamiento de los términos convectivos y de la condición de incompresibilidad en las ecuaciones de fluido y el modelado y seguimiento de la superficie libre.
Estos problemas desaparecen si se utiliza una descripción lagrangiana para formular las ecuaciones de gobierno de los dominios del fluido y de la estructura. En la formulación lagrangiana se sigue el movimiento de cada una de las partículas de líquido o del sólido de forma individual. Esta es la base de la técnica denominada smooth particle hydrodynamics (SPH), que está cobrando gran popularidad en todo el mundo [13] . Por el contrario, esta formulación presenta algunas dificultades de menor importancia en el MEF, como el tratamiento de las condiciones de contorno o la condición de incompresibilidad del fluido
En los últimos años, CIMNE ha desarrollado una clase particular de formulación lagrangiana para resolver un gran abanico de problemas, entre los que se encuentran los de dinámica de fluidos. El método se denomina método de partículas y elementos finitos (particle finite element method , PFEM). El PFEM trata los nodos en la malla, tanto en los dominios del fluido como de la estructura, como partículas que pueden moverse libremente e incluso separarse del dominio principal del fluido representando, por ejemplo, el efecto de gotas o chorreones de agua. Una malla de elementos finitos conecta los nodos que definen el dominio discretizado donde se resuelven las ecuaciones de gobierno de la mecánica de fluidos (para el líquido) y de la mecánica de sólidos (para la estructura) en la forma estándar del MEF. La calidad de la solución numérica depende del tamaño de la malla utilizada, como en el MEF. Se han desarrollado técnicas de mallado adaptativo que permiten definir diferentes tamaños de malla dentro del dominio de análisis.
La formulación lagrangiana es de gran utilidad para seguir el movimiento de las partículas del fluido en flujos en donde existen grandes desplazamientos de la superficie libre, como en el caso de olas que rompen sobre una estructura. El caso de los desagües de fondo es especialmente complicado debido a que 2 fluidos de características muy diferentes (agua y aire) interaccionan y por lo tanto ambos deben ser considerados en el cálculo. En el PFEM la malla de elementos finitos se utiliza fundamentalmente para obtener los valores de las variables de estado (por ejemplo, las velocidades, presiones, etc.) en los nodos.
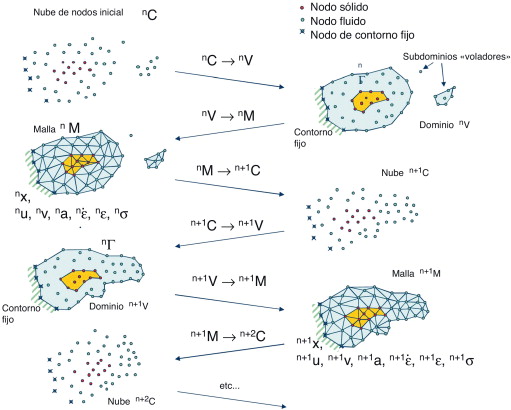
A continuación se describen brevemente las etapas que se siguen en la resolución mediante el PFEM, que se muestran esquematizadas en la figura 3 .
- Partir en cada paso de tiempo de una nube de puntos que discretiza los dominios de fluido y de sólido. Así, n C denota este conjunto de puntos en el instante t = tn (fig. 3 ).
- Identificar los contornos externos para los dominios del fluido y del sólido para definir el dominio de análisis n V. Esta es una etapa esencial ya que algunos contornos (como la superficie libre en los fluidos) pueden haberse distorsionado severamente durante el proceso de solución, incluyendo la separación y reentrada de nodos. El código utiliza una técnica basada en el método de alpha shape[14] para la definición de los nodos del contorno.
- Discretizar el dominio mediante una malla de elementos finitos n M. El método utiliza una técnica de malla basada en una teselación extendida de Delaunay [15] .
- Resolver las ecuaciones acopladas del movimiento lagrangiano para los dominios del fluido y de la estructura. Calcular las variables de estado relevantes en ambos dominios en cada paso de tiempo: las velocidades, la presión y las tensiones viscosas en el fluido, y los desplazamientos, las deformaciones y las tensiones en la estructura.
- Mover los nodos de la malla a la nueva posición n+1 C, donde n + 1 indica el paso de tiempo t + Δt, función del tamaño del paso del tiempo. Esta etapa es típicamente una consecuencia del proceso de solución de la etapa 4.
- Volver a la etapa 2 y repetir el proceso de solución para el paso de tiempo siguiente para obtener n+2 C (fig. 3 ).
|
|
|
Figura 3. Secuencia de etapas que comprende la resolución de las ecuaciones mediante el PFEM para actualizar un dominio que comprende un fluido y un sólido, entre el tiempo n (t = tn ) y n + 2 (t = tn + 2Δt). |
El lector interesado en una descripción detallada del método puede consultar las bases de la formulación en las referencias [15] y [16] , y sus aplicaciones más recientes en [17] , [18] , [19] y [20] .
2.3. Criterios de modelación numérica
La geometría de la compuerta se ha definido a partir de la información aportada por INHISA sobre las válvulas de asiento plano y paso circular instaladas en los desagües de fondo de la presa de Susqueda, en Cataluña (España). El resto de la geometría del modelo (sistema de aireación y conducto de desagüe) se ha diseñado de modo que permitiera medir el caudal de aire circulante por el conducto del sistema aireador. Con el fin de conocer la influencia de diversos parámetros en la demanda de aire, se realizó la campaña de experimentación numérica a partir de un modelo base.
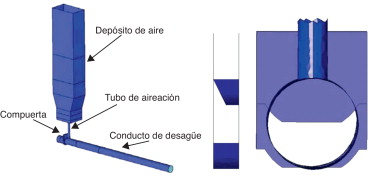
El modelo base (fig. 4 ) consta de: a) un conducto de desagüe horizontal de 1,5 m de diámetro y 30,0 m de longitud; b) una compuerta de asiento plano, 0,3 m de espesor, paso circular y diferentes grados de apertura; c) un conducto de aireación vertical circular de 0,5 m de diámetro y 4,0 m de longitud, situado aguas abajo de la compuerta de desagüe, y d) un depósito prismático de aire de sección rectangular y una altura de 30,0 m del que parte el conducto de aireación. Este depósito (d) es un artificio de modelación que sirve para almacenar las partículas del fluido «aire» que atravesarán el conducto durante la simulación, pudiendo medir así su caudal.
|
|
|
Figura 4. Izquierda: vista global de la geometría del modelo en 3D. Centro: vista lateral de la compuerta de asiento plano y paso circular, parcialmente abierta. Derecha: alzado desde aguas abajo. |
Como condición de contorno de aguas arriba se fija la velocidad de entrada del agua en una sección situada a 2 m de la compuerta. El caudal circulante en el desagüe se calcula previamente con las condiciones de cada caso particular (carga hidráulica, apertura de compuerta y pérdidas de carga). El valor de la velocidad se obtiene a partir de la ecuación de continuidad:
|
|
( 5) |
donde v es la velocidad de entrada, que se utiliza posteriormente como condición de contorno en el cálculo (m/s), Q es el caudal circulante (m3 /s) y S es la sección del conducto de desagüe (m2 ). Se ha admitido que la velocidad es constante en módulo y paralela al eje del conducto en toda la sección de entrada al modelo.
Inicialmente todos los conductos se encontraban llenos de aire que posteriormente es arrastrado por la circulación de agua hacia la salida. Este efecto crea la demanda de aire proveniente del sistema de aireación, que es alimentado desde el depósito de aire.
Se ha utilizado una malla de tetraedros de 0,1 m de lado en la zona de interés, que es la próxima a la compuerta y la correspondiente al conducto de aireación. La mitad de aguas abajo del conducto de desagüe se ha mallado con un tamaño de 0,2 m. Para la parte superior del depósito de aire se ha utilizado una malla mayor (de hasta 0,4 m), ya que únicamente sirve para aplicar la condición de presión a la entrada del conducto de aireación.
2.4. Campaña de experimentación numérica
Sobre el modelo numérico de base descrito anteriormente, se han realizado modificaciones con objeto de analizar el efecto de diferentes parámetros: la longitud del conducto de desagüe, el grado de apertura de compuerta, el nivel de embalse considerado y el diámetro del conducto aireador.
En una primera fase, se han comparado los resultados obtenidos en modelos 2D y 3D en cuanto a la relación entre el caudal de aire medido y el grado de apertura de compuerta.
Posteriormente se han planteado modelos 3D con diferente longitud del conducto de desagüe. Estudios anteriores indican que este parámetro puede influir en el sentido de circulación del aire, de modo que puede provenir del depósito de aire y circular a través del aireador, o bien de la salida del desagüe. Los modelos utilizados para el análisis del resto de parámetros tienen una longitud de 30 m para poder considerar como único punto de entrada de aire el conducto de aireación.
El grado de apertura se ha estudiado de forma discreta, generando la geometría correspondiente en la compuerta. Los porcentajes de apertura analizados son: 25, 38, 50, 60, 65, 75, 80 y 100%. El objeto de esta forma de proceder es tratar de detectar la posición de la compuerta que produce el máximo caudal de demanda de aire.
Los niveles de embalse considerados fueron de 5, 30 y 50 m, y para cada uno de ellos se varió la apertura de compuerta. En función del nivel de embalse se escogió la velocidad correspondiente de entrada de agua en la tubería teniendo en cuenta las pérdidas de carga en la conducción y la entrada.
Al variar la geometría del sistema de aireación los diámetros escogidos fueron de 0,5 y de 1,0 m para establecer las comparaciones en el flujo de aire. Para ambos casos se hizo variar el grado de apertura de compuerta.
2.5. Criterios de validación
La validación previa de los resultados se ha realizado de un modo cualitativo, comparando los flujos de aire que se producen con los descritos en [3] (fig. 1 ).
Con objeto de realizar una comprobación cuantitativa, se compararon los coeficientes de aireación obtenidos a partir de los experimentos llevados a cabo por Sharma [9] para flujo en lámina libre. Estos experimentos sirvieron para determinar las fórmulas de cálculo de β (2), (3) y (4). Si bien los resultados pueden dar una idea en cuanto al orden de magnitud, no puede esperarse una correspondencia exacta, por las diferencias existentes en la geometría de los modelos físico y numérico.
Para cada modelo se calcula el número de Froude en la zona contraída de la lámina de agua (Fc ), que a su vez depende de la velocidad del agua (Vc ) y del calado en ese punto (hc ):
|
|
( 6) |
3. Resultados y discusión
3.1. Modelación 2D y 3D
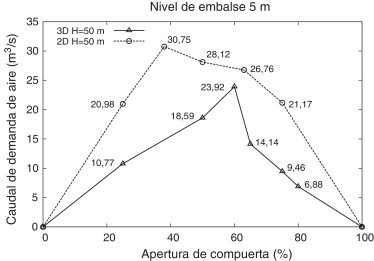
Los resultados obtenidos de caudales de aire con diferentes aperturas de compuerta se expresan en forma de gráficas comparativas entre un modelo 2D y otro 3D en la figura 5 .
|
|
|
Figura 5. Resultados de caudales de aire (m3 /s) medidos en modelos 2D y 3D en función del grado de apertura de compuerta y con una carga de agua en el embalse de 50 m. |
El resultado es una demanda de aire mayor para los modelos 2D que en los casos análogos tridimensionales para cualquier grado de apertura. Así mismo, se ha apreciado que el grado de apertura para el que se registra la demanda máxima de aire es menor en 2D (38%) que en 3D (65%).
En modelación numérica es habitual el uso de modelos en 2D para conseguir un importante ahorro en número de elementos considerados y tiempo de cálculo. En desagües de fondo de presas, especialmente si tienen sección circular, como es el caso del presente trabajo, parece claro que la simplificación bidimensional no reproduce adecuadamente el fenómeno real. No obstante, se ha realizado una batería de casos en 2D como una primera validación cualitativa del código, y para ver si se podía establecer algún tipo de correspondencia con los casos en 3D en cuanto al caudal de demanda de aire.
Los modelos 2D se pueden asemejar a secciones rectangulares de profundidad transversal unitaria, que no tienen en cuenta el efecto de las paredes laterales del conducto. Por lo tanto, la relación entre el área de la sección transversal del aireador y la del conducto de desagüe es mayor en 2D que en 3D. Así, este resultado podría ser un indicador de que para mayores secciones del dispositivo aireador, el caudal demandado de aire será mayor y además su máximo se dará para menores aperturas de compuerta.
3.2. Longitud del conducto de desagüe
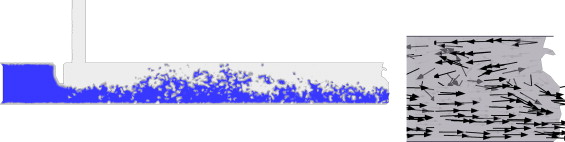
Uno de los parámetros que intervienen en la interacción agua-aire es la longitud del conducto de desagüe aguas abajo de la compuerta. Los ensayos en modelos numéricos realizados han dado como resultado que, a igualdad del resto de parámetros, con una longitud del conducto de desagüe de 12 m o menor se produce la entrada de aire desde el orificio de salida de este (fig. 6 ). Este caudal de aire avanza por la parte superior de la sección hasta llegar al punto inmediatamente aguas abajo de la compuerta, que es donde se producen las presiones más bajas del sistema. En cambio, con una longitud del conducto de desagüe de 30 m o mayor solo se produce entrada de aire desde el conducto de aireación.
|
|
|
Figura 6. Sección longitudinal por el eje del caso 3D con apertura del 50% y conducto de desagüe de 12 m. Izquierda: situación del agua (oscuro) y el aire (claro). Derecha: detalle del campo de velocidades en el extremo de aguas abajo, donde se observa que el agua sale por la parte inferior del conducto, mientras que el aire entra por la parte superior del mismo. |
Los resultados obtenidos son coherentes con las conclusiones de otros autores que estudiaron este mismo efecto, como Safavi et al. [10] y Oveson [21] . En general, puede afirmarse que la longitud relativa del conducto (L/D) es determinante en la procedencia del caudal de aire. Así:
- Si L/D es menor que un determinado valor, el aire necesario procederá de la salida del túnel, que a su vez estará más próxima a la compuerta. En el caso estudiado en este trabajo el valor límite es L/D = 8.
- Si L/D es mayor que un determinado valor, todo el aire necesario procederá del conducto de aireación. En nuestro caso, este límite es L/D = 20.
- Para valores intermedios el aire procede parcialmente de cada una de las entradas posibles.
Sin embargo, otros parámetros pueden influir en el sentido de circulación del caudal de aire, como son la apertura de compuerta o el diámetro del conducto de aireación. Así, a menores aperturas de compuerta, el caudal de agua liberado es menor y existe más espacio en el conducto de desagüe, lo cual facilita la entrada de aire desde aguas abajo; a menores diámetros del conducto de aireación, aumenta la dificultad de entrada de aire desde el mismo, lo cual facilita la entrada de aire desde la salida del desagüe.
3.3. Grado de apertura de la compuerta
La figura 7 muestra la relación entre el caudal de aire medido en los modelos analizados y el grado de apertura de compuerta.
|
|
|
Figura 7. Caudales de aire en función del porcentaje de apertura de compuerta con diferentes valores de nivel de embalse (H). |
Se resalta que el máximo de la demanda de aire se alcanza para la apertura del 60%, independientemente de la carga hidráulica aguas arriba. En otros apartados se puede apreciar que la geometría del modelo influye en la posición de este máximo.
La mayor parte de las referencias concluyen que la máxima demanda de aire en el aireador se produce para el 80% de apertura de compuerta. Este valor es el recomendado por CNEGP para el diseño del sistema de aireación [3] . Sin embargo, en la revisión bibliográfica realizada se ha detectado una variación importante de la posición de la compuerta que produce el máximo de demanda en cada caso. USACE [7] publicó un estudio de la demanda de aire en varias presas donde la posición del máximo varía entre el 60 y el 80% según las características de cada instalación. Por su parte, Tullis y Larchar [11] llevaron a cabo una campaña en modelo reducido en la que la mayor demanda de aire se producía para una apertura de en torno al 50%.
Por lo tanto, la geometría de cada caso y el propio diseño del sistema de aducción determinarán el porcentaje de apertura de compuerta que exige la máxima demanda de aire.
3.4. Nivel del embalse
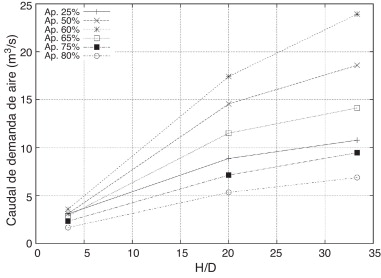
En la figura 8 se muestra la relación entre el caudal de aire circulante por el conducto de aireación y el parámetro H/D, que es el cociente entre el nivel de embalse y el diámetro del conducto de desagüe.
|
|
|
Figura 8. Caudales de aire demandados en función del nivel de embalse. Cada línea corresponde a un porcentaje de apertura de compuerta (Ap.). D: diámetro del conducto de desagüe; H: nivel de embalse. |
En la figura se representan modelos con 3 valores de la carga hidráulica aguas arriba, cada uno de los cuales se ha calculado con diferentes aperturas de compuerta. En los resultados se aprecia que un aumento de la carga hidráulica provoca una mayor demanda de aire, y que esta influencia es más importante cuando la carga hidráulica es pequeña.
3.5. Diámetro del conducto aireador
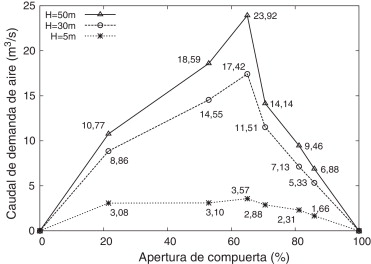
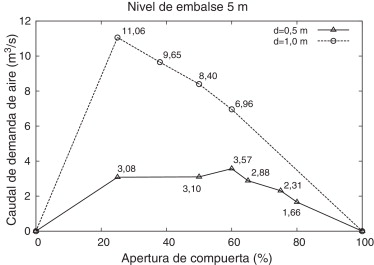
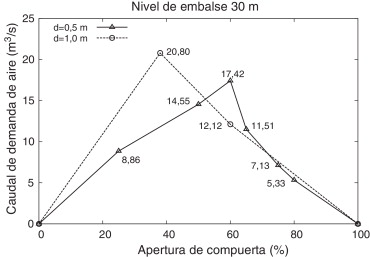
Los resultados obtenidos en la campaña de experimentación se reflejan en la figura 9 (para nivel de embalse de 5 m) y en la figura 10 (para nivel de embalse de 30 m). En cada una de ellas se muestra el caudal de aire para 2 diámetros diferentes del conducto de aireación (0,5 y 1,0 m).
|
|
|
Figura 9. Caudales de aire en función del porcentaje de apertura de compuerta y del diámetro del aireador (d). Nivel de embalse: H = 5 m. |
|
|
|
Figura 10. Caudales de aire en función del porcentaje de apertura de compuerta y del diámetro del aireador (d). Nivel de embalse: H = 30 m. |
En los modelos realizados se ha detectado que el porcentaje de apertura de compuerta para el cual se produce la máxima demanda de aire depende del diámetro del conducto aireador.
En los casos con el aireador de 0,5 m de diámetro, la máxima demanda de aire se ha registrado para una apertura de compuerta del 60%. Sin embargo, con el aireador de mayor diámetro se observa que el grado de apertura de compuerta que provoca la demanda de aire máxima es menor. A pesar de que los resultados obtenidos son de carácter discreto, se puede afirmar que se encontrará netamente por debajo del 60% registrado con el aireador de menor sección.
Se concluye así que existe una importante relación entre el diámetro del conducto aireador y el porcentaje de apertura de compuerta para el cual se obtiene la máxima demanda de aire.
3.6. Validación
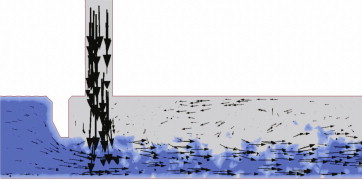
En la figura 11 se muestra el campo de velocidades que resulta en un caso típico de los analizados, en la zona inmediatamente aguas abajo de la compuerta. Es un corte longitudinal por el eje de la conducción, realizado sobre uno de los modelos tridimensionales.
|
|
|
Figura 11. Vectores de velocidad de partículas en el plano de simetría longitudinal de un modelo tridimensional con H = 30 m y 50% de apertura de compuerta. Zona aguas abajo de la compuerta. |
La comparación cualitativa con los flujos de aire indicados en la figura 1 ha mostrado resultados satisfactorios. Se puede apreciar que las velocidades de mayor módulo se producen en el conducto de aireación. Las partículas de aire parecen formar remolinos en el conducto de desagüe, con un flujo a contracorriente situado en la zona superior. Se observa además que la mezcla entre agua y aire produce un aumento del calado hacia aguas abajo.
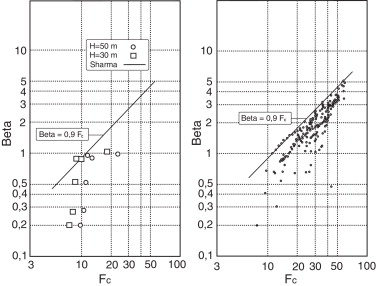
Por otra parte, la figura 12 muestra los resultados obtenidos mediante modelación numérica en comparación con los obtenidos mediante modelación física por Sharma [9] , así como con los que resultan de aplicar la fórmula correspondiente (5). Dicha fórmula representa una envolvente de los máximos para cada valor del número de Froude.
|
|
|
Figura 12. Izquierda: resultados de la modelación numérica con 30 y 50 m de nivel de embalse, en comparación con los obtenidos con (4). Derecha: adaptación del gráfico original de Sharma [9] , donde se observa que la fórmula que propone aproxima los máximos, así como la dispersión de los resultados. |
Los resultados experimentales presentan una importante dispersión respecto de dicha envolvente. Los casos analizados con el PFEM cubren una parte del rango de números de Froude analizados por Sharma [9] y los valores máximos obtenidos encajan con los que resultan de la aplicación de (5). Así, los modelos numéricos realizados se corresponden con los valores del tipo de flujo en lámina libre, no pudiendo considerarse como flujos de tipo pulverizado o con resalto hidráulico.
4. Conclusiones
- El PFEM permite la modelación numérica del flujo de agua en un desagüe de fondo a su paso bajo la compuerta de operación, así como del arrastre de aire que produce desde el sistema de aireación hacia la cara posterior de la compuerta.
- La longitud del conducto del desagüe de fondo aguas abajo de la compuerta es determinante en el origen del flujo de aire. En conductos cortos la mayor parte del flujo de aire entra al sistema desde la salida del túnel. Si por el contrario el desagüe es suficientemente largo, todo el aire necesario es suministrado desde el conducto aireador y posteriormente es arrastrado por el agua a lo largo del conducto hasta el exterior. No obstante, se ha detectado que en la circulación del aire también influyen decisivamente las dimensiones del aireador y el grado de apertura de la compuerta.
- Cuanto mayor es el nivel de embalse, mayor es el caudal de aire, a igualdad del resto de parámetros. La ley de variación se puede aproximar por una parábola (fig. 9 ) de pendiente positiva y decreciente a medida que aumenta la carga de agua, si bien hasta el momento solo se cuenta con resultados correspondientes a 3 niveles de embalse diferentes.
- La máxima demanda de aire en el modelo analizado se ha registrado para aperturas de compuerta del 60%. No obstante, se ha encontrado que este valor varía apreciablemente al modificar el diámetro del conducto de aireación. Concretamente, con diámetros mayores, el máximo caudal de aire se produce con aperturas de compuerta más pequeñas.
- Al aumentar el diámetro del aireador aumenta también el valor del caudal máximo de demanda de aire.
- El campo de velocidades obtenido (fig. 12 ) resulta concordante con el indicado por CNEGP [3] . En cuanto al caudal máximo de aire, los valores obtenidos con el PFEM se corresponden con los resultantes de aplicar la fórmula de Sharma [9] para flujos del tipo en lámina libre.
Agradecimientos
El trabajo presentado se ha desarrollado en el marco del proyecto VADIVAP (CIT 460000-2009-5), financiado por el Ministerio de Ciencia e Innovación. Está incluido en el «Plan Nacional de Investigación Científica, Desarrollo e Innovación Tecnológica 2008-2011».
Así mismo, el citado proyecto ha sido parcialmente financiado por el Fondo Europeo de Desarrollo Regional (FEDER) de la Comisión Europea.
Para el desarrollo de la investigación ha sido imprescindible la importante y continua colaboración por parte de M.A. Celigueta, E. Oñate, R. Morán y F. Riquelme, así como de los miembros de CIMNE y CIMNE-Madrid y del departamento de Ingeniería Civil: Hidráulica y Energía, de la Universidad Politécnica de Madrid.
Bibliografía
- [1] P.C.F. Erbisti; Design of Hidraulic Gates; Balkeman, Rotterdam (2004)
- [2] R.M. Gutiérrez Serret, Aireación en las estructuras hidráulicas de las presas: aliviaderos y desagües profundos [tesis doctoral]. Biblioteca ETS. Ingenieros de Caminos, Universidad Politécnica de Madrid. Documento (1995) 360718.
- [3] Comité Nacional Español de Grandes Presas. Guía Técnica de Grandes Presas n.° 5: Aliviaderos y Desagües, Anejo n.° 2 Aireación. 1997.
- [4] D.L. Vischer, W.H. Hager; Dam Hydraulics; John Wiley & Sons, Chichester (1997)
- [5] A.A. Kalinske, J.M. Robertson; Air entrainment in closed conduits flow; Trans. Am. Soc. Civ. Eng., 108 (1943), pp. 1435–1516
- [6] F.B. Campbell, B. Guyton; Air demand in Gated Conduits; IAHR Symposium, Minneapolis (1953)
- [7] U.S. Army Corps of Engineers. Hydraulic Design Criteria, Air Demand, Regulated Outlet Works, Sheet 050-1. (1964).
- [8] L. Levin, Calcul Hydraulique des Conduits d’Aération des Vidanges de Fond et Dispositifs Deversants, La Houille Blanche, No. 2. (1965).
- [9] H.R. Sharma; Air-Entrainment in High-Head Gated Conduits; Proceedings of ASCE, Journal of the Hydraulics Division, HY11 (1976)
- [10] K. Safavi, A.R. Zarrati, J. Attari; Experimental study of air demand in high head gated tunnels; Proc. ICE, Water Management, 161 (2) (2008), pp. 105–111
- [11] B.P. Tullis, J. Larchar; Determining air demand for small- to medium-sized embankment dam low-level outlet works; J. Irrig. Drain Eng., 137 (12) (2011), pp. 793–800
- [12] K.W. Frizell; Hydraulic Model Studies of Aeration Enhancements at the Folsom Dam Outlet Works: Reducing Cavitation Damage Potential; Water O&M Bulletin, 185 (September) (1998)
- [13] M.B. Liu, G.R. Liu; Smoothed particle hydrodynamics (SPH): an overview and recent developments; Arch. Comput. Methods Eng., 17 (1) (2010), pp. 25–76
- [14] H. Edelsbrunner, E.P. Mucke; Three dimensional alpha shapes; ACM Trans Graphics, 13 (1999), pp. 43–72
- [15] S.R. Idelsohn, E. Oñate, E.N. Calvo, F. del Pin; The meshless finite element method; Int. J. Num. Meth. Eng., 58 (6) (2003), pp. 893–912
- [16] E. Oñate, S.R. Idelsohn, F. del Pin, R. Aubry; The particle finite element method: an overview; Int. J. Comp. Meth., 1 (2004), pp. 267–307
- [17] A. Larese, R. Rossi, E. Oñate, S.R. Idelsohn; Validation of the particle finite element method (PFEM) for simulation of free surface flows; Int. J. for Computer-aided Engineering and Software, 25 (4) (2008), pp. 385–425
- [18] E. Oñate, S.R. Idelsohn, M.A. Celigueta, R. Rossi; Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows; Comp. Methods in Apll. Mech. And Eng., 197 (2008), pp. 1777–1800
- [19] F. Salazar, E. Oñate, R. Morán; Modelación numérica de deslizamientos de ladera en embalses mediante el método de partículas y elementos finitos (PFEM); Rev. Int. Mét. Num. Cálc. Dis. Ing., 28 (2) (2012), pp. 112–123
- [20] E. Oñate, M.A. Celigueta, S.R. Idelsohn, F. Salazar, B. Suárez; Possibilities of the particle finite element method for fluid-soil-structure interaction problems; Comput. Mech., 48 (2011), pp. 307–318
- [21] D.P. Oveson, Air Demand in Free Flowing Gated Conduits (2008). All Graduate Theses and Dissertations. Paper 3. Disponible en: http://digitalcommons.usu.edu/etd/3 [consultado 22 Ene 2013].
Document information
Published on 01/03/14
Accepted on 07/11/12
Submitted on 27/12/11
Volume 30, Issue 1, 2014
DOI: 10.1016/j.rimni.2012.11.002
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?