Abstract
The objective of this monograph is the derivation and implementation of a robust Finite Element formulation for the solution of solid-pore fluid coupled problems in multi-fractured porous media.
A coupled displacement-pore pressure FEM formulation for solving solid-pore fluid interaction problems is first introduced. The interaction between both components is governed by two equations: the balance of momentum for the mixture solid-fluid and the mass balance for the pore fluid.
Under nearly undrained-incompressible conditions, such formulation suffers from instability problems because of the violation of Babuska-Brezzi conditions. In order to work with elements of equal order interpolation for the displacement and pore pressure, the formulation is stabilized by means of the Finite Increment Calculus method (FIC). The FIC-stabilized formulation is tested against stable elements with a higher order interpolation for the displacement field in 2D and 3D examples.
Continuum damage mechanics is the basis of the crack growth strategy for the proposed fracture propagation technique. The strain softening models used for quasi-brittle materials favour spurious strain localization and ill-posedness of the boundary value problem if the damage variable only depends on the strain state at the point under consideration.
An integral-type non-local damage model associated to a characteristic length parameter is presented as a method to control the size of the fracture process zone and fully regularize the problem. Two examples are solved assessing the robustness of the model in front of changes in the spatial discretization.
Quasi-zero-thickness interface elements are formulated to represent discontinuities in the porous domain. A bilinear cohesive fracture model is used to describe its mechanical behaviour, and a formulation derived from the cubic law models the fluid flow through the crack.
Finally, a new methodology for the simulation of fracture propagation processes in saturated porous media is presented. The non-local damage model is used in conjunction with the interface elements to predict the degradation pattern of the domain and insert new fractures followed by remeshing. Fluid-driven fracture propagation examples in 2D and 3D are presented to illustrate the accuracy of the proposed technique.
Acknowledgements
After three years of hard work I can say that most of the objectives set at the beginning have been achieved. The time spent in the research and elaboration of this monograph has been truly rewarding for the acquired knowledge and for all the gained friends. Indeed, this project would have been impossible without all the people around me that have helped me in some way.
First, I would like to express my sincere gratitude to Prof. Eugenio Oñate for offering me the opportunity of working at CIMNE in this monograph. As my supervisor he always gave me wise advice and helped me work better, but he also gave me freedom to think for myself and let me grow as a researcher, which I really appreciate. I also want to thank him along with Sonia Sagrista for encouraging me to go on a three-month secondment at Tsinghua University (Beijing) in the framework of the TCAINMAND project. I can say that it has been one of the best experiences in my life.
I specially want to thank all the officemates at CIMNE that have been close to me kindly clarifying all my doubts, and with whom I enjoyed several meals during these years: Salva Latorre, Pablo Agustín Becker, Ferran Arrufat, Merce López, Guillermo Casas, Lorenzo Gracia, Miguel Ángel Celigueta, Miquel Santasusana and Roberto Flores.
I am deeply grateful to Prof. Zhuo Zhuang as the supervisor of my secondment in Tsinghua University. Although I was very far from home, he always made me feel comfortable. I really appreciate all the interesting discussions we had every Thursday during the group meetings. In the same way, I would like to thank Prof. Zhanli Liu and all the officemates, specially: Tao Wang, Qinglei Zeng, Yue Gao, Liu Fengxian, Liyuan Wang, Ramiro Mena and Jan Rojek. I am also very thankful to my room mate in Tsinghua Jaime Santirso, and to Duan Wenjie.
I would also like to thank other colleagues at CIMNE that have helped me in various matters: Fernando Salazar, Enrique Escolano, Miguel Pasenau, Javi Gárate, Josep Maria Carbonell, Pooyan Dadvand, Riccardo Rossi, Jordi Cotela, Carlos Roig, Rubén Zorrilla and Vicente Mataix.
I also acknowledge the Agencia de Gestió d'Ajuts Universitaris i de Recerca (AGAUR) for the financial support.
Finally, this work is dedicated to my family: Lluís, Marta, Oriol, MªAngels and Gabriel. They are the most important people in my life and represent a fundamental and unique support.
1 Introduction
1.1 Motivation and presentation
Problems involving the flow of a fluid through a porous medium have always been the object of special interest in geomechanics. Many geomaterials contain pores and other cavities that are filled with fluid in saturated or unsaturated conditions. The pressure of such fluid and the deformation of the solid medium are closely related in a challenging problem that must be analysed in a coupled manner.
Further complexity is added when one takes into consideration fluid-driven fracture propagation in the solid domain. Indeed, depending on the fluid pressure distribution and the external efforts acting over the domain, not only pre-existing discontinuities can open and close, but they can also propagate and conform new fractures, introducing an additional degree of coupling.
From the classical contributions of Terzaghi [1] and Biot [2] important effort has been made in the last decades to develop competent numerical methods in poromechanics that allow analysing and understanding the complexity of the mechanisms involved in problems with a coupling between a solid skeleton and a fluid phase. Such techniques are becoming essential tools of for different fields and applications.
In hydrogeology, for instance, these numerical methods are important to represent the water flow through porous soil when characterizing aquifers performance (storage capacity, water transmissivity, water content, etc.), and also to study the dispersion and transport of dissolved contaminants [3].
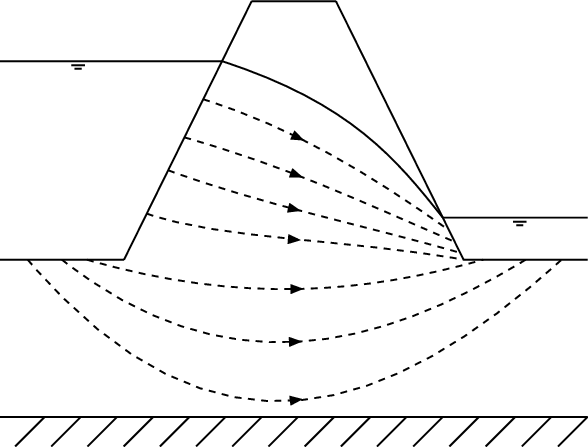
For soil mechanics, these tools are specially interesting for solving problems in which the seepage flow and pressures interact with the dynamic behaviour of the solid skeleton (Figure 1a).
|

|
| (a) Seepage through earth dam. | (b) Simplified scheme of an hydraulic fracturing process. |
| Figure 1: Examples of problems with important interaction between a solid skeleton and a fluid phase. | |
An important field of application is in petroleum engineering. Here, the oil-gas-soil interaction takes the leading role along with the hydraulic fracturing (Figure 1) as a common technique to enhance reservoir permeability and well efficiency [4,5].
Other applications for numerical methods in poromechanics have recently emerged for a variety of fields, including the underground storage of carbon dioxide [6], the geothermal energy production [7], the analysis of interstitial flow in bone tissue [8], and even the study of fractures in epithelial cell sheets [9,10].
There are clearly different applications for this kind of problem, but in all of them one can always distinguish, at least, two distinct components: a solid skeleton and a fluid phase. The solid medium is usually composed by particles of different shapes and sizes enclosing little cavities that can be totally or partially filled by the fluid.
It seems natural that a proper analysis of these kind of problems should require taking into account both parts, i.e. solid and fluid, for the derivation of the governing equations and the definition of the boundary conditions.
Thereby, when solving this coupled problem, it will be necessary to capture the seepage of the fluid through the porous medium, and the deformations of the solid skeleton at any point of the domain. From the numerical perspective, one of the most widespread approaches is the displacement-pressure formulation, in which the main unknowns are the displacements of the solid skeleton and the pore pressure .
However, in the limit of nearly incompressible pore fluid and small permeability, coupled poromechanics formulations suffer from instability problems. Finite elements exhibit locking in the pressure field and spurious oscillations appear due to the violation of the so-called Babuska-Brezzi conditions [11,12]. The oscillations can be overcome by locally refining the mesh or by using shape functions of the displacement field one order higher than those of the pressure field. In practical applications this is, however, not feasible because of the increment in the computational cost. In this sense, stabilization methods have been found to be powerful tools to circumvent the Babuska-Brezzi conditions violation without compromising the efficiency of the computation.
Discontinuities in porous materials such as concrete, soil and rock have a noticeable influence in the mechanical and hydraulic behaviour of a multi-phase system. They represent a jump in the displacement field as well as in the stress and strain fields. The presence of these fracture planes modifies the global material response in terms of strength and stiffness, and introduces directional preferences in the deformation of the solid and in the fluid flow. It is thereby essential to properly describe the initiation and propagation of these discontinuities with a suitable fracture mechanics approach.
In the context of the Finite Element Method (FEM), modelling of discontinuities can be done by means of interface elements. These special elements, which can be used to define pre-existing or propagating cracks, act as joints between the discontinuities in the displacement field and can be used to represent the enhanced conductivity of the medium.
Thereby, in the modelling of the fractured domain, it is necessary to implement a constitutive model that allows determining the initiation and propagation of new failure zones, and a model characterizing the mechanical behaviour of the fractures. In this regard, the combination of a “smeared crack” model with a “discrete crack” approach permits working with pre-defined discontinuities and, at the same time, insert new joint elements when necessary.
Concerning the propagation of fractures, suitable regularization methods and remeshing techniques become essential to minimize the mesh dependency when determining the direction of the crack growth.
Kratos framework
This work has been implemented in Kratos Multiphysics [13]. Kratos is an Open-Source framework for building parallel multi-disciplinary simulation software. Modularity, extensibility and High Performance Computing (HPC) are some of its main objectives. Kratos has BSD licence and is written in C++ with extensive Python interface.
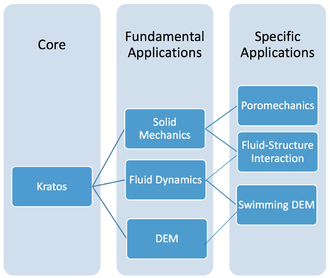
It features a “core and applications approach”, where standard tools (databases, linear algebra, solvers, etc.) come as part of the “core” and are available as building blocks in the development of “applications”, which derive from the core and focus on the solution of particular problems of interest (see Figure 2). We note here that all the implementations of this monograph gave as a result the “Poromechanics Application” in Kratos.
|
| Figure 2: Kratos' “core and applications approach”. |
1.2 Objectives
The main objective of this work is to advance in the development of finite element methods for the analysis of coupled solid-pore fluid problems in which the initiation and propagation of cracks represents a key issue and is strongly influenced by the interaction between the different media. To this end, the following goals were set for the three-years of work:
- Derivation and testing of a stable FEM formulation for coupled solid-pore fluid problems under fully saturated conditions for 2D and 3D analysis.
- Implementation and validation of a robust continuum damage model for the analysis of degradation of quasi-brittle materials.
- Development of special interface elements compatible with the implemented formulation, and valid for the definition of pre-existing fractures in the porous media as well as propagating cracks.
- Development of a crack tracking technique based on the analysis of the damage pattern around the crack tip.
- Implementation of an efficient technique to insert new interface elements in the domain and remesh the model every time the crack propagates.
- Application of the previous implementations for solving a problem of interest in engineering. An example of a problem where all the components are required is the analysis of hydraulic fracture processes.
1.3 State of the art
1.3.1 Coupled solid-pore fluid formulation
The first work regarding the coupling between a fluid and a porous medium can be attributed to Terzaghi, who proposed a one-dimensional theory of consolidation in 1943 [1]. The generalization to three-dimensional cases was presented by Biot who also described methods for determining the elastic coefficients of the theory [2,14,15]. Although these first works were restricted to linear elastic materials, they have been the basis for a lot of subsequent works in geophysics, soil and rock mechanics.
The transition between Biot's theoretical formulation and the first successful numerical results is found in Ghaboussi and Wilson's work, in which the assumption of incompressibility of fluid and solid particles was relaxed [16]. Zienkiewicz and Bettes [17] proposed a formulation based only on the displacement of solid and the pore pressure, which is suitable for the low-frequency situations such as earthquake problems.
De Boer and Kowalski [18] developed a plasticity theory for saturated porous media and, due to the increasing interest in non-linear applications, Zienkiewicz and co-workers expanded the theory to a generalized incremental form for non-linear material behaviour and large strain effects for liquefaction analysis of soil structures [19,20].
In order to overcome the violation of Babuska-Brezzi conditions, several stabilization techniques can be found in the literature in the context of fluid mechanics and solid mechanics, and have been also extended to poromechanics problems.
Some of these techniques are based on the pioneer work of Chorin [21] and use special time stepping schemes to generate stabilization terms [22,23,24].
Other types of approaches have also achieved good stabilized results by modifying the fluid mass balance equation with the addition of a characteristic term that needs to be calibrated [25,26,27,28]. Here one can also include the methods based on the concept of Polynomial-Pressure-Projections, in which the stabilizing terms use element-local projections of the pressure field to counteract the inherent instabilities [29,30,31,32].
There is an additional group of stabilization techniques that make use of the Finite Increment Calculus method (FIC) developed by Oñate and co-workers. In this approach, stabilization terms are derived by expanding the residual of the governing equations in a Taylor series. Previously stabilized FEM formulations for quasi and fully incompressible fluids and solids were based on the first order form of the FIC balance equation in space [33,34,35,36], while recent works are based on the second-order FIC form of the mass balance equation [37,38].
1.3.2 Fracture modelling
In the last decades various authors have developed numerical methods for the initiation and propagation of fractures in the context of porous media.
One approach that has obtained notable attention in the last years is the extended finite element method (XFEM) developed for crack analysis [39,40,41,42,43,44]. The XFEM handles discontinuities in an approximation space with jump functions, i.e. local enrichment functions, and so there is no need to represent cracks in a mesh. This considerably reduces the cost of remeshing during crack growth, but in return, the method demands a higher computational cost in terms of number of degrees of freedom and numerical integration.
The other obvious approach that has shown significant impact includes the group of numerical techniques purely based on the finite element method (FEM). In this group, numerous methods can be found in the literature, but probably two main subgroups can be distinguished: the “smeared crack” approaches, continuum based methods in which the influence of developing fractures is incorporated into the constitutive stress-strain law [45,46,47,48], and the “discrete crack” models, in which each single discontinuity is represented explicitly [49,50,51,52].
For the analysis of material degradation and crack initiation in porous media, most of the techniques developed for continuum damage mechanics are applicable.
The concept of damage was introduced by Kachanov in 1958 in the context of creep rupture in metals [53]. Rabotnov [54] gave the problem physical meaning by suggesting that the reduction of the sectional area was measured by means of the damage parameter.
The thermodynamic formalism involved in the irreversible process of damage was developed by Lemaitre and Chaboche [55], and other important contributions to our knowledge were given by: Mazars and Pijaudier-Cabot [56], Simo and Ju [57], Oller et al. [58], Oliver et al. [59,60], and Cervera et al. [61,62], to name but a few.
If the damage parameter depends only on the strain state at the point under consideration, numerical simulations exhibit a pathological mesh dependence and the energy consumed by the system tends to zero as the mesh is refined. Classical constitutive models require an extension in the form of a characteristic length to properly model the thickness of localized zones.
Such extension can be introduced by means of second gradient models [63], micro-polar [64], strain gradient [65], viscous [66] and non-local terms [67].
Non-local elasticity was developed by Eringen [68] who later extended it to non-local elasto-plasticity [69]. Subsequently, it was found that certain non-local formulations could act as efficient localization limiters with a regularizing effect on problems with strain localization [70].
Modelling of discontinuities between two bodies in contact has been performed via contact elements in solid mechanics [71,72,73], and the idea has also been used in fracture mechanics to model cohesive forces by means of cohesive elements [74,75].
Since Goodman et al. proposed the “zero-thickness” interface element to describe the mechanical behaviour of pre-existing joints in rock masses [76], many authors have developed strategies to adapt that element for the solution of fracture processes in solid-pore fluid coupled problems.
Similarly as in the formulation of the continuum solid-pore fluid mixture, two equilibrium equations usually govern the coupled behaviour of the fractures. One equation deals with the mechanical behaviour of the crack, whereas the other equation describes the balance of fluid mass within the fracture.
Concerning the modelling of the fluid flow through the discontinuity, three different types of zero-thickness interface elements can be found in the literature: single, double and triple noded elements (Figure 3). The single-noded elements are the simplest ones and represent pipe elements that are superimposed onto the standard continuum element edges [77]. With this elements the hydraulic head is uniform across the discontinuity and thus only the longitudinal conductivity is taken into account. The triple-noded elements allow including the influence of a transversal conductivity through the discontinuity [78]. The two nodes at each side of the interface represent the potentials in the pore pressure between the two sides of the discontinuity. The third node, placed at the middle of the interface, stores the average potential of the longitudinal fluid through the fracture. Finally, the double-noded elements take into account both types of conductivity but the middle node variable is eliminated in terms of the variables of the external nodes. Ng and Small [79] used this double-noded zero-thickness interface element to model flow problems with pre-existing discontinuities but with no hydraulic potential drop between the two interface walls. Segura and Carol [80] introduced the transversal conductivity for zero-thickness elements to account for the exchange of fluid between the discontinuity and the porous material.
For analysing the mechanical behaviour of fractures, we find essentially two different approaches: those based on linear elastic fracture mechanics (LEFM), and those based on non-linear fracture mechanics (NLFM). LEFM techniques were first proposed to solve fracture propagation problems by means of remeshing without considering a fracture process zone (FPZ) before the crack tip. This approach is applicable in large structures where the size of the FPZ is negligible. However, for quasi-brittle analyses, the consideration of a non-linear fracture process zone where the energy is dissipated before it completely fails was found to be essential. In those cases the NLFM technique is usually applied and a softening law relates the cohesive stress to the crack opening in the FPZ. The first procedure based on the cohesive fracture model was originally introduced by Barenblatt [81,82] for brittle materials and by Dugdale [83] for plastic materials. Hillerborg et al. [84] developed the first fictitious crack model for Mode I fracture. It was extended later for the mixed mode fracture, from which Camacho and Ortiz [85] proposed a suitable fracture criterion that is widely used in the literature.
A crucial part in the modelling of fracture propagation is the criterion for determining the direction of the crack growth. Some criteria are based on the local evaluation of the stress field at the crack tip, e.g. the maximum circumferential stress criterion [86]. Others are based on the energy distribution at the fractured zone, such as the minimum strain energy density criterion [87] or the maximal strain energy release rate criterion [88]. There is also another group of crack growth criteria based on continuum damage mechanics [89].
Schrefler et al. [90] and Secchi et al. [91] implemented the double-noded interface element with cohesive fracture model, working together with an adaptive mesh refinement technique in porous materials. Also, Khoei et al. implemented a model of cohesive crack growth using an adaptive mesh refinement procedure for two-dimensional problems [92]. In that work, a bilinear cohesive law originally proposed by Espinosa and Zavattieri [93] is adopted, and a modified superconvergent patch recovery (SPR) technique is used for the error estimation.
More recently, Moës et al. presented an alternative technique combining fracture mechanics with level set procedures [94,95].
1.4 Organization
The book is organized as follows.
In Chapter 2 the displacement-pore pressure formulation is described, starting from the governing equations of the problem and the fully coupled system of equations to be solved. Following that, the instability produced under undrained-incompressible conditions is presented and the stable formulation based on the second-order FIC form of the mass balance equation in space is thoroughly detailed. Two academic examples are solved at the end of the chapter comparing the FIC-FEM elements of equal order interpolation to stable elements with a higher order interpolation for the displacement field.
Chapter 3 starts introducing the essential concepts on continuum damage mechanics. Details are given on the fundamental concepts of the isotropic damage theory, including the equivalent strain forms and damage evolution laws that have been implemented in this work. Next, the regularization techniques developed to overcome the problems associated to strain localization are illustrated. Special attention is given to the integral-type non-local damage model, highlighting the most relevant aspects of its numerical implementation. Two examples are shown at the end, where we assess the robustness of the implemented damage models against changes in the spatial discretization.
In Chapter 4 the formulation of the developed quasi-zero-thickness interface elements is detailed, explaining the mechanical behaviour of the fracture and the model governing the fluid flowing in it. After that, we present the proposed fracture propagation technique combining the non-local damage model with the interface elements. Finally, two plane-strain examples are solved to test the accuracy of the crack propagation methodology, and one additional case is included to show the performance of the generalized 3D formulation.
Chapter 5 summarizes the most relevant conclusions of this work, pointing out its main contributions. In the end, the new perspectives to future works are briefly commented.
1.5 Related publications
The following publications have emanated from the work carried out in this monograph. The list is ordered chronologically.
- I. de Pouplana and E. Oñate. Combination of a non-local damage model for quasi-brittle materials with a mesh-adaptive finite element technique. Finite Element in Analysis and Design, vol. 112, pp. 26-39, 2016. DOI: 10.1016/j.finel.2015.12.011
- I. de Pouplana and E. Oñate. A FIC-based stabilized mixed finite element method with equal order interpolation for solid-pore fluid interaction problems. International Journal for Numerical and Analytical Methods in Geomechanics, vol. 41, pp. 110-134, 2016. DOI: 10.1002/nag.2550
- I. de Pouplana, L. Gracia, F. Salazar and E. Oñate. Cracking of a concrete arch dam due to seasonal temperature variations. Theme A - International Benchmark Workshop on the Numerical Analysis of Dams, 2017.
- L. Gracia, I. de Pouplana, F. Salazar and E. Oñate. Static and seismic analysis of an arch-gravity dam. Theme B - International Benchmark Workshop on the Numerical Analysis of Dams, 2017.
- I. de Pouplana and E. Oñate. Finite element modelling of fracture propagation in saturated media using quasi-zero-thickness interface elements. Article sent to Computers and Geotechnics, 2017.
- E. Oñate and I. de Pouplana. A methodology for analysis of delamination in composites using joint elements. In preparation.
2 Coupled Solid-Pore Fluid Interaction Problem
2.1 Introduction
Sometimes two or more physical systems interact with each other in such a way that it is not possible to obtain a solution independent of any of the systems without considering all the systems at the same time. It is said that those systems belong to a coupled problem, with the coupling being stronger or weaker depending on the level of interaction between each system.
Our problem of interest belongs to the type of coupled problems in which the different domains of the physical systems overlap. In such cases, the coupling occurs through the governing differential equations describing the different physical phenomena. In particular, we are going to study solid-pore fluid interaction problems in which a unique mesh represents a porous medium.
The problem falls in the field of poromechanics [96], a branch of physics that studies porous materials whose mechanical behaviour is significantly influenced by the pore fluid.
A porous medium is composed of a matrix, containing solid components of different shape and size, and a porous space, that can be totally or partially filled by a fluid. Thereby, any infinitesimal volume of a porous medium can be treated as the superimposition of two material particles: the skeleton particle and the fluid particle (Figure 4).

|
| Figure 4: Infinitesimal volume of porous medium as a combination of two phases: a solid skeleton and a fluid medium. |
A continuous description of such an heterogeneous medium requires taking into account the mechanical coupling between the solid skeleton and the fluid phase when formulating the governing equations of the problem.
In the last decades important effort has been made in the development of powerful numerical methods for poromechanics that allow analysing porous media considering the mechanical coupling between the solid and the fluid phase.
A one-dimensional theory of consolidation was first proposed by Terzaghi in 1943 [1] and then Biot extended it to three-dimensional cases [2,14,15]. Although these first works were restricted to linear elastic materials, they have been the basis for a lot of subsequent works in geophysics, soil and rock mechanics.
The first numerical solution of Biot's formulation was obtained by Ghaboussi and Wilson [16] and the work was further developed by Zienkiewicz et al. [97,17]. Later on, due to the increasing interest in non-linear applications, Zienkiewicz and co-workers expanded the theory to a generalized incremental form for non-linear materials and large deformation problems [19,20].
The mathematical formulation of solid skeleton and pore fluid interaction presented here is based on the model proposed by Zienkiewicz et al. [97]. The problem was originally formulated for fully saturated conditions in terms of the solid matrix displacement , the mean fluid velocity relative to the solid phase and the fluid pore pressure , but in many geo-mechanical problems with no high-frequency phenomena involved, the fluid relative velocity can be neglected and so the equations can be simplified to work with only two main variables: and [98].
In the limit of nearly incompressible pore fluid and small permeability, the coupled poromechanics formulations suffer from instability problems. Finite elements exhibit locking in the pressure field and spurious oscillations in the numerical solution for the pressure appear due to the violation of the so-called Babuska-Brezzi conditions [11,12]. The oscillations can be overcome by locally refining the mesh and by using shape functions of the displacement field one order higher than those of the pressure field. In practical applications this is, however, not the best approach because of the increment in the computational cost. In this sense, stabilization methods have been found to be powerful tools to circumvent the Babuska-Brezzi conditions violation without compromising the efficiency of the computation.
Several stabilization techniques have been investigated in the past years in the context of computational fluid dynamics [21,25,26,22,33,34] and (incompressible) solid mechanics [99,100,28,35,36], and have been also extended to poromechanics problems [27,23,24,101,29].
Although each stabilization approach has its differential aspects, they can be classified in three main categories.
The first category comprises those techniques in which special time stepping schemes are applied in order to generate stabilization terms. Probably the earliest work in this category is due to Chorin [21] who proposed a technique to deal with incompressible fluid problems which is now referred as the fractional step method or the operator-splitting method. Such a staggered time stepping algorithm has been found to provide stabilization in the steady-state when used in a convenient form [21,22,23,24].
The second type of techniques are more direct stabilization methods based on the perturbation of the fluid mass conservation equation. Instead of using special time-stepping algorithms that give additional terms in the steady-state approximation, the fluid balance equation is modified by adding a stabilization term multiplied by a parameter that needs to be carefully calibrated [25,26,27,28]. This group also includes the methods based on the concept of Polynomial-Pressure-Projections, in which the additional stabilizing terms use element-local projections of the pressure field to counteract the inherent instabilities [29,30,31,32].
The third category considered here is the Finite Increment Calculus method (FIC) [33,34,35,36,37,38], which is the approach also adopted in the present work. The FIC technique is based on expressing the equations of balance of mass and momentum in a space/time domain of finite size, and retaining higher order terms in the Taylor series expansion typically used for expressing the change in the transported variables within the balance domain. Apart from the standard terms of infinitesimal theory, the FIC form of the balance equations contains derivatives of the classical differential equations multiplied by characteristic distances in space and/or time.
Previously stabilized FIC-FEM formulations were based on the first-order form of the FIC balance equation in space and can be found in the literature for quasi and fully incompressible fluids and solids [33,34,35,36], and even for 1D and 2D poromechancis problems [102]. In this work, the more recent second-order FIC form of the mass balance equation [37,38] has been adopted as the basis for deriving the stabilized FIC-FEM formulation for 2D and 3D poromechanics problems. This new formulation takes advantage of the second order derivatives terms to provide a simpler procedure for obtaining a residual-based stable form of the mass balance equation suitable for finite element analysis. Proof of the good results of this formulation regarding convergence and mass conservation are given in [38].
This chapter is organized as follows. First, the finite element formulation is introduced, starting from the governing equations of the problem and the fully coupled system of equations to be solved. After that, the instability problem is stated and the stabilization by means of the second-order FIC form of the mass balance equation in space is thoroughly detailed. Finally, two examples are solved in order to test the implemented FIC-stabilized element and compare it to stable elements with a higher order interpolation for the displacement field.
2.2 Finite element formulation
|
|
(2.1) |
where is the Kronecker delta and is Biot's coefficient [103]:
|
|
(2.2) |
with being the bulk modulus of the solid phase and the bulk modulus of the porous medium:
|
|
(2.3) |
where is the Young's modulus and is the Poisson's ratio.
In order to account for the coupling between the solid and fluid phases, the behaviour of a saturated porous medium is governed by the combination of two equations: the balance of momentum for the mixture solid-fluid, and the mass balance for the pore fluid.
Balance of momentum for the mixture solid-fluid
|
|
(2.4) |
where is the body force per unit mass, is the acceleration of the solid skeleton and is the density of the solid-fluid mixture , being the porosity of the soil, the density of the fluid and the density of the solid.
Let us introduce the general definition for the effective stress (2.1) into the balance of momentum equation (2.4). This gives
|
|
(2.5) |
Mass balance for the pore fluid
|
|
(2.6) |
where is the fluid mass content per unit volume and represents the flow rate. It should be noted that Equation (2.6) is in a linearized form of the general mass balance expression as the fluid density variation effect has been ignored.
The mass balance equation is modified as follows. Let us first consider the constitutive equation presented in [2] relating the fluid mass content per unit volume with the volumetric strain of the solid skeleton and the pore pressure
|
|
(2.7) |
where is a combined compressibility of the fluid-solid phases, also called Biot's modulus [103]
|
|
(2.8) |
being the bulk modulus of the fluid phase.
Let us now make use of the generalized form of Darcy's law
|
|
(2.9) |
where is the dynamic viscosity of the fluid and is the intrinsic permeability matrix of the porous medium.
Taking into account the relations from equations (2.7) and (2.9), the mass balance equation (2.6) can be rewritten as
|
|
(2.10) |
Equations (2.5) and (2.10) have to be supplemented by a constitutive law for the solid skeleton. In general, for any non-linear material we may consider an incremental form with a tangent constitutive tensor as
|
|
(2.11) |
with
|
|
(2.12) |
The boundary conditions for this problem are specified as:
|
where and are the prescribed displacements and surface tractions, respectively.
|
where and are the prescribed pore pressure and the normal flow rate, respectively.
In order to express the resultant system of equations in a more compact manner, we rewrite equations (2.5) and (2.10) in matrix form using Voigt notation as follows.
- Balance of momentum
|
|
(2.17) |
- Mass balance
|
|
(2.18) |
For a general 3D case, we have
|
|
(2.19) |
|
|
(2.20) |
|
|
(2.21) |
The above system of partial differential equations (2.17) and (2.18) can be discretized by interpolating the displacement and pressure fields as: and where denotes nodal values and
|
|
(2.22) |
|
|
(2.23) |
with and being, respectively, the shape functions of the displacement and pressure interpolations, which do not necessarily need to coincide.
Following the standard Galerkin technique [104,105], we left multiply Equation (2.17) by test functions and Equation (2.18) by test functions and integrate them over the spatial domain to obtain the following set of ordinary differential equations
- Balance of momentum
|
|
(2.24) |
- Mass balance
|
|
(2.25) |
where and are the residual vectors for the momentum and the mass balance equation, and
|
|
(2.26) |
|
|
(2.27) |
|
|
(2.28) |
|
|
(2.29) |
with .
The time derivatives of and are approximated using the Generalized Newmark scheme. Thus, for a new time step , we use the GN22 scheme for displacements [106]:
|
|
(2.30.a) |
|
|
(2.30.b) |
and the GN11 scheme for pressure:
|
|
(2.31) |
which are unconditionally stable for , and [107].
The residual vectors for the momentum and mass balance equations can be rewritten as
|
|
(2.32) |
|
|
(2.33) |
where and are the nodal unknowns at time , and , and stand for values that are computed from known parameters at time as:
|
|
(2.34) |
|
|
(2.35) |
|
|
(2.36) |
The Newton-Raphson method is used to solve the problem iteratively. Thus, at a time step and the iteration we have:
|
|
(2.37) |
|
|
(2.38) |
where is the tangent stiffness matrix:
|
|
(2.39) |
Note that the system of equations (2.38) can be made symmetric by multiplying Equation (2.33) by .
2.3 Stabilization using Finite Increment Calculus (FIC)
2.3.1 Introduction to the FIC-stabilization procedure
For a quasi-static problem the term involving the mass matrix is omitted. Also, in the undrained-incompressible limit, i.e. when and , the matrices and vanish and the system of equations (2.38) becomes
|
|
(2.40) |
The resultant system matrix is almost identical to that frequently encountered in the solution of incompressible elasticity or incompressible fluid mechanics problems [36,26]. In such cases, the spaces used to approximate the displacement (or the velocity) and pressure fields must fulfill the Babuska-Brezzi conditions [11,12] or the Zienkiewicz-Taylor patch test [108,109] in order to avoid spurious oscillations and locking in the pressure field.
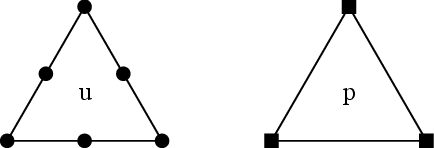
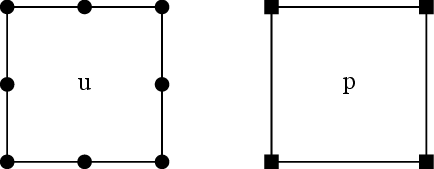
With the equations presented so far, these conditions can be accomplished using shape functions for the displacement field one order higher than those for the pressure field. Some examples of “stable” 2D elements are depicted in Figure 5.
|
|
| (a) Quadratic displacement and linear pressure. | (b) Biquadratic displacement and bilinear pressure. |
| Figure 5: Some 2D elements that fulfil the Babuska-Brezzi conditions. | |
However, low order finite elements with equal order interpolation for the displacements and the pressure are very attractive due to their simplicity and efficiency, and so stabilization techniques must be applied if one aims at solving large scale 3D computations.
The stabilization approach implemented in this work relies on the Finite Increment Calculus (FIC) method [33,34,35,36,37,38] and affects only the continuity equation with the balance of momentum remaining unchanged.
For the sake of clarity, let us redefine the mass balance equation (2.10) as:
|
|
(2.41) |
As stated in the introduction, this technique is based on the second-order FIC form of the mass balance equation in space for a quasi-incompressible fluid. This can be written as [38]:
|
|
(2.42) |
where are the number of space dimensions (i.e. for 3D problems).
In a 2D case Equation (2.42) is obtained by expressing the balance of mass in a rectangular domain of finite size with dimensions , where are arbitrary distances, and retaining up to third-order terms in the Taylor series expansions used for expressing the change of mass within the balance domain [37]. The derivation of Equation (2.42) for a 1D problem is shown in [38].
The FIC term in Equation (2.42) plays the role of a space stabilization term, in which are space dimensions related to the characteristic element dimensions. Note that for the standard form of the mass balance equation (2.41), as given by the infinitesimal theory, is recovered.
Equation (2.42) can be interpreted as a particular class of residual-based stabilization methods applied to the strong form of the mass conservation equation. This ensures the consistency of the stabilization method in the discretized problem.
2.3.2 Modified FIC-stabilized form of the mass balance equation
Let us first expand Equation (2.42) using Equation (2.41) as
|
|
(2.43) |
Next we split the stress tensor into its deviatoric and volumetric components as
|
|
(2.44) |
where is the deviatoric stress tensor and is the hydrostatic pressure defined as .
In the same way, we split the strain tensor into its deviatoric and volumetric parts as
|
|
(2.45) |
with being the deviatoric strain tensor and the volumetric dilation.
Now let us write the isotropic linear elastic constitutive equations:
|
|
(2.46) |
where is the shear modulus,
|
|
(2.47) |
where is the mean effective stress and is the Biot's coefficient defined in Equation (2.2).
Combining Equations (2.44), (2.45), (2.46) and (2.47), we express the stress tensor as
|
|
(2.48) |
At this point, we substitute the above expression in the balance of momentum (2.4). This gives
|
|
(2.49) |
From this point forward, in the derivation of equations (2.43), (2.49) and in the following, we neglect the space and time changes of , , and in the derivatives.
If we now apply the divergence operator to both sides of Equation (2.49), differentiate it with respect to time, and rearrange the terms we can obtain
|
|
(2.50) |
In the previous equation the term can be neglected and the term involving the third derivative of the displacements with respect to time can be obtained from the mass balance equation. Thus if we differentiate Equation (2.10) twice with respect to time assuming that the time derivative of the body force per unit mass is negligible, and we take into account the definition of the volumetric strain , we obtain
|
|
(2.51) |
Introducing (2.51) into (2.50) gives
|
|
(2.52) |
At this point, we can already substitute the above relation in Equation (2.43) giving
|
|
(2.53) |
The above equation can be simplified if we take into account that the last term involves the fourth order spatial derivative of the pore pressure and the third order spatial derivative of the body force per unit mass. In practical problems these terms are either zero (for constant body forces) or much smaller than the others. Hence, these terms will be omitted for the rest of this work. Furthermore, numerical results have shown that the terms and can be neglected without loss of accuracy. Thereby, Equation (2.53) is written in the simpler form as
|
|
(2.54) |
In the following we will assume where is a characteristic length related to a typical average dimension of each element in the mesh. After rearranging terms, Equation (2.54) can be rewritten as
|
|
(2.55) |
where is a stabilization parameter given by
|
|
(2.56) |
The form of the stabilization parameter in Equation (2.56) resembles that typically used in other stabilized procedures. We note that this term has naturally formed from the FIC formulation.
In the examples solved in this work we have chosen , where is a characteristic element length that, for 2D problems, is taken as the diameter of a circle with the area of the element, while for 3D problems, it is the diameter of a sphere with the volume of the element. In essence
|
|
(2.57) |
|
|
(2.58) |
where and represent the area and the volume of the element, respectively.
The presence of the characteristic element length in Equation (2.56) helps us control the diffusion of the stabilized solution, avoiding over-diffusive numerical results provided that fine enough discretizations are used. This fact is clearly shown in the example of Section 2.4.2.
2.3.3 Variational form of the FIC-stabilized mass balance equation
The variational expression of the FIC-stabilized mass balance equation is obtained by multiplying Equation (2.55) by arbitrary test functions and integrating over the domain to give
|
|
(2.59) |
Integrating by parts the last two integrals of Equation (2.59) and applying the divergence theorem yields
|
|
(2.60) |
where are the components of the unit normal vector to the external boundary of .
Introducing the boundary condition (2.16) and rearranging terms we have
|
|
(2.61) |
Using the stress decomposition in (2.48), we can rewrite the boundary condition (2.14) as
|
|
(2.62) |
Next if we apply the divergence operator to both sides of Equation (2.62), differentiate it with respect to time and rearrange terms we have
|
|
(2.63) |
In all typical problems the divergence of the traction vector is zero and so it is the term . Moreover, numerical tests have shown that the results are not affected by the term . Consequently, the stabilized mass balance equation is rewritten as
|
|
(2.64) |
where is the derivative of in the direction of the normal to the external boundary. This derivative can be approximated as shown in Figure 6.

|
| Figure 6: Computation of the term at the side of a triangle adjacent to the external boundary . |
Using the previous argument, the stabilized FIC form for the mass balance equation (2.64) finally becomes
|
|
(2.65) |
where is an arbitrary distance in the normal direction to the boundary. In our work has been taken as the characteristic length of the element adjacent to the external boundary.
2.3.4 Discretized form of the momentum and FIC-stabilized mass balance equations
Combining the discretized form of Equation (2.65) along with the residual obtained from the original balance of momentum equation (2.24), the system of equations to be solved reads
- Balance of momentum
|
|
(2.66) |
- Mass balance
|
|
(2.67) |
with the stabilizing terms
|
|
(2.68) |
|
|
(2.69) |
|
|
(2.70) |
where and the matrix appears due to the difference between the strain tensor and the strain vector expressed in Voigt notation. For a general 3D case
|
|
(2.71) |
Note that since the test functions are zero on the Dirichlet boundaries , matrix must be only computed on those external boundaries where no pressure Dirichlet conditions are imposed.
Using the stabilized residual vector (2.67), the system of equations for a linear elastic material, quasi-static and undrained-incompressible limit case becomes
|
|
(2.72) |
with
|
|
(2.73) |
|
|
(2.74) |
Note that the diagonal of the iteration matrix is now different from zero. Matrices and emerging from the stabilized FIC formulation are essential for ensuring the consistency of the residual-based stabilization method used.
The consistency of residual does not directly affect the diffusion of the numerical solution, but it helps improving the condition number of the system matrix and facilitates the convergence of the Newton-Raphson scheme.
We highlight that the FIC-FEM formulation presented is applicable to equal order interpolation approximations of the displacements and the pressure of any degree. In this work we have implemented the FIC-FEM formulation using 3-noded triangles and 4-noded quadrilaterals for 2D problems, and 4-noded tetrahedra and 8-noded hexahedra for 3D problems, with equal order interpolation for the displacements and pressure.
2.4 Examples
This section includes two academic examples designed to assess the performance of the stabilized FIC-FEM formulation in situations near the undrained-incompressible limit. The first example is an elastic soil column subjected to a surface load. The second problem is an elastic soil foundation also subjected to a surface load.
The soil column problem is analysed in a 2D framework under plane strain conditions, whereas the soil foundation case is tackled as a 3D problem. The problems have been solved with simple elements with equal order interpolation for the displacements and the pore pressure, using the direct (non-stabilized) formulation and the FIC-stabilized formulation presented in the previous sections. Stable mixed elements with higher order interpolation for the displacements have been used to validate the FIC-stabilized element.
In both problems, the porous medium is under totally saturated conditions with isotropic permeability. The effect of gravity is not considered.
2.4.1 Elastic soil column subjected to surface loading
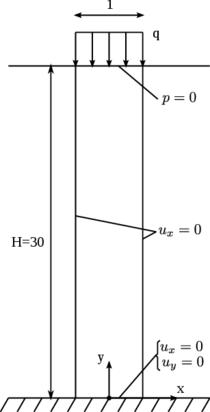
This example consists on a column of saturated soil subjected to a surface loading that lies on a rigid rock bed. The geometry and boundary conditions of the problem are shown in Figure 7.
|
| Figure 7: Elastic soil column subjected to surface loading. Geometry and boundary conditions. Dimensions in . |
The material properties of the soil column are summarized in Table 1. It must be noticed that the indices 1 and 2 in the solid bulk modulus , the fluid bulk modulus and the intrinsic permeability denote the different cases that have been considered here. Index 1 corresponds to the nearly undrained-incompressible limit, and index 2 corresponds to a more relaxed condition.
| Property | Value |
| Young modulus () | |
| Poisson's ratio () | 0.2 |
| Solid density () | |
| Fluid density () | |
| Porosity () | 0.3 |
| Dynamic viscosity () | |
| Solid bulk modulus 1 () | |
| Fluid bulk modulus 1 () | |
| Intrinsic Permeability 1 () | |
| Solid bulk modulus 2 () | |
| Fluid bulk modulus 2 () | |
| Intrinsic Permeability 2 () |
This problem is solved in a 2D configuration under plane strain conditions. The geometry is discretized with a structured mesh of 20 quadrilateral elements. We have solved the problem using 4-noded quadrilateral elements with bilinear shape functions for both the pressure and the displacements (Q4P4), and 9-noded quadrilateral elements with biquadratic shape functions for the displacements and bilinear shape functions for the pressure (Q9P4).
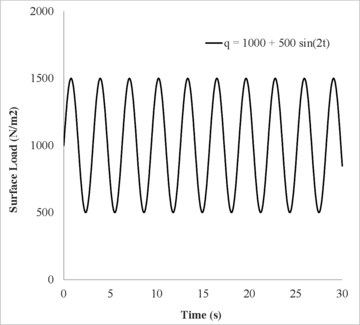
Two different load cases have been considered: a surface step loading (Figure 8) and a surface cyclic loading (Figure 10).
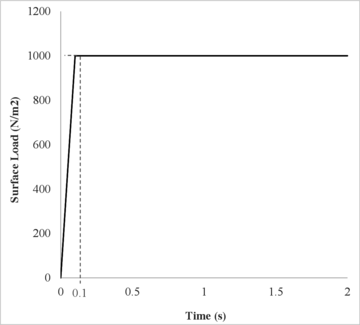
Step loading case
The main purpose of this first case is to verify that the FIC-stabilized formulation captures properly the pressure distribution along the soil column under undrained-incompressible conditions.
|
| Figure 8: Surface step loading applied in the elastic soil column problem. |
Figure 9 shows the normalized pore pressure along the normalized height of the soil column for nearly undrained conditions at a time .
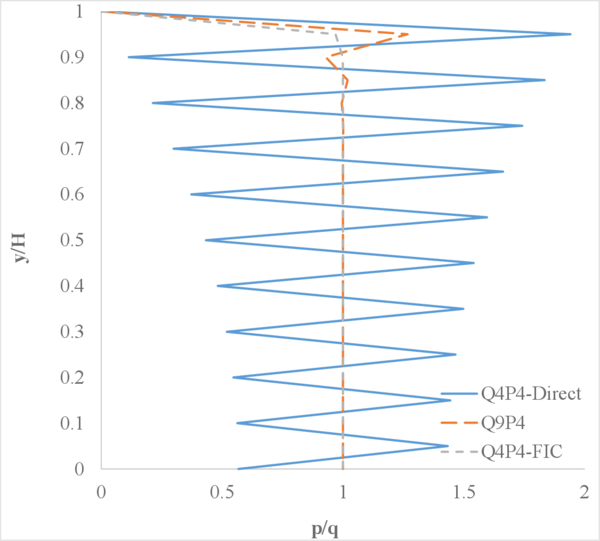
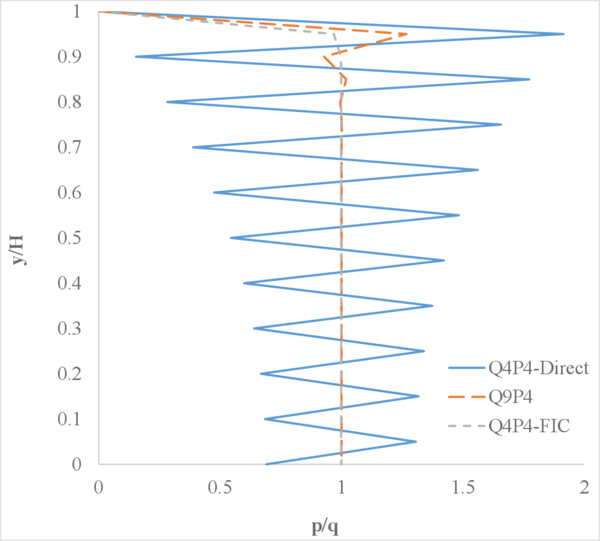
Understanding the results of Figure 9 requires taking into account the fact that gravity is not considered. Indeed, since the only force acting over the soil column is the surface load, the pressure applied by the surface load is completely transferred to the pore pressure throughout the column height and thus the ratio should equal 1.
The results obtained with the non-stabilized formulation and the 4-noded quadrilaterals (hereafter called Q4P4-Direct) are not able to properly capture the pressure distribution along the column. The element locks and the pressure oscillates with arbitrary values. In contrast, by using the Q4P4 element stabilized with the FIC approach presented in this work (here called Q4P4-FIC), the correct pressure distribution is obtained. Similar good results are obtained with the Q9P4 element, as expected.
Comparing the graphs in Figures 9a and 9b one can see the effect of the compressibility of the materials on the sought solution. Certainly, as we decrease the value of Biot's modulus , or equivalently, the bulk modulus of the solid and fluid phases and , the amplitude of the pressure oscillations obtained with the Q4P4-Direct element decreases near the rock bed. On the other hand, the results obtained with the Q4P4-FIC and Q9P4 elements remain unaltered.
|
|
| (a) Quasi-incompressible limit (). | (b) Relaxed incompressibility (). |
| Figure 9: Normalized pore pressure along the soil column (, , ). | |
Cyclic loading case
In this second case the objective is to analyse the evolution of the pore pressure in time, and assess the effect of the soil permeability on the dissipation of the pore pressure.
|
| Figure 10: Surface cyclic loading applied in the elastic soil column problem. |
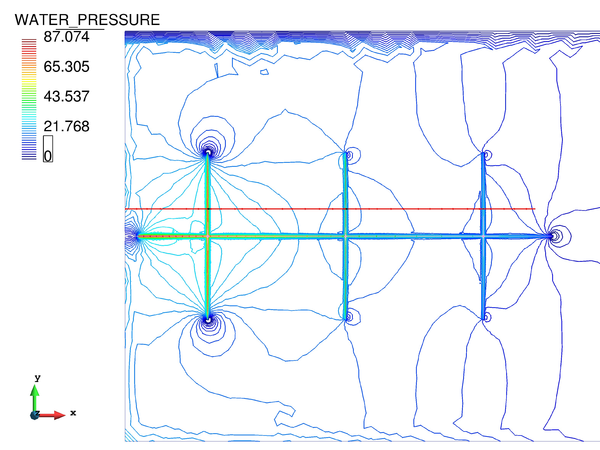
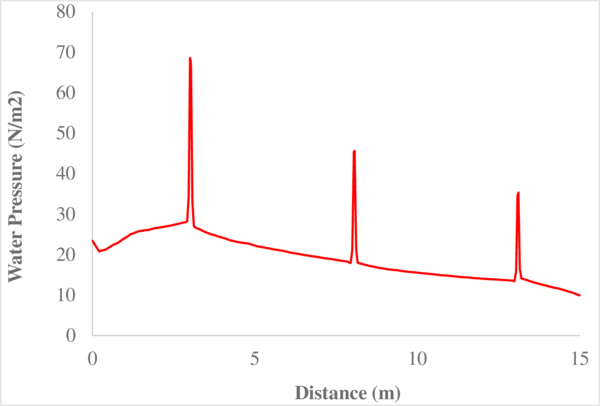
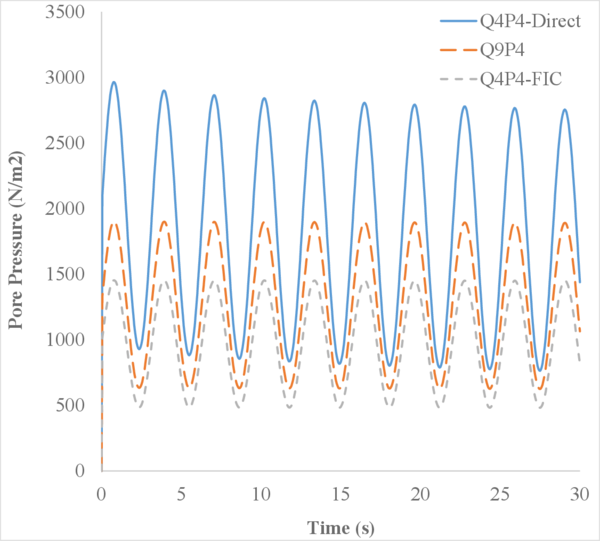
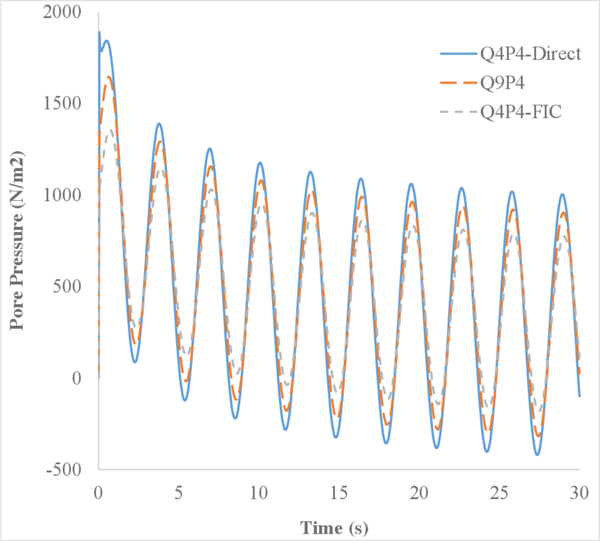
To that purpose, Figure 11 shows the temporal evolution of the pore pressure at a node located 1.5 m below the surface.
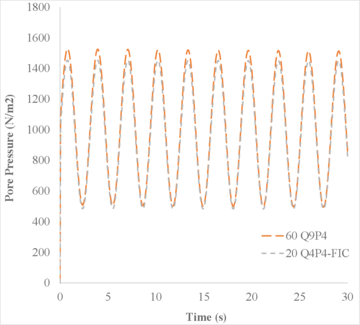
Like in the previous case, the pressure obtained here should reflect the load applied on the surface. From the results in Figure 11, it is clear that the three tested elements show sinusoidal pressure evolutions in time. However, from the nearly undrained case of Figure 11a, it appears that while the Q4P4-FIC element shows a pressure that correctly oscillates from 500 to 1500 , the Q4P4-Direct element presents pressure values that vary from 1000 to 3000 , making no sense. One must notice that although the Q9P4 element shows higher pressures than the stabilized element, after refining the mesh up to 60 elements, the Q9P4 results are in good agreement with the solution obtained with 20 Q4P4-FIC elements (Figure 12). This evidences the good accuracy of the stabilized FIC-FEM Q4P4 element.
|
|
| (a) Quasi-undrained limit (). | (b) Partially drained (). |
| Figure 11: Evolution of the pore pressure with time at a node near the surface (, ). | |
Looking at the graph depicted in Figure 11b one can see that, by increasing the intrinsic permeability , the problem is no longer as bad conditioned as before, and so the gap in the amplitude of the three elements diminishes. Moreover, a greater permeability implies that the water can flow towards the surface due to the deformation of the column. Thereby, a dissipation in the pore pressure occurs as the computation advances in time.
Finally, it is also interesting to notice that the pressure becomes negative after the soil has drained a certain amount of water. This is easily understood if one thinks about the elastic behaviour considered for the porous medium. Since the applied load is oscillating, the deformation of the elastic soil experiments a similar behaviour. In consequence, when the soil recovers its initial position as the load reduces, a suction appears that makes the pore pressure negative at some points near the surface.
|
| Figure 12: Time evolution of the pore pressure. Comparison between 20 Q4P4-FIC elements and 60 stable Q9P4 elements (, , ). |
2.4.2 Elastic soil foundation subjected to surface loading
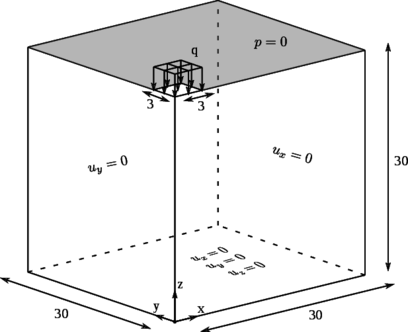
This second example consists on a pillar foundation on a saturated soil stratum lying over a rigid rock bed. The geometry and boundary conditions are sketched in Figure 13.
|
| Figure 13: Elastic soil foundation subjected to surface loading. Geometry and boundary conditions. Dimensions in . |
The material properties for the soil are the same as for the previous example (Table 2).
| Property | Value |
| Young modulus () | |
| Poisson's ratio () | 0.2 |
| Solid density () | |
| Fluid density () | |
| Porosity () | 0.3 |
| Dynamic viscosity () | |
| Solid bulk modulus 1 () | |
| Fluid bulk modulus 1 () | |
| Intrinsic Permeability 1 () | |
| Solid bulk modulus 2 () | |
| Fluid bulk modulus 2 () | |
| Intrinsic Permeability 2 () |
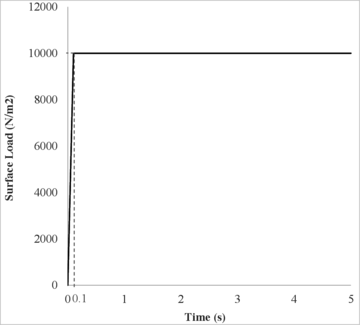
In this case the soil is subjected to a surface step loading of applied in a linear increment during (Figure 14).
|
| Figure 14: Surface step loading applied in the elastic soil foundation problem. |
As stated before, this problem is solved by means of a 3D analysis. We use 4-noded tetrahedral elements with linear interpolation for the displacements and the pressure in the non-stabilized form (T4P4-Direct) and the FIC-stabilized formulation (T4P4-FIC). Ten-noded stable tetrahedral elements with quadratic shape functions for the displacement field and linear shape functions for the pressure field (T10P4) have also been used in the analysis for comparison purposes.
This example has two objectives. First, it should help analysing the effect of the spatial discretization on the solution obtained with the FIC-stabilized formulation. Second, it may allow us to assess whether the three element types considered here converge to the expected solution when the mesh is refined.
In order to do so, two different unstructured spatial discretizations have been used: a coarse uniform mesh (Figure 15a) and a refined non-uniform mesh (Figure 15).
|

|
| (a) Coarse uniform mesh: 9985 elements. | (b) Refined non-uniform mesh: 13532 elements. |
| Figure 15: Spatial discretizations used for the elastic soil foundation problem. | |
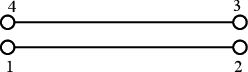
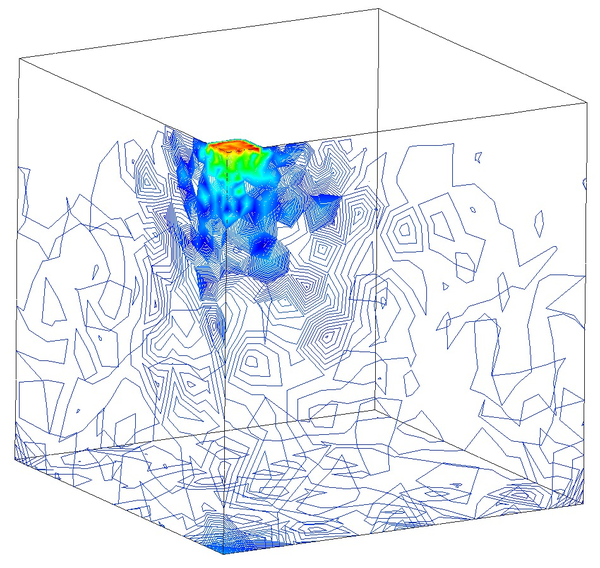
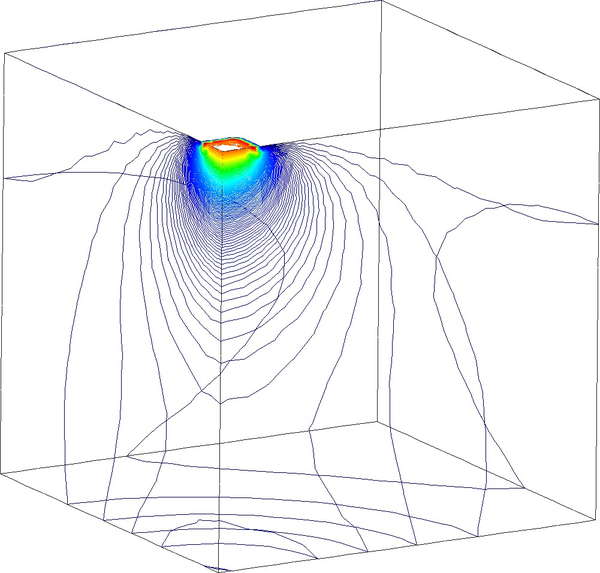
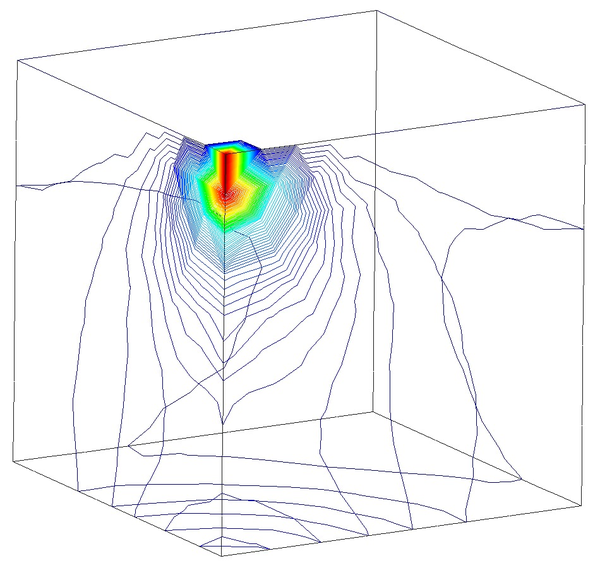
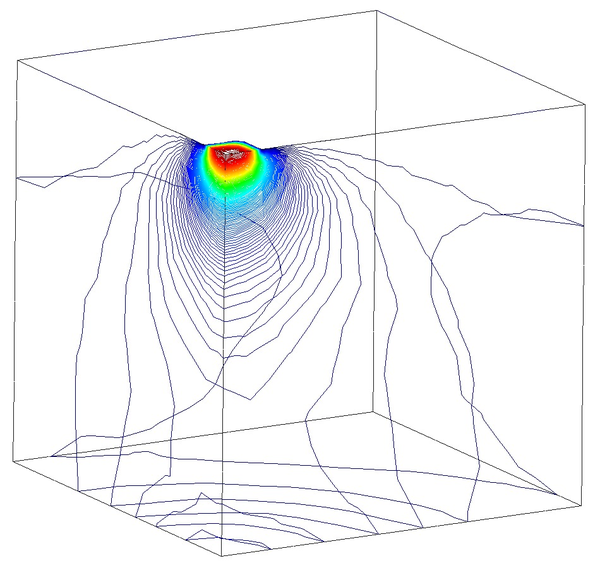
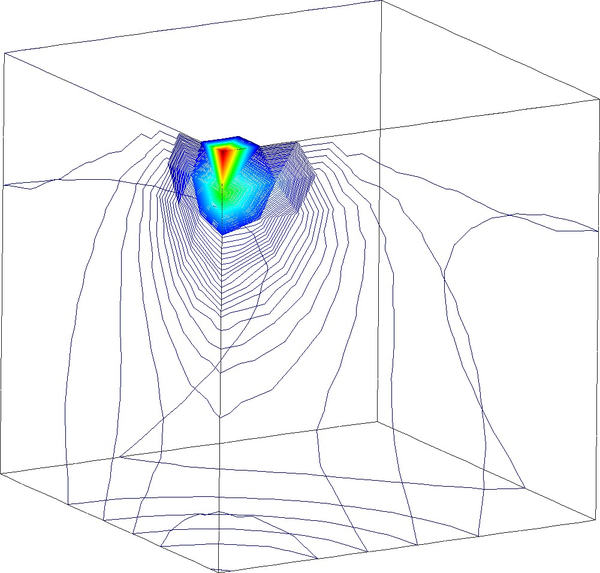
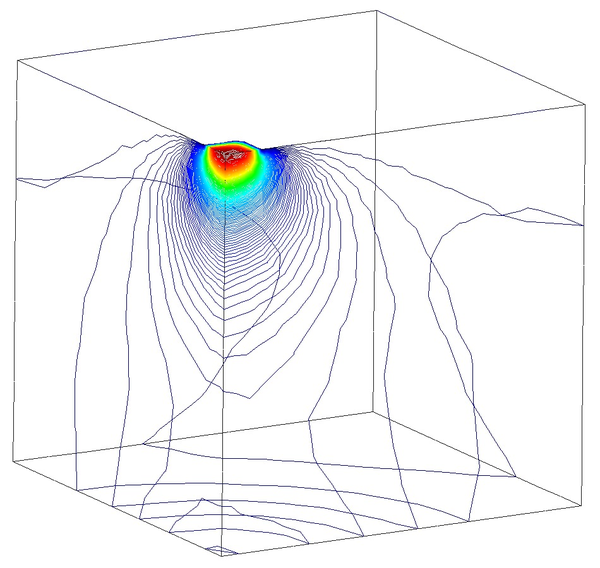
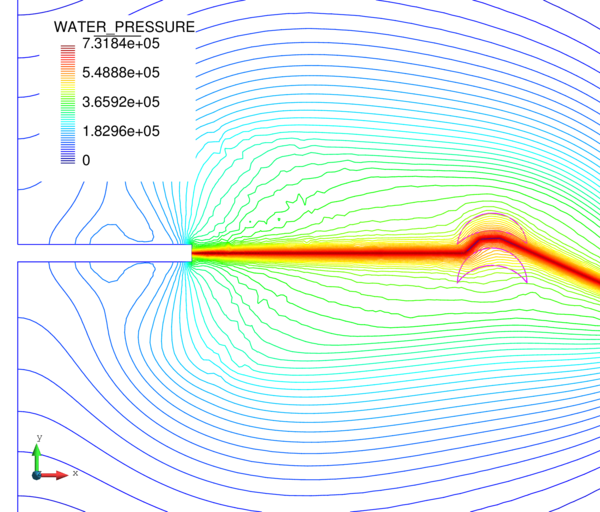
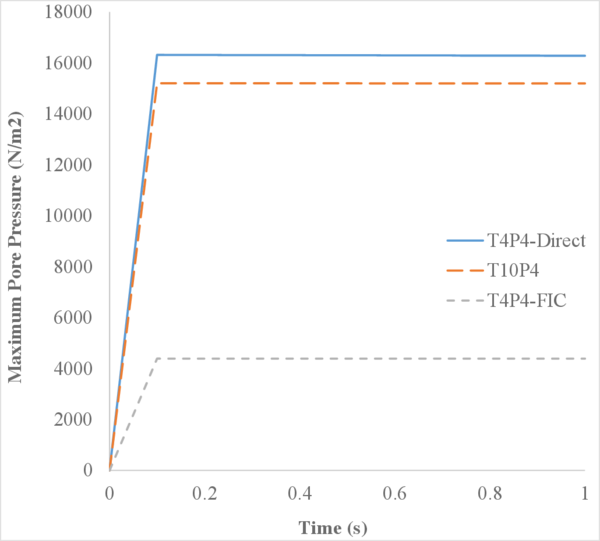
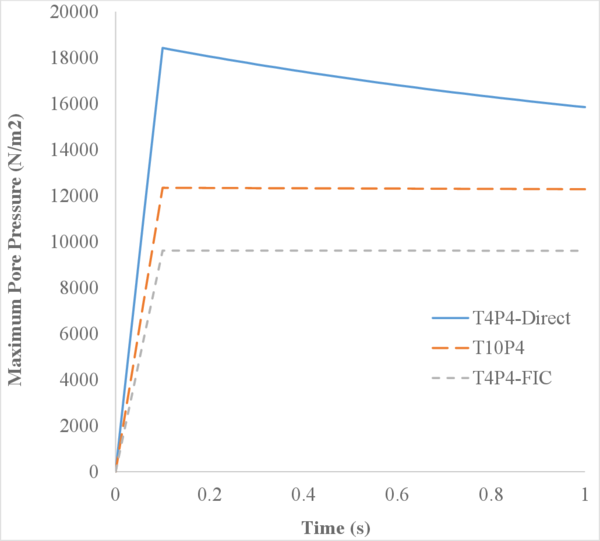
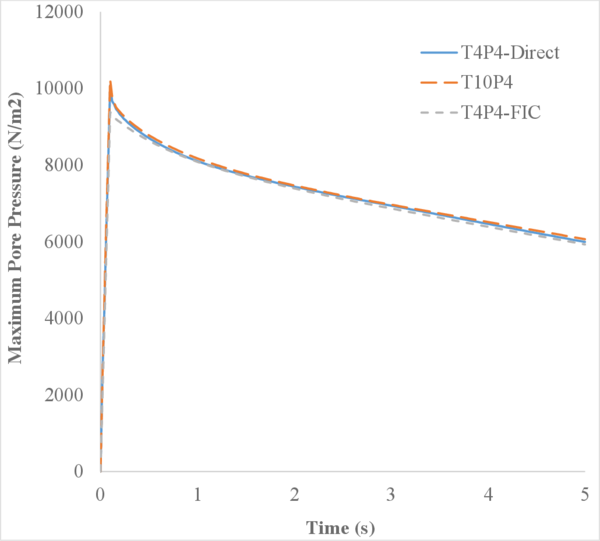
In Figure 16 we represent the evolution of the maximum pore pressure with time under nearly undrained-incompressible conditions for both the coarse and refined meshes using . The impermeability of the case makes that the pore pressure remains constant after the first of application of the load for the two stable elements, the T10P4 and the T4P4-FIC. We see, though, a different behaviour in the unstable T4P4-Direct element, showing a certain dissipation for the finer mesh.
Comparing the T10P4 and the T4P4-FIC elements we notice that, while the first one surpasses the threshold of for both meshes, the latter is always below the value of the applied load. In any case, both elements approach the expected solution as the mesh is refined, which indicates a consistent response.
|
|
| (a) Coarse mesh. | (b) Refined mesh. |
| Figure 16: Time evolution of the maximum pore pressure under undrained-incompressible conditions (, , ). | |
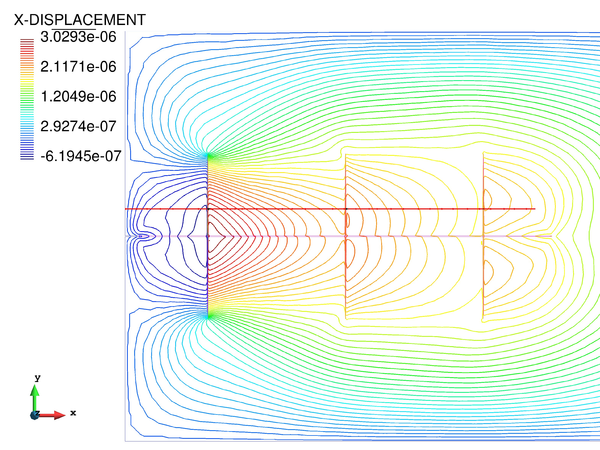
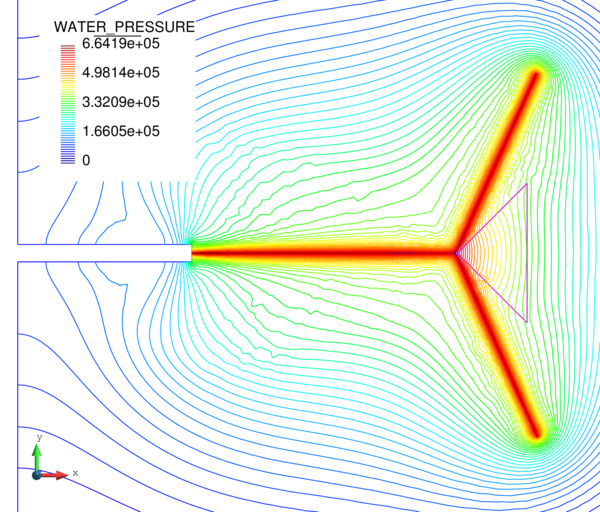
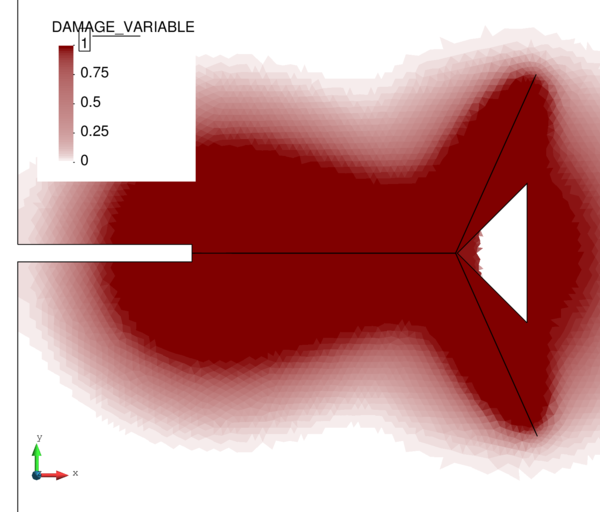
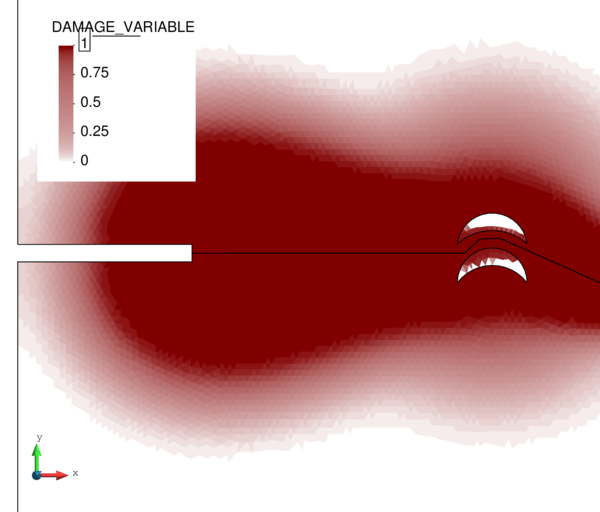
If we look at the contour lines of the pore pressure distribution obtained at time in Figure 17, we can understand the abnormal behaviour of the T4P4-Direct element. Indeed, the direct mixed formulation with equal order interpolation elements locks under undrained-incompressible conditions which leads to the incoherent pressure distribution obtained.
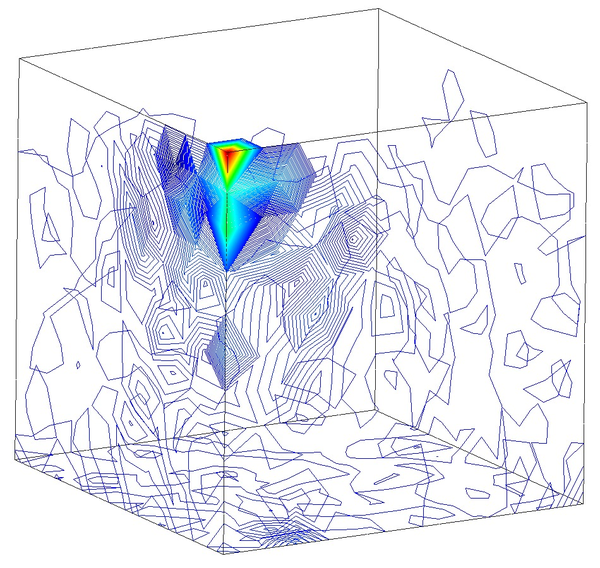
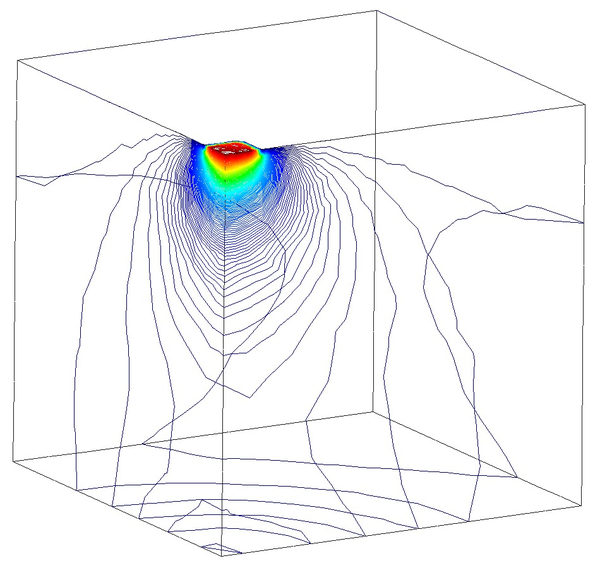
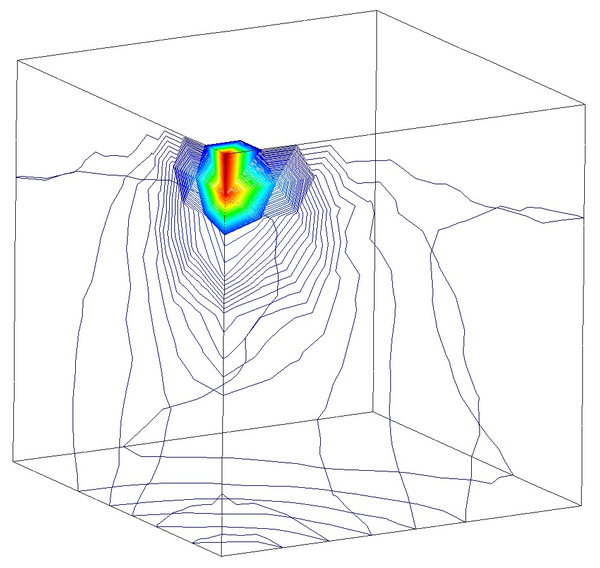
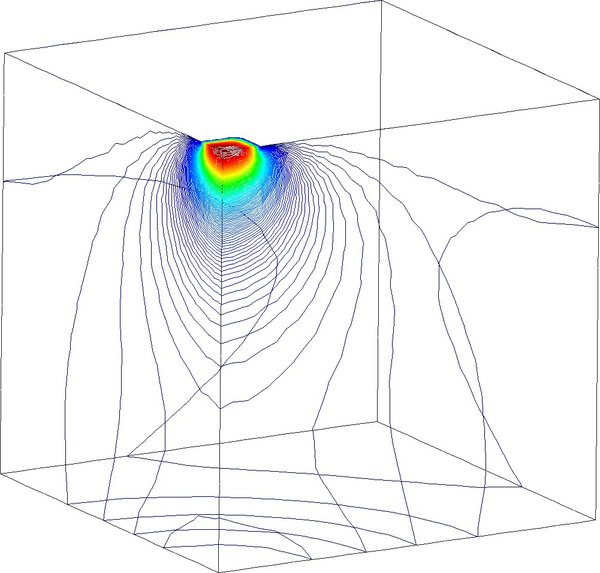
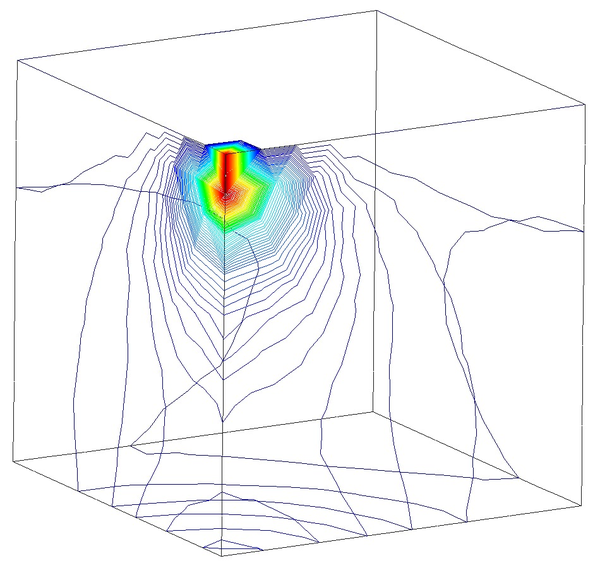
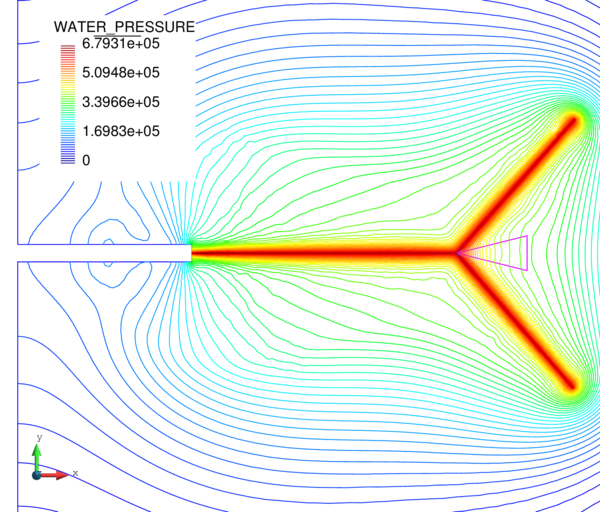
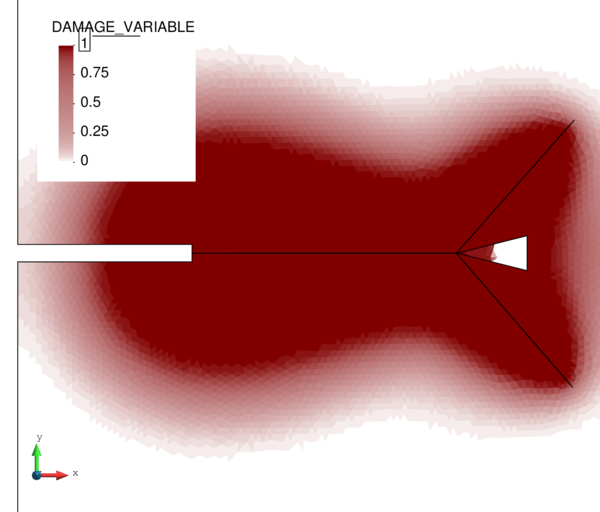
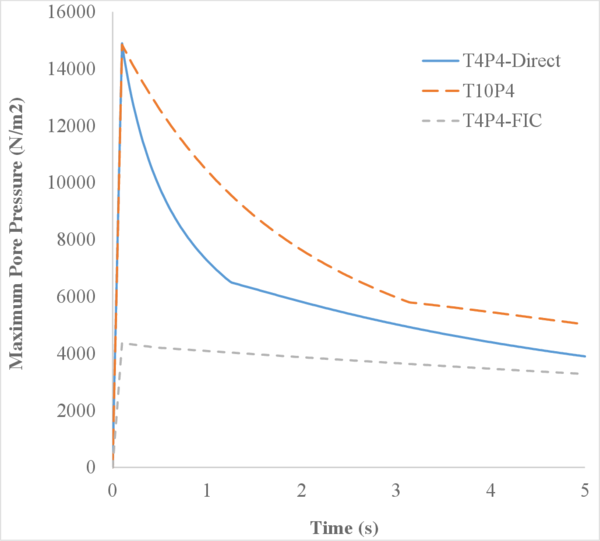
Next we evaluate the capabilities of the FIC stabilized formulation to reproduce a solution where stabilization is not needed. For this purpose the previous problem has been solved for partially drained and compressible conditions up to s (Figure 18). Results are again shown at s for s (Figure 19). Under these relaxed conditions, the equal order interpolation mixed element with the direct formulation is able to capture acceptable pressure distributions as expected (Figures 19a and 19b).
The higher permeability of this second case also permits capturing the so-called Mandel-Cryer effect, i.e. the increase of pore pressure due to the application of the load is immediate, but the dissipation due to the outflow of the pore fluid is delayed by the permeability of the porous medium [110]. Figures 18a and 18b show that, after the first 0.1 s of loading, the fluid starts draining due to the consolidation of the soil.
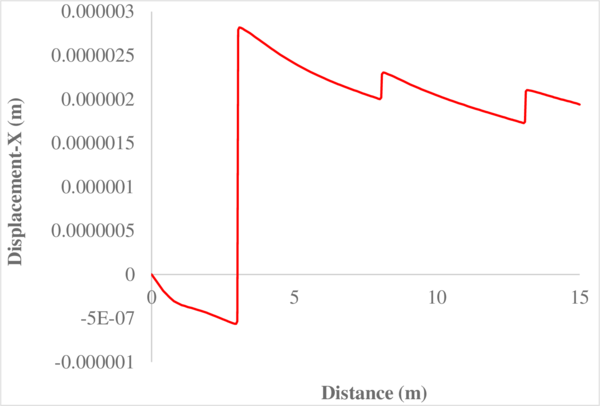
In order to properly understand the low peak pore pressure obtained with the T4P4-FIC element in Figure 18a, it is useful to recall the definition of the stabilization parameter in Equation (4.56) and observe carefully the mesh in Figure 15a. It can be noticed that the area of application of the load is covered by only two triangular faces. This implies that the characteristic element length around that particular zone is relatively large, and so it is the stabilization parameter. As a result, one obtains an over-diffusive solution that leads to an underestimation of the maximum pore pressure.
However, it is interesting to see that the larger peak pore pressure obtained with the T4P4-Direct and the T10P4 elements, caused by an initial locking of the pressure field, converges to the solution obtained with the T4P4-FIC element after the soil consolidates.
On the other hand, the results for the maximum pressure obtained with the refined non-uniform mesh (Figures 18b, 19b, 19d and 19f) converge all to an almost identical value. This evidences that the FIC stabilization does not alter negatively the solution obtained with the original non-stabilized mixed formulation.
|
|
| (a) Coarse mesh. | (b) Refined mesh. |
| Figure 18: Time evolution of the maximum pore pressure for partially compressible and drained conditions (, , ). | |
3 Continuum Damage Mechanics
3.1 Introduction
Many engineering materials subjected to unfavourable mechanical and environmental conditions undergo micro-structural changes that decrease their strength. Since these changes impair the mechanical properties of these materials, the term damage is generally used.
This effect is particularly relevant and difficult to predict in brittle or quasi-brittle materials such as concrete, rocks, mortar or other geo-materials. For instance, concrete is a highly heterogeneous, anisotropic, brittle material with a very complex non-linear mechanical behaviour due to the occurrence of the localization of deformation. This localization of deformation can appear as cracks, if cohesive properties are dominant, or as shear zones, if frictional properties prevail. As a result of strain localization, material softening takes place and a significant reduction of the material stiffness occurs during cyclic loading. A good understanding of the mechanism of the formation of such localization is of crucial importance because it acts as a precursor of fracture and failure.
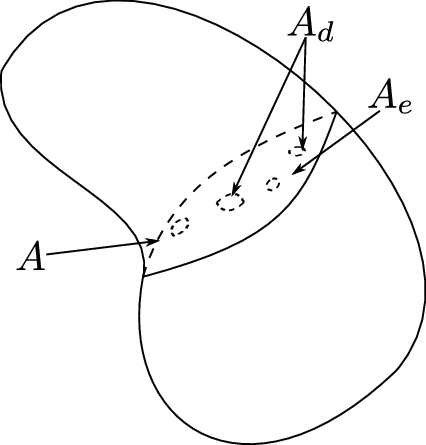
Continuum damage mechanics is a branch of continuum mechanics that describes the progressive loss of material integrity due to the propagation and coalescence of micro-cracks, micro-voids, and similar defects (Figure 20). These changes in the micro-structure lead to an irreversible material degradation, characterized by a loss of stiffness that can be observed on the macro-scale.
|
| Figure 20: Generic damaged section. |
The main objective of standard continuum damage mechanics is to propose a continuum-mechanics based framework that allows to characterize, represent and model at the macroscopic scale the effects of distributed defects and their growth on the material behaviour.
The term “continuum damage mechanics” was first used by Hult [111], but the concept of damage was introduced by Kachanov in 1958 in the context of creep rupture [53]. In that work Kachanov introduced the concept of effective stress, and by using continuum damage he solved problems related to creep in metals. Rabotnov [54] gave the problem physical meaning by suggesting that the reduction of the sectional area was measured by means of the damage parameter.
The thermodynamic formalism involved in the irreversible process of damage was developed by Lemaitre and Chaboche [55]. Other important contributions on damage mechanics include: Mazars and Pijaudier-Cabot [112,56], Simo and Ju [57], Oller et al. [58], Oliver et al. [59,60], and Cervera et al. [61,62,113].
If the damage parameter depends only on the strain state at the point under consideration, and non enriched kinematics are adopted to regularize the problem, numerical simulations exhibit a pathological mesh dependence and the energy consumed by the fracture process tends to zero as the mesh is refined. This is the typical behaviour of the so-called local damage models, which are not able to properly describe both the thickness of localization and the distance between damaged zones. They suffer from mesh sensitivity (for size and alignment) and produce unreliable results. Strains concentrate in one element wide zones and the computed force-displacement curves are mesh-dependent. The reason behind these misbehaviours is that the differential equations of motion change their type, from elliptic to hyperbolic in static problems, and the boundary value problem becomes ill-posed [114].
Classical constitutive models require an extension in the form of a characteristic length to properly model the thickness of localized zones. Such extension can be done by means of second gradient models [63], micro-polar [64], strain gradient [65], viscous [66] and non-local terms [67]. In this monograph we have worked with the latter approach using a weighted spatial averaging of the internal variables. In this manner the kinematic and equilibrium equations remain standard, and the notions of stress and strain keep their usual meaning.
The first non-local models of this type, proposed in the 1960s, aimed at improving the description of elastic wave dispersions in crystals. Non-local elasticity was further developed by Eringen [68] who later extended it to non-local elasto-plasticity [69]. Subsequently, it was found that certain non-local formulations could act as efficient localization limiters with a regularizing effect on problems with strain localization [70].
The chapter is organized as follows. First, the basic concepts on continuum damage mechanics are introduced. Details are given on the essential components of the isotropic damage theory, including the equivalent strain forms and damage evolution laws implemented for this work. Following that, the regularization techniques developed to overcome the difficulties associated to strain localization are illustrated. Special attention is given to the integral-type non-local damage model, pointing out the most relevant aspects of its numerical implementation. Two examples are shown at the end, in order to assess the robustness of the implemented damage models against changes in the spatial discretization.
3.2 Isotropic damage theory
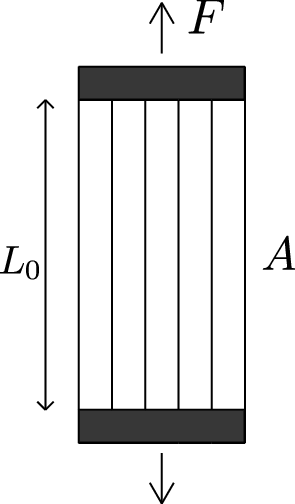
Damage models work with certain internal variables that characterize the density and orientation of micro-defects. To introduce its concepts and understand the fundamental theory of damage mechanics, let us explain the stress evolution in a simple uniaxial tensile case (Figure 21).
|
| Figure 21: Idealized material for the description of the uniaxial damage theory. |
For a better understanding, the material is idealized as a bundle of fibres parallel to the loading direction (Figure 21). Initially, all the fibres respond elastically, and the stress is carried by the total cross section of all fibres (Figure 22.1). As the applied strain is increased some fibres start breaking (Figure 22.2). Each fibre is assumed to be perfectly brittle, meaning that the stress in the fibre drops down to zero immediately after a critical strain level is reached. However, since the critical strain can differ from one fibre to another, the effective area (the area of unbroken fibres that can still carry stress) decreases gradually from to . Of course, when the applied force diminishes (Figure 23.2), the affected fibres remain broken and so the damaged area of the specimen is irrecoverable.

|
| Figure 22: Scheme of a uniaxial damage model through a monotonic loading process. |

|
| Figure 23: Scheme of a uniaxial damage model through a non-monotonic loading process. |
It is important to make a distinction between the nominal stress , defined as the force per unit initial area of the cross section, and the effective stress , defined as the force per unit effective area1. The nominal stress enters the Cauchy equations of equilibrium on the macroscopic level, while the effective stress is the “actual” stress acting in the material micro-structure. Since the external applied force is the same regardless of the definition of the stress, i.e. , we can write:
|
|
(3.1) |
The ratio of the effective area to the total area, , is a scalar characterizing the integrity of the material. Within the classical approach, a very simple measure of the damage amplitude in a given plane is obtained by measuring the area of the intersection of all defects with that plane. Thereby, we can define the damage variable as:
|
|
(3.2) |
where is the damaged part of the area. An undamaged material is characterized then by , i.e. by . Due to propagation of micro-defects and their coalescence, the damage variable grows and at the late stages of degradation process it approaches asymptotically the limit value , corresponding to a complete damaged material with effective area reduced to zero.
In the simplest version of the presented scheme, each fibre is supposed to remain linear elastic up to the strain level at which it breaks. Consequently, the 1D effective stress is related to the elastic strain of the material by the uniaxial Hooke's law:
|
|
(3.3) |
where is the elastic modulus of the undamaged material. Combining (2.1), (3.2) and (3.3), it is straightforward to see that the constitutive law for the nominal stress takes the form:
|
|
(3.4) |
For the uniaxial model formulation, Equation (3.4) must be complemented with the damage evolution law, which can be characterized by the dependence between the damage variable and the applied strain:
|
|
(3.5) |
Function affects the shape of the stress-strain diagram and can be directly identified from a uniaxial test.
The evolution of the effective stress, damage variable, and nominal stress in a material that remains elastic up to the peak stress is shown in Figure 22. This description is valid only for monotonic loading by an increasing applied strain .
When the material is first stretched up to a certain strain level that induces damage and then the strain decreases (Figure 23), the damaged area remains constant and the material responds as an elastic material with a reduced Young's modulus . This means that, during unloading and partial reloading, the damage variable in (5.4) must be evaluated from the largest previously reached strain and not from the current strain . This means that it is crucial to introduce an internal state variable characterizing the maximum strain level reached in the previous history of the material up to a given time :
|
|
(3.6) |
The above expression implies that , where is the so-called damage threshold, a material parameter that represents the value of strain at which damage starts. In this formula, is not necessarily the physical time (it can be any monotonically increasing parameter controlling the loading process). The damage evolution law (3.5) is then rewritten in the form:
|
|
(3.7) |
which remains valid not only during monotonic loading but also during unloading and reloading. The evolution of the effective stress, damage variable, and nominal stress in a non-monotonic test is shown in Figure 23. Note that, upon a complete removal of the applied force, the strain returns to zero (due to elasticity of the unbroken fibres), i.e. the pure damage model does not take into account any permanent strains. Nevertheless, the material state is different from the initial virgin state because, according to (3.6) and (3.7), when the state variable becomes greater than , the damage variable will not be zero again and thus the stiffness and strength mobilized in a new tensile loading process will be smaller than their initial values. Therefore, we can say that the loading history is always reflected by the value of the internal state variable .
Instead of defining the variable like in (3.6), we can introduce a loading function and postulate the loading-unloading conditions in the Kuhn-Tucker form:
|
|
(3.8) |
The first condition indicates that can never be smaller than , while the second condition means that cannot decrease. Finally, according to the third condition, can grow only if the current values of and are equal.
At this point, we can already formulate the extension of the uniaxial damage theory to general multiaxial stress states.
In this work we have chosen the simple isotropic damage model with a unique scalar variable. Isotropic damage models are based on the simplifying assumption that the stiffness degradation is isotropic, i.e. the stiffness moduli corresponding to different directions decrease proportionally, independently of the direction of loading. Since an isotropic elastic material is characterized by two independent elastic constrains, a general isotropic damage model should deal with two damage variables. The model with a single variable makes use of the additional assumption that the relative reduction of all the stiffness coefficients is the same, in other words, that the Poisson's ratio is not affected by damage. In this regard, the stress-strain law in Voigt notation is postulated as:
|
|
(3.9) |
where is the elastic constitutive matrix of the intact material. One can clearly notice that (3.9) is a generalization of (3.4). Also, Equation (3.9) can alternatively be written as:
|
|
(3.10) |
which is the multidimensional generalization of (3.1), and where is the effective stress vector defined as:
|
|
(3.11) |
Similarly as in the uniaxial case, we introduce a loading function specifying the elastic domain and the states at which damage grows. The loading function now depends on the strain vector , and on a variable that controls the evolution of the elastic domain. Physically. represents a scalar measure of the largest strain level ever reached in the history of the material. States for which are supposed to be below the current damage threshold. Damage can grow only if the current state reaches the boundary of the elastic domain, i.e. when . Essentially, we can postulate the damage criterion for a multiaxial isotropic damage model with:
- The loading function:
|
|
(3.12) |
- The loading-unloading conditions (3.8)
in Eq (3.12) is the equivalent strain, a scalar magnitude of the strain level, and is the largest value of equivalent strain calculated in the previous deformation history of the material up to its current state. In this regard, (3.6) can now be generalized to:
|
|
(3.13) |
An important advantage of an isotropic damage model is that the stress evaluation algorithm is usually explicit and there is no need to use an iterative solution for non-linear equations.
Thereby, for a particular strain increment, the corresponding stress is obtained by computing the current value of equivalent strain, updating the maximum previously reached equivalent strain and the damage variable, and reducing the effective stress according to (3.10). In essence, one must follow the scheme of Table 3.
| Step |
| 1. Evaluate effective stress: |
| 2. Compute the new equivalent strain: |
| 3. Update with (3.13): If |
| 4. Update damage variable: |
| 5. Compute nominal stress: |
(1) Note that this concept is different from Terzaghi's effective stress defined in Eq (2.1).
3.2.1 Elastic-damage tangent constitutive tensor
The material non-linearity introduced by the damage model requires solving the system of equations by means of incremental-iterative techniques such as the Newton-Raphson's method. If one aims at achieving reasonable convergence rates, it is crucial to properly compute the tangent constitutive tensor.
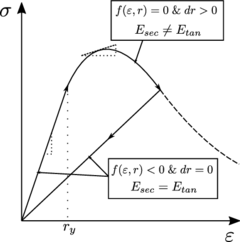
To that purpose, it is essential to understand that the global stiffness of the structure changes through any damage process. In 1D problems one can easily distinguish the secant Young's modulus from the tangent one and compute them as:
|
|
(3.14) |
Figure 24 shows the stress-strain relation on a unidimensional damage process. The branch on the left side of the curve corresponds to the elastic loading case. The stress increases proportionally to the strain growth, and goes back following the same path when the strain diminishes. The secant and tangent elastic modulus coincide through all this stage. After a certain strain value is reached, i.e. , the relation between the stress and the strain becomes non-linear as the material starts degrading. In this situation, the secant and tangent Young's moduli diverge and the internal state variable starts increasing (). Finally, since no plastic deformation is considered, the strain is fully recovered upon unloading following a branch with a lower stiffness than the original.
|
| Figure 24: Unidimensional stress-strain diagram throughout a damage process. |
Understanding the previous concepts is not so straightforward in a general 3D case and so it is convenient to derive a general expression for the elastic-damage tangent constitutive tensor .
Let us remind first that the tangent constitutive tensor defines the tangent stiffness matrix (2.39) and must satisfy the following relation:
|
|
(3.15) |
Considering the stress vector defined in (3.9) as a function of the strain vector and the damage variable, i.e. , we compute its total derivative as:
|
|
(3.16) |
Like in the 1D case (Figure 24), we distinguish two possible situations, bearing in mind that the Kuhn-Tucker conditions hold (Eq (3.8)):
- Elastic loading or unloading process ()
Whenever the structure is under an elastic loading or unloading process, there is no change in the internal historical variable (3.13). As a result, the damage variable also remains constant () and so the expression in (3.16) results:
|
|
(3.17) |
Consequently, in this case the tangent constitutive tensor coincides with the secant constitutive tensor:
|
|
(3.18) |
- Loading process with growing damage ()
If the structure is under a loading process with the equivalent strain exceeding the damage threshold , the internal state variable increases with time, and so the damage variable ().
From the definitions in (3.7), (3.12) and (3.13), we compute the total derivative of the damage variable as:
|
|
(3.19) |
Where the derivative of the equivalent strain with respect to the strain vector is estimated by means of the perturbation method [115]. This method is actually convenient as it allows us to compute the previous derivative regardless of the form of the equivalent strain:
|
|
(3.20) |
with being the perturbation vector of the strain component.
|
|
(3.21) |
Now, introducing Equation (3.19) into (3.16) and rearranging terms gives
|
|
(3.22) |
And so the expression defining the tangent constitutive tensor reads
|
|
(3.23) |
The typical scheme for the numerical implementation of the tangent constitutive tensor is summarized in Table (4).
| Step | |
| 1. Compute secant constitutive tensor: | |
| If | 2. Compute damage function derivative: |
| 3. Calculate equivalent strain derivative: | |
| 4. Compute tangent constitutive tensor: | |
3.2.2 Equivalent strain
To some extent, the equivalent strain presented in (3.12) plays a role similar to the yield function in plasticity, because it directly affects the shape of the elastic domain (Figure 25).
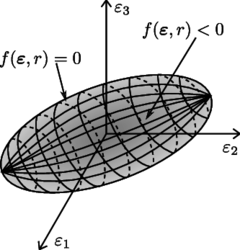
|
| Figure 25: 3D elastic domain for a generic equivalent strain. |
There are numerous forms for the equivalent strain in the literature, but the simplest choice is to define it as the Euclidean norm of the strain vector:
|
|
(3.24) |
or as the energy norm:
|
|
(3.25) |
The two norms of introduced above, lead to symmetric elastic domain in tension and compression (Figure 26a). Nevertheless, several materials (rocks, concrete, ceramics, etc.) often show a non symmetric damage surface, i.e., the yield value in compression can be several times the value in tension. In order to overcome this limitation, it is necessary to adjust the definition of the equivalent strain.

|

|
| (a) Symmetric energy norm. | (b) Adapted Simo & Ju norm. |

|

|
| (c) Mazars norm. | (d) Modified von Mises norm. |
| Figure 26: Damage surfaces in the 2D principal stress space. | |
In this regard, one may work wit a definition of the equivalent strain based on the model proposed by Simo and Ju [57], using the energy norm of the strain and modifying it to take into account the different degradation rate in tension and compression of concrete-like materials (Figure 26b). Such definition takes the form:
|
|
(3.26) |
where the variable is a weighting factor computed from the eigenvalues of the effective stress tensor:
|
|
(3.27) |
with denoting the “positive part” operator or McAuley brackets. For scalars , i.e.,
|
|
(3.28) |
The parameter in (3.26) is defined as the ratio between the compression elastic limit and the tension elastic limit, i.e.
|
|
(3.29) |
Eq (3.26) is not the only possible form of equivalent strain valid for quasi-brittle materials. Micro-cracks in concrete grow mainly if the material is stretched, and so it is natural to take into account only strains that are positive (tensile strains) and neglect those that are negative (compressive strains). This leads to the so-called Mazars definition of equivalent strains [116]:
|
|
(3.30) |
where are the principal values of the strain tensor.
Alternatively, the modified von Mises definition [117], reads:
|
|
(3.31) |
where is the first invariant of the strain tensor and is the second invariant of the deviatoric strain tensor. Given a generic symmetric strain tensor:
|
|
(3.32) |
The first invariant is the trace of the strain tensor:
|
|
(3.33) |
Also, one can always decompose the strain tensor into its volumetric and deviatoric parts :
|
|
(3.34) |
|
|
(3.35) |
From the deviatoric strain tensor we can calculate and :
|
|
(3.36) |
|
|
(3.37) |
The Mazars form of equivalent strain (3.30) and the modified von Mises equation (3.31) lead to different damage surfaces as shown in Figures 26c and 26d. However, in both cases the elastic limit in tension is considerably lower than the elastic limit in compression , and thus they are convenient for modelling damage progression of quasi-brittle materials such as rocks or concrete.
3.2.3 Damage evolution law
Once we have defined the energy norm in the strain space or equivalent strain , let us introduce the law governing the evolution of the damage variable (3.7).
There are various damage governing laws that can be effectively used to model damage growth in geo-materials. One option, especially suited for simplified analyses, is the linear softening law:
|
|
(3.38) |
Such a relation limits the range of the internal state variable between the damage threshold and a maximum admissible value , and leads to a linear softening branch in the stress-strain curve (Figure 27a).
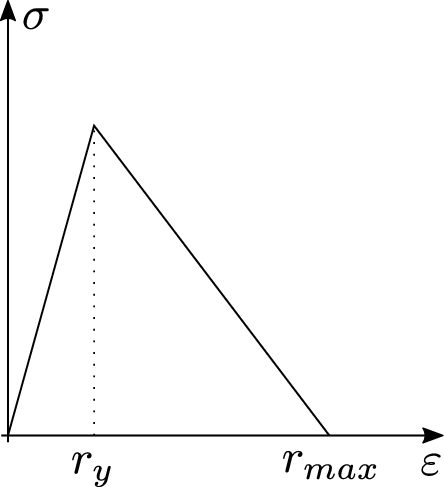
|
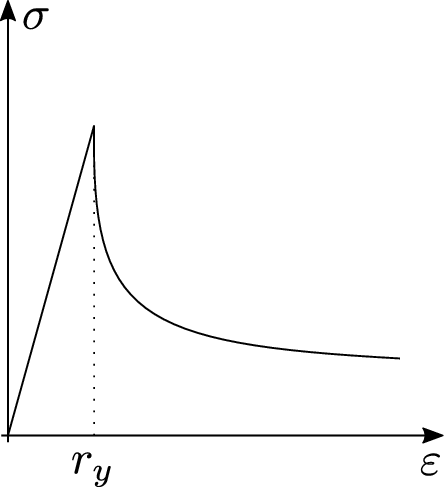
|
| (a) Linear softening law. | (b) Polynomial softening law. |
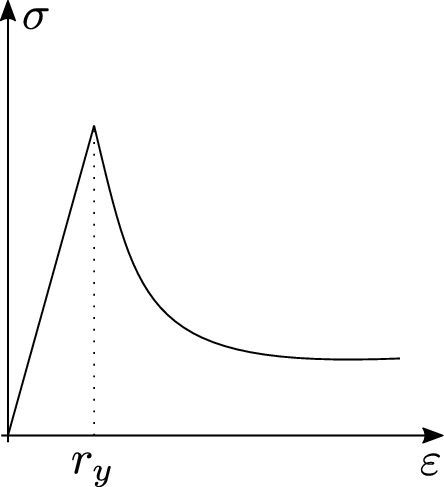
| |
| (c) Exponential softening law. | |
| Figure 27: Generic unidimensional stress-strain curves for different softening laws. | |
Two typical choices to describe the evolution of degradation in quasi-brittle materials are the polynomial law [118]:
|
|
(3.39) |
and the exponential softening law [112]:
|
|
(3.40) |
In the above expressions, the parameter is associated to the residual strength of the material, whereas the parameter softening slope controls the slope of the softening branch after the peak of the stress-strain curve.
The polynomial equation (3.39) and the exponential softening law (3.40) mainly differ from the linear law (3.38) in that the material preserves some residual strength in the post-peak branch, as shown in the 1D stress-strain curves of Figures 27b and 27c.
An alternative exponential softening model was proposed in [59]:
|
|
(3.41) |
The parameter is obtained from the following expression:
|
|
(3.42) |
where is the specific fracture energy per unit area, is the characteristic length for the fractured domain, usually taken as the characteristic length of the finite elements, and is the aforementioned damage threshold which, for quasi-brittle materials, can be estimated from the tensile strength :
|
|
(3.43) |
Another popular damage evolution law specifically designed for concrete was proposed by Mazars [116,112]. He divided the damage variable in two components: and , which are computed from the equivalent strain of Eq (3.30), but using two different damage laws: and . Function is characterized by the uniaxial compressive test, while corresponds to the uniaxial tensile test. Both functions were proposed in the same exponential form of (3.40):
|
|
(3.44) |
|
|
(3.45) |
The damage evolution law results from the combination of the two parts:
|
|
(3.46) |
The coefficient ranges from to and takes into account the character of the stress state. It is evaluated from:
|
|
(3.47) |
where are the principal strains due to positive effective stresses (or tensile stresses).
The parameter in (3.46) was equal to in the original version of the model [116]. For values higher than , allows to slow down the evolution of damage under shear loading (when principal stresses have different sign).
The definition of tells us that if all principal stresses are negative then and , corresponding to a “purely compressive” stress state. On the other hand if all principal stresses are positive, i.e. in a “purely tensile” stress states, we have and .
3.3 Local and Non-local Damage Models
In the last section we have presented the fundamental theory of the isotropic damage models with a unique scalar variable . Although these models are relatively simple, they are often used to model the failure of concrete, rocks and other quasi-brittle materials that show important strain localization. If the damage parameter depends only on the strain state at the point under consideration, the numerical simulations exhibit a pathological mesh dependence, and physically unrealistic results are obtained.
This is the typical behaviour of the so-called local damage models, which are not able to properly describe both the thickness of localization and distance between them. They suffer from mesh sensitivity (for size and alignment) and produce unreliable results. The strains concentrate in one element wide zones and the computed force-displacement curves are mesh-dependent. The reason is that differential equations of motion change their type (from elliptic to hyperbolic in static problems) and the rate boundary value problem becomes ill-posed [114].
Classical constitutive models require an extension in the form of a characteristic length to properly model the thickness of localized zones. Such extension can be done with micro-polar [64,119], strain gradient [65,120,121], viscous [66,122,123] and non-local terms [124,70,67,125]. In this work we have developed the latter approach.
First of all, we present the problems derived from the strain localization phenomenon, using a simple uniaxial case as example. Following that, the basic concepts of the implemented non-local damage model are introduced.
3.3.1 Strain localization phenomenon
The idea of modelling damaged concrete and other quasi-brittle materials as strain-softening continua, was not immediately accepted by all the scientific community. Actually, most of the early analyses were not truly objective and, upon mesh refinement, their results would not converge to a robust solution. Let us explain the nature of the problem by means of a unidimensional example.
Consider a straight bar with a constant cross section and a total length under uniaxial tension (Figure 28). The material is assumed to obey a simple stress-strain law with linear elasticity up to the peak stress , followed by linear softening (Figure 29). If the bar is loaded in tension by an applied displacement at its right extreme, the response remains linear elastic up to , instant at which the force transmitted by the bar (reaction at the support) attains its maximum value . After that, the resistance of the bar starts decreasing until the strain reaches and the transmitted stress completely disappears.
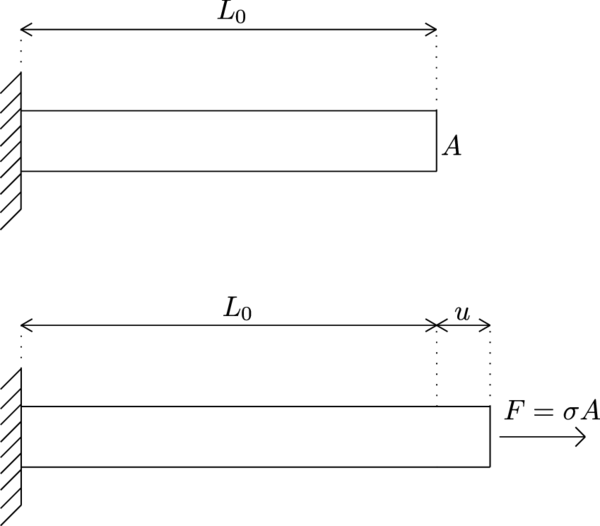
|
| Figure 28: Bar under uniaxial tension. |
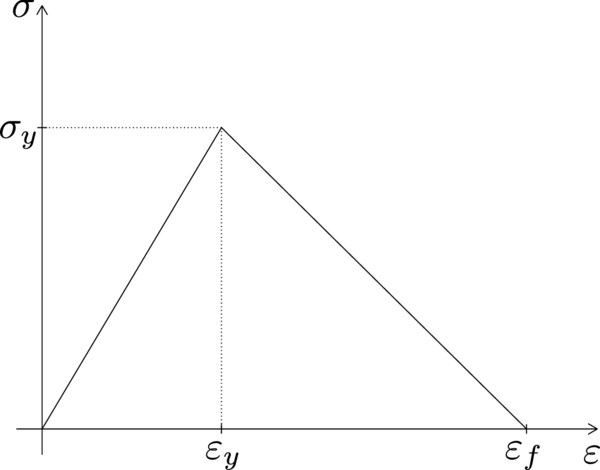
|
| Figure 29: Stress-strain diagram of the linear softening law. |
The equilibrium equations at a section in the middle imply that the axial forces are constant along the bar and so the stress profile must remain also uniform (Figure 30).
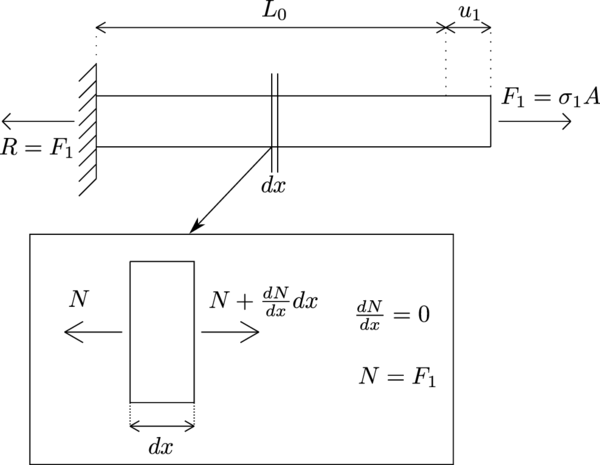
|
| Figure 30: Axial force acting along the bar. |
However, at a given stress level between and , there are actually two values of strain, and , that satisfy the constitutive equation (Figure 31). This is quite straightforward if one considers that any cross section can either be damaged, or undamaged. Indeed, an undamaged section is on the elastic branch with , whereas a damaged one falls in the softening branch with .
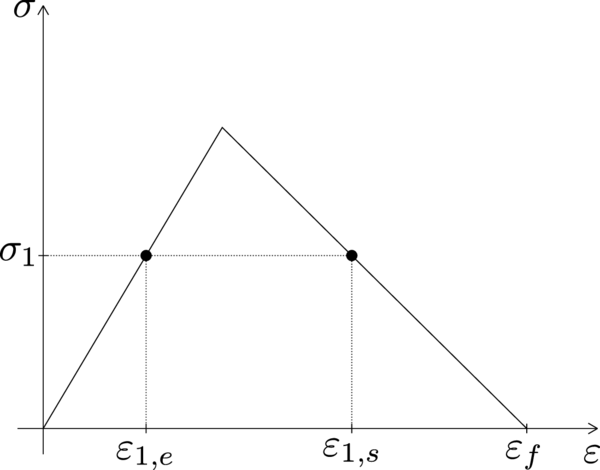
|
| Figure 31: Possible strain values corresponding to the same stress level. |
Thereby, the strain profile along the bar does not have to be necessarily uniform. In fact, any piecewise constant strain distribution that jumps between the two possible strain values represents a valid solution.
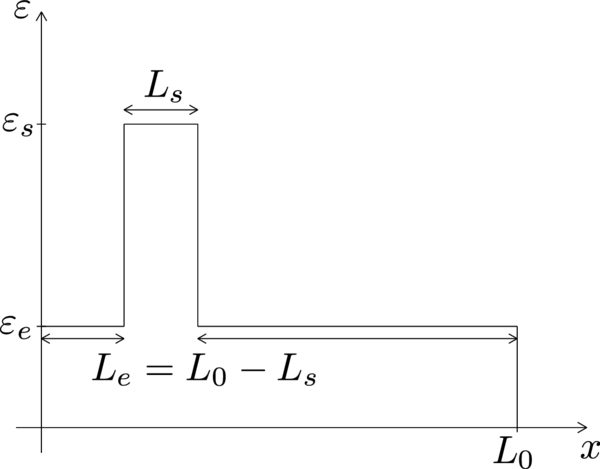
|
| Figure 32: Piecewise constant strain profile along the bar. |
In Figure 32 we have denoted by the cumulative length of the softening regions and by the cumulative length of the elastic regions. When the stress is completely relaxed, the strain in the elastic region is and the strain in the softening branch is . Thus the total elongation of the bar in this case is . At this point, although is perfectly known from the linear softening law (Figure 29), is totally undetermined. This means that the problem has infinite possible solutions with its corresponding post-peak branches in the load-displacement diagram (Figure 33).
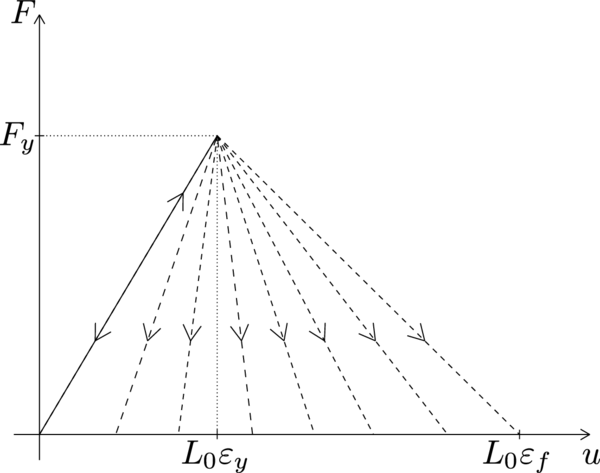
|
| Figure 33: Fan of possible post-peak branches of the load-displacement diagram. |
This fan of post-peak branches is bounded on one side by the solution with uniform softening () and on the other side by the solution with uniform elasticity (). The first limit corresponds to a totally damaged bar while the latter represents the case in which the bar is unloaded before any damage takes place. All the other solutions describe processes in which a part of the bar is damaged. However, it is not trivial to determine which of all these solutions is the one that reflects better the actual failure process.
The ambiguity is removed if imperfections are taken into account. The material properties and sectional dimensions of a real bar are not perfectly uniform. Thereby, supposing that there is a small region where the strength is lower than in the remaining portion of the bar, when the applied stress reaches the peak of that weaker region, softening starts and the stress decreases. Consequently, the material outside the damaged region must unload elastically because its strength has not been exhausted. This leads to the conclusion that the size of the softening region is related to the size of the region with minimum strength. The problem is that such a region can be arbitrarily small and so the corresponding softening branch is arbitrarily close to the elastic unload branch. Therefore, the standard strain-softening continuum formulation leads to a solution with several pathological features:
- The softening region is infinitely small.
- The load-displacement diagram always shows snap-back, regardless of the size of the structure and the ductility of the material.
- The total amount of energy dissipated during the failure process tends to zero.
From the mathematical point of view, these problematic features are related to the loss of ellipticity of the governing differential equation. As a result, the boundary value problem no longer has a unique solution with continuous dependence on the given data.
From the numerical point of view, these inconveniences are manifested by a pathological sensitivity of the results to the size of the finite elements.
For instance, let us assume that the bar is uniformly discretized by two-node elements with linear displacement interpolation and that the weakest region is located at the middle of the bar. The numerical algorithm will capture a very localized solution with a softening region extending over one only element. In consequence, the softening length will decrease as the number of elements increases () and thus the softening post-peak branch will completely depend on the number of elements of the mesh.
Indeed, as it is shown in Figure 34a, for all the bar is damaged and the softening length is the total length of the bar , whereas for the softening region is more localized with strains becoming especially important at the damaged element. In the limit case of the softening branch would coincide with the elastic branch (see Figure 34b).
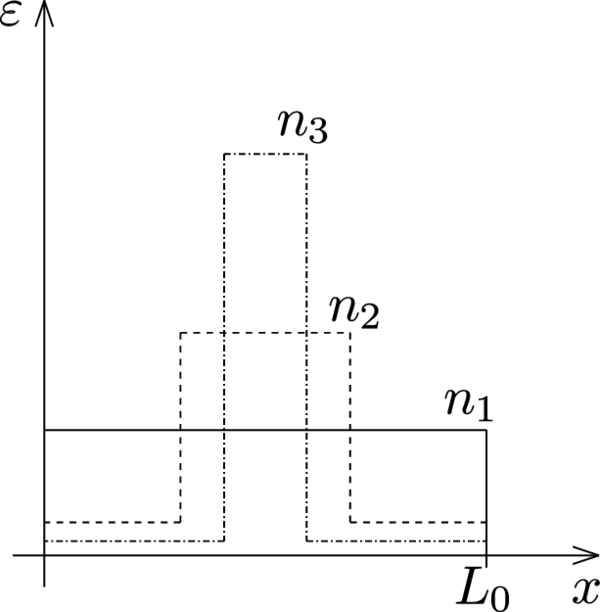
|
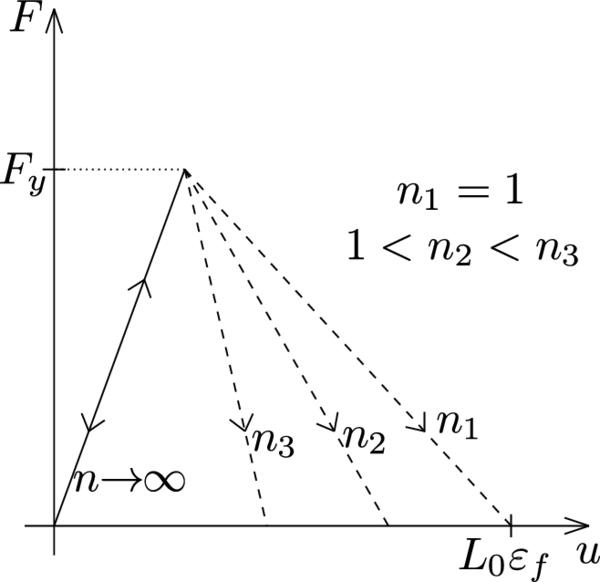
|
| (a) Strain profiles for a prescribed imposed displacement. | (b) Load-displacement diagrams for different number of elements. |
| Figure 34: Mesh dependence of the numerical results. | |
In this section we presented a problem that commonly arises in the simulation of damage processes involving quasi-brittle materials: the strain localization phenomenon. Although only a uniaxial case has been discussed, this problem is also present in multidimensional problems with similar effects on the numerical results.
The simple one-dimensional example illustrates the essence of the problem with localization of inelastic strain into a zone of an arbitrarily small width. In uniaxial cases, localization occurs when the peak of the stress-strain diagram is reached, independently of the specific constitutive model used. In multiple dimensions, the analysis of the localization process is more complicated and the derivation of a criteria for the start of localization represents a challenging problem.
Mesh refinement in multiple dimensions leads to a reduction of the total dissipated energy (area under the load-displacement curve) with a lower peak load and a more brittle response. Apart from this, upon further refinement, one can also face convergence difficulties due to the abrupt change of strain distribution, from a smoothly distributed to a highly localized one. These effects will be shown more clearly with the simulation of a bi-dimensional case later in this chapter (see Section 3.4).
3.3.2 Regularization of the problem
When simulating fracture propagation processes, it is essential to ensure that the direction of crack growth is not affected by numerical conditioners such as the mesh size or the type of element. For this reason, in the present work two different continuum damage models for the porous medium were implemented in the research of a robust method that avoids the pathological sensitivity of the finite element results to the mesh size.
Partially regularized local damage model
As a first attempt, we used a simple partially regularized local damage model, based on the crack band models [126]. We combined the equivalent strain form of Eq (3.26) and the damage evolution law in Eq (3.41).
Essentially, the model is an isotropic damage model following the classical local damage theory, in which an energy based adjustment of the stress-strain diagram, depending on the size of the element, is introduced in the definition of the damage parameter.
Indeed, the damage evolution law in (3.41) depends on the characteristic length of the fractured domain included in the definition of the variable (3.42). This characteristic length of the fractured domain is what, in the end, partially regularizes the damage model. If the mesh size is modified, the energy dissipated by the structure is scaled according to the element characteristic length and, ideally, the energy consumption should remain unaltered by the changes on the spatial discretization.
Thereby, before updating the damage variable, one just needs to compute the characteristic length of the element , which can be estimated from the dimensions of the element like it was done in Equations (2.57) and (2.58). In a two-dimensional analysis, for instance, the characteristic length of the element can be defined as the diameter of the circle that contains the area of the element (see Figure 35).
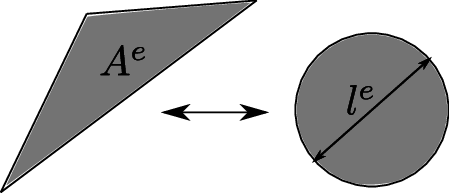
|
| Figure 35: Characteristic length of a 2D finite element. |
This approach is endowed with some, but not all of the properties of fully regularized damage models. It can ensure a correct energy dissipation in a localized damage band, but the width of the numerically resolved fracture process zone depends on the element size and tends to zero as the mesh is refined. This is why this approach cannot be considered as a true localization limiter. It provides only a partial regularization of the problem in the sense that global response characteristics do not exhibit spurious mesh sensitivity, but the mesh-induced directional bias is still present.
Moreover, the scaling of the stress-strain diagram is straightforward only for models that explicitly control the evolution of inelastic strain, e.g. for softening plasticity [127] or smeared crack models [59]. In those cases, the desired scaling effect is achieved just by modifying the hardening modulus (derivative of stress with respect to inelastic strain). Nevertheless, in continuum damage mechanics, non-linearity and softening are controlled by the damage evolution law, and the reduction factor multiplies the total strain. For this reason, it is not easy to scale only the post-peak part of strain localization while keeping the unloading part unaffected.
In some cases, diffuse softening damage patterns in certain parts of the structure can coexist with localized cracks in other parts, and they may even change during the loading process. In such cases it is virtually impossible to define a coherent rule for the adjustment of the stress-strain diagram according to the element size.
Fully regularized non-local damage model
The introduction of a characteristic length into the constitutive model, and the formulation of a non-local strain-softening model, have been shown to prevent the spurious localization of strain-softening damage, to regularize the boundary value problem, and to ensure numerical convergence to physically meaningful solutions [69,70,125].
Fully regularized description of localized inelastic deformation is achieved by a proper generalization of the underlying continuum theory. Two different approaches are normally used: generalization of the kinematic relations, i.e. continua with micro-structure (Cosserat-type continua or strain gradient theories), and continua with non-local strain (non-local elasticity); and generalization of constitutive equations, i.e., material models with gradients of internal variables, and materials models with weighted spatial averages of internal variables.
In this monograph we have worked with the second kind of generalization, because kinematic and equilibrium equations remain standard, and the notions of stress and strain keep their usual meaning. Also, in the generalization of constitutive equations through non-local models, we have focused on the integral-type methods.
Integral-type non-local models abandon the classical assumption of locality and admit that stress a certain point depends, not only on the state variables at that point, but also on the distribution of the state variables over the whole body, or over a finite neighbourhood of the point under consideration.
In a general manner, the non-local integral approach consists in replacing a certain local variable by its non-local counterpart, which is usually obtained by a weighted averaging over a spatial neighbourhood of each point under consideration.
Let be some local field in a domain . The corresponding non-local field is defined as:
|
|
(3.48) |
where is the non-local weighting function.
In an infinite, isotropic and homogeneous medium, the weighting function depends only on the distance distance between the source point , and the receiver point . Thereby, we usually write , where is usually chosen as a non-negative function monotonically decreasing for .
One possible choice for is the Gauss distribution function:
|
|
(3.49) |
where is the characteristic length, a material parameter reflecting the internal length of the non-local continuum.
If a bounded support is preferred, one can also truncate the previous function as follows:
|
|
(3.50) |
where the interaction radius is a parameter related to the characteristic length . In the present work, we have considered .
In this monograph we worked with the previous Gauss distribution (3.50), but there are other alternatives that can be effectively used, e.g. the following truncated quartic polynomial function:
|
|
(3.51) |
In essence, the interaction radius represents the smallest distance between points and at which the interaction weight vanishes (for weighting functions with a bounded support) or becomes negligible (for weighting functions with an unbounded support). It must be carefully chosen as it controls the size of the softening region.
The interval, circle, or sphere of radius , centered at , is called the domain of influence of point . In the vicinity of the boundary of a finite body, it is simply assumed that the averaging is performed only on the part of the domain of influence that lies within the body (Figure 36).
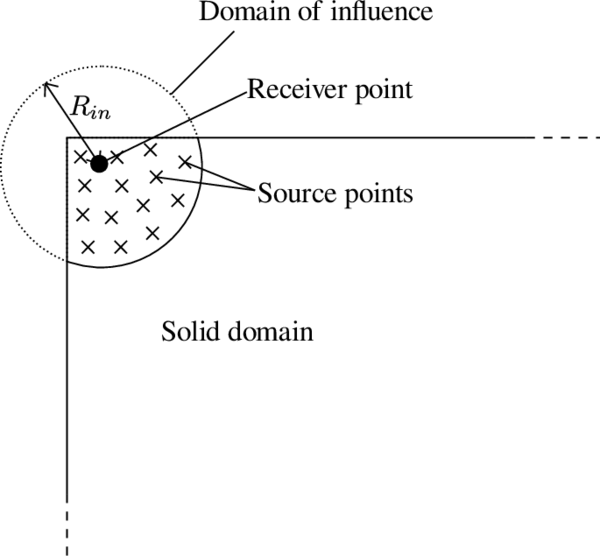
|
| Figure 36: Domain of influence protruding through the boundary of a body. |
Thereby, if a weighting function with bounded support is chosen, the non-local average of (3.48) is calculated as a weighted sum over the values at all the finite element integration points lying within the non-local interaction radius .
In the application to softening materials, it is often required that the non-local operator do not alter a uniform field (consistency of order ), which means that the weighting function must satisfy the normalizing condition:
|
|
(3.52) |
In order to satisfy (3.52), the weighting function is usually rescaled as:
|
|
(3.53) |
In the present work, the damage variable is computed from the non-local equivalent strain, which corresponds to a suitable non-local damage formulation that restores well-posedness of the boundary value problem [128].
Therefore, in the loading function (3.12), the local equivalent strain is replaced by its weighted spatial average:
|
|
(3.54) |
And the internal state variable is then the largest previously reached value of the non-local equivalent strain:
|
|
(3.55) |
It is important to note that while the damage variable is evaluated from the non-local equivalent strain , the strains used in (3.9) to compute the stresses are considered as local. This way, during the elastic range, when the damage variable remains equal to zero, the stress-strain relation is completely local. The process for the evaluation of stresses with the non-local damage model is schematically represented in Table 5.
| Step |
| 1. Evaluate effective stress: |
| 2. Compute the new local equivalent strain: |
| 3. Compute the new non-local equivalent strain (3.54): |
| 4. Update with (3.55): If |
| 5. Update damage variable: |
| 6. Compute nominal stress: |
As it can be deduced from Table 5, the numerical implementation of the non-local damage model based on averaging of the equivalent strain is relatively simple. The evaluation of the stresses remains explicit, and no internal iteration is required. One just needs to implement the algorithm of weighted spatial averaging and, before damage is evaluated, replace the local equivalent strain by its non-local counterpart.
The values of the non-local equivalent strain must be traced at the individual Gauss integration points of the finite element mesh, because these are the points at which stresses are computed.
Thereby, the averaging integral in (3.54) is evaluated numerically as follows:
|
|
(3.56) |
where is a coefficient containing the product of the determinant of the Jacobian and the integration weight of Gauss point , and is the aforementioned weight of non-local interaction between points and , computed as:
|
|
(3.57) |
In the previous two equations, subscript represents the receiver point under consideration, whereas indexes and correspond to source points. Since the chosen weighting function (3.50) has bounded support, vanishes if the distance between points and is larger than the interaction radius . Therefore, the sums in (3.56) and (3.57) do not need to be taken over all Gauss points, but only over those that are located inside the domain of influence of point .
Note that, at least around the damage process zone, one must always use an element size smaller than the interaction radius in order to account for the non-local interaction. Otherwise the damage model would become local. In this regard, an interaction radius relatively small can restrict the applicability of non-local models to small or medium size domains because of very fine meshes being necessary.
Each Gauss point must have a non-local interaction table that gives access to its neighbours. This table must be constructed at the beginning of the problem and every time the model is remeshed. In this work, the search of neighbours is performed by means of a grid-based algorithm. A general rectangular grid is defined in the entire domain and all the integration points are positioned in the cells. This way, the neighbour search that must be performed for each Gauss point is restricted to a limited number of cells, i.e. the ones that fall inside the domain of influence of the considered point (see Figure 37).
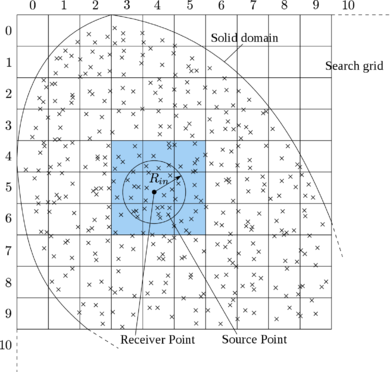
|
| Figure 37: Grid-based non-local search. |
The stress evaluation procedure (Table 5), repeatedly called during the incremental-iterative strategy, makes use of the non-local interaction tables when the non-local equivalent strain is computed. To obtain we first compute the local equivalent strains at all Gauss points, and then we calculate the non-local counterpart using (3.56).
Finally, if one aims to obtain an iterative solver with quadratic convergence when working with a non-local damage model, it is necessary to construct the tangent stiffness matrix in a consistent manner, which slightly differs from the standard procedure already explained in Section 3.2.1. Here we derive the analytical expression of the tangent stiffness matrix, but we also note that some authors report complete consistency when obtaining the global tangent operators by finite-differencing the residuals [129].
Let us start expressing the tangent stiffness matrix (2.39) as a numerical integration over the Gauss points of the model:
|
|
(3.58) |
Using the stress-strain law in (3.9) and the classical strain-displacement relation , we expand Eq (3.58) as follows:
|
|
(3.59) |
Since the damage variable depends on the nodal displacements through the equivalent strain, we compute first the derivative of the damage variable with respect to the displacement vector . Taking into account that (3.7), depends on (3.55), and depends on through the interpolated strains, we use the chain rule to write the derivative of the damage variable for an integration point as follows:
|
|
(3.60) |
where is the derivative of the damage evolution law with respect to the internal state variable , and is the loading-unloading factor that is in an elastic loading or in an unloading regime, and in a loading regime with growing damage:
|
|
(3.61) |
Using expression (3.56), we can differentiate the non-local equivalent strain of a Gauss point with respect to the nodal displacements as
|
|
(3.62) |
The derivative of the equivalent strain with respect to the strain vector is a row matrix that depends on the chosen form of equivalent strain.
At this point, we can already differentiate Eq (3.59), substitute (3.60) and rearrange terms to obtain the following expression:
|
|
(3.63) |
Note that the first term in (3.63) is the secant stiffness matrix, which coincides with the tangent matrix in an elastic loading or in an unloading regime (). The second term in Eq (3.63) is the non-local part of the tangent stiffness matrix. Substituting (3.62) into (3.63) yields:
|
|
(3.64) |
Defining for convenience the column matrix , the row matrix , and the coefficient , Equation (3.64) can be rewritten as:
|
|
(3.65) |
The double index of the sum, caused by the non-local interaction, implies that the term on the right part of Equation (3.65) cannot be assembled only from the standard element loop. Essentially, each pair of Gauss points and contributes to the global stiffness matrix with a block of the same size as that of the classical element stiffness matrix. The difference is that the assembling routine differs from the usual one because in this case one needs to take into account the elements of both points and (Figure 38). As a consequence, the global stiffness matrix is always non-symmetric and its bandwidth increases due to the non-local interaction.
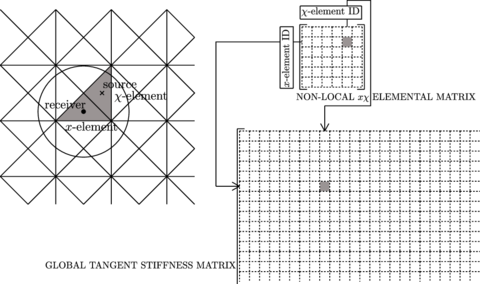
|
| Figure 38: Non-local assembly process. |
In order to avoid the additional non-zero entries that the non-local interaction introduces into the global stiffness matrix, one could neglect the non-local terms by using , where is the Kronecker delta. This way, Equation (3.65) reduces to
|
|
(3.66) |
where the sum is performed over one index only. Note that the resulting local tangent matrix is no longer consistent, and quadratic convergence is lost.
Probably the most important issue caused by non-locality is the evolutionary character of the profile of the stiffness matrix. For the simulation of quasi-brittle materials like concrete or rock, the consistent stiffness matrix remains local through the elastic branch, and so the initial distribution of non-zero entries is the same as in the local case. However, when the damage threshold is exceeded and the damage zone starts propagating, new non-zero entries appear due to the non-local interaction between Gauss points belonging to different elements, and the profile of the stiffness matrix must be dynamically adapted. The number of additional non-zero entries depends on each particular case, but if a finer mesh is used in the expected softening zones, this number can be relatively high.
Thereby, although the non-local damage model completely removes the pathological sensitivity to the mesh size and substantially alleviates the mesh-induced directional bias, it also increases the computational cost with respect to the local model, specially in the memory usage.
Figure 39 compares the general scheme for the stress evaluation and stiffness matrix assembly between the local and non-local damage models. Apart from a greater memory usage, the non-local damage model requires performing more elements loops than the classical local model.

|

|
| (a) Local damage model. | (b) Integral-type non-local damage model. |
| Figure 39: General scheme for the stress evaluation and stiffness matrix assembly. | |
3.4 Examples
The fundamental concepts on damage mechanics theory and the most relevant aspects concerning the implementation of a non-local damage model within the Finite Element Method have already been introduced.
This section is devoted to test and validate the presented damage models by solving two classical examples in the damage mechanics field: the three-point bending test, and the four-point shear test.
For each one of the tests, we solve the problem with the two implemented damage models: the partially regularized local damage model, and the integral-type non-local damage model. The objective of this experiment is to analyse and compare both models, pointing out the strengths and limitations of the approaches, and assessing whether the non-local procedure is a valid and robust technique.
Both examples are carried out under a 2D plane stress framework. The problems are solved as quasi-static step by step loading cases by means of the so-called modified Riks-Wempner arc-length strategy. Self weight is not taken into account.
3.4.1 Three-Point Bending Test
This test is performed with a notched beam subjected to three-point bending (TPB). The beam has a square cross section of , a span of , and the notch is thick and extends over one tenth of the beam depth (see Figure 40).
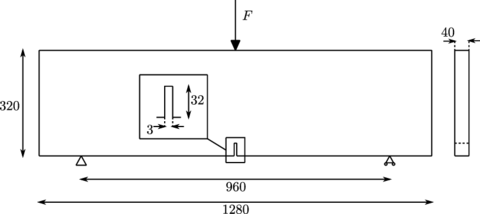
|
| Figure 40: TPB test. Geometry and boundary conditions. Dimensions in . |
Plane stress conditions are assumed, and the geometry is meshed by means of bilinear 4-node quadrilaterals with integration points.
We solve the problem using two different damage models: a partially regularized local damage model using the form of the equivalent strain proposed by Simo and Ju (3.26) and the damage evolution law presented in (3.41), and a non-local damage approach, which is defined with the Mazars model regarding the equivalent strain (3.30) and the damage evolution law (3.46). The weighting function for the non-local interaction relies on a Gauss distribution function of bounded support (3.50).
The material properties for the local damage model are summarized in Table 6 and have been obtained after some calibration, trying to fit the experimental results in [130]. For the non-local approach we use the same material parameters of [130] (see Table 7).
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Compressive strength () | |
| Tensile strength () | |
| Fracture energy () |
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Damage threshold () | |
| Residual strength in compression () | |
| Softening slope in compression () | |
| Residual strength in tension () | |
| Softening slope in tension () | |
| Characteristic length () |
In order to assess the robustness of the models in terms of mesh sensitivity, we solve the problem for different spatial discretizations. Here we use three unstructured meshes of quadrilaterals with a refined area in the center (see Figure 41). The first model was obtained from a characteristic element size of , with a resultant mesh of elements and nodes. The second mesh, with elements and nodes, resulted from an element size of . The third model was obtained after defining a characteristic element size of and lead to a mesh of elements and nodes.
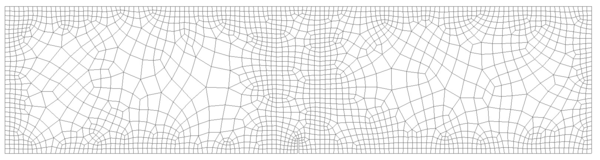
|
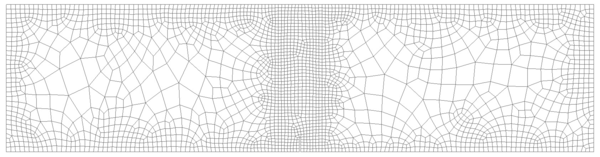
|
| (a) : elements. | (b) : elements. |

| |
| (c) : elements. | |
| Figure 41: TPB test. Spatial discretizations. | |
Figure 42 shows the relation between the applied load and the vertical deflection of the beam. As one can see from the discontinued equilibrium curves, we had serious difficulties in tracing the response of a full test. The reason behind the convergence problems could be the use of a too global arc-length method. Indeed, to account for the localized nature of quasi-brittle failure, a more specific control parameter, like the Crack Mouth Opening Displacement (CMOD), could help improving the convergence near snap-back zones.
That aside, if we look at the curves in Figure 42a we can see that, although there is no relevant difference between the response obtained with the two coarser meshes, the peak force actually decreases with the finest mesh, and so the total dissipated energy. On the other hand, the response diagram in Figure 42b shows virtually the same peak load for the three meshes.
|
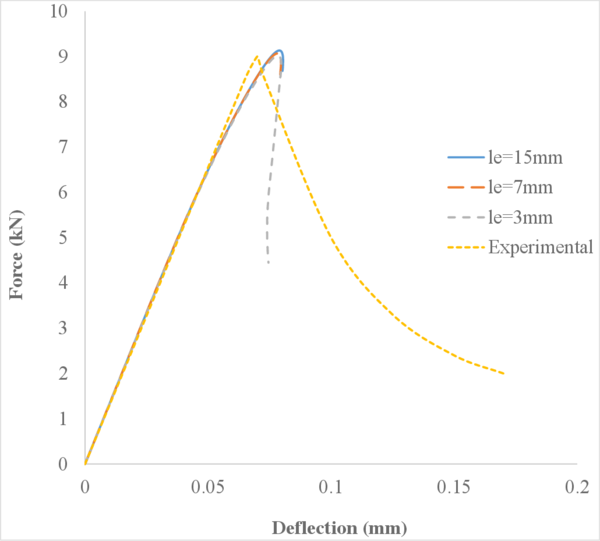
|
| (a) Partially regularized local damage model. | (b) Non-local damage model. |
| Figure 42: TPB test. Force-vertical deflection diagrams. | |
Focusing on Figure 42b and comparing the computed results with the experimental solution [130], one sees that the non-local damage model properly captures the peak load of the expected solution for all meshes.
Nonetheless, the post-peak branch of the numerical solution falls faster than in the reference solution, and even shows a certain amount of snap-back behaviour. Moreover, looking at the elastic branch of the responses, it seems that the stiffness degradation starts before in the numerical curves and, in consequence, the peak is slightly displaced to the right.
Using an advancing technique purely based on the control of displacements instead of the mentioned arc-length method would reduce the differences in the post-peak response.
From the depicted curves in Figure 42, it seems that the partially regularized local damage model is more sensitive to changes in the spatial discretization than the non-local model. In any case, though, the behaviour of the numerical model seems more brittle than the observed in experiments.
In order to properly understand the response of both damage models, let us present some snapshots with the damage distributions.
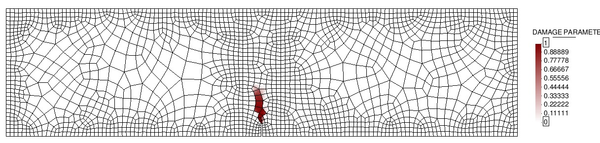
|
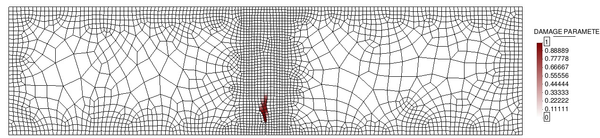
|
| (a) Model with . | (b) Model with . |
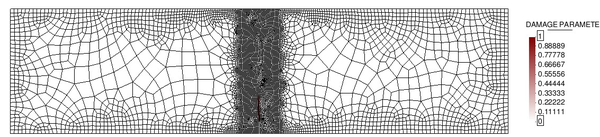
| |
| (c) Model with . | |
| Figure 43: TPB test. Damage initiation in the local model. | |
Figures 43 and 44 show an initial stage of damage progression in the local and non-local model, respectively. Just by looking at the size and shape of the damaged zone, we can clearly state the most differential trait of each model: localization on the one hand, and diffusion on the other. This concept is crucial to understand the observed behaviour in the load-deflection diagrams of Figure 42.
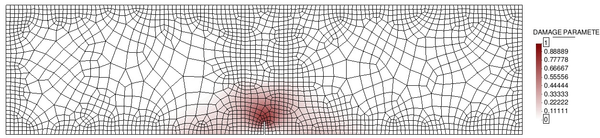
|
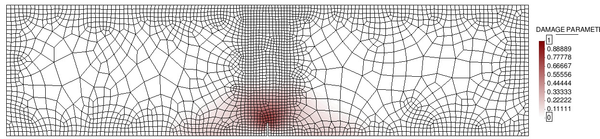
|
| (a) Model with . | (b) Model with . |

| |
| (c) Model with . | |
| Figure 44: TPB test. Damage initiation in the non-local model. | |
Essentially, in the local approach, damage starts at the most stressed element and then “jumps” to the next one when the first is totally damaged. As a result, shape and direction of progression of damage strongly depends on the size and distribution of the elements of the mesh (see Figure 45).
|
|
| (a) Model with . | (b) Model with . |
| Figure 45: TPB test. Zoom of damage growing in the local model. | |
On the other side, in Figures 44a, 44b and 44c we see a very similar diffusive damaged area. Indeed, in the non-local approach, the damage size is controlled by the interaction radius and thus even when reducing the size of the elements the damaged area is practically unaltered.
The distinction between localization and diffusion can also be seen in the evolution of the damage variable depicted in Figure 46.
While in the local damage model (Figures 46a, 46c and 46e) only a thin line of damage is propagated, i.e. a line of the size of the elements, in the non-local case (Figures 46b, 46d and 46f) damage occupies a wider area corresponding to the defined crack length , and even some zones at each side of the notch are affected by the damage progression at the center, stressing the idea that the damage depends, not only on the state of the point under consideration, but also on the state of the neighbouring points.
3.4.2 Four-Point Shear Test
In this second example a single-edge notched beam is subjected to four-point shear (FPS). The analysed beam has a square cross section of , a span of , and the notch is thick and depth (see Figure 47).
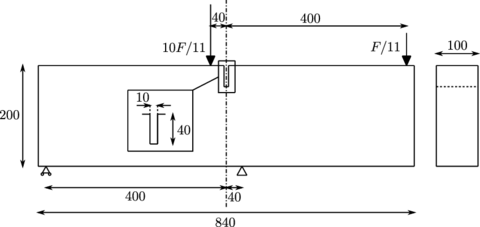
|
| Figure 47: FPS test. Geometry and boundary conditions. Dimensions in mm |
Plane stress conditions have been again assumed, but in this case the geometry is meshed by means of linear 3-node triangular elements with one integration point.
Again, we solve the problem using the two implemented damage models. The local approach is modelled with the same Simo and Ju model of the previous example, using the material parameters shown in Table 8. On the other hand, the non-local damage model is defined in this case using the equivalent strain form of the modified von Mises model (3.31), and the exponential damage evolution law that we presented in (3.40). The material parameters for the non-local approach have been obtained from [131] and are summarized in Table 9.
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Compressive strength () | |
| Tensile strength () | |
| Fracture energy () |
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Damage threshold () | |
| Compressive to tensile strength ratio () | |
| Residual strength () | |
| Softening slope () | |
| Characteristic length () |
As we did for the previous example, we solve the problem for three different unstructured meshes of triangles (Figure 48). The first model was obtained by refining the central area with a characteristic element size of , which resulted in a mesh of elements and nodes. The second model is represented by a mesh of elements and nodes and was obtained from an element size of . The last spatial discretization is the result of defining a characteristic element size of and lead to a total of elements and nodes.
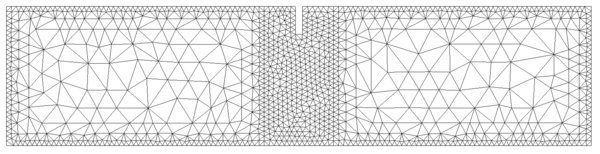
|
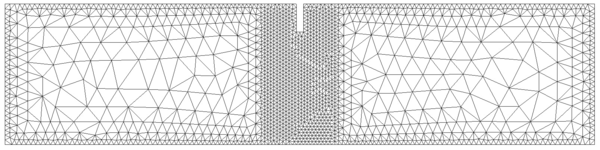
|
| (a) : 2216 elements. | (b) : 3502 elements. |
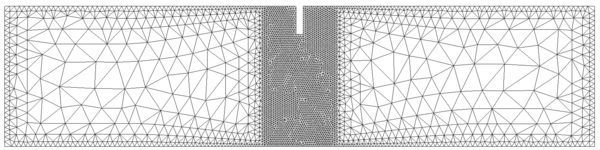
| |
| (c) : 7183 elements. | |
| Figure 48: FPS test. Spatial discretizations. | |
In Figure 49 we represent the relation between the applied load and the Crack Mouth Sliding Displacement (CMSD) for each mesh. The curves in Figure 49a show that in this case the peak and the dissipated energy also decrease as the mesh is refinement. However, this reduction is not so clear as in the previous example. On the other hand, Figure 49b shows virtually the same peak load for the three meshes. Also, although one can notice some oscillations in the post-peak region for the mesh with and the mesh with , we can say that the residual force at the right part of the graph is actually similar for all cases.
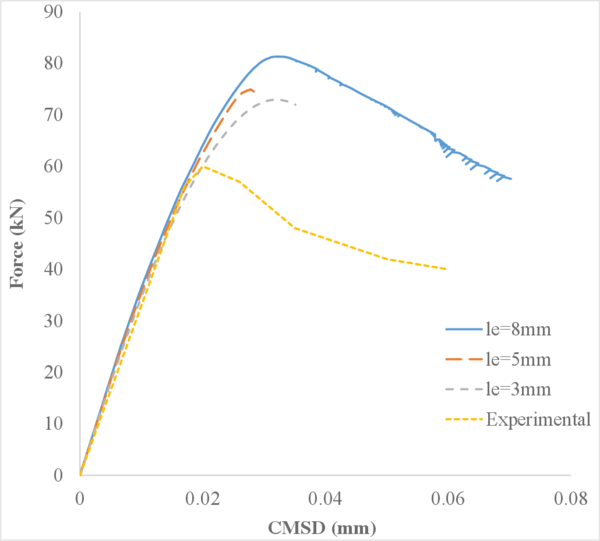
|
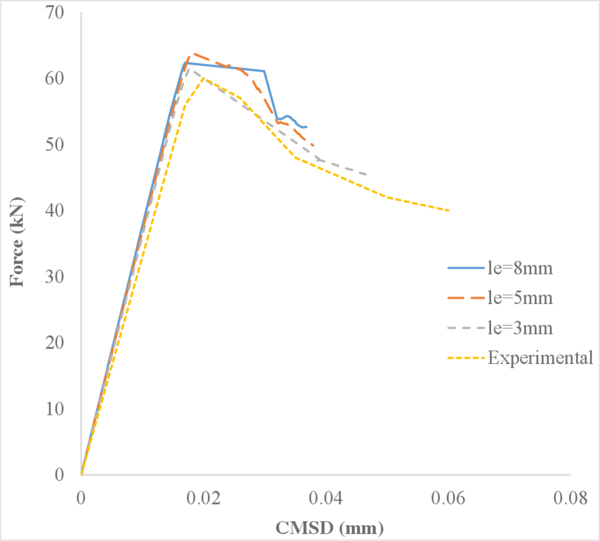
|
| (a) Partially regularized local damage model. | (b) Non-local damage model. |
| Figure 49: FPS test. Force-Crack Mouth Sliding Displacement curves. | |
We note that the “bilinear-like response” obtained with the finest mesh of in Figure 49b is due to the low precision of the arch-length strategy used in this problems. Again, an advancing technique based on the control of displacements, like the CMSD, could be better suited in this case.
Like in the previous case, we can compare the curves obtained from the non-local damage model with an experimental solution [132].
Thereby, focusing on Figure 49b we can see that the computed responses are very similar to the experimental solution, specially for the mesh with . Also, if one carefully looks at the elastic loading branches, it may be noticed that the numerical solutions exhibit a slightly stiffer behaviour than the experimental curve in the beginning of the degradation process. However, this difference is subtle and the post-peak branches converge to the results of the experiment.
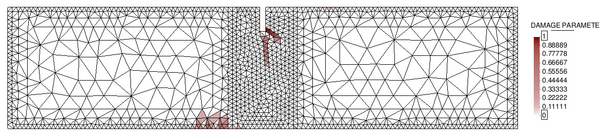
|
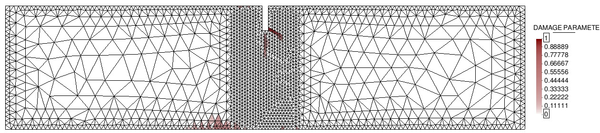
|
| (a) Model with . | (b) Model with . |
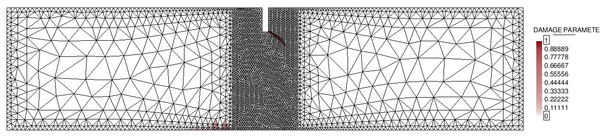
| |
| (c) Model with . | |
| Figure 50: FPS test. Damage progression in the local model. | |
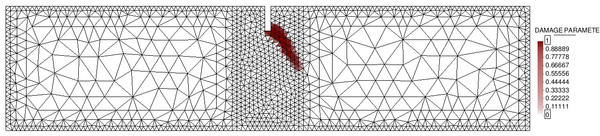
|
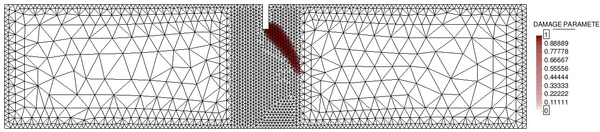
|
| (a) Model with . | (b) Model with . |

| |
| (c) Model with . | |
| Figure 51: FPS test. Damage progression in the non-local model. | |
Figures 50 and 51 show the damage progression in the peak-load region of the response, for the local and non-local model, respectively. Like before, from the size and shape of the damaged zone, we can clearly see a more localized response in the local damage model, and a more diffusive response in the non-local case.
Comparing the different damage patterns of the local model (Figures 50a, 50b and 50c), we notice an additional vertical damage line that appears only in the coarser meshes, stressing the idea that the local model suffers from mesh sensitivity.
The damage patterns in the non-local damage model (Figures 51a, 51b and 51c) are virtually identical for all meshes.
Finally, a comparative evolution of the damage variable with the mesh corresponding to is represented in Figure 52. We can see that, at the beginning of damage propagation (Figures 52a and 52b) both approaches show a very similar damage zone. The initially localized damage zone in the non-local model is mainly due to the small interaction radius of this example . After that, the difference between both models is clear, with a wider damage mark of the order of the characteristic length in the non-local case.
4 Modelling Discontinuities in Porous Media
4.1 Introduction
Modelling the fluid flow in a multi-fractured porous domain implies taking into account that the cracks in the solid skeleton introduce preferential flow paths, apart from jumps in the displacement field. A proper understanding of discontinuities is crucial not only because they influence the behaviour of the local surroundings of the cracks, but also because they modify the global permeability and the mechanical response of the medium, specially whenever it undergoes a crack growth process.
In the last decades, many efforts have been made to develop numerical models for the accurate analysis of discontinuities in solids and porous media.
The extended finite element method (XFEM) has obtained notable attention in the past years [39,41,43,44]. The essential idea of the XFEM is to enhance the solution by decomposing the displacement field into a continuous and a discontinuous part. The discontinuity is captured by means of enrichment functions that introduce the jumps in the displacement field. The most remarkable advantage of the method is that there is no need to explicitly represent cracks in a mesh provided that enriched nodes are considered (Figure 53a). This avoids the necessity of remeshing during crack growth, but in return it demands a higher computational cost in terms of number of degrees of freedom and numerical integration.
The present work focuses on the methods purely based on the finite element method (FEM). In this category, numerous methods can be found in the literature, but two main subgroups can be distinguished: the "smeared crack" approaches (Figure 53b), continuum based methods in which the influence of developing fractures is incorporated into the constitutive stress-strain law [45,46,47,48], and the "discrete crack" models (Figure 53), in which each single discontinuity is represented explicitly [49,50,51,52].
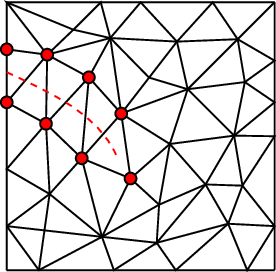
|
|
| (a) XFEM. Enriched nodes have been coloured red. | (b) FEM: smeared crack approach. |
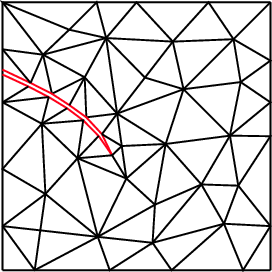
| |
| (c) FEM: discrete crack approach. | |
| Figure 53: Different methods to represent discontinuities. | |
Since Goodman et al. proposed the "zero-thickness" interface element to describe the mechanical behaviour of pre-existing joints in rock masses [76] many authors have developed strategies to adapt this element for the solution of fracture processes in coupled solid-pore fluid problems.
Three different types of zero-thickness interface elements can be found in the literature concerning the way the fluid is modelled: single, double and triple noded elements. The single-noded element is the simplest one and only considers longitudinal conductivity with no pressure drop across the interface [77]. The triple-noded element was meant to include the effect of the transversal conductivity through the discontinuity [78]. The two nodes at each side of the interface represent the potentials in the pore pressure, while the third node in the middle stores the average potential of longitudinal fluid through the fracture. Finally, the double-noded elements take into account both types of conductivity but the external nodes variables substitute the middle node. Ng and Small used this double-noded zero-thickness interface element to model flow problems with pre-existing discontinuities, but did not consider hydraulic potential drop between the two interface walls [79]. Segura and Carol introduced the transversal conductivity in double-noded zero-thickness elements to account for the exchange of fluid between the discontinuity and the porous media [80].
Regarding the mechanical behaviour of fractures, two different approaches are typically used: the linear elastic fracture mechanics (LEFM), and the non-linear fracture mechanics (NLFM). LEFM was first proposed to solve fracture propagation problems by means of remeshing without considering a fracture process zone (FPZ) before the crack tip. This approach is applicable in large structures where the size of the FPZ is negligible. However, for quasi-brittle analyses, the consideration of a non-linear fracture process zone where the energy is dissipated before it completely fails was found to be essential. In those cases NLFM is usually applied and a softening law relates the cohesive stress to the crack opening in the FPZ. The first technique based on the cohesive fracture model was originally introduced by Barenblatt for brittle materials [81,82] and by Dugdale for plastic materials [83]. Hillerborg et al. developed the first fictitious crack model for Mode I fracture [84]. It was extended later for the mixed mode fracture, from which Camacho and Ortiz proposed a suitable fracture criterion that is widely used in the literature [85].
One of the most important parts in the modelling of fracture propagation is the criterion for determining the direction of the crack growth. Some methodologies are based on the local evaluation of the stress field at the crack tip, such as the maximum circumferential stress [86] and the maximum principal stress criteria [133,92]. Others measure the energy distribution at the fractured zone, e.g. the minimum strain energy density criterion [87] or the maximum strain energy release rate criterion [88]. Finally, some authors have developed crack growth criteria based on continuum damage mechanics [89] and, more recently, combined with level sets [94,95].
In order to minimize the mesh-induced directional bias, in this work we use the non-local damage model of Chapter 5 in combination with a discrete crack approach, in which discontinuities are represented by quasi-zero-thickness interface elements. A special utility allows us inserting new interface elements according to the computed damage map, finishing with a remeshing of the model to ensure a conformal spatial discretization. The low permeability and high compressibility of fluid-driven fracture propagation problems makes the pressure field oscillate spuriously if equal order interpolation elements are used without stabilization. Here we solve the solid-pore fluid interaction problem with the FIC-FEM stabilized formulation presented in Chapter 4.
The present chapter is organized as follows. First, the formulation of the developed quasi-zero-thickness interface elements is detailed, explaining the mechanical behaviour of the fracture and the model governing the fluid flowing in it. After that, we present the proposed fracture propagation technique combining the non-local damage model with the interface elements. Finally, two plane-strain examples are solved to test the accuracy of the crack propagation methodology, and one additional case is included to show the performance of the generalized 3D formulation.
4.2 Quasi-zero-thickness interface elements
Before going through the governing equations of the interface elements, let us clarify the “quasi-zero-thicknes” adjective used in this work.
Essentially, the quasi-zero-thickness interface elements follow the same idea as the double-noded zero-thickness interface elements of [79] or [80] but, in fact, they are surface elements in 2D and volume elements in 3D and so they can be defined using a width larger than zero if necessary.
This fact is particularly useful in case we need to define pre-existing joints with a certain opening, or when we want to capture the distribution of the fluid flow in the intersection between fractures (Figure 54).
|
| Figure 54: Fluid flow inside a crack with bifurcation. |
However, one can also define them with a zero thickness. In such case, the interface elements work as double lines in 2D or as a double surfaces in 3D, which is useful to represent very thin layers or closed faults that could eventually open (Figure 55).
|
| Figure 55: Consolidation problem with a vertical fault. |
Three different types of geometries for joint elements have been implemented: a 4-node quadrilateral interface element with two Lobatto integration points for bi-dimensional problems (Figure 56a), a 6-node wedge interface element with three Lobatto points and an 8-node hexahedral interface element with four Lobatto points for three-dimensional cases (Figures 56b and 56c). The 6-node prismatic interface element is used in problems where the porous domain is meshed with tetrahedra, whereas the hexahedral interface element is meant for problems meshed with hexahedra in the rest of the domain.
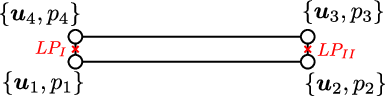
|
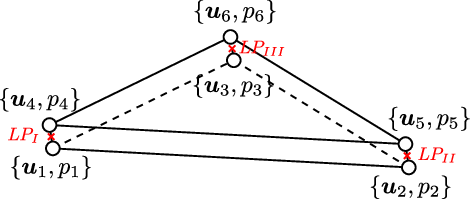
|
| (a) Four-node quadrilateral. | (b) Six-node triangular prism. |
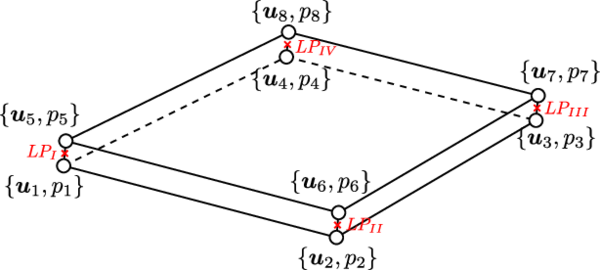
| |
| (c) Eight-node hexahedron. | |
| Figure 56: Quasi-zero-thickness interface elements. | |
It is important to note that the choice of Lobatto integration over Gauss integration responds to the spurious traction oscillations that may appear in joint elements with a stiff cohesive zone [73,134,135]. As it has been reported in the literature, a common strategy to overcome this issue is to make use of reduced Lobatto integration along the mid plane of the element [136,137,138].
Furthermore, it is essential to understand that the quantities of interest in the interface elements are in a different coordinate system from the one used to solve the standard elements in the porous domain.
Indeed, while for the porous domain we work in a unique coordinate system to obtain the global deformations of the structure, for each interface element we aim at obtaining the normal and tangential relative displacements at any point along the crack, and so we must work in the local coordinate system of the fracture. Moreover, as it is usually done for beams (in 2D) or shells (in 3D), this local system is located at the mid plane of the interface element, and it is necessary to distinguish the upper and lower faces of the joint to compute its relative displacements (Figure 57).
|
| Figure 57: Scheme of a generic hexahedral interface element. Global and local coordinate system. |
Let us first define the vector of relative displacements in a joint as the difference between the displacements at the upper and lower faces:
|
|
(4.1) |
The vector of nodal displacements in global axis is written as in Chapter 2. For a general 3D case it reads:
|
|
(4.2) |
where is the number of nodes of the element.
We also define the matrix of shape functions for the displacements at the interface element as:
|
|
(4.3) |
in which the shape functions are preceded by a negative sign for nodes located at the lower face of the joint and by a positive sign for nodes at the upper face.
Thereby, taking into account the definition in Eq (4.1), we can compute the vector of relative displacements at any point of the interface as:
|
|
(4.4) |
Also, in order to obtain the normal and tangential relative displacements, we need to transform the computed relative displacements from the global to the local coordinate system. To do so, we need to compute a rotation matrix from the direction cosines between the global (, , ) and local (, , ) coordinates (Figure 57). In essence:
|
|
(4.5) |
The transformation is written then as:
|
|
(4.6) |
In the following paragraphs, we present the governing equations of the implemented quasi-zero-thickness interface elements.
Similarly to the formulation presented for the continuum solid-pore fluid mixture, two equilibrium equations govern the behaviour of the interface elements. One equation deals with the mechanical behaviour of the crack, whereas the other equation describes the balance of fluid mass within the fracture.
It is important to stress here that the formulation of the interface elements is completely compatible with the displacement-pore pressure formulation presented in Chapter 2. Thereby, one can combine both type of elements in the same problem and solve them together in a unique coupled system of equations.
4.2.1 Mechanical behaviour of the fracture
The starting point is the strong form of the balance of momentum equation for the solid-fluid mixture (4.5) defined at the fracture plane. We discretize the relative displacements at the joint and integrate the equation by parts to obtain the following weak form:
|
|
(4.7) |
Equation (4.7) shows the same structure as Equation (4.24), but the resulting matrices and vectors are defined in the coordinate system in which the interface element is solved, i.e.:
|
|
(4.8) |
|
|
(4.9) |
where is the deformation matrix of the interface element, defined as:
|
|
(4.10) |
with joint width being the distance between the two faces of the interface (Figure 57). If the interface is closed, then we use a small value to avoid dividing by zero.
It is important to note that the terms in (4.7) are integrated over a quasi-zero-thickness interface element and thus:
|
|
(4.11) |
The effective stress vector in the fracture must be computed first in the local coordinate system and then transformed into the global one as
|
|
(4.12) |
Also, the vector comes from the definition of the local effective stresses in the joint:
|
|
(4.13) |
The constitutive law governing the mechanical behaviour of the interface element is a bilinear cohesive fracture model based on the fracture criteria of Camacho and Ortiz [85] and Song et al. [139] (see Figure 58).
The fundamental concept behind the cohesive fracture model is that, although the interface element represent discontinuities, the stress field can still be transferred through the crack sides of the cohesive zone (Figure 58a). From the micro-mechanical point of view, the cohesive zone is the local region ahead of the crack tip where the micro-voids or micro-cracks initiate, grow and coalesce with the main crack.
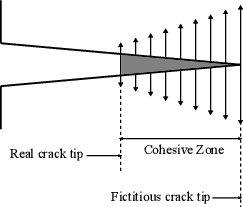
|
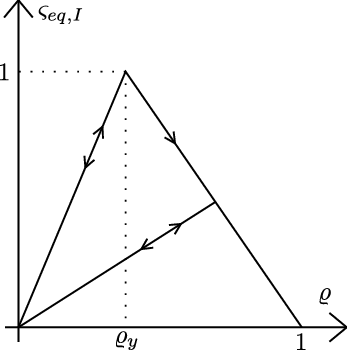
|
| (a) Cohesive fracture zone. | (b) Bilinear cohesive law. |
| Figure 58: Bilinear cohesive fracture model. | |
Figure 58b relates the normalized equivalent stress with the internal state variable and shows that the evolution of the cohesive zone is, in essence, an irreversible damage process.
The variable plays the same role as the internal scalar variable (Eq (5.13)) and thus it characterizes the maximum strain level reached in the previous history of the joint:
|
|
(4.14) |
Here is the damage threshold of the joint, a material parameter ranging from to that represents the value of strain at which damage starts.
The chosen model is suitable for mixed mode fracture and thus the evolution of the damage propagation in the cohesive zone must depend on the simultaneous activation of tangential and normal relative displacements. We define the equivalent strain of the interface as
|
|
(4.15) |
where is the critical relative displacement of the interface, i.e. it is the relative displacement at which the cohesive zone stops transmitting forces.
Expression (4.14) implies that , which shows that, in fact, the internal state variable can also be seen as the damage variable of the cohesive fracture zone.
Similarly as in Eq (4.15) we can define the normalized equivalent stress as:
|
|
(4.16) |
with being the yield stress at the cohesive zone, i.e. the stress at which the cohesive zone starts damaging. Each local component of the effective stress is computed as follows:
|
|
(4.17) |
The definition of the equivalent strain in (4.15) and the expressions of the stresses in (4.17) are valid only for cases in which the two faces of the joint are separated by a certain gap ().
However, in any interface it is possible that both faces push each other whenever they get in contact (Figure 59). In such cases, it is necessary to redefine some variables to properly model the mechanical behaviour of the joint.
|
|
| (a) Mesh in the original position. | (b) Vertical displacement after contact. |
| Figure 59: Contact between two beams connected by interface elements. | |
Thereby, when there is contact between the two opposite bodies of an interface () the tangential effective stresses in Eq (4.17) are defined as the shear strength of the Mohr-Coulomb criterion:
|
|
(4.18) |
|
|
(4.19) |
where is the friction coefficient, and and are the tangential cohesive stresses. They are computed as:
|
|
(4.20) |
|
|
(4.21) |
We note that the absolute values in Equations (4.18) and (4.19) are used to represent that, regardless of the sign of the stresses, the cohesion and the friction terms have always the same sign.
The definition of the normal component of the effective stress also changes during contact. It imitates the expression for the normal force between two neighbouring rigid particles in the Discrete Element Method (DEM) [140,141].
Let us assume that the interface is composed by linear springs with a stiffness per unit area of (Figure 60).
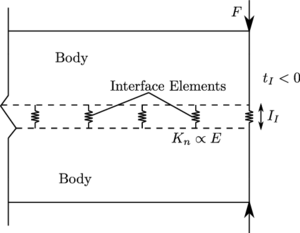
|
| Figure 60: Scheme of a contact with interface elements. |
The normal effective stress in contact is computed as:
|
|
(4.22) |
where is the indentation between the two faces of the joint.
Also, supposing that during contact , the equivalent strain of the interface is computed as:
|
|
(4.23) |
Finally, in order to compute the stiffness matrix of the interface element , one just needs to derive the term in Equation (4.7) with respect to the displacement vector :
|
|
(4.24) |
where is the tangent constitutive tensor of the interface in the global reference system. It is obtained from:
|
|
(4.25) |
The matrix in Eq (4.25) is the local tangent constitutive tensor per unit length, which can be obtained by deriving the stresses in the interface with respect to their relative displacements:
|
|
(4.26) |
Considering that the definition of the stresses in Eq (4.17) are used, the expressions defining the local tangent constitutive tensor of the interface (4.26) can be analytically derived. Taking into account that , we can distinguish two different scenarios:
- Elastic loading or unloading process ():
|
|
(4.27) |
- Loading process with growing damage ():
|
|
(4.28) |
4.2.2 Fluid flow in the fracture
The fluid flow in the fracture is modelled by the following mass balance equation:
|
|
(4.29) |
where
|
|
(4.30) |
|
|
(4.31) |
|
|
(4.32) |
The pressure at the joint is interpolated as we did in Chapter 2, i.e. . Thereby, the compressibility matrix (4.30) is virtually the same as the one used in standard elements (4.27), with the only difference being the domain of integration (4.11).
Matrix (4.31) introduces the enhanced permeability of the fractures in the porous medium. It is assumed that the longitudinal flow is coupled to the interface opening according to the so-called cubic law [142,143].
The name “cubic law” comes from the expression of the flow in the joint as a function of the cube of the local aperture . Such relation arises from the Reynolds equation [144]:
|
|
(4.33) |
Equation (4.33) originates from the lubrication theory, which was formulated for fluid flows in narrow and smooth parallel plates. The terms on the left hand side correspond to the flow induced by a pressure gradient or Poiseuille flow (Figure 61a), whereas the terms on the right hand side are given by the shear flow or Couette flow, generated by the movement of the upper face with a velocity (Figure 61).
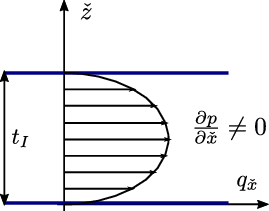
|
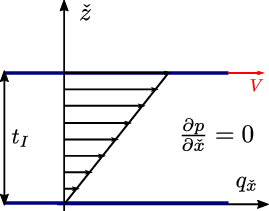
|
| (a) Poiseuille flow. | (b) Couette flow. |
| Figure 61: Velocity profiles between two smooth parallel plates. | |
The cubic law is naturally incorporated in the matrix of Equation (4.31) through the gradient of the matrix of shape functions and the intrinsic permeability matrix .
The matrix is defined as [145]:
|
|
(4.34) |
The two first rows in (4.34) allow computing the derivatives of the pressure with respect to the tangential directions of the joint and , whereas the third row approximates the derivative of the pressure in the normal direction by means of the pressure drop between the upper and lower faces of the interface:
|
|
(4.35) |
In essence, the computation of the derivatives of the shape functions with respect to the three coordinates of the space , and requires obtaining first the complete Jacobian matrix and then compute its inverse. The problem is that, when working with quasi-zero-thickness interface elements, the Jacobian matrix can be singular if the joint is nearly closed. Because of that, the tangential derivatives of the pressure are computed in the mid plane of the joint, i.e. a line in 2D and a triangle or a quadrilateral in 3D (Figure 62). The normal derivative is computed through finite differences as in (4.35).
|
| Figure 62: Natural coordinates at the mid plane of an hexahedral interface element. |
If we define and as the two natural coordinates at the mid plane of an interface element (Figure 62), we can obtain the expression for the derivative of the shape functions with respect to the local directions and by deriving the shape functions with respect to the natural coordinates and applying the chain rule. For every node we have:
|
|
(4.36) |
or equivalently:
|
|
(4.37) |
And so the derivatives of the shape functions with respect to the local tangential directions are computed as:
|
|
(4.38) |
The terms of the Jacobian matrix in (4.37) are obtained by rotating the derivatives of the global coordinates with respect to the natural coordinates:
|
|
(4.39) |
Regarding the intrinsic permeability matrix of the fracture (4.31), we make a distinction between the permeability in the tangential directions and the permeability in the normal one.
|
|
(4.40) |
where and are defined as [142]:
|
|
(4.41) |
The parameter represents the transversal permeability of the fracture, which is usually given a value similar to the intrinsic permeability of the porous domain.
Let us note that, although we write a for the exponential of the joint width in Eq (4.41), we actually have the expected of the cubic law if we take into account the additional appearing when integrating over the interface domain (4.11).
The anisotropic permeability introduced in the permeability matrix of the joint (4.40) can become a problem whenever we have intersection of different fractures. Indeed, an intersection between two cracks represents a void in the porous domain through which fluid can flow towards any direction. In this case there are not clear longitudinal and transversal directions for the flow because all directions can be preferential, and thus a variant of the conventional interface element with a modified intrinsic permeability matrix is introduced:
|
|
(4.42) |
Figure 63 exemplifies the effect that a set pre-defined interface elements introduce in a porous medium. Water is injected at a constant rate of through the left side of the horizontal crack, and after only , the displacement and pore pressure fields show noticeable jumps between each side of the joints (see Figures 63a, 63b, 63c and 63d).
Figure 63 also displays an application case of the modified intrinsic permeability matrix (4.42). The cyan square element in Figure 63e has the same structure as the rest of interface elements in pink, and just by using matrix , a proper flow distribution is captured at the intersection of each fracture (Figure 63f).
4.3 Fracture propagation approach
After introducing the quasi-zero-thickness interface element as a means to represent discontinuities in the porous domain, the current section is devoted to describe the proposed method for propagating cracks through the solid skeleton.
There are essentially two main strategies for solving fracture propagation problems by means of interface elements. The first technique has been widely used in the literature [146,147,139,148] and is based on the definition of an initial finite element mesh in which the joint elements are introduced at every possible location between standard finite elements (Figure 64).

|
| Figure 64: Finite element mesh with interface elements at all possible edges. |
Such an approach requires defining a number of interface elements much larger than the strictly necessary, which may alter the mechanical response of the solid skeleton and condition the permeability of the whole porous domain. In addition, when predicting the propagation of fractures, it is crucial that the type of the mesh does not affect the direction of propagation. With the mentioned method the influence of the mesh on the obtained crack path is virtually unavoidable.
The alternative method that can be encountered in the literature is based on the insertion of new interface elements where the strength of the porous domain reaches a threshold value [149,145,150]. This method provides a realistic approach for the simulation of dynamic crack propagation, but it requires remeshing the potential fracture zone after the insertion of every new interface element.
In this work, the fracture propagation strategy is based on the latter approach.
4.3.1 Crack path estimation
Essentially, we combine the integral-type non-local damage model introduced in Chapter 3 with the presented quasi-zero-thickness interface elements (Section 4.2). The fundamental idea is to use the information of the damaged points around the crack tip to determine, as accurately as possible, the direction of the fracture propagation.
The implemented method relies on two main assumptions:
- Any crack growth process must start from a predefined crack tip.
- Such propagation can either follow one direction, or bifurcate in two.
The first assumption implies that the implemented method can not model crack initiation. However, this is not major inconvenience because one can always use the damage model to determine the initial damage pattern, and then insert crack tips to model fracture propagation. The second assumption means that the presented approach allows capturing crack branching for any propagation process.
Next, we present the main steps configuring the crack path estimation technique.
Crack tip neighbours search
The information of the damaged elements around the crack tip is used to estimate the direction of the crack path. In order to do so, a neighbour search must be performed at the beginning of each time step.
Let be the propagation length, a material parameter determining the domain of influence of the fracture . For each fracture tip, we search the neighbouring Gauss points falling inside a circle (or a sphere in 3D) of radius (Figure 65a).
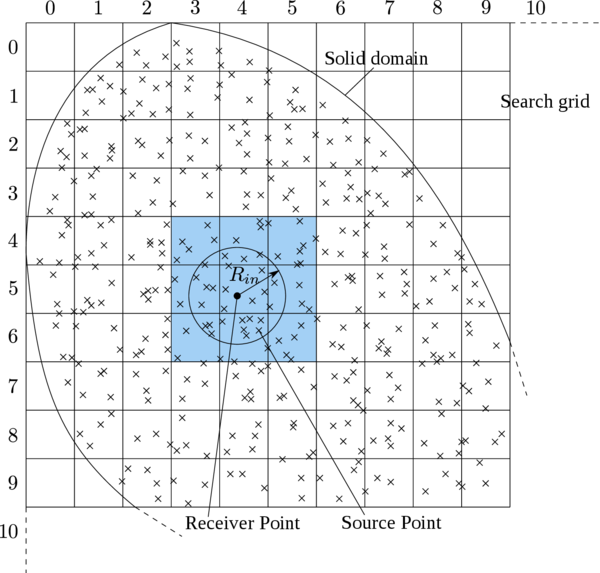
|
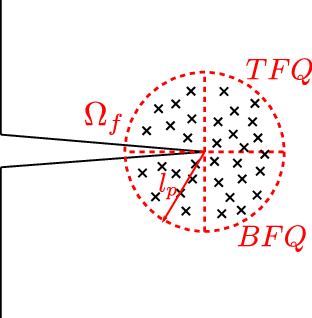
|
| (a) Grid-based search around the tip. | (b) Division of into quarters. |
| Figure 65: Crack tip neighbours search. | |
At this stage we also divide the domain of influence into quarters and distribute the neighbour points between the Top-Front-Quarter (TFQ) and the Bottom-Front-Quarter (BFQ) (Figure 65).
Crack growth
In order to determine the start of the crack growth, we estimate the damage at the crack tip and compare it with a prefixed threshold value, called propagation damage .
Damage at the crack tip is defined here as a non-local measure of the damage inside the region of influence of the fracture . This measure follows the same idea as the non-local average performed in Chapter 3 for the equivalent strain (Eq (3.56)). The damage at the tip is evaluated as:
|
|
(4.43) |
where is the coefficient with the product of the determinant of the Jacobian and the integration weight of Gauss point , and is the weight of non-local interaction between the tip and any other point , defined as in Eq (3.57), i.e.
|
|
(4.44) |
When the damage at the tip exceeds the threshold value () the crack is supposed to grow, but it is still necessary to discern the direction of propagation. First, we compute the potential location for the new crack tip by weighted averaging the coordinates of all the points in front of the crack tip.
Unlike the average performed in (4.43), the coordinates are weighted in terms of the damage of each Gauss point under consideration. In essence, the coordinate of the new crack tip is computed as:
|
|
(4.45) |
where is a modified version of the weighting function in (4.44) as
|
|
(4.46) |
Once the coordinates for the new crack tip have been found, it is necessary to check whether it is at a feasible location of the domain. Basically, the new crack tip must fulfil the following two conditions:
- It must fall inside an existing element in the mesh.
- The average damage at the element must be larger than a minimum value
The first condition is obviously necessary to avoid propagating the fracture outside the limits of the model, whereas the second condition prevents propagating the fracture towards undamaged regions.
In case one of the two conditions is not fulfilled, we recalculate two possible coordinates for the crack tip, distinguishing the elements of the top-front-quarter (TFQ) and the bottom-front-quarter (BFQ) as
|
|
(4.47) |
Of course, the two coordinates in (4.47) must also fulfil the aforementioned conditions to make sure they are feasible crack tips. In this regard, three different scenarios are possible. If the two new tips are valid, then the fracture bifurcates in two separate ways. If only one of the computed coordinates is feasible, then the fracture will propagate only towards that valid tip. Finally, if neither of the tips is valid, the fracture does not grow.
4.3.2 Interface elements insertion
After estimating direction of the propagating fracture, one can actually insert new interface elements into the model.
To do so, it is essential to make sure that the mesh after the insertion is conformal, and that the primary unknowns and internal variables are properly mapped from the old mesh to the new one.
Insertion and remeshing
For the insertion of new interface elements and regeneration of the model, we take advantage of the meshing capacities of the pre and post-processor GiD [151].
Thereby, not only GiD meshes the geometry at the beginning of the numerical simulation, but it is also GiD which generates the new spatial discretization every time we need to adapt the model with new interface elements.
The flexible design of GiD makes it possible to expand its basic features by means of customizable modules called “Problem-Types”. Such modules are quite versatile and allow, not only to create a graphical user interface (GUI) for defining the conditions and properties of the problem, but also to perform automatic GiD procedures by means of Tcl scripts.
Essentially, the computation of any problem starts with a Tcl procedure from the Problem-Type that writes the necessary input files with the conditions defined in the GUI:
- ProjectName.mdpa: lists the material properties, the nodes and the elements.
- ProjectParameters.json: saves the parameters for the project such as the dimension, the time step or the linear solver, and writes all the boundary conditions of the problem.
- FracturesData.json: registers all the pre-defined fracture tips in the model.
The “FracturesData.json” file must contain all the necessary information of the pre-existing crack tips in the model so as to perform the crack path estimation procedure already explained. This information includes the coordinates of all the points defining every crack tip.
In this regard, it is essential to have a clear image of how the crack tip is designed. In 2D any crack tip can be defined from just three points (Figure 66a), but in 3D this is not so straightforward. In the present work, the three-dimensional fracture tip is assumed to be conical, but it is approximated as a pyramid of quadrilateral base (Figure 66b).
|
|
| (a) 2D tip. | (b) 3D tip. |
| Figure 66: Scheme of the implemented crack tips. | |
The input files are read by the main Python script of the program, and then the first step of the problem is solved in a C++ strategy. Next, another method is called to check whether any of the pre-existing fractures propagates. If none of the crack tips progresses, the calculation simply jumps to the next time step, and in case one of the fractures propagates, the new crack tips are estimated following the procedure presented in Section 4.3.1, and the information of these tips is saved in another file called “PropagationData.tcl”.
Python calls then another Tcl procedure from the Problem-Type, which reads the “PropagationData.tcl” file, draws the new fractures in the geometry, and regenerates the model making sure that the new mesh is conformal.
In this work, a uniform mesh is generated for simplicity, but one could also apply the method proposed in [152] for adapting the mesh of the whole domain in a non-structured manner according to the stress state. The spatial discratization could be then finer around the cracks and coarser in those areas where no damage appears, thus making the computation cost more efficient.
After the mesh is generated, the input files are updated with the new configuration of fractures, and the problem continues in the next time step after a mapping of variables between the old and new meshes is performed.
In the end, the implemented fracture propagation technique is based on the combination of the modelling capabilities of GiD with the solving power of Kratos. It is schematically represented in Figure 67.
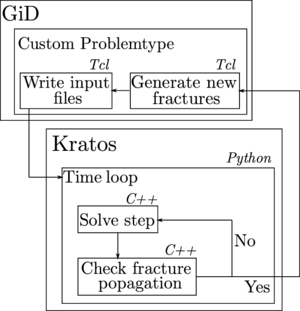
|
| Figure 67: Flow chart of the fracture propagation technique. |
Mapping of variables
After the new model is generated, a final step must be performed: the mapping of primary unknowns and internal variables between the old and new meshes.
In essence, if one aims at continuing the analysis from the current state, instead of restarting it from scratch every time the model is regenerated, it is necessary to apply some transfer algorithms so as not to lose the nodal unknowns, and the history variables at the Gauss points.
The mapping of the primary unknowns, i.e. nodal displacements and nodal pore pressure, is achieved by using the shape function projections. To do so, we first place each new node inside an old element, by means of another grid-based search, and then we interpolate the displacements of the old nodes at the position of the new one (Figure 68a).
On the other hand, the mapping of the internal state variables, i.e. and respectively governing the damage evolution of the standard elements and the interface elements, is done through a weighted spatial averaging similar to the one used in the non-local damage model (5.48). The difference is that, in this case, the source points are the integration points of the old mesh, and the receiver points are the integration points of the new mesh (Figure 68). Like before, an efficient grid-based search is performed in order to determine the Gauss points of the old mesh that fall inside the interaction radius of each new Gauss point.
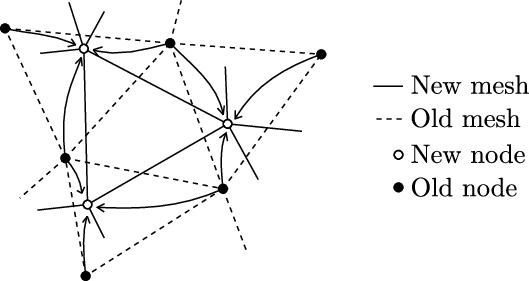
|
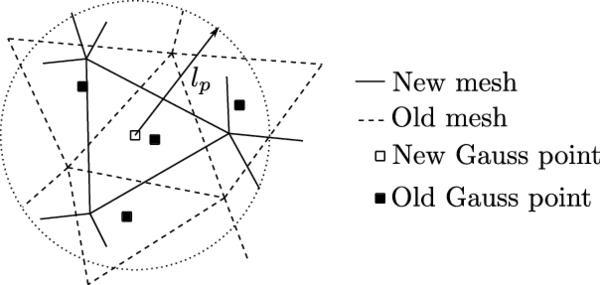
|
| (a) Nodal variables mapping. | (b) Internal state variables mapping. |
| Figure 68: Mapping of variables between meshes. | |
4.4 Examples
This section includes three test cases devoted to assess the performance of the presented fracture propagation strategy and the behaviour of the implemented interface elements. The first example is meant to validate the fracture propagation approach against an analytical solution, whereas the second and third cases are used to test the proposed technique under complex conditions and evaluate its strengths and limitations.
The three examples model fluid-driven fracture propagation problems in nearly undrained-incompressible porous media. FIC-stabilized elements of equal order interpolation for the displacements and the pore pressure have been used in that regard.
In all cases, the material of the porous domain is considered to undergo isotropic degradation by means of the same non-local damage model as the one used in Section 5.4.2. In essence, the equivalent strain form is defined as the von Mises model (3.31), and the damage follows the exponential law presented in (3.40).
The two first problems are analysed in a 2D framework under plane strain conditions, and the last test is solved with a 3D model. The porous medium is considered to have isotropic permeability and the effect of gravity is neglected.
4.4.1 Fluid-driven fracture propagation test
This example consists on a semi-cylindrical portion of soil of radius, laying on a rectangle high that has a notch of at the center. Water is injected at a constant rate of through an incipient crack tip of thick and long, which results in a volumetric flow of . The geometry and boundary conditions of the problem are shown in Figure 69.
The material of the porous domain is defined as a non-local damage model combining the von Mises equivalent strain form of Eq (3.31) with the exponential damage law in (3.40). The material parameters are summarized in Table 10.
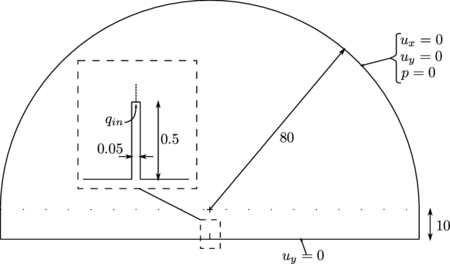
|
| Figure 69: Fluid-driven fracture propagation test. Geometry and boundary conditions. Dimensions in . |
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Solid density () | |
| Fluid density () | |
| Porosity () | |
| Solid bulk modulus () | |
| Fluid bulk modulus () | |
| Intrinsic permeability () | |
| Dynamic viscosity () | |
| Damage threshold () | |
| Compressive to tensile strength ratio () | |
| Residual strength () | |
| Softening slope () | |
| Characteristic length () |
On the other hand, the predefined crack tip is represented by quasi-zero-thickness interface elements with the properties in Table 11.
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Solid density () | |
| Fluid density () | |
| Porosity () | |
| Solid bulk modulus () | |
| Fluid bulk modulus () | |
| Transversal permeability () | |
| Dynamic viscosity () | |
| Damage threshold () | |
| Minimum joint width () | |
| Critical displacement () | |
| Yield stress () | |
| Friction coefficient () | |
| Propagation length () | |
| Propagation damage () |
As commented above, this problem is approached in a 2D configuration under plane-strain assumption. The porous domain is solved with the FIC-stabilized formulation, using 3-noded triangular elements with linear interpolation for the displacements and the pore pressure. The interface elements of the crack tip are 4-noded quadrilateral elements.
The main objective of this test is to validate the implemented propagation technique against an analytical solution obtained by Spence and Sharp [153] and replicated by Khoei et al. [145]. The fluid pressure along the crack mouth, the crack length and the crack width have been monitored through seconds of simulation. In order to assess the robustness of the numerical solution, a convergence analysis was performed in terms of the mesh size and the time step.
|
|
| (a) : elements. | (b) : elements. |
| |
| (c) : elements. | |
| Figure 70: Fluid-driven fracture propagation test. Initial meshes. | |
The influence of the mesh size was analysed by fixing the time step at and solving the problem for three different spatial discretizations (Figure 70). The first model was obtained from a characteristic element size of , with a resultant mesh of elements and nodes. The second mesh, with elements and nodes, resulted from an element size of . The third model was obtained after defining a characteristic element size of and lead to a mesh of elements and nodes.
In order to study the effect of the time step on the solution, we fixed the mesh size at and run the case for three different time steps: , and .
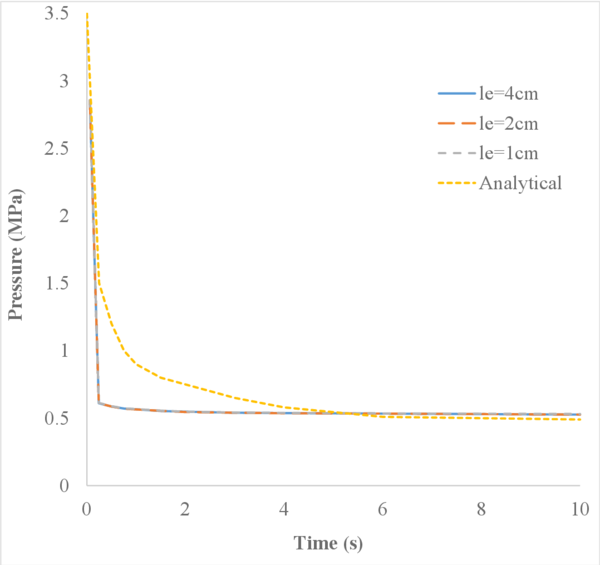
|
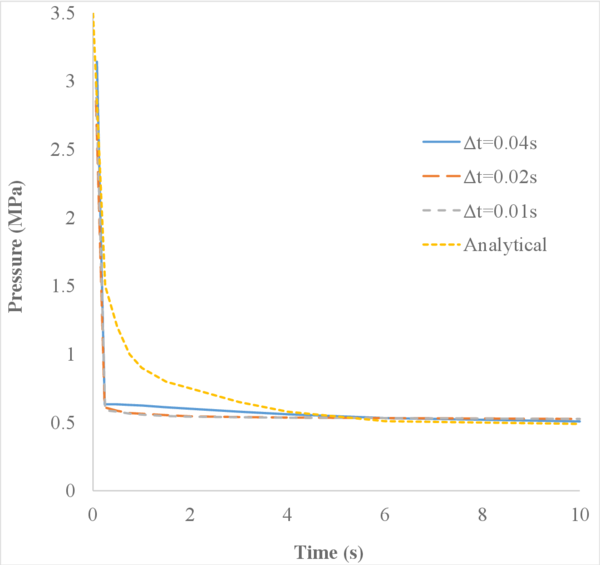
|
| (a) Pressure for different mesh sizes with . | (b) Pressure for different time steps with . |
| Figure 71: Fluid-driven fracture propagation test. Time evolution of the pressure. | |
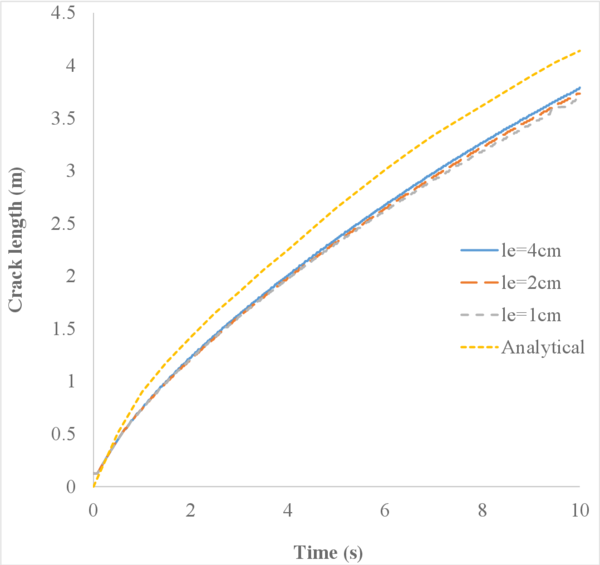
|
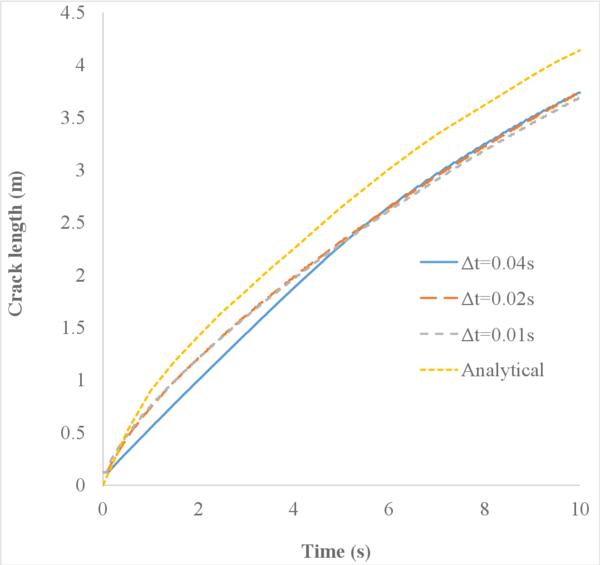
|
| (a) Crack length for different mesh sizes with . | (b) Crack length for different time steps with . |
| Figure 72: Fluid-driven fracture propagation test. Time evolution of the crack length. | |
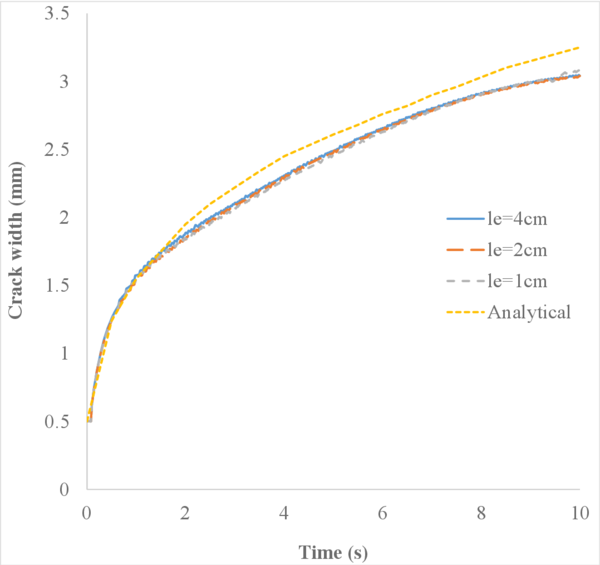
|
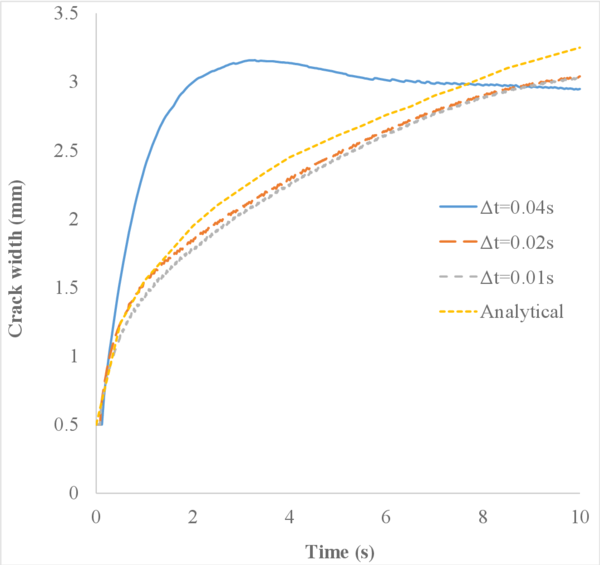
|
| (a) Crack width for different mesh sizes with . | (b) Crack width for different time steps with . |
| Figure 73: Fluid-driven fracture propagation test. Time evolution of the crack width. | |
Figures 71a, 72a and 73a show the pressure, crack length and crack width for different mesh size and . We highlight that the combination of an integral-type non-local damage model with the insertion of interface elements has no mesh dependence.
The results displayed in Figures 71b, 72b and 73b evidence that the time step is an important parameter in this kind of problems. Indeed, despite integrating the time variable with an unconditionally stable Newmark scheme, a large time step together with the material non-linearity of the problem lead to inaccurate results. Such effect is particularly remarkable in Figure 73b, mainly because of the greater sensitivity of the crack width variable (in the range of millimetres) with respect to the crack length and the pore pressure variables (in the range of meters and mega pascals, respectively). In any case, using a small enough time step ensures obtaining consistent results. In this case good results have been obtained for .
Regarding the validation of the present test, a general good agreement is observed between the numerical and the analytical curves. Looking at Figures 71a and 71b, it is evident that the pressure at the mouth falls faster in the beginning of the numerical solutions. Such pressure drop is related to a sudden lost of integrity of the soil, and thus an accurate calibration of the parameters could smooth this effect. However, after a few seconds all curves converge to the same value of , which remains virtually constant due to the near undrained condition of the soil.
In Figures 72a and 72b, one observes that the computed crack grows at a slightly slower pace than the expected solution. This fact is clearly linked to the fast drop in the pressure already commented.
Finally, it is noticeable the similarity between the theoretical crack width and the numerical one. Except for the solution with , the slope of the curve and the maximum value reached in the rest of the cases are virtually identical to the analytical result.
4.4.2 Crack tracking test
This second test models a rectangular saturated porous domain of . The same notch and crack tip of the previous example have been horizontally placed at the left side of the model, with equivalent conditions at the inlet. In this case, an incursion of stronger soil is defined over apart from the initial crack tip, as represented in Figure 74.
| Figure 74: Crack tracking test. Geometry and boundary conditions. Dimensions in . |
The porous media and the crack tip are characterized with the same properties of the previous example (see Tables 10 and 11). The only difference is in the material incursion in front of the crack tip, the properties of which are listed in Table 12.
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Solid density () | |
| Fluid density () | |
| Porosity () | |
| Solid bulk modulus () | |
| Fluid bulk modulus () | |
| Intrinsic permeability () | |
| Dynamic viscosity () | |
| Damage threshold () | |
| Compressive to tensile strength ratio () | |
| Residual strength () | |
| Softening slope () | |
| Characteristic length () |
Again, this case is solved as a plane-strain 2D problem, and FIC-stabilized 3-noded triangles are used to circumvent the violation of Babuska-Brezzi conditions due to the impermeability of the porous medium. Also, the characteristic element size chosen is and .
The main purpose of the present test is to verify the “crack-tracking” capabilities of the implemented approach against anisotropic porous domains. In order to do so, three different “obstacles” have been placed in front of the propagating crack (Figure 75). The first two incursions (Figures 75a and 75b) are meant to simulate branching situations for different bifurcation angles, whereas the third obstacle introduces an irregular preferential path for the advancing fracture (Figure 75c).
|
|
| (a) Obstacle 1: -- isosceles triangle. | (b) Obstacle 2: -- isosceles triangle. |
| |
| (c) Obstacle 3: moon shape incursions. | |
| Figure 75: Crack tracking test. Material incursions in front of the crack tip. | |
The three crack paths, after seconds of simulation, are displayed in Figure 76. The fluid pressure and the damage of the porous domain are also illustrated to give a deeper insight into the current analysis.
Focusing first on Figures 76a, 76c and 76e, it is evident that the proposed technique captures the anisotropy introduced in the model, and the inserted interface elements properly represent the enhanced permeability of the porous medium. Moreover, the smooth contour lines of the pressure field show that the FIC-stabilized 3-noded triangles have an excellent behaviour near the undrained-incompressible conditions. It is interesting to note that the maximum water pressure is different for each case, with the highest value in Figure 76e and the lowest in Figure 76a. Although the difference is subtle, one may infer that the pressure dissipates faster in a branching case with a wider angle of bifurcation.
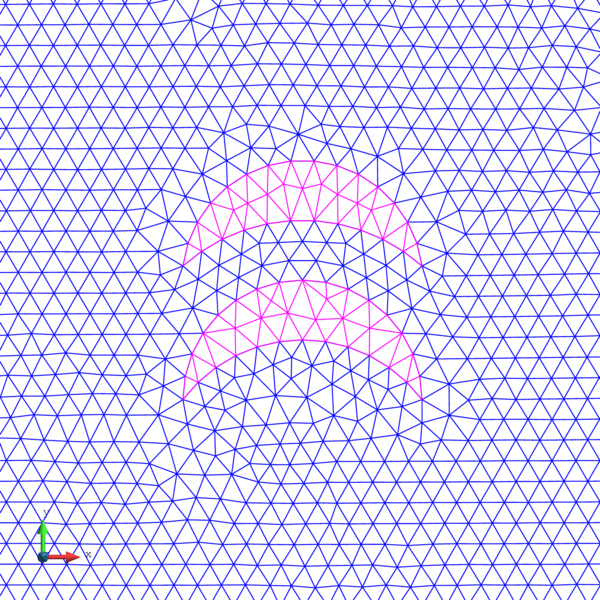
|
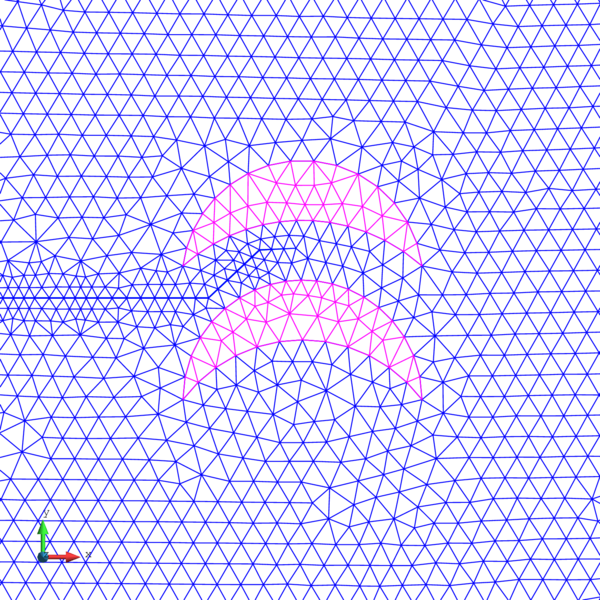
|
| (a) Mesh at initial stage. | (b) Mesh at intermediate stage. |
| |
| (c) Mesh at advanced stage. | |
| Figure 77: Crack tracking test. Fracture passing between moon shape incursions. | |
In Figures 76b, 76d and 76f, the non-locality of the damage model is clearly visible in the width of the damage mark around the crack. Indeed, with a characteristic length of , the crack tip is surrounded by a damaged area with a diameter of over . Such diffusive damage pattern is what leads the crack through the right path, avoiding mesh-induced directional bias. Thereby, in the first two cases (Figures 76b and 76d) the fracture eventually runs into the stronger incursion and, given the low degradation of the material in front of the tip, the crack bifurcates with an angle that depends on the shape of the incursion. For the moon shape obstacles (Figure 76f), the undamaged areas on both sides of the tip let the crack no choice but to pass between the two obstacles. A detailed view of the mesh is shown in Figure 77.
4.4.3 Parallel fracture propagation test
This last example consists on a block of soil with two parallel crack tips separated by a distance . Water is injected at a constant rate of through each one of the cracks of thick and long, giving a total volumetric flow of around . A scheme of the geometry and the boundary conditions is represented in Figure 78.
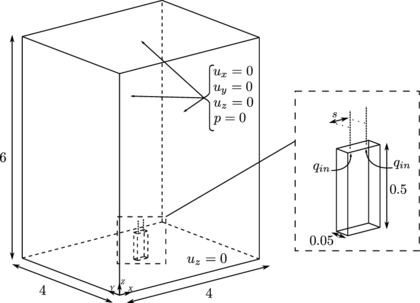
|
| Figure 78: Parallel fracture propagation test. Geometry and boundary conditions. Dimensions in . |
In this case a softer material has been defined in order to reduce the maximum pore pressure and minimize the computational cost. The material properties of the porous domain and the two incipient cracks are given in Tables 13 and 14, respectively.
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Solid density () | |
| Fluid density () | |
| Porosity () | |
| Solid bulk modulus () | |
| Fluid bulk modulus () | |
| Intrinsic permeability () | |
| Dynamic viscosity () | |
| Damage threshold () | |
| Compressive to tensile strength ratio () | |
| Residual strength () | |
| Softening slope () | |
| Characteristic length () |
| Property | Value |
| Young's modulus () | |
| Poisson's ratio () | |
| Solid density () | |
| Fluid density () | |
| Porosity () | |
| Solid bulk modulus () | |
| Fluid bulk modulus () | |
| Transversal permeability () | |
| Dynamic viscosity () | |
| Damage threshold () | |
| Minimum joint width () | |
| Critical displacement () | |
| Yield stress () | |
| Friction coefficient () | |
| Propagation length () | |
| Propagation damage () |
Since the problem is approached in a 3D framework, the porous domain is represented by stabilized 4-noded tetrahedra with linear interpolation for the displacements and the pore pressure. The two crack tips are meshed with six-node wedge interface elements. In this case, the characteristic element size and the time step are larger than in previous examples with and .
Basically, the purpose of this problem is to analyse the influence of the distance between neighbouring cracks in a parallel fracture propagation case. Thereby, in order to give a more realistic insight and account for the Poisson's effect in the transversal deformation of the soil, a 3D configuration has been chosen for this last test.
As reported in [154], to ensure the efficiency of a hydraulic fracturing process, the spacing between parallel cracks should be of the order of . Here three different spacings have been studied: , and , and the crack length in each case has been measured after seconds of simulation. Table 15 summarizes the results along with the obtained crack growth velocity.
The values in Table 15 show that the closer the initial cracks are defined, the faster they propagate, as expected. However, the relation between the spacing and the crack growth velocity seems to be not linear, which also makes sense if one takes into account the material non-linearity of this problem.
| Spacing | Crack Length at | Crack growth velocity |
In order to properly appreciate the previous results, the contour lines of the pressure field and the damage variable are represented on two orthogonal planes cutting both cracks (Figure 79).
Looking first at the pressure field in Figures 79a, 79c and 79e, it is quite clear that a closer spacing between cracks makes the pore pressure grow, and consequently the propagation velocity also increases. Also, to understand the interaction between two parallel cracks, it is useful to observe Figures 79b, 79d and 79f. Indeed, the non-local damage model generates a diffusive damage mark around the cracks that extends up to the radius of influence . In Figures 79b and 79d, in which the spacing is smaller than twice the characteristic length of the material, the damage patterns of the cracks seem to overlap each other. In Figure 79f, with , the two damage marks are almost independent and hence the velocity of propagation noticeably decreases.
This example shows that the characteristic length of the non-local damage model is not only a mathematical parameter used to regularize the strain localization problem, but it actually has a physical meaning.
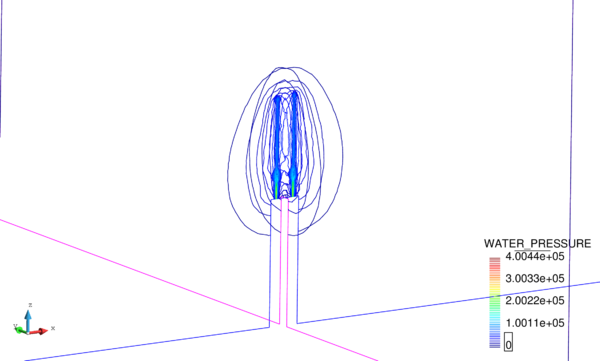
|
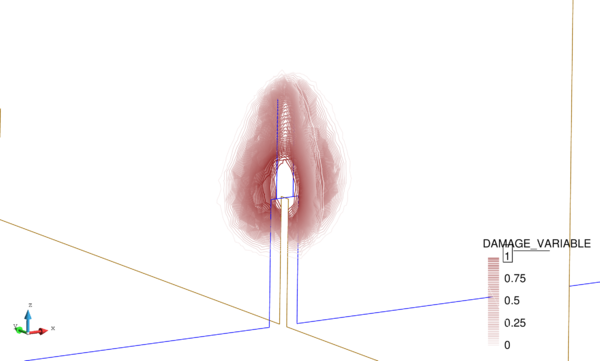
|
| (a) Pressure with . | (b) Damage with . |
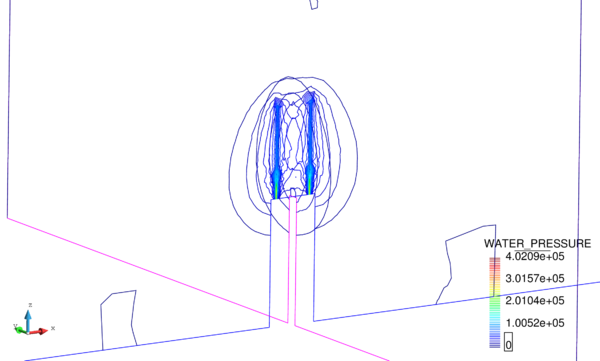
|
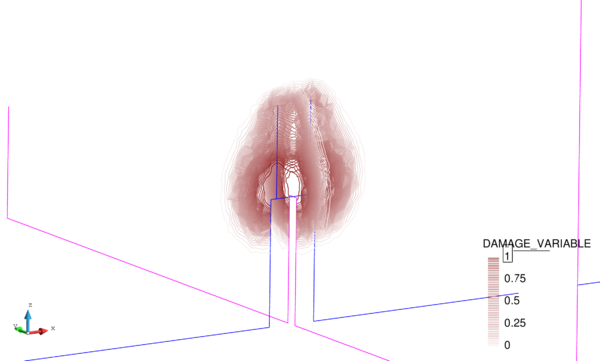
|
| (c) Pressure with . | (d) Damage with . |
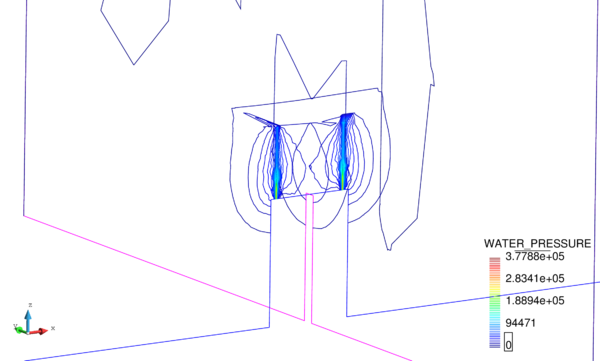
|
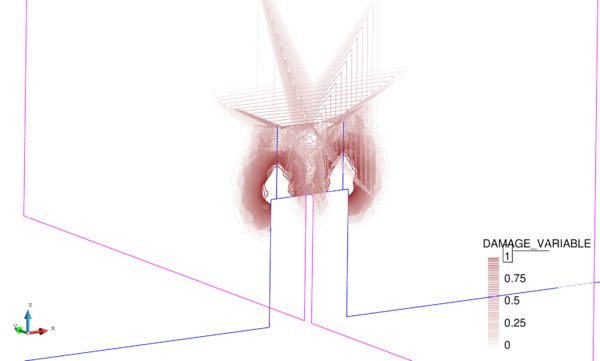
|
| (e) Pressure with . | (f) Damage with with . |
| Figure 79: Parallel fracture propagation test. Pore pressure and damage at . | |
5 Conclusions and Future Lines of Research
5.1 Conclusions and contributions
The main objective of this monograph was the derivation of a robust Finite Element formulation for the solution of solid-pore fluid coupled problems with multi-fracture propagation. The following conclusions can be highlighted.
A displacement-pore pressure FEM formulation for solving coupled solid-pore fluid interaction problems has been successfully implemented for 2D and 3D analysis, and stabilized by means of the Finite Increment Calculus method (FIC). In this formulation, a unique mesh represents a porous medium composed by two phases: a solid skeleton and a fluid phase. The interaction between both components is governed by means of the coupling of two equations: the balance of momentum for the mixture solid-fluid and the mass balance for the pore fluid.
The derived FIC-FEM formulation represents the first application of the second order FIC mass balance equation in space to the stabilization of a poromechanics problem. In the presented approach, the balance of momentum equation is unaltered and only the continuity equation is modified with the stabilization terms.
Comparing this work with other classical stabilization methods, we notice that the FIC stabilization allows solving the problem in a fully coupled manner without relying on time stepping algorithms. It also avoids the calibration of the stabilization parameter, which simply depends on the characteristic element size.
The presented FIC-based approach does not require additional basis functions or element level condensation, but relies on higher-order derivatives to obtain the terms that ensure the consistency of the residual-based procedure.
As presented in the Examples' section in Chapter 2, the FIC-FEM formulation has been used to solve an elastic saturated soil column subjected to surface loading in a 2D problem under plane strain conditions. It has proven to avoid arbitrary oscillations along the column, and it has shown consistent results for both transient and cyclic loading cases, despite modifying the material compressibility and permeability.
Additionally, the FIC-FEM element has been tested in a 3D problem of an elastic saturated soil foundation. The effect of the spatial discretization on the solution has been addressed in this case. This problem has shown that the residual-based character of the FIC-stabilization favours that the numerical solution converges to the expected solution as the mesh is refined. Moreover, when relaxing the undrained-incompressible conditions, the FIC stabilization does not alter negatively the response obtained in the original non-stabilized formulation, and yields an accurate solution.
Since the proposed fracture propagation technique relies on continuum damage mechanics for the estimation of the crack path, Chapter 3 focuses on the seek of a robust damage model for the analysis of the degradation and failure of quasi-brittle materials.
We saw that a local damage model, although partially regularized with an energy based adjustment, shows mesh sensitiveness and presents severe mesh-induced directional bias, which makes it virtually unusable for tracking the crack path.
However, we must also notice that for certain cases and if carefully calibrated, a partially regularized local damage model can become a useful tool to obtain a first estimation of the damage pattern with a very low computational cost.
Of course, in solid-pore fluid coupled problems, where cracks represent preferential paths for the fluid flow and have a critical influence on the global permeability of the porous medium, it is essential to work with a fully regularized damage model. In this regard, the implemented integral-type non-local damage model has shown a robust behaviour for different spatial discretizations, avoiding pathological mesh sensitivity and mesh-induced directional bias.
An important aspect to note about the non-local approach is that the neighbour search and the averaging performed to account for the non-local interaction, considerably increase the computational cost of the solution, as compared to the classical local approach, and also modify the traditional assembly process of the global tangent stiffness matrix.
Both damage models have been tested in a 2D three-point bending test under plane stress assumption. Excluding the mesh-dependent local model, the non-local damage model based on the Mazars definition of the equivalent strain has proved to properly capture the peak load of the Force-Deflection curve for all meshes. Nonetheless, the post-peak branch of the numerical solution is more brittle than in the reference solution, and even shows a certain snap-back behaviour. The use of an advancing technique based on the control of displacements should smooth the behaviour in the post-peak region and improve the convergence of the solution.
Furthermore, a plane stress four-point shear test has been solved to check that the non-local damage model accurately reproduces the Force-CMSD curve and converges to the expected solution as the mesh is refined. This last test also showed that the non-local form of the modified von Mises definition of the equivalent strain, along with the exponential damage evolution law actually represent an effective combination given its remarkable robustness and convergence, in spite of its simplicity, specially when compared to the tested alternatives.
Chapter 4 presents the quasi-zero-thickness interface elements which, combined with the coupled formulation of Chapter 2 and the non-local damage model of Chapter 3, are used to develop a methodology for the 2D and 3D analysis of fracture propagation problems in saturated porous media.
The quasi-zero-thickness interface elements are governed by the same two equations presented in Chapter 2, i.e. the balance of momentum for the mixture solid-fluid and the mass balance for the pore fluid, but they are conveniently adapted to account for the special behaviour of the joints. This fact is particularly useful as it allows combining the standard elements with the interface elements in the same model and solve a unique coupled system of equations.
The formulation of the interface elements, distinguishing its upper and lower faces, has shown to adequately introduce jumps in the displacement field, and capture the enhanced permeability of the porous medium.
Three examples involving crack propagation have been analysed with different objectives. In the 2D fluid-driven fracture propagation test, the combination of the non-local damage model with the automatic insertion of interface elements has shown to be robust and effective. It has been validated against analytical values of the pressure at the crack mouth, the crack length, and the crack width with promising results.
Furthermore, as seen in Chapter 3, the integral-type non-local damage model fully regularized the boundary value problem and thus the curves of the monitored variables during crack propagation were virtually unaffected by the changes in the spatial discretization.
On the other hand, the time step appeared as an important parameter in problems involving material non-linearities and fluid diffusion. A small enough value must be used to ensure accurate results.
In the crack tracking test, we checked that the search of damaged points around the crack tip, combined with the non-local damage model, is a robust tool for predicting the crack path in anisotropic media, including the possibility of branching when the proper conditions are met.
The FIC-stabilized elements of equal order interpolation for the displacements and the pore pressure have also been proved to prevented the blocking of the pressure field during crack propagation.
Finally, the proposed technique has been positively tested in a 3D configuration for the analysis of the complex interaction between parallel cracks. As expected, the crack growth velocity is inversely proportional to the spacing between fractures.
Moreover, this example provided useful information to understand that the characteristic length of the non-local damage model is not only a numerical parameter, but it actually has a physical meaning, as it plays a crucial role in the interaction between parallel cracks.
We note that the memory usage in 3D fracture problems is remarkable due to the storage of the neighbours for the non-local damage model and thus the computational cost can be intense. The optimization of the code is therefore essential before the characteristic element size can be reduced.
In conclusion, the main contributions and innovative points of the present work can be summarized in the following list:
- Derivation of a stable FIC-FEM formulation for the solution of coupled solid-pore fluid interaction problems, which is based on the second order FIC mass balance equation in space.
- Evolution and assessment of a modular 2D and 3D integral-type non-local damage model, relying on a grid-based search of Gauss points neighbours.
- Generalization of the interface elements presented in [80,145], in the form of 2D and 3D quasi-zero-thickness interface elements, which are valid for the solution of the fully coupled solid-pore fluid problem.
- Development of a crack tracking technique based on the non-local evaluation of the region of influence around the crack tip.
- Implementation of a innovative utility for the automatic insertion of interface elements for fracture propagation and bifurcation using GiD.
5.2 Lines of future work
This monograph opens new perspectives to feasible and attractive future works. The most relevant are outlined below.
The porous domain has been considered as a two-phase medium composed by a solid skeleton and a fluid phase. In reality, though, this is not usually the case and the porous space can be partially filled by a fluid and partially filled by a gas. In this regard, the generalization to three-phase problems, such as those encountered in unsaturated soils or in oil-gas-soil interaction, are possible extensions of the numerical approach presented here.
Fredlund and Morgenstern considered an unsaturated soil as a four-phase system, with the air-water interface being the fourth phase, and proposed suitable stress state variables based on the equilibrium of forces for each phase [155]. A simple extension of two phase formulation to semi-saturated problems was proposed by Zienkiewicz et al. [156] based on the assumption that the air or gas present in the pores remains at atmospheric pressure. Alonso et al. [157] formulated a constitutive model within the framework of hardening plasticity for describing the stress-strain behaviour of partially saturated soils which are slightly expansive.
Further development has been done by Gawin and Schrefler [158], and Khoei et al. [159] for solving geotechnical problems of unsaturated soils. A more recent application of a solid-fluid-gas formulation is found in the underground storage of carbon dioxide [6].
Another possible expansion of the current formulation is the inclusion of the temperature field as a variable of the problem. A particularly interesting application is in the modelling of geothermal energy production where the solid-pore fluid-thermal formulation can be combined with interface elements in a displacement-pore pressure-temperature system of equations [7].
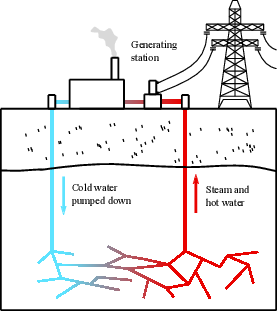
|
| Figure 80: Scheme of the geothermal energy production. |
Figure 80 schematically represents the process for the generation of geothermal energy: water is injected into deep formations and, because of the higher temperatures of the underground rocks, steam and hot water is returned to the surface, driving turbines and electricity generators.
Regarding future enhancements for the current code, we highlight two main topics: the generalization of the presented fracture propagation technique, and the optimization of the code for improving its speed and efficiency.
In the fracture propagation utility, many advances can be introduced. The most important are summarized below:
- Automatically generate interface elements from a cloud of damaged points, so as to avoid pre-defining initial crack tips.
- Introduce the technique presented in [152] to adapt the mesh according to the stress state after the insertion of new interface elements.
- Implement alternative crack designs for 3D fracture propagation.
- Add the possible scenario of two different cracks crossing each other.
In terms of code optimization, there is still room for cleaning the implemented procedures to make them more efficient. However, there is one aspect that should be addressed first: the parallel programming.
As commented in Chapter 1, the code has been implemented inside the Kratos programming framework based on C++ language. Kratos is prepared for parallel computing using OpenMP (Open Multiprocessing) and MPI (Message Passing Interface) (Figure 81). However, certain features of the code, such as the non-local damage model or the crack tracking utility, are currently designed to work only in OpenMP configuration, but not in MPI. In order to develop a computational technology that can compete with other commercial software, specially in large 3D problems, the extension of all the code to MPI can not be a secondary task.
|
| Figure 81: MPI domain partitioning in sections. |
Finally, this work is also related to alternative lines of research that, although differ from the main topic of the monograph, are supplied with features that derive from it and will be further developed in the near future.
One of these lines of work is the numerical analysis of concrete dams through the finite element method.
This work was involved in a convenient synergy between the ACOMBO project for the development of numerical tools for the thermo-mechanical analysis of arch dams, and Lorenzo Gracia's PhD thesis “Unified finite element modelling of the life cycle of concrete dams”.
The main objective of both the ACOMBO project and Lorenzo Gracia's work is the development of numerical tools that help analyse the behaviour of a concrete dam from the design period to the end of its service life. Such analysis is divided in three different stages: construction of the dam, in which the evolution of the heat of hydration is studied to prevent uncontrolled cracking, operation period, where the solution of a thermo-mechanical problem considering the temperature variations of the year is used to detect possible anomalies when compared to monitor devices, and extraordinary events, which include non-linear analysis for the study of damage initiation and crack propagation and dynamic analysis for the prevention of catastrophic failure under seismic loading.
The present monograph took also part in that synergy as the main contributor in the development of damage models and interface elements. Although the quasi-zero-thickness interface elements were initially implemented for modelling fractures in saturated porous media, the project required them for the definition of joints in the body of the dam or in the rock formation, and for the modelling of the contact between the dam and the rock foundation.
The ACOMBO project, which congregates Jesús Granell Engineering, Endesa, Universidad Politécnica de Madrid and CIMNE, gave a practical insight into the derived formulations in the monograph, and provided useful data to understand the applicability of the implemented numerical tools.
An example of this synergy is displayed in Figure 82, where the joints of Baserca's arch dam open because of the thermal contraction produced by the cold temperatures of winter.
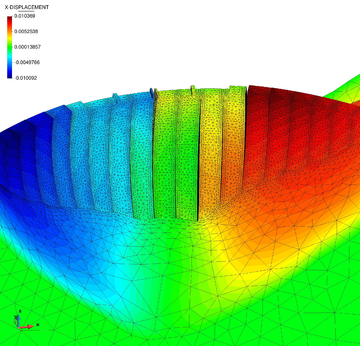
|
| Figure 82: Opening of the joints of Baserca's arch dam during winter. Deformation is exaggerated times. |
Related to the numerical analysis of dams, two publications have already been generated for the ICOLD Benchmark Workshop 2017. They are listed in Chapter 1.
Additionally, the implemented interface elements open another alternative line of work: the analysis of interlaminar cracks in laminated composite materials.
Essentially, the idea is to take advantage of the natural definition of the interface elements to perform a direct numerical simulation of composite delamination. This means that every layer of the composite is modelled as a solid material, and quasi-zero-thickness interface elements are placed in between them.
As it is widely known, 3D finite element analysis is the more appropriate tool to accurately model plates and shells of laminated composite material. Combined with cohesive interface elements it can effectively reproduce delamination in composite beams, as it is shown in Figure 83. However, for composites with hundreds of piles, such model becomes considerably expensive, specially if we take into account that interface elements introduce duplicated nodes at every layer.
|
| Figure 83: Multi-delamination of a 3-layered beam. |
In order to partially alleviate the computational cost, an innovative strategy for the deactivation and activation of interface elements has already been implemented.
In essence, all the interface elements between the layers of the laminate would be initially defined as inactive, so that no extra degrees of freedom are solved. As the beam is loaded, the interface elements with a stress value higher than a pre-fixed threshold would be dynamically activated along with its corresponding nodes. We remark that no remeshing is required here to activate the interface elements, because they are all defined at the beginning of the problem.
If this technique is combined with efficient MPI parallel computing, solving problems that had been prohibitively expensive in the past could be now feasible.
A publication regarding the analysis of composite delamination using the mentioned approach is currently in preparation.
Bibliography
[1] Terzaghi, Karl. (1943) "Theoretical soil mechanics". Wiley, New York
[2] Biot, Maurice A. (1941) "General theory of three-dimensional consolidation", Volume 12. Journal of applied physics 2 155–164
[3] Berkowitz, Brian and Bear, Jacob and Braester, Carol. (1988) "Continuum models for contaminant transport in fractured porous formations", Volume 24. Wiley Online Library. Water Resources Research 8 1225–1236
[4] Adachi, J and Siebrits, E and Peirce, A and Desroches, J. (2007) "Computer simulation of hydraulic fractures", Volume 44. Elsevier. International Journal of Rock Mechanics and Mining Sciences 5 739–757
[5] Carrier, Benoit and Granet, Sylvie. (2012) "Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model", Volume 79. Elsevier. Engineering fracture mechanics 312–328
[6] Jha, Birendra and Juanes, Ruben. (2014) "Coupled modeling of multiphase flow and fault poromechanics during geologic CO storage", Volume 63. Elsevier. Energy Procedia 3313–3329
[7] Zimmermann, Gunter and Reinicke, Andreas. (2010) "Hydraulic stimulation of a deep sandstone reservoir to develop an Enhanced Geothermal System: laboratory and field experiments", Volume 39. Elsevier. Geothermics 1 70–77
[8] Cowin, S C and Cardoso, L. (2013) "Interstitial flow in the hierarchical pore space architecture of bone tissue". ASCE. Poromechanics V 1203–1212
[9] Casares, Laura and Vincent, Romaric and Zalvidea, Dobryna and Campillo, Noelia and Navajas, Daniel and Arroyo, Marino and Trepat, Xavier. (2015) "Hydraulic fracture during epithelial stretching", Volume 14. Nature Research. Nature materials 3 343–351
[10] Lucantonio, Alessandro and Noselli, Giovanni and Trepat, Xavier and DeSimone, Antonio and Arroyo, Marino. (2015) "Hydraulic fracture and toughening of a brittle layer bonded to a hydrogel", Volume 115. APS. Physical review letters 18 188105
[11] Babuska, Ivo. (1973) "The finite element method with Lagrangian multipliers", Volume 20. Springer. Numerische Mathematik 3 179–192
[12] Brezzi, Franco. (1974) "On the existence, uniqueness and approximation of saddle-point problems arising from lagrangian multipliers", Volume 8. Revue francaise d'automatique, informatique, recherche opérationnelle. Analyse numérique 2 129–151
[13] . (2017) "Kratos Multiphysics"
[14] Biot, M A. (1955) "Theory of elasticity and consolidation for a porous anisotropic solid", Volume 26. AIP Publishing. Journal of applied physics 2 182–185
[15] Biot, Maurice A. (1956) "Theory of propagation of elastic waves in a fluid-saturated porous solid. I: Low-frequency range. II: Higher frequency range", Volume 28. Acoustical Society of America. the Journal of the Acoustical Society of America 2 168–191
[16] Ghaboussi, Jamshid and Wilson, Edward L. (1973) "Flow of compressible fluid in porous elastic media", Volume 5. Wiley Online Library. International Journal for Numerical Methods in Engineering 3 419–442
[17] Zienkiewicz, O C and Bettess, P. (1982) "Soils and other saturated media under transient, dynamic conditions: general formulation and the validity of various simplifying assumptions". Wiley, New York. Soil mechanics - transient and cyclic loads 1–16
[18] De Boer, R and Kowalski, S J. (1983) "A plasticity theory for fluid saturated porous media", Volume 21. International Journal of Engineering Science 11–16
[19] Zienkiewicz, O C. (1982) "Basic formulation of static and dynamic behaviour of soil and other porous media". Numerical methods in geomechanics. Springer 39–55
[20] Zienkiewicz, O C and Shiomi, T. (1984) "Dynamic behaviour of saturated porous media; The generalized Biot formulation and its numerical solution", Volume 8. Wiley Online Library. International journal for numerical and analytical methods in geomechanics 1 71–96
[21] Chorin, Alexandre Joel. (1967) "A numerical method for solving incompressible viscous flow problems", Volume 2. Elsevier. Journal of Computational Physics 1 12–26
[22] Zienkiewicz, Olgierd C and Codina, Ramon. (1995) "A general algorithm for compressible and incompressible flow. Part I. The split, characteristic-based scheme", Volume 20. Wiley Online Library. International Journal for Numerical Methods in Fluids 8-9 869–885
[23] Pastor, M and Zienkiewicz, O C and L. Xiaoqing, T Li and Huang, M. (1999) "Stabilized finite elements with equal order of interpolation for soil dynamics problems", Volume 6. Springer. Archives of Computational Methods in Engineering 1 3–33
[24] Huang, Maosong and Wu, Shiming and Zienkiewicz, O C. (2001) "Incompressible or nearly incompressible soil dynamic behaviour–a new staggered algorithm to circumvent restrictions of mixed formulation", Volume 21. Elsevier. Soil Dynamics and Earthquake Engineering 2 169–179
[25] Brezzi, F and Pitkäranta, J. (1984) "On the Stabilization of Finite Element Approximations of the Stokes Equations", Volume 10. Efficient Solutions of Elliptic Systems. Vieweg, Wiesbaden 11–19
[26] Hughes, Thomas J R and Franca, Leopoldo P and Balestra, Marc. (1986) "A new finite element formulation for computational fluid dynamics: V. Circumventing the Babuska-Brezzi condition: A stable Petrov-Galerkin formulation of the Stokes problem accommodating equal-order interpolations", Volume 59. Elsevier. Computer Methods in Applied Mechanics and Engineering 85–99
[27] Zienkiewicz, O C and Huang, M and Pastor, M. (1994) "Computational soil dynamics – A new algorithm for drained and undrained conditions". Computer Methods and Advances in Geomechanics. Balkema, Rotterdam 47–59
[28] Chiumenti, Michele and Valverde, Quino and De Saracibar, C Agelet and Cervera, Miguel. (2002) "A stabilized formulation for incompressible elasticity using linear displacement and pressure interpolations", Volume 191. Elsevier. Computer Methods in Applied Mechanics and Engineering 46 5253–5264
[29] White, Joshua A and Borja, Ronaldo I. (2008) "Stabilized low-order finite elements for coupled solid-deformation/fluid-diffusion and their application to fault zone transients", Volume 197. Elsevier. Computer Methods in Applied Mechanics and Engineering 49 4353–4366
[30] Sun, WaiChing and Ostien, Jakob T and Salinger, Andrew G. (2013) "A stabilized assumed deformation gradient finite element formulation for strongly coupled poromechanical simulations at finite strain", Volume 37. Wiley Online Library. International Journal for Numerical and Analytical Methods in Geomechanics 16 2755–2788
[31] Choo, Jinhyun and Borja, Ronaldo I. (2015) "Stabilized mixed finite elements for deformable porous media with double porosity", Volume 293. Elsevier. Computer Methods in Applied Mechanics and Engineering 131–154
[32] Sun, WaiChing. (2015) "A stabilized finite element formulation for monolithic thermo-hydro-mechanical simulations at finite strain", Volume 103. Wiley Online Library. International Journal for Numerical Methods in Engineering 11 798–839
[33] Oñate, Eugenio. (1998) "Derivation of stabilized equations for numerical solution of advective-diffusive transport and fluid flow problems", Volume 151. Elsevier. Computer Methods in Applied Mechanics and Engineering 1 233–265
[34] Oñate, Eugenio. (2000) "A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation", Volume 182. Elsevier. Computer Methods in Applied Mechanics and Engineering 3 355–370
[35] Oñate, Eugenio and Taylor, Robert L and Zienkiewicz, Olgierd C and Rojek, J. (2003) "A residual correction method based on finite calculus", Volume 20. MCB UP Ltd. Engineering Computations 5/6 629–658
[36] Oñate, Eugenio and Rojek, Jerzy and Taylor, Robert L and Zienkiewicz, Olgierd C. (2004) "Finite calculus formulation for incompressible solids using linear triangles and tetrahedra", Volume 59. Wiley Online Library. International Journal for Numerical Methods in Engineering 11 1473–1500
[37] Oñate, Eugenio and Idelsohn, Sergio R and Felippa, Carlos. (2011) "Consistent pressure Laplacian stabilization for incompressible continua via higher-order finite calculus", Volume 87. Wiley Online Library. International Journal for Numerical Methods in Engineering 1-5 171–195
[38] Oñate, Eugenio and Franci, Alessandro and Carbonell, Josep M. (2014) "Lagrangian formulation for finite element analysis of quasi-incompressible fluids with reduced mass losses", Volume 74. Wiley Online Library. International Journal for Numerical Methods in Fluids 10 699–731
[39] Belytschko, Ted and Black, Tom. (1999) "Elastic crack growth in finite elements with minimal remeshing", Volume 45. International Journal for Numerical Methods in Engineering 5 601–620
[40] Moës, Nicolas and Dolbow, John and Belytschko, Ted. (1999) "A finite element method for crack growth without remeshing", Volume 46. International Journal for Numerical Methods in Engineering 1 131–150
[41] Réthoré, Julien and De Borst, René and Abellan, Marie-Angele. (2007) "A two-scale approach for fluid flow in fractured porous media", Volume 71. Wiley Online Library. International Journal for Numerical Methods in Engineering 7 780–800
[42] Lecampion, Brice. (2009) "An extended finite element method for hydraulic fracture problems", Volume 25. John Wiley & Sons. Communications in Numerical Methods in Engineering 2 121–133
[43] Lin, Zhijia and Zhuang, Zhuo and You, Xiaochuan and Wang, Heng and Xu, Dandan. (2012) "Enriched goal-oriented error estimation applied to fracture mechanics problems solved by XFEM", Volume 25. Elsevier. Acta Mechanica Solida Sinica 4 393–403
[44] Zeng, Qinglei and Liu, Zhanli and Xu, Dandan and Wang, Heng and Zhuang, Zhuo. (2015) "Modeling arbitrary crack propagation in coupled shell/solid structures with X-FEM". Wiley Online Library. International Journal for Numerical Methods in Engineering
[45] Rashid, Y R. (1968) "Ultimate strength analysis of prestressed concrete pressure vessels", Volume 7. Elsevier. Nuclear Engineering and Design 4 334–344
[46] Lubliner, J and Oliver, J and Oller, Sand and Oñate, E. (1989) "A plastic-damage model for concrete", Volume 25. Elsevier. International Journal of Solids and Structures 3 299–326
[47] Camanho, P P and Bessa, M A and Catalanotti, G and Vogler, M and Rolfes, R. (2013) "Modeling the inelastic deformation and fracture of polymer composites – Part II: smeared crack model", Volume 59. Elsevier. Mechanics of Materials 36–49
[48] Heinrich, Christian and Waas, Anthony M. (2013) "Investigation of progressive damage and fracture in laminated composites using the smeared crack approach", Volume 35. CMC-Computers Mater Continua 155–181
[49] Hillerborg, A. (1985) "Numerical methods to simulate softening and fracture of concrete". Fracture mechanics of concrete: Structural application and numerical calculation. Springer 141–170
[50] Cervenka, Jan. (1994) "Discrete crack modeling in concrete structures". University of Colorado at Boulder
[51] Geiler, G and Netzker, C and Kaliske, M. (2010) "Discrete crack path prediction by an adaptive cohesive crack model", Volume 77. Elsevier. Engineering Fracture Mechanics 18 3541–3557
[52] Etse, Guillermo and Caggiano, Antonio and Vrech, Sonia. (2012) "Multiscale failure analysis of fiber reinforced concrete based on a discrete crack model", Volume 178. Springer. International journal of fracture 1-2 131–146
[53] Kachanov, L M. (1958) "On the time of fracture under conditions of creep". Izv. AN SSSR, Otd. Tekh. Nauk 8 26–35
[54] Rabotnov, Y N. (1963) "Damage from creep", Volume 2. Zhurn. Prikl. Mekh. Tekhn. Phys 113–123
[55] Lemaitre, J and Chaboche, J L "Mécanique des matériaux solides, 1985". Dunod, Paris
[56] Mazars, Jacky and Pijaudier-Cabot, Gilles. (1996) "From damage to fracture mechanics and conversely: a combined approach", Volume 33. Elsevier. International Journal of Solids and Structures 20 3327–3342
[57] Simo, J C and Ju, J W. (1987) "Strain-and stress-based continuum damage models-I. Formulation", Volume 23. Elsevier. International journal of solids and structures 7 821–840
[58] Oller, S and Oñate, E and Oliver, J and Lubliner, J. (1990) "Finite element nonlinear analysis of concrete structures using a “plastic-damage model”", Volume 35. Elsevier. Engineering Fracture Mechanics 1 219–231
[59] Oliver, J and Cervera, M and Oller, S and Lubliner, J. (1990) "Isotropic damage models and smeared crack analysis of concrete", Volume 2. Second international conference on computer aided analysis and design of concrete structures. Pineridge Press 945–958
[60] Oliver, J and Cervera, M and Oller, S and Lubliner, J. (1990) "A simple damage model for concrete, including long term effects", Volume 2. Second International Conference on Computer Aided Analysis And Design of Concrete Structures 945–958
[61] Cervera, M and Chiumenti, M and de Saracibar, C Agelet. (2004) "Shear band localization via local J 2 continuum damage mechanics", Volume 193. Elsevier. Computer Methods in Applied Mechanics and Engineering 9 849–880
[62] Cervera, M and Chiumenti, M. (2006) "Mesh objective tensile cracking via a local continuum damage model and a crack tracking technique", Volume 196. Elsevier. Computer Methods in Applied Mechanics and Engineering 1 304–320
[63] Chambon, René and Caillerie, Denis and Matsuchima, Takashi. (2001) "Plastic continuum with microstructure, local second gradient theories for geomaterials: localization studies", Volume 38. Elsevier. International Journal of Solids and Structures 46 8503–8527
[64] Mühlhaus, H B. (1986) "Shearband analysis in antigranulocytes material by cosserat-theory", Volume 56. SPRINGER VERLAG 175 FIFTH AVE, NEW YORK, NY 10010. Ingenieur Archiv 5 389–399
[65] Zbib, H M and Aifantis, E C. (1989) "A gradient-dependent flow theory of plasticity: application to metal and soil instabilities", Volume 42. American Society of Mechanical Engineers. Applied Mechanics Reviews 11S S295–S304
[66] Loret, Benjamin and Prevost, Jean H. (1990) "Dynamic strain localization in elasto-(visco-) plastic solids, Part 1. General formulation and one-dimensional examples", Volume 83. Elsevier. Computer Methods in Applied Mechanics and Engineering 3 247–273
[67] Jirásek, Milan and Rolshoven, Simon. (2003) "Comparison of integral-type nonlocal plasticity models for strain-softening materials", Volume 41. Elsevier. International Journal of Engineering Science 13 1553–1602
[68] Eringen, A Cemal and Edelen, DGB. (1972) "On nonlocal elasticity", Volume 10. Elsevier. International Journal of Engineering Science 3 233–248
[69] Eringen, A Cemal. (1981) "On nonlocal plasticity", Volume 19. Elsevier. International Journal of Engineering Science 12 1461–1474
[70] Pijaudier-Cabot, Gilles and Bazant, Zdenek P. (1987) "Nonlocal damage theory", Volume 113. American Society of Civil Engineers. Journal of Engineering Mechanics 10 1512–1533
[71] Ghaboussi, Jamshid and Wilson, Edward L and Isenberg, Jeremy. (1973) "Finite element for rock joints and interfaces", Volume 99. ASCE. Journal of the Soil Mechanics and Foundations Division 10 849–862
[72] Bfer, G. (1985) "An isoparametric joint/interface element for finite element analysis", Volume 21. Wiley Online Library. International journal for numerical methods in engineering 4 585–600
[73] Schellekens, J C J and De Borst, R. (1993) "On the numerical integration of interface elements", Volume 36. Wiley Online Library. International Journal for Numerical Methods in Engineering 1 43–66
[74] Ortiz, M and Suresh, S. (1993) "Statistical properties of residual stresses and intergranular fracture in ceramic materials", Volume 60. American Society of Mechanical Engineers. Journal of Applied Mechanics 1 77–84
[75] Xu, X P and Needleman, Alan. (1994) "Numerical simulations of fast crack growth in brittle solids", Volume 42. Elsevier. Journal of the Mechanics and Physics of Solids 9 1397–1434
[76] Goodman, Richard E and Taylor, Robert L and Brekke, Tor L. (1968) "A model for the mechanics of jointed rock". Journal of the Soil Mechanics and Foundations Division
[77] Andersson, Johan and Dverstorp, Björn. (1987) "Conditional simulations of fluid flow in three-dimensional networks of discrete fractures", Volume 23. Wiley Online Library. Water Resources Research 10 1876–1886
[78] Guiducci, Chiara and Pellegrino, Antonio and Radu, Jean-Pol and Collin, Frédéric and Charlier, Robert. (2002) "Numerical modeling of hydro-mechanical fracture behavior". Balkema. NUMOG VIII 293–299
[79] Ng, K L A and Small, J C. (1997) "Behavior of joints and interfaces subjected to water pressure", Volume 20. Elsevier. Computers and Geotechnics 1 71–93
[80] Segura, J M and Carol, I. (2004) "On zero-thickness interface elements for diffusion problems", Volume 28. Wiley Online Library. International journal for numerical and analytical methods in geomechanics 9 947–962
[81] Barenblatt, G I. (1959) "The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks", Volume 23. Elsevier. Journal of Applied Mathematics and Mechanics 3 622–636
[82] Barenblatt, Grigory Isaakovich. (1962) "The mathematical theory of equilibrium cracks in brittle fracture", Volume 7. Advances in Applied Mechanics 1 55–129
[83] Dugdale, D S. (1960) "Yielding of steel sheets containing slits", Volume 8. Elsevier. Journal of the Mechanics and Physics of Solids 2 100–104
[84] Hillerborg, Arne and Modéer, Mats and Petersson, P-E. (1976) "Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements", Volume 6. Elsevier. Cement and concrete research 6 773–781
[85] Camacho, Godofredo T and Ortiz, M. (1996) "Computational modelling of impact damage in brittle materials", Volume 33. Elsevier. International Journal of Solids and Structures 20 2899–2938
[86] Erdogan, Fazil and Sih, G C. (1963) "On the crack extension in plates under plane loading and transverse shear", Volume 85. American Society of Mechanical Engineers. Journal of Fluids Engineering 4 519–525
[87] Sih, George C. (1974) "Strain-energy-density factor applied to mixed mode crack problems", Volume 10. Springer. International Journal of Fracture 3 305–321
[88] Hussain, M A and Pu, S L and Underwood, J. (1974) "Strain Energy Release Rate for a Crack Under Combined Mode I and Mode II", Volume 560. Fracture Analysis 1
[89] Van Vroonhoven, J C W and De Borst, R. (1999) "Combination of fracture and damage mechanics for numerical failure analysis", Volume 36. Elsevier. International Journal of Solids and Structures 8 1169–1191
[90] Schrefler, Bernhard A and Secchi, Stefano and Simoni, Luciano. (2006) "On adaptive refinement techniques in multi-field problems including cohesive fracture", Volume 195. Elsevier. Computer Methods in Applied Mechanics and Engineering 4 444–461
[91] Secchi, Stefano and Simoni, Luciano and Schrefler, Bernhard A. (2007) "Mesh adaptation and transfer schemes for discrete fracture propagation in porous materials", Volume 31. International Journal for Numerical and Analytical Methods in Geomechanics 2 331
[92] Khoei, A R and Moslemi, H and Ardakany, K Majd and Barani, O R and Azadi, H. (2009) "Modeling of cohesive crack growth using an adaptive mesh refinement via the modified-SPR technique", Volume 159. Springer. International Journal of Fracture 1 21–41
[93] Espinosa, Horacio D and Zavattieri, Pablo D. (2003) "A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part I: Theory and numerical implementation", Volume 35. Elsevier. Mechanics of Materials 3 333–364
[94] Moës, Nicolas and Stolz, Claude and Bernard, P E and Chevaugeon, Nicolas. (2011) "A level set based model for damage growth: the thick level set approach", Volume 86. Wiley Online Library. International Journal for Numerical Methods in Engineering 3 358–380
[95] Cazes, Fabien and Moës, Nicolas. (2015) "Comparison of a phase-field model and of a thick level set model for brittle and quasi-brittle fracture", Volume 103. Wiley Online Library. International Journal for Numerical Methods in Engineering 2 114–143
[96] Coussy, Olivier. (2004) "Poromechanics". John Wiley & Sons
[97] Zienkiewicz, O C and Chang, C T and Bettess, P. (1980) "Drained, undrained, consolidating and dynamic behaviour assumptions in soils", Volume 30. Thomas Telford. Géotechnique 4 385–395
[98] Zienkiewicz, O C and Chan, A H C and Pastor, M and Paul, D K and Shiomi, T. (1990) "Static and dynamic behaviour of soils: a rational approach to quantitative solutions. I. Fully saturated problems", Volume 429. The Royal Society. Proceedings of the Royal Society of London 1877 285–309
[99] Pastor, Manuel and Quecedo, M and Zienkiewicz, Olgierd C. (1997) "A mixed displacement-pressure formulation for numerical analysis of plastic failure", Volume 62. Elsevier. Computers & Structures 1 13–23
[100] Zienkiewicz, O C and Rojek, J and Taylor, R L and Pastor, M. (1998) "Triangles and tetrahedra in explicit dynamic codes for solids", Volume 43. Wiley Online Library. International Journal for Numerical Methods in Engineering 3 565–583
[101] Masud, Arif and Hughes, Thomas J R. (2002) "A stabilized mixed finite element method for Darcy flow", Volume 191. Elsevier. Computer Methods in Applied Mechanics and Engineering 39 4341–4370
[102] Preisig, Matthias and Prévost, Jean H. (2011) "Stabilization procedures in coupled poromechanics problems: A critical assessment", Volume 35. Wiley Online Library. International Journal for Numerical and Analytical Methods in Geomechanics 11 1207–1225
[103] Biot, Maurice A and Willis, D G. (1957) "The elastic coefficients of the theory of consolidation", Volume 24. Journal of applied mechanics 594–601
[104] Galerkin, Boris Grigoryevich. (1915) "Series solution of some problems of elastic equilibrium of rods and plates", Volume 19. Vestnik Inzhenerov i Tekhnikov 7 897–908
[105] Biezeno, Cornelis Benjamin and Grammel, Richard. (1939) "Technische Dynamik". Springer-Verlag
[106] Newmark, Nathan M. (1959) "A method of computation for structural dynamics", Volume 85. ASCE. Journal of the Engineering Mechanics Division 3 67–94
[107] Daniel, W J T. (1980) "Modal methods in finite element fluid–structure eigenvalue problems", Volume 15. Wiley Online Library. International Journal for Numerical Methods in Engineering 8 1161–1175
[108] Zienkiewicz, O C and Qu, S and Taylor, R L and Nakazawa, S. (1986) "The patch test for mixed formulations", Volume 23. Wiley Online Library. International Journal for Numerical Methods in Engineering 10 1873–1883
[109] Zienkiewicz, Olgierd Cecil and Taylor, Robert Leroy and Zhu, J Z. (2005) "The Finite Element Method", Volume 1. Butterworth-Heinemann, 6th Edition
[110] Verruijt, Arnold. (2013) "Theory and problems of poroelasticity". Delft University of Technology
[111] Hult, J. (1974) "Creep in continua and structures". Topics in applied continuum mechanics. Springer 137–155
[112] Mazars, Jacky. (1986) "A description of micro-and macroscale damage of concrete structures", Volume 25. Elsevier. Engineering Fracture Mechanics 5 729–737
[113] Cervera, Miguel and Pela, Luca and Clemente, Roberto and Roca, Pere. (2010) "A crack-tracking technique for localized damage in quasi-brittle materials", Volume 77. Elsevier. Engineering Fracture Mechanics 13 2431–2450
[114] Bazant, Zdenek P and Belytschko, Ted B and Chang, Ta-Peng. (1984) "Continuum theory for strain-softening", Volume 110. American Society of Civil Engineers. Journal of Engineering Mechanics 12 1666–1692
[115] Martínez, Xavier. (2008) "Micro-mechanical simulation of composite materials using the serial/parallel mixing theory". Unpublished doctoral dissertation) Universidad Politécnica de Cataluña. Spain
[116] Mazars, Jacky. (1984) "Application de la mécanique de l'endommagement au comportement non linéaire et a la rupture du béton de structure"
[117] De Vree, J H P and Brekelmans, W A M and Van Gils, M A J. (1995) "Comparison of nonlocal approaches in continuum damage mechanics", Volume 55. Elsevier. Computers & Structures 4 581–588
[118] Pijaudier-Cabot, Gilles and Huerta, Antonio. (1991) "Finite element analysis of bifurcation in nonlocal strain softening solids", Volume 90. Elsevier. Computer methods in applied mechanics and engineering 1 905–919
[119] Tejchman, J and Wu, W. (1993) "Numerical study on patterning of shear bands in a Cosserat continuum", Volume 99. Springer. Acta Mechanica 1-4 61–74
[120] Mühlhaus, H B and Alfantis, E C. (1991) "A variational principle for gradient plasticity", Volume 28. Elsevier. International Journal of Solids and Structures 7 845–857
[121] Meftah, F and Reynouard, J M. (1998) "A multilayered mixed beam element in gradient plasticity for the analysis of localized failure modes", Volume 3. Wiley Online Library. Mechanics of Cohesive-frictional Materials 4 305–322
[122] Prevost, Jean H and Loret, Benjamin. (1990) "Dynamic strain localization in elasto-(visco-) plastic solids, part 2. Plane strain examples", Volume 83. Elsevier. Computer Methods in Applied Mechanics and Engineering 3 275–294
[123] Ehlers, W and Graf, T. (2003) "Adaptive computation of localization phenomena in geotechnical applications". Bifurcations and Instabilities in Geomechanics, Swets, Zeitlinger 247–262
[124] Bazant, Zdeněk P. (1986) "Mechanics of distributed cracking", Volume 39. American Society of Mechanical Engineers. Applied Mechanics Reviews 5 675–705
[125] Rodríguez-Ferran, Antonio and Morata, Irene and Huerta, Antonio. (2005) "A new damage model based on non-local displacements", Volume 29. Wiley Online Library. International Journal for Numerical and Analytical Methods in Geomechanics 5 473–493
[126] Bazant, Zdenek P and Oh, Byung H. (1983) "Crack band theory for fracture of concrete", Volume 16. Springer. Matériaux et construction 3 155–177
[127] Pietruszczak, S T and Mroz, Z. (1981) "Finite element analysis of deformation of strain-softening materials", Volume 17. Wiley Online Library. International Journal for Numerical Methods in Engineering 3 327–334
[128] Bazant, Zdenek P and Jirásek, Milan. (2002) "Nonlocal integral formulations of plasticity and damage: survey of progress", Volume 128. American Society of Civil Engineers. Journal of Engineering Mechanics 11 1119–1149
[129] Pérez-Foguet, Agustí and Rodríguez-Ferran, Antonio and Huerta, Antonio. (2000) "Numerical differentiation for local and global tangent operators in computational plasticity", Volume 189. Elsevier. Computer Methods in Applied Mechanics and Engineering 1 277–296
[130] Le Bellégo, Caroline. (2001) "Couplages chimie-mécanique dans les structures en béton attaquées par l'eau: Étude expérimentale et analyse numérique". LMT-ENS Cachan
[131] Rodríguez Ferran, Antonio and Arbós, Ivan and Huerta, Antonio and others. (2001) "Adaptive analysis based on error estimation for nonlocal damage models"
[132] Carpinteri, Alberto and Valente, Silvio and Ferrara, G and Melchiorrl, G. (1993) "Is mode II fracture energy a real material property?", Volume 48. Elsevier. Computers & structures 3 397–413
[133] Bouchard, Pierre Olivier and Bay, Francois and Chastel, Yvan. (2003) "Numerical modelling of crack propagation: automatic remeshing and comparison of different criteria", Volume 192. Elsevier. Computer methods in applied mechanics and engineering 35 3887–3908
[134] Kaliakin, V N and Li, J. (1995) "Insight into deficiencies associated with commonly used zero-thickness interface elements", Volume 17. Elsevier. Computers and Geotechnics 2 225–252
[135] Simone, A. (2004) "Partition of unity-based discontinuous elements for interface phenomena: computational issues", Volume 20. Wiley Online Library. Communications in Numerical Methods in Engineering 6 465–478
[136] Hashagen, Frank and De Borst, Rene. (1997) "An interface element for modelling the onset and growth of mixed-mode cracking in aluminium and fibre metal laminates", Volume 5. Structural Engineering and Mechanics 6 817–837
[137] De Borst, René. (2003) "Numerical aspects of cohesive-zone models", Volume 70. Elsevier. Engineering fracture mechanics 14 1743–1757
[138] Svenning, Erik. (2016) "A weak penalty formulation remedying traction oscillations in interface elements", Volume 310. Elsevier. Computer Methods in Applied Mechanics and Engineering 460–474
[139] Song, Seong Hyeok and Paulino, Glaucio H and Buttlar, William G. (2006) "A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material", Volume 73. Elsevier. Engineering Fracture Mechanics 18 2829–2848
[140] Oñate, Eugenio and Zárate, Francisco and Miquel, Juan and Santasusana, Miquel and Celigueta, Miguel Angel and Arrufat, Ferran and Gandikota, Raju and Valiullin, Khaydar and Ring, Lev. (2015) "A local constitutive model for the discrete element method. Application to geomaterials and concrete", Volume 2. Springer. Computational particle mechanics 2 139–160
[141] Santasusana, Miquel and Irazábal, Joaquín and Oñate, Eugenio and Carbonell, Josep Maria. (2016) "The Double Hierarchy Method. A parallel 3D contact method for the interaction of spherical particles with rigid FE boundaries using the DEM", Volume 3. Springer. Computational Particle Mechanics 3 407–428
[142] Snow, David Tunison. (1965) "A parallel plate model of fractured permeable media". University of California, Berkeley
[143] Witherspoon, Paul Adams and Wang, Joseph S Y and Iwai, K and Gale, John E. (1980) "Validity of Cubic Law for fluid flow in a deformable rock fracture", Volume 16. Wiley Online Library. Water Resources Research 6 1016–1024
[144] Reynolds, Osborne. (1886) "On the Theory of Lubrication and Its Application to Mr. Beauchamp Tower's Experiments, Including an Experimental Determination of the Viscosity of Olive Oil.", Volume 40. The Royal Society. Proceedings of the Royal Society of London 242-245 191–203
[145] Khoei, A R and Barani, O R and Mofid, M. (2011) "Modeling of dynamic cohesive fracture propagation in porous saturated media", Volume 35. Wiley Online Library. International Journal for Numerical and Analytical Methods in Geomechanics 10 1160–1184
[146] Carol, Ignacio and López, Carlos M and Roa, Olga. (2001) "Micromechanical analysis of quasi-brittle materials using fracture-based interface elements", Volume 52. Wiley Online Library. International Journal for Numerical Methods in Engineering 1-2 193–215
[147] Caballero, A and López, C M and Carol, I. (2006) "3D meso-structural analysis of concrete specimens under uniaxial tension", Volume 195. Elsevier. Computer Methods in Applied Mechanics and Engineering 52 7182–7195
[148] Caballero, A and Willam, K J and Carol, I. (2008) "Consistent tangent formulation for 3D interface modeling of cracking/fracture in quasi-brittle materials", Volume 197. Elsevier. Computer Methods in Applied Mechanics and Engineering 33 2804–2822
[149] Zhou, Fenghua and Molinari, Jean-Francois. (2004) "Dynamic crack propagation with cohesive elements: a methodology to address mesh dependency", Volume 59. Wiley Online Library. International Journal for Numerical Methods in Engineering 1 1–24
[150] Barani, O R and Khoei, A R and Mofid, M. (2011) "Modeling of cohesive crack growth in partially saturated porous media; a study on the permeability of cohesive fracture", Volume 167. Springer. International Journal of Fracture 1 15–31
[151] . (2017) "GiD The Personal Pre And Post Processor"
[152] de-Pouplana, Ignasi and Oñate, Eugenio. (2016) "Combination of a non-local damage model for quasi-brittle materials with a mesh-adaptive finite element technique", Volume 112. Elsevier. Finite Elements in Analysis and Design 26–39
[153] Spence, D A and Sharp, P. (1985) "Self-similar solutions for elastohydrodynamic cavity flow", Volume 400. The Royal Society. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 1819 289–313
[154] Chau, Viet T and Bazant, Zdenek P and Su, Yewang. (2016) "Growth model for large branched three-dimensional hydraulic crack system in gas or oil shale", Volume 374. The Royal Society. Phil. Trans. R. Soc. A 2078 20150418
[155] Fredlund, Delwyn G and Morgenstern, Norbert R. (1977) "Stress state variables for unsaturated soils", Volume 103. Journal of Geotechnical and Geoenvironmental Engineering ASCE 12919
[156] Zienkiewicz, O C and Xie, Y M and Schrefler, B A and Ledesma, A and Bicanic, N. (1990) "Static and dynamic behaviour of soils: a rational approach to quantitative solutions. II. Semi-saturated problems", Volume 429. The Royal Society. Proceedings of the Royal Society of London 1877 311–321
[157] Alonso, Eduardo E and Gens, Antonio and Josa, Alejandro. (1990) "A constitutive model for partially saturated soils", Volume 40. Thomas Telford. Géotechnique 3 405–430
[158] Gawin, Dariusz and Schrefler, Bernhard A. (1996) "Thermo-hydro-mechanical analysis of partially saturated porous materials", Volume 13. MCB UP Ltd. Engineering Computations 7 113–143
[159] Khoei, A R and Azami, A R and Haeri, S M. (2004) "Implementation of plasticity based models in dynamic analysis of earth and rockfill dams: A comparison of Pastor–Zienkiewicz and cap models", Volume 31. Elsevier. Computers and Geotechnics 385–410
Document information
Published on 01/01/2018
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?