Abstract
This paper attempts to present a method for differentiating between multi-attribute decision procedures and to identify some competent procedures for major decision problems, where a matrix of alternative-measure of effectiveness and a vector of weights for the latter are available. In this respect, several known multi-attribute analysis procedures are chosen, and the same procedures are exploited to evaluate themselves, based on some evaluation criteria. This is done from an engineering viewpoint and in the context of a transportation problem, using a real case light rail transit network choice problem for the City of Mashhad, and the results are presented. Two concepts have been proposed in this respect and used in this evaluation; peer evaluation and information evaluation, which are investigated in this paper.
In the evaluation of five multi-attribute decision procedures, based on nine criteria, and with the help of these procedures themselves in the context of the case under study, the results revealed that these procedures found Electre, Linear Assignment, Simple Additive Weighting, TOPSIS, and Minkowski Distance better than others, in the same order as given. This is backed by a wide range of sensitivity analyses. Nevertheless, despite specific conclusions made regarding the better decision procedures among those evaluated, this paper finds its contribution mainly in the approach to such evaluations and choices.
Keywords
Decision analysis ; Information valuation ; Light rail transit ; Multi-attribute procedures ; Multiple criteria analysis ; Peer evaluation
1. Introduction
Many multi-attribute analysis techniques have been presented in the past few decades to respond to the growing need for suitable decision-making procedures to apply to complex decision problems. The need for multi-attribute analysis stems from the fact that in most problems, several attributes, associated with different weights, are crucial for a just and appropriate decision to be made from among the alternatives. Furthermore, such analysis methods bring transparency to the decision making process. There are different approaches in deriving preferences among alternatives and making decisions in this regard. In addition, there are different kinds of information, with various degrees of confidence and certainty, in many situations.
To give an indication of the importance of, and the need for, multi-criteria decision making procedures, in practice, it may be interesting to mention the work of Behzadian et al. [1] , who administered a comprehensive literature review of methodologies and applications of a specific family of Multiple Criteria Decision Analysis (MCDA) procedures, namely; PROMETHEE (preference ranking organization method for enrichment evaluations), in a wide range of areas. They report covering 217 scholarly papers, in 100 journals, in at least 14 wide areas of decision making. On the other hand, Zopounidis and Doumpos [2] mention that an arsenal of different MCDA methods exist, each of which are suitable for a particular decision problem. The differences between various analysis methods lead to different decisions for the same problem [3] . This leads to an ambiguity in choosing a method of analysis for a decision problem, and is found important enough to identify it as a future direction in research and practice [2] . Triantaphyllou [4] describes identification of the best of the MCDA methods for a given problem as a most important and challenging one. This is found to be due to the indeterminacy of the quality of these methods. The fact that many researchers compare these methods in solving a particular problem (see the references given in Section 2 ) is strong evidence of the aforementioned ambiguity, in both theoretical as well as practical aspects of the matter.
Mela et al. [5] and Guitouni and Martel [6] , among others, emphasize the need for application of the MCDA methods to various fields, and believe that differences should be expected among these methods in various areas. The fact that problems differ themselves, and results for a specific problem may be hardly transferred to another, adds to the ambiguity mentioned above. Such problems add to the already complex real world implementation issues, some of which were analyzed by De Bruijn and Veeneman [7] for light rail projects in the Netherlands.
In this paper, some well-known multi-attribute decision procedures are chosen and evaluated for solving a major engineering decision problem. Engineering decision problems that concern this paper are problems in which a set of alternative projects, each with a vector of attribute values, compete to be selected. The attributes have known weights. The purpose of this paper is to create a platform for the evaluation of MCDA techniques for a particular problem, whose results could become beneficial in the long run. This platform is based on the peer review or evaluation concept, in which alternative techniques vote for the good one(s) among themselves. The purpose of this paper is neither to review such alternative techniques, nor to advocate a particular procedure for a decision problem per se. These are done extensively in the literature through many books (see, e.g. [8] , [9] , [10] and [11] ), and papers (see, e.g. [2] and [12] ).
Section 2 briefly reviews previous work relevant to this study. Section 3 sets the stage for evaluation of MCDA procedures, where the sub-sections perform as follows: First, the approach of this paper for the evaluation of MCDA methods and the concept behind them are introduced in Section 3.1 . Next, Section 3.2 introduces the set of selected multi-attribute decision-making procedures for illustration of the evaluation technique. Section 3.3 specifies the kind and context of the decision problem of concern in this study. Section 3.4 devises a set of evaluation criteria that we expect every good MCDA method should observe, and describes how to quantify these criteria for the case under study.
Section 4 evaluates the selected procedures for a base case, which is later complemented by a sensitivity analysis in Section 5 . The latter analysis enjoys a new concept, namely information valuation. The paper is summarized and concluded in Section 6 , where further research avenues are suggested.
The approach of selecting the better evaluation procedure; peer evaluation, is methodological, and the rankings of the selected procedures is a case-specific result of this study. It can, also, form a basis for the choice of such analysis techniques in other cases (say, political decisions), and other decision analysis techniques suitable in other contexts (say, with partial or inconsistent information). The proposed method of evaluation of alternative decision procedures can act as a guide to better understand these procedures, and, thus, lead to better choices for various cases and contexts, which hopefully will lead to better decisions in the long run.
2. A review of the literature in evaluation of multi-attribute decision procedures
There are many text books and articles that present, review, compare, or attempt to evaluate, alternative multi-attribute decision procedures, as mentioned above. An early and good endeavor in this regard is presented by Hwang and Yoon [8] , who described many of the well-known MCDA methods, and compared the results of their applications on same example problems. A more recent endeavor of a similar nature belongs to Triantaphyllou [4] , who compares cases of MCDA, theoretically, empirically, and critically.
Triantaphyllou and Mann [13] compare four MCDA methods, namely; weighted sum model, weighted product model, the Analytic Hierarch Process (AHP), and the revised analytic hierarch process, based on two criteria. One of these criteria was “to remain an accurate method in a single dimension case if it happens to be accurate in a multi-dimensional one”. The other criterion was “the stability of the method in yielding the same outcome when a non-optimal alternative was replaced with a worse alternative”. They simulated decision problems randomly, and reached a paradox of deciding on a single best method. They, also, presented the results of the comparisons of the four methods, without resolving the seeming paradox. We will refer to this work, again, later, in Section 3.4 .
Buede and Maxwell [14] compared the top-ranked options resulting from the Multi-Attribute Value Theory (MAVT), AHP, Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), and a fuzzy algorithm, in a series of simulation experiments. These experiments demonstrated that MAVT and AHP identified the same alternatives as “best”. The other methods were found less consistent with MAVT. Moreover, they also echoed the point that other issues, such as problem structuring and weight determination, may be more important in the solution of the problem than the choice between computational algorithms.
Triantaphyllou and Mann [13] , despite showing their doubt about finding the “perfect” MCDA method, have encouraged users to be aware of main controversies in this field. They, further, assert that despite the continuous search for finding the best MCDA method, research in this area of decision making is critical and valuable.
Guitouni and Martel [6] describe that none of the MCDA methods can be considered the “super method”, appropriate to all decision making situations. They argue that the existence of numerous methods for the solution of multi-criteria decision problems show that these methods did not produce good recommendations in all cases. They criticize the current practice of familiarity and affinity with a specific method, leading to the choice of MCDA method for the solution of a problem, as being non-productive, since it adapts the problem to the method, and not vice versa. They also note that surveying all different methods is practically impossible. Furthermore, they propose a conceptual framework for guiding the choice among MCDA methods for a decision making situation. They stress that these guidelines cannot be considered as criteria. They, then, compared several well-known MCDA procedures based on these guidelines, considering their work as a first step in a methodological approach to select a proper MCDA method to a specific decision making situation.
Guitouni et al. [15] state none of the MCDA procedures is perfect, nor applicable, to all decision problems. They, also, call the identification of a specific MCDA method to a specific decision situation, a challenge. They assess a framework for choice engineering of a MCDA procedure to a decision-making situation, in which they associate different MCDA procedures with a pair of (input, output), and where inputs (outputs) characterize the admissible (produced) information by a MCDA procedure.
Zanakis et al. [16] studied a decision matrix of criteria weights and rankings of alternatives on each criterion. They investigated the performance of 8 methods, namely elimination et choice translating reality (ELECTRE), TOPSIS, Multiplicative Exponential Weighting (MEW), Simple Additive Weighting (SAW), and four versions of AHP. They administered a simulation comparison of the selected methods, with parameters as the number of alternatives, number of criteria, and their distributions. They analyzed the solutions with the help of 12 measures of similarity of performance, through which similarities and differences in the behavior of the methods are investigated.
Salminen et al. [17] considered studying the performance of four MCDA methods, namely; ELECTRE III, PROMETHEE I and II, and simple multiattribute rating technique (SMART), in some real case environmental decision problems, as well as a set of randomly generated problems. They concluded that “the choice in practice will not be easy”. They, like others, observed similarities among the methods, as well as great differences in particular situations. This is why they suggest use of several methods for the same problem in converging to a particular alternative. However, they are among the few researchers who name a particular method, here, ELECTRE III, when such multiple applications of methods are not feasible.
Bohance and Rajkovic [18] advocate the application of the expert system shell decision expert (DEX) in qualitative MCDA, particularly in industrial areas.
Parkan and Wu [19] highlight the frustration of a decision maker who is trying to act logically by using a formal multi-attribute decision making method, and finds different MCDA approaches end in dissimilar results. They note that this confusion results in discomfort in using such methods, when the person thinks that there must be one best solution, except for the unusual cases of multiple similar solutions. They present a new MCDA method, called Operational Competitiveness Rating (OCRA), and compare the results of the application of OCRA to a process selection problem, with those of AHP and Data Envelopment Analysis (DEA). They tried to reach a conclusion regarding the similarities and differences of these three MCDA methods with the hope of bringing some insight into their behavior.
Munda [20] , in an interesting philosophical discussion regarding multi-criteria assessment, argued that a multi-criteria problem is ill defined mathematically. Consequently, a wide range of multi-criteria methods exists. One way to deal with the difficulty of a choice among these methods, the author suggests, is to search for the right method for the right problem. Quoting Roy [21] and [22] , Munda [20] states that the solution of a multi-criteria decision problem is more in the “creation” than in the “discovery” of the solution. Thus, in this sense, there is no wonder that different MCDA techniques can possibly present different solutions.
Opricovic and Tzeng [23] undertake another endeavor in comparing the compromise ranking method of VIKOR and the method of TOPSIS. Both of these methods use aggregating functions to measure proximity to an ideal entity. They used a small numerical example to compare these two methods in search of similarity and differences. They conclude that a difference between these two methods is the dependence of the normalized aggregation measure in TOPSIS on the evaluation unit of a criterion, a characteristic that does not exist for VIKOR.
Hajkowicz [3] administered a study to compare the MCDA method and an unaided decision in an environmental management context. He used four MCDA methods, namely weighted summation, lexicographic ordering, ELECTRE, and multi-criteria evaluation with mixed qualitative and quantitative data (Evamix), in association with five weighting methods. The results of application of the MCDA procedures in environmental decisions, as opposed to unaided or intuitive approaches, differed significantly. He suggests that MCDA methods should “equally”, if not “primarily”, be concerned with finding the right process, as well as the right answer”.
Hajkowicz and Higgins [24] applied MCDA techniques to six water management decision problems. They used weighted summation, range of value, PROMTHEE II, Evamix, and compromised programming methods for this purpose. They showed that different methods show strong agreement in their rankings, while strong disagreements did also occur where mixed ordinal-cardinal data were present. Thus, they concluded that, except where ordinal-cardinal data are present, results of discrete choices in the cases studied are relatively insensitive to variations in MCA methods.
Mostert [25] emphasizes multi-criteria analysis to cover values other than those related to current human use, for the management of water resource infrastructures.
They emphasize, despite the importance of MCDA technique selection, that criteria selection and decision options are more important.
Al-Ani et al. [26] chose a MCDA method; weighted summation, for assessing storm-water management alternatives in Malaysia, because of its simplicity and ease of understanding by the decision makers. The erosion and sedimentation of soil are responsible for degradation of water quality and fish spawning areas, and the reduction of water depth, which endangers ship movement and flood control measures, among others. They employed some criteria in each of the following categories: Technical, economical, environmental, and social and community benefits. Alternative measures of controlling erosion and sedimentation, due to storm-water from construction sites, were defined, and small groups of stakeholders were selected and interviewed for ranking all criteria, to come up with their weights. This analysis helped to arrive at the better storm-water control measure that should be adopted for different construction stages.
Mela et al. [5] administered a comparative study of MCDA methods for building design. They believe that conflicting aspects in construction management decisions, particularly in the conceptual design phase of building projects, is a major reason for the need of MCDA methods to aid the decision process. They noted the effect of number of criteria and number of alternatives on algorithmic performance. They chose two to four criteria in their test problems, and employed six alternative methods for comparison. The selected methods are weighted sum, weighted product. VIKOR, TOPSIS, PROMETHEE II, and a PEG-theorem based method (PEG = Pareto–Edgeworth–Grierson). They chose to apply the MCDA methods to multi-criteria optimization problems that have been documented in the literature. They could not decide on the best method; instead, they provided information regarding the performance of these methods in building design problems. They, like many other authors described in this paper, believe in the existence of the differences between the methods, and expected these differences to appear.
One important observation in the evaluation of MCDA is that most of the comparisons of these methods are done in the context of cases in the fields of engineering or planning. In this respect, conclusions may be limited for being case-oriented, and the results of the application of the methods in the same case may differ, as reported by the researchers, and as may be expected to appear. However, there is considerable agreement among the results, as also expected. Nevertheless, some of these methods have fewer short-comings, and are less exposed to pitfalls. Thus, we should not be looking for a philosopher’s stone: There is no such thing as the best method for all cases and situations. However, it is advantageous to know about robust MCDA methods that act logically, irrespective of case, field, criteria, alternatives, weights, etc.; or prove to be better than others under certain conditions.
3. Evaluation of MCDA procedures
3.1. The study approach
In this section, we introduce the approach of this study for comparison and evaluation of multi-attribute decision making procedures. These procedures are designed to choose the better alternatives for the solution of the original problem based on some attributes. First, note that comparison of multi-attribute decision-making procedures can be, by itself, a multi-criteria decision problem [13] . The effectiveness of the choice procedure depends on its characteristics, which may be measured on scales of some criteria. Suppose that one may define such criteria, which together define the effectiveness, goodness, robustness, etc. of the procedures, in identifying a better decision for the original problem.
Now, a question arises as to what would be a good, and, of course, just decision method in identifying the better decision procedure for the original problem. In practice, the choice of the decision procedure may be done using the analysts’ experience or familiarity with these procedures. More skeptical analysts may resort to the results of reports in comparative studies of similar problems. Still, more scientific analysts may adhere to simulation or analytic approaches. The approach of this paper in choice of a MCDA procedure is to consider these procedures as some alternatives which are to be evaluated based on their performance measures, called criteria, in making a decision. All alternative decision procedures are envisaged to be members of an assembly, voting to select their president, thus, the term peer evaluation in the title of this work. In other words, the selection is done by defining a set of evaluation criteria, using the same procedures to evaluate themselves, and, then, concluding, based on a sensitivity analysis and an information valuation concept. In doing this, the approach is more practical or engineering oriented. For example, we take the liberty of identifying certain evaluation measures and quantifying them. Furthermore, assume that all MCDA procedures of concern are rational; in that a higher/lower value of positive/negative measure of effectiveness of a project would positively affect the choice of that particular project (see Lemma 1 in this section). Then, all procedures do their best to introduce the best procedure(s), including themselves. This is, clearly, a just and “democratic” method, based on global wisdom.
We demonstrate this approach by practicing it on a real case. This study has chosen one area of an engineering problem, for which one may confidently assume the existence of a model that provides reliable information on a sufficient number of measures of effectiveness (moe’s), as well as the relative weight (or importance) of these moe’s. Moreover, it defines a set of nine evaluation criteria of the MCDA procedures of concern, as a first attempt. Furthermore, it assigns a set of weights or importance to these criteria that are further studied for the sensitivity of the study approach decisions to such values. Nevertheless, definition of MCDA procedures for particular problem contexts, evaluating criteria for these procedures, and assigning weights to these criteria, is worthy of further wide-range scrutiny and case-based close examination.
Despite specific conclusions made regarding the better decision procedures among those evaluated, this paper finds its contribution mainly in the approach to such evaluations. There are two concepts that are proposed: peer evaluation, and information valuation, which will be investigated further later in this paper.
In this paper, the terms multi-attribute (decision) procedure, alternatives or projects, and attributes or moe, are reserved for the original engineering alternative project choice problem; and the respective synonyms of multiple criteria decision analysis, procedures, and criteria, are reserved for the procedure choice problem.
3.2. The MCDA procedures of concern to this study
This paper concerns itself with MCDA procedures that assume availability of an alternative-attribute table and a vector of weights for the attributes. The selected methods were known and studied well before the early work of Hwang and Yoon [8] . The methods that apply to cases of incomplete, inconsistent, imprecise, or partial, information (see e.g. [27] , [28] and [29] ), whether in preference, parameters of the analysis method, or in the alternative-attribute table; or those that try to gather additional information by case-based multiple criteria analysis (see, e.g. [30] ), are not treated in this paper. Nevertheless, with such information, some of the other methods may turn into one of the methods studied in this paper. For example, as Samson [31] reports, AHP (see, e.g. [32] and [33] ) presents the same ranking of the alternatives as suggested by simple additive weighting, if it uses the same weights as those in the SA method. However, if the decision maker decides to use the AHP method, rather than SA, and the weights used in it, because the decision maker is unwilling or unable to give the vector of weights for the attributes, then, one has to make pair-wise comparisons of the attributes to determine their weight [34] . This takes the decision context out of the circle of concern in this study.
For the methods of concern in this paper, the following information is available. is the set of alternatives, and the set of measures of effectiveness, , and . is the value of the measure of effectiveness (moe) for the alternative ( ; and ). is the set of ’s, for which higher (lower) values of moe are preferred. It is sometimes referred to as a positive (negative) attribute set. Clearly, , and . is the dimensionless measure of , defined as follows: if , otherwise, (if ) . Finally, is the weight of moe . Note that , and higher values of are preferable to lower values of it. Moreover, and . ’s and ’s are all that are required to operate the methods of concern to this study.
There are some other procedures, also discussed in Hwang and Yoon [8] , which have certain shortcomings that prevent them from being a viable method of multi-attribute decision-making. Thus, we excluded the procedures mentioned below from further consideration for the following reasons: the ability to narrow down the preferred alternatives, efficient utilization of information provided, and computational complexity: dominance, maximin, maximax, maximin–maximax, lexicographic, semi-lexicographic, satisficing method, and permutation. The selected procedures for evaluation are: (1) Electre (El), (2) TOPSIS (TO), (3) linear assignment (LA), (4) simple additive weighting (SA), and (5) Minkowski distance (MD). The algorithms of these five procedures are given in Appendix A .
Three points are in order here. First, the method of permutation has not been selected for its formidable computational burden for cases with high numbers of alternatives. (We have 29 alternatives in the case we study, for which there will be comparisons.) Second, although we may undertake a sensitivity analysis to compensate for the unavailability of (the power of the distance measure in the Minkowski procedure), this parameter has been chosen to be 2.0 in evaluating alternative projects and decision procedures for the following reasons: (a) To be more specific in the evaluation of a procedure, and (b) at , the Minkowski procedure connotes the Euclidean distance, or bears the notion of least square “error”. (At it is equivalent to SA, which is present in this study.) Finally, one may assert that the selected procedures are rational procedures, as stated below.
Lemma 1.
Procedures El, TO, LA, SA, and MD are rational, in that a higher value of a positive/negative attribute for an alternative results in a non-decreasing/non-increasing potential for that alternative choice by either of these procedures.
Proof.
See Appendix B . □
3.3. The decision problem: case of the city of Mashhad
The decision problem is the problem of choosing a network of Light Rail Transit (LRT) from a set of such networks for the City of Mashhad, and which suits the city best. This choice is based on a set of attributes and respective weights. The city has a population forecast of about 3.1 million in the target year of 2021. The estimated Origin–Destination (O/D) trips by vehicles for the target year is about 5.4 million per day, and 384 000 per hour of the morning peak period. The demand estimation procedure comprises a rather extensive set of models, including car-ownership, activity allocation, trip production and attraction, trip distribution, mode choice, and a multi-class user equilibrium flow assignment routine with a bus and rapid transit assignment. The algorithm of Frank and Wolfe [35] solves the auto user equilibrium flow problem, and the transit assignment uses the optimal strategy routine [36] . The demand for goods transportation is treated separately within a multi-class user equilibrium flow problem. All routines are assembled in EMME/2 environment [37] .
The city is about 10×20 km×km, and has a road transportation network of over 500 km in length, represented by over 700 nodes and 1300 (two-way or one-way) links. The existing bus system has a fleet of about 1000 buses and about 110 bus lines of about 1300 km in length (one-way).
Alternative LRT lines are identified based on public transportation passenger desired routes, the feasibility of the link to embody an LRT line at ground or underground level, expert opinion regarding good routes, and analyses of network loadings for various future demand forecasts. A combination of these candidate lines created alternative network configurations of 1–4 lines. Several interim analyses have reduced the alternative configurations to 29, of which, one is the do nothing alternative ( , no LRT line, or only bus network). There are two 1-line networks , eight 2-line networks , ten 3-line networks , and eight 4-line networks , as shown in Table 1 . The last alternative in this table ( ) is an irrelevant alternative created for analysis purposes, which will be discussed later in this paper.
| Alternative | moea | ||||
|---|---|---|---|---|---|
| Monetary cost of users of the system | Investment cost of the system operator | Monetary cost of limited resources | Cost to environment (CO) | Choice diversity of modes | |
| 1 | 3134 | 274 | 929 | 273 | 0 |
| 2 | 2779 | 423 | 829 | 239 | 39 |
| 3 | 2773 | 439 | 827 | 238 | 42 |
| 4 | 2732 | 542 | 826 | 236 | 61 |
| 5 | 2689 | 539 | 813 | 233 | 65 |
| 6 | 2768 | 508 | 833 | 239 | 60 |
| 7 | 2723 | 516 | 819 | 236 | 59 |
| 8 | 2709 | 582 | 821 | 235 | 85 |
| 9 | 2725 | 519 | 822 | 236 | 61 |
| 10 | 2666 | 582 | 807 | 229 | 70 |
| 11 | 2673 | 564 | 807 | 231 | 56 |
| 12 | 2680 | 630 | 817 | 234 | 82 |
| 13 | 2636 | 714 | 812 | 229 | 107 |
| 14 | 2591 | 729 | 791 | 223 | 102 |
| 15 | 2622 | 707 | 808 | 229 | 108 |
| 16 | 2684 | 679 | 822 | 234 | 106 |
| 17 | 2654 | 682 | 809 | 230 | 107 |
| 18 | 2645 | 686 | 812 | 231 | 101 |
| 19 | 2649 | 679 | 812 | 230 | 99 |
| 20 | 2643 | 699 | 812 | 230 | 108 |
| 21 | 2641 | 688 | 809 | 230 | 102 |
| 22 | 2662 | 781 | 818 | 232 | 150 |
| 23 | 2598 | 804 | 805 | 226 | 128 |
| 24 | 2602 | 790 | 801 | 226 | 129 |
| 25 | 2592 | 811 | 801 | 225 | 128 |
| 26 | 2610 | 796 | 806 | 227 | 128 |
| 27 | 2590 | 802 | 798 | 225 | 128 |
| 28 | 2609 | 806 | 807 | 227 | 129 |
| 29 | 2551 | 859 | 785 | 220 | 131 |
| 30 | 2708 | 527 | 833 | 238 | 42 |
a. All monetary values are in billions of (2003) Rials per year, CO is in 1000 of tons per year, and mode diversity in km of one-way rail length.
Detail operational and cost characteristics are available from the model of network flow built for this study. Such characteristics may be converted to several more aggregate measures of effectiveness, as follows, which collectively cover the transportation system fairly: (1) User costs, (2) Operator costs, (3) Limited resources costs, and (4) Cost to environment. The first three are monetary costs at market price, and the fourth measure is in kg of CO. A fifth measure of effectiveness is defined to measure the benefit of mode choice diversity, which is measured in km of one-way LRT lines (higher values indicating availability of one new public transit mode to more people in the city). An independent survey of the politicians, decision-makers, experts, managers, and operators of the transport sector and systems of the city under study revealed the following weights by these influential decision bodies for moe’s 1–5 mentioned above: 0.21, 0.22, 0.22, 0.20, and 0.15 [38] . These values are the average values of the weights assigned to the objectives associated with the above moe’s by the above-mentioned bodies.
This is the original multi-attribute decision problem which will be given to the selected alternative procedures to solve. The performance of these procedures in solving the stated problem is measured on several criteria, which will be discussed below. To give an idea of the suitable networks for the city, it is worth mentioning that different analysis methods, extensive sensitivity analyses of the parameters of the problem, and expert opinion, have revealed that alternatives (alt’s.) 2, 5, 14, and 29 are, respectively, the better 1, 2, 3, and 4-line LRT networks for the city. Alt. 2 is a network with one lower NW-SE line; alt. 5 is alt. 2 plus a NE-SW line; alt 14 is alt. 5 plus an upper NW-SE line; and alt. 29 is alt. 14 plus a N-SE line. This is a striking coincidence! This happenstance, of course, has roots in the merits of each of the above-mentioned LRT lines.
3.4. Evaluation criteria for the alternative evaluation procedures
We have chosen the following 9 criteria to evaluate the 5 alternative multi-attribute decision procedures (El, TO, LA, SA, and MD): (a) Demand for information; (b) Information utilization and generation, including: (b.1) Degree of information utilization; and (b.2) Frequency of using given information to form new information; (c) Creation of a spectrum of solution; (d) Computation speed; (e) Effect upon the solution, including: (e.1) Successive application of the method to obtain clearer solutions; (e.2) Effect of an irrelevant attribute upon the solution; (e.3) Effect of an irrelevant alternative upon the solution; and (f) Distance of the solution from a general consensus. These criteria are not necessarily exhaustive. They have formed a reasonable set of evaluation criteria, used for illustrative purposes, which are backed by logic, common sense, and the literature in decision making, since, at least, the early work of de Neufville and Stafford [39] .
It is worth noting that a similar approach to that in this study was employed by Triantaphyllou and Mann [13] to evaluate MCDA techniques. However, the noted work was recently introduced to the authors of the present paper, and the two types of research are completely independent. There are several differences between the former and present research. Unlike the noted research, this one is established on a real-world case study. While the former work used only two attributes to compare MCDA techniques, namely; the effect of a (special) irrelevant alternative upon the solution and the difference between the solutions and a standard solution, the present work benefits from employing all attributes noted in the previous paragraph, which cover those of the former study. This research overcomes the difficulty posed by the paradox noted by Traintaphyllou and Mann [13] , wherein the true best alternative is not known, by considering general consensus as a standard (instead of SAW method’s solution). Moreover, we introduce the information valuation, explained in Section 5.2 of this paper, to value the decisions made by each technique proportional to the credit received from the others. Furthermore, by employing various attributes to evaluate these techniques, we increase the reliability of the results. In passing, the reader recalls from Section 3.2 that the present paper normalizes the measures of effectiveness, as recommended in the literature (e.g. [8] ), while the previous work did not stress such normalizations.
3.4.1. Measurements of the evaluation criteria for the decision procedures
This section will quantify the evaluation criteria mentioned above for the multi-attribute decision making procedures specified in Section 3.2 . There are two important points to note in this quantification. First, the definition of measures of effectiveness is a matter of art and science, and it is particularly so in the field of decision science. To verify this, one may have a glance through the measures defined by the inventors of the MCDA procedures chosen in this paper, or the measures in procedures presented elsewhere in the literature (e.g. [30] ). In this sense, it is sufficient for a moe to be a logical and sensitive meter of the respective objective. However, the measures are always open to improvement, which also forms a basis for the introduction of new decision procedures. For instance, TOPSIS, which measures the distance of an alternative to both an ideal and an opposing-to-ideal alternative, may be regarded as an improvement and generalization of the Minkowski distance, which only considers the first distance measure. Second, in this study, we may frequently choose the top 3 alternatives in several analyses. This is based on the feeling that 3 for the tops is a “magic” number in most competitions; a number which can be easily comprehended by any person, as well as the decision-makers. There is no reason behind this choice, other than the logic behind this widespread accepted convention. Interested analysts may choose other numbers that suit their problems most. We, now, turn to the measurements of the criteria:
(a) Demand for information . Higher needs for information for a given performance implies higher cost and longer time to make a decision procedure functional, and, thus, is considered a negative attribute for a decision procedure for a given performance level. All of the selected procedures need only the alternative-moe (alt-moe, for short) table and the moe weights, except for the linear assignment and Minkowski procedures. In the linear assignment method, one only needs the rankings of alternatives based on each moe separately. However, when the number of alternatives is high (e.g., greater than 5, as in our case, which is 29), specifying this ranking precisely without having the alt-moe table is practically difficult, if not impossible. Thus, it will be assumed in this study that the linear assignment procedure also needs the information of this table. The Minkowski procedure needs extra information, , the power of the distance measure. Note that specification of is equivalent to a significant amount of computation, since compensating for this lack of information requires a sensitivity analysis on , e.g., through analyzing decisions in terms of the length of the range of in which the alternative LRT networks remain one of the top (say, 3) alternatives.
We assume in this study that the effort required to obtain the three types of information of the moe table ( ), moe weights ( ), and the level of risk-taking behavior ( ) for the Minkowski procedure is equal to 1 unit. Thus, for a maximum demand for information of 1.0, all procedures demand a value of 2/3, and the Minkowski’s procedure needs 1.0, resulting and 0.0, respectively, owing to the fact that . This argument leaves or , where “′” represents “transpose”.
(b.1) The degree of information utilization . This criterion is a measure of the degree of utilization of the information resources, which are paid for by money or time. A procedure which does not fully utilize the information that it asks for, may lose ground to capture all aspects of the problem and waste the resources. This criterion differentiates procedures such as maximin [8] , which uses only a small portion of the alt-moe table information, from the selected procedures. All decision procedures under study use all the information provided, except the linear assignment procedure, which uses each moe column to produce a ranking of the alternatives and does not pay attention to the values of differences of the alternatives in the dimensions of these moe’s. Considering equal weight for the and information, and equal importance for cardinal and order data, the linear assignment procedure looses 1/4 of the maximum utilization of data 1.0 (i.e., 1/2 of 1/2 of the total information of order data), resulting , noting that criterion 2 is a positive one (more utilization of information is better).
(b.2) Frequency of using given information to form new useful information . This is generally considered a positive criterion, recognizing the fact that there is a limit to such use because of generating correlated and non-independent information. In Electre, for the two alternatives, and , pair-wise comparisons of and for all moe’s, , produce concordance and discordance sets, ’s, and ’s. So, every entry of the alt-moe table is used times ( is the number of alternatives), which is 28 in our case of LRT network selection. Note that knowing implies identification of . Also, note that this study does not consider arithmetic operations on existing information as “new“information. TOPSIS defines two ideal and opposite-to-ideal alternatives and uses the alt-moe table entries twice to compute the distances of alternatives to the above two fictitious alternatives. So, TOPSIS uses each alt-moe entry 2 times. The linear assignment procedure uses the entries of the alt-moe table once to create the information needed by the procedure. The same is true for the simple additive weighting and the Minkowski procedures. Hence, one may write , or .
(c) Creation of a spectrum of solutions . This positive criterion recognizes the need to give the decision-makers options to choose, e.g., in the range of high benefit and capital intensive to low benefit and low cost alternatives, or in the range of high-technology to traditional technology, etc. We may value a certain number of competing alternative solutions (say, 3) most (i.e., 1.0), and devalue any number of alternative solutions which is more, or less, than that. This choice of alternative solutions is based on the fact that lower numbers (here, 2 or 1) leave no spectrum, and higher numbers (say, 4, 5, or more) require another decision aid to bring them down to a comprehensible level. Since all procedures either introduce a subset of competing alternatives (e.g., Electre), or a ranking of the alternatives, we consider them to produce an almost similar type of information to present the top few (3, in this study) alternatives. Also, we select 3 alternatives with higher net concordance index, NCI, and lower net discordance index, NDI, values in the Electre procedure in this study. Thus (see Table 2 , Application No. 1), .
| Appl. no. | Top 3 rank | (1) Electre | (2) TOPSIS | (3) Linear assign. | (4) Simple additive weighting | (5) Minkowski procedure | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Net concordance index | Net discordance index | Network ID | Similarity measure | Network ID | Network ID | SAW measure | Network ID | Minkowski distance | ||||
| Network ID | NCI measure | Network ID | NDI measure | |||||||||
| 1 | 1 | 29 | 15.94 | 24 | −0.61 | 22 | 0.562 | 29 | 22 | 0.259 | 8 | 0.101 |
| 2 | 27 | 13.95 | 27 | −0.54 | 8 | 0.541 | 14 | 24 | 0.248 | 5 | 0.108 | |
| 3 | 24 | 13.83 | 29 | −0.49 | 17 | 0.539 | 27 | 27 | 0.246 | 9 | 0.109 | |
| 2 | 1 | 29 | 7.54 | 24 | −0.51 | 22 | 0.563 | 29 | 22 | 0.177 | 8 | 0.058 |
| 2 | 27 | 5.55 | 29 | −0.46 | 24 | 0.4891 | 14 | 24 | 0.168 | 5 | 0.070 | |
| 3 | 24 | 4.07 | 27 | −0.42 | 17 | 0.4890 | 27 | 27 | 0.167 | 10 | 0.070 | |
| 3 | 1 | 29 | 2.32 | 27 | −0.11 | 22 | 0.560 | 29 | 22 | 0.169 | 8 | 0.039 |
| 2 | 27 | 1.2 | 29 | −0.06 | 24 | 0.4858 | 14 | 24 | 0.161 | 12 | 0.051 | |
| 3 | – | – | – | – | 17 | 0.4856 | 27 | 27 | 0.159 | 16 | 0.053 | |
| 4 | 1 | 22 | 0.552 | 29 | 22 | 0.169 | 16 | 0.030 | ||||
| 2 | 8 | 0.464 | 14 | 24 | 0.161 | 17 | 0.031 | |||||
| 3 | 24 | 0.440 | 27 | 27 | 0.159 | 19 | 0.032 | |||||
(d) Computation speed . This is a differentiating measure for some of the time consuming multi-criteria procedures, but, for most of these procedures, computation speed is not a major concern, because it is in the order of seconds, or even fractions of seconds, with modern computers. In this study, to reduce reliance on the lapsed time computation precision of computer systems, the decision problem of concern has been solved 10,000 times by each procedure, to reach a more accurate estimate of the procedure’s computation time. The results (in seconds, on a PC) are as follows: . These times include 0.89 s for 10,000 times computation of the ( ) matrix. This would result in .
(e.1) Successive applications of the method to obtain clearer solutions . Justification for this criterion stems from the introduction of a subset of the original set of alternatives as non-inferior or competing alternatives by many of the multi-criteria decision-making procedures. Then, a good procedure should rank the better alternatives the same, if it had to choose once again from its selected (solution) subset in the previous application(s). Variation in this ranking is an undesirable characteristic of the decision procedure. In this study, each procedure has been applied successively until the final subset of the solution contains 3, or less, alternatives. In case the procedure ranks the alternatives, if the top 3 alternatives in each application of the procedure remain the same, then (changes), which corresponds to an value of 1.0 owing to the negativity of this criterion (higher variations in the solution set or rankings are less desirable). Permutations of the top 3 alternatives were considered no change, and, thus, no negative point. Change is measured with respect to the previous application top 3 alternative set. In this study, for 4 applications of each procedure, there could be a maximum of 9 changes in the successive solution sets. A value of may be assigned to the maximum value of 5 changes, which happened in our case, on a scale of 0–1.
The Electre procedure produced 14, 5, and 2 networks in the 1st, 2nd, and 3rd applications of the method, respectively, having 1 change in the top 3 alternative network sets, as shown in Table 2 . (In fact, alternative network 24 could not resist staying in the top 3 list in the 3rd application.) Four successive applications of the other procedures to the case under study resulted in 2, 0, 0, and 5 changes in the top 3 alternative lists for TOPSIS, linear assignment, simple additive weighting, and Minkowski distance (for ), respectively. Thus, , and , owing to the negativity of this criterion.
(e.2) The effect of an irrelevant attribute upon the solution . A good decision procedure is one that is not affected by the presence of an attribute which is unrelated to the problem, or is redundant. To measure the sensitivity of decision procedures regarding irrelevant attributes, the following three experiments have been conducted:
(a) Two outcomes of vehicle-kilometers traveled and vehicle-hours spent by the demand are added to the existing list of attributes. The first measure relates to the cost of limited resources (fuel, here) and the cost to the environment (CO emission, here). The second measure relates to the monetary cost of travel to the users of the network. The weight of each of the existing attributes (fuel, CO, and user monetary cost of travel) reduced by one half, and the new related attribute received the other half.
(b) A third attribute is devised by dividing veh-km by veh-hr to yield the average network speed, which is obviously dependent upon the two attributes making it. This is added to the attribute list in the experiment (a) above. Due to this very dependence, the weights of the two attributes, veh-km and veh-hr, are reduced to one half, and the new dependent attribute received the other halves.
(c) In the third experiment, all three new attributes are present. The weights of user monetary cost, limited resource cost, and cost to the environment are reduced to half the respective original values, and the sum of the other halves are equally distributed among the three new attributes. This is, in fact, case with different moe weighting.
The alternative decision procedures are applied to the three new cases mentioned above, and the results compared with those of the original case. The number of changes in the list of the top 3 alternatives of the new cases, as compared to the original, or base, case, is chosen as the measure of the vulnerability of the decision procedure to the misleading nature of irrelevant attributes. The results of this endeavor are summarized in Table 3 , where , or .
| Top 3a alternative list | No. of changes in top 3 list | ||||
|---|---|---|---|---|---|
| Base case | Irrelevant attributes included | ||||
| (a)Veh-Km & Veh-hr | (b)Veh-Km, Veh-hr & ave. veh. speed | (c) Case (b) with different moe weighting | |||
| Electre | 29 | 29 | 29 | 29 | 1 |
| 24 | 27 | 27 | 27 | ||
| 27 | 24 | 24 | 25 | ||
| TOPSIS | 22 | 22 | 22 | 22 | 2 |
| 8 | 8 | 8 | 29 | ||
| 17 | 17 | 17 | 24 | ||
| Linear assignment | 29 | 29 | 29 | 29 | 0 |
| 14 | 14 | 14 | 14 | ||
| 27 | 27 | 27 | 27 | ||
| Simple additive weighting | 22 | 22 | 22 | 29 | 1 |
| 24 | 24 | 24 | 22 | ||
| 27 | 27 | 27 | 27 | ||
| Minkowski distance (α=2) | 8 | 8 | 8 | 22 | 5 |
| 5 | 5 | 5 | 29 | ||
| 9 | 6 | 6 | 24 | ||
a. List contains rank 1 alternative on top and rank 3 at the bottom.
(e.3) Effect of an irrelevant alternative upon the solution . Given the proper attribute set for the evaluation of the projects, a good procedure is one wherein the introduction of a new alternative not related to the solution of the problem does not affect its rating of the alternatives. In the case under study, the problem is to solve the transportation problem of the city of Mashhad by the introduction of a new network of public rail transit. One irrelevant alternative could be to serve private automobile transportation demand by building 12 interchanges for the reduction of intersection delay. This alternative transportation system, alternative 30, has the estimates of moe’s, as given in Table 1 . To see the difference between this alternative and a rapid rail transit alternative, one may compare the values of the moe’s for this alternative (30) with the respective ones of alternative rail network 29, which is a top ranking alternative according to many decision procedures under study. As Table 1 shows, the irrelevant alternative is only better in the investment cost, whereas alternative 29 is better in the other 4 dimensions. Table 4 shows the changes in the rankings of alternatives as a result of the inclusion of the above-mentioned irrelevant alternative to the list of the alternatives. According to this table, no change has occurred in the top 3 alternative lists of the procedures under study. This results in , or .
| Electre | TOPSIS | Linear assignment | Simple additive weighting | Minkowski dist. ( ) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NCI | NDI | Similarity measures | Rankings | SAW measure | Dist. measure | ||||||||||||
| Alt. rank | Alternative ID | Alt. rank | Alternative ID | Alt. rank | Alternative ID | Alt. rank | Alternative ID | Alt. rank | Alternative ID | Alt. rank | Alternative ID | ||||||
| Without irr. Alt. | With irr. Alt. | Without irr. Alt. | With irr. Alt. | Without irr. Alt. | With irr. Alt. | Without irr. Alt. | With irr. Alt. | Without irr. Alt. | With irr. Alt. | Without irr. Alt. | With irr. Alt. | ||||||
| 1–9 | the | same | 1–30 | the | same | 1–29 | the | same | 1–25 | the | same | 1–28 | the | same | 1–27 | the | same |
| 10 | 13 | 10 | 30 | – | 30 | 26 | 3 | 30 | 29 | 1 | 30 | 28 | 29 | 30 | |||
| 11 | 21 | 13 | 27 | the | same | 30 | – | 1 | 29 | 1 | 29 | ||||||
| 12 | 17 | 21 | 28 | 2 | 3 | 30 | – | 1 | |||||||||
| 13 | 20 | 27 | 29 | 1 | 2 | ||||||||||||
| 14 | 19 | 20 | 30 | – | 1 | ||||||||||||
| 15 | – | 19 | |||||||||||||||
| 16–30 | None | ||||||||||||||||
(f) Deviation of the rankings of a procedure from a general consensus . Define a general consensus for an alternative as the global wisdom of a collection of all/other competing procedures in identifying the better alternatives. The feeling is that all alternative decision procedures are rational methods of evaluation of multiple alternatives. Thus, collectively, they should make sense. It might first occur to some that this is a restraint for conservatism, preventing break-thorough methods to flourish. Or, it might seem that this criterion prevents considerations of the extreme solutions (as compared to the solutions of the other rational procedures) as good solutions. However, such arguments lose ground if one takes into account the information value: valuing each procedure’s information as much as it is trusted. So, to measure this criterion for the procedures under consideration, we need to introduce a concept, called; information valuation. We define two general consensus measures in the next section, in relation to information value.
3.4.2. Measures of distance to general consensus
Let be the ranking of alternative (LRT) project , as evaluated by alternative decision procedure ( ; and ). Let be the value of the information supplied by the alternative procedure, . Initially, as unbiased estimates, , a constant for all , as we are not aware of the degree of “correctness” of the information given by each alternative procedure in terms of project rankings. However, project rankings by different procedures provide some information in this regard, which may be used in weighting the information supplied by the procedures in project rankings, as will be described later.
Now, let , initially , and let be the rank of project , according to the values of collective ranks of the decision procedures, . In fact, , which is the weighted rank of project , may be regarded as a measure of general consensus. And, hence, may be viewed as the ranking of project based on global wisdom. In general, a project with lower values of , or , is expected to be preferred by more alternative procedures. One may exclude in the computation of for procedure , i.e. set in the above summation expression for . However, the authors believe that is also another sensible method and, thus, should contribute to the value of . Moreover, this prevents from being dependent on and being a variable (not a fixed) reference point. Then, the following index reflects the distance of alternative procedure rankings from those of the “general consensus”: . The lower is, the closer are ’s rankings to those of the “general consensus”.
However, in measuring the sensibility, or “correctness”, of the evaluating procedures in ranking the projects (here, LRT alternatives), except for the top few (here, 3) chosen projects by the evaluating procedure, which are of importance to them, incorrect rankings of the other alternatives are not of any concern. Thus, one may ask about the rankings of the top (3) projects chosen by alternative , as given by all evaluating procedures, (including ), and use a weighted sum of such rankings as a measure of general consensus. Let , and be rank 1–3 (LRT) projects, according to the evaluating procedure , then, , and . Now, define:
|
|
( 1) |
where is as defined before (initially, ), and represents the set of the top 3 projects of procedure . Hence, is the average rank of the 1st rank project of alternative procedure . So;
|
|
( 2) |
is a measure of the deviation of the choice of the top (3) projects of alternative procedure from the general consensus on them. (Later in this section, superscript on and identifies their corresponding values in iteration .)
Numerical analysis of the case under study reveals , 16.45, 15.22, 13.97, and 23.66 for , TOPSIS, linear assignment, simple additive weighting, and Minkowski distance (for ), respectively.
4. MCDA of the decision procedures
Table 5 summarizes the results of the analyses of the five selected decision procedures in solving the original decision problem of the case under study. In this table, there are 9 measures of effectiveness for the 5 alternative decision procedures, as discussed in Section 3.2 . The alternative decision procedures are now used to evaluate themselves in solving the problem of the case under study. To do this, a weighting system is required to measure the relative importance of the measures of effectiveness. One such weighting is given in Table 5 , which weighs more important moe’s (approximately) twice ( ), the less important ones ( ), and one moe, the computation speed, is considered not important for the procedures of concern (but, of course, is important when procedures such as permutation come into play). The last line of Table 5 indicates whether the respective criterion of each entry of this line is positive or negative.
| Row | Evaluation method | moe | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Demand for information | Degree of information utilization | Frequency of using given information | Creation of a spectrum of solution | Computation time | Solution changes in successive applications | Effect of irrelevant attribute | Effect of irrelevant alternative | Deviation of solution from general consensus | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 | Electre | 2 | 1 | 28 | 1 | 156.39 | 1 | 1 | 0 | 12.99 |
| 2 | TOPSIS | 2 | 1 | 2 | 1 | 4.89 | 2 | 2 | 0 | 16.45 |
| 3 | Linear assignment | 2 | 0.75 | 1 | 1 | 2013.14 | 0 | 0 | 0 | 15.22 |
| 4 | Simple add. weight. | 2 | 1 | 1 | 1 | 2.08 | 0 | 1 | 0 | 13.97 |
| 5 | Minkowski dist. (α=2.0) | 3 | 1 | 1 | 1 | 3.66 | 5 | 5 | 0 | 23.66 |
| Weight 1 (w1) | 0.15 | 0.08 | 0.08 | 0.08 | 0.00 | 0.15 | 0.15 | 0.15 | 0.15 | |
| Sign of attributes | − | + | + | + | − | − | − | − | − | |
Table 6 shows the results of applying the five decision procedures to choose from the five target procedures. The rankings of the evaluating methods are shown in this table. Based on the results of Table 6 , the average rankings of the decision procedures (1) Electre, (2) TOPSIS, (3) Linear Assignment, (4) Simple Additive Weighting, and (5) Minkowski Distance , using equal weight for alternative procedure , are 1.40, 4.10, 2.00, 2.60, and 4.90, respectively (with average rank 4.5 for the non-selected procedures by Electre).
| Alternative procedure rank | Evaluating method: | ||||
|---|---|---|---|---|---|
| (1) Electre | (2) TOPSIS | (3) Linear Assignment | (4) Simple additive weighting | (5) Minkowski distance ( ) | |
| 1 | El | El | SA | El | El |
| 2 | LA | LA | LA | LA | LA |
| 3 | SA | SA | El | SA | SA |
| 4 | – | TO | TO | TO | TO |
| 5 | – | MD | MD | MD | MD |
a. The letters abbreviate the evaluating procedures’ names.
Thus, according to these average rankings, the five different selected alternative decision procedures may be named in the order of these average ranks as follows: (1) Electre, (3) Linear Assignment, (4) Simple Additive Weighting, (2) TOPSIS, and (5) Minkowski Distance.
5. Sensitivity analysis and information valuation
We now extend the analysis in two dimensions: First, evaluate the information given by the evaluating procedures proportional to their ranks; and second, analyze the sensitivity of the decisions regarding the better procedures, with respect to the weights of the evaluation criteria.
5.1. Sensitivity analysis
Aside from the base case weighting system, , as described in Table 5 and Table 10 other alternative weights, as in Table 7 , are specified to represent a range of weights on different evaluation criteria of the alternative procedures, in order to perform a sensitivity analysis of the decisions made by different decision procedures. These are a range of reasonable weighting systems devised to complement the weighting system, , to represent possible variants of the weights. Weight number 1, , represents the equal importance of the group of criteria (with each criterion within a group getting an equal share of this total assigned group weight). In the other weighting systems, it is assumed that the weight of (effect upon the solution) > the weight of (distance to general consensus) > the weight of (demand for information) = the weight of (information utilization and generation) = the weight of (solution spectrum) ≥ the weight of (computation speed); and three cases are considered for each main category. In the last three weighting systems in Table 7 , extreme cases check the stability of the solutions.
| Weight number ( ) | Evaluation criteria groupa | Remarks | |||||
|---|---|---|---|---|---|---|---|
| 0 | 2 | 2 | 1 | 0 | 6 | 2 | Base case weights |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | Equal weight |
| 2 | 1 | 1 | 1 | 0 | 3 | 2 | Group f weighted twice each of groups a to c, and group e weighted more. Group d is ignored |
| 3 | 1 | 1 | 1 | 0 | 4 | 2 | |
| 4 | 1 | 1 | 1 | 0 | 5 | 2 | |
| 5 | 2 | 2 | 2 | 1 | 4 | 3 | Group d is weighted 1, with each group a to c weighted twice, and group e more |
| 6 | 2 | 2 | 2 | 1 | 6 | 3 | |
| 7 | 2 | 2 | 2 | 1 | 8 | 3 | |
| 8 | 0 | 0 | 0 | 0 | 1 | 1 | Extreme weights |
| 9 | 0 | 0 | 0 | 0 | 2 | 1 | |
| 10 | 0 | 0 | 0 | 0 | 3 | 1 | |
a. ( ) Demand for information; ( ) Information utilization, and creation; ( ) Spectrum of solution; ( ) Computation speed; ( ) Effect upon solution: successive applications, irrelevant attribute, irrelevant alternative; and ( ) Distance of solution from general consensus.
To obtain the weights of each evaluation criterion mentioned above, one may proceed as follows: for each weight number , the weight of each group of criteria ( to ) may be obtained by dividing the figure in the respective cell in Table 7 by the sum of these figures in row . Each evaluation criterion in each group gets an equal share of the weight of the respective group.
5.2. Information valuation
Consider, once again, the results in Table 6 , which show how an evaluation procedure is viewed from the eyes of the other procedures. Let be the rank of alternative procedure, , by the evaluating procedure, , in iteration . Let be the weight of the information supplied by the evaluating procedure, , in iteration . (This is initially set as 1/5 for the procedures under study, representing an unbiased estimator for the no-information, or equally informative, case.) At any iteration , compute:
|
|
( 4) |
Lower rank alternative procedure ( ), according to index , is a procedure which is judged by the evaluating procedures ( ’s) to be better in identifying the superiority of the alternatives. Thus, it is justifiable to value the information supplied by lower rank alternatives more.
The value of the information supplied by an alternative procedure, , in iteration , is defined as follows:
|
|
( 5) |
where is a proportionality constant. Alternatively, one may define it by other suitable functions, such as:
|
|
( 6) |
Thus, the relative information value supplied by alternative procedure may be defined and modified in the course of an iterative procedure (using Eq. (5) ), as:
|
|
( 7) |
The reader recalls that one of the evaluating criteria in Table 5 , the “deviation of solution from general consensus”, , depends on . Thus, we may revise the respective vector in Table 5 and solve the problem once again, and repeat this process to convergence, i.e., when the respective weights of alternative procedures in two successive iterations (or the average ranks of alternative procedures in these iterations) remain (approximately) the same. (Proof of convergence depends on the procedures selected, and the case under study, as well as the assumed information, such as the weights of the evaluation criteria. Thus, attempts to prove such convergences may only be done for a unified situation, in which assumptions are made regarding these degrees of freedom. In our study case, this convergence has practically happened very rapidly.) The following algorithm formalizes the computations in the above discussion.
Peer Evaluation-Information Valuation Algorithm (PEIVA) .
Specify the weighting system, , and procedure (= (1) El, (2) TO, (3) LA, (4) SA, and (5) MD).
- Set , and use Eq. (7) to compute the relative information value of alternative procedure , .
- If , where is a pre-specified positive value, STOP. Otherwise, GO TO Step 2 with the new information values, ’s. □
- (= 5, in this paper).
- Identify the top (= 3, in this paper) alternative projects, , by applying procedure on the original decision problem, and find . Then, for this case, , 2, and 3 for , and , respectively. (In Electre, rank the alternative projects by the help of concordance and discordance indices.)
- Use Eq. (1) to compute the weighted rank of top projects: .
- Use Eq. (2) (or Eq. (3) , for ) to compute the deviation of the solution by procedure from general consensus: . (This prepares a table, like Table 5 , for the weighting system, , and sets the stage for the evaluation of decision procedures ( ’s) by peers ( ’s).)
- Apply the evaluating method, , to rank alternative decision procedures, ’s, and find to ; and to . (This prepares a table, like Table 6 .)
- Use Eq. (4) to compute the weighted average rank of procedure as seen by peers:
|
|
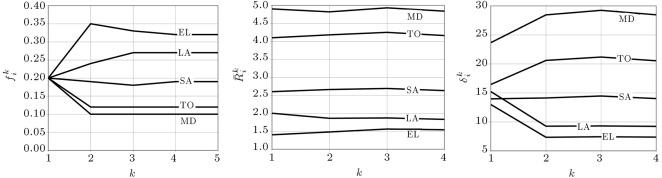
The results of four iterations of the above algorithm for the weighting system, , are shown in Figure 1 , which also shows rapid convergence of three key elements of the algorithm ( , and ). According to this analysis, the evaluating procedures Electre, linear assignment, simple additive weighting, TOPSIS, and Minkowski distance , with , 1.83, 2.63, 4.16, and 4.84, respectively, are the better multi-attribute decision procedures, in that order.
|
|
|
Figure 1. Convergence of the information values , the weighted average ranks , and the deviation of solution from general consensus , with iteration number , for the evaluation procedure and case of . |
Table 8 summarizes the information values, , of various evaluating procedures, , at iteration , starting from equal information values, , for each of them, to convergence at iteration , where further iterations render approximately the same values for all evaluating procedures. Depending on the importance of the information supplied by each procedure, the effects of these procedures in forming the general consensus vary, which changes the deviation of the solution of each procedure ( ) from this general consensus in identifying the better LRT networks ( , for iteration ). Columns 3, 4 and 5 in Table 8 show the rapid convergence of , and , to some limiting values, respectively. This happens for each weight, to in this table.
| Weight | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TO | LA | SA | MD | TO | LA | SA | MD | EL | TO | LA | SA | MD | |||||
| 1 | 2 | 3 | 4 | 5 | |||||||||||||
| w0 | 1 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 1 | 12.99 | 16.45 | 15.22 | 13.97 | 23.66 | 1.40 | 4.10 | 2.00 | 2.60 | 4.90 |
| 2 | 0.35 | 0.12 | 0.24 | 0.19 | 0.10 | 2 | 7.34 | 20.60 | 9.26 | 14.12 | 28.45 | 1.48 | 4.18 | 1.86 | 2.66 | 4.82 | |
| 3 | 0.33 | 0.12 | 0.27 | 0.18 | 0.10 | 3 | 7.43 | 21.18 | 9.30 | 14.46 | 29.23 | 1.56 | 4.25 | 1.87 | 2.69 | 4.93 | |
| 4 | 0.32 | 0.12 | 0.27 | 0.19 | 0.10 | 4 | 7.38 | 20.54 | 9.22 | 14.02 | 28.47 | 1.54 | 4.16 | 1.83 | 2.63 | 4.84 | |
| 5 | 0.32 | 0.12 | 0.27 | 0.19 | 0.10 | ||||||||||||
| w1 | 4 | 0.36 | 0.17 | 0.12 | 0.25 | 0.11 | 3 | 8.88 | 18.28 | 11.64 | 12.75 | 27.34 | 1.37 | 2.92 | 4.26 | 2.01 | 4.59 |
| w2 | 4 | 0.44 | 0.10 | 0.22 | 0.15 | 0.09 | 3 | 6.38 | 22.08 | 8.10 | 15.28 | 29.29 | 1.00 | 4.22 | 2.00 | 3.00 | 4.78 |
| w3 | 5 | 0.33 | 0.12 | 0.25 | 0.20 | 0.10 | 4 | 7.40 | 20.70 | 9.36 | 14.10 | 28.80 | 1.51 | 4.21 | 2.02 | 2.53 | 4.88 |
| w4 | 4 | 0.33 | 0.12 | 0.25 | 0.20 | 0.10 | 3 | 7.37 | 20.37 | 9.31 | 13.88 | 28.41 | 1.50 | 4.16 | 2.00 | 2.50 | 4.83 |
| w5 | 4 | 0.44 | 0.11 | 0.13 | 0.22 | 0.09 | 3 | 7.34 | 20.57 | 9.26 | 14.12 | 28.45 | 0.99 | 3.87 | 3.28 | 1.98 | 4.73 |
| w6 | 6 | 0.33 | 0.12 | 0.25 | 0.20 | 0.10 | 5 | 7.41 | 20.52 | 9.44 | 13.94 | 28.74 | 1.50 | 4.16 | 2.00 | 2.50 | 4.83 |
| w7 | 5 | 0.33 | 0.12 | 0.25 | 0.20 | 0.10 | 4 | 7.40 | 20.70 | 9.36 | 14.10 | 28.79 | 1.51 | 4.21 | 2.02 | 2.53 | 4.88 |
| w8 | 6 | 0.28 | 0.11 | 0.35 | 0.16 | 0.10 | 5 | 7.20 | 21.31 | 8.62 | 14.55 | 28.81 | 1.65 | 4.14 | 1.35 | 3.00 | 4.86 |
| w9 | 4 | 0.21 | 0.12 | 0.36 | 0.21 | 0.10 | 3 | 7.54 | 19.44 | 9.35 | 12.80 | 27.95 | 2.32 | 4.06 | 1.33 | 2.29 | 4.85 |
| w10 | 6 | 0.17 | 0.12 | 0.35 | 0.26 | 0.10 | 5 | 7.65 | 19.23 | 9.58 | 12.40 | 28.20 | 2.83 | 4.08 | 1.35 | 1.82 | 4.21 |
In another set of experiments, to see the stability of the weighted average ranks of the procedures, the limiting values of information rendered by various procedures were reversed: weights of information for ranks 1 and 5, and ranks 2 and 4, were interchanged, leaving the information weight of rank 3 procedure unchanged, as shown in Table 9 , for the weighting system . In this table, -reverse is the reversed information values of in Table 8 . Similar computations, as in Table 8 , reveal that the procedure converges to original information weights, as in Table 8 , within 2 iterations. (Compare the respective values of in Table 9 and in Table 8 .) A summary of the results of similar computations as in Table 9 for all weighting systems, to , are given in Table 10 . As is evident in this table, for a wide spectrum of weighting systems, to , and even for a reversed information valuation of the procedures, the rankings of these procedures converge to the respective values given in Table 8 . Moreover, this convergence is found to be rather fast for the case under study.
| Row | Procedure : | Electre | TOPSIS | Linear assignment | Simple additive weighting | Minkowski distance | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | fi5-reverse | 0.10 | 0.27 | 0.12 | 0.19 | 0.32 | ||||||||||
| 2 | θl5 | 16.15 | 9.84 | 11.61 | 11.51 | 8.93 | 6.06 | 16.15 | 14.8 | 11.61 | 11.54 | 9.84 | 11.61 | 8.93 | 13.75 | 14.89 | |
| 3 | δi | 19.11 | 12.98 | 21.62 | 15.71 | 18.50 | |||||||||||
| 4 | Rji5 | SA, TO, EL, LA, MD | EL, LA, SA, TO, MD | SA, LA, TO, EL, MD | EL, LA, SA, TO, MD | EL, SA, LA, TO, MD | |||||||||||
| 5 | R¯i5 | 1.56 | 3.68 | 2.56 | 2.24 | 5.0 | |||||||||||
| 2 | 1 | fi6 | 0.33 | 0.14 | 0.20 | 0.23 | 0.10 | ||||||||||
| 2 | θl6 | 7.47 | 5.16 | 6.08 | 13.33 | 15.96 | 8.04 | 7.47 | 9.19 | 6.08 | 13.33 | 5.16 | 6.08 | 15.95 | 18.64 | 19.71 | |
| 3 | δi | 7.83 | 19.29 | 10.15 | 13.10 | 27.92 | |||||||||||
| 4 | Rji5 | EL, LA, SA, (TO, MD) | EL, LA, SA, TO, MD | SA, LA, EL, TO, MD | EL, LA, SA, TO, MD | EL, LA, SA, TO, MD | |||||||||||
| 5 | R¯i5 | 1.4 | 4.16 | 2.0 | 2.93 | 4.84 | |||||||||||
| fi7 | 0.36 | 0.12 | 0.25 | 0.17 | 0.10 | ||||||||||||
| Weight | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TO | LA | SA | MD | TO | LA | SA | MD | TO | LA | SA | MD | ||||||
| 1 | 2 | 3 | 4 | 5 | |||||||||||||
| w0 | 1 | 0.10 | 0.27 | 0.12 | 0.19 | 0.32 | 1 | 19.11 | 12.98 | 21.62 | 15.71 | 18.50 | |||||
| 3 | 0.36 | 0.12 | 0.25 | 0.17 | 0.10 | 2 | 7.83 | 19.29 | 10.15 | 13.10 | 27.92 | 1.40 | 4.16 | 2.00 | 2.93 | 4.84 | |
| w1 | 1 | 0.11 | 0.17 | 0.25 | 0.12 | 0.36 | 1 | 18.53 | 16.92 | 19.75 | 18.48 | 19.38 | |||||
| 4 | 0.36 | 0.17 | 0.11 | 0.24 | 0.11 | 3 | 9.63 | 17.71 | 12.40 | 12.88 | 26.54 | 1.33 | 2.89 | 4.28 | 2.00 | 4.49 | |
| w2 | 1 | 0.09 | 0.15 | 0.22 | 0.10 | 0.44 | 1 | 20.68 | 14.91 | 22.11 | 18.89 | 16.22 | |||||
| 3 | 0.45 | 0.13 | 0.17 | 0.15 | 0.09 | 2 | 9.18 | 18.44 | 11.73 | 13.31 | 26.92 | 1.00 | 3.63 | 2.63 | 2.95 | 4.81 | |
| w3 | 1 | 0.10 | 0.25 | 0.12 | 0.20 | 0.33 | 1 | 19.08 | 13.23 | 21.49 | 15.94 | 18.41 | |||||
| 3 | 0.37 | 0.12 | 0.24 | 0.18 | 0.10 | 2 | 8.51 | 18.48 | 11.17 | 12.60 | 27.59 | 1.31 | 4.20 | 2.02 | 2.73 | 4.88 | |
| w4 | 1 | 0.10 | 0.25 | 0.12 | 0.20 | 0.33 | 1 | 19.08 | 13.23 | 21.49 | 15.94 | 18.41 | |||||
| 3 | 0.37 | 0.11 | 0.24 | 0.18 | 0.10 | 2 | 7.82 | 18.48 | 10.39 | 12.44 | 27.38 | 1.29 | 4.13 | 1.98 | 2.67 | 4.78 | |
| w5 | 1 | 0.09 | 0.22 | 0.13 | 0.11 | 0.44 | 1 | 22.52 | 14.40 | 24.11 | 19.56 | 15.10 | |||||
| 3 | 0.44 | 0.12 | 0.13 | 0.22 | 0.09 | 2 | 10.33 | 16.17 | 13.25 | 11.83 | 22.50 | 0.99 | 3.74 | 3.33 | 1.98 | 4.80 | |
| w6 | 1 | 0.10 | 0.25 | 0.12 | 0.20 | 0.33 | 1 | 19.30 | 13.50 | 21.68 | 16.26 | 18.55 | |||||
| 3 | 0.38 | 0.12 | 0.20 | 0.20 | 0.10 | 2 | 8.92 | 18.09 | 11.70 | 12.53 | 27.30 | 1.27 | 4.21 | 2.39 | 2.40 | 4.88 | |
| w7 | 1 | 0.10 | 0.25 | 0.12 | 0.20 | 0.33 | 1 | 19.08 | 13.23 | 21.49 | 15.94 | 18.41 | |||||
| 4 | 0.35 | 0.12 | 0.24 | 0.19 | 0.10 | 3 | 7.36 | 20.56 | 9.49 | 14.06 | 28.72 | 1.41 | 4.23 | 2.02 | 2.63 | 4.86 | |
| w8 | 1 | 0.11 | 0.28 | 0.10 | 0.16 | 0.35 | 1 | 20.41 | 12.98 | 22.85 | 16.70 | 17.45 | |||||
| 6 | 0.27 | 0.11 | 0.37 | 0.15 | 0.10 | 5 | 7.35 | 20.56 | 9.24 | 14.08 | 28.45 | 1.75 | 4.17 | 1.25 | 3.00 | 4.86 | |
| w9 | 1 | 0.21 | 0.21 | 0.10 | 0.12 | 0.36 | 1 | 19.16 | 15.72 | 21.00 | 18.12 | 18.30 | |||||
| 3 | 0.17 | 0.12 | 0.37 | 0.25 | 0.10 | 2 | 8.56 | 17.95 | 10.97 | 11.60 | 27.66 | 2.87 | 4.12 | 1.30 | 1.89 | 4.97 | |
| w10 | 1 | 0.17 | 0.26 | 0.10 | 0.12 | 0.35 | 1 | 19.87 | 14.40 | 22.04 | 17.44 | 17.90 | |||||
| 3 | 0.15 | 0.11 | 0.44 | 0.22 | 0.09 | 2 | 7.85 | 17.55 | 10.59 | 10.55 | 27.99 | 3.03 | 4.11 | 1.01 | 2.02 | 4.97 | |
6. Conclusions and further recommendations
Comparison of multi-attribute decision-making procedures can be, by itself, a multi-criteria decision problem. The effectiveness of the procedures depends on their characteristics, which may be measured on scales of some criteria. Suppose that such criteria may be defined, which together define the effectiveness, goodness, robustness, etc. of the procedures, in identifying the better decision for the original problem. This paper presents an approach in evaluating alternative evaluation procedures. This approach connotes “peer evaluation”, which, although existing in practice, was not seen as an effective and serious tool to evaluate various alternative procedures.
The decision context of concern in this paper is the one in which a set of alternatives are contrasted against a set of criteria, as in most engineering problems, forming a matrix of alternative-criteria, where a vector of weights or importance levels associates with the criteria. A set of 5 known and popular multi-attribute decision procedures have been selected in this context from the literature. These procedures were exploited to evaluate themselves, based on 9 criteria, as they perform in solving an original decision problem of selecting a light rail transportation network for a real case large metropolitan area. These procedures are Electre (El), TOPSIS (TO), Linear Assignment (LA), Simple Additive Weighting (SA), and Minkowski Distance (MD).
The results of this analysis show that Electre was elected as the better procedure among El, LA, SA, TO, and MD, and the other better procedures are found in this order for the case under study. A sensitivity analysis on a wide range of evaluation attribute weights accentuated this finding for the case. However, it is to be emphasized that, despite specific conclusions made regarding the better decision procedures among those evaluated, this paper finds its contribution mainly in the approach to such evaluations. More specifically, the paper presents two concepts of peer evaluation, and information valuation. By peer evaluation, it is meant to exploit the same procedures to find the better one(s) among themselves. The information valuation concept introduces higher weights to the information supplied by the alternative procedures, which are deemed to be more appropriate, by peers giving them higher ranks. The peer evaluation-information valuation is iterated to convergence. It is shown, for the case under study, that the proposed iterative method is rapidly convergent to the same point, even under a reversed weighting situation of evaluation criteria.
The proposed approach is demonstrated in this study by practicing it on a real engineering case. The analysis enjoyed an engineering approach toward the selection problem: It defined certain evaluation criteria, assumed measures to quantify them, and specified weights to show their relative importance. It assumed functions to valuate information, or to measure distance from general consensus. Moreover, convergence is shown practically to happen for the case under study. All these endeavors are done to set forth the two concepts mentioned above.
We propose the following directions of research in continuation of this study: (a) Devising new evaluation criteria, as in Section 3.4 , and agreeing over what should be expected from a good MCDA method; (b) Administration of similar endeavors, as in the case of LRT in this study, to conclude the better analysis techniques in various areas of decision-making (in engineering, the environment, science, medicine, politics, social-sciences, etc.), as well as in various decision-making contexts (full/ partial information, with/without uncertainty, etc.); (c) Improvement of the study approach in various dimensions, such as information valuation function, and last, but not least; (d) provision of convergence proofs for specific agreed upon cases of PEIVA. The authors believe that a collection of similar endeavors may complement the findings in this paper, and build a bank of information regarding the better DM procedures on different cases. It is expected that future critical discussions by interested professionals in this area, based on such an information bank, would establish a more solid foundation for the introduction of better MCDA methods in different situations.
Appendix A.
A.1. ELECTRE method (EL)
Electre has several variants. The following is one such procedure, used in this paper: (a) Construct the concordance set of two alternatives and as , and the discordance set , for all ; and l; (b) Calculate the concordance index of two alternatives and as and , where and , and where denotes the cardinality of the set ; (c) Compute the Net Concordance and Net Discordance Indices of alternative as, , and , respectively for all ; and (d) The set of alternatives with and are defined as the set of non-dominated alternatives. □
A.2. TOPSIS (TO)
TOPSIS is based on the concept that the better alternatives should be closer to an “ideal” alternative and farther from an “opposing-to-ideal“alternative. The procedure may be defined as follows: (a) create alternatives and 0, such that and ; (b) Calculate the (weighted) distances of the alternatives ( ) to the ideal , and opposite-to-ideal , alternatives as follows and ; (c) Calculate the relative closeness of alternative to ideal solution as ; and (d) Rank alternatives based on the increase in value of and pick the top of the list alternative(s) as the best one(s). □
for the ideal alternative (since ), and for the opposite-to-ideal alternative (since ), so that , for all .
A.3. Compensatory linear assignment (LA)
This method is based on separate rankings of alternatives for each moe with a given weight. The procedure is as follows: (a) Construct the elements of matrix , as if alternative is ranked when compared to other alternatives based on moe j. (b) Compute the elements of matrix as , where if , otherwise . (c) Solve the following linear programming problem for ’s: , and , for all , (d) Find the optimal ordering of the alternatives by , where is the vector of alternatives and the matrix of optimal permutation. □
This method works for ordinal, rather than cardinal, input data.
A.4. Simple additive weighting (SA)
This widely used method of multi-attribute decision making procedure may be stated as follows: (a) Compute . (b) Find the best alternative which has the maximum value of . □
A.5. Minkowski distance (MD)
This method of alternative evaluation is similar to TOPSIS, but computes only one measure of distance to the ideal alternative: (a) Create the ideal alternative characteristics as ; (b) Calculate the distance of alternative to the ideal alternative as , for a given ; (c) Rank alternatives in the order of increasing , and choose the alternative in the top of this list. □
This method reduces to the Simple Additive Weighting method when . Lower values of (close to 1.0) permit compensation among moe’s in making the distance to the ideal alternative. As increases (to, say, 5.0 or more), values of moe’s, which are significantly different from the respective values of the ideal alternative, become more influential in determining the distance, pushing the alternatives with such different moe’s further away from the ideal alternative. Thus, lower values may represent risk-prone decision-makers, while the higher values may be attributable to more risk-averse individuals.
Appendix B. Proof of Lemma 1
(a) For Electre: For an alternative , the cardinality of the set , is a non-decreasing function of a positive attribute value for any other alternative ; and, thus, is a non-decreasing function of that attribute value. Similarly, and , for all other alternatives , are non-increasing functions of negative attribute value. At the same time, and are non-increasing, and and are non-decreasing functions of such an attribute value. Therefore, is non-decreasing, and is non-increasing for a positive attribute value, which collectively increase the potential of alternative to be in the set of non-dominated alternatives.
(b) For TOPSIS: is a non-decreasing function of positive attribute value, and higher values of such attributes for an alternative shortens the distance of the alternative to the ideal alternative , and, thus, increases the closeness index to the ideal alternative, , which would, in turn, decrease the (value of the) rank of alternative . Similar reasoning show that is non-increasing function of negative attribute value, and that lower values of such attributes for an alternative shortens (the distance to the opposite-to-ideal alternative), and, thus, decreases , which would, in turn, increase the (value of the) rank of alternative .
(c) For Compensatory Linear Assignment: Higher value of a positive attribute would decrease for alternative , which would, in turn, raise the weight of higher rank position for . That is, is a non-decreasing function for lower values (i.e., higher ranks). Thus, the chance of to be assigned to higher ranks is a non-decreasing function of positive attribute values. Similar reasoning would show the reverse for negative attribute values.
(d) For Simple Additive Weighting: Higher value of a positive attribute, , for an alternative, , would increase , and, thus, the chance of being maximum would be non-decreasing. The reverse is true for a higher value of a negative attribute.
(e) For Minkowski Distance is a non-decreasing function of the value of a positive attribute, , for an alternative, . So, (2.0) is a non-increasing function of the value of , which makes the rank of non-increasing. The reverse is true for a value of negative attribute: higher values of such attributes for alternative would make the rank of non-decreasing. □
References
- [1] M. Behzadian, R.B. Kazemzadeh, A. Albadvi, M. Aghdasi; PROMETHEE: a comprehensive literature review on methodologies and applications; European Journal of Operational Research, 200 (2010), pp. 198–215
- [2] C. Zopounidis, M. Doumpos; Multi-criteria classification and sorting methods: a literature review; European Journal of Operational Research, 138 (2002), pp. 229–246
- [3] S. Hajkowicz; A comparison of multiple criteria analysis and unaided approaches to environmental decision making; Environmental Science & Policy, 10 (2007), pp. 177–184
- [4] E. Triantaphyllou; Multi-Criteria Decision Making Methods: A Comparative Study, Applied Optimization Series, 44, , Springer (2000)
- [5] K. Mela, T. Tiainen, M. Heinisuo; Comparative study of multiple criteria decision making methods for building design; Advanced Engineering Informatics, 26 (4) (2012), pp. 716–726
- [6] A. Guitouni, J.-M. Martel; Tentative guidelines to help choosing an appropriate MCDA method; European Journal of Operational Research, 109 (1998), pp. 501–521
- [7] H. De Bruijn, W. Veeneman; Decision-making for light rail; Transportation Research Part A, 43 (2009), pp. 349–359
- [8] C.L. Hwang, K. Yoon; Multiple Attribute Decision Making: Methods and Applications, A State-of-the-Art Survey; Springer-Verlag, Berlin (1981)
- [9] B. Roy; Multi-Criteria Methodology for Decision Aiding; Kluwer, Dordrecht (1996)
- [10] V. Belton, T.J. Stewart; Multiple Criteria Decision Analysis; Kluwer, Dordrecht (2001)
- [11] J. Figueira, S. Greco, M. Ehrgott (Eds.), Multiple Criteria Decision Analysis: State of the Art Surveys, Springer, New York (2009)
- [12] B.S. Ahn, K.S. Park; Comparing methods for multi-attribute decision making with ordinal weights; Computers and Operations Research, 35 (2008), pp. 1660–1670
- [13] E. Triantaphyllou, S.H. Mann; An examination of the effectiveness of multi-dimensional decision-making methods: a decision-making paradox; Decision Support Systems, 5 (1989), pp. 303–312
- [14] D.M. Buede, D.T. Maxwell; Rank disagreement: a comparison of multi-criteria methodologies; Journal of Multi-Criteria Decision Analysis, 4 (1995), pp. 1–21
- [15] Guitouni, A., Martel, J.-M., Vincke, P., North, P.B. and Val-bblair, O.G.X “A framework to choose a discrete multi-criterion aggregation procedure”, Accessed by CiteSeerX (October 2012).
- [16] S.H. Zanakis, A. Solomon, N. Wishart, S. Dublish; Muti-attribute decision making: a simulation comparison of select methods; European Journal of Operational Research, 107 (1998), pp. 507–529
- [17] P. Salminen, J. Hokkanen, R. Lahdelma; Comparing multi-criteria methods in the context of environmental problems; European Journal of Operational Research, 104 (1998), pp. 485–496
- [18] M. Bohanec, V. Rajkovic; Multi-attribute decision modeling: industrial applications of DEX; Informatica, 23 (1999), pp. 487–491
- [19] C. Parkan, M.-L. Wu; Comparison of three modern multi-criteria decision making tools; International Journal of Systems Science, 31 (4) (2000), pp. 497–517
- [20] G. Munda; Multi-criteria assessment; Internet Encyclopedia of Ecological Economics, International Society for Ecological Economics (2003) (accessed October 2012)
- [21] Roy, B. “Methodologie Multicritere Daide a la Decision”, In Economica , Paris (1985).
- [22] B. Roy; Decision aid and decision making; C.A. Bana e Costa (Ed.), Readings in Multiple Criteria Decision Aid, Springer-Verlag, Heidelberg (1990), pp. 17–35
- [23] S. Opricovic, G.-H. Tzeng; Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS; European Journal of Operational Research, 156 (2004), pp. 445–455
- [24] S. Hajkowicz, A. Higgins; A comparison of multiple criteria analysis techniques for water resource management; European Journal of Operational Research, 184 (2008), pp. 225–265
- [25] E. Mostert; Managing water resources infrastructure in the face of different values; Physics and Chemistry of the Earth, 33 (2008), pp. 22–27
- [26] Al-Ani, I.A., Sidek, L.M., Desa, M.N.M. and Basri, N.E.A. “Development of decision support tools for urban storm drainage”, Proceedings of 12th International Conference on Urban Drainage , Porto Alegre, Brazil, pp. 1–8 (11–16 September 2011).
- [27] V. Mousseau, L. Dias, J. Figueira; Dealing with inconsistent judgments in multiple criteria sorting models; 4OR: A Quarterly Journal of Operations Research, 4 (2006), pp. 145–158
- [28] Y.S. Eum, K.S. Park, S.H. Kim; Establishing dominance and potential optimality in multi-criteria analysis with imprecise weight and value; Computers and Operations Research, 28 (2001), pp. 397–409
- [29] C.W. Kirkwood, R.K. Sarin; Ranking with partial information: a method and an application; Operations Research, 23 (1985), pp. 38–49
- [30] R. Vetschera, Y. Chen, K.W. Hipel, D.M. Kilgour; Robustness and information levels in case-based multiple criteria sorting; European Journal of Operational Research, 202 (3) (2009), pp. 841–852
- [31] Samson, D. “Managerial decision analysis”, In The Irwin Series in Quantitative Analysis for Business, Ill , US (1988).
- [32] T.L. Saaty, L.G. Vargas; Decision Making with the Analytic Network Process, Economic, Political and Technological Applications with Benefits, Opportunities, Costs and Risks; Springer, New York (2006)
- [33] T.L. Saaty; Fundamentals of Decision Making and Priority Theory, with the Analytic Hierarchy Process, AHP Series, VI, , RWS Publications, Pittsburgh, PA, USA (2000)
- [34] R.V. Rao; Decision Making in the Manufacturing Environment; Springer-Verlag, London (2007)
- [35] Y. Sheffi; Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods; Prentice-Hall, NJ, USA (1985)
- [36] H. Spiess, M. Florian; Optimal strategies: a new assignment model for transit networks; Transportation Reserarch Part B, 23 (1989), pp. 83–102
- [37] INRO, “EMME/2 User’s Manual”, Software Release 9.2, Montreal, Canada (1999).
- [38] H. Poorzahedy, H.Z. Aashtiani, Y. Shafahi, M. Kermanshah; Analysis of the results of an opinion survey regarding Mashhad public transportation systems; Mashhad Integrated Public Transportation Studies; Report No. 82-01, The Institute for Transportation Studies and Research, Sharif Univ. of Tech., Tehran, Iran (2003) (in Farsi)
- [39] R. de Neufville, J.H. Stafford; System Analysis for Engineers and Managers; McGraw-Hill Book Co., New York (1971)
Document information
Published on 06/10/16
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?