Robust Design Optimization applied to aeronautics combining stochastic calculus with evolutionary algoritms

Resumen

Las incertidumbres son un problema cotidiano en la ingeniería aeroespacial y en sus aplicaciones. Los métodos de optimización robusta utilizan, normalmente, y para asegurar la robustez de las soluciones, la generación aleatoria de los valores con incertidumbres así como criterios de selección multi-punto para la determinación del óptimo. Desde un punto de vista computacional, la aplicación a problemas de fluido-dinámica (CFD) o interacción fluido-estructura (FSI) puede ser extremadamente cara. Este trabajo presenta el acoplamiento entre el cálculo estocástico y los algoritmos evolutivos para la definición de un procedimiento de optimización robusta. Se propone, en primer lugar, una metodología para el cálculo estocástico, que a continuación se aplica a la solución de problemas de optimización. Estos métodos propuestos se han aplicado a dos tipos de problemas; un problema de CFD y otro de FSI orientados a la reducción de la resistencia aerodinámica y del fenómeno de estabilidad estructural conocido por «flutter», respectivamente.

Abstract

Uncertainties are a daily issue to deal with in aerospace engineering and applications. Robust optimization methods commonly use a random generation of the inputs and take advantage of multi-point criteria to look for robust solutions accounting with uncertainty definition. From the computational point of view, the application to coupled problems, like fluid-dynamics (CFD) or fluid-structure interaction (FSI), can be extremely expensive. This work presents a coupling between stochastic analysis techniques and evolutionary optimization algorithms for the definition of a stochastic robust optimization procedure. At first, a stochastic procedure is proposed to be applied into optimization problems. The proposed method has been applied to both CFD and FSI problems for the reduction of drag and flutter, respectively.

Palabras clave

Optimizació robusta ; Incertidumbre ; Cálculo estocástico ; Algoritmos evolutivos ; Fluido-dinámica ; Aero-estructuras

Keywords

Robust design optimization ; Uncertainty ; Stochastic calculus ; Evolutionary algorithms ; Fluid dynamics ; aero-structures

1. Introducción

Los problemas de optimización son un punto de encuentro de diferentes disciplinas, incluyendo aquellas relacionadas con las herramientas de análisis como los códigos de CFD y estructurales. Gracias a los avances en ciencias de la computación, que permiten una mayor rapidez de cálculo, los problemas de CFD y aero-elásticos han pasado a ser de resolución cotidiana, y lo que ahora está en la punta de lanza es la resolución de problemas con incertidumbres en los datos.

La cuantificación de la incertidumbre es un concepto importante a tener en cuenta durante la simulación y la optimización de los procesos. La gestión de la incertidumbre produce mejores resultados al asegurar la robustez de la solución ante variaciones de los datos. Existe incertidumbre al modelar un proceso debido a las simplificaciones de las ecuaciones de gobierno o a las aproximaciones de la discretización, pero en este trabajo el foco está en las incertidumbres de los parámetros que definen el proceso. Estas están generalmente relacionadas con el comportamiento del fenómeno natural o con las tolerancias de fabricación que acaban perjudicando el punto nominal de trabajo. Las incertidumbres se pueden clasificar en dos categorías, según Helton y Davis [1] .

La primera es la llamada incertidumbre aleatoria. El comportamiento de la naturaleza, con su variabilidad inherente, es un buen ejemplo. Gracias a la observación empírica este tipo de incertidumbre puede ser modelada de forma precisa, y representada a través de métodos probabilísticos.

La segunda categoría es la llamada incertidumbre epistémica que viene de una falta de conocimiento acerca del proceso o sistema. Normalmente es difícil de modelar utilizando métodos probabilísticos y se tiende a modelar por intervalos (véase ref. [2] ).

El objetivo del presente trabajo es definir una nueva metodología para los problemas de optimización en aerodinámica, o problemas acoplados aero-estructurales. Esta metodología tiene que permitir la definición estocástica de los parámetros de entrada para una mejor representación de la incertidumbre asociada a los mismos. Esta metodología será eficiente, de manera que se reducirán al máximo el número de evaluaciones comparado con la dimensión del espacio de las soluciones. Tiene que ser robusta, y encontrar el valor óptimo dada cualquier topología del espacio de búsqueda. Se tiene que tener en cuenta que los problemas de ingeniería, y en especial los relacionados con la aerodinámica y las aero-estructuras, requieren no únicamente el punto de trabajo óptimo, sino también operar en un amplio rango de condiciones.

Este artículo está organizado en cuatro secciones. Después de esta introducción, la segunda sección se centra en la definición del procedimiento de definición de los valores estocásticos. La tercera sección está destinada a la integración del procedimiento estocástico con los métodos de optimización, basados en algoritmos evolutivos. Esta sección presenta un ejemplo ilustrativo de la metodología completa. Finalmente, la cuarta sección subraya las conclusiones y plantea el trabajo de desarrollo a realizar a partir de los resultados obtenidos.

2. Procedimiento estocástico

En los problemas de ingeniería existen varias fuentes de incertidumbre. Falta de información o conocimiento acerca del fenómeno estudiado, o bien errores en las pruebas o errores numéricos pueden crear incertidumbre en los datos que pueden provocar una gran variabilidad en los resultados, lo que puede conducir a unas conclusiones erróneas. Tan importante es asegurar la buena comprensión del fenómeno físico como de la incertidumbre asociada.

Los procedimientos estocásticos se basan en acoplar un generador de valores aleatorios con el programa de análisis. Las variables de entrada son entonces definidas a partir de su función de densidad de probabilidad (PDF); las distribuciones gaussianas y las uniformes son las más utilizadas. A partir de esta información se genera una nube de puntos aleatorios que representan un estado fenómeno y en el que se evaluará la función objetivo. El conjunto de resultados obtenidos se analiza con herramientas estadísticas.

Esta sección presenta diferentes ejemplos de análisis estocásticos, aplicando variabilidad a diferentes parámetros de definición del problema, así como las conclusiones de dichos ejemplos.

Los casos analizados pretenden verificar que los resultados obtenidos con el procedimiento de cálculo estocástico permiten aplicarlo en desarrollo de una técnica de optimización de diseño robusto. Los resultados se evaluarán en comparación con el comportamiento físico conocido, de manera que se obtenga una validación desde el punto de vista del procedimiento pero también del sentido de los resultados.

En esta investigación, el código STAC se ha utilizado para generar los valores aleatorios a partir de la información probabilística. STAC es una herramienta de gestión del cálculo estocástico. STAC utiliza los desarrollos de Hurtado y Barbat [3] para la generación de los valores estocásticos a partir de muestreos de Monte-Carlo o de hipercubo latino. El entorno gráfico de STAC desarrollado en CIMNE facilita un pre y pos-procesado de la información de manera fácil y eficaz. El programa permite la definición de distintas funciones de densidad de probabilidad, tanto continuas como discretas.

En los ejemplos mostrados donde existen varias variables con incertidumbre, se ha definido una combinación de casos estocásticos que permite comparar e identificar las variables que introducen mayor variabilidad en los valores de salida.

Dos ejemplos, uno de fluido-dinámica (CFD) y otro de aero-elasticidad, serán expuestos en las próximas secciones. En el ejemplo de fluido-dinámica, el principal objetivo es analizar la variabilidad de los coeficientes de sustentación y de resistencia respecto a un ángulo de ataque (AoA) y un número de Mach (M) con incertidumbres. El problema aero-elástico se define para capturar la variabilidad de los valores aerodinámicos y estructurales para identificar la aparición del fenómeno de inestabilidad estructural conocido como «flutter». Los valores de salida analizados son el coeficiente de sustentación (Cl) y la resistencia de presión (Cdp), así como la rotación angular y la deformación vertical del ala. Se aplica incertidumbre a M, AoA, la coordenada x del eje elástico, los coeficientes de amortiguación del movimiento angular y vertical, y el cociente de masas. Desde un punto de vista ingenieril, el problema CFD permite determinar la mejor configuración para la reducción de la resistencia y la maximización de la sustentación, mientras que el problema aero-elástico ayuda a entender el problema de seguridad de la inestabilidad estructural.

2.1. Ejemplo de análisis estocástico de CFD

Para ilustrar la operativa del análisis estocástico se ha analizado un perfil RAE2822 bajo condiciones de incertidumbre en los parámetros de entrada. Se ha aplicado incertidumbre en el análisis fluido-dinámico del perfil. A cada uno de los parámetros de entrada escogidos se les ha aplicado diferentes definiciones estocásticas, y se ha analizado el comportamiento de las variables de salida. La combinación de múltiples casos ha permitido detectar la influencia de cada entrada en los valores de salida.

Se han planteado 8 casos diferentes que combinan diferentes análisis estocásticos. La tabla 1 muestra los casos analizados y su definición. El primero de ellos solo ha considerado el número de Mach (M) como valor estocástico, y el ángulo de ataque (AoA) se ha mantenido constante. En el segundo caso es el AoA el parámetro estocástico y M se mantiene constante. Los casos 3 a 8 han considerado AoA y M como parámetros estocásticos, pero definidos a partir de diferentes PDF.

Tabla 1. Definición de los casos analizados

Condiciones de flujo	Ángulo de ataque Media/Dev std	Número de Mach Media/Dev std
Caso 1: PDF gaussiana	4/--	0,7/0,08
Caso 2: PDF gaussiana	4/0,5	0,7/--
Caso 3: PDF gaussiana	4/0,5	0,7/0,08
Caso 4: PDF gaussiana	4/1,0	0,7/0,08
Caso 5: PDF gaussiana	4/1,5	0,7/0,08
Caso 6: PDF gaussiana	4/0,5	0,7/0,04
Caso 7: PDF gaussiana	4/0,5	0,7/0,12
	Low- Up bounds	Low- Up bounds
Caso 8: PDF uniforme	2,5–4,5	0,45–0,95

Para cada uno de los 8 casos, STAC ha definido un conjunto de muestras, 250 en concreto, a partir de la definición de probabilidad y utilizando el método de Monte-Carlo. Para cada muestra correspondiente a los dos valores generados para las condiciones de flujo se ha obtenido una solución del problema de CFD. La herramienta utilizada es un código llamado PUMI desarrollado en CIMNE por Flores y Ortega [4] . Está basado en las ecuaciones de Euler y utiliza una técnica de estabilización añadida a un esquema de Galerkin para evitar soluciones no físicas. La robustez de la solución se asegura a través de una integración temporal basada en un esquema explícito multi-etapa de Runge-Kutta. Especial atención se tomó en cuanto a la eficiencia del código para poder lidiar con problemas de alta complejidad y reducir los requisitos computacionales. Otros códigos de CFD pueden acoplarse a la rutina descrita. Uno con los que se han realizado algunos test es XFOIL [5] , que permite trabajar en casos subsónicos con número de Mach bajos.

Una vez analizadas todas las muestras, los resultados, el coeficiente de fuerza de sustentación y el coeficiente de resistencia (C_l and C_dp ), se han analizado estadísticamente. La media y la desviación estándar de cada coeficiente se han calculado para poder capturar el comportamiento bajo incertidumbres y detectar alguna correlación entre parámetros. El análisis numérico se ha definido utilizando GiD [6] como la herramienta de pre y pos-proceso. Se ha generado una malla no-estructurada, permitiendo un análisis con mayor exactitud de todos los casos. Se ha definido un tamaño de malla más fino en torno al perfil. Para asegurar la convergencia en un amplio rango de geometrías, la configuración del código se ha adaptado al problema a solucionar. Detalles acerca de los parámetros de configuración se pueden encontrar en [7] .

La tabla 2 muestra la lista de valores obtenidos para los mínimos, máximos, desviación estándar y valor medio de los resultados, los coeficientes C_l y C_dp , para los 8 casos definidos.

Tabla 2. Condiciones de flujo en los casos analizados

Flow Conditions	Cl	Cdp
Caso 1: PDF gaussiana
Mínimo	0,196710	0,000660
Máximo	0,801520	0,116290
Dev std	0,112927	0,023424
Media	0,575257	0,014833
Caso 2:PDF gaussiana
Mínimo	0,448210	-0,001500
Máximo	0,677780	0,004160
Dev std	0,045442	0,000812
Media	0,563089	0,001467
Caso 3: PDF gaussiana
Mínimo	0,217150	-0,000300
Máximo	0,887760	0,124900
Dev std	0,126863	0,027027
Media	0,581701	0,017832
Caso 4: PDF gaussiana
Mínimo	0,249090	-0,000100
Máximo	1,031040	0,103300
Dev std	0,150591	0,020772
Media	0,578093	0,014280
Caso 5: PDF gaussiana
Mínimo	0,152880	-0,002500
Máximo	1,049770	0,137490
Dev std	0,168275	0,027084
Media	0,565699	0,016121
Caso 6: PDF gaussiana
Mínimo	0,401550	-0,000100
Máximo	0,861750	0,054020
Dev std	0,085143	0,008020
Media	0,562241	0,006400
Caso 7: PDF gaussiana
Mínimo	0,156320	0,000580
Máximo	0,871920	0,123860
Dev std	0,146843	0,031274
Media	0,559294	0,020944
Caso 8: PDF uniforme
Mínimo	0,125770	-0,000900
Máximo	0,844940	0,124070
Dev std	0,163701	0,044329
Media	0,465643	0,033504

El análisis de estos valores permite confirmar la relación entre sustentación y resistencia y AoA y M. Estas conclusiones sirven de validación del método estocástico definido.

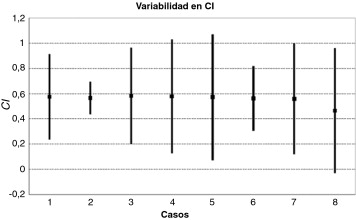
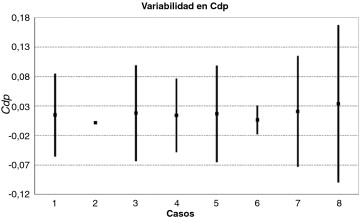
Las Figura 1  and Figura 2 muestran, respectivamente, los valores medios de C_l y C_dp para cada caso con su correspondiente rango + - 3σ. Un resultado con un rango + - 3σ amplio significa una mayor dispersión en el comportamiento de los resultados del análisis estocástico. Una mayor dispersión significa además una mayor dependencia con respecto a las variables de entrada. Por el contrario, una dispersión menor define una menor sensibilidad de los resultados frente a variaciones en las entradas.

Figura 1. Medias y rangos de la desviación estándar para Cl .

Figura 2. Medias y rangos de la desviación estándar para Cdp .

En las Figura 1  and Figura 2 se puede analizar esta sensibilidad y su relación con los diferentes parámetros de entrada.

La comparación entre los coeficientes de variación de los parámetros de entrada y de salida puede ser utilizada como una medida de la dispersión. El coeficiente de variación se define como el cociente entre la desviación estándar y la media. Valores bajos significan una dispersión menor. De todas formas, si los coeficientes de dos parámetros son iguales, esto significa que las variabilidades son idénticas. Con esto es fácil identificar la relación entre los parámetros de entrada y salida.

En la tabla 3 , los coeficientes de variación de los parámetros de entrada, AoA y M, y las variables de salida, C_l y C_dp , se han tabulado. De ahí se deduce que la distribución de C_dp es más sensible que la de C_l .

Tabla 3. Coeficientes de variación

Condiciones de flujo	AoA	M	Cl	Cdp
Caso 1: Gaussiana	0	0,114	0,196	1,579
Caso 2: Gaussiana	0,125	0	0,081	0,553
Caso 3: Gaussiana	0,125	0,114	0,218	1,516
Caso 4: Gaussiana	0,25	0,114	0,260	1,455
Caso 5: Gaussiana	0,375	0,114	0,297	1,680
Caso 6: Gaussiana	0,125	0,057	0,151	1,253
Caso 7: Gaussiana	0,125	0,171	0,263	1,493
Caso 8: Uniforme	0,048	0,060	0,352	1,323

Los casos 1 y 2 muestran el comportamiento cuando AoA y M se mantienen constantes. M produce un efecto mayor que AoA para ambos casos de C_l y de C_dp , que presentan un valor del coeficiente menor. En el resto de casos, la diferencia se observa en los valores de los coeficientes. Mientras que los valores para C_l son menores de 1 sobre 0,25 de media, los valores para C_dp son mayores de 1 hacia 1,4 de media. Esto significa un orden de magnitud mayor. Además, los valores correspondientes a C_l son similares a los valores de los parámetros de entrada, todo lo contrario en el caso de C_dp .

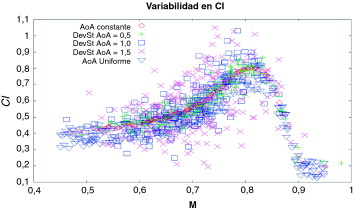
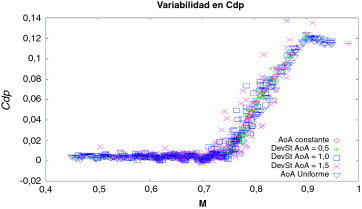
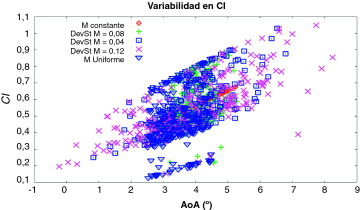
Para completar las conclusiones derivadas del análisis de los coeficientes de variación, las siguientes figuras muestran un análisis gráfico de los resultados. Las Figura 3  and Figura 4 muestran los valores de los coeficientes aerodinámicos frente al número de Mach, M. En la figura 5 el coeficiente de sustentación se representa frente al ángulo de ataque AoA.

Figura 3. Cl vs M con varias distribuciones del AoA.

Figura 4. Cdp vs M con varias distribuciones del AoA.

Figura 5. Cl vs AoA con varias distribuciones de M.

En la figura 3 se observa como el valor de C_l crece con M hasta el punto donde aparece el choque sónico, que provoca su decremento. La curva sigue la pauta de la curva polar, aunque en este caso M se ha definido a través de su distribución gaussiana. Los valores de M se concentran alrededor de su valor medio con una mayor densidad. Para valores de M sub-sónicos, la dispersión crece rápidamente con el incremento de la desviación estándar. Por contra, en régimen transónico la dispersión se reduce.

En la figura 4 , el coeficiente de resistencia C_dp muestra un valor cercano a cero hasta la aparición de ondas de choque. Esto es debido al ruido numérico de las simulaciones, por tener que mantener la malla constante sean cuales sean las condiciones de simulación. El simulador PUMI, basado en las ecuaciones de Euler, no calcula la resistencia aerodinámica en estos rangos de M. A partir del régimen transónico, los valores muestran un rango de variación pequeño con la variación de la desviación estándar del AoA.

La figura 4 muestra una menor variabilidad de C_dp con el AoA. En este caso, la variabilidad se incrementa con M por la presencia de las ondas de choque.

En la figura 5 se observa una línea recta, que no es más que una porción de la curva polar del perfil. Este comportamiento es el esperado incluso introduciendo la variabilidad del número de Mach, M.

En todas las figuras se puede detectar el efecto de las distribuciones estadísticas aplicadas a M o AoA. En las Figura 3  and Figura 4 , la densidad de los valores es más grande alrededor de M = 0,734, que es el valor medio de M. En el otro lado, la figura 5 se muestra como la variabilidad de AoA produce gráficos más dispersos que aumentan su grosor con el aumento de la desviación estándar del ángulo.

La variabilidad de los resultados se ha analizado para el caso del perfil RAE2822. Los resultados obtenidos siguen las tendencias esperadas. Se puede concluir que la variable de entrada que produce la mayor dispersión de los valores de los parámetros de salida es el número de Mach.

Estos análisis proporcionan información de cómo la sustentación y la resistencia se ven afectadas por la variabilidad en las condiciones del flujo, es decir, el ángulo de ataque y número de Mach. No solo la relación entre ellos se puede identificar en las gráficas, sino también el efecto combinado de ambas variables al mismo tiempo y para varias distribuciones estadísticas. Obviamente, la mejor representación de esta relación se puede ver cuando una de las variables se mantiene constante, pero también puede ser identificada cuando los efectos de la variabilidad aparecen en la gráfica, aunque la gráfica se vuelve más gruesa (más dispersa) debido a la representación de la variabilidad.

El procedimiento estocástico se ha aplicado sin dificultades en un entorno CFD. El uso del coeficiente de variación ha demostrado ser muy eficaz y útil para comparar la dispersión de los resultados con la dispersión en los valores de entrada. Debido al hecho de que los valores de los coeficientes de sustentación y la resistencia tiene una orden de una magnitud de diferencia, los valores promedio y desviación estándar no son comparables. La forma más sencilla para comparar las distribuciones de Gauss es normalizar los valores de desviación estándar a través de la utilización del coeficiente de variación.

El hecho de que PUMI CFD se basa en las ecuaciones de Euler debe ser tomado en consideración. Por lo tanto, el cálculo de la resistencia es una aproximación que puede afectar al comportamiento final de los resultados. Este hecho demuestra la necesidad de conocer el programa de análisis y la comprensión de su uso. Si no, puede fácilmente conducir a conclusiones erróneas.

STAC permite la definición de las muestras utilizando Monte-Carlo y las técnicas de hipercubo latino. Las pruebas realizadas concluyen que ambas técnicas de muestreo proporcionan resultados similares. Esta conclusión se debe al hecho de que el análisis de comparación utiliza la media como su principal función objetivo, y es bien conocido que el hipercubo latino mejora la convergencia de la covarianza en comparación con el método de Monte-Carlo, pero no necesariamente el valor medio.

2.2. Ejemplo del análisis aero-elástico estocástico

Se ha definido el problema aero-elástico de manera equivalente al caso anterior. El perfil RAE2822 es, de nuevo, la geometría base. Se ha definido incertidumbre en los parámetros aerodinámicos y los parámetros estructurales. Los parámetros aerodinámicos son el número de Mach y el ángulo de ataque. Los parámetros estructurales son los coeficientes de amortiguamiento del movimiento vertical (z-dp) y la oscilación angular (a-dp), y la coordenada X del eje elástico (x-EA). Todos ellos han sido definidos estocásticamente mediante una distribución gaussiana estadística (fig. 4 ). Para cada análisis estocástico, un conjunto de 200 muestras han sido generadas utilizando la técnica del hipercubo latino muestreo.

Se han definido tres tipos diferentes de análisis: el primero es un análisis determinista que utiliza los valores medios de todos los parámetros como valores de entrada, sin tener en cuenta su carácter estocástico. Este primer análisis ha sido definido para ser utilizado como una referencia (caso 0). El segundo análisis considera un comportamiento estocástico simultáneo de todos los parámetros de entrada (caso 1). El tercer análisis es, en realidad, un conjunto de diferentes casos estocásticos. En cada uno de estos casos, solo uno de los cinco parámetros de entrada se ha considerado como estocástico (casos 2A a 2E), mientras que el resto se han mantenido como en el caso determinista.

Un código aero-elástico desarollado en CIMNE y basado en el método de partículas finitas [8][9] se ha seleccionado como la herramienta principal de análisis. Este se basa en las ecuaciones de Euler para el cálculo de flujo, junto con un modelo estructural de dos grados de libertad (cabeceo y caída). La salida analizada es theta, θ, que es la oscilación angular del fenómeno de «flutter» o «aleteo».

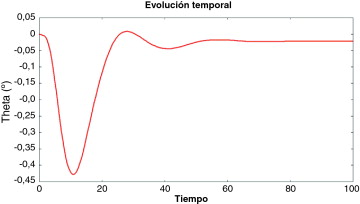
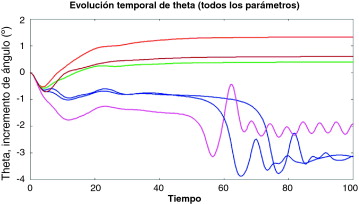
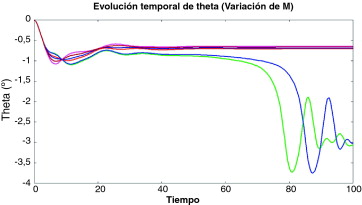
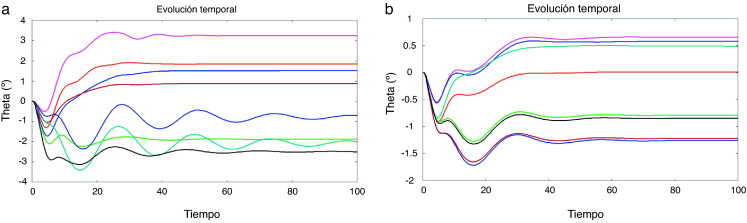
Las Figura 6 , Figura 7 , Figura 8 , Figura 9 , Figura 10 , Figura 11  and Figura 12 muestran una comparación entre los resultados obtenidos para cada uno de los análisis y los casos definidos. Todas las figuras muestran la evolución del ángulo de oscilación del perfil a través del tiempo. Las figuras se utilizan para comparar los efectos en la introducción de la variabilidad de algunas de las variables de diseño. La figura 6 muestra los resultados para el caso determinista. En este caso, el comportamiento elástico del ala produce una primera oscilación que disminuye en 0,45° el ángulo real de ataque, pero después de ese punto el flujo se estabiliza alrededor del perfil y se puede considerar que el ángulo real de ataque se mantiene constante en 0,21° por debajo del valor nominal. La figura 7 muestra algunos ejemplos entre el conjunto de resultados del análisis cuando todos los parámetros son estocásticamente definidos de manera simultánea. Se muestra un conjunto de gráficas que representan todos los casos analizados. El primer punto importante a destacar de este conjunto de resultados es que la gráfica sigue un patrón similar para el caso determinista. La forma y el comportamiento de las curvas en la figura 7 son similares a los que se muestran en la figura 6 . La segunda observación importante es el fenómeno de aleteo que aparece en algunos casos. Después de una aparente tendencia que lleva a la convergencia, algunos valores de los parámetros estocásticos producen una falta de convergencia y la oscilación vuelve a crecer con el tiempo. Este fenómeno de aleteo, que es un efecto estructural no deseado, es producido por algunas de las combinaciones de los valores de los parámetros de entrada.

Figura 6. Evolución temporal de la oscilación angular en el caso determinista.

Figura 7. Evolución temporal de la oscilación temporal para una definición estocástica de todos los parámetros.

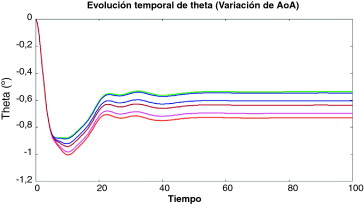
Figura 8. Evolución temporal de la oscilación temporal con el AoA estocástico.

Figura 9. Evolución temporal de la oscilación temporal con M estocástico.

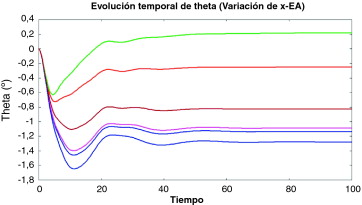
Figura 10. Evolución temporal de la oscilación temporal con x-EA estocástico.

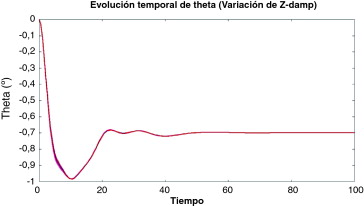
Figura 11. Evolución temporal de la oscilación temporal con z-dp estocástico.

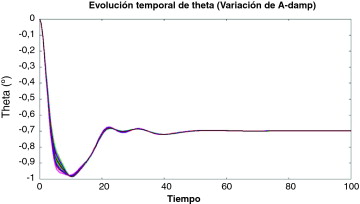
Figura 12. Evolución temporal de la oscilación temporal con a-dp estocástico.

Con el fin de detectar cuáles de los parámetros estocásticos induce el aleteo, se ha realizado un análisis estocástico por separado para cada variable de entrada. La figura 8 muestra algunas curvas ejemplo de la evolución temporal de la oscilación cuando solo el ángulo de ataque se define estocásticamente. La primera oscilación es mayor que la obtenida en el caso determinista. Sin embargo, el valor de convergencia final es inferior. De todos modos, se observa que todos los casos analizados convergen a un valor estable de θ.

Por otro lado, la figura 9 muestra algunos de los resultados cuando el número de Mach se define estocásticamente. Ahora, se detecta fácilmente la falta de convergencia de algunas muestras. La evolución temporal no sigue el mismo patrón de otros análisis.

Las Figura 10 , Figura 11  and Figura 12 muestran algunos de los resultados correspondientes a la definición estocástica de x_EA, z-dp y a-dp, respectivamente. En todos los casos, la evolución de la oscilación angular converge a un valor estable. La figura 11 muestra cómo el coeficiente de amortiguamiento vertical produce una variabilidad muy pequeña, incluso considerando unos pocos ejemplos. El rango de valores estocásticos de este coeficiente es lo suficientemente pequeño como para asegurar una variabilidad pequeña del ángulo de oscilación. Es fácilmente comprensible que el coeficiente de amortiguamiento del movimiento vertical no afecte directamente al ángulo de oscilación.

Ambos coeficientes de amortiguamiento presentan una variabilidad muy pequeña (Figura 11  and Figura 12 ). En el primer caso, el movimiento vertical de amortiguación tiene un efecto casi nulo en la variabilidad del ángulo theta (θ), como podría suponerse a priori. Lo que era difícil de predecir es que el coeficiente de amortiguamiento angular también tiene un efecto muy pequeño en la variabilidad de theta. Las desviaciones estándar de ambos coeficientes de amortiguamiento se han definido como el 10% del valor medio, que son valores similares a los definidos para otros parámetros. En la tabla 5 , se observa el escaso efecto en la variabilidad de los resultados.

Tabla 5. Coeficientes de variación

Caso	AoA	M	x-EA	a-dp	z-dp
1	0,0927	0,0133	0,0980	0,0960	0,0930
2a	0,0972	0,0	0,0	0,0	0,0
2b	0,0	0,0130	0,0	0,0	0,0
2c	0,0	0,0	0,1084	0,0	0,0
2d	0,0	0,0	0,0	0,1069	0,0
2e	0,0	0,0	0,0	0,0	0,0981

	Th(min)	h/c(max)	Cd(min)	Cl(min)	Cm(min)
1	-0,6952	0,1332	-0,7412	10,2331	-0,6719
2a	-0,0487	0,0502	-0,2456	0,0602	-0,0376
2b	-0,6854	0,0120	-0,3253	7,0153	-0,6480
2c	-0,3362	0,1583	-0,4269	0,1032	-0,3340
2d	-0,0077	0,0223	-0,0103	0,0094	-0,0061
2e	-0,0018	0,0026	-0,0633	0,0041	-0,0038

La tabla 4 es un breve resumen de todos los casos analizados y los valores aplicados en cada uno. Ambos coeficientes de amortiguamiento tienen menor desviación estándar, lo que conduce a los resultados obtenidos.

Tabla 4. Casos analizados para el estudio de sensibilidad

Caso	AoA		M		x-EA
	M	DevSt	M	DevSt	M	DevSt
1	2,79	0,279	0,734	0,01	0,4	0,04
2a	2,79	0,279	0,734	--	0,4	--
2b	2,79	--	0,734	0,01	0,4	--
2c	2,79	--	0,734	--	0,4	0,04
2d	2,79	--	0,734	--	0,4	--
2e	2,79	--	0,734	--	0,4	--

	a-dp		z-dp
	M	Devst	M	DevSt
1	0,25	0,025	0,25	0,025
2a	0,25	--	0,25	--
2b	0,25	--	0,25	--
2c	0,25	--	0,25	--
2d	0,25	0,025	0,25	--
2e	0,25	--	0,25	0,025

Cada uno de estos casos se ha utilizado para analizar el comportamiento de los parámetros de salida adicionales, como el movimiento vertical del perfil, y los coeficientes aerodinámicos de sustentación, resistencia y momento.

Otras variables de salida, como los coeficientes aerodinámicos (sustentación, resistencia y momento), o los parámetros estructurales como la deformación vertical del ala se pueden analizar de la misma manera como se ha hecho con θ, la oscilación angular del perfil. La descripción de los resultados se ha centrado en θ con el fin de simplificar la presentación. Sin embargo, las mismas conclusiones se pueden tomar de otros parámetros de salida.

Los resultados se pueden resumir mediante el coeficiente de variación obtenido para todos los análisis. En la tabla 5 se muestran los coeficientes obtenidos.

3. Optimización CFD estocástica

El análisis estocástico de CFD es la base del procedimiento definido por la optimización evolutiva estocástica. El método bien conocido de optimización evolutiva, junto con la herramienta de análisis estocástico, se integra para analizar estocásticamente cada individuo dentro del proceso de optimización. En este enfoque, el análisis clásico determinista de cada individuo se sustituye por un análisis estocástico completo. El análisis estocástico de un determinado individuo ofrece ahora una nube de puntos, y la función objetivo se calcula mediante la media de los resultados, que se utiliza como objetivo estocástico. La desviación estándar de los resultados también se puede utilizar como una medida de la solidez del diseño en comparación con la variabilidad del valor de entrada (véase la ref. [10]  and [11] ).

El análisis estocástico requiere una cantidad significativa de evaluaciones diferentes, y el correspondiente coste computacional global puede ser muy elevado. Si se multiplica el coste de cada individuo por el total necesario en un proceso de optimización evolutiva, el coste total puede ser más que prohibitivo. Esto justifica el uso de un modelo de sustitución. En este trabajo se ha seleccionado el uso de redes neuronales artificiales (RNA), ya que su capacidad para hacer frente a una amplia gama de problemas diferentes (ver ref. [12] , [13] , [14]  and [15] ). Esta red neuronal se integrará en el algoritmo evolutivo en paralelo con la herramienta estocástica.

Basado en un algoritmo evolutivo validado, como es el NSGA-II [16] , [17]  and [18] , se han realizado algunas pruebas con el fin de mostrar las capacidades de la metodología propuesta. Los parámetros utilizados para configurar el algoritmo genético son:

• Tamaño de la población: 16
• Número de generaciones: 100
• Probabilidad de crossover: 0,99
• Probabilidad de mutación: 0,25

3.1. Optimización determinista

A modo de ejemplo, se muestran en primer lugar los resultados correspondientes a un problema de optimización multi-objetivo determinista. El problema se define como:

Minimizar

${\begin{array}{c}f_{1}=1/C_{l}\\f_{2}=C_{dp}\end{array}}$

( 1)

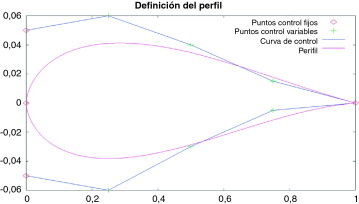
Tomando como punto de partida la geometría del perfil RAE2822, y definiento la misma mediante los nodos de las curvas de Bezier (fig. 13 ).

Figura 13. Curvas de Bezier y sus puntos de control para la definición de las variables de diseño.

La tabla 6 muestra las restricciones aplicadas a las coordenadas de los nodos de la parametrización geométrica.

Tabla 6. Restricciones geométricas

	X	Y	Límite inferior	Límite superior
Pt x1s, y1s	0	0	-	-
Pt x2s, y2s	0	0,05	-	-
Pt x3s, y3s	0,25	Variab	0,05	0,085
Pt x4s, y4s	0,5	Variab	0,03	0,06
Pt x5s, y5s	0,75	Variab	0,01	0,02
Pt x6s, y6s	1	0	-	-
Pt x2l, y2l	0	-0,05	-	-
Pt x3l, y3l	0,25	Variab	-0,06	-0,03
Pt x4l, y4l	0,5	Variab	-0,035	-0,02
Pt x5l, y5l	0,75	Variab	-0,015	-0,005

A fin de comparar las soluciones obtenidas mediante un problema de optimización determinista y otro de optimización estocástica, se ha resuelto en primer lugar el problema determinista. Se han aplicado los siguientes valores para el ángulo de ataque (AoA) y el número de Mach (M):

• El ángulo de ataque; AoA = 2,79
• Número de Mach, M = 0,734

Se han utilizado un optimizador basado en el NSGA-II y un modelo de sustitución por redes neuronales. Se han definido los siguientes parámetros para configurar el algoritmo:

• Tamaño de la población: 24
• Número de generaciones: 300
• Probabilidad de cruce: 0,95
• Probabilidad de mutación: 0,166667

La figura 14 muestra la población total y el frente de Pareto obtenidos como solución del problema determinista.

Figura 14. Optimización determinista multi-objectivo.

3.2. Integración del análisis estocástico y los algoritmos evolutivos

Del ejemplo determinista al estocástico se ha trabajado el acoplamiento del análisis estocástico y el algoritmo evolutivo. El problema ahora es:

Minimizar

${\begin{array}{c}f_{1}=\mu \left(1/C_{l}\right)\\f_{2}=\mu \left(C_{dp}\right)\end{array}}$

( 2)

Para un perfil definido mediante curvas de Bézier, que utiliza el perfil RAE2822 como punto de partida, y como en la figura 13 . Los valores de la tabla 6 se aplican también en este caso para las restricciones de las coordenadas de los nudos de las curvas de Bezier, utilizadas para la parametrización geométrica del perfil.

La tabla 7 muestra los valores de la media y la desviación estándar que corresponde a una definición gaussiana del AoA y M. Los valores medios son los mismos que los valores deterministas previamente definidos. Utilizando el método de Monte-Carlo se ha generado un único conjunto de 250 muestras para modelar los parámetros de entrada, y se aplican para el análisis de todos los individuos en el proceso de optimización.

Tabla 7. Restricciones estocásticas

	M	DevSt
Ángulo de ataque	2,79	0,279
Número de Mach	0,734	0,05

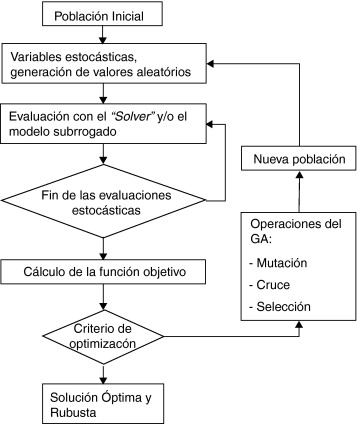
La propuesta de integración define el flujo de trabajo mostrado en la figura 15 .

Figura 15. Flujo de trabajo del caso estocástico.

El uso de un modelo de sustitución es casi obligatorio para reducir el coste computacional de todo el proceso. La red neuronal artificial (RNA) se ha entrenado con el fin de proporcionar resultados con menos del 1% de error.

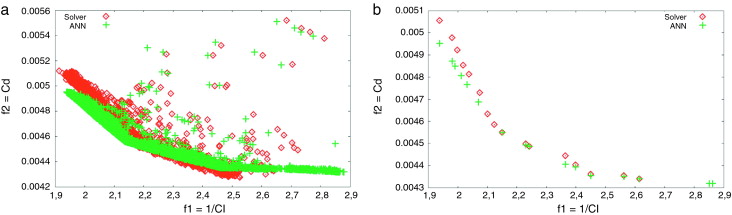
Con el fin de garantizar la viabilidad del uso de la RNA, se han comparado los frentes de Pareto obtenidos utilizando la herramienta de análisis directo y la ANN. La figura 16 (a) muestra la diferencia entre la población general obtenido en ambos casos. La figura 16 (b) muestra los dos frentes de Pareto y la diferencia que existe entre ellos. Esta diferencia se mantiene por debajo de un 3% que ha sido considerado como aceptable.

Figura 16. Resultados de la optimización utilizando el simulador y la RNA (a) Población total (b) frente de Pareto.

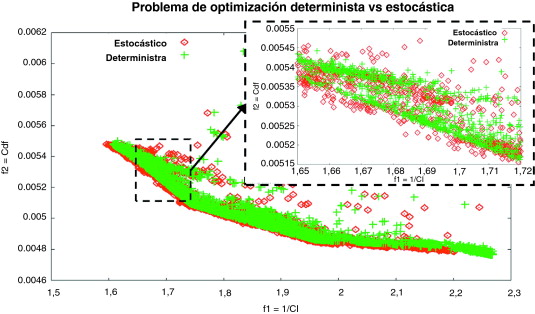
La figura 17 muestra una comparación entre las soluciones deterministas y las soluciones de la optimización estocástica. Ambos utilizan la misma definición del problema a excepción del AoA y la M, que son las variables estocásticas. Tanto el uso de RNA, junto con el optimizador utilizan la misma configuración y datos de entreno.

Figura 17. Comparación entre los resultados deterministas y estocásticos.

Se aprecia que las formas de ambos frentes son similares, pero un frente se desplaza con respecto al otro. El frente estocástico está claramente retrasado, como se puede ver en la imagen ampliada de la figura 17 . Las soluciones son diferentes porque la solución estocástica utiliza la media de una nube de evaluaciones en lugar de un valor único como es el caso determinista. Desde el punto de vista físico, algunos de estos puntos se ven afectados por la presencia de una onda de choque cercana, mientras que la optimización determinista no tiene en cuenta la posibilidad este fenómeno. Desde este punto de vista, la definición estocástica produce una solución más robusta. Esta situación no se produciría si estuviésemos tratando con flujos claramente subsónicos.

3.3. Aplicación de la definición probabilística de los datos de entrada

Con el fin de simplificar, el proceso estocástico de optimización anterior se ha definido utilizando el mismo conjunto de valores estocásticos del AoA y M para todos los individuos analizados. Esto es, de hecho, un caso extremo de un problema de optimización multi-punto con un número elevado de puntos. De todos modos, una evaluación multi-punto no es realmente representativa del carácter probabilístico de las variables de entrada y el siguiente paso ha sido la de considerar realmente la generación al azar de un conjunto diferente de muestras para las variables de entrada para el análisis de cada individuo.

Se podría considerar que el uso de una definición única al azar durante el proceso de optimización es suficiente. Sin embargo, la definición estadística de las variables de entrada tiene la intención de capturar su comportamiento aleatorio, principalmente. Una muestra diferente para cada individuo presenta una variabilidad adicional que aumenta la robustez de los resultados. Por lo tanto, las muestras aleatorias se generan ahora para cada generación e individuo es la llamada definición variable aleatoria.

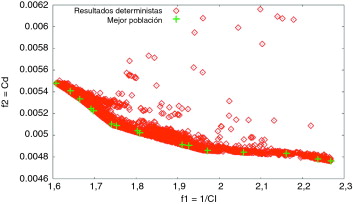
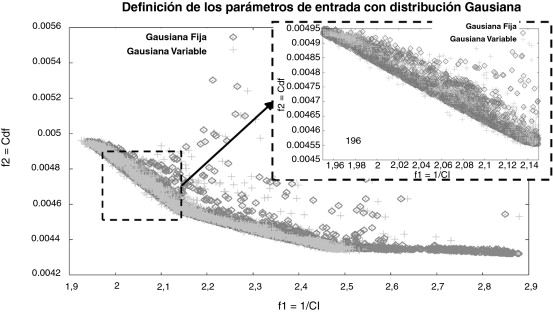
La figura 18 muestra la comparación entre los resultados obtenidos con una única definición fijada al azar y los obtenidos con una definición diferente al azar para cada individuo. Se puede detectar cómo la definición fija también corrige la parte frontal de la solución, definiendo claramente una tendencia lineal, mientras que la definición variable rompe esta regularidad. Esto significa que la definición de la variable afecta a la evaluación de la función objetivo que permite capturar los mejores resultados.

Figura 18. Comparación entre las definiciones fijas o aleatorias de las muestras estocásticas.

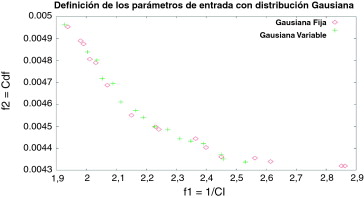
Si se analiza solo la forma de los frentes de Pareto, la figura 19 muestra cómo la definición fija limita negativamente el rango de valores de las funciones objetivo. La definición variable conduce a un frente más estrecho, produciendo resultados con valores más bajos para la función f₁ .

Figura 19. Comparación entre los frentes de Pareto para muestras fijas o aleatorias.

También se ha realizado una comparación de dos tipos diferentes de PDF. Se han utilizado la gaussiana y la uniforme y se han aplicado al análisis de cada individuo durante el ciclo de optimización sin detectar ninguna diferencia relevante entre ellos.

4. Optimización de diseño aero-elástico estocástica

4.1. Optimización determinista multi-objetivo

La definición determinista del problema aero-elástico se utiliza ahora como base de una optimización multi-objetivo. La solución de este caso se ha utilizado como referencia para su comparación con la optimización estocástica que se presenta en los siguientes apartados. El problema se basa en un perfil RAE2822. Este es el diseño de referencia para resolver un problema cuyo objetivo es buscar el comportamiento más suave de la evolución temporal de la oscilación angular (θ(t)) y la evolución temporal de la resistencia coeficiente (Cdp(t)). Se pretende que estos sean más suaves en el sentido de reducir la integral total de la curvatura, la segunda derivada de cada función del tiempo. El problema se puede formular como:

Minimizar

${\begin{array}{c}f_{1}=\sum _{i=0}^{N_{t}}{\frac {{\partial }^{2}{\theta }_{i}\left(t\right)}{\partial t^{2}}}\\f_{2}=\sum _{i=0}^{N_{t}}{\frac {{\partial }^{2}C_{d_{i}}\left(t\right)}{\partial t^{2}}}\end{array}}$

( 3)

Siendo Nt el número de pasos de tiempo utilizados para el cálculo de la evolución temporal. La función objetivo es el sumatorio del valor de la curvatura.

• Se consideran los siguientes rangos de diseño:
• Rango de la coordenada X del eje elástico; x_EA: [0,25 0,65]
• Rango de la coordenada X del centro de gravedad; x_cg: [0,35 0,60]
• Rango del cociente de masas, μ: [30,0 65,0]
• Rango del coeficiente de amortiguamiento de la deformación vertical, ξh: [0,15 0,35]
• Rango del coeficiente de amortiguamiento para el giro angular, ξθ: [0,15 0,45]

Por último, el ángulo de ataque y el número de Mach se definen como valores constantes en:

• Ángulo de ataque: 2,79
• Número de Mach: 0,734

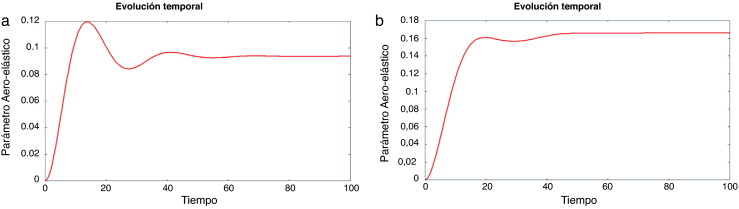
El método de optimización busca una forma de θ(t) y Cdp(t) tal que las curvas deben seguir una tendencia como la que se muestra en la figura 20 b, que es más suave que la que se muestra en la figura 20 a. Los resultados óptimos deben llegar a formas suaves para las dos funciones objetivo.

Figura 20. Ejemplos de un comportamiento poco suave (a) y un comportamiento suave (b).

El procedimiento de optimización con las poblaciones iniciales que presentan una gran variabilidad, como se muestra en las Figura 21  and Figura 22 . El proceso de optimización consigue obtener poblaciones con carácter más estable. Las figuras 21 b y 22b muestran en conjunto la evolución temporal de estas poblaciones y su comportamiento más suave.

Figura 21. (a) Población inicial para θ(t), (b) Población óptima para θ(t).

Figura 22. (a) Población inicial para Cdp (t). (b) Población óptima para Cdp (t).

Pero no solo la suavidad de las curvas es mejor, también la dispersión se reduce. En ambos casos, θ(t) y C_dp (t), la población inicial presenta una gran variabilidad, es decir, una gran dispersión entre los miembros de la población, así como también una diferencia significativa entre el comportamiento de cada miembro. Algunos de ellos presentan una convergencia rápida, pero otros convergen después de una mayor cantidad de pasos de tiempo. Por otro lado, el comportamiento de las mejores poblaciones es mucho más homogénea, ya que puede verse en las Figura 21  and Figura 22 .

La integración de la definición estocástica del problema aero-elástico con un optimizador multi-objetivo ofrece toda una población y un frente de Pareto que siguen el comportamiento habitual de este tipo de análisis. La población inicial presenta un mal comportamiento, que mejora continuamente en cada iteración hasta el más óptimo, como muestra la figura 23 .

Figura 23. Detalle de (a) toda la población y (b) frente de Pareto del proceso de optimización.

La optimización determinista se planteó como una validación de la definición del problema. Así como una referencia para los próximos casos. Comparando los resultados obtenidos para el óptimo y la población inicial, se puede observar el comportamiento más homogéneo de los óptimos en comparación con los iniciales. Incluso la dispersión se reduce, aunque cada uno de los individuos óptimos tiene su propio comportamiento.

4.2. Optimización multi-objetivo estocástica

En este caso, las dos funciones objetivo son los valores promedio de la suma total de la curvatura de las dos variables de salida: la evolución temporal de la oscilación angular del perfil (θ(t)) y la evolución temporal del coeficiente de resistencia (Cdp (t)). El análisis está dirigido a comparar si el procedimiento estocástico es capaz de encontrar soluciones robustas, sin definir la desviación estándar del resultado principal como una de sus funciones objetivo, que sería el caso de un problema de diseño robusto clásico.

El problema se define como:

Minimizar

${\begin{array}{c}f_{1}=\mu \left(\sum _{i=0}^{N_{t}}{\frac {{\partial }^{2}{\theta }_{i}\left(t\right)}{\partial t^{2}}}\right)\\f_{2}=\mu \left(\sum _{i=0}^{N_{t}}{\frac {{\partial }^{2}C_{dp}\left(t\right)}{\partial t^{2}}}\right)\end{array}}$

( 4)

Siendo N_t el número de pasos de tiempo utilizado para calcular el movimiento angular, por lo que la suma total de los valores de la curvatura se obtiene y se utiliza como función objetivo. Teniendo en cuenta las variables de diseño tal como se define en el anterior caso determinista. Por último, el ángulo de ataque y el número de Mach se definen como variables estocásticas:

El ángulo de ataque sigue una distribución de Gauss, con una media: 2,79 y desviación estándar: 0,01

Número de Mach sigue una distribución de Gauss, con una media: 0,734 y desviación estándar: 0,01

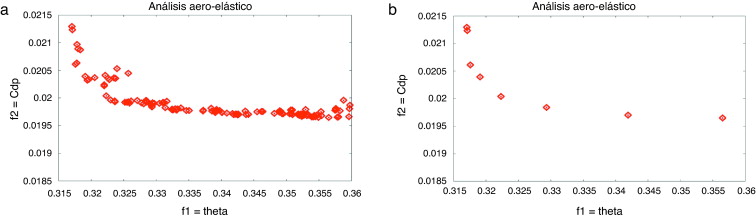
Una vez más, el problema está principalmente destinado a buscar el comportamiento más suave de las dos curvas. Los resultados pueden ser analizados mediante un esquema similar al que se ha utilizado en los casos anteriores. En la figura 24 , se aprecia cómo la función f₁ tiene mayor dispersión que f₂ si se analiza la población total. Cuando la atención se centra solo en el frente de Pareto se puede apreciar que los rangos de valores de la dispersión son similares.

Figura 24. Análisis estocástico; población total y frente de Pareto.

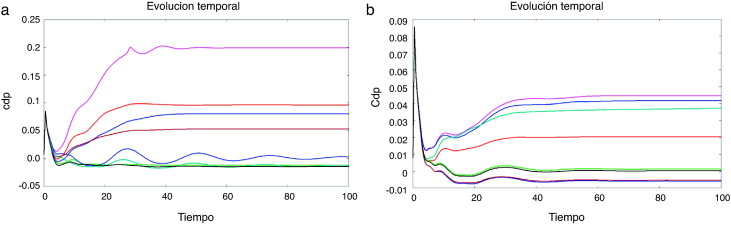
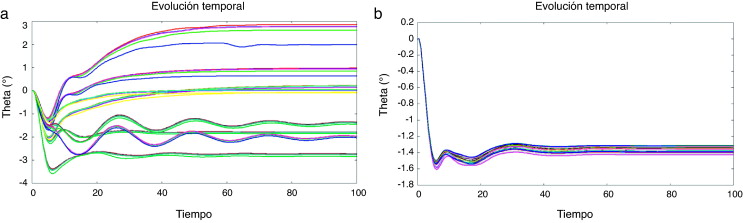
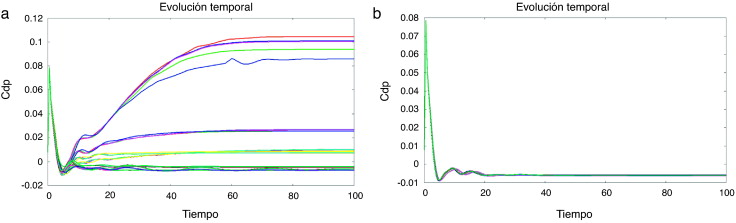
Se puede establecer otra comparación entre la evolución temporal de la población inicial, con sus cinco evaluaciones estocásticas, y la evolución en el tiempo de los individuos óptimos. Las Figura 25  and Figura 26 muestran la evolución temporal de θ(t) y C_dp (t). En este caso, ni siquiera con la definición de la desviación estándar como una de las funciones objetivo se alcanza una reducción de la dispersión. Ambos θ(t) y las curvas de C_dp (t) se suavizan después de la optimización, pero aún mantienen una cierta inestabilidad inicial.

Figura 25. (a) inicial y (b) las mejores poblaciones de la theta, θ, la evolución.

Figura 26. (a) inicial y (b) las mejores poblaciones de la CDP (t) la evolución.

Al comparar las poblaciones iniciales y óptimas de las Figura 25  and Figura 26 se entiende cómo el proceso de optimización tiende a buscar los individuos más aptos. En comparación con los resultados deterministas, la dispersión entre los individuos óptimos se reduce y las curvaturas de todos los óptimos tienden a ser bastante similares.

4.3. Optimización multi-objetivo estocástica con diseño robusto

El mismo problema aero-elástico se utiliza ahora como base de la optimización robusta. El problema se define ahora como:

Minimizar

${\begin{array}{c}f_{1}=\mu \left(\sum _{i=0}^{N_{t}}{\frac {{\partial }^{2}{\theta }_{i}\left(t\right)}{\partial t^{2}}}\right)\\f_{2}=\sigma \left(\sum _{i=0}^{N_{t}}{\frac {{\partial }^{2}{\theta }_{i}\left(t\right)}{\partial t^{2}}}\right)\end{array}}$

( 5)

Teniendo en cuenta las variables de diseño y límites definidos en el caso estocástico.

El problema está principalmente destinado a buscar el comportamiento más suave y robusto de θ(t). No solo se considera la curvatura de cada individuo, sino también el comportamiento de todo el conjunto de individuos generados estocásticamente. Como se muestra en la figura 27 , pequeñas variaciones de los parámetros de entrada pueden provocar una gran variabilidad en los resultados.

Figura 27. (a/b) Ejemplos de la oscilación angular de un conjunto de muestras estocásticas.

La principal diferencia con el problema de optimización determinista, en cuanto a la definición de las funciones objetivo, es el hecho de que ahora la desviación media y estándar son las funciones seleccionadas. En cuanto a la definición del problema, está claro que la definición estocástica del ángulo y el número de Mach es la diferencia principal.

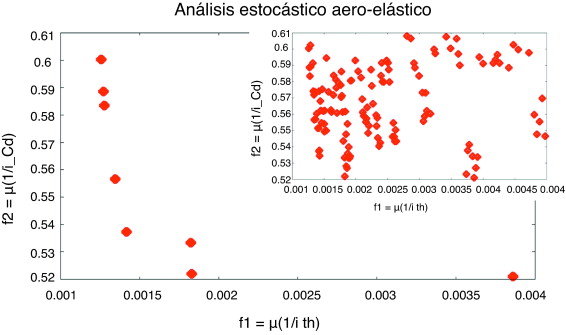
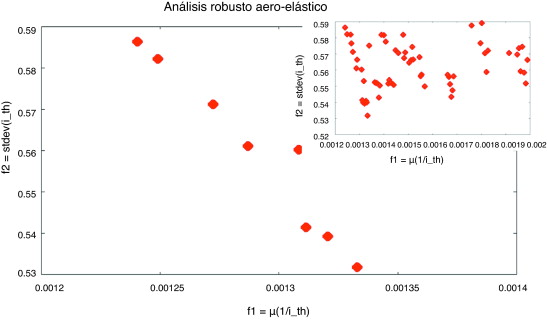
Los resultados pueden ser analizados mediante un esquema similar al que se ha hecho en el caso determinista. En primer lugar, se realiza una comparación entre la población inicial y la óptima. La gráfica en la figura 28 muestra el conjunto de la población y la figura 29 muestra el comportamiento físico de estos individuos, lo que demuestra que los individuos iniciales están lejos de los valores óptimos. Una vez más, el proceso de optimización es capaz de tender al óptimo.

Figura 28. Análisis robusto; población total y Pareto.

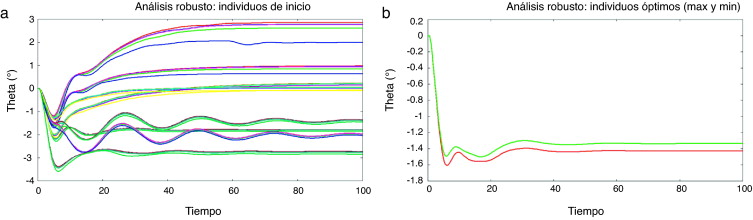
Figura 29. (a) población inicial y (b) óptima.

El acoplamiento entre el procedimiento estocástico y la herramienta de análisis aero-elástica funciona como se espera, sin mayores problemas. En la figura 28 , se muestran tanto el frente de Pareto obtenido como la población total.

Otra comparación se puede establecer entre la evolución temporal de los individuos iniciales y el comportamiento de sus evaluaciones estocásticas, y la evolución en el tiempo de los individuos óptimos y sus evaluaciones estocásticas. Es fácil darse cuenta de cómo la población inicial es más dispersa, en todos los sentidos. Cada individuo difiere mucho de los demás, así como el conjunto de evaluaciones estocásticas de cada individuo también presenta una variabilidad mayor respecto al resto de individuos. Por otro lado, el conjunto de las soluciones óptimas tiende hacia un mismo comportamiento, con una menor variabilidad comparada con el resto de individuos.

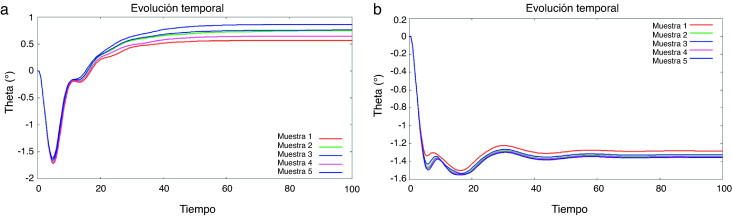
Información adicional tomada de la gráfica de las figuras 29 (a) y (b), que muestran las evoluciones temporales de theta θ(t), es de gran interés para validar los resultados finales de este test.

Las gráficas en la figura 29 muestran los individuos iniciales y cómo no siguen ninguna tendencia. En la figura 29 (b), donde solo se muestran los límites extremos del conjunto de curvas obtenidas para mayor simplicidad, se muestra cómo el proceso de optimización conduce a formas suaves (disminución de la curvatura), y estandariza la forma optimizada para el conjunto de los valores óptimos. Es importante notar que la función objetivo es fuertemente dependiente del tiempo, aunque esto no afecta a la capacidad del optimizador de llegar a una solución óptima.

Comparando los resultados entre los casos estocástico y robusto, el caso robusto aumenta la dispersión en los valores óptimos. Esto es efecto de la definición en las funciones objetivo. A partir de los valores deterministas, el estocástico se enfrenta con los valores medios el robusto con la media y la desviación estándar.

Se ha trabajado con un acoplamiento perfecto entre el problema aero-elástico y el procedimiento estocástico. En estos casos no se utiliza ningún tipo de información geométrica, sino que se utiliza una geometría fija a partir de un perfil de RAE2822. El algoritmo evolutivo controla otro tipo de parámetros de entrada, como la proporción de masas o el coeficiente de amortiguamiento, que están directamente relacionados con el comportamiento elástico del perfil.

Una contribución adicional de este caso es el uso de la media y desviación estándar como funciones objetivo. La robustez de la solución ha sido reforzada por la definición estocástica de las variables de entrada, que introduce el concepto de incertidumbre en el análisis, así como también con la variabilidad como un objetivo de la optimización, lo que garantiza la minimización de esta variabilidad.

5. Conclusiones

Se ha definido un nuevo procedimiento de optimización estocástica. La integración de un algoritmo evolutivo y una herramienta de análisis estocástico ha sido comparada con unos primeros casos de validación [19]  and [20] . Varias opciones se han evaluado en relación con la definición estocástica de los parámetros y cómo la incertidumbre podría extenderse a través del análisis numérico.

Se han definido tres casos: la solución determinista clásica, que no considera ninguna incertidumbre, el estocástico, que define los valores medios de la función objetivo de la optimización, y la robusta, que define tanto la media y la desviación estándar como las funciones objetivo de la optimización. La comparación entre los casos determinista, estocástico y los casos de diseño robusto muestra como progresa el estudio de los efectos de la variabilidad. Al comparar la solución determinista con la estocástica y la robusta, uno puede darse cuenta de como la introducción de la definición estocástica conduce a resultados completamente nuevos. Los casos estocástico y robusto son capaces de reducir la dispersión de los resultados, al tiempo que garantizan la robustez de la solución.

Las técnicas de Monte-Carlo, así como las del hipercubo latino, son computacionalmente costosas. El uso de un modelo de sustitución, como una red neuronal artificial, es altamente aconsejable. Si está bien entrenada y validada, se ha demostrado que el error de aproximación del modelo de sustitución es lo suficientemente bajo para no reducir la exactitud de las soluciones óptimas. Es importante tener en cuenta que la variabilidad intrínseca del método estocástico, debido a su definición estadística de las variables, se añade al error del modelo de sustitución. Es importante, entonces, para mantener bajo control tanto la variabilidad y el error de aproximación, y por debajo de un límite deseable, a fin de no dar lugar a resultados erróneos. La cantidad de muestras aleatorias definidas para la definición estocástica de los valores de entrada es de gran importancia. Una gran cantidad de muestras produce una variabilidad más grande y una mejor representación de la naturaleza aleatoria de las variables de entrada. Sin embargo, cuanto mayor sea la cantidad de muestras, mayor es el coste computacional.

Con el fin de obtener un método competitivo, es urgente seguir trabajando en la paralelización. Además, se están analizando los nuevos desarrollos en los métodos de «probabilistic collocation» para comprobar si la reducción de las evaluaciones compensa el carácter multi-punto de estos métodos.

La definición estocástica ha demostrado su robustez frente a los dos casos, el caso estocástico y el caso robusto. El primero utiliza la media, mientras que el segundo utiliza la media y los valores de desviación estándar. En ambos casos se han dirigido a las mejores soluciones que cumplan los requisitos. La definición de la desviación estándar como función objetivo no representa una mayor complejidad. La robustez está garantizada por la definición estocástica de la entrada, y la desviación estándar proporciona información adicional.

Agradecimientos

Este trabajo ha sido parcialmente financiado por la Comisión Europea a través del proyecto de FP6 NODESIM-CFD (Contrato 030959) y por el Ministerio de Ciencia e Innovación español con el proyecto DPI2011-27834.

Bibliografía

1. [1] J.C. Helton, F.J. Davis; Latin Hypercube sampling and the propagation of uncertainty in analyses of complex systems; Reliab Engng System Safety, 81 (2003), pp. 23–69
2. [2] K. Durga Raoa, H.S. Kushwaha, A.K. Verma, A. Srividya; Quantification of epistemic and aleatory uncertainties in level-1 probabilistic safety assessment studies; Reliab Engng System Safety, 92 (2007), pp. 947–956
3. [3] J.E. Hurtado, A.H. Barbat; Monte-Carlo techniques in computational stochastics mechanics; Arch Comput Methods Eng, 5 (1998), pp. 3–29
4. [4] R. Flores, E. Ortega; PUMI: an explicit 3D unstructured finite element solver for Euler equations; CIMNE (2008) PI326
5. [5] M. Drela; XFOIL–An analysis and design system for low Reynolds number airfoils, Low Reynolds number aerodynamics; Proceedings of the Conference, Notre Dame, IN; GERMANY, FEDERAL REPUBLIC OF; 5-7 June 1989 (1989), pp. 1–12
6. [6] GiD, The pre and post-processor tool. CIMNE. [consultado 1/9/2011]. Disponible en: www.gid.cimne.com .
7. [7] P.H. Cook, M.A. McDonald, M.C.P. Firmin, Aerofoil RAE 2822 - Pressure Distributions, and Boundary Layer and Wake Measurements, Experimental Data Base for Computer Program Assessment, AGARD Report AR 138, 1979.
8. [8] E. Ortega, E. Oñate, S. Idelshon; An Improved finite point method for a three dimensional potential flows; Comput Mech (2007)
9. [9] E. Ortega, E. Oñate, S. Idelshon; A finite point method for adaptive three-dimensional compressible flow calculations; Int J Numer Meth Fluids (2009)
10. [10] Z. Tang, J. Periaux, G. Bugeda, E. Oñate; Lift maximization with uncertainties for the optimization of high-lift devices; Int J Numer Meth Fluids (2010)
11. [11] Z. Tang, J. Periaux, G. Bugeda, E. Oñate; Lift Maximization with Uncertainties for the Optimization of High Lift Devices using Multi-Criterion Evolutionary Algorithms, CEC2009; 2009 IEEE Congress on Evolutionary Computation, Tronheim (Norway) (2009)
12. [12] R. López, A1. Flood; An open source Neural Networks C++ Library User Guide; CIMNE (2007)
13. [13] López R., Neural Networks for Variational Problems in Engineering, PhD Thesis, 2008.
14. [14] R. López, E. Oñate; A variational formulation for the Multilayer Perceptron, Artificial Neural Networks, ICANN 2006; Lecture Notes in Computer Science, 4132 (I) (2006), pp. 159–168
15. [15] R. López, E. Balsa-Canto, E. Oñate; Neural networks for variational problems in engineering; Int J Numer Meth Fluids (2008)
16. [16] K. Deb, A. Pratap, S. Agarwal, T. Meyarivan; A Fast and Elitist Multi-Objective Genetic Algorithm: NSGA-II; IEEE Transactions on Evolutionary Computation, 6 (2002), pp. 182–197
17. [17] M. Papadrakakis, N.D. Lagaros, Y. Tsompanakis; Structural optimization using evolution strategies and neural networks; Comput Methods Appl Mech Engrg, 156 (1998), pp. 309–333
18. [18] D. Quagliarella, A. Vicini; Designing high-lift airfoils using Genetic Algorithms; Proceedings of EUROGEN 1999 (1999)
19. [19] J. Pons-Prats, E. Oñate, F. Zárate, G. Bugeda, J. Hurtado; Non-deterministic shape optimization in aeronautics; Proc. of MAO AIAA-ISSMO Conf, Victoria, Canada, AIAA (2008)
20. [20] J. Pons-Prats, G. Bugeda, E. Oñate, F. Zárate, J. Hurtado; Robust shape optimization in aeronautics; Proc. of WCSMO-8 Conf, Lisbon, Portugal (2009)