Summary
A special type of the gas engine with external combustion is called Stirling engine. The mechanism has two pistons with two volumes inside. The pistons are connected together through cooler, regenerator and warmer. The engine effectivity depends on the piston movement behaviour. The usual sinusoidal time curve leads to low effectiveness. The quick movement from lower to upper position with a certain delay in both top and bottom dead centres is more effective. The paper deals with three types of mechanisms, analyzing the piston movement, and their behavior. Special emphasize is taken to the piston movement regime.
Keywords
Combustion ; Gas engine ; Effectivity ; Kinematic solution ; Driving mechanism
Introduction
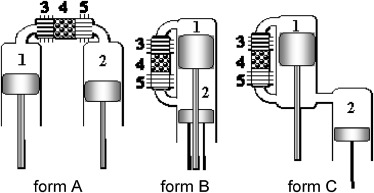
The special type of the gas engine with external combustion is called Stirling engine. The kinematic driving mechanism of the engine consists of two pistons (working and transferring) with two volumes (compressive and expansive) inside, connected together through cooler, regenerator and warmer. The design of the engine can have three forms (see Fig. 1 , where 1 is expansive volume, 2 is compressive volume, 3 is warmer, 4 is regenerator and 5 is cooler).
|
|
|
Figure 1. Three forms of the Stirling engine. |
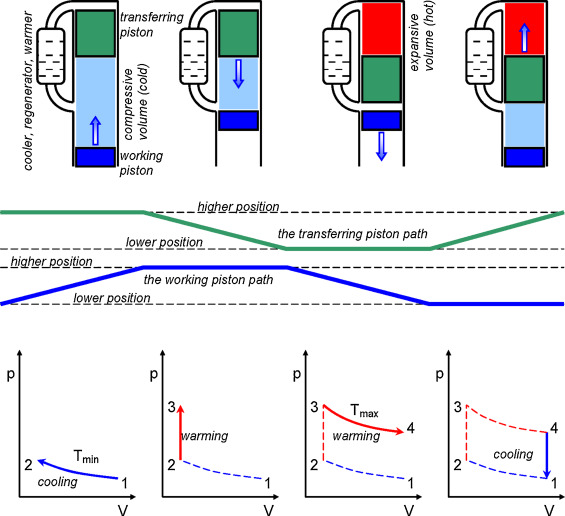
The ideal cycle of the Stirling engine is shown in Fig. 2 . The cycle has 4 phases (Míka, 2004 ).
- Point 1 to point 2 in Fig. 2 . The working piston is in the lower position; compressive volume is large and cold. The transferring piston is in the higher position, expansive volume is near zero. The working piston moves upward, the compressive volume decreases but due to cooling the gas keeps its low temperature.
- Point 2 to point 3 in Fig. 2 . The working piston is in the higher position; compressive volume is small and cold. The transferring piston moves downward and presses the gas from compressive volume through warmer to expansive volume. The total volume keeps the temperature and pressure increase.
- Point 3 to point 4 in Fig. 2 . The transferring piston is in the lower position; the compressive volume is near zero. The working piston moves downward drawing the gas from expansive volume through warmer to increasing compressive volume. Due to warming the gas keeps its high temperature.
- Point 4 to point 1 in Fig. 2 . The working piston is in the lower position. The transferring piston moves upward pressing the rest of the gas from expansive volume through cooler to the compressive volume. The total volume keeps, due to cooling, the temperature decreases.
|
|
|
Figure 2. The ideal cycle of the Stirling engine. |
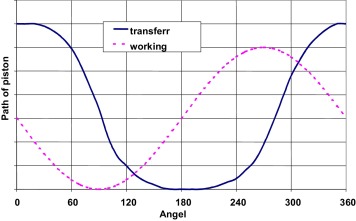
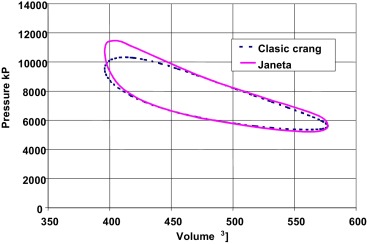
The motions of both pistons are similar; the working piston is late in the phase. The efficiency of the engine is higher if the transferring piston moves from one position to another more quickly and then stays in the position for a certain time (see Fig. 3 , solid curve). This leads to the higher pressure in the p –V diagram (see Fig. 4 ) in the beginning of the expansion phase and subsequently higher torsion moment. The piston path depends on the gear mechanism, realizing the piston motion.
|
|
|
Figure 3. The path of the working and transferring piston. |
|
|
|
Figure 4. The comparison of the p –V curve for sinusoidal and non-sinusoidal transferring piston path. |
Solution with the crank mechanism
The scheme of the crank mechanism is shown in Fig. 5 .
|
|
|
Figure 5. The crank mechanism. |
The piston path–crank rotation relationship (Vinogradov, 2000 and Huston, 2002 ) is:
|
|
( 1) |
The corresponding curve is shown in Fig. 6 . The piston path has a good course only for extremely short connecting rod (solid curve in the figure). This causes design problems.
|
|
|
Figure 6. The piston path–crank rotation curve. |
The Janeta design of the piston gear mechanism
There are several types of the piston gear mechanism. In the paper the three types of the mechanism, coming from the firm of Mr. Janeta, Orlova, Czech Republic, will be evaluated with respect to the transferring piston path.
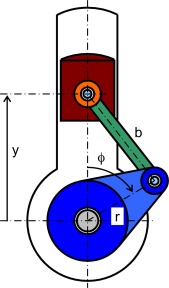
The mechanism with banked plate
The scheme is shown in Fig. 7 .
|
|
|
Figure 7. Mechanism with banked plate, kinematic scheme. |
The motion of the banked plate is determined by two rotations. Rotation about vertical axis (the rotational angle ϕ ) and rotation about slanting bearing axis (the rotational angle ψ ).
Transformation of the unit vector due to rotation about vertical axis z is (see Brát, 1981 and Brát et al., 1987 ):
|
|
( 2) |
where α is constant slope angle of the banked plate, ϕ is rotational angle about vertical axis z .
Transformation of the unit vector due to rotation about slanting bearing axis is (Brát, 1981 and Brát et al., 1987 ):
|
|
( 3) |
where ψ is rotational angle about slanting bearing axis. The condition, that both transformations must lead to the same vertical plane y –z , gives the formula:
|
|
( 4) |
and subsequently:
|
|
( 5) |
The z -coordinate of the unit vector gives the angle of the crank arm γ (see scheme in Fig. 7 ):
|
|
( 6) |
Then for the crank mechanism is:
|
|
( 7) |
where r is the arm length, b is the connecting rod length, γ is the arm angle and δ is the slope angle of the rod. Finally the piston lift path is:
|
|
( 8) |
The mechanism allows changing the parameters α (the plate angle) and b (the rod length) in large range.
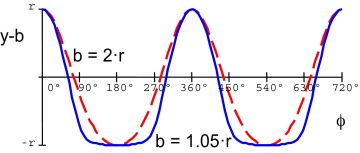
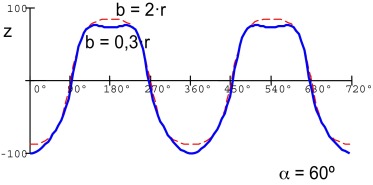
The curve shape is slightly influenced by the plate angle α , but the angle has direct influence to the piston lift amplitude (compare solid curve for α = 60° and dashed curve for α = 15° in Fig. 8 ). The rod length b slightly varies the curve shape (see Fig. 9 ). The mechanism is easy to realize but the possibilities to modify the lift curve are limited.
|
|
|
Figure 8. The piston lift path. |
|
|
|
Figure 9. The lift path. |
The mechanism with the Hooks joint
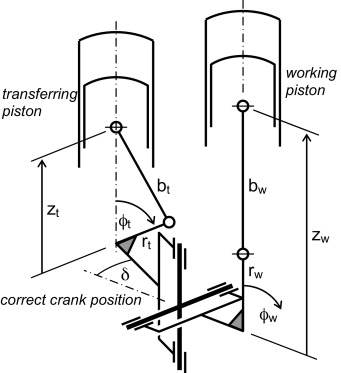
The design consists of the two crank mechanisms (for working and transferring piston) with the Hooks joint between. The working piston crank rotates steadily while the transferring piston crank behind the Hooks joint rotates non-steadily (Vinogradov, 2000 and Huston, 2002 ).
The relationship between the angle ϕw (working piston crank) and (transferring piston crank) is:
|
|
( 9) |
If the transferring piston crank foreruns the working piston crank by the phase angle ψ (usually ψ = 90°) then the transferring piston crank rotational angle is:
|
|
( 10) |
Both working piston and transferring piston lift path are:
|
|
( 11) |
where r is the crank arm length, b is the connecting rod length.
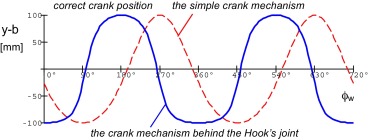
While the working piston lift path (simple crank mechanism, dashed curve in Fig. 11 ) is near sinusoidal (depending on the crank arm length to connecting rod length ratio), the transferring piston lift path (behind the Hooks joint, solid curve in Fig. 11 ) is near rectangular.
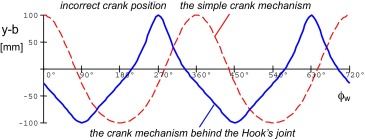
It is very important to arrange both crank mechanisms in the right position to the cradles of the Hooks joint (as shown in Fig. 10 ). If the position will be opposite, then the transferring piston lift path will not satisfying (see solid curve in Fig. 12 ).
|
|
|
Figure 10. Mechanism with Hooks joint, kinematic scheme. |
|
|
|
Figure 11. The piston path–crank rotation curve. |
|
|
|
Figure 12. The piston path–crank rotation curve. |
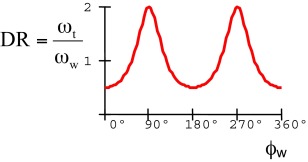
It is clear that the transferring piston moves from one position to the opposite with higher speed than the working piston. The ratio between these speeds is determined by the drive ratio of the Hooks joint – the first derivative of the ϕt –ϕw relationship.
|
|
( 12) |
The drive ratio expresses the ratio between the angular velocity of the transferring piston crank and the working piston crank. The DR–ϕw curve is in Fig. 13 .
|
|
|
Figure 13. The drive ratio. |
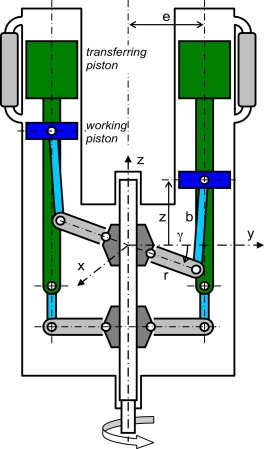
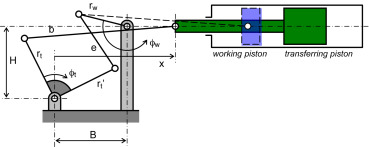
The four-joints mechanism
The kinematic scheme is shown in Fig. 14 .
|
|
|
Figure 14. The four-joint mechanism, kinematic scheme. |
The solution of the four-joint mechanism is determined by two equations (Vinogradov, 2000 and Huston, 2002 ):
|
|
( 13) |
where rw is the length of the working piston crank, e is the length of the connecting rod, is the length of the transferring piston lever arm, ϕw is the angle of the working piston crank to the horizontal direction, ϑ is the angle of the connecting rod to the vertical direction, is the angle of the transferring piston lever arm to the horizontal direction. Finally B and H is horizontal and vertical distance between the working piston crank joint and transferring piston lever joint.
Then
|
|
( 14) |
where ϕt is the angle of the transferring piston crank to the vertical direction, ψ is the angle between the transferring piston crank and lever arm. For the transferring piston crank mechanism is:
|
|
( 15) |
where b is the connecting rod length and δ is the angle of the connecting rod to the horizontal direction. Finally:
|
|
( 16) |
is the transferring piston path.
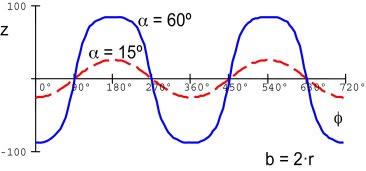
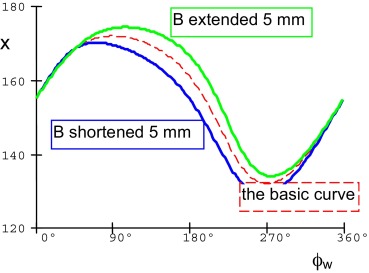
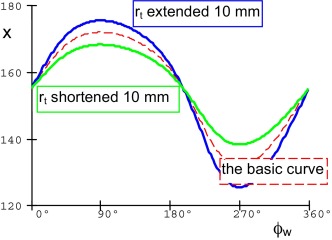
The mechanism has many “tuning parameters”, but the reached piston lift path curve is not satisfying. Fig. 15 expresses the sensitivity to the change of the B distance; Fig. 16 expresses the sensitivity to the change of the rt length.
|
|
|
Figure 15. The piston path–angle curve. |
|
|
|
Figure 16. The piston path–angle curve. |
Any kind of parameter changing does not lead to reach the requested shape of the transferring piston lift path.
Conclusion
The Stirling engine is the interesting alternative way to commercialize the waste heat. One of the ways to increase the effectiveness is to find the optimal mechanism to gear the engine pistons and optimize its parameters (dimensions).
The first question, to find the mechanism, is rather intuitive. The success depends on the designers idea, inspiration. The second question, to optimize the parameters, is analytical work. It can be done if the designer has a needed knowledge in mechanics.
Evaluating four mechanisms the mechanism with the Hooks joint seems to be very satisfying. It is simple, easy to design and realize and it leads to the good shape of the transferring piston path.
Conflict of interest
The authors declare that there is no conflict of interest.
Acknowledgment
The paper was prepared with support of the faculty project SP2015/98.
References
- Brát, 1981 V. Brát; Maticové metody; Academia, Praha, Czech Republic (1981)
- Brát et al., 1987 V. Brát, J. Rosenberg, V. Jáč; Kinematika; SNTL, Praha, Czech Republic (1987)
- Huston, 2002 H.J.R.L. Huston; Dynamics of Mechanical Systems; CRC Press, London (2002)
- Míka, 2004 J. Míka; Kogenerace s pístovými motory s vnitřním a vnějším spalováním. Habilitační práce; VŠB – Technical University of Ostrava, Ostrava, Czech republik (2004)
- Vinogradov, 2000 O. Vinogradov; Fundamentals of Kinematics and Dynamics of Machines and Mechanisms; CRC Press, London (2000)
Document information
Published on 05/10/16
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?