Optimization of hydraulic parts using adjoint optimization

Summary

Modern fluid mechanics examines understanding, predicting and directing of fluids in the fluid structures. But new computational methods need to find out the optimal solution of each hydraulic system because of minimization of power losses. Consequently, this article looks through the shape optimization of hydraulic parts using adjoint optimization method. It is most used gradient-based method. This approach enables to calculate the objective function sensitivities in consideration of the design variables (Kyriakos and Papadimitriou, 2008 ).

Many producers talk about the optimized solutions, but only small part from them use all possibilities for finding the best one. It is motivation why in this paper the shape optimization of the hydraulic valve component with respect to minimization of pressure losses is presented.

Keywords

Optimization ; Adjoint method ; Hydraulics

Introduction

Any part of any hydraulic system that people have ever produced has had its dimensions designed in order to fulfill some shape, power, flow, pressure parameters or criteria. In most cases it is simply the shape design that makes the important work functions possible. But this solution is not the optimal solution with the best parameters and options. From the beginning it is necessary to say a few words about theory of mathematical flow models, the adjoint optimization and the computational methods.

Mathematical flow model for incompressible fluids is resulted from the law of conservation of mass. Generally, the law is expressed by the continuity relation. Differential configuration of equation for incompressible flow is

${\frac {\partial u_{j}}{\partial x_{j}}}=0$

( 1)

From the law of momentum conservation resulted that the force of inertia is equal the sum of mass and surface (pressure and friction) forces. After substitution and reducing of operators we can write differential equation for momentum conservation known as Navier–Stokes equations (Kozubková, 2009 )

${\frac {\partial u_{i}}{\partial t}}+{\frac {\partial u_{i}}{\partial x_{j}}}u_{j}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial x_{i}}}+v{\frac {\partial ^{2}u_{i}}{\partial u_{j}\partial u_{j}}}+f_{i}$

( 2)

The computational elaboration and simulation of the mathematical flow models with the aim of the description of the flow parameters has got a lot of benefits. With the fast improvement of a computational capacity the mathematical analysis begins to be effective during a proposition and design of hydraulic machines and in a lot of engineering applications. The aim of the numerical methods is to find a discrete solution defined in sufficiently small domains with the aid of the system of differential (algebraic) equations. The oldest classical method for differential equations is the method of finite differences. There is used a reduction in the Taylor series. The finite element method was used only for the structural analysis in the past but later this method started to be applied for flow calculations. A big benefit is the possibility to use the inconsecutive meshes for the discretization of geometry. Now it is used for the flow solutions with the smaller Reynolds numbers. The third described method combines benefits of two previous methods. The finite volume method is used for integration of partial differential equations that describe the flow of compressible and uncompressible fluids. The discrete finite volumes are defined using non-staggered scheme where all values are calculated in the middle of the finite volumes.

In this article we specify the term of the shape optimization in hydraulic application which is calculated using a partial differential equation and the design of the part assigns the geometrical domain of the PDE. The general description of this problem is:

${\underset {F\in D}{\mbox{min}}}J(x,F)$

( 3)

subject to

$L(u)=f{\mbox{   }}{\mbox{in}}{\mbox{   }}\Omega (F)$

( 4)

and

$B(u)=g{\mbox{   }}{\mbox{on}}{\mbox{   }}\partial \Omega (F)$

( 5)

where F designates the shape, D the set of acceptable shapes, L the differential operator of partial differential equation, Ω(F ) the domain as function of the shape, B an operator defining the boundary conditions and f and g are given functions ( Schneider, 2006 ).

Material and methods

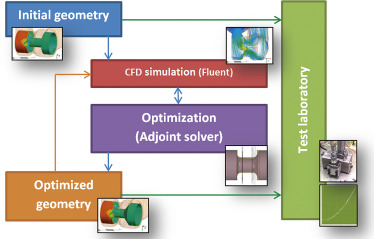
In our case the adjoint method was applied on the optimization of a hydraulic valve part. As the first step, numerical analysis of the flow field in the initial geometry of the hydraulic valve was carried out. For the calculation the full flow model of the valve cavities was used with one type of the pressure compensator located in the circuit. For geometry optimization a simplified geometry was used with the cavities around the hydraulic component assuming the symmetry of boundary conditions (asymmetry boundaries have no foundation for this type of spool of the pressure compensator) and with the reduction of the model size and so the computing time.

The models of initial and optimized geometry were calculated with very fine mesh options on the high-power computational station.

In the last step the geometries were compared using the test measurements. Significant difference between the initial versus optimized geometry of the pressure compensator was confirmed (Fig. 1 ).

Figure 1. Process of the optimization.

Optimization step by step

Generally this optimization process used three geometries. As the first the detailed model of initial geometry was prepared for one position of the compensator spool. This position is the most probable working position for the pressure compensator of the selected dimensions and the mass flow rate. The prepared geometry was meshed with very fine grid. The quality of grid elements was controlled by the orthogonal number criteria before it was exported to the Ansys Fluent CFD software. In the next step mathematical model for the calculation of the actual geometry was set up in Ansys Fluent. All calculations were solved as steady turbulent flow for one position of the compensator spool in the cavity of the valve. The two-equation standard SST k –ω turbulent model was applied. Defined boundary conditions were the velocity inlet and the pressure outlet. In all calculations the velocity inlet was calculated for maximum value of the mass flow rate of 220 lpm and with the pressure outlet equal to zero.

The second geometry was specially created for the adjoint optimization of the compensator spool. The shape optimization of fluid systems belongs to the most complicated computational cases. With respect to that it is necessary to choose only the part of geometry which is the subject of optimization. Other elements and connected accessories in the circuit that are not optimized must be eliminated. So a simplified geometry was used without cavities of the valve and with a symmetric flow through the compensator spool. This model had to be calculated with the Realizable k –ɛ model of turbulence, which is recommended for a combination with adjoint optimization. The third model had the same geometry as the first one (initial – detailed) but with new optimized geometry of the compensator spool.

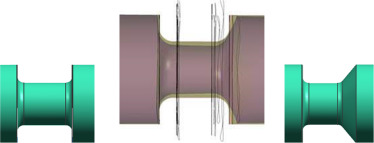
The optimization was based on adjoint optimization method. As the observable value the pressure-drop was used. The adjoint solver offers various type of observables, as force, moment of force, swirl, etc. (Eggenspieler, 2011 ). With these options the adjoint solver modifies the walls of the geometry with respect to minimization of pressure drop between the inlet and outlet (Ansys, 2013 ). During this set up it is possible to check actual value of the examined parameter. In the adjoint solution control the stabilized scheme of the advancement controls was checked. In the next step convergence criteria were set up. After setting of all necessary options the solution of the optimization could start. After calculation we could compare a lot of sensitivities of the geometry. In this case the shape modification was evaluated. For the editing the morphing control was used. The modified geometry was exported for the next analysis. In the picture below we can see the modified geometry versus the initial one. The diameter of the spool neck was changed and the wall opposite to the flow direction is under 53° angles. This value ensues from the geometry configuration and the boundary conditions (Fig. 2 ).

Figure 2. The initial design (left), the recommended shape from the optimization (middle), and the used optimized design (right).

The third model was generated as combination of initial compensator geometry and the new optimized spool geometry. The set up of the mathematical model and boundary conditions was the same to enable comparison of numerical analysis carried out with the first and third model.

Experimental

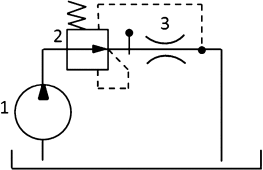
The pressure compensator was tested in the open circuit. As we can see in Fig. 3 the circuit consists of the pump (1), the pressure compensator (2) and the orifice (3). In this simply hydraulic schema are not any measuring accessories. The pressure compensator was tested in the two modifications – initial and optimized design. Both variants were tested for the pressure ramp of 0–300 bar with the mass flow rate of 220 lpm. A lot of compensator compression springs with the different spring stiffness were compared during measurements.

Figure 3. Hydraulic scheme of the tested valve without the measuring accessories.

Results

The goal of the described work was to optimize the design of the pressure compensator with the minimization of the pressure drop. All results of the simulation were verified with the testing data. From the comparison of the pressure drop before and after the optimization we can state about 7% improvement. But from the analyses and the testing there were expressive changes in the forces acting on the compensator spool. The radial force has significantly increased (more than 50%) in the optimized design and had a negative influence on the spool function during the testing. This influence was reduced using a modification of the cavities. This has brought both the radial force reduction and further improvement of about 2% of the pressure drop (Fig. 4 ).

Figure 4. Velocity streamlines of the initial versus optimized design.

Discussion and conclusions

Generally, optimization is of great importance during the design procedure of new hydraulic components and equipment. Application of optimization techniques can be a helpful tool in the most effective, efficient solutions to various engineering problems. The importance of optimizations is even stronger in todays difficult times of economic competiveness and rapidly changing market. Only good quality products manufactured at reasonable costs maintain their place on store shelves.

Conflict of interest

The author declares that there is no conflict of interest.

References

1. Ansys, 2013 ANSYS, Inc. Southpointe; ANSYS Fluent Adjoint Solver (Adjoint Solver Module Manual); ANSYS, Inc. Southpointe (2013) 74 pp. http://148.204.81.206/Ansys/150/ANSYS%20Fluent%20Adjoint%20Solver%20Manual.pdf
2. Eggenspieler, 2011 G. Eggenspieler; Ansys Fluent Adjoint Solver; Ansys, Inc (2011) 38 pp. http://www.ansys.com/staticassets/ANSYS/Conference/Confidence/San%20Jose/Downloads/optimization-adjoint-solver-9.pdf
3. Kyriakos and Papadimitriou, 2008 G.C. Kyriakos, D.I. Papadimitriou; Adjoint Method for Shape Optimization; , 978-3-540-72152-9Springer, Berlin, Heidelberg (2008)
4. Kozubková, 2009 M. Kozubková; Matematické modely kavitácie a hydraulického rázu; Vysoká Škola Baňská – Technická Univerzita Ostrava (2009) 130 pp., ISBN: 978-80-248-2043-93
5. Schneider, 2006 R. Schneider; Applications of the Discrete Adjoint Method in Computational Fluid Dynamics; The University of Leeds School of Computing (2006) http://www.comp.leeds.ac.uk/research/pubs/theses/schneider.pdf