Simulation of a cross-flow air classifier at high solid feed rates

Resumen

El clasificador de polvo de flujo cruzado es un equipo de clasificación que trabaja por vía seca. El uso de este tipo de dispositivos se evalúa actualmente para reemplazar a los métodos húmedos de clasificación en la producción de arena de trituración. La influencia del contenido de polvo es de importancia crítica para el diseño del proceso. Una manera de estimar esta influencia es a través de simulación numérica. En éste trabajo se simula el proceso de clasificación de polvo mediante fluidodinámica computacional (CFD). La interacción entre partículas se modela mediante un método de elementos discretos (DEM). Las simulaciones se optimizan para minimizar el error a través de la elección entre dos modelos de turbulencia y entre dos modelos para la inyección de sólidos. Se simula la clasificación de polvo con tres distintos contenidos de polvo. Se establece que el contenido de sólidos alimentados al clasificador tiene una gran influencia en el proceso de clasificación, por lo que es un parámetro crítico para el correcto diseño del clasificador.

Abstract

The cross-flow air classifier is a dry process device. The use of such separators is being evaluated to replace the wet classification methods in the production of manufactured sand. The influence of the solid feed rate is critical for the correct design of the process. One method to analize the influence of the feed is by using numerical simulation. In this work, the powder classification process is simulated by computational fluid dynamics (CFD). The particle-particle interaction is modeled with a discrete element method (DEM). Simulations are optimized to better represent the experimental data by choosing between two turbulence models and two models for the injection of solids. Dust classification at three different solid rates is simulated. It is established that the amount of solids has a great influence in the classification process. This fact indicates that the solids content is a critical parameter for a proper design of the device.

Palabras clave

CFD-DEM;Clasificación de Polvo;Arenas de Trituración

Keywords

CFD-DEM;Air Clasification;Manufactured Sands

1. Introduction

Los agregados finos para la producción de hormigón han sido conformados históricamente por arenas naturales extraídas de lechos de ríos y/o depósitos naturales. Sin embargo, estas fuentes están en extinción o su explotación requiere de costos cada vez más elevados. Una alternativa para la producción de agregados finos es el uso de arenas de trituración para reemplazar a las arenas naturales [1] ;  [2]. La distribución de tamaño de partículas (DT) de las arenas de trituración hace que se requiera de un tratamiento previo a su utilización como agregado fino. El principal problema es que estas arenas presentan un exceso de polvo (partículas con tamaño menor a 75 μm) [3] ;  [4].

El método de eliminación de polvo en arenas de trituración más usado en la actualidad es el lavado con agua. El proceso de lavado elimina el polvo de manera efectiva. Sin embargo, genera problemas como el tratamiento y secado del lodo efluente. Además, el proceso húmedo requiere de una alta disponibilidad de agua que no es posible recuperar completamente. Por las razones anteriores, el proceso de lavado es cada vez menos aplicado y se lo considera dañino para el medio ambiente [1] ;  [3].

Una alternativa al proceso de lavado es la clasificación por vía seca o clasificación por aire. Se basa en usar las fuerzas de gravedad, centrífugas y el arrastre del aire sobre las partículas para clasificarlas por tamaño [5]. Esta tecnología tiene dos aplicaciones clásicas, la más antigua en el control de la polución del aire y la más recientemente en la obtención de polvos con tamaño de partícula controlado. En los últimos años, se han desarrollado distintos tipos de clasificadores, algunos de los cuales han sido aplicados a la industria de agregados [6]; [7]; [8] ;  [9].

El clasificador de polvo cruzado es uno de los equipos capaces de controlar la cantidad de polvo en las arenas de trituración. Una de las ventajas que presenta es la clasificación del material en más de una fracción con un moderado consumo de energía. Datos de estudios previos sugieren que el rendimiento de estos clasificadores está influenciado por el caudal de sólidos que ingresan al clasificador [10]. Cuando se opera con grandes caudales de polvo, el comportamiento de las partículas en su interior no es el ideal. Como consecuencia, la eficiencia disminuye y el diámetro de corte se aleja del valor de diseño.

Una manera de poder analizar el comportamiento del flujo dentro del clasificador es a través de la fluidodinámica computacional o CFD. Esta herramienta permite resolver las ecuaciones que modelan el comportamiento de los fluidos, mediante una discretización de las ecuaciones diferenciales y de modelos de turbulencia específicos para cada sistema. El uso de CFD es de gran utilidad para problemas de ingeniería como: análisis aerodinámico de estructuras sometidas a flujo externo [11] ;  [12], modelado de deslizamientos de laderas [13], simulación de flujos en tanques de agitación [14], ductos [15], lechos porozos [16] y flujos bifásicos en torres de enfriamiento [17]. La simulación de flujos bifásicos aire-polvo puede llevare a cabo mediante el uso de CFD y el método de elementos discretos (DEM, Discrete Element Method). Con éste método se puede modelar la interacción entre partículas y entre las partículas y el fluido. La combinación de estas técnicas de CFD-DEM posibilita la observación y comprensión de los fenómenos involucrados [18]; [19] ;  [20].

Distintos modelos de turbulencia pueden usarse para la simulación de flujos bifásicos [21]; [10]; [9]; [6]; [8] ;  [17]. El más utilizado por su simpleza es el modelo κ − ϵ. Otros modelos de turbulencia más complejos, como el del tensor de esfuerzos de Reynolds (RSM) o el modelo κ − ϵ realizable (RKE), pueden dar información más detallada del flujo dentro del clasificador [22] ;  [23]. El modelo RSM tiene un requerimiento computacional mayor que el κ − ϵ y sus variantes debido a la mayor cantidad de ecuaciones diferenciales en su formulación. Sin embargo, el RSM es utilizado cuando el problema de flujo es de elevada complejidad [24].

El objetivo de este trabajo es simular el proceso de clasificación de material particulado dentro de un clasificador de flujo cruzado. Las simulaciones se llevan a cabo mediante las técnicas combinadas de CFD-DEM considerando un contenido de polvo de 1.5 kg/m³. Dos modelos de turbulencia y dos métodos de inyección de polvo son evaluados en comparación con datos experimentales de la literatura. Sobre esta base, se establece el método más apropiado de simulación. Se procede luego a realizar nuevas simulaciones con mayores contenidos de polvo para obtener información fuera del rango reportado para el clasificador.

2. Materiales y Métodos

2.1. Descripción del clasificador de flujo cruzado

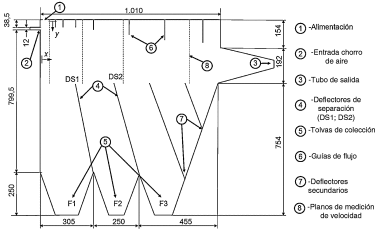
Un esquema del clasificador de flujo cruzado puede verse en la figura 1. El material sólido a clasificar ingresa por la parte superior a través de una tolva de dosificación (Punto 1). Las partículas son interceptadas por un chorro de aire proveniente de una hendija (Punto 2). La corriente de aire trasporta las partículas según la magnitud de las fuerzas que actúen sobre ellas. El flujo de aire escapa de la cámara por el tubo de salida (Punto 3). Las partículas son separadas en tres fracciones mediante los deflectores de separación DS1 y DS2 (Punto 4). Las partículas grandes son más afectadas por la gravedad y caen en la tolva de colección F1 (Punto 5). Las partículas finas son especialmente afectadas por el arrastre del aire y se colectan en las tolvas F2 y F3. Una pequeña cantidad de partículas finas escapan con el aire por el tubo de salida. El clasificador cuenta con guías que conducen el flujo de aire hasta el tubo de salida (Punto 6). Hay una pequeña abertura entre los deflectores secundarios y la pared del clasificador que permite la colección de las partículas más finas en F3 (Punto 7). Esta abertura no es tomada en cuenta para las simulaciones.

Figura 1. Esquema del clasificador de flujo cruzado. Unidades en mm.

2.2. Descripción del proceso experimental

Wang y Hafenbradl [10] ;  [25], reportan datos experimentales referidos a la clasificación de esferas de vidrio de densidad 2650 kg/m³ y un rango de tamaños entre 0.05 a 1.1 mm. El rango de velocidades entre los cuáles se realizó la clasificación es de 8 a 12 m/s y un contenido de sólidos de 0.1 a 4.5 kg/m³. También se informa la velocidad del flujo medida en planos ubicados a diferentes distancias de la entrada de aire (véase figura 1). La granulometría de la alimentación es conocida, así como también la de las fracciones colectadas en las distintas tolvas.

2.3. Descripción del proceso de simulación

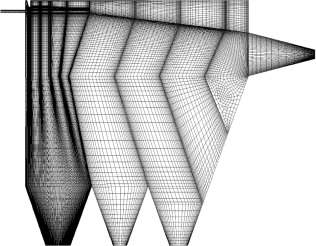
En este trabajo se realizan simulaciones empleando un marco de referencia Euleriano-Lagrangiano. El aire se considera una fase continua y su comportamiento está modelado por las leyes de Navier-Stokes y continuidad para flujos incompresibles. El flujo dentro del clasificador ha sido caracterizado como turbulento por lo que el campo de presiones y velocidades se calcula utilizando las ecuaciones promediadas RANS, (Reynolds Averaged Navier-Stokes), basadas en los valores medios de las variables de flujo [22] ;  [23]. Las partículas son tratadas como una fase dispersa que puede intercambiar momento con la fase continua. Las posiciones de las partículas se calculan a través de ecuaciones de movimiento dentro del flujo que ha sido calculado previamente [18] ;  [26]. Las simulaciones se llevan a cabo mediante una discretización del dominio en volúmenes finitos utilizando el software ANSYS-FLUENT [27]. El campo de velocidades y presiones es resuelto de manera transiente hasta llegar a valores estables en el tiempo. Luego, se simula la inyección de partículas y su trayectoria hasta que se clasifican en las tolvas. Dos diferentes modelos de turbulencia son evaluados para la simulación del proceso de clasificación. El primero es el RSM y el segundo el RKE. En ambos casos se utilizaron funciones de pared escalables con lo que se evita resolver completamente la capa límite. El uso de las funciones de pared reduce la cantidad de elementos necesarios para la simulación. Sin embargo, es necesario tener precaución respecto de la distancia del primer nodo a la pared. El dominio es simplificado para poder llevar a cabo una simulación en dos dimensiones. Tres mallas conteniendo 15000; 35000 y 58000 elementos fueron utilizadas para poner a prueba la independencia de la solución. Las mallas cuentan con un sector de tipo estructurado cerca de la entrada de aire y un sector de tipo no estructurado en la zona cercana a la salida del mismo. En todos los casos la distancia y⁺, del primer nodo a la pared, se mantuvo en el rango 20-100 [23] ;  [22]. Debido a que el valor de y⁺ depende de condiciones locales de flujo se utilizaron funciones de pared escalables. Este tipo de funciones de pared evitan un deterioro de los resultados en caso de que alguno de los nodos se encuentre por debajo de y⁺ ≤ 11 [27]. El refinamiento de las mallas se realizó tomando en cuenta los principales gradientes de flujo y el número de elementos en la capa límite turbulenta. Sin embargo, mallas con un número de elementos mayor a 35000 no presentan una mejora significativa en la simulación del flujo con ninguno de los modelos de turbulencia usados. La malla de 35000 elementos, presentada en la figura 2, es utilizada para las simulaciones siguientes.

Figura 2. Malla utilizada para las simulaciones.

Las condiciones de borde impuestas fueron las de velocidad en la entrada (Velocity Inlet) y presión a la salida (Pressure Outlet). Las condiciones de borde turbulentas a la entrada del aire fueron los valores de la energía cinética turbulenta k_in = 1.5 m²s⁻² y la tasa de disipación de la energía turbulenta ϵ_in = 18.6 m²s⁻³. Estos valores se calcularon a partir de correlaciones tomando en cuenta los valores de la velocidad de entrada del aire, el ancho de la hendija y una intensidad turbulenta I = 10%. Los esquemas numéricos utilizados para la resolución del problema de flujo pueden verse en la tabla 1. Las simulaciones se llevan a cabo considerando un error en la convergencia menor a 1 × 10⁻⁴.

Tabla 1. Ecuaciones de transporte y esquemas usados para su resolución

Ecuación de Transporte	Esquema
Algoritmo velocidad-presión	SIMPLEC
Gradiente	LSCB
Presión	Segundo Orden
Energía cinética turbulenta	Segundo Orden (upwind)
Tasa de disipación turbulenta	Segundo Orden (upwind)
Tensores de Reynolds	Segundo Orden (upwind)
Temporal	Segundo Orden (upwind)
Seguimiento de partículas	Implícito

La trayectoria de las partículas se modela integrando en el tiempo las ecuaciones de Newton aplicadas a cada partícula [18] ;  [19]. El efecto de la turbulencia se tiene en cuenta a través del modelo Random Walk. Este modelo considera las fluctuaciones de las componentes de la velocidad en el cálculo de las trayectorias. Las partículas intercambian momento con la fase continua. Esto se modela como una generación de cantidad de movimiento dentro de las ecuaciones RANS. Además, el movimiento de las partículas puede generar o amortiguar la turbulencia del flujo [27]. Las partículas no sólo interactúan con la fase continua sino que también lo hacen entre sí. El choque entre dos partículas se modela como la acción conjunta de un resorte y un amortiguador usando el paquete de colisiones DEM propio del software [18] ;  [27]. Las interacciones mencionadas son función de la masa y tamaño de las partículas. Mayores contenidos de polvo generan un aumento de estas interacciones creando un flujo cada ves más complejo. Los parámetros necesarios para el modelado y cálculo de las trayectorias de las partículas se presentan en la tabla 2.

Tabla 2. Parámetros del modelado de las interacciones entre partículas

Parámetro	Valor
Longitud característica	1 × 10−5 m
Factor de forma	0.7
Paso temporal de las partículas	1 × 10−4 s
Longitud de la malla de colisión	6 × 10−3 m
Constante del resorte	5 × 104 N m−1
Coeficiente de amortiguamiento	0.3
Coeficiente de fricción (sticking)	0.3
Coeficiente de fricción (gliding)	0.3
Coeficiente de fricción límite	0.3
Coeficiente de restitución normal	0.3
Coeficiente de restitución tangencial	0.6

La granulometría del polvo de alimentación es representada de dos maneras diferentes. La primera se basa en la suposición de que la granulometría sigue un tipo de distribución tipo Rosin-Rammler [28]. La ventaja de éste método es la fácil introducción de los parámetros al software y la capacidad de dividir el rango de tamaños en cantidades definidas por el usuario. La segunda es mediante el método de multi-inyección. Cada clase o tamaño de partícula representa una inyección de polvo independiente. El caudal másico de cada inyección está determinado por la distribución granulométrica y el caudal total de polvo alimentado. Esta estrategia es más laboriosa ya que se deben realizar tantas inyecciones como tamaños se desee tener en cuenta. Las simulaciones se realizaron para una velocidad de entrada de aire de 10 m/s y un contenido de polvo de 1.5 kg/m³. Los casos estudiados se resumen en la tabla 3. Los Casos 1 y 2 se utilizaron para conocer cuál de los modelos de turbulencia representa mejor el flujo de aire. Los Casos 3 y 4 consideran la distribución granulométrica de la alimentación. Los Casos 5 y 6 simulan el proceso de clasificación con un contenido de polvo 5 y 10 veces mayor al reportado por Wang.

Tabla 3. Casos de estudio realizados. V_IN: Velocidad de entrada; C: Contenido de sólidos

Caso	VIN(m/s)	N. Elem.	C (kg/m3)	Turbulencia	Inyección
1	10	35000	–	RSM	–
2	10	35000	–	RKE	–
3	10	35000	1.5	RSM	Rosin-Rammler
4	10	35000	1.5	RSM	Multi-Inyección
5	10	35000	7.5	RSM	Multi-Inyección
6	10	35000	15	RSM	Multi-Inyección

2.4. Caracterización del desempeño del clasificador

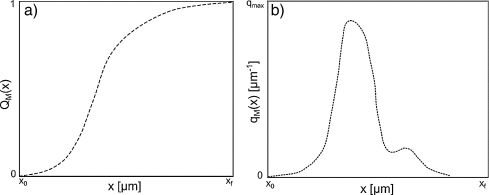
El proceso de clasificación dentro del separador puede ser caracterizado mediante las granulometrías del polvo obtenido en cada tolva. Una manera de hacerlo es mediante la distribución acumulada pasante, representada en la figura 3a. A esta distribución se la denomina Q_M(x) y representa la fracción en masa de la población que está compuesta por partículas menores que x[28] ;  [29]. En algunos casos la distribución puede ser modelada mediante la distribución Rosin-Rammler (Ecuación (1)). Los parámetros ${\textstyle {\overline {x}}}$ y n se pueden encontrar ajustando datos experimentales por mínimos cuadrados [28]

$Q_{M}(x)=1-e^{-{\left(x/{\overline {x}}\right)}^{n}}$

(1)

Figura 3. Caracterización de la población: a) Distribución acumulada pasante; b) Función de densidad de distribución.

Si se utiliza el método de multi-inyección, las fracciones másicas referentes a cada tamaño de partícula se pueden encontrar restando la distribución acumulada pasante de dos tamaños contiguos, Ecuación (2)

$M(x_{i})=Q(x_{i+1})-Q(x_{i})$

(2)

Esta fracción multiplicada por el caudal total de alimentación determina el caudal másico de partículas de ese tamaño en particular.

Otra forma de representar la granulometría es mediante la función de densidad de distribución en masa, esquematizada en la figura 3b. A esta función se la denomina q_M(x) y representa la fracción de la población formada por partículas con tamaños comprendidos entre x y x + dx. Ambas distribuciones están relacionadas por la Ecuación (3)

$q_{M}(x)={\frac {{dQ}_{M}(x)}{dx}}$

(3)

La utilidad de la función de densidad reside en que el máximo de la función coincide con la moda de la distribución, de esta manera es posible caracterizar a la población a través de un solo parámetro.

El proceso de clasificación dentro del equipo también se puede caracterizar cuantitativamente mediante el diámetro de corte y la selectividad [10]. El diámetro de corte del deflector DP1, x₅₀, representa el tamaño de la partícula cuya eficiencia de clasificación en F1 es de 50% [10] ;  [5]. De igual manera, el diámetro de corte del deflector DP2 representa el tamaño de la partícula cuya eficiencia de clasificación en F2 es de 50%. Este último se denomina y₅₀. Los diámetros de corte son obtenidos realizando una curva de eficiencia por tamaños y leyendo el diámetro de partícula para el cual la eficiencia es 50%.

La selectividad de la clasificación, k, es un cociente dado por:

$k={\frac {x_{25}}{x_{75}}}$

(4)

El parámetro x₂₅ es el diámetro de partícula para el cual la eficiencia de colección es de 25%. De manera similar, ocurre con x₇₅ y una eficiencia de 75%. Para una clasificación ideal el parámetro k es cercano a uno y la curva de eficiencia se parece a un “escalón”. En una curva de eficiencia real esto no ocurre debido a la acción de la turbulencia, aglomeración e interacción entre partículas.

3. Resultados y Discusión

3.1. Simulación del flujo de aire

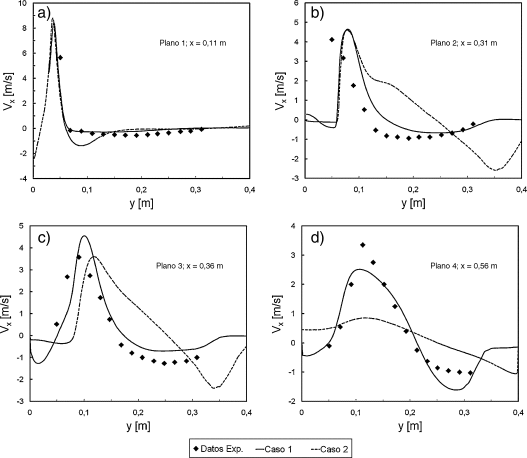
La variación de la componente x de la velocidad, V_x, con la distancia al límite superior del clasificador, y, fue medida experimentalmente en diferentes planos normales al flujo. Los planos están situados a 0.11, 0.31, 0.36 y 0.56 m de la rendija de entrada de aire (véase figura 1. Punto 8). En la figura 4 se presenta la comparación entre los datos experimentales y los resultados de las simulaciones de los Casos 1 y 2 utilizando el modelo RSM y el RKE respectivamente. El modelo RKE representa la elección por defecto en la mayoría de los casos de estudio que involucren flujos turbulentos [22] ;  [23]. Sin embargo, su rendimiento es limitado y se ha encontrado que el modelo falla al describir flujos en geometrías complejas o con grandes esfuerzos de deformación como por ejemplo dentro de separadores tipo ciclón [24]. Además, Wang [10] presenta resultados significativamente diferentes al resolver el flujo dentro del clasificador con una malla estructurada y una no estructurada utilizando el modelo κ − ϵ estándar.

Figura 4. Comparación entre la componente x de la velocidad estimada con la experimental: a) Plano 1; b) Plano 2; c) Plano 3; d) Plano 4 (véase fig. 1).

Puede observarse que el Caso 1 representa mejor al flujo que el Caso 2. Sin embargo, el Caso 1 presenta algunas diferencias con los datos experimentales en el Plano 2. Se observa que sobreestima el valor máximo de velocidad en el Plano 3, y lo subestima en el Plano 4. El Caso 2 con el modelo RKE presenta grandes diferencias con los datos experimentales. De la comparación se observa que el modelo RSM presenta un error aceptable dada la complejidad del flujo y predice el comportamiento de los datos experimentales con mayor exactitud.

La magnitud de la velocidad de flujo para una velocidad de entrada de 10 m/s, para el Caso 1, se muestra en la figura 5. Se observa claramente la trayectoria del flujo y las zonas de máxima y mínima velocidad del aire. También se observan zonas de recirculación o remolinos entre las guías de flujo. Este fenómeno ocurre en distintos tipos de clasificadores y afectan al proceso de clasificación [10] ;  [9]. Los remolinos en las zonas de recirculación captan las partículas más finas y las transportan corriente arriba influyendo en la selectividad de la clasificación.

Figura 5. Representación de la magnitud de la velocidad (m/s) dentro del clasificador para una velocidad de entrada de 10 m/s.

El modelo de turbulencia RSM representa los datos experimentales con muy buena concordancia y permite una visualización detallada del flujo dentro del clasificador. En consecuencia, este modelo se elige para continuar con las simulaciones.

3.2. Comparación con datos granulométricos

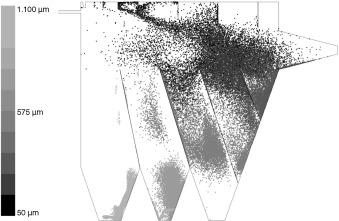
En la figura 6 se presenta una descripción gráfica de la simulación del proceso de clasificación. Se muestra la posición instantánea de las partículas inyectadas al clasificador para el Caso 4, luego de terminada la inyección. El tamaño de las partículas se describe mediante una escala de grises. Se observa que las partículas de mayor tamaño, entre 700 y 1100 μm se asientan en la tolva de colección F1. Partículas con tamaños entre 700 y 500 μm en F2 y las menores que 500 μm alcanzan la tolva F3. Se aprecia la influencia de los remolinos que se producen en las zonas de recirculación. Una parte de las partículas de polvo, de tamaño menor a 75 μm, son atrapadas en los remolinos y se dispersan dentro de la cámara. Como consecuencia, partículas de este tamaño pueden encontrarse en las tolvas F1 y F2.

Figura 6. Posición instantánea de las partículas dentro del clasificador para una velocidad de entrada de 10 m/s.

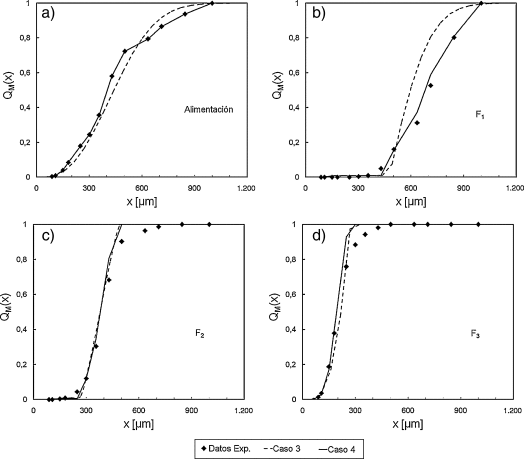
En la figura 7 se presentan los resultados experimentales y de simulación en términos de la distribución acumulada pasante para los materiales colectados. Se comparan los datos obtenidos en el Caso 3 con la inyección de tipo Rosin-Rammler y el Caso 4 con el método de multi-inyección.

Figura 7. Distribuciones acumuladas pasantes para los materiales colectados a 10 m/s: a) alimentación; b) F1; c) F2; d) F3.

La figura 7a representa la granulometría de la alimentación usada para los estudios experimentales y las usadas para las simulaciones. Las figuras 7b a 7d representan las distribuciones acumuladas para las F1 a F3.

En el Caso 4 se observa un muy buen modelado de la granulometría del polvo a la entrada del clasificador mientras que el Caso 3 presenta diferencias en la mayoría de los puntos.

La granulometría estimada para la tolva F1 en el Caso 4 está en excelente concordancia con los datos experimentales. Por otra parte, el Caso 3 sobreestima el valor de la curva en el rango de 500 a 900 μm.

Ambos casos sobreestiman el valor de la distribución a partir de 500 μm para F2 y 300 μm para F3. Sin embargo, las diferencias entre los casos y los datos experimentales no son significativas en estas tolvas.

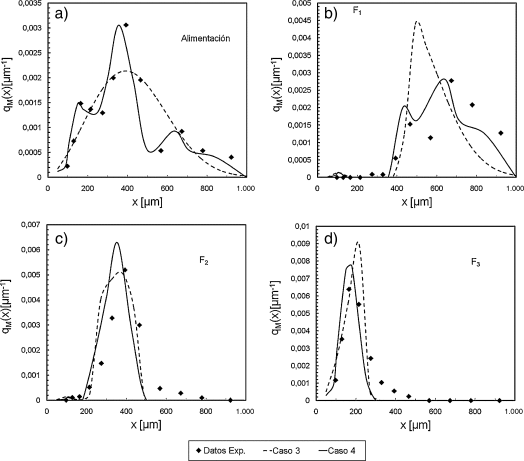
Los resultados de los Casos 3 y 4 también pueden compararse mediante la función de densidad de distribución presentada en la figura 8. La figura 8a presenta los datos correspondientes a la alimentación y las figuras 8b a 8d los de las tolvas de colección. En todos los casos, las curvas de función de densidad revelan mayores diferencias entre los datos estimados y los calculados a partir de datos experimentales.

Figura 8. Funciones de densidad para los materiales colectados a 10 m/s: a) alimentación; b) F1; c) F2; d) F3.

La figura 8a muestra que el Caso 3 describe una curva unimodal mientras que el material claramente describe una curva con tres máximos. El Caso 4 describe mejor la curva granulométrica del polvo.

La comparación de los resultados de F1, confirman la sobreestimación del contenido de partículas en el rango de 500 a 900 μm. El Caso 3 estima un máximo de la distribución en 500 μm que no se observa en los datos experimentales o en el Caso 4. En el caso de F2 y F3 las predicciones difieren en la magnitud y tamaño de partícula donde se encuentran sus máximos. Además, presentan diferencias en el ancho de la campana. Ambos casos fallan al estimar la presencia de partículas mayores a 600 μm en F2 y 300 μm para F3. Este efecto podría deberse a que la simulación sobreestima la influencia de las partículas sobre el flujo. Se produce un apantallamiento de la velocidad del aire que afecta el arrastre sobre las partículas. Como consecuencia, la trayectoria de las partículas es mas corta y las más gruesas no alcanzan a las tolvas más alejadas. Por otra parte, las figuras 8b y 8c reportan la presencia de partículas de tamaño cercano a 100 μm en las tolvas. Esto indica que estas partículas se colectan en F1 o F2 por acción de la dispersión turbulenta o la interacción con partículas más gruesas.

La distribución tipo Rosin-Rammler no logra una buena representación del polvo de alimentación. El error es arrastrado en la estimación de las poblaciones de las tolvas. Las simulaciones con el método multi-inyección presentan una mejor representación de los datos experimentales y serán usadas para estimar la influencia del polvo sobre el mecanismo de clasificación.

3.3. Efecto del contenido de sólidos sobre la clasificación

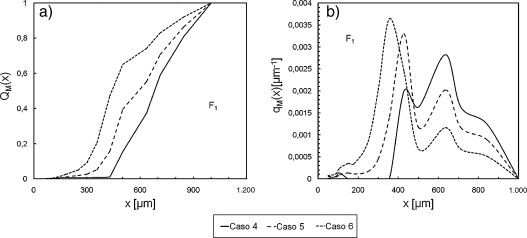
Los Casos 5 y 6 se simularon para extender la información en un mayor alcance que el reportado en la literatura. Las figuras 9a y 9b muestran los datos para la granulometría de la tolva F1. Como se observa en la figura 9a, un aumento en el contenido de polvo tiene como consecuencia un incremento en la cantidad de partículas pequeñas colectadas en F1. El mismo efecto se confirma observando la figura 9b, donde el máximo de la curva se desplaza hacia diámetros más pequeños. Además, el máximo secundario disminuye tendiendo a la unimodalidad. El material colectado en F1 se enriquece en partículas finas cuando se incrementa el caudal de sólidos.

Figura 9. Efecto del contenido de sólidos en la tolva F1: a) Distribución acumulada pasante; b) Función de densidad de distribución.

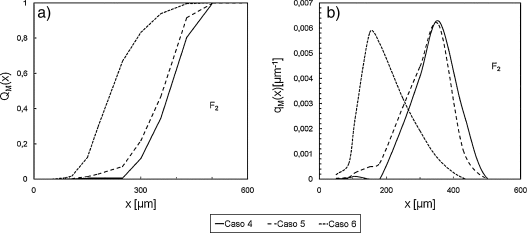
Las figuras 10a y 10b muestran los resultados para la tolva F2. La tendencia observada es similar a la de F1, pero en este caso se observa un salto abrupto en el diámetro de partícula correspondiente a los máximos de los Casos 5 a 6 (fig. 10b). El corrimiento del máximo de la densidad de distribución hacia diámetros más pequeños puede atribuirse al incremento en el contenido de sólidos.

Figura 10. Efecto del contenido de sólidos en la tolva F2: a) Distribución acumulada pasante; b) Función de densidad de distribución.

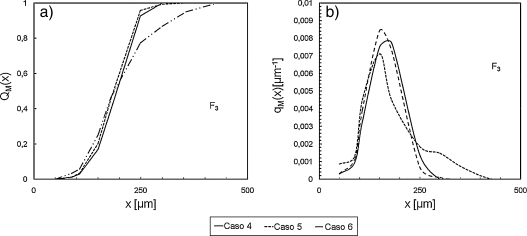
Las figuras 11a y 11b muestran los resultados de las simulaciones para la tolva F3. A diferencia de los casos anteriores, no se observa un corrimiento de la distribución con el contenido de polvo. Los gráficos muestran una distribución acumulada que tiende a un escalón a medida que aumenta el contenido de sólidos (fig. 11a). Además, el máximo de la función de densidad se incrementa y la campana tiende a ser más estrecha. Esto conduce a una homogeneización de la distribución, para dar un material de un diámetro característico de alrededor de 150 μm.

Figura 11. Efecto del contenido de sólidos en la tolva F1: a) Distribución acumulada pasante; b) Función de densidad de distribución.

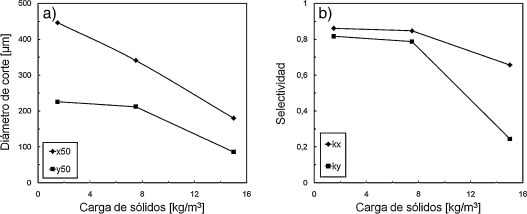
El diámetro de corte y selectividad también son útiles para caracterizar el efecto del contenido de polvo sobre la calidad de la clasificación. Las figuras 12a y 12b presentan los resultados obtenidos por simulación para los diámetros de corte y selectividad en función de la carga de sólidos. Los diámetros de corte, x₅₀ e y₅₀, disminuyen con el caudal de alimentación. Ambos parámetros presentan a 15 kg/m³ un valor cercano al 50% de su valor a 1.5 kg/m³. Esto concuerda con lo observado en las figuras 9 y 10.

Figura 12. Efecto del contenido de sólidos en la clasificación: a) diámetro de corte; b) selectividad.

La disminución del diámetro de corte con la carga de sólidos puede atribuirse al mayor contacto partícula-partícula y a una disminución de la velocidad efectiva del aire. La selectividad presenta un comportamiento similar, ya que disminuye con el caudal de sólidos. Un aumento en la cantidad de sólidos hace que los choques entre partículas sean más frecuentes. Como consecuencia, más partículas finas quedan atrapadas en el material grueso. La turbulencia también juega un papel importante ya que atrapa y dispersa las partículas finas evitando su clasificación.

4. Conclusiones

Las técnicas CFD-DEM se utilizaron para simular el proceso de clasificación dentro de un clasificador de polvo de flujo cruzado. La mejor representación de los datos experimentales se obtuvo utilizando el modelo de turbulencia RSM y el método de multi-inyección. Las simulaciones revelaron la existencia de zonas de remolinos entre las guías de flujo que afectan el proceso de clasificación.

El contenido de polvo es un parámetro crítico en el diseño del proceso de clasificación. La distribución de tamaños de las partículas colectadas en las tolvas es fuertemente influenciada por este parámetro.

La influencia de la carga de sólidos se manifiesta en las granulometrías de los polvos obtenidos en las tres tolvas de colección. Las primeras tolvas, F1 y F2, colectan material de menor tamaño a medida que la cantidad de sólidos aumenta. El efecto en la tolva F3 es diferente ya que el material colectado tiende a homogeneizarse en un diámetro de aproximadamente 150 μm.

Los diámetros de corte y selectividad disminuyen notablemente a medida que se incrementa el contenido de sólidos. Como consecuencia, el proceso de clasificación es menos definido.

Agradecimientos

Los autores agradecen a la Comisión Nacional de Investigaciones Científicas y Técnicas (CONICET), al Centro de Investigaciones en Física e Ingeniería del Centro de la Provincia de Buenos Aires (CIFICEN), a la Universidad Nacional del Centro de la Provincia de Buenos Aires (UNCPBA), a la Comisión de Investigaciones Científicas de la Provincia de Buenos Aires (CICPBA) y a la Planta Piloto de Ingeniería Química (PLAPIQUI) por el apoyo brindado al realizar este trabajo.

References

1. [1] H. Pettingell; An effective dry sand manufacturing process from Japan potential to replace natural sand entirely in concrete; Quarry Management Magazine (2008), pp. 1–6
2. [2] D. Morrow; Why Manufactured Sand?, Metsos customer magazine for the mining and construction industries; Results Minerals & Aggregates, 1 (2011), pp. 26–27
3. [3] K. Aasly Aslaksen, S. Danielsen, J. Wigun, S.-H. Norman, R. Cepuritis, T. Onnela, Review report on dry and wet classification of filler materials for concrete, COIN Project report 52 - 2014. URL www.coinweb.no.
4. [4] R. Cepuritis, S. Jacobsen, T. Onnela; Sand production with VSI crushing and air classification: Optimising fines grading for concrete production with micro-proportioning; Minerals Engineering, 78 (0) (2015), pp. 1–14 https://doi.org/10.1016/j.mineng.2015.03.025 URL http://www.sciencedirect.com/science/article/pii/S0892687515001156
5. [5] M. Shapiro, V. Galperin; Air classification of solid particles: a review; Pneumatic Conveying and Handling of Particulate Solids, 44 (2) (2005), pp. 279–285 https://doi.org/10.1016/j.cep.2004.02.022 URL http://www.sciencedirect.com/science/article/pii/S0255270104000984
6. [6] R. Johansson, M. Evertsson; CFD simulation of a gravitational air classifier; Computational Modelling, 33 (0) (2012), pp. 20–26 https://doi.org/10.1016/j.mineng.2012.01.007 URL http://www.sciencedirect.com/science/article/pii/S089268751200009X
7. [7] R. Johansson, M. Evertsson; An empirical study of a gravitational air classifier; Physical Separation, 31 (0) (2012), pp. 10–16 https://doi.org/10.1016/j.mineng.2012.01.004 URL http://www.sciencedirect.com/science/article/pii/S0892687512000064
8. [8] R. Johansson, Air Classification of Fine Aggregates, Ph.D. thesis, Chalmers University of Technology, Gotemburg, Sweden, iSBN: 978-91-7597-136-0 (Dec. 2014).
9. [9] Y. Li, X. Zhang, X. Shen, H. Li, K. Gao; Experiment and simulation study on optimized structure of a gravitational air classifier; International Journal of Mineral Processing, 141 (2015), pp. 44–50 https://doi.org/10.1016/j.minpro.2015.06.007 URL http://www.sciencedirect.com/science/article/pii/S0301751615001490
10. [10] Q. Wang, M.C. Melaaen, S.R. De Silva; Investigation and simulation of a cross-flow air classifier; Powder Technology, 120 (3) (2001), pp. 273–280 https://doi.org/10.1016/S0032-5910(01)00282-0 URL http://www.sciencedirect.com/science/article/pii/S0032591001002820
11. [11] G. Balbastro, V. Sonzogni; Uso de CFD para estudio de presiones del viento en cubiertas curvas aisladas; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 28 (1) (2012), pp. 49–54 https://doi.org/10.1016/j.rimni.2011.11.003 URL http://www.sciencedirect.com/science/article/pii/S021313151100037X
12. [12] F. Nieto, J. Jurado, S. Hernández, I. Kusano; Aplicación de métodos computacionales en la evaluación de la respuesta aeroelástica de puentes soportados por cables; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 30 (2) (2014), pp. 136–144 https://doi.org/10.1016/j.rimni.2013.03.001 URL http://www.sciencedirect.com/science/article/pii/S0213131513000618
13. [13] F. Salazar, E. Oñate, R. Morán; Modelación numérica de deslizamientos de ladera en embalses mediante el Método de Partículas y Elementos Finitos (PFEM); Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 28 (2) (2012), pp. 112–123 https://doi.org/10.1016/j.rimni.2012.03.004 URL http://www.sciencedirect.com/science/article/pii/S0213131512000181
14. [14] L. Battaglia, J. D’Elía, M. Storti; Simulación numérica de la agitación en tanques de almacenamiento de líquidos mediante una estrategia lagrangiana euleriana arbitraria; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 28 (2) (2012), pp. 124–134 https://doi.org/10.1016/j.rimni.2012.02.001 URL http://www.sciencedirect.com/science/article/pii/S0213131512000119
15. [15] D. Pozo, F. Salazar, M. Toledo; Modelación del funcionamiento hidráulico de los dispositivos de aireación de desagües de fondo de presas mediante el método de partículas y elementos finitos; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 30 (1) (2014), pp. 51–59 https://doi.org/10.1016/j.rimni.2012.11.002 URL http://www.sciencedirect.com/science/article/pii/S0213131512000715
16. [16] M. Toledo, R. Morán, H. Campos; Modelación del movimiento del agua en medios porosos no lineales mediante un esquema de diferencias finitas. Aplicación al sobrevertido en presas de escollera; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 28 (4) (2012), pp. 225–236 https://doi.org/10.1016/j.rimni.2012.02.002 URL http://www.sciencedirect.com/science/article/pii/S0213131512000144
17. [17] B. Zamora, A. Kaiser; Simulación numérica del flujo turbulento de aire con gotas dispersas de agua a través de separadores de torres de refrigeración; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 28 (3) (2012), pp. 148–160 https://doi.org/10.1016/j.rimni.2012.03.008 URL http://www.sciencedirect.com/science/article/pii/S0213131512000223
18. [18] P. Traoré, J.-C. Laurentie, L. Dascalescu; An efficient 4 way coupling CFD-DEM model for dense gas-solid particulate flows simulations; Computers & Fluids, 113 (2015), pp. 65–76 https://doi.org/10.1016/j.compfluid.2014.07.017 URL http://www.sciencedirect.com/science/article/pii/S0045793014003028
19. [19] F. Zhou, S. Hu, Y. Liu, C. Liu, T. Xia; CFD-DEM simulation of the pneumatic conveying of fine particles through a horizontal slit; Particuology, 16 (0) (2014), pp. 196–205 https://doi.org/10.1016/j.partic.2014.03.015 URL http://www.sciencedirect.com/science/article/pii/S1674200114000911
20. [20] F. Alobaid, N. Baraki, B. Epple; Investigation into improving the efficiency and accuracy of CFD/DEM simulations; Particuology, 16 (0) (2014), pp. 41–53 https://doi.org/10.1016/j.partic.2013.11.004 URL http://www.sciencedirect.com/science/article/pii/S1674200113002289
21. [21] D. Sambasivam, A.K. Bhattacharya; Synthesis of CFD and Monte-Carlo simulations for improved design and operation of Dense Medium Cyclones; Computers & Fluids, 96 (2014), pp. 47–62 https://doi.org/10.1016/j.compfluid.2014.02.012 URL http://www.sciencedirect.com/science/article/pii/S004579301400067X
22. [22] J. Blazek; Computational Fluid Dynamics: Principles and Aplications; (1st Edition)Elsevier, United Kingdom (2001)
23. [23] J. Tu, G.H. Yeoh, C. Liu; Computational Fluid Mechanics: A practical Approach; (1st Edition)Elsevier (2008)
24. [24] K. Elsayed, C. Lacor; CFD modeling and multi-objective optimization of cyclone geometry using desirability function, artificial neural networks and genetic algorithms; Applied Mathematical Modelling, 37 (8) (2013), pp. 5680–5704 https://doi.org/10.1016/j.apm.2012.11.010 URL http://www.sciencedirect.com/science/article/pii/S0307904X12007263
25. [25] F. Von Hafenbradl, S. Da Silva, B. Anja, The Development of a Cross-Flow Air Classiffier, Postec Newsletter 16.
26. [26] F. Alobaid, B. Epple; Improvement, validation and application of CFD/DEM model to dense gas-solid flow in a fluidized bed; Particuology, 11 (5) (2013), pp. 514–526 https://doi.org/10.1016/j.partic.2012.05.008 URL http://www.sciencedirect.com/science/article/pii/S167420011200171X
27. [27] ANSYS-Fluent, Theory Guide, Release 14.0, 2011.
28. [28] R. King; Modeling and Simulation of Mineral Processing Systems; (2nd Edition)Society for Mining, Metallurgy, and Exploration, Inc. (SME) (2012)
29. [29] M. Rhodes; Introduction to Particle Technology; (2nd Edition)John Wiley and Sons (2008)