Resumen
Las afecciones cardiovasculares constituyen en la actualidad una causa frecuente de muerte. Una de estas afecciones es la ateroesclerosis, la cual provoca la reducción de la luz arterial. En aras de solucionar tal afección se han desarrollado varios tratamientos, ganando terreno la Angioplastia Coronaria Transluminar Percutánea (PTCA) con colocación de estent. En la actualidad muchos de estos dispositivos son recubiertos para aumentar la biocompatibilidad y disminuir los riesgos de reestenosis. Dado la posibilidad de fallas o roturas de los recubrimientos y los riesgos asociados a estas, es de gran importancia el estudio del comportamiento de la unión estent-recubrimiento durante la fase de expansión del estent. En esta investigación se estudia la posible ocurrencia de delaminación del recubrimiento durante la expansión de un estent y la influencia de parámetros como el espesor y el material del mismo. El estudio parte de la obtención de un modelo geométrico de una celda del estent Sirius Carbostent para su posterior procesamiento por el Método de Elementos Finitos. La simulación por tal método, se desarrolló, aplicando restricciones al movimiento de forma tal que la celda modelada simule su comportamiento durante la expansión de un estent. Considerando estos aspectos fue posible evaluar la integridad del recubrimiento. Con los modelos desarrollados se logró predecir la ocurrencia de delaminación durante la expansión del estent y se determinó que al aumentar el espesor del recubrimiento aumenta el riesgo de ocurrencia de la misma. Se obtuvo además una ecuación general que permite determinar el esfuerzo máximo de contacto para celdas en forma de U.
Abstract
The cardiovascular diseases constitute one of the main causes of death worldwide. One of the main diseases is atherosclerosis, which causes narrowing of the arterial lumen. In order to solve this condition, several treatments have been developed; and Percutaneous Transluminal Coronary Angioplasty (PTCA) with the placement of stent have gained relevancy. Many of these devices are currently coated to increase the biocompatibility and to decrease the restenosis risks. The biomechanical studies of the stent-coating interface behavior are necessary given the associated risks to possibility of failures or breakages of the coating during stent deployment. In this study the possible occurrence of coating delamination during stent deployment and the influence of parameters as the thickness and material were studied. The study starts by obtaining a geometric model of a stent unit of the Sirius Carbostent stent for the further processing by the Finite Element Method. The simulation was developed by applying restrictions so that the modeled stent hinge simulates his behavior during stent deployment. Considering these aspects it was possible to evaluation the coating integrity. With this model it was possible to predict the occurrence of delamination during stent deployment and to determine that the delamination risks increases with increasing the coating thickness. Finally, it was obtained a general function that allows to determine the maximal contact stress for a stent hinge with an U shape.
Palabras clave
Estent;Aterosclerosis;Angioplastia;Recubrimiento;Método de elementos finitos;Delaminación
Keywords
Stent;Atherosclerosis;Angioplasty;Coating;Finite element method;Delamination
1. Introducción
Las enfermedades cardiovasculares (ECV) se consideran un problema global de la salud, siendo una de las principales causas de muerte [1] ; [2]. Dentro de las enfermedades cardiovasculares más comunes se encuentra la ateroesclerosis que consiste en la obstrucción parcial o total de la sección de un vaso sanguíneo. Debido a esto pueden ocurrir accidentes vasculares como el infarto agudo del miocardio (IAM) que provoca serias amenazas para la salud y en ocasiones la muerte súbita. Si el estrechamiento es pequeño el tratamiento más utilizado es la angioplastia coronaria transluminal percutánea (ACTP). Este tratamiento es mínimamente invasivo y tiene asociado tiempos de recuperación cortos. Durante el procedimiento puede ser colocada una endoprótesis denominada estent. Este dispositivo constituye un implante permanente que mantiene la arteria abierta, asegurando así el adecuado flujo de sangre [2] ; [3].
Uno de los problemas asociados a la colocación de estent es la reestenosis. Estudios realizados en Europa y en Estados Unidos evidenciaron menor incidencia de reestenosis y mejores resultados a largo plazo con el uso del estent que con la ACTP con balón; suponiendo esto un avance importante en este campo. No obstante, en la actualidad son innumerables las investigaciones que se desarrollan en aras de continuar disminuyendo tal afectación. Una de ellas es el recubrimiento de los dispositivos para aumentar la biocompatibilidad e introducir medicamentos antiploriferativos (los llamados estents liberadores de drogas o fármacos) [4].
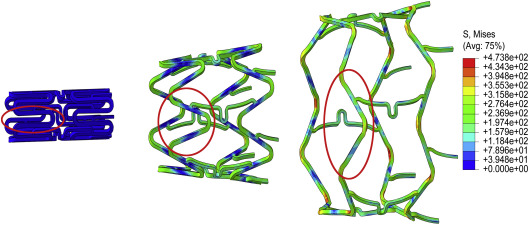
Frente a las grandes ventajas que presentan los estents recubiertos, fundamentalmente los liberadores de fármacos, los investigadores se han centrado en la búsqueda de recubrimientos más eficientes para la transportación y entrega de los medicamentos. Este hecho ha descuidado el análisis del comportamiento de la unión estent-recubrimiento. En estudios desarrollados se han evidenciado fallos del recubrimiento en las zonas de mayores esfuerzos y deformaciones durante la expansión de los estents (ver fig. 1) [5]; [6]; [7] ; [8]. Estos fallos por lo general provocan complicaciones en los pacientes, como pueden ser, trombosis o micro-embolismos [9]. Teniendo en cuenta estos aspectos los estudios del comportamiento de los recubrimientos durante la expansión de los estent son un paso vital para la mejora continua de estas endoprótesis.
|
|
|
Figura 1. Delaminación del recubrimiento después de la expansión del estent. |
Debido a la complejidad de realizar pruebas experimentales y los altos costos relacionados con las mismas, se ha hecho necesario el uso de alternativas más viables para la comprobación y estudio de los estents. Una alternativa es el uso del Método de los Elementos Finitos (MEF); herramienta que ha ganado importancia y ha permitido estudiar el comportamiento mecánico de tales dispositivos. Partiendo de la experiencia alcanzada en estudios anteriores [10]; [11] ; [12], en este estudio se analiza la integridad del recubrimiento de un estent coronario durante la expansión.
2. Materiales y métodos
2.1. Desarrollo geométrico de la sección a modelar
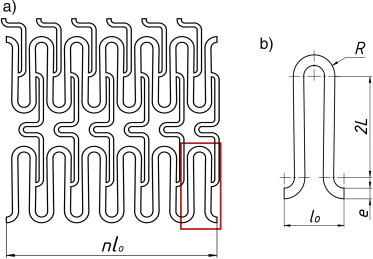
Teniendo en cuenta la complejidad de la geometría de los estents, su simetría y que la delaminación ocurre en las zonas de mayores esfuerzos y deformaciones (zona central de las celdas), solo se tomará una celda para el análisis [13]. Considerando además que varios estudios han mostrado que la delaminación ocurre principalmente en las superficies del estent normales a la dirección circunferencial, una simplificación acertada es considerar la celda plana [9]. Esto es posible también, ya que los mayores esfuerzos y deformaciones se obtienen por la apertura de la celda y no por su desplazamiento radial al aumentar el diámetro del estent (ver fig. 2) [14]; [15]; [16] ; [17]
|
|
|
Figura 2. Apertura que sufre la celda durante el proceso de expansión del estent. Distribución de los esfuerzos de Von Mises (los valores están dados en MPa). |
La celda desarrollada posee forma de U por ser una de las configuraciones más ampliamente utilizadas en la fabricación de estent. Dicha geometría representa una aproximación de una celda del estent Sirius Carbostent (Sorin Biomedical S.p.A., Saluggia, Italy) [12]. Uno de los parámetros que debe ser definido es el ancho inicial de la celda; para ello es necesario partir del desarrollo de un anillo del estent. La longitud de este desarrollo es calculada a partir del diámetro medio del estent empleando la ecuación del cálculo de longitud de una circunferencia. Teniendo en cuenta que el anillo posee una cantidad n de celdas, la longitud de las mismas se puede calcular a partir de la siguiente expresión:
|
|
(1) |
donde l0 es el ancho inicial de la celda, d0 es diámetro exterior inicial del estent (1.2mm), e el espesor del alambre (0.1mm) y n la cantidad de celdas que tiene un anillo (6 celdas) [12] (ver fig. 3).
|
|
|
Figura 3. Geometría empleada. a) Desarrollo de una sección de estent; delimitando con el recuadro la geometría de una celda (n, cantidad de celdas que posee un anillo y l0, ancho inicial de la celda). b) Parámetros geométricos fundamentales de la celda (e, espesor del alambre; 2 L, longitud del tramo recto de la celda y R, radio de curvatura de la celda). |
Sustituyendo en (1) los valores de d0, e y n es posible calcular el ancho inicial de la celda (l0 = 0.576mm). Para completar la geometría fueron asumidos los valores del radio de curvatura de la celda (R = 0.2mm) y la longitud del tramo recto de la misma (2L = 0.95mm) a partir de la obtención de un modelo geométrico completo del estent.
2.2. Modelación por el método de elementos finitos
El problema de la deformación de múltiples capas con forma de arco circular ha sido investigado por diferentes autores con el fin de estimar la distribución de tensiones en la estructura y especialmente en la zona de contacto entre las capas [16]. Estos estudios han evidenciado que los mayores esfuerzos normales del contacto se obtienen en la zona central del arco mientras que el esfuerzo tangencial del contacto es cero en dicha zona [16] ; [17]. Teniendo en cuenta que este tipo de estructura es típica de los estents, especialmente del estent objeto de estudio, y según resultados como los obtenidos por Hopkins et al. en el 2010 en la modelación de estents recubiertos, se puede predecir que la delaminación del recubrimiento en estos dispositivos comienza principalmente en el centro de la curvatura de la celda (zona crítica), cuando el esfuerzo normal a tracción de la unión supera cierto valor [16] ; [18]. A este valor límite, a partir del cual ocurre la delaminación, se le denomina esfuerzo crítico de la unión (σcrit).
Producto a la localización de la zona crítica es posible analizar la ocurrencia de la delaminación sin incluir en el modelo la arteria ni la placa ateromática obteniéndose resultados certeros [18]. Teniendo en cuenta todos estos aspectos, para el estudio de la delaminación del recubrimiento, fue implementado un modelo cohesivo de forma tal que las superficies en contacto entre el estent y el recubrimiento permanezcan siempre unidas [9]. Esto permite evaluar el esfuerzo generado en el contacto, especialmente en la zona central y compararlo con la condición límite para la separación. Por tales motivos y teniendo en cuenta que el modelo cohesivo usado no permiten la separación de las superficies en contacto, los modelos desarrollados están orientados hacia la determinación de la posible ocurrencia de la delaminación (cuando el esfuerzo normal del contacto en el centro de la celda es mayor que el esfuerzo límite) y no a la magnitud de la misma.
Para el análisis de la unión estent-recubrimiento se desarrollaron varios modelos. Estos modelos fueron obtenidos en el software ABAQUS/Standard, en el cual se efectuaron posteriormente las simulaciones. En dichos modelos se emplearon diferentes materiales y espesores del recubrimiento en aras de determinar la influencia de los mismos en el comportamiento de la unión. Los modelos fueron discretizados con elementos hexaédricos de ocho nodos y la sensibilidad de la malla fue definida a partir de pruebas de convergencia del mallado [12] ; [15]. Los resultados de estas pruebas para los diferentes modelos desarrollados arrojaron una cantidad de elementos en un rango entre 168 521 y 184 722, con un número de nodos en un rango entre 195 894 y 213 048 respectivamente. La malla definitiva adoptada para cada modelo, asegura errores menores del 0.2% en los esfuerzos normales del contacto.
2.3. Modelo de comportamiento del material para el recubrimiento
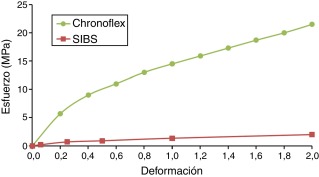
El material empleado para la modelación del estent (sustrato) fue el acero inoxidable 316L por ser uno de los materiales más empleados en la fabricación de estent y en particular el utilizado para la obtención del Sirius Carbostent [17]. El comportamiento elasto-plástico fue definido a partir de un trabajo publicado por Auricchio et al., donde el Módulo de Young es 196 GPa, el coeficiente de Poisson 0.3, el límite de fluencia 205 MPa y límite de rotura de 515 MPa[19] ; [20]. Los polímeros usados para el recubrimiento fueron escogidos por su relevancia comercial en los estents liberadores de fármacos. Estos son el poliuretano biomédico con el nombre comercial Chronoflex® AR (AdvanSource Biomaterials Corporation, MA, USA) [21] y el poli-estireno-b-isobutileno-b-estireno (SIBS) [7]. Este último es usado para recubrir los estents Taxus, liberadores de fármacos. El comportamiento de material de estos polímeros se tomó de un trabajo publicado por Hopkins et al.[18]. En dicho trabajo se publican los resultados de un ensayo de tracción realizado a tres polímeros, entre ellos el Chronoflex y el SIBS. En la figura 4 se puede observar que en el rango de deformaciones de 0 - 40%, el Chronoflex y el SIBS exhiben una relación esfuerzo-deformación relativamente lineal con los módulos de Young de 23 MPa y 2 MPa, respectivamente [18]. Según el estudio de estos autores, durante la expansión del estent las deformaciones del recubrimiento no superan el valor de deformación antes mencionado.
|
|
|
Figura 4. Datos de esfuerzos en función de la deformación para los polímeros Chronoflex y SIBS. |
2.4. Condiciones de contorno y sistema de cargas
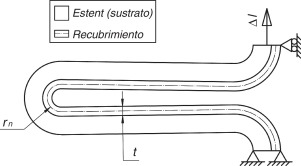
Para asignar las restricciones al movimiento y las condiciones de carga es necesario tener en cuenta que al expandir el estent, el aumento del radio está asociado a la apertura de las celdas. Entonces, para recrear tal situación al modelar solo una celda, esta es fijada en uno de sus extremos y en el otro, se le aplican desplazamientos (Δl) que representen el aumento de diámetro del estent (ver fig. 5).
|
|
|
Figura 5. Condiciones de contorno y geometría del recubrimiento; Δl desplazamiento impuesto a la celda, t espesor del recubrimiento y rn radio de curvatura del recubrimiento medido sobre la línea neutra del mismo. |
3. Resultados y discusión
Para el análisis de la integridad del recubrimiento se desarrollaron seis modelos. Se emplearon los dos materiales para recubrimiento ya mencionados y cada uno se modeló con tres espesores diferentes; 5 μm, 10 μm y 15 μm.
El contacto entre la celda del estent y el recubrimiento como se mencionó fue definido mediante una interacción fuerte sin separación. Entonces, al comparar el esfuerzo máximo a tracción que se genera en la unión durante la apertura de la celda, con el valor del esfuerzo crítico de la unión, se puede definir si ocurre o no la delaminación. Según el estudio desarrollado por Hopkins et al. para celdas de estent de acero inoxidable, recubiertas con varios polímeros entre ellos el Chronoflex y el SIBS, el esfuerzo crítico de la unión es de 0.05 MPa[3].
Para un mejor estudio de los resultados es conveniente hacer el análisis en relación al diámetro del estent y no al ancho de la celda. Para ello, (1) puede ser reescrita de forma general y despejar en ella el diámetro exterior del estent:
|
|
(2) |
donde di es el diámetro exterior del estent correspondiente a cada ancho impuesto a la celda (li) mediante el desplazamiento de uno de sus extremos.
El ancho de la celda fue aumentado hasta alcanzar un valor correspondiente con el diámetro exterior del estent de 4.25 mm. Los valores del esfuerzo normal máximo a tracción del contacto, obtenidos para cada material del recubrimiento y correspondiente a cada espesor fueron registrados y graficados en función del diámetro exterior del estent.
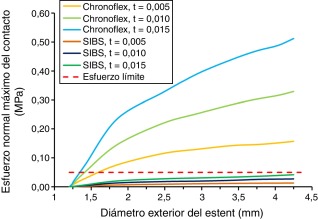
En la figura 6 se observa que el estent recubierto con Chronoflex presenta delaminación para todos los espesores estudiados. Esto se debe a que el valor del esfuerzo normal máximo del contacto supera el valor del esfuerzo crítico (0.05 MPa, línea roja). Para este material en el caso del espesor de 5 μm la delaminación ocurre antes de que el diámetro del estent alcance los 1.75 mm y en el caso de los espesores de 10 μm y 15 μm el diámetro no supera los 1.42 mm. Al recubrir el estent con SIBS se aprecia que para ninguno de los espesores simulados se presenta delaminación.
|
|
|
Figura 6. Gráfico del comportamiento del esfuerzo normal máximo a tracción del contacto en función del diámetro del estent. En la gráfica se presentan los resultados de los 6 modelos desarrollados y el valor del esfuerzo crítico (línea roja) planteado por Hopkins et al. |
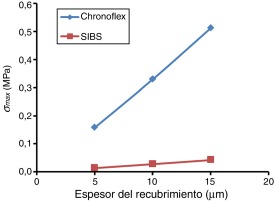
Un resultado significativo es que al aumentar el espesor del recubrimiento aumenta el valor del esfuerzo normal del contacto, siendo este fenómeno más significativo para el Chronoflex que para el SIBS. Esto demuestra que la reducción del espesor del recubrimiento reduce los riesgos de delaminación [21]. Lo antes mencionado se refleja con mayor claridad en la gráfica de la figura 7, donde se presentan los valores del esfuerzo normal máximo de la unión para el diámetro final del estent (4.25 mm) contra el espesor del recubrimiento. En esta gráfica, se observa que la recta correspondiente al recubrimiento de Chronoflex posee mayor pendiente que la correspondiente al recubrimiento de SIBS. Esta diferencia demuestra que el recubrimiento de Chronoflex posee una mayor sensibilidad del esfuerzo normal máximo de la unión al aumentar el espesor. En este gráfico, se observa también como para todos los espesores del recubrimiento de Chronoflex, cuando el estent alcanza el diámetro máximo, los esfuerzos normales de contacto superan el valor del esfuerzo crítico, no ocurriendo así para los recubrimientos de SIBS.
|
|
|
Figura 7. Esfuerzo normal máximo de la unión (σmax) en función del espesor del recubrimiento, cuando el estent alcanza los 4.25 mm de diámetro. |
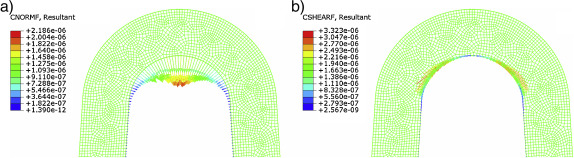
Por otra parte, las simulaciones desarrolladas permitieron analizar la distribución de las fuerzas que se generan en el contacto producto a la expansión del estent. Estas evidenciaron que la delaminación del recubrimiento se inicia bajo la acción del modo I de separación, es decir, bajo la acción de la fuerza normal. En la figura 8a se puede observar que la fuerza normal alcanza sus valores máximos en el centro de la celda y va disminuyendo a medida que se aleja de dicho punto. Sin embargo en la ver figura 8b se aprecia que en el centro de la celda la fuerza tangencial es prácticamente despreciable y va aumentando a medida que se aleja del mismo. Este comportamiento conlleva a que la delaminación comience por el efecto de la fuerza normal (modo I de separación), posteriormente se propaga por la influencia combinada de la fuerza normal y tangencial (modo mixto de separación) hasta cierto punto, a partir del cual la delaminación avanza por la acción dominante de la fuerza tangencial (modo II de separación).
|
|
|
Figura 8. Distribución de las fuerzas que se generan en la unión estent-recubrimiento al expandir el estent (los valores de las escala son dados en Newton). a) Distribución de fuerzas normales, b) distribución de fuerzas tangenciales. Las imágenes mostradas pertenecen al recubrimiento de Chronoflex con espesor de 5μm, en el momento en que el esfuerzo del contacto es aproximadamente igual al esfuerzo crítico (0.05MPa). |
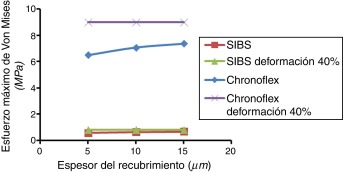
Otro aspecto analizado fue el comportamiento del esfuerzo máximo de Von Mises en los recubrimientos al variar el material y el espesor de los mismos. Para ello se analizaron los esfuerzos correspondientes al mayor diámetro de expansión (4.25 mm). En la gráfica de la figura 9 se muestra que los esfuerzos alcanzados por los recubrimientos de Chronoflex son superiores a los alcanzados por los recubrimientos de SIBS. Se observa además que para ambos materiales a medida que se incrementa el espesor del recubrimiento aumentan los esfuerzos máximos de Von Mises. Estos esfuerzos al igual que el esfuerzo de contacto máximo se encuentran ubicados en la zona correspondiente al centro de la celda.
|
|
|
Figura 9. Gráfico de esfuerzo máximo de Von Mises para cada material y espesor del recubrimiento cuando el estent alcanza los 4.25 mm de diámetro. Las curvas Chronoflex deformación 40% y SIBS deformación 40% representan los valores de esfuerzos correspondientes al 40% de deformación de cada material. |
En esta gráfica se aprecia que los esfuerzos máximos de Von Mises, obtenidos durante las simulaciones, son menores que los esfuerzos correspondientes al 40% de deformación de cada material del recubrimiento. Esto ratifica que durante la expansión del estent las deformaciones que sufren los recubrimientos son menores del 40%.
Otro aspecto analizado en este estudio es la relación existente entre los parámetros geométricos de la celda, las propiedades de material del recubrimiento, el diámetro de expansión del estent y el esfuerzo normal máximo que se genera en el contacto. Un estudio realizado por Hopkins et al. a los estents Cypher y Taxus, evidenció que para una celda de estent en forma de U, la relación entre los parámetros antes mencionados se comporta de forma no lineal y prácticamente con la misma tendencia, independientemente de los valores que adopten los parámetros geométricos o las propiedades del material [18].
La relación entre todos los parámetros antes mencionados se realiza a partir de la definición de dos términos. En primer lugar y teniendo en cuenta que la expansión del estent se debe en su mayoría a la apertura de las celdas, se define el término de deformación circunferencial por unidad de longitud de la celda como [18]:
|
|
(3) |
donde es la deformación circunferencial correspondiente a cada ancho impuesto a la celda, L la mitad de la longitud del tramo recto de la celda y el diámetro medio del estent correspondiente a cada ancho impuesto a la celda. Por otra parte se define un parámetro que caracteriza la resistencia del contacto (). El mismo tiene en cuenta el esfuerzo normal máximo del contacto (σmax), la geometría y el material del recubrimiento.
|
|
(4) |
donde Er es el Módulo de Young del material del recubrimiento, t el espesor del recubrimiento y k la curvatura del recubrimiento. Esta curvatura del recubrimiento es calculada a partir del radio de curvatura del mismo medido sobre la línea neutra (rn) mediante la siguiente expresión:
|
|
(5) |
Los valores de t, rn y L se obtienen directamente del modelo desarrollado para cada espesor de recubrimiento y los valores de k se obtienen empleando (5) (ver tabla 1).
| t (mm) | rn (mm) | k (mm) | L (mm) |
|---|---|---|---|
| 0.005 | 0.0975 | 10.2564 | 0.475 |
| 0.010 | 0.0950 | 10.5263 | 0.475 |
| 0.015 | 0.0925 | 10.8108 | 0.475 |
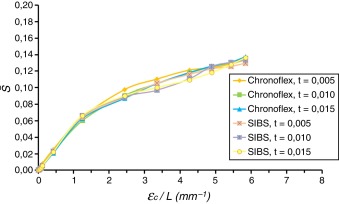
Teniendo en cuenta los resultados obtenidos en las modelaciones, empleando (3) y (4), es posible calcular el parámetro y la deformación circunferencial por unidad de longitud de la celda para cada modelo desarrollado. En la gráfica de la figura 10 se muestran los resultados obtenidos para cada material y espesor de recubrimiento.
|
|
|
Figura 10. Curvas que relacionan el parámetro con la deformación circunferencial por unidad de longitud de la celda para cada modelo desarrollado. |
Obsérvese en esta figura que todos los modelos presentan un comportamiento similar con independencia del material o el espesor que se emplee para el recubrimiento. Esto posibilita el desarrollo de una ecuación que permita relacionar los parámetros estudiados. Por las características de las curvas y con el objetivo de seleccionar posteriormente la que mejor se ajuste a los resultados, se desarrollaron dos formulaciones; una logarítmica y otra exponencial de dos términos. En el caso del desarrollo de la función logarítmica se parte de la formulación:
|
|
(6) |
donde a y b son coeficientes que se determinan mediante el ajuste de la ecuación a los datos obtenidos de las simulaciones. El valor de la unidad es adicionado en el argumento del logaritmo para garantizar la condición inicial ( cuando ɛc = 0). El mejor ajuste logrado mediante esta ecuación corresponde con los valores de a = 0.145 y b = 1.266, ofreciendo un coeficiente de correlación R2 = 0.9965
|
|
(7) |
En (7) se aprecia la segunda formulación propuesta (exponencial); la cual consta de dos términos para lograr un mejor ajuste a los datos especialmente a partir de ɛc ≥ 3. La formulación exponencial de un solo término a partir de este valor (ɛc ≥ 3) se comienza a alejar considerablemente de los datos obtenidos. Por tanto, inicialmente la función exponencial de dos términos está compuesta por cuatro coeficientes (a, b, c y d ). Al analizar las condiciones iniciales ( cuando ɛc = 0) se aprecia que para cualesquiera sean los valores de b y d la función solo se anula si c = − a; por tanto:
|
|
(8) |
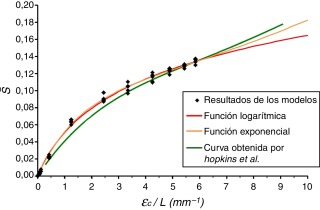
Al realizar el ajuste correspondiente de la ecuación, se obtuvo el valor de los tres coeficientes; donde a = 0.088, b = 0.073 y d = −0.731. Con estos valores se obtiene un ajuste a los datos con un coeficiente de correlación R2 = 0.9972. En el gráfico de la figura 11 fueron comparadas las funciones desarrolladas con los resultados obtenidos por Hopkins et al.
|
|
|
Figura 11. Ajuste de las funciones propuestas. Comparación entre los resultados obtenidos en este trabajo y los resultados presentados por Hopkins et al. |
Al observar esta figura se aprecia que las simulaciones desarrolladas arrojan resultados similares a los obtenidos por los autores antes citados. En una primera zona los valores del parámetro obtenidos en este trabajo son ligeramente superiores a los obtenidos por Hopkins et al. No obstante, a partir de una relación ɛc/L = 4 se observa que los resultados de ambos estudios son prácticamente iguales. Es importante observar que la función exponencial desarrollada no solo tiene mejor ajuste a los resultados de las simulaciones (R2 = 0.9972) es decir, hasta valores de ɛc/L cercanos a 6, sino que para valores de ɛc/L ≥ 6 (no simulados en este trabajo) también presenta mayor similitud a los resultados obtenidos por Hopkins et al. En el caso de la función logarítmica se puede apreciar que para valores de ɛc/L ≥ 6 comienza a distanciarse de los resultados presentados por Hopkins et al. Teniendo en cuenta los aspectos antes mencionados, la función exponencial es la que mejor se ajusta a los estudios realizados. Si se sustituye (4) y los coeficientes a, b, y d en (8), se puede despejar el esfuerzo normal máximo a tracción de la interfaz en función de los parámetros geométricos de la celda, el material del recubrimiento y la deformación circunferencial
|
|
(9) |
Mediante (9) es posible definir el comportamiento del esfuerzo máximo a tracción que se genera en la interfaz estent-recubrimiento de una celda genérica en forma de U al ser expandida. Por tanto, de ser conocido el esfuerzo crítico de la unión es posible predecir si para determinadas condiciones geométricas y de expansión ocurrirá o no la delaminación. Interpretada de otra forma, esta formulación permite determinar el esfuerzo crítico necesario para que bajo determinadas condiciones geométricas y de expansión no ocurra la delaminación (σcrit ≥ σmax).
4. Conclusiones
Los modelos desarrollados permiten predecir la ocurrencia de fallas por delaminación del recubrimiento en estents coronarios recubiertos. Este estudio permitió evaluar la influencia del espesor del recubrimiento en los esfuerzos de contacto generados en la interfase estent-recubrimiento durante la expansión. Se pudo apreciar que a medida que aumenta el espesor del recubrimiento aumentan los esfuerzos de contacto. En el caso del estent modelado (Sirius Carbostent) se aprecia que al recubrirlo con Chronoflex es muy probable que presente delaminación del recubrimiento (para todos los espesores simulados) antes de que el dispositivo alcance el diámetro máximo. En el caso del SIBS, por el contrario, no presenta peligro de delaminación para ninguno de los espesores simulados. Se determinó también que la resistencia del contacto durante la expansión del dispositivo presenta el mismo comportamiento para todas las celdas de estent en formas de U, si se tienen en cuenta los parámetros geométricos de las mismas. Este último aspecto permitió obtener una función exponencial para estimar el esfuerzo normal máximo del contacto estent-recubrimiento para cada valor de deformación circunferencial de un estent, siempre que este esté formado por celdas en forma de U. Al comparar los resultados obtenidos con trabajos desarrollados por autores reconocidos en el tema se evidencia que los modelos desarrollados y la ecuación propuesta constituyen una buena herramienta para la predicción de la ocurrencia de delaminación en los estents coronarios recubiertos. A pesar de estos resultados es importante conocer que el trabajo presentado posees determinadas limitaciones. En primer lugar, los resultados obtenidos solo son aplicables a estents con celdas en forma de U. Los análisis de delaminación solo se realizaron en las zonas centrales de las celdas y no en todo el estent. No se tuvo en cuenta la fricción entre el recubrimiento y otros elementos que intervienen durante el proceder como son la arteria, la placa ateromática y el balón. Con los modelos desarrollados es posible predecir la ocurrencia de la delaminación pero no es posible determinar su magnitud.
Referencias
- [1] G. Vilalta, Y. Dago, J. O’connor, H. Calas, J. Figueredo; Análisis de la variación del flujo sanguíneo en la bifurcación carótida con diferentes grados de estenosamiento utilizando MEF; Ingeniería Mecánica, 2 (2008), pp. 21–28
- [2] F. Harewood, J. Grogan, P. Mchugh; A multiscale approach to failure assessment in deployment for cardiovascular stents; Journal of Multiscale Modelling, 02 (2010), pp. 1–22
- [3] C.G. Hopkins, P.E. Mchugh, J.P. Mcgarry; Computer modeling of cardiovascular stent coating damage; Proceedings of the ASME 2008 Summer Bioengineering Conference (SBC2008) (2008)
- [4] J. Iqbal, J. Gunn, P.W. Serruys; Coronary stents: historical development, current status and future directions; Br. Med. Bull., 106 (2013), pp. 193–211
- [5] A. Abizaid, J.R. Costa; New Drug-Eluting Stents. An Overview on Biodegradable and Polymer-Free Next-Generation Stent Systems; Circ. Cardiovasc. Interv., 3 (2010), pp. 384–393
- [6] Y. Fujimoto, Y. Kobayashi, M. Yamaguchi; Delamination of Abluminal Polymer of Biolimus-Eluting Stent; JACC Cardiovasc. Interv., 5 (2012), pp. e5–e6
- [7] M.W.Z. Basalus, K. Tandjung, H. Sen, A. Van Apeldoorn, D.W. Grijpma, C. Von Birgelen; Recent Insights from Scanning Electron Microscopic Assessment of Durable Polymer-Coated Drug-Eluting Stents; Interventional Cardiology, 4 (2012), pp. 661–674
- [8] M.W.Z. Basalus, M. Joner, C. Von Birgelen, R.A. Byrne; Polymer coatings on drug-eluting stents: Samsons hair and Achilles’ heel?; EuroIntervention, 9 (2013), pp. 302–305
- [9] S. Lee, W. Chang Lee, C.-S. Kim; FEA Study on the Stress Distributions in the Polymer Coatings of Cardiovascular Drug-Eluting Stent Medical Devices; Ann. Biomed. Eng., 42 (2014), pp. 1952–1965
- [10] F. Migliavacca, L. Petrini, V. Montanari, I. Quagliana, F. Auricchio, G. Dubini; A predictive study of the mechanical behaviour of coronary stents by computer modelling; Med. Eng. Phys., 27 (2005), pp. 13–18
- [11] C. Dumoulin, B. Cochelin; Mechanical behaviour modelling of balloon-expandable stents; J. Biomech., 33 (2000), pp. 1461–1470
- [12] F. Migliavacca, L. Petrini, M. Colombo, F. Auricchio, R. Pietrabissa; Mechanical behavior of coronary stents investigated through the finite element method; J. Biomech., 35 (2002), pp. 803–811
- [13] M. Azaouzi, A. Makradi, S. Belouettar; Deployment of a self-expanding stent inside an artery: A finite element analysis; Mater. Des., 41 (2012), pp. 410–420
- [14] O. Pérez Acosta, T. Rodríguez Moliner, Análisis del comportamiento mecánico de un estent durante la expansión, 17 Convención de Ingeniería y Arquitectura. Congreso Cubano de Ingeniería Mecánica y Metalúrgica, 2014, La Habana. pp. 8. ISBN: 5456444646.
- [15] A. Schiavone, L.G. Zhao, A.A. Abdel-Wahab; Effects of material, coating, design and plaque composition on stent deployment inside a stenotic artery—Finite element simulation; Mater. Sci. Eng., C, 42 (2014), pp. 479–488
- [16] É.Ó. Máirtín, G. Parry, G.E. Beltz, J.P. Mcgarry; Potential-based and non-potential-based cohesive zone formulations under mixed-mode separation and over-closure. Part II: Finite element applications; J. Mech. Phys. Solids., 63 (2014), pp. 363–385
- [17] G. Parry, J.P. Mcgarry; An analytical solution for the stress state at stent–coating interfaces; J. Mech. Behav. Biomed. Mater., 10 (2012), pp. 183–196
- [18] C.G. Hopkins, P.E. Mchugh, J.P. Mcgarry; Computational Investigation of the Delamination of Polymer Coatings During Stent Deployment; Ann. Biomed. Eng., 38 (2010), pp. 2263–2273
- [19] F. Auricchio, M. Di Loreto, E. Sacco; Finite-element Analysis of a Stenotic Artery Revascularization through a Stent Insertion; Comput. Method. Biomec., 00 (2000), pp. 1–15
- [20] F. Auricchio, A. Constantinescu, G. Scalet; Fatigue of 316L stainless steel notched lm-size components; Int. J. Fatigue., 68 (2014), pp. 231–247
- [21] C. Hopkins, P.E. Mchugh, N.P. O’dowd, Y. Rochev, J.P. Mcgarry; A combined computational and experimental methodology to determine the adhesion properties of stent polymer coatings; Comp. Mater. Sci., 80 (2013), pp. 104–112
Document information
Published on 20/12/17
Accepted on 24/05/17
Submitted on 24/05/17
Volume 33, Issue 4, 2017
DOI: 10.1016/j.rimni.2016.04.011
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?