Resumen
Los modelos numéricos de transferencia de calor y de flujo de fluido empleados en la simulación del proceso de soldadura por fricción-agitación (FSW) han contribuido a la comprensión del proceso. Sin embargo, existen ciertos parámetros de entrada a los modelos que no pueden determinarse fácilmente a partir de principios fundamentales o de las condiciones de soldadura. Como resultado, las predicciones de estos modelos no siempre están de acuerdo con los resultados experimentales. En este trabajo se usa el método de Levenberg-Marquardt (LM) para estimar de manera no lineal los parámetros desconocidos presentes en los modelos de transferencia de calor y de flujo de fluido, ajustando las temperaturas obtenidas con los modelos a mediciones experimentales de temperatura. Estos modelos se implementan en un programa de propósito general que emplea una formulación numérica desarrollada a partir del método de los elementos finitos (MEF). Los parámetros que se desconocen son: el coeficiente de fricción y la cantidad de adherencia del material a la superficie de la herramienta, el coeficiente de transferencia de calor en la superficie inferior y la cantidad de disipación viscosa convertida en calor. Los resultados obtenidos revelan una mejora de las predicciones de los modelos numéricos a partir de la incorporación de técnicas de estimación de parámetros.
Abstract
Numerical models of heat transfer and fluid flow used in the simulation of the friction-stir welding (FSW) process have contributed to the understanding of the process. However, there are some input model parameters that cannot be easily determined from fundamental principles or the welding conditions. As a result, the model predictions are not always in agreement with experimental results. In this work, the Levenberg-Marquardt (LM) method is used in order to perform a non-linear estimation of the unknown parameters present in the heat transfer and fluid flow models, by adjusting the temperatures results obtained with the models to temperature experimental measurements. These models are implemented in a general-purpose software that uses a numerical formulation developed from the finite element method (FEM). The unknown parameters are: the friction coefficient and the amount of adhesion of material to the surface of the tool, the heat transfer coefficient on the bottom surface and the amount of viscous dissipation converted into heat. The obtained results show an improvement in the numerical model predictions from the incorporation of parameter estimation techniques.
Palabras clave
Estimación de parámetros ; Problema inverso ; Friction stir welding
Keywords
Estimation of parameters ; Inverse problem ; Friction stir welding
1. Introducción
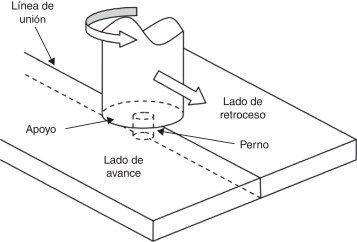
El proceso de soldadura friction stir welding (FSW) fue desarrollado en Inglaterra en el año 1991 por The Welding Institute (TWI). Se trata de un proceso de unión en estado sólido, es decir, el material no alcanza su temperatura de fusión durante el mismo. La herramienta de soldadura está construida generalmente en una sola pieza y, básicamente, se diferencian 2 partes: un perno y un apoyo ( fig. 1 ).
|
|
|
Figura 1. Esquema del modelo. |
El proceso comienza con la herramienta girando y la introducción del perno entre las piezas que se van a unir hasta que el apoyo hace contacto con las superficies de las piezas. A continuación se le impone una velocidad de avance a la herramienta en dirección a la línea de soldadura. La intensa fricción entre la herramienta y el material de las piezas, así como la gran deformación plástica del material alrededor de la herramienta, contribuyen a producir un aumento de la temperatura en una zona cercana a la herramienta. El ablandamiento del material alrededor del perno –debido a las altas temperaturas– y la acción combinada de la rotación y la traslación de la herramienta conducen al material del frente hacia detrás del perno, generando la unión de las piezas. Debajo de las placas se coloca una base que sirve de soporte para restringir el movimiento y absorber los esfuerzos que surgen de la presión de la herramienta y que, además, participa en la extracción del calor.
Existen diversos trabajos de simulación numérica del proceso de soldadura FSW en los que se emplean modelos de flujo viscoplástico con acoplamiento termomecánico [1] , [2] , [3] , [4] , [5] , [6] , [7] and [8] . Si bien han contribuido a la comprensión del proceso de soldadura por FSW, estos trabajos incluyen ciertos parámetros de entrada a los modelos cuyos valores no pueden determinarse fácilmente a partir de principios fundamentales o de las condiciones de soldadura. En este sentido, se han llevado a cabo trabajos que aplican distintas alternativas para mejorar la confiabilidad de los resultados en base a datos experimentales.
Entre ellos, se destaca el trabajo de Zhu et al. [9] en modelado térmico de acero inoxidable 304L. En este trabajo el valor de la fuente de generación de calor y la resistencia al flujo de calor hacia la placa base se obtuvieron haciendo análisis inverso. Por otra parte, Nandan et al. [10] aplicaron técnicas de estimación de parámetros a un modelo de flujo viscoplástico y de transferencia de calor de un acero AISI 1018 laminado en caliente, donde imponen una resistencia al flujo de calor hacia la placa soporte y consideran una generación de calor compuesta de 2 aportes: una de fricción y otra de deformación plástica, asignando un deslizamiento relativo entre las superficies en contacto tomado del proceso de laminado. Asimismo, Larsen et al. [11] determinaron la magnitud y la distribución espacial del coeficiente de transferencia de calor, o conductancia térmica, hacia la placa de respaldo, minimizando la diferencia entre mediciones experimentales de temperatura y temperaturas obtenidas usando un modelo de elementos finitos tridimensional.
El propósito del presente trabajo es obtener, a través de una técnica de estimación de parámetros, el valor de 4 parámetros de entrada al modelo de elementos finitos del proceso de soldadura FSW, considerando el ajuste de los resultados numéricos de temperatura a datos experimentales.
2. Desarrollo
2.1. Modelado numérico del proceso
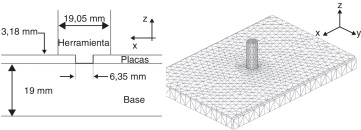
La geometría del modelo se compone de la herramienta, de las piezas que soldar y de la placa base (fig. 2 ). La forma y las dimensiones de la herramienta, así como el espesor, el ancho y la longitud de las piezas por soldar y de la placa base, se corresponden con las de los datos del trabajo de Zhu et al. [9] .
|
|
|
Figura 2. Geometría del modelo. |
La simulación numérica del proceso incluye la resolución acoplada de un modelo de flujo viscoplástico y de transferencia de calor. El primero de ellos está gobernado por las ecuaciones de conservación de la cantidad de movimiento (segundo principio de Newton) para un medio continuo y por la ecuación de conservación de la masa para un fluido incompresible:
|
|
( 1) |
|
|
( 2) |
donde uk son las velocidades, xm son las coordenadas espaciales, t es el tiempo, ρ es la densidad del material, gk son las fuerzas de volumen y σkm son las componentes del tensor de Cauchy.
De acuerdo con la formulación de flujo adoptada, el tensor de Cauchy adquiere la forma general:
|
|
( 3) |
donde δkm es el delta de Kronecker, p es la presión hidrostática y τkm es el tensor desviador de tensiones. Este último se puede relacionar con el tensor de velocidades de deformación dkm por medio de la viscosidad μ , según la siguiente relación:
|
|
( 4) |
|
|
( 5) |
|
|
( 6) |
donde σf es la tensión efectiva o el segundo invariante de la tensión, y es la velocidad de deformación efectiva o el segundo invariante de la velocidad de deformación, que puede obtenerse por:
|
|
( 7) |
Se asume que el material tiene un comportamiento viscoplástico y rígido para el cual la tensión de flujo depende de la velocidad de deformación y de la temperatura representada por la siguiente relación constitutiva propuesta por Sellars et al. [12] :
|
|
( 8) |
|
|
( 9) |
donde A , α y nc son constantes del material, Z es el parámetro de Zener-Hollomon, Q es la energía de activación, R es la constante universal de los gases y T es la temperatura absoluta. Los valores de las constantes se obtuvieron del trabajo de Jorge Jr. et al. [13] y son α = 0, 012 MPa−1 , Q = 401 kJ·mol−1 , A = 8, 30 · 1015 y nc = 4,32.
Se considera como marco de referencia a la herramienta rotando a una velocidad ω sin avanzar, y como resultado la placa base se mueve hacia ella con una velocidad .
Por otro lado, se asume una condición de deslizamiento relativo entre las superficies en contacto de la herramienta y del material de las placas por soldar. Es decir, la velocidad que se impone al material sobre dicha superficie no es directamente la velocidad de la herramienta, sino que se encuentra afectada por un coeficiente. Este coeficiente responde a la siguiente relación extraída del proceso de laminado [10] :
|
|
( 10) |
donde δ es la fracción de deslizamiento, δ0 es una constante (parámetro por estimar), r es la distancia radial y Rs es el radio exterior del apoyo. Una condición de adherencia completa se indica por δ = 0.
El segundo modelo responde a la ecuación de conservación de la energía, que incluye la generación de calor interna por disipación de potencia viscoplástica γ :
|
|
( 11) |
|
|
( 12) |
donde Cp es la capacidad calorífica, K es la conductividad térmica, T la temperatura y η la fracción de potencia que no es absorbida en defectos microestructurales (parámetro por estimar).
Se asume que la presión en el apoyo de la herramienta y en el fondo del perno es la misma en todos los puntos. La presión en la mitad frontal del perno cilíndrico es mucho menor que la anterior, por lo que se la desprecia. De esta manera, el calor generado en la interfaz herramienta/material (se considera que se distribuye en partes iguales hacia la herramienta y hacia el material) está dado por las presiones y por la velocidad del material según:
|
|
( 13) |
donde PN (la fuerza axial es FA = 31.138 kg·m·s−2 ) es la presión normal a la superficie y μf es el coeficiente de fricción entre la herramienta y el material. Este último varía con la distancia radial según [10] :
|
|
( 14) |
donde μ0 es una constante (parámetro por estimar) y λf es una constante que tiene en cuenta las unidades (10−3 cm·s−1 ). Sobre la superficie de entrada del modelo se impone una temperatura de 25 °C y se consideran los fenómenos de transmisión de calor por convección (h = 10 W·m−2 ·C−1 ) y radiación con el medio:
|
|
( 15) |
donde T0 es la temperatura del medio externo, ɛ es la emisividad de la superficie y B es la constante de Stefan-Boltzmann.
Entre las superficies en contacto se considera una condición de resistencia al flujo de calor, representada en el modelo por la siguiente ecuación:
|
|
( 16) |
donde q es el calor que se transmite, hb es la conductancia térmica (parámetro por estimar) y ΔT es la diferencia de temperaturas entre las superficies.
Las constantes de los materiales que forman parte del modelo se presentan en la tabla 1 :
| ρ [kg·m−3 ] | Cp [J·kg−1 · °C−1 ] | K [W·m−1 ·°C−1 ] | ɛ | |
|---|---|---|---|---|
| Placas (SS 304L) | 8,0 ·103 | 0,5 ·103 | 2,41 | 0,17 |
| Herramienta (acero) | 7,8 ·103 | 0,5 ·103 | 43,0 | 0,8 |
| Base (acero) | 7,8 ·103 | 0,5 ·103 | 43,0 | – |
2.2. Estimación de parámetros
La función costo que minimizar es la siguiente:
|
|
( 17) |
donde β son los parámetros por estimar, M es la cantidad de mediciones, son las temperaturas medidas experimentalmente y Ti son las temperaturas calculadas numéricamente.
Minimizando F con respecto a los parámetros βj , y a través del método de Levenberg-Marquard [14] , se llega al siguiente esquema de resolución iterativo:
|
|
( 18) |
donde λ es un parámetro que se ajusta durante el curso de la estimación para asegurar la convergencia del algoritmo, los supraíndices n y n + 1 corresponden a las iteraciones anterior y actual, respectivamente, y X es la matriz de sensibilidad de componentes Xij , llamados coeficientes de sensibilidad. Cada uno de estos coeficientes corresponde a la primera derivada de las temperaturas obtenidas del modelo para la medición i con respecto al parámetro βj :
|
|
( 19) |
2.3. Matriz de sensibilidad
Existen distintas maneras de encontrar la matriz de sensibilidad. En el presente trabajo se realiza una aproximación a la matriz utilizando un método numérico: diferencias finitas.
Para ello, se calcula la temperatura que resulta de efectuar pequeños incrementos, llamados perturbaciones, sobre cada uno de los parámetros de forma independiente. De esta manera, los coeficientes de la matriz de sensibilidad se obtienen según:
|
|
( 20) |
donde Δβj es la perturbación del parámetro j y β* son los parámetros por estimar con el elemento j perturbado.
2.4. Datos de entrada
Los parámetros por estimar son 4 (NP = 4): las 2 constantes que se encuentran incluidas en las ecuaciones que corresponden al coeficiente de fricción (μ0 ) y a la fracción de deslizamiento (δ0 ) del material en contacto con la superficie de la herramienta; el coeficiente de transferencia de calor en la superficie inferior (hb ), y la cantidad de disipación viscosa convertida en calor (η ).
Para los valores iniciales de los parámetros se tuvieron en cuenta algunos trabajos anteriores [9] and [10] , cuyos valores son: δ0 = 0, 4, η = 0, 5, μ0 = 0, 5 y hb = 400 W·m−2 ·°C−1 .
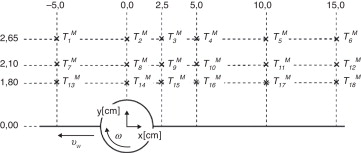
Las mediciones de temperatura que se tomaron como referencia ( ) se extrajeron del trabajo de Zhu et al. [9] . Se consideraron un total de 18 puntos (M = 18) sobre la superficie superior de las placas (fig. 3 ).
|
|
|
Figura 3. Posición de los puntos de las temperaturas medidas. |
2.5. Resolución
Para la simulación del proceso se construyó una malla de elementos finitos tetraédricos del tipo Taylor-Hood [15] , es decir, tetraedros P2-P1, con interpolaciones cuadráticas para las velocidades y lineales para las presiones, con el fin de lograr la estabilidad de las interpolaciones de presión por la condición de divergencia nula junto con una adecuada captura de los gradientes de tensión en las capas límite. Para las temperaturas se emplearon elementos tetraédricos con interpolación cuadrática en coincidencia con los nodos de velocidad. La malla resultó tener aproximadamente 52.800 elementos con 71.000 nodos de velocidad.
Se implementó una formulación de elementos finitos con estabilización Streamline Upwind Petrov-Galerkin (SUPG) [16] con un esquema de avance en el tiempo totalmente implícito, usado fundamentalmente como precondicionador del sistema de ecuaciones para llegar a la solución estacionaria. Asimismo, se agregó pseudocompresibilidad artificial del tipo de Chorin [17] .
El algoritmo de resolución consiste en 2 subpasos: en el primero de ellos se obtiene el campo de velocidades asumiendo como fijo el campo de temperaturas. Se itera por reemplazos sucesivos para adaptar no linealmente los valores de viscosidad de acuerdo con las velocidades de deformación obtenidas en la iteración anterior. En el segundo subpaso se resuelve el campo de temperaturas asumiendo el campo de velocidades resultante en el primer subpaso. En este caso, la no linealidad reside en el término de generación de calor.
El método de resolución numérica del sistema de ecuaciones lineales para cada iteración es el mismo en ambos subpasos. Se emplea el método de gradientes conjugados cuadrados con un precondicionador de factorización incompleta de tipo LU de acuerdo con el esquema propuesto por Saad [18] en SparseKit.
Con la solución obtenida de la simulación se interpolan las temperaturas en los puntos que corresponden a las posiciones de las temperaturas medidas ( ) y se evalúa la función costo (F ). Se perturban cada uno de los parámetros de manera independiente y se vuelve a requerir la solución estacionaria del problema para cada una de las perturbaciones. De esta manera, en cada iteración se construye la matriz de sensibilidad (X ) que permite obtener nuevos valores de los parámetros (β ).
3. Resultados y discusión
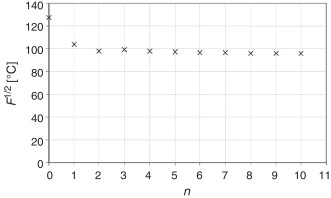
En la figura 4 se muestra gráficamente la raíz cuadrada de la función costo (F ) en cada iteración (n ), para el problema considerado. Se observa que en las 2 primeras iteraciones la magnitud de F1/2 disminuye significativamente respecto al valor inicial, pasando de un valor de 127,8 a 97,7°C (tabla 2 ). A partir de aquí, el valor se mantiene aproximadamente constante.
|
|
|
Figura 4. Valores que toma la raíz cuadrada de la función costo (F ) en cada iteración. |
| δ0 | η | μ0 | hb [W·m−2 ·°C−1 ] | F1/2 [°C] | |
|---|---|---|---|---|---|
| Valor inicial | 0,400 | 0,500 | 0,500 | 400 | 127,8 |
| Valor final | 0,589 | 0,386 | 0,707 | 531 | 97,7 |
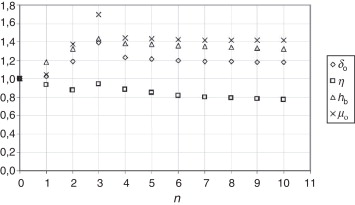
En la figura 5 se muestra gráficamente el valor que toman los 4 parámetros (δ0 , η , μ0 y hb ), cada uno dividido por su valor inicial, en cada iteración (n ), para el problema considerado.
|
|
|
Figura 5. Valores que toman los parámetros (δ0 , η , μ0 y hb ) en cada iteración. |
Es importante establecer cuál es la influencia de los parámetros sobre los resultados térmicos para comprender el significado del resultado de la estimación. En el caso de η y μ0 , un aumento en los parámetros significa un aumento de la temperatura, mientras que en el caso de hb significa una disminución. Es decir, en el primer caso es mayor el calor generado por disipación y por fricción superficial de la herramienta y, en el segundo, es mayor el calor que se transfiere a la placa base. En el caso de δ0 la cuestión es más compleja, ya que un aumento en el parámetro significa un menor calor generado por esfuerzos viscosos (menor flujo de material) pero un mayor calor generado por fricción superficial de la herramienta.
En consecuencia, la evolución de los parámetros (figura 5 ) indica mayor calor generado por la fricción superficial de la herramienta (debido al aumento de μ0 y de δ0 ), menor calor generado por el trabajo plástico –potencia de las tensiones– (debido a la disminución de η y al aumento de δ0 ) y una mayor pérdida de calor hacia la base (por aumento de hb ).
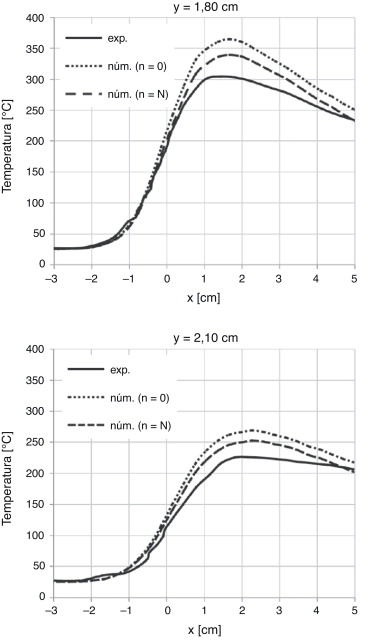
En la figura 6 se comparan las temperaturas medidas experimentalmente (exp.) y las del modelo numérico (num.), obtenidas con los valores de los parámetros inicial (n = 0) y final (n = N ), a 2 distancias distintas de la línea de unión: y = 1,80 cm y y = 2,10 cm.
|
|
|
Figura 6. Temperaturas experimentales y numéricas en los puntos de medición. |
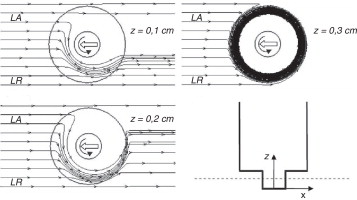
En la figura 7 se muestran las líneas de corriente del modelo en planos horizontales a distintas alturas (z) respecto a la superficie inferior de las placas por soldar.
|
|
|
Figura 7. Líneas de corriente del modelo. |
Comparando estas 3 imágenes puede verse que el flujo de material alrededor del perno aumenta cerca del apoyo de la herramienta. Asimismo, las líneas de corriente indican que el material es conducido principalmente por el lado de retroceso (LR). Lejos del apoyo, el material viaja alrededor del perno por el lado de retroceso y se ubica aproximadamente a un diámetro del perno detrás de su posición original. Esta característica del flujo se encuentra de acuerdo las visualizaciones de flujo de Reynolds [19] .
4. Conclusiones
Se pudieron estimar parámetros involucrados en un modelo de elementos finitos del proceso de soldadura FSW resolviendo un problema inverso. Se empleó el procedimiento iterativo consistente en minimizar una función costo a través de un desarrollo de errores de primer orden modificado por el método de Levenberg-Marquardt.
Estos nuevos parámetros permitieron mejorar el ajuste de los resultados numéricos de temperatura a mediciones experimentales. Asimismo, los cambios de los parámetros en relación con sus valores iniciales evidencian la influencia de los fenómenos físicos considerados sobre los resultados del modelo.
Los valores numéricos hallados son válidos específicamente para el material de las piezas y, en principio, es posible emplearlos para modelar ensayos sobre el mismo material con otras variables de procesamiento: velocidad de avance, velocidad de giro, presión y geometría de herramienta.
Los resultados obtenidos revelan el interés en la incorporación de técnicas de estimación de parámetros para mejorar las predicciones de los modelos numéricos.
Bibliografía
- [1] P. Ulysse; Three-dimensional modeling of the friction stir-welding process; Int. J. Mach. Tools Manuf., 42 (2002), pp. 1549–1557
- [2] C.M. Chen, R. Kovacevic; Finite element modeling of friction stir welding - thermal and thermomechanical analysis; Int. J. Mach. Tools Manuf., 43 (2003), pp. 1319–1326
- [3] D. Santiago, G. Lombera, S. Urquiza, A. Cassanelli, L. de Vedia; Numerical modeling of joints welded by “friction stir welding” process; Mater. Res., 7 (2004), pp. 569–574
- [4] D. Santiago, G. Lombera, G. Cassanelli, A. S.Urquiza, L. de Vedia; Analisis térmico en soldadura por fricción; Mec. Comp., 24 (2005), pp. 2781–2793
- [5] P.A. Colegrove, H.R. Sherclif; 3-Dimensional CDF modelling of flow round a threated friction stir welding tool profile; J. Mat. Process. Tech., 169 (2) (2005), pp. 320–327
- [6] R. Nandan, G.G. Roy, T.J. Lienert, T. Debroy; Three-dimensional heat and material flow during friction stir welding of mild steel; Acta Mater., 55 (2007), pp. 883–895
- [7] N. Dialami, M. Chiumenti, M. Cervera, C. Agelet de Saraciba; An apropos kinematic framework for the numerical modeling of friction stir welding; Comput. Struct., 117 (2013), pp. 48–57
- [8] H.-H Cho, S.-T Hong, J.-H Roh, H.-S Choi, H. Kang Suk, J. Steel Russell, N. Han Heung; Three-dimensional numerical and experimental investigation on friction stir welding processes of ferritic stainless steel; Acta Mater., 61 (7) (2013), pp. 2649–2661
- [9] X.K. Zhu, Y.J. Chao; Numerical simulation of transient temperature and residual stresses in friction stir welding of 304L stainless steel; J. Mat. Process. Tech., 146 (2004), pp. 263–272
- [10] R. Nandan, B. Prabu, A. De, T. Debroy; Improving Reliability of Heat Transfer and Materials Flow Calculations during Friction Stir Welding of Dissimilar Aluminum Alloys; Weld. J., 86 (2007), pp. 313–322
- [11] A. Larsen, M. Stolpe, J.H. Hattel; Estimating the workpiece-backingplate heat transfer coefficient in friction stir welding; Eng. Computation., 29 (1) (2012), pp. 65–82
- [12] C.M. Sellars, W.J. McG Tegart; La relation entre la résistance et la structure dans la déformation á chaud; Mémoires Sci. rev. met., 63 (9) (1966), pp. 731–746
- [13] A.M. Jorge Jr., O. Balancin; Prediction of Steel Flow Stresses under Hot Working Conditions; Mat. Research, 8 (2005), pp. 309–315
- [14] R. Aster, B. Borchers, C. Thurber; Parameter Estimation and Inverse Problems, Int. Geophysics Series, v. 90; Elsevier Academic Press (2003)
- [15] O.C. Zienkiewicz, R.L. Taylor, The Finite Element Method, Mc Graw Hill, London, 1 1989, 2 1991.
- [16] T.J.R. Hughes; The finite element Method; Prentice-Hall, Englewood Cliffs, New Jersey (1987)
- [17] A.J. Chorin; Numerical solution of the Navier-Stokes equations; Math. Comput., 22 (1968), pp. 745–762
- [18] Y. Saad, SPARSEKIT: a basic tool kit for sparse matrix computation (version 2), University of Illinois, Disponible en: http://www-users.cs.umn.edu/∼saad/software/SPARSKIT/ , 1994 [consultado 1 Abr 2010].
- [19] A.P. Reynolds; Flow visualization and simulation in FSW; Scr. Mater., 58 (2008), pp. 338–342
Document information
Published on 01/09/14
Accepted on 29/04/13
Submitted on 24/10/13
Volume 30, Issue 3, 2014
DOI: 10.1016/j.rimni.2013.04.007
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?