Abstract
A theoretical study on free vibration behavior of pre-stressed functionally graded material (FGM) beam is carried out. Power law variation of volume fraction along the thickness direction is considered. Geometric non-linearity is incorporated through von Kármán non-linear strain–displacement relationship. The governing equation for the static problem is obtained using minimum potential energy principle. The dynamic problem for the pre-stressed beam is formulated as an eigenvalue problem using Hamiltons principle. Three classical boundary conditions with immovable ends are considered for the present work, namely clamped–clamped, simply supported–simply supported and clamped–simply supported. Four different FGM beams, namely Stainless Steel–Silicon Nitride, Stainless Steel–Zirconia, Stainless Steel–Alumina and Titanium alloy–Zirconia, are considered for generation of results. Numerical results for non-dimensional frequency parameters of undeformed beam are presented. The results are presented in non-dimensional pressure-displacement plane for the static problem and in non-dimensional frequency-displacement plane for the dynamic problem. Comparative frequency-displacement plots are presented for different FGMs and also for different volume fraction indices.
Keywords
Functionally graded material ; Large deflection ; Timoshenko beam ; Pre-stressed beam ; Loaded natural frequency
1. Introduction
Functionally graded materials (FGMs) are inhomogeneous composites that have smooth and continuous variation of material properties in space. In most of the existing and potential future applications, FGM is considered mainly as a mixture of ceramic and metal in varying proportion. With the strength and toughness of metals, and the thermal and wear resistance of ceramics, FGM components possess good qualities of both the metals and ceramics. This makes it suitable for the FGM structures or components to be used in high temperature environment. FGM components are found in various applications, such as in aerospace, nuclear, automotive, civil, biomechanical, optical, electronic, mechanical, chemical and shipbuilding industries [1] . FGM components have applications in astronautic structures, such as rocket launch-pad, space vehicles [2] , etc., because rocket launch-pad is subjected to tremendous thermal and mechanical loading, whereas, space vehicles are subjected to extreme thermal conditions. FGMs having excellent thermal and mechanical properties are suitable for such various astronautic structures. It is to be mentioned that the present work deals with FGM beams, which are often found in various structures in the fields of aerospace, mechanical, automotive, civil engineering, etc.
FGM beams are mainly designed for applications under thermal environment. But its behavior under mechanical loadings at ambient condition is also important in order to ascertain its performance when thermal loadings are absent. Knowledge of free vibration behavior of pre-stressed FGM beams under mechanical loading is important from design point of view. It is known that the amplitude of forced vibration becomes excessively large when the excitation frequency falls in the vicinity of the natural frequency of vibration of a loaded beam. To avoid such undesirable vibration levels, the natural frequency of vibration of the loaded beam must be known to the designer. Hence the present work is meant to investigate such dynamic behavior of FGM beams. The literature review of some related works by other notable researchers are given in the next few paragraphs.
Ke et al. [3] investigated the nonlinear vibration behavior of FGM beams based on Euler–Bernoulli beam theory and von Kármán geometric nonlinearity. Fallah and Aghdam [4] and [5] presented large amplitude free vibration analysis of FGM Euler–Bernoulli beams resting on nonlinear elastic foundation subjected to both mechanical and thermal loadings. Fu et al. [6] carried out nonlinear free vibration analysis of piezoelectric FGM beams under thermal environment employing Euler–Bernoulli beam theory. Lai et al. [7] obtained the accurate analytical solutions for large amplitude vibration of thin FGM beams using Euler–Bernoulli beam theory. Based on Euler–Bernoulli beam theory, Yaghoobi and Torabi [8] studied the nonlinear vibration behavior of geometrically imperfect FGM beams resting on nonlinear elastic foundation subjected to axial force. Hemmatnezhad et al. [9] studied the large-amplitude oscillations of FGM Timoshenko beams using finite element formulation. Rahimi et al. [10] performed free vibration analysis of FGM Timoshenko beams in the vicinity of a buckled equilibrium configuration.
Kapuria et al. [11] presented a theoretical finite element model for vibration analysis of layered FGM beams with experimental validation. Aydogdu and Taskin [12] studied free vibration behavior of simply supported FGM beams using different beam theories. Free vibration characteristics of simply supported FGM beams were investigated by Şimşek and Kocatürk [13] using Lagranges equations under the assumptions of the Euler–Bernoulli beam theory. Thermo-mechanical vibration analysis of FGM beams resting on variable elastic foundation was carried out by Pradhan and Murmu [14] . Free vibration analysis of FGM beams based on a different first order shear deformation theory was carried out by Sina et al. [15] . Fundamental frequency analysis of FGM beams was carried out by Şimşek [16] using different higher-order beam theories. Giunta et al. [17] addressed free vibration behavior of functionally graded beams via several axiomatic refined theories. Using finite element method, Alshorbagy et al. [18] presented the free vibration characteristics of FGM beams with material graduation axially or transversally through the thickness based on the power law.
Free vibration characteristics of layered functionally graded beams were studied by Wattanasakulpong et al. [19] using Ritz method. Thai and Vo [20] investigated free vibration behavior of FGM beams based on various higher-order beam theories. Free vibration analysis of FGM beams for different boundary conditions was carried out by Pradhan and Chakraverty [21] using Euler–Bernoulli and Timoshenko beam theories. Free vibration behavior of axially loaded rectangular FGM beams was investigated by Nguyen et al. [22] based on the first-order shear deformation beam theory. The dynamic stiffness method was used by Su et al. [23] to investigate the free vibration behavior of FGM beams. Wattanasakulpong and Mao [24] investigated the dynamic response of Timoshenko FGM beams supported by various classical and non-classical boundary conditions.
Esfahani et al. [25] studied free vibration behavior of a thermally pre/post buckled FGM beam resting over a nonlinear hardening elastic foundation. Free vibration behavior of a thermo-electrically post-buckled rectangular FGM piezoelectric beams was studied by Komijani et al. [26] . Thermal buckling analysis of FGM beams with temperature-dependent material properties was carried out by Kiani and Eslami [27] and [28] . Esfahani et al. [29] carried out non-linear thermal stability analysis of temperature-dependent FGM beams resting on non-linear hardening elastic foundation. Thermo-electrical stability analysis of piezoelectric FGM beams had been carried out by Kiani et al. [30] , Kargani et al. [31] and Komijani et al. [32] , whereas thermal stability analysis of piezoelectric FGM beams was carried out by Kiani et al. [33] .
The present work is based on Timoshenko beam theory, which considers uniform distribution of transverse shear stress across the beam thickness. It is worthwhile to mention some of the research works using higher shear deformation theories (HSDT) developed in the recent years for analysis of plate and beam structures. Tounsi et al. [34] carried out thermo-elastic bending analysis of functionally graded sandwich plates using a refined trigonometric shear deformation theory (RTSDT). The thermo-mechanical bending behavior of FGM plates resting on Winkler–Pasternak elastic foundations was studied by Bouderba et al. [35] using RTSDT. Buckling and free vibration behaviors of exponentially graded sandwich plates were investigated by Ait Amar et al. [36] using simple refined shear deformation theory. Static and dynamic analyses of FGM and sandwich plates had been carried out by Hebali et al. [37] and Mahi et al. [38] using new hyperbolic shear deformation theory. Using higher-order shear deformation theories, wave propagation analysis in porous FGM plates, and bending and vibration analysis of FGM plates, were carried out by Ait Yahia et al. [39] and Belabed et al. [40] respectively. Recently, Bourada et al. [41] developed a refined trigonometric higher-order beam theory to investigate static and dynamic behaviors of FGM beams. In that work, the authors have included stretching deformation effect along the thickness direction and eliminated the need of shear correction factor. Bousahla et al. [42] presented a new trigonometric higher-order theory for the static analysis of FGM plates employing the physical neutral surface concept. Hamidi et al. [43] presented a sinusoidal plate theory for the thermo-mechanical bending analysis of functionally graded sandwich plates. Bessaim et al. [44] developed a new higher-order shear and normal deformation theory for investigating the bending and free vibration behavior of sandwich plates with functionally graded isotropic face sheets. Thermo-elastic bending analysis of functionally graded sandwich plates was carried out by Bouchafa et al. [45] using a refined hyperbolic shear deformation theory. Houari et al. [46] , using a new higher-order shear and normal deformation theory, simulated the thermo-elastic bending of FGM sandwich plates.
From the literature review presented, it is clear that an exhaustive study on free vibration behavior of transversely loaded beam for different FGM materials and different classical boundary conditions is scarce. Most of the published works are involved with either free vibration behavior of undeformed FGM beam or large amplitude free vibration behavior of FGM beam. Hence, in the present work, free vibration frequencies of FGM beam are computed for different pre-stressed configurations under uniform transverse pressure. Pre-stressed configurations are obtained through a geometrically non-linear static analysis. The linear vibration frequency of the pre-stressed beam, hereafter termed as loaded natural frequency, is then computed through an eigenvalue problem that includes the effect of pre-stressing using the displacement fields of the static problem. The effect of geometric non-linearity is included using von Kármán non-linear strain–displacement relationship. Timoshenko beam theory is used to consider the effects of shear deformation for the static problem and of rotary inertia for the subsequent dynamic problem. Suitable energy-based variational principles are used to derive the governing equations for both parts of the problem. Four different functionally graded materials and three different immovable classical boundary conditions are considered to show the pre-stressed dynamic behavior of beams.
2. Mathematical formulation
The present work aims at finding loaded natural frequency of pre-stressed FGM Timoshenko beam. A uniform rectangular beam with length L , height h and width b is considered. A beam with symbolic dimensions is shown in Fig. 1 , where, x , y and z denote the coordinate axes along the length, width and thickness directions respectively. As mentioned earlier, two distinct but interrelated problems are formulated and solved to obtain the desired solution. The purpose of the first one, the static problem, is to obtain the pre-stressed configuration of the beam under the application of uniform transverse pressure. And the second problem, named as the dynamic problem, is utilized to obtain the loaded natural frequency of the deformed beam. It must be mentioned that the static configurations for different loadings are obtained through a geometrically non-linear analysis to address the large deflection effect.
|
|
|
Fig. 1. Beam with dimensions and coordinate axes. |
2.1. Modeling of FGM beam
The present work considers continuous variation of graded material properties across the beam thickness. A continuous variation of volume fraction of ceramic ( ) and metal ( ) constituents across the thickness is assumed in accordance with the power-law given by and respectively [47] . Here, is the volume fraction index. Hence the effective material property of any FGM layer is determined using the Voigt model, which is given by , where and are the material properties of the ceramic and metal constituents respectively. So any effective material property at any layer z is given by . For the present FGM beam model, the top layer ( ) is purely ceramic and the bottom layer ( ) is purely metal. It is to be mentioned that the subscripts m and c refer to the metal and ceramic constituents respectively.
Any material property of the individual constituent is temperature-dependent and such temperature dependence is considered using the relationship , where is the temperature in K and , , , and are the coefficients of temperature. The relevant effective material properties for the present problem are elastic modulus , shear modulus , Poissons ratio and density . The temperature coefficients [47] of the material properties for the ceramic or metal constituents considered are given in Table 1 . For the present problem, the beam is assumed to be at ambient temperature , which is also considered to be the temperature at which thermal stress is zero. Hence all the required material properties are calculated at .
| Constituent material | Property |
|
|
|
|
| |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SUS304 | (Pa) | 201.04 × 109 | 0 | 3.079 × 10−4 | −6.534 × 10−7 | 0 | |||||||||||||||
|
0.3262 | 0 | −2.002 × 10−4 | 3.797 × 10−7 | 0 | ||||||||||||||||
| (kg m−3 ) | 8166 | 0 | 0 | 0 | 0 | ||||||||||||||||
| Ti-6Al-4V | (Pa) | 122.56 × 109 | 0 | −4.586 × 10−4 | 0 | 0 | |||||||||||||||
|
0.2884 | 0 | 1.121 × 10−4 | 0 | 0 | ||||||||||||||||
| (kg m−3 ) | 4429 | 0 | 0 | 0 | 0 | ||||||||||||||||
| Si3 N4 | (Pa) | 348.43 × 109 | 0 | −3.070 × 10−4 | 2.160 × 10−7 | −8.946 × 10−11 | |||||||||||||||
|
0.2400 | 0 | 0 | 0 | 0 | ||||||||||||||||
| (kg m−3 ) | 2370 | 0 | 0 | 0 | 0 | ||||||||||||||||
| ZrO2 | (Pa) | 244.27 × 109 | 0 | −1.371 × 10−3 | 1.214 × 10−6 | −3.681 × 10−10 | |||||||||||||||
|
0.2882 | 0 | 1.133 × 10−4 | 0 | 0 | ||||||||||||||||
| (kg m−3 ) | 3000 | 0 | 0 | 0 | 0 | ||||||||||||||||
| Al2 O3 | (Pa) | 349.55 × 109 | 0 | −3.853 × 10−4 | 4.027 × 10-7 | −1.673 × 10−10 | |||||||||||||||
|
0.2600 | 0 | 0 | 0 | 0 | ||||||||||||||||
| (kg m−3 ) | 3750 | 0 | 0 | 0 | 0 |
2.2. Static problem
The governing equation of the static problem is obtained using the minimum potential energy principle [48] given by,
|
|
( 1) |
where is the strain energy developed due to external loadings, is the potential energy of the external loadings, and is the variational operator. The strain energy consists of two parts, i.e., , where and are the strain energies due to axial strain and shear strain respectively. Using the proportionality of stress and strain (i.e., linear elastic material), and using suitable strain–displacement relationships, the strain energies can be expressed in terms of the displacement fields. The three displacement fields considered for the present problem are the following: , the in-plane displacement field, , the transverse displacement field, and , the rotational field of beam cross section due to bending. Here , and are defined at the mid-plane of the beam and are functions of the axial coordinate x .
The expressions of axial strain and shear strain are given by,
|
|
( 2) |
and
|
|
( 3) |
It is to be mentioned that the first term of Eq. (2) is von Kármán type non-linear strain–displacement relationship. Hence the strain energies and are given by,
|
|
( 4) |
and
|
|
( 5) |
The stiffness coefficients used in Eqs. (4) and (5) are given below:
and . In Eq. (5) , is the shear correction factor, which is taken to be 5/6 for rectangular cross section. It is to be mentioned that the shear modulus is given by, .
The potential energy of the applied uniform transverse pressure is given by,
|
|
( 6) |
where is defined as the force per unit length of the beam.
Following Ritz method, the displacement fields are approximated as finite linear combinations of admissible functions and unknown coefficients given as,
|
|
( 7) |
Here, , and are set of orthogonal admissible functions for the displacement fields , and respectively; and , and are the number of functions used to approximate , and respectively. It is to be noted that is the set of unknown coefficients, which are to be determined from the governing equations. The admissible functions satisfy the boundary conditions of the beam. The lowest order functions for each of the displacement fields are selected suitably and the corresponding higher-order functions are developed numerically following Gram–Schmidt orthogonalization scheme. Three boundary conditions with immovable ends are considered for the present work. And these are clamped–clamped (CC), simply supported–simply supported (SS) and clamped–simply supported (CS). The selected lowest order admissible functions for each of the displacement fields are given in Table 2 for all the three boundary conditions considered.
| Displacement field | Boundary | Conditions | Function | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
CC |
|
| |||||||||
| SS | ||||||||||||
| CS | ||||||||||||
|
CC |
|
| |||||||||
| SS | ||||||||||||
| CS | ||||||||||||
|
CC |
|
| |||||||||
| SS |
|
| ||||||||||
| CS |
|
|
Using the expression of various potential energies, given by Eqs. (4) , (5) and (6) into Eq. (1) and using the approximate displacement fields, given by Eq. (7) , the governing algebraic equations are obtained in the form given below:
|
|
( 8) |
where and are the stiffness matrix and load vector, respectively, each of dimension . The elements of and are given in the Appendix. It can be seen that the set of governing equations is non-linear in nature as the stiffness matrix is a function of the unknown coefficients. To solve this set of non-linear equations, a multi-dimensional secant method known as Broydens method [49] and [50] is used. The solution of Eq. (8) gives the statically deflected configuration of a pre-stressed beam. The next stage of the problem is now to determine the loaded natural frequency of the pre-stressed beam and its mathematical formulation is discussed in the next section.
2.3. Dynamic problem
The governing equation of the dynamic problem is derived using Hamiltons principle [48] given by,
|
|
( 9) |
where is the kinetic energy of the vibrating beam and is the time. The present work is a free vibration problem of a pre-stressed beam, in which the pre-stressed configuration is already obtained in the previous step of static problem. Hence the potential energy of the external loadings is zero in this case. Taking as the effective density of any FGM layer, the expression of is as follows:
|
|
( 10) |
where the inertia coefficients and are given by . The expression of remains the same as given for the static problem.
The approximate dynamic displacement fields, which are assumed to be separable in space and time, are given by,
|
|
( 11) |
where and are a new set of unknown parameters for the dynamic problem. The complete set of the space part of the dynamic displacements, i.e., , and , is the same as taken for the static problem. In Eq. (11) , denotes the natural frequency of vibration of the beam.
Using the expressions of strain energy (Eqs. (4) and (5) ), kinetic energy (Eq. (10) ) and dynamic displacements (Eq. (11) ), the governing equation is obtained as follows:
|
|
( 12) |
where and are the stiffness matrix and mass matrix respectively. The elements of are the same as given in the Appendix and the elements of are given below:
|
|
( 13) |
The off-diagonal elements of are zero. Eq. (12) is an eigenvalue problem, in which the square root of the eigenvalues gives the natural frequency of vibration of various vibration modes and is the corresponding eigen vectors used to obtain the vibration mode shapes. It must be noted that the stiffness matrix given in Eq. (12) is non-linear in nature. But as the dynamic problem is to be formulated at the pre-stressed beam configuration, the non-linear terms of the stiffness matrix are updated with the pre-stressed beam displacement fields obtained from the static problem [51] . Hence the solution of Eq. (12) gives the linear loaded natural frequency of vibration of the pre-stressed beam.
3. Results and discussion
The present work is carried out to determine the natural frequency of the first mode of vibration of pre-stressed FGM beams. It is to be mentioned that the frequency determined is of small amplitude vibration of pre-stressed beam. So the dynamic behavior is presented graphically in non-dimensional plane, where is the non-dimensional loaded natural frequency of first vibration mode and is the normalized maximum transverse deflection of pre-stressed beam. Hence such plots present the dynamic behavior in terms of loaded natural frequency of vibration as a function of maximum beam deflection. On the other hand, the static equilibrium path of the beam is presented graphically in plane, where is the non-dimensional uniform transverse pressure. The non-dimensional parameters are defined as: , , and , where is the elastic modulus of metal constituent, is the maximum transverse deflection, is the density of metal constituent, is the cross sectional area, and is the area moment of inertia of the beam cross section about the centroidal axis. The results are generated for and .
Four different functionally graded materials are considered for the present work, namely Stainless Steel (SUS304)–Silicon Nitride (Si3 N4 ), Stainless Steel–Zirconia (ZrO2 ), Stainless Steel–Alumina (Al2 O3 ) and Titanium alloy (Ti-6Al-4V)–Zirconia, and hereafter these are termed as FGM 1, FGM 2, FGM 3 and FGM 4 respectively. Using the temperature coefficients for the constituents of these FGM compositions given in Table 1 , the various material properties are calculated at . These are presented in Table 3 . The static and dynamic behaviors of these FGM beams are presented for three boundary conditions, i.e., CC, SS and CS.
| Material property | SUS304 | Ti-6Al-4V | Si3 N4 | ZrO2 | Al2 O3 | |||
|---|---|---|---|---|---|---|---|---|
| (GPa) | 207.79 | 105.70 | 322.27 | 168.06 | 320.24 | |||
|
0.318 | 0.298 | 0.240 | 0.298 | 0.260 | |||
| (kg m−3 ) | 8166 | 4429 | 2370 | 3000 | 3750 |
3.1. Validation study
The non-dimensional frequency parameter of undeformed FGM beam is compared with the results of Ref. [9] for different volume fraction indices and also for different boundary conditions. The comparison is made for Steel–Alumina FGM beam for a length-thickness ratio L/h = 20. The material properties used for comparison purpose are as follows: , , , , , and . The comparison is presented in Table 4 . The comparison shows good agreement of the present results with Ref. [9] . This validates the free vibration dynamic behavior of undeformed FGM beam analyzed by the present method.
| Boundary condition | Non-dimensional frequency parameter, | |||||||
|---|---|---|---|---|---|---|---|---|
| k = 0 | k = 0.1 | k = 0.2 | k = 0.5 | k = 1 | k = 2 | k = 5 | ||
| CC | Present | 6.4864 | 6.2664 | 6.0896 | 5.7504 | 5.4617 | 5.2340 | 5.0333 |
| Ref. [9] . | 6.4971 | 6.2737 | 6.1001 | 5.7575 | 5.4713 | 5.2413 | 5.0390 | |
| SS | Present | 4.3311 | 4.1980 | 4.0653 | 3.8402 | 3.6652 | 3.5203 | 3.3863 |
| Ref. [9] . | 4.3371 | 4.1889 | 4.0753 | 3.8554 | 3.6742 | 3.5244 | 3.3803 | |
| CS | Present | 5.4099 | 5.2240 | 5.0820 | 4.8056 | 4.5385 | 4.3759 | 4.2091 |
| Ref. [9] . | 5.4086 | 5.2228 | 5.0786 | 4.7951 | 4.5590 | 4.3688 | 4.1990 | |
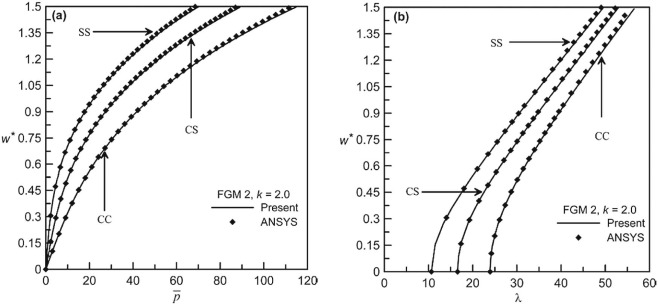
The validation plots of pre-stressed Stainless Steel–Zirconia (FGM 2) beam are presented in Fig. 2 (a–b) for k = 2.0. Fig. 2 (a) presents the static equilibrium path in plane, whereas Fig. 2 (b) presents the pre-stressed free vibration behavior in plane. The validation is carried out with finite element package ANSYS (version 10.0). The comparison plots are presented for CC, SS and CS boundary conditions. The comparative plots in Fig. 2 show very good agreement of the present method with ANSYS for both the static and dynamic behaviors. The finite element model in ANSYS is created using BEAM 188 element, and the results are generated with 30 elements. It must be noted that a layered variation of material properties is used to create the finite element model in ANSYS.
|
|
|
Fig. 2. Validation plots of pre-stressed beam: (a) static behavior and (b) free vibration behavior. |
3.2. Natural frequency of vibration of undeformed FGM beam
The non-dimensional frequency parameter of undeformed CC beam for all the four functionally graded materials considered is presented in Table 5 for different volume fraction indices. The list presented in Table 5 includes results for L/h = 10 and L/h = 25. Similar lists for SS and CS FGM beams are presented in Table 6 and Table 7 respectively. As seen from these tables, the non-dimensional frequency parameter decreases with increase in values of k , and this is true for all the four FGMs considered. Only exception to this occurs for FGM 2 with L/h = 25, where increases from k = 20 to k = 50. It is to be mentioned that higher k values indicate more metal content in the beam. It is also seen that the non-dimensional frequency parameter increases with L/h ratio but the change is very little. The effect of L/h ratio on non-dimensional frequency of vibration remains insignificant for pre-stressed beam also. Hence the results, as presented in the following section, for pre-stressed FGM beams are generated for L/h = 25.
| k | L/h = 10 | L/h = 25 | ||||||
|---|---|---|---|---|---|---|---|---|
| FGM 1 | FGM 2 | FGM 3 | FGM 4 | FGM 1 | FGM 2 | FGM 3 | FGM 4 | |
| 0.0 | 48.595 | 31.128 | 38.477 | 32.142 | 51.212 | 32.872 | 40.537 | 33.943 |
| 0.1 | 43.041 | 29.308 | 35.828 | 30.774 | 45.334 | 30.915 | 37.723 | 32.470 |
| 0.2 | 39.411 | 28.051 | 33.864 | 29.715 | 41.448 | 29.597 | 35.751 | 31.378 |
| 0.5 | 33.475 | 25.815 | 30.290 | 27.617 | 35.312 | 27.260 | 31.870 | 29.106 |
| 1.0 | 29.326 | 24.070 | 27.502 | 25.862 | 30.803 | 25.413 | 28.969 | 27.268 |
| 2.0 | 26.288 | 22.657 | 25.320 | 24.425 | 27.742 | 23.896 | 26.728 | 25.802 |
| 5.0 | 23.853 | 21.563 | 23.445 | 23.102 | 25.246 | 22.712 | 24.771 | 24.430 |
| 10.0 | 22.697 | 21.198 | 22.499 | 22.358 | 24.001 | 22.348 | 23.799 | 23.581 |
| 20.0 | 21.953 | 21.052 | 21.847 | 21.802 | 23.204 | 22.190 | 23.099 | 23.055 |
| 50.0 | 21.390 | 20.984 | 21.350 | 21.350 | 22.579 | 22.135 | 22.552 | 22.547 |
| k | L/h = 10 | L/h = 25 | ||||||
|---|---|---|---|---|---|---|---|---|
| FGM 1 | FGM 2 | FGM 3 | FGM 4 | FGM 1 | FGM 2 | FGM 3 | FGM 4 | |
| 0.0 | 22.457 | 14.410 | 17.789 | 14.880 | 22.393 | 14.596 | 17.804 | 15.072 |
| 0.1 | 19.873 | 13.573 | 16.532 | 14.234 | 20.200 | 13.920 | 16.718 | 14.514 |
| 0.2 | 18.208 | 12.998 | 15.637 | 13.759 | 18.303 | 13.270 | 15.796 | 14.043 |
| 0.5 | 15.522 | 11.969 | 14.046 | 12.829 | 15.692 | 12.186 | 14.249 | 12.915 |
| 1.0 | 13.635 | 11.159 | 12.794 | 12.048 | 13.772 | 11.279 | 12.989 | 12.230 |
| 2.0 | 12.243 | 10.500 | 11.803 | 11.399 | 12.250 | 10.472 | 12.031 | 11.613 |
| 5.0 | 11.098 | 9.999 | 10.909 | 10.746 | 11.234 | 10.140 | 11.133 | 10.924 |
| 10.0 | 10.566 | 9.819 | 10.461 | 10.401 | 10.561 | 9.986 | 10.586 | 10.497 |
| 20.0 | 10.168 | 9.747 | 10.147 | 10.119 | 10.258 | 9.811 | 10.310 | 10.286 |
| 50.0 | 9.934 | 9.704 | 9.886 | 9.889 | 10.042 | 9.873 | 10.152 | 9.953 |
| k | L/h = 10 | L/h = 25 | ||||||
|---|---|---|---|---|---|---|---|---|
| FGM 1 | FGM 2 | FGM 3 | FGM 4 | FGM 1 | FGM 2 | FGM 3 | FGM 4 | |
| 0.0 | 34.326 | 22.013 | 27.203 | 22.730 | 35.330 | 22.785 | 28.021 | 23.527 |
| 0.1 | 30.411 | 20.740 | 25.306 | 21.783 | 31.326 | 21.558 | 25.969 | 22.512 |
| 0.2 | 27.831 | 19.853 | 23.940 | 21.017 | 29.007 | 20.403 | 24.488 | 21.737 |
| 0.5 | 23.681 | 18.276 | 21.416 | 19.527 | 24.481 | 18.867 | 22.181 | 19.990 |
| 1.0 | 20.728 | 17.036 | 19.472 | 18.310 | 21.457 | 17.507 | 20.152 | 18.861 |
| 2.0 | 18.622 | 16.034 | 17.934 | 17.298 | 19.166 | 16.534 | 18.662 | 18.033 |
| 5.0 | 16.889 | 15.252 | 16.615 | 19.373 | 17.299 | 15.773 | 17.022 | 17.098 |
| 10.0 | 16.094 | 14.998 | 15.934 | 15.845 | 16.395 | 15.463 | 16.504 | 16.321 |
| 20.0 | 15.553 | 14.899 | 15.482 | 15.444 | 19.120 | 15.330 | 16.050 | 16.026 |
| 50.0 | 15.146 | 14.842 | 15.113 | 15.112 | 15.649 | 15.321 | 15.572 | 15.662 |
3.3. Effect of material and volume fraction index on static and dynamic behavior
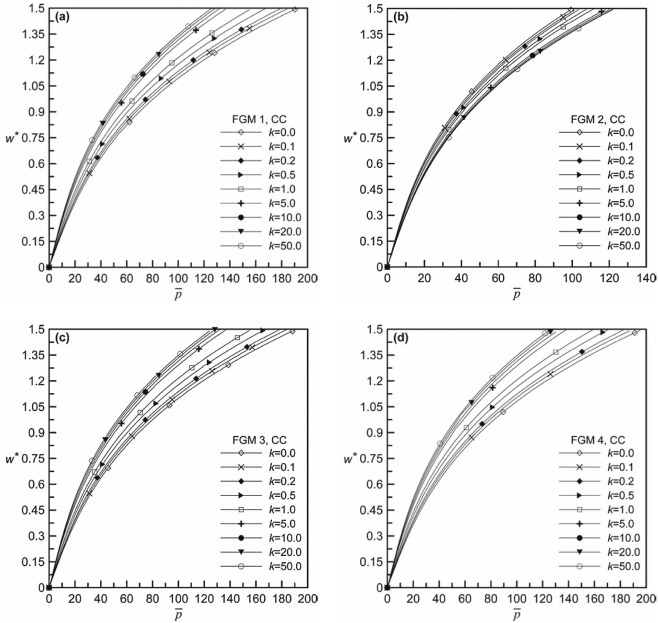
The static deflection behavior of CC beam in plane is presented in Fig. 3 (a–d) for FGM 1, FGM 2, FGM 3 and FGM 4 respectively. In each of these figures, the static equilibrium path is presented for a set of volume fraction indices, i.e., for k = 0.0, 0.1, 0.2, 0.5, 1.0, 2.0, 5.0, 10.0, 20.0, 50.0. The plots are useful in finding the non-dimensional pressure value corresponding to a static deflection level, at which the loaded natural frequency is found out. As seen from Fig. 3 , the beam exhibits non-linear hardening type load-deflection behavior. This is due to stiffening effect induced in the beam as a result of generation of tensile membrane forces due to immovable ends. With increase in k , i.e., the increase in metal content, FGM 1, FGM 3 and FGM 4 beam shows decreased stiffness levels as the elastic modulus of ceramic constituent is greater than its metal counterpart, as can be seen from Table 3 . The trend is completely reverse for FGM 2 beam as the elastic modulus of its ceramic constituent is lesser than that of its metal part.
|
|
|
Fig. 3. Non-dimensional pressure-deflection behavior for different volume fraction indices of CC beams: (a) FGM 1, (b) FGM 2, (c) FGM 3 and (d) FGM 4. |
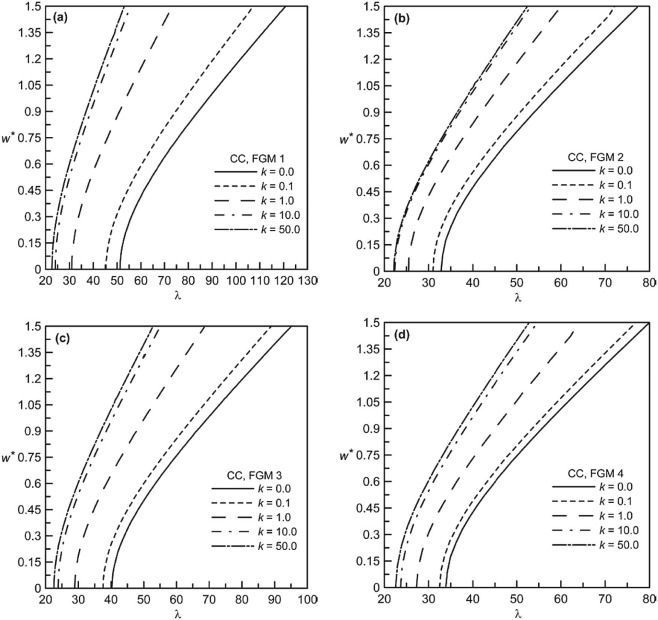
The loaded natural frequency versus maximum transverse deflection plots in non-dimensional plane is presented in Fig. 4 (a–f) for k = 0.0, 0.2, 0.5, 5.0, 20.0 and 50.0, respectively, for CC FGM beam. In each of the figures, free vibration behavior is shown for FGM 1, FGM 2, FGM 3 and FGM 4 beams. In accordance with the static behavior, the loaded natural frequency is shown to be increasing with increased deflection level as a result of enhanced stiffening effect. With regard to the comparative behavior among different FGMs considered, FGM 1 shows highest frequency of vibration with FGM 3, FGM 4 and FGM 2 coming next in order of exhibiting decreasing vibration frequency at any common deflection levels. This is true irrespective of the values of the volume fraction index. It is also seen that the relative differences in frequency-deflection behavior of various FGMs diminish with increase in k values. At higher k values, the dynamic behavior becomes almost identical for all the FGMs considered.
|
|
|
Fig. 4. Non-dimensional frequency-deflection behavior of different CC FGM beams: (a) k = 0.0, (b) k = 0.2, (c) k = 0.5, (d) k = 5.0, (e) k = 20.0 and (f) k = 50.0. |
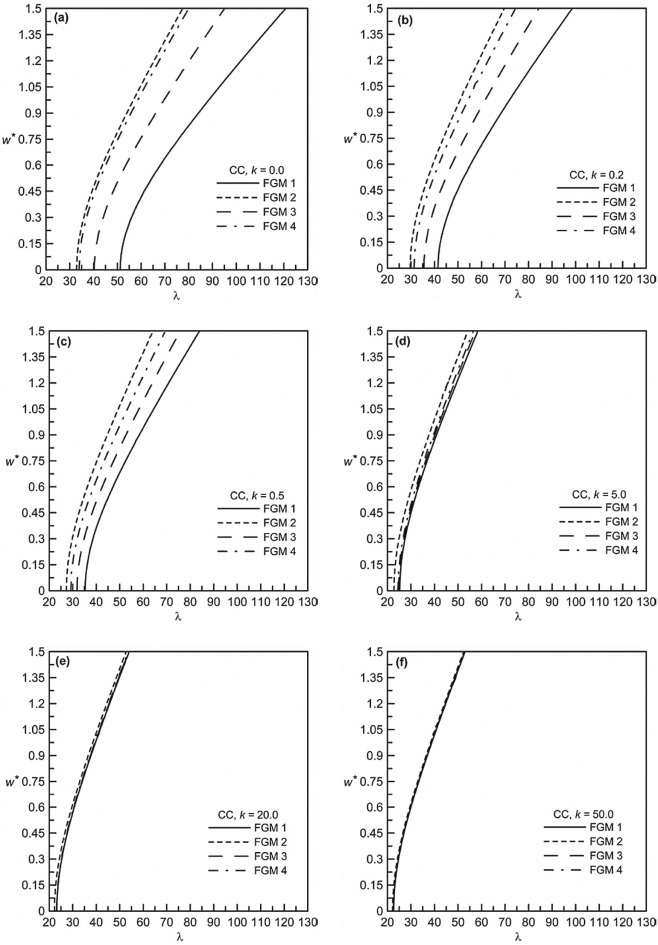
It is also important to study the dynamic behavior of pre-stressed FGM beam for different volume fraction indices. Fig. 5 (a–d) shows such non-dimensional frequency-deflection plots for FGM 1. FGM 2, FGM 3 and FGM 4, respectively, each showed comparative behavior for k = 0.0, 0.1, 1.0, 10.0, 50.0. It can be seen that the loaded natural frequency decreases with increase in k values for any particular deflection level. This is true for all the FGMs considered. The explanation for the variation of loaded natural frequency with k cannot be given by seeing only the static deflection behavior as shown in Fig. 3 . Because in predicting the dynamic behavior, both the relative density values and the relative elastic modulus values of the constituents are to be considered.
|
|
|
Fig. 5. Non-dimensional frequency-deflection behavior of CC beams for different volume fraction indices: (a) FGM 1, (b) FGM 2, (c) FGM 3 and (d) FGM 4. |
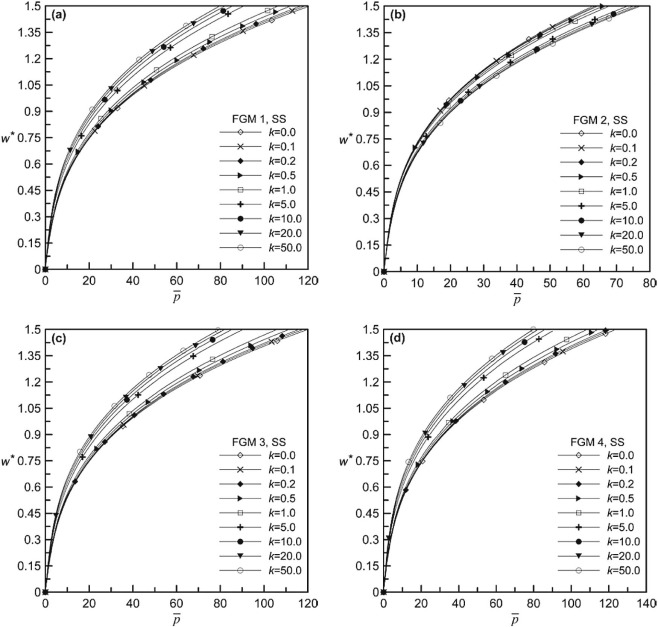
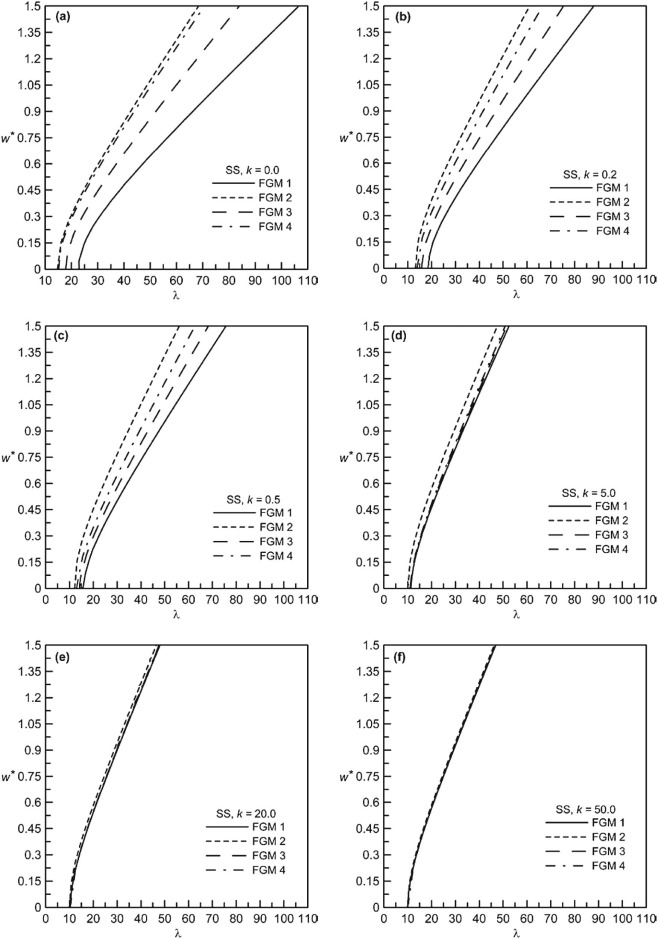
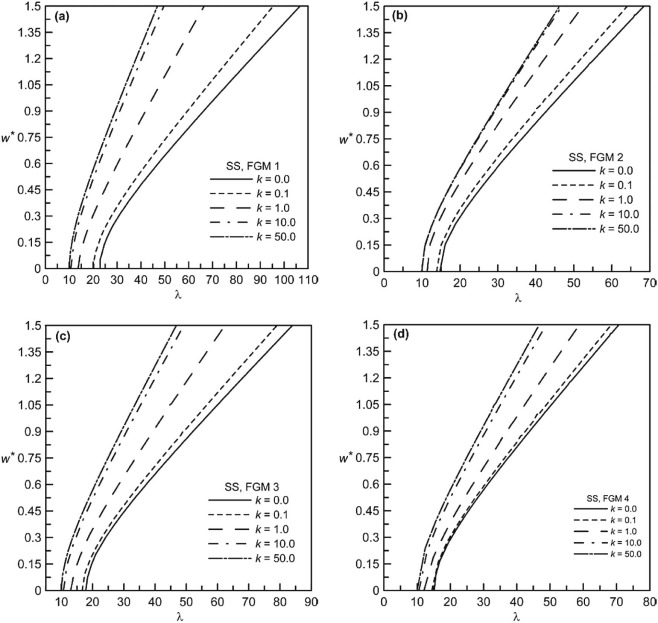
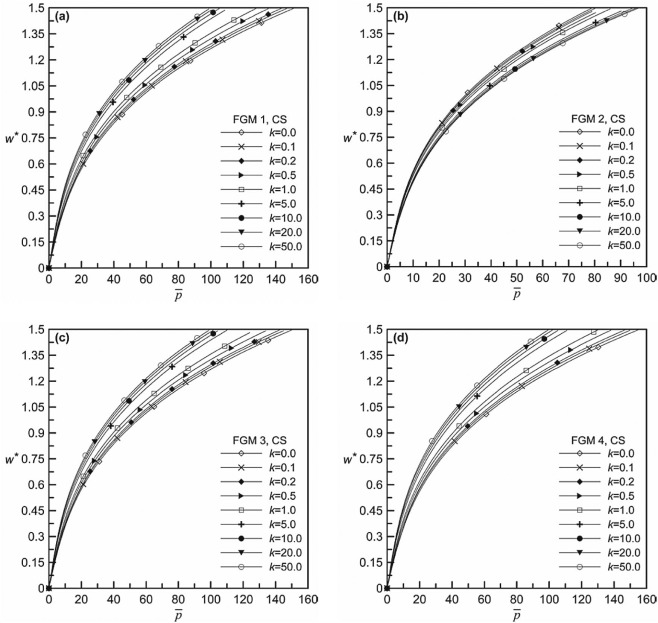
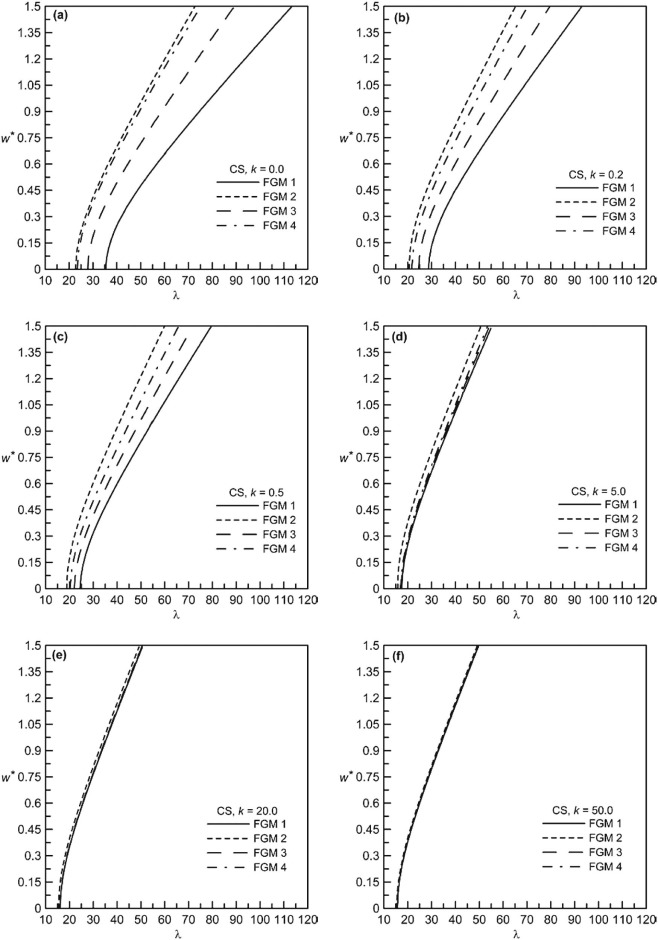
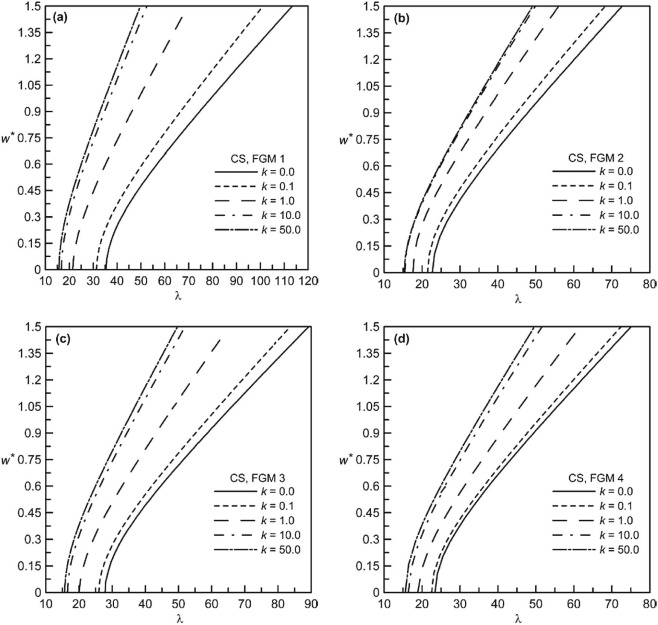
The non-dimensional static deflection behavior for different volume fraction indices is presented in Fig. 6 (a–d) for SS beams each for different functionally graded materials. Also the non-dimensional frequency-deflection plots of SS beams are shown in Fig. 7 (a–f) for different k values and in Fig. 8 (a–d) for different FGMs. As for CS beams, static deflection behavior is presented in Fig. 9 (a–d), whereas the dynamic behavior in terms of frequency-deflection plots is shown in Fig. 10 (a–f) for different k values and in Fig. 11 (a–d) for different FGMs. For both these boundary conditions, the nature of static and dynamic behavior is similar in nature as described for CC beams. The relative behavior for these three different boundary conditions, although not shown in a single plot, differs obviously due to the stiffness effects contributed from the support conditions. Because it is known that CC beam exhibits the highest transverse stiffness, with CS and SS beam being next in order of decreasing stiffness levels.
|
|
|
Fig. 6. Non-dimensional pressure-deflection behavior for different volume fraction indices of SS beam: (a) FGM 1, (b) FGM 2, (c) FGM 3 and (d) FGM 4. |
|
|
|
Fig. 7. Non-dimensional frequency-deflection behavior of different SS FGM beams: (a) k = 0.0, (b) k = 0.2, (c) k = 0.5, (d) k = 5.0, (e) k = 20.0 and (f) k = 50.0. |
|
|
|
Fig. 8. Non-dimensional frequency-deflection behavior of SS beams for different volume fraction indices: (a) FGM 1, (b) FGM 2, (c) FGM 3 and (d) FGM 4. |
|
|
|
Fig. 9. Non-dimensional pressure-deflection behavior for different volume fraction indices of CS beam: (a) FGM 1, (b) FGM 2, (c) FGM 3 and (d) FGM 4. |
|
|
|
Fig. 10. Non-dimensional frequency-deflection behavior of different CS FGM beams: (a) k = 0.0, (b) k = 0.2, (c) k = 0.5, (d) k = 5.0, (e) k = 20.0 and (f) k = 50.0. |
|
|
|
Fig. 11. Non-dimensional frequency-deflection behavior of CS beams for different volume fraction indices: (a) FGM 1, (b) FGM 2, (c) FGM 3 and (d) FGM 4. |
4. Conclusions
An energy based mathematical model is presented to study the free vibration behavior of pre-stressed FGM Timoshenko beams. The entire work is carried out in solving two different but interrelated problems, namely the static problem and the dynamic problem. The static problem is used to determine the pre-stressed configuration of FGM beam under uniform transverse pressure. And the dynamic problem, formulated as an eigenvalue problem, is used to determine the loaded natural frequency of the pre-stressed beam. Four different FGMs, namely Stainless Steel–Silicon Nitride, Stainless Steel–Zirconia, Stainless Steel–Alumina and Titanium alloy–Zirconia, are used to generate results for different volume fraction indices. Numerical results for non-dimensional frequency parameters of undeformed beam are presented for different functionally graded materials with CC, SS and CS boundary conditions. Effects of material as well as the volume fraction index on non-dimensional frequency-deflection behavior of pre-stressed beams are studied. The results are presented for three boundary conditions, i.e., CC, SS and CS. Static equilibrium paths in non-dimensional plane are also presented in order to relate the applied pressure with loaded natural frequency through the static deflection level. The results can serve as benchmarks for further study in this field.
Appendix
Elements of stiffness matrix and load vector
|
|
|
|
|
|
|
|
|
|
|
|
|
|
References
- [1] M. Zidi, A. Tounsi, M.S.A. Houari, E.A. Adda Bedia, O. Anwar Bég; Bending analysis of FGM plates under hygro-thermo-mechanical loading using a four variable refined plate theory; Aerosp. Sci. Technol, 34 (2014), pp. 24–34
- [2] M. Bennoun, M.S.A. Houari, A. Tounsi; A novel five variable refined plate theory for vibration analysis of functionally graded sandwich plates; Mech. Adv. Mater. Str, 23 (2016), pp. 423–431
- [3] L.L. Ke, J. Yang, S. Kitipornchai; An analytical study on the nonlinear vibration of functionally graded beams; Meccanica, 45 (2010), pp. 743–752
- [4] A. Fallah, M.M. Aghdam; Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation; Eur. J. Mech. A Solid, 30 (2011), pp. 571–583
- [5] A. Fallah, M.M. Aghdam; Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation; Compos. Part B, 43 (2012), pp. 1523–1530
- [6] Y. Fu, J. Wang, Y. Mao; Nonlinear analysis of buckling, free vibration and dynamic stability for the piezoelectric functionally graded beams in thermal environment; Appl. Math. Model, 36 (2012), pp. 4324–4340
- [7] S.K. Lai, J. Harrington, Y. Xiang, K.W. Chow; Accurate analytical perturbation approach for large amplitude vibration of functionally graded beams; Int. J. Nonlinear Mech, 47 (2012), pp. 473–480
- [8] H. Yaghoobi, M. Torabi; Post-buckling and nonlinear free vibration analysis of geometrically imperfect functionally graded beams resting on nonlinear elastic foundation; Appl. Math. Model, 37 (2013), pp. 8324–8340
- [9] M. Hemmatnezhad, R. Ansari, G.H. Rahimi; Large-amplitude free vibrations of functionally graded beams by means of a finite element formulation; Appl. Math. Model, 37 (2013), pp. 8495–8504
- [10] G.H. Rahimi, M.S. Gazor, M. Hemmatnezhad, H. Toorani; On the postbuckling and free vibrations of FG Timoshenko beams; Compos. Struct, 95 (2013), pp. 247–253
- [11] S. Kapuria, M. Bhattacharyya, A.N. Kumar; Bending and free vibration response of layered functionally graded beams: a theoretical model and its experimental validation; Compos. Struct, 82 (2008), pp. 390–402
- [12] M. Aydogdu, V. Taskin; Free vibration analysis of functionally graded beams with simply supported edges; Mater. Des, 28 (2007), pp. 1651–1656
- [13] M. Şimşek, T. Kocatürk; Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load; Compos. Struct, 90 (2009), pp. 465–473
- [14] S.C. Pradhan, T. Murmu; Thermo-mechanical vibration of FGM sandwich beam under variable elastic foundations using differential quadrature method; J. Sound Vib, 321 (2009), pp. 342–362
- [15] S.A. Sina, H.M. Navazi, H. Haddadpour; An analytical method for free vibration analysis of functionally graded beams; Mater. Des, 30 (2009), pp. 741–747
- [16] M. Şimşek; Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories; Nucl. Eng. Des, 240 (2010), pp. 697–705
- [17] G. Giunta, D. Crisafulli, S. Belouettar, E. Carrera; Hierarchical theories for the free vibration analysis of functionally graded beams; Compos. Struct, 94 (2011), pp. 68–74
- [18] A.E. Alshorbagy, M.A. Eltaher, F.F. Mahmoud; Free vibration characteristics of a functionally graded beam by finite element method; Appl. Math. Model, 35 (2011), pp. 412–425
- [19] N. Wattanasakulpong, B.G. Prusty, D.W. Kelly, M. Hoffman; Free vibration analysis of layered functionally graded beams with experimental validation; Mater. Des, 36 (2012), pp. 182–190
- [20] H.T. Thai, T.P. Vo; Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories; Int. J. Mech. Sci, 62 (2012), pp. 57–66
- [21] K.K. Pradhan, S. Chakraverty; Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method; Compos Part B, 51 (2013), pp. 175–184
- [22] T.K. Nguyen, T.P. Vo, H.T. Thai; Static and free vibration of axially loaded functionally graded beams based on the first-order shear deformation theory; Compos Part B, 55 (2013), pp. 147–157
- [23] H. Su, J.R. Banerjee, C.W. Cheung; Dynamic stiffness formulation and free vibration analysis of functionally graded beams; Compos. Struct, 106 (2013), pp. 854–862
- [24] N. Wattanasakulpong, Q. Mao; Dynamic response of Timoshenko functionally graded beams with classical and non-classical boundary conditions using Chebyshev collocation method; Compos. Struct, 119 (2015), pp. 346–354
- [25] S.E. Esfahani, Y. Kiani, M. Komijani, M.R. Eslami; Vibration of a temperature-dependent thermally pre/postbuckled FGM beam over a nonlinear hardening elastic foundation; J. Appl Mech, 81 (2014), p. 011004-1
- [26] M. Komijani, Y. Kiani, S.E. Esfahani, M.R. Eslami; Vibration of thermo-electrically post-buckled rectangular functionally graded piezoelectric beams; Compos. Struct, 98 (2013), pp. 143–152
- [27] Y. Kiani, M.R. Eslami; Thermal buckling analysis of functionally graded material beams; Int. J. Mech. Mater. Des, 6 (2010), pp. 229–238
- [28] Y. Kiani, M.R. Eslami; Thermomechanical buckling of temperature-dependent FGM beams; Lat. Am. J. Solids Str, 10 (2013), pp. 223–246
- [29] S.E. Esfahani, Y. Kiani, M.R. Eslami; Non-linear thermal stability analysis of temperature dependent FGM beams supported on non-linear hardening elastic foundations; Int. J. Mech. Sci, 69 (2013), pp. 10–20
- [30] Y. Kiani, M. Rezaei, S. Taheri, M.R. Eslami; Thermo-electrical buckling of piezoelectric functionally graded material Timoshenko beams; Int. J. Mech. Mater. Des, 7 (2011), pp. 185–197
- [31] A. Kargani, Y. Kiani, M.R. Eslami; Exact solution for nonlinear stability of piezoelectric FGM Timoshenko beams under thermo-electrical loads; J. Therm. Stresses, 36 (2013), pp. 1056–1076
- [32] M. Komijani, Y. Kiani, M.R. Eslami; Non-linear thermoelectrical stability analysis of functionally graded piezoelectric material beams; J. Intel. Mater. Syst. Str, 24 (2013), pp. 399–410
- [33] Y. Kiani, S. Taheri, M.R. Eslami; Thermal buckling of piezoelectric functionally graded material beams; J. Therm. Stresses, 34 (2011), pp. 835–850
- [34] A. Tounsi, M.S.A. Houari, S. Benyoucef, E.A. Adda Bedia; A refined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates; Aerosp. Sci. Technol, 24 (2013), pp. 209–220
- [35] B. Bouderba, M.S.A. Houari, A. Tounsi; Thermomechanical bending response of FGM thick plates resting on Winkler–Pasternak elastic foundations; Steel Compos. Str, 14 (2013), pp. 85–104
- [36] M.M. Ait Amar, H.H. Abdelaziz, A. Tounsi; An efficient and simple refined theory for buckling and free vibration of exponentially graded sandwich plates under various boundary conditions; J. Sand. Str. Mater, 16 (2014), pp. 293–318
- [37] H. Hebali, A. Tounsi, M.S.A. Houari, A. Bessaim, E.A. Adda Bedia; A new quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates; J. Eng. Mech, 140 (2014), pp. 374–383
- [38] A. Mahi, E.A. Adda Bedia, A. Tounsi; A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates; Appl. Math. Model, 39 (2015), pp. 2489–2508
- [39] S. Ait Yahia, H. Ait Atmane, M.S.A. Houari, A. Tounsi; Wave propagation in functionally graded plates with porosities using various higher-order shear deformation plate theories; Str. Eng. Mech, 53 (2015), pp. 1143–1165
- [40] Z. Belabed, M.S.A. Houari, A. Tounsi, S.R. Mahmoud, B.O. Anwar; An efficient and simple higher order shear and normal deformation theory for functionally graded material (FGM) plates; Compos. Part B, 60 (2014), pp. 274–283
- [41] M. Bourada, A. Kaci, M.S.A. Houari, A. Tounsi; A new simple shear and normal deformations theory for functionally graded beams; Steel Compos. Str, 18 (2015), pp. 409–423
- [42] A.A. Bousahla, M.S.A. Houari, A. Tounsi, E.A. Adda Bedia; A novel higher order shear and normal deformation theory based on neutral surface position for bending analysis of advanced composite plates; Int. J. Comput. Meth, 11 (2014), p. 1350082
- [43] A. Hamidi, M.S.A. Houari, S.R. Mahmoud, A. Tounsi; A sinusoidal plate theory with 5-unknowns and stretching effect for thermomechanical bending of functionally graded sandwich plates; Steel Compos. Str, 18 (2015), pp. 235–253
- [44] A. Bessaim, M.S.A. Houari, A. Tounsi, S.R. Mahmoud, E.A. Adda Bedia; A new higher-order shear and normal deformation theory for the static and free vibration analysis of sandwich plates with functionally graded isotropic face sheets; J. Sand. Str. Mater, 15 (2013), pp. 671–703
- [45] A. Bouchafa, B.M. Bachir, M.S.A. Houari, A. Tounsi; Thermal stresses and deflections of functionally graded sandwich plates using a new refined hyperbolic shear deformation theory; Steel Compos. Str, 18 (2015), pp. 1493–1515
- [46] M.S.A. Houari, A. Tounsi, O. Anwar Bég; Thermoelastic bending analysis of functionally graded sandwich plates using a new higher order shear and normal deformation theory; Int. J. Mech. Sci, 76 (2013), pp. 467–479
- [47] H.S. Shen; Functionally Graded Materials Nonlinear Analysis of Plates and Shells; CRC Press, USA (2009)
- [48] I.H. Shames, C.L. Dym; Energy and Finite Element Methods in Structural Mechanics; New Age International Publishers, Delhi (2009)
- [49] W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery; Numerical Recipes in Fortran 77: The Art of Scientific Computing; Cambridge University Press, New York, NY (1992)
- [50] D. Das, P. Sahoo, K. Saha; A numerical analysis of large amplitude forced beam vibration under different boundary conditions and excitation patterns; J. Vib. Control, 18 (2011), pp. 1900–1915
- [51] D. Das, P. Sahoo, K. Saha; Large-amplitude dynamic analysis of simply supported skew plates by a variational method; J. Sound Vib, 313 (2008), pp. 246–267
Document information
Published on 10/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?