Cost modeling of lithium-ion battery cells for automotive applications

Abstract

The purpose of this study was to highlight the technical and economic issues arising in lithium-ion cells for automotive applications, and to indicate some potential solutions to lower the cost. This topic has already been the subject of some studies, but, although of primary importance, the role on cost of a cell design parameter, the electrode coating thickness, has rarely been described. This study intends to explore particularly the influence of this parameter. To do so, the cost of cells with four positive electrode materials (NMC, NCA, LFP, and LMO), and the same negative electrode material are compared at several electrode thickness. The cost of these cells is computed using an innovative model and varies between 230 and 400 $ per kWh. With the assumptions used, it appears that the potential savings resulting from doubling the electrode coating thickness from 50 to 100 μm at a given porosity represent roughly 25% of the cell cost. The electrode coating thickness emerges as an essential parameter for an unbiased cells cost comparison. This article gives a view of the current lithium-ion cells costs, and provides guidelines to lower cells cost.

Introduction

Lithium-ion batteries are newcomers on the automotive market, with a high growth potential. More and more vehicles contain this type of battery, from small hybrids to all-electric cars. The price of these vehicles is higher than that of an internal combustion engine car, largely due to the high battery cost [1-4]. Currently, government incentives all around the world are driving car electrification development, but electric vehicle cost reduction will be essential for long-term market sustainability. Therefore, battery costs must be lowered.

A lithium-ion battery is a complex system with various components [5]. The central part is the cell, where the energy storage through electrochemical reactions takes place. The characteristics of a battery are directly linked to the number of cells inside the pack and to the cells properties. This study is done at the cell level, in order to focus only on material and cell design choices, and thus avoiding the interference of side effects at the battery level.

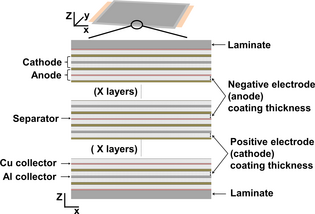
Figure 1 gives a schematic on the inside of a prismatic cell, which is basically a stack of positive electrode, separator, and negative electrode layers, soaked with an electrolyte and enclosed in a container. Both electrodes are based on a lithium intercalation compounds, and lithium ions move from the negative electrode to the positive one during discharge, and inversely during charging (by convention, the term «cathode» refer to the positive electrode and « anode » refer to the negative electrode). The separator and the electrolyte are used for the electronic isolation and ionic conduction between the two electrodes.

Figure 1. Definition of the electrode coating thickness: inside view of a prismatic cell.

Within this study, one key parameter of the cell design is studied: the electrode thickness. In order to avoid any misunderstanding, we choose to use the term “electrode coating thickness.” It is so clear that only the layer containing active material, without the current collector is considered, as illustrated in Figure 1.

The literature on lithium-ion battery cost reduction is mainly focused on new materials with better properties, while fewer studies are devoted to the subject of battery engineering for cost reduction. Yet, significant cost reduction can be achieved by optimizing current battery design. Today, many materials and cell designs are possible for lithium-ion batteries, all with direct impacts on battery behavior [6-8]. Thus, determining the best battery configuration is a complex matter requiring a rigorous method of comparison, encompassing technical and economic aspects.

In the literature, several works have focused on the lithium-ion battery cost. One of the most complete works on the topic is the freely available Battery Performance and Cost (BatPac) model of the Argonne National Laboratory [9, 10], which contains both a cell design model and a cell cost analysis model. It allows the user to calculate the cost of a wide range of battery configurations. Circa 10 years before the publication of this tool, the Argonne national laboratory had already published a comprehensive report from Gaines and Cuenca [11], on the lithium-ion batteries cost analysis.

Another useful work available for battery cost optimization is the TIAX work, presented each year since 2009 at the United States Department of Energy (DOE) merit review [12]. This document gives precious indications on electrode design, especially surface capacity, and material choices for a cost-effective battery. A study by Brodd and Helou focused on another cost aspect: the effect of plant location on cost [13]. Other studies propose methods to evaluate battery cost: with a bottom-up cost model [3, 14, 15], experience curve [16], review and extrapolation of existing models [17-22], or empiric formulae [23, 24].

Battery cost has thus been the subject of many studies, several of which take the influence of materials into account. By contrast, the effect of the cell design on cost, especially of the electrode coating thickness, has been much less studied. Rempel et al. [12], Xue et al. [25], and Nelson et al. [10] have suggested that electrode coating thickness plays a major role on cost. While numerous articles are dealing with the technical effects of thick or thin electrodes [26-36], none are dedicated to the study of the effects on cost.

Within this document, a hypothesis will be introduced: the electrode coating thickness should be used as a pivotal parameter during a cell cost analysis. To demonstrate this hypothesis we will first present our method for cell cost modeling. Then, we will observe the results, and explain the various phenomena acting. Finally, we will analyze the possible bias or limitations of this study. Thus, we are able to conclude on the accuracy of our hypothesis.

Method

During the initial phase of our study, we designed 90 Wh cells using a cell design software. Cells from this size are currently used in battery electric vehicles (BEV) or in plug-in hybrid electric vehicles (PHEV), as for example in the Volkswagen e-golf [37] or the Ford C-Max Plug-in Hybrid [38]. These cells were designed with four cathode materials and six different electrode coating thicknesses. Then, we calculated the cost of these cells for a volume of 10 million cells per year using our own cost model.

Battery design

The cells were designed using the cell design model from the Argonne National Laboratory (BatPac) [9, 10]. Despite some slight limitations, the model provides results with a level of accuracy sufficient for our study [10, 39]. The cells designed are stacked cells in a pouch container (see Fig. 1), a widespread cell design in the battery industry [40], used by several car makers on their EVs and PHEVs, as Ford [41], General Motors [41], Nissan [42], or Renault.

All cells designed for this project had the same total energy of 90 Wh. Cell voltage and capacity depend on the cell materials. The four cathode materials used were as follows: LiFePO₄ referred to as LFP, Li(Ni_0.33Co_0.33Mn_0.33)O₂ referred to as NMC, LiNi_0.8Co_0.15Al_0.05O₂ referred to as NCA, and LiMn₂O₄ referred to as LMO, while the anode material was always graphite (Gr).

For this study, ceramic coated separator has been considered. Compared to classic polyolefin separators used in the cell design model, ceramic coated ones enhance the thermal stability of cells, and improve the cell behavior during safety tests, which is of primary importance for automotive applications [43]. Furthermore, this type of separator facilitates the manufacturing of cell, by improving the global cell wettability [44-46]. This explains why, according to our vision of the market, these separators are widespread for automotive applications. The thickness, porosity, and density of the considered separator are, respectively, 24 μm, 41%, and 1 g cm⁻³.

For cathode materials other than LFP (NMC, LMO, and NCA), the electrode porosity was taken at 32%, as it is in the cell design model (BatPac [9]). For LFP cathode, the design model porosity of 50% was reduced to 40%, which appears to be an accurate value for this material [29, 31, 47]. Since porosity is a sensitive parameter for cell density and cost, this avoids an unfair comparison of the materials within this study.

The effect of electrode coating thickness as defined in Figure 1 was studied. Generally, the positive and negative electrodes of a cell have not the same coating thickness. Depending on the material volumetric capacity (mAh cm⁻³) and of the balancing, the thickest electrode can be the positive or the negative one. The balancing is defined as the anode to cathode ratio of surface capacity (mAh cm⁻²). This ratio depends on the materials, but is always higher than 1, to avoid lithium plating and enhance cell durability.

We chose to use the electrode coating thickness of the thickest electrodes as a parameter. Our assumption was indeed that the electrode coating limitation concerned the two electrodes, and should be applied to both. To illustrate this hypothesis, Table 1 shows the thickness of both electrodes for each material for a maximum electrode thickness of 50 μm. The electrode with the maximum coating thickness is the positive one in the LMO and LFP cell, while the negative one is the thicker electrode in the NMC and NCA cells.

Table 1. Thickness of the positive and negative electrodes for each material for a maximum coating thickness of 50 μm

	Positive electrode coating thickness (μm)	Negative electrode coating thickness (μm)
NMC // Gr	49.0	50.0
NCA // Gr	45.0	50.0
LMO // Gr	50.0	30.4
LFP // Gr	50.0	34.2

Since the designed batteries are for EVs or PHEVs, we take the 50 μm coating thickness as the lower limit. Thinner electrodes will not be economically viable for such automotive applications. A coating thickness of 100 μm is taken as the upper coating limit because, according to the literature, it appears to be the current maximum realistic thickness in automotive applications, for durability, process ability, mechanical integrity, and rate capability reasons [10, 30, 32, 33, 47].

The cell footprint (i.e., width and length of the electrodes within the cell) is a fixed parameter (100 × 200 mm) in this study. Cell thickness is not fixed, and thus slightly changes between each cell. The cell thickness variation range is between 14.1 and 8.7 mm for all cells designed within this study.

Material cost

The material cost data used were provided by material suppliers during the second half of 2011 in the context of the European project “Helios” [48]. “Requests for information” were sent to certain major suppliers, asking them to give an estimation of their prices for a material with four different quantity scenarios. The Helios data were summarized in prices fitting the quantities required for this study: 10 million of 90 Wh cells per year. The related active material quantities are given in Table 2.

Table 2. Prices of active materials obtained in the European project Helios [48]

	Price ($ kg−1)	Price relatively to NCA (%)	Corresponding volume (kT y−1)
NMC	27	82	1.8
NCA	33	100	1.8
LMO	14	42	2.6
LFP	21	64	2.1
Graphite	18.5	56	1.1

These values should not be considered absolute or definitive. Firstly, under the generic material names, their characteristics (such as metal content, particle size and shape, morphology, distribution, and crystallite size) may vary between suppliers, thus the properties can be slightly different [35, 49]. Secondly, material prices are dependent on raw material prices. The given prices are based on the main metal prices of 22 $ kg⁻¹ for Nickel and 38 $ kg⁻¹ for Cobalt (September 2011). Finally, since these prices were obtained during a project without commercial applications, they are possibly above the prices that could be achieved through actual negotiation.

Our values are of the same magnitude as data found in the literature [10, 12]. However, since the metal prices and volumes are not the same, we cannot make a direct price comparison. But it appears that, in relation to the other materials (price relatively to NCA on Table 2), the NMC price obtained during the Helios project is slightly lower compared with these studies.

The costs for the materials common to all cells and electrodes are displayed in Table 3. The costs of the binder, binder solvent (NMP for positive electrode and water for negative electrode), and aluminum foil were taken from BatPac [10], while the remaining costs were provided by the Helios project [48].

Table 3. Prices of cell materials and components

Carbon black conductor	7.15 $ kg−1
NMP binder	27.6 $ kg−1
Electrolyte	19.5 $ kg−1
Aqueous binder	10 $ kg−1
Binder solvent	3.2 $ kg−1
Current collector, Al	0.8 $ m−2
Current collector, Cu	1.7 $ m−2

For the separator, specific to our cells, the quantity required per year has an influence on the cost. For an electrode coating thickness twice as high, the same energy per cell is achieved with half the quantity of separators. Thus, a price evolution of this component with the quantity required per year is taken into account. The separator price is 2.5 $ m⁻² if more than 15.10⁶ m² are needed per year, else the price is 2.7 $ m⁻².

Total cost calculation

For this study, an innovative cell cost model has been developed, based on our knowledge of the current lithium-ion cells manufacturing. This model has been validated internally with tests on several offers from lithium-ion batteries suppliers. The reasons for the choice of this model instead of models from the literature are presented in 'Model accuracy and contribution'. Our model is described below. The total cell cost is divided into three parts: purchase cost, process cost, and overheads and other fees.

Purchase cost

The purchase cost is computed using the mass of materials and components of the cell, and their cost per kilogram. The total material cost is also calculated as follows:

${\mbox{Purchase cost}}=\sum ({\mbox{Sr}}_{i}\times m_{i}\times C_{i})$

where Sr _i is the scrap rate, m_i is the weight of component or material i (kg), and C_i is the cost of component or material i ($ kg⁻¹). A single scrap rate (1.09) is used for the cell materials and components affected by a fabrication loss. This is a rather high value in comparison with other industries, linked to the immaturity of the industry.

Process cost

The process cost includes direct labor, equipment depreciation, operating and maintenance costs, indirect factory costs, and infrastructure costs. Our model is based on a standard hypothesis: the factory of the supplier manufactures cells for several customers. The cost of one cell is calculated in function of the supplier lines occupation for this cell. This occupation time is estimated from a reference cell, using adequate ratios. Ratio parameter used depends on the manufacturing step, and we found that four parameters have an influence on the manufacturing cost. The process cost is divided into three parts with different ratio parameters: electrode manufacturing, cell stacking, and cell filling and formation, with:

${\mbox{Electrode manufacturing cost}}={\mbox{Pro}}_{electrodes}\times {\left(T/T_{ref}\right)}^{0.2}\times S$

where Pro_electrodes is the electrode manufacturing related portion ($ m⁻²), S is the surface of electrode per cell, T is the electrode coating thickness, and T_ref is the electrode coating reference thickness (70 μm). The ratio parameters for the estimation of electrode manufacturing cost are also the surface of electrode per cell (S), and the electrode coating thickness (T). Pro_electrodes corresponds to the electrode manufacturing cost of the reference, divided by the surface of electrode for the reference cell.

The modeling of this cost considers the electrode coating thickness as a cost inductor, through the correction factor (T/T_ref)^0.2: the thicker the electrode, the harder the coating and the drying step, the more expensive the process. The correction factor choice is an empiric hypothesis based on our observations of the relation between electrode manufacturing speed and electrode coating thickness.

${\mbox{Cell stacking cost}}={\mbox{Pro}}_{cell\quad assy}\times N$

where Pro_{cell assy} is the cell assembly related portion ($ per bicells, with bicells definition of Nelson et al. [10]) and N the number of bicells per cell. The ratio parameter for the estimation of cell stacking cost is also the number of bicells per cell (N). Pro_{cell assy} corresponds to the cell stacking cost of the reference cell, divided by the number of bicells for the reference cell.

${\mbox{Cell filling and formation cost}}={\mbox{Pro}}_{fixed}$

Pro_fixed is the filling and formation related portion ($ per cell). This part of the manufacturing process is considered as the same for each cell. The ratio parameter for the cell filling and formation cost is also the cell.

The process coefficients, Pro_electrodes, Pro_{cell assy}, and Pro_fixed, have been determined based on our own knowledge and on discussions with several manufacturer, as follows: Pro_electrodes = 1.93 $ m⁻², Pro_{cell assy} = 0.05 $ per bicell, and Pro_fixed = 1.79 $ per cell. They do not depend on the number of cells manufactured per year: this reflect the fact that the modeled factory manufactures cells for several customers.

Overheads and other fees

The third part of our model encompasses overheads and other fees: the purchasing and sales departments, administration, R&D, licenses and royalties, financial charges, margin, and warranty. It is indexed on the process cost (66% of this cost, representative value according to our survey), plus a warranty and insurance part (5.6% of the overall cost). The overheads and other fees cost was also calculated as follows:

${\mbox{Overheads and other fees}}=66\%\times ({\mbox{Process cost}})+$$5.6\%\times ({\mbox{Purchase cost}}+{\mbox{Process cost}}+$$66\%\times ({\mbox{Process cost}}))$

The accuracy of our model has been tested and validated on several suppliers’ offers. The coefficients used here are representative of the manufacturing cost on a high volume factory (capacity of 1–10 GWh per year). Naturally, it is not an absolute cost, since each suppliers has it is own manufacturing cost, depending on his competitiveness.

Results

Within this section, the results of our simulations are presented and analyzed. At first, the impact of the cathode material on cost is quantified. Then, the electrode coating thickness effect on cost is shown, as well as his effect on cell properties. Finally, a comparison with another design parameter is done.

Impact of positive electrode material on cost

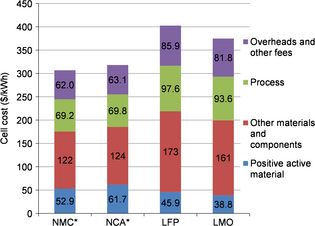
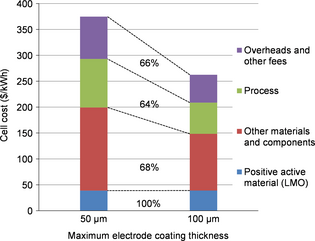
According to our results shown in Figure 2, the cheapest cell for an electrode coating thickness of 50 μm is the one using NMC. This result was expected, since NMC is one of the most widely used materials in automotive lithium-ion batteries [15, 40]. The NCA cell is slightly more expensive (+3.7%). The LMO and LFP cells are the most expensive: the NMC cell is 18.2% cheaper than the LMO cell and 23.8% cheaper than the LFP cell.

Figure 2. Cell cost breakdown for each material for a maximum thickness of coating of 50 μm (*the negative electrode is the limiting electrode).

According to Figure 2, the LFP and LMO material costs per cell are lower than the NMC cost. However, the entire NMC cell is cheaper, since other material portions as well as the process, overheads, and other fees are cheaper. This is due to better properties, giving the NMC more energy per kilogram and per cubic centimeter compared with LMO or LFP. Thus, two effects are combined.

Firstly, a material with more energy per kilogram than another one requires a lower quantity of material to obtain the same energy. Thus, if the material is more expensive per kilogram, the extra cost would be lower or even reversed on the material cost per kilowatt hour. This explains, for example, why the LMO material cost per cell is only 27% less than NMC, while the material cost per kilogram of LMO is 48% less.

Secondly, a material with more energy per cubic centimeter needs less volume to produce the same energy. Thus, for a fixed electrode coating thickness and porosity, less current collector surface area requires coating. The extra active material cost is saved via the reduction of nonactive parts (current collector and separator), the reduction of process time, and overheads and other fees linked to less material handling. The combination of these two effects results in a NMC cell that is cheaper than the LMO cell.

The cell costs indicated in Figure 2 correspond to the cost per kilowatt hour (total energy) of 307 $ kWh⁻¹ for the NMC cell, 318 $ kWh⁻¹ for the NCA cell, 375 $ kWh⁻¹ for the LMO cell, and 402 $ kWh⁻¹ for the LFP cell. For optimized battery durability, BatPac recommends to limit the useable energy at 85% of the total energy for EV applications, that is, 76.5 Wh [10]. Thus, if this useable energy is considered, the cell cost values are as follows: 361 $ kWh⁻¹ for the NMC cell, 374 $ kWh⁻¹ for the NCA cell, 473 $ kWh⁻¹ for the LMO cell, and 441 $ kWh⁻¹ for the LFP cell.

These cell costs are slightly above some recent estimations available in the literature [50, 51]. This is mainly due to the electrode coating thickness limited to 50 μm. Furthermore, since the goal of this study was to understand the effect of electrode coating thickness on cost rather than estimate precisely the current cost for cells suppliers, we did not try to obtain market challenging output values.

Impact of electrode coating thickness on cost

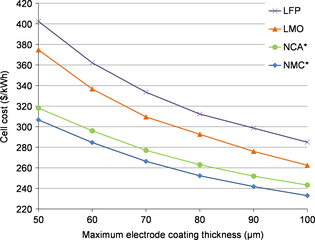
The cost per kilowatt hour of a cell according to the electrode coating thickness is shown on Figure 3. The cost reduction between the ranges of 50 and 100 μm is: 24% for NMC, 24% for NCA, 29% for LFP, and 30% for LMO. This indicates that the cell cost can be reduced by 25% if the coating thickness is doubled, with the hypothesis used in our model. For an increase in thickness of 10 μm (from 50 to 60 μm), the NMC cell cost is 7% lower (285 $ kWh⁻¹ instead of 307). And for 20 μm thicker electrodes (70 μm), the cost is 13% lower (266 $ kW⁻¹).

Figure 3. Cell cost comparison for four positive electrode materials and a variable maximum coating thickness (*the negative electrode is the limiting electrode).

The major role on cell cost of the electrode coating thickness for a cell cost analysis appears also clearly on Figure 3. Costs of the cells clearly depend on this parameter. This figure also suggests that electrode coating thickness seems to influence the cost comparison of several positive electrode materials. This is why we propose to fix the electrode coating thickness at a given porosity for such a comparison.

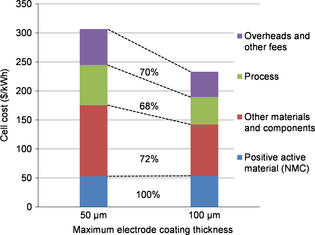
Figure 4 shows the cost breakdown for the same cell (NMC), with two different electrode coating thicknesses. The material and components portion is affected, thanks to the reduction of nonactive components. The process cost is also reduced, thanks to the electrode surface and number of layers per cell reduction. Overheads and other fees are also decreased due to the reduction of purchases to be handled, and the process cost improvement. Savings on process are proportionally slightly more significant (32%) than savings on purchasing (28% without cathode active material).

Figure 4. Cost breakdown of an NMC cell cost for two coating thicknesses (50 and 100 μm).

Figure 5 shows the cost breakdown with two different electrode coating thicknesses, but this time with LMO as positive electrode. Savings on process (36%) and purchasing (32% without cathode active material) for the LMO cells are more significant than savings for the NMC cells. For the NCA cells, the cost evolution is close to the NMC cells (Fig. 4), and thus as not been represented. The LFP cells cost evolution is close to the LMO cells (Fig. 5).

Figure 5. Cost breakdown of an LMO cell cost for two coating thicknesses (50 and 100 μm).

The potential savings due to an electrode coating thickness reduction have been quantified and clearly indicate a substantial improvement. Figure 3 shows also the key role of this parameter to compare several cells cost. This is why we have formulated the following hypothesis: this parameter has to be fixed for an unbiased comparison of several cathode materials. To investigate the accuracy of this suggestion, the technical and economic role of this parameter will be further investigated thereafter.

Effect of electrode coating thickness on cell properties

The major parameters impacted by the electrodes thickness, according to our research on the topic are presented below.

Cell power

The required power has an influence on the cell design, especially for a PHEV battery, due to the low energy of the battery [52]. Accordingly, power will be a key parameter in determining the electrode coating thickness. On the contrary, if the power requirement is less stringent, such as in a purely EV applications, the power requirement has less influence on battery design and cost.

Manufacturing ability

The manufacturing ability of an electrode is another parameter influenced by the electrode thickness: it is easier to handle thin electrodes. We found little information in the literature on this topic, although it is a key parameter form an industrial point of view [49]. Nevertheless, our model encompasses this effect in the study range of thickness (50–100 μm), through the factor (T/T_ref)^0.2 (see 'Process cost').

Durability

Battery durability depends on several phenomena among which the electrode thickness: the thicker the coating, the worse the aging capability. This link between electrode coating thickness and capacity fade has been occasionally described in the literature, and is hardly quantifiable. [32, 53-55]. Although this parameter is worth mentioning, the quantification of his effect is beyond the scope of this study. The topic is broad and complex, and must be further investigated, as suggested by Zheng et al. [32].

Mass and volume

Cell volume and mass have an impact on the total battery cost: the smaller and lighter the cell, the simpler and cheaper the modules and pack. Furthermore, carmakers are willing to pay more for a lightweight battery, since it improves energy consumption. They are also willing to pay more for a lower battery volume, for integration reasons, especially for a PHEV.

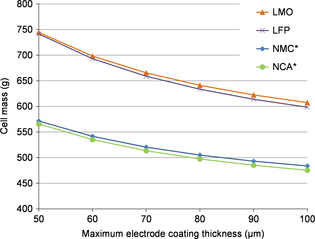
Figure 6 shows that NMC and NCA allow more lightweight cells. In addition to reducing cost, increasing the coating thickness also reduces the cell mass, as it has already been largely suggested on the literature [36, 56-58]. This is due to the reduction of the nonactive parts of the cell. Cell mass as cell volume reductions of circa 15% are achieved between the electrode coating thicknesses of 50 and 100 μm.

Figure 6. Cell mass according to coating thickness and positive electrode material (*the negative electrode is the limiting electrode).

Other parameter effects

In this study, only the electrode coating thickness is studied. The effects of an electrode composition modification or of an electrode porosity change are interesting ways to improve cells’ design. These parameters offer opportunities to reduce cells cost, with different impacts on cell behavior than electrode coating thickness. Except for the LFP cathode porosity, these parameters have been kept as they were in the cell design model. More challenging values are probably currently used by lithium-ion cells suppliers [28, 29, 33, 56, 58-61].

Impact of electrode surface capacity on cost

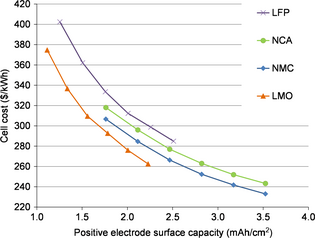
Within this study, we are suggesting to compare the influence on cost of several cathode materials at the same electrode coating thickness (at a given porosity). The cost classification obtained so (Fig. 3: NMC cost < NCA cost < LMO cost < LFP cost) seems to be in contradiction with some results in the literature [12, 15]. Yet, if the coating thickness parameter is replaced by the electrode surface capacity as in Figure 7, the material cost classification is largely modified.

Figure 7. Comparison of cell cost for four positive electrode materials according to the positive electrode surface capacity (points correspond to coating thickness between 50 and 100 μm, with an increment of 10 μm).

Both parameters are bound: the surface capacity correspond to the electrode coating thickness multiply by the electrode volume capacity. Since the porosity is the same (32%) for all of the materials in this study except LFP (40%), for a given electrode coating thickness, the surface capacity will be higher for materials with a better volume density. The electrode volumetric capacities (electrode composition and porosity included) are as follows: NMC = 359 mAh cm⁻³, NCA = 392 mAh cm⁻³, LFP = 251 mAh cm⁻³, and LMO = 223 mAh cm⁻³. With the same coating thickness and porosity, NCA has also a far better capacity than LMO.

For a coating thickness of 50 μm, the electrode surface capacity of NMC and NCA is 1.76 mAh cm⁻², as it is 1.11 mAh cm⁻² for LMO and 1.26 mAh cm⁻² for LFP. This explains why the chemistry cost ranking is different for the electrode surface capacity parameter versus the electrode coating thickness (Fig. 3 vs. Fig. 7).

This remark raises an issue: which design parameter is the most suitable for the cost classification of the materials? As there are a lot of scenarios, it is not possible to answer to this question generally. But for high-energy applications, where low currents are used, the overpotential and thus losses within the cell are not crucial. Our point of view, based on discussions with several cell suppliers, is that the main reason for the limitation of the electrode coating thickness is the manufacturing process (quality of the coating, homogenous particles distribution, mechanical strength of the electrode, processing speed). This is why we have used this parameter for the comparison of cost of cells for energy applications.

Discussion

Model accuracy and contribution

Although there are already several battery cost models available in the literature [3, 13, 14, 16, 19, 20, 22, 24], a new one has been developed for this study. In our view, the cost tool developed by the Argonne National Laboratory (Batpac) [9, 10] is the state-of-the-art battery cost model, but some hypothesis are unsatisfactory.

Firstly, the modeled factory is dedicated to one customer, which is not a usual hypothesis for cost analysis of automotive parts. Secondly, the number of layers per cell is not a cost inductor for the process cost. Finally, process slowing down related to thicker electrodes is not taken into account. For all of these reasons, we used our own model, which fits better to the aim of this work: the study of the electrode coating thickness.

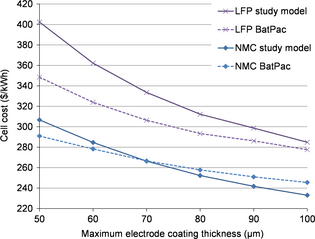
To better understand the impact of this choice, we compared the results of the two models (Fig. 8). We substituted the material prices of the BatPac cost model with our data (see Table 2). Thus, the differences between the two models are only due to the process and the overheads and other fees costs.

Figure 8. Comparison of the results from our internal model with the results from the BatPac cost model [9].

The results are shown in Figure 8 for NMC and LFP. The cost reduction is more pronounced with our model. This means that the cost is more impacted by the electrode coating thickness, because the number of layers and the electrode coating thickness are cost inductors in our model. The electrode coating thickness effect on cost is also sharpened up with our model.

The cost difference between LFP and NMC cells is bigger with our model as with the BatPac model. This is mainly related to the fact that, contrary to BatPac, our model is influenced by the number of layers inside the cells. Since LFP cells have a high number of layers (e.g., 54 bicells at 50 μm instead of 35 bicells for NMC), the modeled cost of cell stacking is higher.

Sensitivity to active material prices

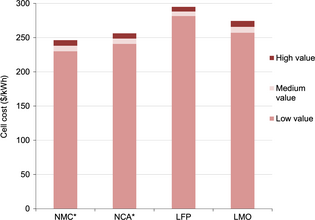
The uncertainty linked with estimating the cost of lithium-ion cells depends on several factors. An evaluation of the spread in the calculated cell price if the inputs are in error allows a critical view of the results. Different methods for this topic can be found in the literature, including statistical analysis [9, 10] or Monte Carlo analysis [12, 62].

Since only active material price varies between each cell, a sensitivity study on this parameter has been made. For each material, a minimum and a maximum value have been estimated, based on our expertise and on the literature values (Table 4). For NMC and NCA, cobalt and nickel prices represent a high risk for prices, thus the range of values is wider than for LMO and LFP.

Table 4. Range of material costs according to our estimation

	Low value ($ kg−1)	Baseline ($ kg−1)	High value ($ kg−1)
NMC	23	27	31
NCA	29	33	37
LMO	11	14	17
LFP	18	21	24

Figure 9 depicts the maximum and minimum cell cost using the low, baseline, and high values of Table 4, for a coating thickness of 100 μm. Cell cost varies between 6.6% for NMC, 6% for NCA, 4.6% for LFP, and 6.3% for LMO. The NMC and NCA cells remain the cheapest ones and the LFP cell the most expensive.

Figure 9. Sensitivity to material cost for a maximum coating thickness of 100 μm (*the negative electrode is the limiting electrode).

If the active materials prices are lower, then the material share is reduced. Therefore, the percentage in cost reduction due to thicker electrodes will be higher. Thus, with the lower cost hypothesis for NMC (23 $ kg⁻¹), the gain between the electrode thickness of 50 and 100 μm is almost the same in absolute value (74 $ kWh⁻¹), but the relative value is 25% instead of 24% previously. Since materials cost will probably decrease in the future (scale effects, production improvements), the gain obtain with thicker electrodes will be more noticeable.

Other cost drivers

Certain elements were not studied here, but they may nevertheless impact battery cost. We would like to highlight them to avoid any false conclusions.

For certain materials with better thermal stability properties such as LFP, a certain degree of cost reduction may be envisaged, while maintaining the same level of safety for the system [63]. It is possible to increase the cells useable state of charge and thus directly save some dollars per kilowatt hour. It may also be possible to avoid the use of a coated separator. According to our model, the savings on LFP cell cost is 27 and 15 $ kWh⁻¹ for the cells with an electrode coating thickness of 50 and 100 μm. And finally, it may be possible to avoid the use of a cooling system at the battery system level.

The same organic binder solvent was used for all of the positive electrode materials. However, certain active materials, especially LFP, could possibly be handled with water-based electrode formulations, also allowing a cost reduction [64]. According to the BatPac model, the savings would be circa 4 $ kWh⁻¹ on the LFP cell cost.

Furthermore, carmakers are responsible for battery recycling. The recycling cost will depend on several parameters. Batteries with high contents of expensive metals such as NMC and NCA batteries will be cheaper to recycle thanks to the metal resale value. The cost difference between NMC and LFP battery recycling has been studied notably by Kwade et al. [65]. According to the data of this study, the recycling cost difference magnitude between an NMC battery and an LFP battery is of 2 $ kWh⁻¹. This value is highly dependent on metal values.

A high potential strategy, applied by some suppliers, is to use composite cathodes with a blend of two types of materials. Such strategies allow a better fitting of the chemistry to a project needs [41].

Conclusions

The purpose of this study was to highlight the technical and economic issues arising in lithium-ion cells for automotive applications, and to indicate some potential solutions to lower the cost. The electrode coating thickness appears as a key parameter on cell cost analysis. Its major role on cost analysis has rarely been underlined even less quantified in the literature.

Within this article, we have suggested the essential function of this parameter for the cost analysis. Our results have shown that, with the assumptions used, doubling the electrode coating thickness from 50 to 100 μm at a given porosity could save roughly 25% of the cell cost. An increase of the electrode coating thickness is also a promising way to reduce the lithium-ion cells cost.

Four positive electrode materials were compared in this study. The total energy cost of these four cells for an electrode coating thickness of 100 μm was 233 $ kWh⁻¹ for the NMC cell, 243 $ kWh⁻¹ for the NCA cell, 263 $ kWh⁻¹ for the LMO cell, and 285 $ kWh⁻¹ for the LFP cell. Despite their cheaper positive active material (price per kilogram), LFP and LMO cells are more expensive (energy cost) than the other cells for a given electrode coating thickness.

Since high electrode coating thicknesses are attractive to reduce cell cost and mass, but detrimental to the power, aging, and process ability of the cell, we have highlighted that cell cost is the result of a design trade-off. The electrode coating thickness at a given porosity appears as a pivotal parameter for the comparisons of the cost of energy cells with several active materials. Further research on electrode coating thickness will be necessary to better understand the electrochemical limitations on these topics, and after all, improve the behavior of cells with thick electrodes.

In our next step, other materials not currently marketed, such as lithium manganese phosphate, lithium rich, or high-voltage spinel will be included in the future work.

Acknowledgments

This study was prepared for a work partially sponsored by Renault. The views and opinions of the authors expressed herein do not state or reflect those of Renault, and the economic data and the model presented are not related to Renault or to Renault suppliers. The authors gratefully acknowledge the assistance of Pierre Tran-Van and Anna Teyssot in the preparation of this manuscript. The authors also thank the HELIOS project [48] leaders for the kind authorization to use their data.

Conflict of Interest

None declared.

References

1. Börjesson, M., and E. O. Ahlgren. 2012. Assessment of transport fuel taxation strategies through integration of road transport in an energy system model – the case of Sweden. Int. J. Energy Res.36:648–669. doi: 10.1002/er.1824
2. Offer, G. J., D. Howey, M. Contestabile, R. Clague, and N. P. Brandon. 2010. Comparative analysis of battery electric, hydrogen fuel cell and hybrid vehicles in a future sustainable road transport system. Energy Policy38:24–29. doi: 10.1016/j.enpol.2009.08.040
3. Kalhammer, F. R., B. M. Kopf, D. H. Swan, V. P. Roan, and M. P. Walsh. Status and prospects for Zero Emissions Vehicle Technology report of the ARB independent expert panel 2007. 13 April. Available at: http://www.arb.ca.gov/msprog/zevprog/zevreview/zev_panel_report.pdf (accessed 09 July 2013).
4. Delucchi, M. A., and T. E. Lipman. 2010. Pp. 19–60inChapter two – lifetime cost of battery, fuel-cell, and plug-in hybrid electric vehicles. Elsevier, Amsterdam, Electric and Hybrid Vehicles. doi: 10.1016/B978-0-444-53565-8.00002-6
5. Büchler, A. B.2012. Benchmarking Chevrolet Volt/Opel Ampera. Polymotive: Polymers and e-Mobility in the Automotive Industry. ISSN: 1610–7799.
6. Scrosati, B., and J. Garche. 2010. Lithium batteries: status, prospects and future. J. Power Sources195:2419–2430. doi: 10.1016/j.jpowsour.2009.11.048
7. Fergus, J. W.2010. Recent developments in cathode materials for lithium ion batteries. J. Power Sources195:939–954. doi: 10.1016/j.jpowsour.2009.08.089
8. Tarascon, J. M., and M. Armand. 2001. Issues and challenges facing rechargeable lithium batteries. Nature414:359–367. doi: 10.1038/35104644
9. Nelson, P. A., K. G. Gallagher, and I. Bloom. 2013. BatPac (Battery Performance and Cost Model) software version 2.0. Available at: www.cse.anl.gov/batpac (accessed 11 February 2014).
10. Nelson, P. A., K. G. Gallagher, I. Bloom, and D. W. Dees. 2011. Modeling the performance and cost of lithium-ion batteries for electric-drive vehicles. Available at: http://www.cse.anl.gov/batpac/about.html (accessed 19 August 2013).
11. Gaines, L., and R. Cuenca. 2000. Costs of lithium-ion batteries for vehicles. Available at: http://www.transportation.anl.gov/pdfs/TA/149.pdf (accessed 25 February 2014).
12. Rempel, J., B. Barnett, and J. Hyung. 2013. PHEV battery cost assessment. Available at: http://www4.eere.energy.gov/vehiclesandfuels/resources/merit-review (accessed 26 February 2014).
13. Brodd, R. J., and C. Helou. 2013. Cost comparison of producing high-performance Li-ion batteries in the U.S. and in China. J. Power Sources231:293–300. doi: 10.1016/j.jpowsour.2012.12.048
14. USABC. 2007. Final cost model. 23 May. Available at: http://www.uscar.org/guest/article_view.php?articles_id=143 (accessed 04 July 2013).
15. Bernhart, W., and F. J. Kruger. Roland Berger, Technology & market drivers for stationary and automotive battery systems. Batteries 2012 conference, Nice, France, October 24–26, 2012.
16. Mayer, T., D. Kreyenberg, J. Wind, and F. Braun. 2012. Feasibility study of 2020 target costs for PEM fuel cells and lithium-ion batteries: a two-factor experience curve approach. Int. J. Hydrogen Energy37:14463–14474. doi: 10.1016/j.ijhydene.2012.07.022
17. Daniel, C.2008. Materials and processing for lithium-ion batteries. JOM60:43–48. doi: 10.1007/s11837-008-0116-x
18. Cheah, L., and J. Heywood. 2010. The cost of vehicle electrification: a literature review. Available at: http://web.mit.edu/sloan-auto-lab/research/beforeh2/files/PHEV%20costs.pdf (accessed 12 February 2014).
19. Chhaya, S.2010. EPRI, large-format lithium-ion battery costs analysis: critical review of existing PHEV lithium ion battery cost studies, CA. 1019923.
20. Mock, P.2011. Entwicklung eines Szenariomodells zur Simulation der zukünftigen Marktanteile und CO2-Emissionen von Kraftfahrzeugen (VECTOR21). Universitätsbibliothek der Universität Stuttgart, Stuttgart.
21. Kang, S., W. Lu, K. G. Gallagher, S. Park, and V. G. Pol. 2011. Study of Li 1x(Mn 4/9Co 1/9Ni 4/9) 1-xO 2 cathode materials for vehicle battery applications. J. Electrochem. Soc.158:A936–A941.
22. Cluzel, C., and C. Douglas. 2012. Cost and performance of EV batteries. March 21. Available at: http://www.element-energy.co.uk/publications/ (accessed 04 July 2013).
23. Brooker, A., M. Thornton, and J. Rugh. Technology improvement pathways to cost-effective vehicle electrification: NREL/CP-540-47454. SAE 2010 World Congress, Detroit, MI, 13–15 April 2010.
24. English, J., and D. Strong. Optimization of batteries for plug-in hybrid electric vehicles. EMC EV 2012, Conference and Tradeshow, 23–26 October 2012; 51–58.
25. Xue, N., W. Du, T. A. Greszler, W. Shyy, and J. R. R. A. Martins. 2014. Design of a lithium-ion battery pack for PHEV using a hybrid optimization method. Appl. Energy115:591–602. doi: 10.1016/j.apenergy.2013.10.044
26. Srinivasan, V., and J. Newman. 2004. Design and optimization of a natural graphite/iron phosphate lithium-ion cell. J. Electrochem. Soc.151:A1530–A1538.
27. Gaberscek, M.2009. Towards optimized preparation of cathode materials: how can modeling and concepts be used in practice. J. Power Sources189:22–27. doi: 10.1016/j.jpowsour.2008.12.041
28. Chen, Y., C. Wang, X. Zhang, and A. M. Sastry. 2010. Porous cathode optimization for lithium cells: ionic and electronic conductivity, capacity, and selection of materials. J. Power Sources195:2851–2862. doi: 10.1016/j.jpowsour.2009.11.044
29. Fongy, C., A. C. Gaillot, S. Jouanneau, D. Guyomard, and B. Lestriez. 2010. Ionic vs electronic power limitations and analysis of the fraction of wired grains in LiFePO4 composite electrodes. J. Electrochem. Soc.157:A885. doi: 10.1149/1.3432559
30. Lu, W., A. Jansen, D. Dees, P. Nelson, N. R. Veselka, and G. Henriksen. 2011. High-energy electrode investigation for plug-in hybrid electric vehicles. J. Power Sources196:1537–1540. doi: 10.1016/j.jpowsour.2010.08.117
31. Thorat, I. V., T. Joshi, K. Zaghib, J. N. Harb, and D. R. Wheeler. 2011. Understanding rate-limiting mechanisms in LiFePO 4 cathodes for Li-ion batteries. J. Electrochem. Soc.158:A1185–A1193.
32. Zheng, H., J. Li, X. Song, G. Liu, and V. S. Battaglia. 2012. A comprehensive understanding of electrode thickness effects on the electrochemical performances of Li-ion battery cathodes. Electrochim. Acta71:258–265. doi: 10.1016/j.electacta.2012.03.161
33. Yu, S., Y. Chung, M. Song, J. Nam, and W. Cho. 2012. Investigation of design parameter effects on high current performance of lithium-ion cells with LiFePO4/graphite electrodes. J. Appl. Electrochem.42:443–453. doi: 10.1007/s10800-012-0418-0
34. Ramadesigan, V., P. W. C. Northrop, S. De, S. Santhanagopalan, R. D. Braatz, and V. R. Subramanian. 2012. Modeling and simulation of lithium-ion batteries from a systems engineering perspective. J. Electrochem. Soc.159:R31–R45.
35. Ridgway, P., H. Zheng, A. F. Bello, X. Song, S. Xun, J. Chong, et al. 2012. Comparison of cycling performance of lithium ion cell anode graphites. J. Electrochem. Soc.159:A520–A524.
36. Chabot, V., S. Farhad, Z. Chen, A. S. Fung, A. Yu, and F. Hamdullahpur. 2013. Effect of electrode physical and chemical properties on lithium-ion battery performance. Int. J. Energy Res.37:1723–1736. doi: 10.1002/er.3114
37. Green Car Congress. 2014. VW provides details on e-Golf prior to launch at LA auto show. Available at: http://www.greencarcongress.com/2013/11/20131114-egolf.html (accessed 15 February 2014).
38. Schamel, A., P. Schmitz, J. d'Annunzio, and R. Iorio. 2013. Ford C-Max Plug-in Hybrid. MTZ Worldwide74:4–10. doi: 10.1007/s38313-013-0023-6
39. Gallagher, K. G., P. A. Nelson, and D. W. Dees. 2011. Simplified calculation of the area specific impedance for battery design. J. Power Sources196:2289–2297. doi: 10.1016/j.jpowsour.2010.10.020
40. Pillot, C.The worldwide battery market 2011–2025, Avicenne energy. Batteries 2012 conference, Nice, France, 24–26 October 2012.
41. Chikkannanavar, S. B., D. M. Bernardi, and L. Liu. 2014. A review of blended cathode materials for use in Li-ion batteries. J. Power Sources248:91–100. doi: 10.1016/j.jpowsour.2013.09.052
42. Frank, R.2009. Li-ion suppliers try to find the right chemistry with car buyers. Electron. Des.57:34–39.
43. Clostre, I.2012. INERIS références: batteries et sécurité. Available at: http://www.ineris.fr/dossiers-thematiques-ineris/1469 (accessed 11 February 2014).
44. Jeong, H., D. Kim, Y. U. Jeong, and S. Lee. 2010. Effect of phase inversion on microporous structure development of Al2O3/poly(vinylidene fluoride-hexafluoropropylene)-based ceramic composite separators for lithium-ion batteries. J. Power Sources195:6116–6121. doi: 10.1016/j.jpowsour.2009.10.085
45. Kim, K. J., J. Kim, M. Park, H. K. Kwon, H. Kim, and Y. Kim. 2012. Enhancement of electrochemical and thermal properties of polyethylene separators coated with polyvinylidene fluoride–hexafluoropropylene co-polymer for Li-ion batteries. J. Power Sources198:298–302. doi: 10.1016/j.jpowsour.2011.09.086
46. Park, J., W. Park, J. H. Kim, D. Ryoo, H. S. Kim, Y. U. Jeong, et al. 2011. Close-packed poly(methyl methacrylate) nanoparticle arrays-coated polyethylene separators for high-power lithium-ion polymer batteries. J. Power Sources196:7035–7038. doi: 10.1016/j.jpowsour.2010.09.102
47. Wang, M., J. Li, X. He, H. Wu, and C. Wan. 2012. The effect of local current density on electrode design for lithium-ion batteries. J. Power Sources207:127–133. doi: 10.1016/j.jpowsour.2011.12.063
48. Del Corso, F., and H. Mettlach. 2013. Helios website. Available at: http://www.helios-eu.org/ (accessed 05 August 2013).
49. Li, J., C. Daniel, and D. Wood. 2011. Materials processing for lithium-ion batteries. J. Power Sources196:2452–2460. doi: 10.1016/j.jpowsour.2010.11.001
50. Pillot, C.The worldwide battery market 2012–2025, Avicenne energy. Batteries 2013 conference, Nice, France, 14–16 October 2013.
51. Roland Berger. 2012. Lithium-ion batteries – the bubble bursts. Available at: http://www.rolandberger.com/media/pdf/Roland_Berger_Li_Ion_Batteries_Bubble_Bursts_20121019.pdf (accessed 17 July 2013).
52. Pesaran, A.2011. Choices and requirements of batteries for EVs, HEVs, PHEVs. Available at: http://www.nrel.gov/vehiclesandfuels/energystorage/pdfs/51474.pdf (accessed 24 February 2014).
53. Badey, Q.2012. Étude des mécanismes et modélisation du vieillissement des batteries lithium-ion dans le cadre d'un usage automobile. Université Paris Sud, Paris.
54. Barré, A., B. Deguilhem, S. Grolleau, M. Gérard, F. Suard, and D. Riu. 2013. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources241:680–689. doi: 10.1016/j.jpowsour.2013.05.040
55. Vetter, J., P. Novák, M. R. Wagner, C. Veit, K. Möller, J. O. Besenhard, et al. 2005. Ageing mechanisms in lithium-ion batteries. J. Power Sources147:269–281. doi: 10.1016/j.jpowsour.2005.01.006
56. De, S., P. W. C. Northrop, V. Ramadesigan, and V. R. Subramanian. 2013. Model-based simultaneous optimization of multiple design parameters for lithium-ion batteries for maximization of energy density. J. Power Sources227:161–170. doi: 10.1016/j.jpowsour.2012.11.035
57. Dillon, S. J., and K. Sun. 2012. Microstructural design considerations for Li-ion battery systems. Curr. Opin. Solid State Mater. Sci.16:153–162. doi: 10.1016/j.cossms.2012.03.002
58. Tran, H. Y., G. Greco, C. Täubert, M. Wohlfahrt-Mehrens, W. Haselrieder, and A. Kwade. 2012. Influence of electrode preparation on the electrochemical performance of LiNi0.8Co0.15Al0.05O2 composite electrodes for lithium-ion batteries. J. Power Sources210:276–285. doi: 10.1016/j.jpowsour.2012.03.017
59. Shim, J., and K. A. Striebel. 2003. Effect of electrode density on cycle performance and irreversible capacity loss for natural graphite anode in lithium-ion batteries. J. Power Sources119–121:934–937. doi: 10.1016/S0378-7753(03)00235-0
60. Hong, J. K., J. H. Lee, and S. M. Oh. 2002. Effect of carbon additive on electrochemical performance of LiCoO2 composite cathodes. J. Power Sources111:90–96. doi: 10.1016/S0378-7753(02)00264-1
61. Chen, J., J. Liu, Y. Qi, T. Sun, and X. Li. 2013. Unveiling the roles of binder in the mechanical integrity of electrodes for lithium-ion batteries. J. Electrochem. Soc.160:A1502–A1509.
62. Battke, B., T. S. Schmidt, D. Grosspietsch, and V. H. Hoffmann. 2013. A review and probabilistic model of lifecycle costs of stationary batteries in multiple applications. Renew. Sustain. Energy Rev.25:240–250. doi: 10.1016/j.rser.2013.04.023
63. Lamm, A., and P. Wattré. 2013. Battery choices for PHEV applications. Available at: http://www.cars21.com/news/view/5481 (accessed 02 July 2013).
64. Lee, J., J. Kim, Y. C. Kim, D. S. Zang, and U. Paik. 2008. Dispersion properties of aqueous-based LiFePO4 pastes and their electrochemical performance for lithium batteries. Ultramicroscopy108:1256–1259. doi: 10.1016/j.ultramic.2008.04.027
65. Kwade, A., G. Bärwaldt, T. Meinfelder, M. Steinbild, K. Kramer, R. Barenschee, et al. 2012. Recycling von lithium-ionen-batterien. Available at: http://www.erneuerbar-mobil.de/projekte/foerderprojekte-aus-dem-konjunkturpaket-ii-2009-2011/batterierecycling/abschlussberichte-recycling/abschlussbericht-lithorec.pdf (accessed 17 July 2012).