Summary
Mesh simplification is an important problem in computer graphics. Given a polygonal mesh, the goal is to generate another mesh which approximates the underlying shape but includes less polygons, edges and vertices. Early methods focused only on preserving the overall shape of the geometric model, whereas current methods also handle meshes with attributes (normal vectors, colors, texture coordinates) so that both the mesh shape and the mesh appearance are preserved.
The goal of this work is to develop, implement and test a mesh simplification algorithm able to simplify large models in-core using a vertex clustering algorithm. Several detail-preserving techniques will be examined and implemented and a new filter is proposed, taking into account geometry features and nodal defined attributes. We also review recent advances in spatial hash tables to achieve a more compact storage, and we analyze and evaluate their impact in the simplification process.
Acknowledgements
I would like to thank professor Carlos Andújar for its guiding in this project, its suggestions and efforts. I also want to thank Riccardo Rossi and Pooyan Dadvand for their support in providing some of the examples, for their suggestions and help in some of the experiments and providing access to some of the testing platforms. Thanks also to Antonio Chica and the people participating the 'moving-seminars' for providing the inspiration.
Thanks also to the Stanford University for providing the models to the public in their The Stanford 3D Scanning Repository [Standford11]. Models which were used to validate the algorithms. And the patient users of GiD which acted as beta-testers for this new feature. Also the GiD-team for the useful discussions and the demonstrated patience.
I would also like to thank CIMNE for providing support and the resources to develop this work, and also the Instituto Universitario de Investigación Biocomputación y Física de Sistemas Complejos of the Universidad de Zaragoza for letting me run the scalability tests in their Cluster.
Special thanks also to my family and friends for their understanding and support.
1. Introduction
1.1. Motivation
In computational mechanics and computer fluid dynamics, physical or artificial processes are simulated using HPC clusters by means of discretizing the domain with a finite element mesh and solving partial differential equations using different mathematical models and numerical solvers both at node and at element level. The elements used in these meshes can be planar elements, such as triangles, or volumetric elements, such as tetrahedra.
Scientists use several visualization tools to analyze and inspect the results of these programs by extracting information of the meshes using cuts, iso-surfaces, performing particle tracing or visualizing vector fields. With the ever increasing computational capabilities of current HPC clusters, the detail of the simulated 3D models increases accordingly, reaching nowadays billions of elements [Pasenau11, Yilmaz11]. The resolution of 3D scanners is also increasing and meshes with several millions of triangles are being generated. Not to mention the information extracted from medical scanners, like computer tomographies, which are used in biomedical simulations too [Soudah11].
On the other hand commodity hardware can only render at best a few millions of triangles per second. Several simplification techniques have been developed over the years to reduce the original mesh complexity so that the final user can interact with these models [Boubekeur2008]. As the amount of data obtained from the simulations is growing, some data reduction techniques are required to interact easily with these simulation results.
One of the most easily parallelizable simplification methods is the vertex clustering algorithm. This algorithm uses a uniform spatial grid to group vertices of the input mesh; vertices inside each cluster are replaced by a single (representative) vertex.
Some recent developments have been done in the mesh simplification field related to GPU implementations of the vertex cluster algorithm [DeCoro07,Willmot11], which achieve very high simplification rates and attempt to preserve attributes defined in the original mesh.
Several recent spatial hash schemes also take advantage of the GPU architecture to achieve both high insertion and query rates, while providing a compact storage [Alcantara11,Garcia11]. The scheme used by De Coro [DeCoro07] to store the cells of the decimation grid is called 'probabilistic octree' and it resembles a multi-level hash table but without handling collisions.
In a previous work [Pasenau11-2] we already addressed the use of a hash table [Alcantara07] to store the simplification grid efficiently, so that large meshes can be simplified in-core using a vertex clustering algorithm. The resulting algorithm still had some limitations though. On the one hand, classic vertex clustering algorithms might remove some details of the original mesh which may be very important (e.g. the two sides of the a very thin plate), and might create holes in a blade or collapse stretched structures into lines.
On the other hand, the simplification algorithm implemented in [Pasenau11-2] does not handle attributes, like scalar values defined at nodes or colors or texture coordinates defined at vertices. Simply averaging them on a per-cell basis is not appropriate as some discontinuities may turn into smooth changes and turbulences or vortices in a vector field may turn into a low-speed stream.
This work will extend the previous one by incorporating detail-preserving techniques applied not only to the geometry but also to the nodal attributes of the original model. It will also analyze the impact of new hash schemes in the simplification process to support fast simplification of huge 3D models.
1.2. Objectives
The final objective is to develop a tool for simulation engineers allowing them to visualize and interact with large models, either remotely or on a platform with modest graphics. The acceleration of this visualization process will be done by simplifying large triangle meshes coming from the simulation area, and preserving not only geometrical features but also features present in the scalar or vector field defined at nodes. Features in a scalar or vector field can be discontinuities or vortices which may be lost in the simplification process if they are not taken into account.
The resulting algorithm should be fast, robust and use the memory efficiently.
After reviewing the state of the art related to mesh simplification and spatial hash schemes, this work will analyze some of the simplification techniques aimed to preserve details of the original geometry and nodal attributes. It will also examine and compare three major spatial hash schemes presented in the latest years: Alcantara's two- and single-level cuckoo hashes and the coherent parallel hash from Garcia et al.. The goal is to develop a fast simplification algorithm for triangle meshes with a compact storage which also preserves the detail and attributes of the original model. This tool may be used not only to accelerate rendering rates but also, as a daemon running on HPC nodes, to reduce the bandwidth required to interact with huge remote models in a distributed scenario.
To validate the algorithm several models will be used, some of which can be found in the Annex.
1.3. Contributions
Vertex clustering algorithms use a uniform grid to group vertices into clusters. All vertices which fall into the same cell will be replaced by a single vertex (called representative) that provides the better approximation of the geometry. The computation of the best representative vertex for each cell requires some information to be stored in the cell which will be generated from the original mesh.
Since accurate simplification of large models require an arbitrarily large number of cells, we will use spatial hash schemes to store per-cell information. The key to access the hash table will be generated from the integer coordinates (indices) into the simplification grid. The hash schemes will be extended to support 64-bit keys and the information needed in the cell. The access to this decimation grid and the information stored at each cell will depend on the detail-preserving technique and will make use of normals and scalars at the nodes of the original mesh, with a new smoothing normal filter.
An application will be developed, which will run on MS Windows and on Linux, to test the different hash schemes and detail preserving techniques. The algorithms will also form a library which will be used in GiD, a pre- and postprocessor developed at CIMNE [GiD11].
Several benchmarks will be done comparing the speed, scalability and load factor of the different hash schemes.
1.4. Organization
The rest of this document is organized as follows. In the next chapter several articles will be discussed focusing on our particular needs: speed, shape preservation and compact representation. Also the setup of the experiments is described, as well as the metrics used in the benchmarks.
Chapter 3 extends the simplification algorithm of the previous work by building a octree, using the information of normals in the simplification process and incorporating the attributes in the error metrics.
Chapter 4 deals with storage issues and tests several methods to achieve a smaller memory footprint of the simplification algorithm while maintaining speed.
Several benchmarks related to scalability and load factors will be explained in the fifth chapter and some examples will also be shown.
Finally some conclusions will be presented in Chapter 6 and future work will be outlined.
1.5. Concepts
When engineers perform computer simulations they discretize the domain of the simulation, for instance a building structure or the fluid around an airplane, into a mesh of elements. These elements are basic geometrical entities such as lines, triangles, quadrilaterals, tetrahedra, hexahedra and prisms. Usually the Finite Element Method is used to solve the partial differential equations which model the problem to simulate. This method relies on a set of basic geometrical elements connected at the vertices where these equations are solved. This set of elements is called finite element mesh, or simply mesh. The vertices of the mesh are called nodes. Element connectivity is the set of nodes which defines the element. The orientation of an element is the order of the vertices which defines the element, the right-hand rule is used to define this orientation. Boundary edges on a surface mesh are those edges which are incident to one face.
The partial differential equations are solved at nodes or at the elements, and these solvers write results at nodes or at elements. These results may be just scalar values, such as pressures, densities, damage factors, von Misses stress; vectors, such as velocity, displacements, rotational; or matrices, such as tensors. This work will only deal with attributes representing scalars or vectors defined at the vertices of the mesh.
2. State of the Art
The first part of this chapter describes the simplification algorithm and the hash scheme used in the work done by Pasenau in its Final Project [Pasenau11-2] which is used as starting point of the current work. Then some techniques proposed by several authors will be discussed in relation to shape preservation and attribute handling during the simplification process. Two recent hashing schemes will also be explained and their advantages outlined. Finally, in the last section the experimental setup and the benchmark procedure are described.
2.1. Efficient vertex clustering
The starting point of this work is a mesh simplification algorithm [Pasenau11-2] that combines vertex clustering simplification [DeCoro07] with hash tables [Alcantara09]. We now review these two works.
Simplification process
DeCoro's algorithm performs the simplification process in three steps:
1. Creation of the quadric map: for each vertex of each triangle of the original mesh the quadric error function matrix (qef, see below) is calculated, then using the vertex coordinates, the id of the corresponding cell of the decimation grid is calculated, and the qef matrices are accumulated.
2. The optimal representative vertex for each cell of the decimation grid is calculated.
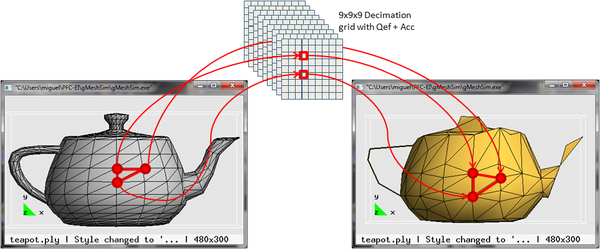
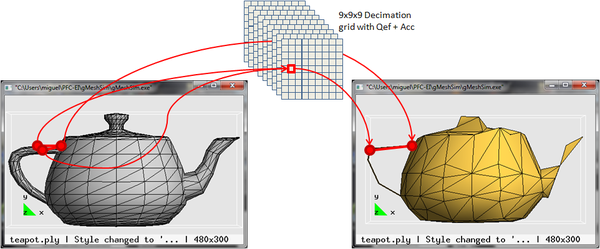
3. Finally, for each vertex of each triangle, the id of the corresponding cell of the decimation grid is calculated and if all three vertices have the same id, then the triangle collapses and is discarded; if only two of them have the same id, then the triangle collapses into a line, otherwise the vertices of the triangle are replaced by the optimal representative vertex of the respective cells. Figure 2.1 shows and example of this simplification step:
|
|
| Figure 2.1: Simplification example using a 9x9x9 decimation grid where one triangle of the original mesh may turn into a triangle in the simplified mesh or into a line. |
The quadric error function used is the one described in [Garland97]. Given a vertex v the quadric error function is defined as the sum of the square distances from this vertex to the set of planes associated to this vertex:
Initially planes(v) is build from the triangles incident to the vertex v. When two vertices are collapsed (a, b) à c, then planes(c) = planes(a) planes(b). Garland explains in its article, [Garland1997], that only the 4x4 matrix has to be stored, instead of storing the set of incident planes. This way, the union of the set of planes turns into a sum of quadrics. And so, on a multi-level octree like approach, the quadric of a node of the tree is the accumulated sum of the quadrics of its sub-tree.
To find the point that best approximates the group of vertices whose quadric error function is the point minimizing this error has to be found. This can be done for example by inverting the QEF matrix:
As explained in the final project [Pasenau11-2], the matrix can be singular and, therefore, is not invertible, or the resulting point may lie outside the decimation cell. To avoid this situation the algorithm checked for both possibilities and if one of the problems is detected then the average of the accumulated vertex coordinates is used instead.
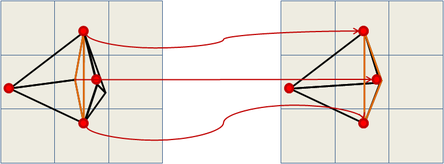
Repeated triangles were also eliminated in the final simplified mesh and, as sometimes the algorithm changes the orientation of some triangles, it checks this and, eventually corrects their orientation, like the one shown in Figure 2.2.
|
| Figure 2.2: The orange triangle flips its orientation in the simplification process |
Data structure
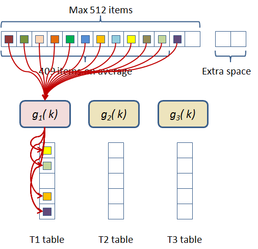
Since space efficiency is critical in vertex clustering simplification, non-empty cells of the decimation grid (along with the qef matrices and the accumulated coordinates) were stored using a hash table, using Alcantara's two level cuckoo hash approach.
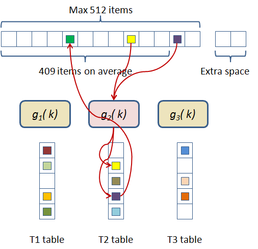
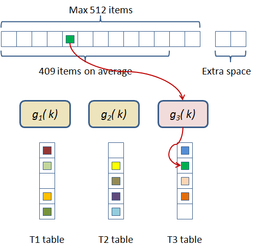
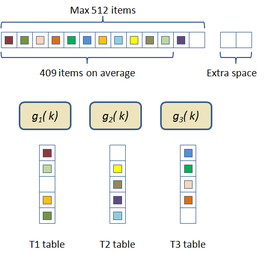
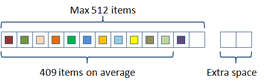
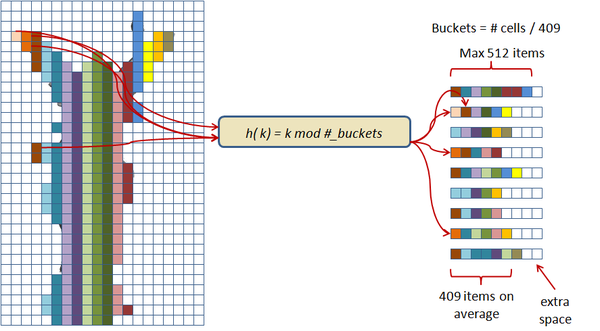
In this scheme the hash table construction is done in two steps: first, entries are grouped in buckets of 409 elements in average and 512 elements at most as shown in Figure 2.3; and then, for each bucket, a cuckoo hash function is build by subdividing the bucket into three sub-tables accessed by three different hash functions and storing a single value per entry. The number of buckets is just the number of items divided by 409. The hash function used for this process is just the modulus function ( ). If the building process of the whole table fails then an alternative hash function is used to distribute the items among the buckets. This alternative is of the form:
being and prime numbers.
|
| Figure 2.3: First step of the two level cuckoo hash: distributing the items into buckets. |
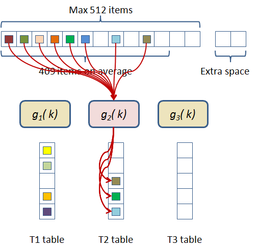
For each bucket the cuckoo building process is performed in parallel and independently between them. Six coefficients are generated by XORing a random seed value with six constants to obtain the three cuckoo hash functions of the form:
This seed is stored in the bucket, and the hash functions are generated each time an item is placed or retrieved.
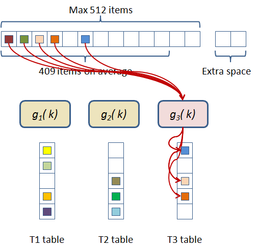
During the building process, an incoming item is inserted in the first sub-table using the first cuckoo hash function if the destination is free. If not, then it looks in the second sub-table using the second hash function. If its position in the second sub-table is not free, then it goes to the third table using the third hash function. If the corresponding entry in this last table is not free then it goes back to the first table and "kicks out" the already stored element and occupies its place. The element which has been "evicted from his nest" tries to place itself in the second sub-table. If the place is occupied, then evicts the stored element and occupies the place, and so on until a maximum number of iterations has been reached. Figure 2.4 displays this construction process graphically. If the construction process fails then a new seed is generated and the process is restarted.
To have enough space for the hash building process to succeed, the buckets are divided in three sub-tables of 191 entries each, adding a total of 573 positions for each bucket.
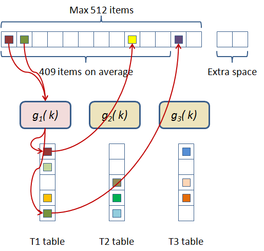
To retrieve an item placed in the table, the first hash function is used to know which bucket needs to be accessed. Then, using the stored seed the three cuckoo hash functions are created and used to access the three sub-tables. If the item is not in the first sub-table, then the second sub-table is accessed and eventually the third.
This hash scheme hash uses 1.4·N space for N items and using the four hash functions guarantees that an item of the table can be retrieved in constant time.
Given a point, the key used in the hash table is a 64-bit unsigned integer generated from the ( i, j, k) indices of the corresponding spatial cell in the simplification grid. The data stored together with the key consist of 14 float numbers corresponding to the 10 floats of the symmetrical quadric error function matrix and the 4 floats used to accumulate the point coordinates: x, y, z and count ( count = number of points accumulated).
Simplification process reviewed
Using the two-level cuckoo hash as data structure adds a fourth step in the simplification process:
1. Creation of the hash table: getting the unique id's used in the simplification grid, create the hash functions using empty values;
2. Creation of the quadric map (calculate the QEF information from the original triangles and accumulate it in the cells corresponding to the vertices of the triangles);
3. Find the optimal representative for each cell of the simplification grid;
4. Generate the simplified mesh by parsing each triangle of the original mesh, locating the cells of their vertices and generate the simplified triangle if it is not collapsed or repeated.
2.2. Detail preserving simplification
Scott Schaefer and Joe Warren in their article "Adaptive Vertex Clustering Using Octrees" [Schaefer03] propose an adaptive vertex clustering algorithm using a dynamic octree with a quadric error function (qef) on each node to control the simplification error and eventually to collapse certain branches. The quadric error function at the leaves is computed as explained in the previous section. The quadric error functions of an internal node is calculated by accumulating the qef's of its sub-tree. Their algorithm is able to simplify meshes without storing them in memory (out of core algorithm). Given a memory budget, the octree is build while reading the original mesh and when the limit is hit, then the sub-trees with less error are collapsed to free memory for new nodes.
The advantage of this algorithm is that it simplifies the original mesh but concentrates the vertices in areas with more detail, generating meshes with better quality than uniform vertex clustering. The main drawback is that the vertices of the mesh should be spatially ordered to guarantee that collapsed sub-trees are not visited again while parsing the original mesh. This sort has a relatively high time cost O(n·log(n)) which represent almost three times the cost of building the octree in some examples of the article.
Christopher DeCoro and Natalya Tatarchuk propose a 'probabilistic octree' in their article "Real-time Mesh Simplification Using the GPU" [DeCoro07]. This octree is in fact a multi-grid data structure in which each level doubles the number of cells with respect to the level above, i.e. follows an octree-like subdivision. Each cell stores the quadric error function for its level and all levels below, by adding the qef's of the cells of its 'sub-tree' like Schaefer. For a certain level, instead of storing all cells, there is a memory limit and a hash function is used to store them in this memory pool. Collisions are not handled and so, as not all cells are stored, a cell has some 'probability' of being stored.
In the building process, the qef calculated for an incoming point is not stored in all levels of the multi-grid, but are randomly distributed among all levels. This random distribution is weighted according to the number of cells on each level. In the simplification step, to obtain the optimal representative for an incoming vertex, the octree level is selected according to the user's error tolerance, given a certain error, and if the cell is not present, as not all cells of a certain level are stored, the cell of the level above is selected, as it 'surely' exists.
In "Rapid Simplification of Multi-Attribute Meshes" Andrew Willmot [Willmot11] proposes a different method to improve the quality of the simplified mesh: shape preservation. Some models have very fine parts such as twigs or antennas, which will be collapsed. In fact, any detail smaller than the cell size in at least one dimension will be removed.
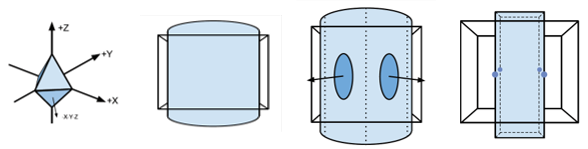
In the vertex clustering algorithm, the label id assigned to each original vertex is extended to contain information about its normal direction, classified according to the sign for each major axis, so 8 tags are possible.
Whit this information, surface vertices with opposite normals will not be collapsed together, as shown in Figure 2.5. This preserves curved surfaces within a cell. Besides reading the vertex position, its normal must be read too. More faces are generated for curved surfaces, but ‘flat’ surfaces are almost unaffected.
2.2. Multi-attributes
In order to handle properties such as colours, textures and surface normals, Michael Garland and Paul Heckbert, in their article "Simplifying Surfaces with Color and Texture using Quadric Error Metrics" [Garland98], extend the quadric error metric to include these and other vertex attributes.
This is accomplished by considering that a point ( x, y, z) and its attributes ( a1, a2, …, an-2) define a point in . Assuming also that all properties are linearly interpolated over triangles, a quadric can be constructed that will measure the squared distance of any point in to this plane.
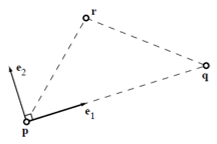
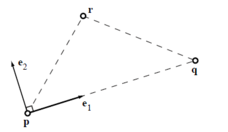
Using the three n-dimensional points of the triangle two orthonormal vectors can be calculated, e1 and e2, which lie in the plane and define a local frame with origin in one of them:
|
|
Using these orthonormal vectors the different parts of the quadric matrix can be calculated:
|
|
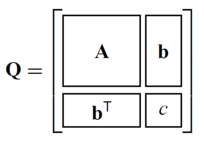
To simplify a mesh a 4x4 matrix is used to represent the quadric error function which then was inverted to calculate the optimal representative of a cell, with their group of original vertices. Considering the different possible attributes results in following matrix dimensions and unique coefficients:
| Simplification criteria | vertex | Q | # unique coefficients | accumulation vector size | |
| geometry only | 4 x 4 | 10 | 4 | ||
| geometry + scalar | 5 x 5 | 15 | 5 | ||
| geometry + colour | 7 x 7 | 28 | 8 | ||
| geometry + vector | 7 x 7 | 28 | 8 | ||
| geometry + normals | 7 x 7 | 28 | 8 | ||
| Table 2.1: Each cell of the simplification grid stores the QEF information and an accumulation vector (accumulates the n coordinates of original points which are grouped into the cell and its number: ; all this will be used to calculate the optimal representative. | |||||
In "Rapid Simplification of Multi-Attribute Meshes" Andrew Willmot [Willmot11] proposes a different technique to preserve discontinuities in the attributes, in its case texture coordinates when the same vertex has different sets of texture coordinates depending on the incident triangle. Instead of repeating the simplified vertex for each incident simplified triangle, repeating texture coordinates, Willmot describes an algorithm to get the boundary edges of the different discontinuities along the original triangles incident to the cell and classify the triangle vertices and determine which ones share the same attribute.
2.4. Parallel spatial hash tables
In his dissertation "Efficient hash tables on the GPU" [Alcantara11], Alcantara experimented with several hash schemes, in two different GPUs: nVidia GTX 280 and nVidia GTX 470. Including the two level cuckoo hash which was later used in Pasenau's final project [Pasenau11-2]. Among other new features, the latest graphics card introduces a cache hierarchy in the GPU architecture and several new memory atomic functions, and the comparison shows the effect of the cache over the different hashing algorithms. While the two-level cuckoo outperforms other hashing methods on the older architecture, the introduction of the cache hierarchy in the latest architectures turns the performance chart upside down, making previously efficient hash schemes become more inefficient. The two level cuckoo required some expensive restarts, memory overhead is difficult to reduce without reducing retrieval speed, and at sub-table level, several tries needs to be done to place and retrieve an item.
To improve performance, according to Alcantara, the algorithm should focus on minimizing memory accesses rather than improving spatial locality. His last proposal consists of a global, single level cuckoo hashing in which the cuckoo hash functions works over the entire hash table instead of using several separated sub-tables, and each thread, instead of trying repeatedly to insert the same element, it atomically swaps the current to-be-placed item with the item in the destination slot. The thread will succeed if the destination slot is empty. An example of this construction process is shown in Figure 2.6.
| Given an item the cuckoo hash functions may place it in any position of the whole hash table | Using the first hash function the location where the element should be placed is not empty. | The existing element is evicted and the hash function used to place this element is selected. |
| Then the next hash function, in round-robin order, is used to calculate the new position for the previous evicted item. | As the new position is again already occupied, the element in the table is evicted and the hash function used for this evicted element selected. | Using the next hash function for the previous evicted element, finally a free slot is found, and the element stored. |
| Figure 2.6: Steps followed to place an incoming item using Alcantara's single level cuckoo hash scheme. | ||
The cuckoo hash functions are of the form:
where ai , bi are randomly generated constants and p a prime number. These hash functions are used as in the other cuckoo scheme, i.e. in round-robin order, and when an item was evicted getting which hash function was used to place it, all functions are recomputed and compared to the current evicted slot index. Then the next hash function is used to place it elsewhere. If the maximum number of iterations is reached, then a restart is required, with other new cuckoo hash functions.
In several conducted experiments, the number of hard-to-place items was very small, 3 out of 10000 trials for table of 10M items. To avoid the restart problem, Alcantara proposed the use of a small stash table. If this stash table is big enough the rebuild probability is reduced to almost nil. In his dissertation Alcantara cites Fredman et al. [Fredman84] who showed that a hash table of size k2 has a high probability to store k items in a collision-free manner using a random hash function of the form
being p a prime number, bigger than the biggest value of k, and x a random number. Because the number of items failing to insert in the main table was almost always less than 5 in Alcantara's experiments, he uses a very small stash table with 101 entries, enough to place 10 items without collisions. Now when the query of a key is performed, the main single-level cuckoo hash table should be checked and the stash table too.
Alcantara also states that using more hash functions helps in packing more data together, so raising the load factor of the hash table, up to a 98 % with five hash functions [Dietzfelbinger10]. As it is increasing difficult to build tables with these higher load factors as the experiments showed, Alcantara suggest a load factor of 80 % to balance construction and retrieval rates for four hash functions.
The single level cuckoo hash outperforms the previous two-level cuckoo hash in both architectures, the older GTX 280 and the newer GTX 470, although its memory access pattern is highly uncoalesced. It is more flexible, allowing different load factors and retrieval rates, and it also reduces the number of probes required to find an item, four in the worst case when four hash functions are used.
Alcantara also showed that other hashing methods, like quadratic probing, perform better than the single-level cuckoo hashing on lower load factors because they take advantage of the cache.
And this is one of the conclusions of his dissertation: although single-level cuckoo hashing takes profit of the faster atomic operations of modern GPUx, it has poor caching because the hash function distributes the elements across the whole table. He proposes several ways to overcome this and pointed also to the work of Dietzfelbinger et al. [Dietzfelbinger11].
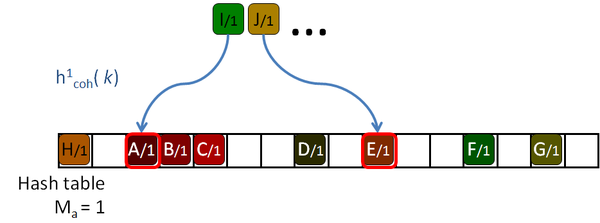
This lack of coherence, which lends to poor caching, is addressed by Garcia in his article "Coherent Parallel Hashing" [Garcia11]. GPU architectures are tailored to exploit spatial coherence, they are optimized to access neighbour memory locations and groups of threads access memory simultaneously. Following this approach, Garcia proposed a Coherent parallel hashing with an early key rejection.
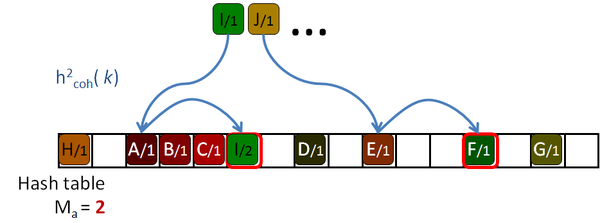
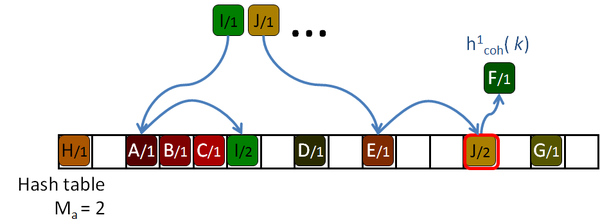
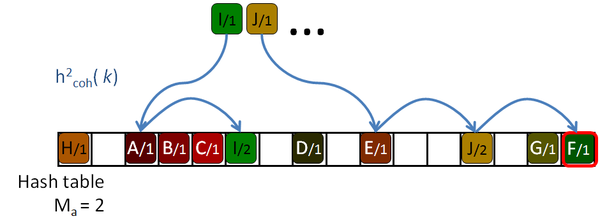
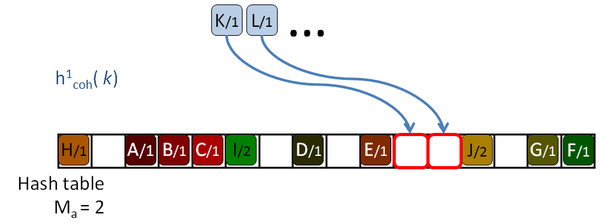
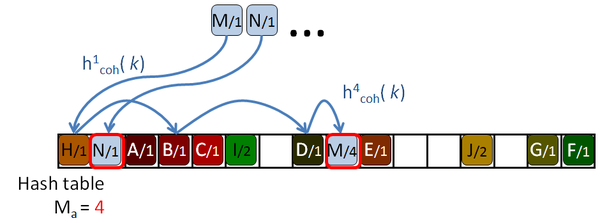
His algorithm is based on a Robin Hood hashing [Celis86], which is an open addressing hashing [Peterson57] with an age reduction technique. On the open addressing hashing, given a table of size |H|, each input key is associated with several hash functions, h1( k) … h|H|( k) which can map the key to every location of the hash table. To insert a key in the hash table, first the first function is used. If the destination slot is occupied then the second hash function is tested, then the third and so on until a free location is found. Peterson defined the age of a key as the number of tries performed until the key is successfully placed in the table. The maximum age of the hash table is the maximum of the ages of all the keys inserted in the table.
So, to insert or query a key in table, the algorithm will take age probes. If an undefined key is queried, then maximum age locations should be checked before rejecting the key. If the amount of undefined queries is larger than the amount of defined keys, as it should be expected for sparse data, this will hurt the performance of the algorithm. The problem is even worse for tables with high load factors, in which the keys are harder to insert, and therefore they get older and older.
The Robin Hood algorithm from Celis solves this problem in that older keys that are to be inserted, evict already placed younger ones. Together with the key, the age of the key is saved and when a key is being inserted, its age is checked against the age of the key already stored in the destination location. If the incoming age is older than the stored one, that is if the incoming key visited more occupied locations than the stored key, then they are swapped. The algorithm continues with the evicted key trying to place it elsewhere. This reduces the age of the keys, and thus the maximum age of the table, drastically. The following pictures show this process with an example:
Garcia et al. states that the expected maximum age for a full table according to [Celis86] is O(log n) and according to Devroye et al. [Devroye04], for nun-full tables, the expected maximum age is reduced to O( log2 log n).
Although Robin Hood hashing reduces the maximum age of the table, the average number of accesses for a given key is very high, specially for undefined ones, compared to the number of accesses of cuckoo hashing, specially for undefined keys.
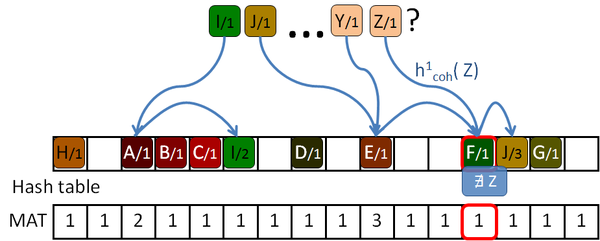
Garcia proposes an addition to the algorithm which helps to reduce the number of access on average, although some of the undefined keys still need to access maximum age locations to discard them. The Early key rejection mechanism stores, for each location of the hash table, H[ p], the maximum of the ages of all the keys whose initial probe location h1( k) is p. These ages are stored in a maximum age table, MAT. So when a key k needs to be queried, only MAT[ h1( k)] tries should be done to discard the key, or less if it's defined, as shown in Figure 2.8.
In all the experiments performed by Garcia, the maximum age was below 16, and so only 4 bits are used to store the age, together with the key and the data in the hash table.
In order to exploit coherence, Garcia uses just translations functions as hash functions:
Where is sequence offsets, large random numbers, independent of and between themselves, and . This way neighbouring keys remain neighbours at each step and threads will access neighbouring memory locations. This does not mean that the keys will be stored as neighbours, because one key can be placed at step and its neighbour at step in another random location, like the example in Figure 2.9:
In his experiments, Garcia shows that when a hash table is build with random sparse data and randomly distributed keys, the single-level cuckoo hashing performs better than the coherent hash algorithm. A robin hood algorithm with a random hash function instead of the translation function, performs slightly better than the coherent hash. Also the results of retrieving random distributed defined keys, the single-level cuckoo and the random hash performs better than the coherent hash. The author states that this is due to the lack of coherence and the overhead of the updated of the MAT table, maximum age table, and the emulation of the CUDA operator atomic MAX over 64-bit operands.
When the input keys of the same random data are sorted before insertion, the construction and querying algorithm doubles the rates of the single-cuckoo, and random hashing. If a coherent data set is used, instead of the random data, and the keys are also inserted in order, then the two-level cuckoo and the coherent hashing perform almost equally, and the single-level cuckoo performs slightly behind. The main difference is that with the coherent robin hood hashing, the hash table can reach higher load factors, up to 99%, compared to the two-level cuckoo and the single-level cuckoo which reach only a factor of 85 % and 95 % respectively. Garcia explains that they never failed to build tables with 99% local factor, but higher factors generate maximum ages above 15, which cannot be stored using only 4 bits.
Also the results for full key tests were presented. In these tests all keys of the domains are scanned, whether they are defined, i.e. pointing to useful data, or undefined, i.e. pointing to empty space. The tests were done over a random data set and a coherent set, an image. In both cases the coherent parallel hashing outperforms the other algorithms by a factor of 4 or more. This can be explained by the early key rejection mechanism and the coherence of the accesses.
The preserved coherence is also reflected in the higher usage of the GPU's cache, which reaches a 40% of cache hits, compared to the meagre 1% or less of the random hashing.
Garcia also experimented with different access patterns, besides the linear incremental one, he also tried the Morton order and the bit-reversal permutation. The conclusion is that the more ordered and predictable the accesses are, the better the coherent parallel algorithm performs.
2.5. Conclusions
The previous simplification algorithm [Pasenau11-2] was able to simplify big meshes very fast but only based on geometrical information and losing some important details, like the shown in Figure 2.10, where holes appear on very thin surfaces:
The octree approach proposed by DeCoro may suppose an advance in preserving some of this details although it supposes more effort in the construction and simplification process.
Willmot's shape preservation feature, which can be seen as subdividing each cell of the simplification grid according to the orientation of the normals on the vertices of the original mesh, may avoid this overhead as the normal orientation is encoded into the label_id calculated for the original vertices.
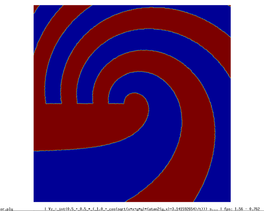
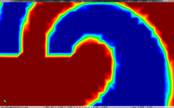
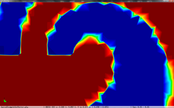
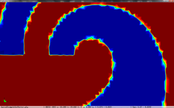
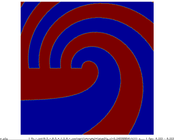
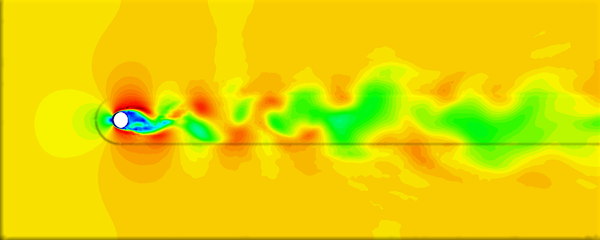
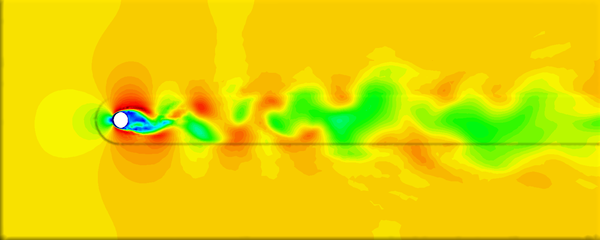
The cell boundary edges mechanism also presented by Willmot, which preserves discontinuities in the cell by grouping triangle vertices with continuous attributes and repeating the simplified vertices as many times as discontinuities are present. This is can be easily be applied on discrete attributes, i.e. vertex attributes whose values are finite or can be grouped clearly in a set of discrete values. As the proposed work should handle scalar and vector fields coming from simulation codes, the nature of these attributes cannot be known beforehand or if so, the discretization may hide some features present in the results of the simulation. Figure 2.11 shows this problem with the velocity modulus field of a fluid around a cylinder:
|

|
| Figure 2.11: The minimum and maximum values, in dark blue and red respectively, of the velocity field are smoothed in the simplified mesh of the bottom image. |
The two level cuckoo hash scheme proposed by Alcantara uses 1.4 N space to store N items. The pair (key, value) used in the simplification algorithm represents a cell of the decimation grid used to simplify the model and is composed by a 64-bit key and the information needed to find the optimal cell representative. This information, as shown in Table 2.1, can be important. The second cuckoo scheme presented also by Alcantara in its dissertation and the coherent parallel hash explained by Garcia in its article may reduce this overhead quite significantly, almost perfect for the later scheme.
Both of these hash functions rely on a very specific feature of CUDA: atomicExchange in the case of the single level cuckoo hash and atomicMax in the case of the coherent parallel hash. Both functions guarantee exclusive access when a thread reads a memory position and stores a new value, in the first case; and when a thread reads a memory position compares its value to the new one and eventually stores a new value, in the second case.
Such atomic memory operations are not present in OpenMP, as the implementation target of this work is the CPU a not GPUs; and therefore the locking mechanism must be used, with its overhead in memory and time.
The two level cuckoo hash scheme proposed by Alcantara, and used the previous project [Pasenau11-2], already achieves very good simplification rates although the cuckoo hash functions introduce a random distribution of neighboring cells. The hash function used to distribute the items into buckets was just a modulus function and the randomness was limited to the bucket area. The single level cuckoo hash scheme extends the randomness of the accesses to the whole table. This can level the advantage of a more compact representation. On the other side, the coherent parallel hash scheme try to maintain the spatial coherence of the input mesh, if the same hash function is used. This feature promises good results, but it should be balanced with a higher memory costs for the maximum age table and the OpenMP locks.
Memory usage is very important as the intention is to extend this simplification algorithm to volume meshes and memory will become a limiting factor in how much can be simplified or how many details can be preserved.
2.6. Experimental setup
Given the three different hash schemes to evaluate and the detail-preservation techniques, we first focus on enhancing the existing simplification schemes by incorporating the following detail preserving techniques and multi-attribute handling:
- Octree: as multi-grid like the one of DeCoro but each upper level will hold all accumulated information their corresponding sub-tree;
- Shape preservation using the normals orientation to classify the points of each cell in the simplification grid;
- Incorporation of a scalar in the quadric error function of the cell and of a vector attribute afterwards.
After the evaluation of these techniques, some experiments will be performed with the hashing schemes and will be compared in terms of simplification time (construction & retrieval) and memory usage.
The timings are averages of several runs to avoid noise, and do not consider the time used to read models, allocate memory for the objects and the calculation of the normals of the input mesh.
Several models will be used to verify and validate the algorithms implemented so that a certain degree of robustness can be guaranteed.
3. Detail preservation and multi-attributes
One of the goals of this work is to develop a simplification algorithm able to preserve not only geometrical features but also the attributes defined at the vertices of the original mesh. In scientific visualization, these attributes represent simulation results on the nodes of the original mesh which may define features that traditional simplification processes may lose. Attributes also include colour components, texture coordinates or even the normals of the original mesh.
This chapter focuses on techniques aiming to enhance the quality of the simplified mesh and the use of attributes to control the simplification process. The hash schemes used to handle and store this information are discussed in the next chapter.
3.1. Octrees
Concept
The simplification process described in the previous chapter proceeds through the following steps:
1. create the hash data structure
2. create the quadric map
3. find the optimal representative for each cell
4. generate the simplified mesh
Following DeCoro's approach [Decoro07], a multi-grid version has been implemented but with some key differences. First, each level stores all occupied cells of the simplifications grid using a two-level cuckoo hashing scheme. Another difference is that the qef information generated from the original mesh is not randomly distributed across all levels of the octree, but stored at the deepest level of the tree. Then, since Schaefer demonstrated that the qef information of an internal node is just the sum of the qef's of its sub-tree, the qef information of the lowest level is accumulated in the levels above until the first level is reached.
Like in DeCoro's octree, given a user's error tolerance, the tree is parsed bottom-up to generate the simplified mesh.
As the original model should still be recognizable in the simplified mesh, the coarser levels are discarded and the implemented octree starts at level 6, corresponding to a decimation grid of 643. The depth of the tree is limited to 11, corresponding to a decimation grid of 20483, but deeper levels have also been tested. In all levels the two-level cuckoo hash scheme has been used to store per-cell information.
Creation
Algorithm 3.1 shows the steps required to create the octree.
Algorithm 3.2 shows how the octree is filled with the qef information calculated from the original mesh:

|
Finding the optimal representatives
To calculate the optimal representatives in the octree, the algorithm visits all the cells of all levels of the octree to calculate the optimal representative in the same way as the previous work, but now the error of the cell's representative is also stored in the cell:
if the qef matrix is not singular then
invert matrix to find the optimal position;
if the optimal position lies inside the cell of the decimation grid then
use it as cell representative
if the qef matrix cannot be inverted or the calculated optimal position lies outside the cell then
use as cell representative the average of the accumulated coordinates
calculate the error of the cell representative
This error is used in the simplification process to compare against the user selected error tolerance.
Simplification using an error tolerance
The simplification process changes somewhat with respect to the previous one. Now for each point of the original mesh, starting from the deepest level, the cell representative which best approximates the user's selected error is selected.
As before if the three representatives of the original triangle are the same, then the triangle is discarded. If two of them are different, then a line is generated. And if all three of them are different then a triangle is generated for the simplified mesh. The resulting triangles are still checked for the correct orientation, i.e. the same orientation as the original triangles, and for duplicates.
One of the advantages of this approach is that once the octree is created, several simplified meshes can be generated using different error tolerances. This cannot be done with the uniform grid approach. If a finer mesh is desired a new grid should be build (including the hash table). Coarser meshes can be obtained by sending the simplified mesh to a coarser grid, but still there is the cost of creating the new hash table.
Results
Two models are used to compare the meshes obtained from the uniform grid simplification and the implemented multi-grid octree-like algorithm.
The first one is the "Lucy" model with 28 million triangles. The second one if the Puget Sound map with 16 million quadrilaterals, which were split into 32 million triangles.
With the "Lucy" model, a side-by-side comparison is performed with different simplification levels, showing differences in the distribution of elements and error.
Refining a little bit more, i.e. using a smaller error, it can be seen that the octree simplifies aggressively on those areas where no much definition is needed, and concentrates elements in areas with more details.
This advantage related to the quality of simplification can also be observed with the Puget Sound map, with 16 millions of quadrilaterals, where with half the triangles the same detail level can be achieved.
This saving in the number of triangles can also be used to obtain a higher resolution in the simplified mesh.
The next sequence of pictures shows different output meshes with different error tolerances, demonstrating how the detail level can be controlled with the multi-grid-octree structure.
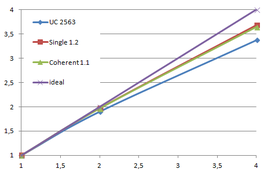
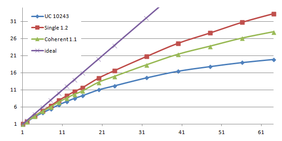
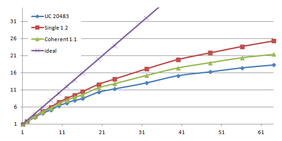
Results
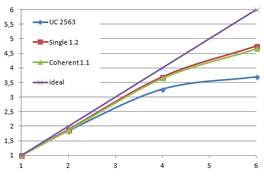
Table 3.1 shows the time, memory requirements and mesh sizes for both algorithms: the one using uniform clustering (UC) and the octree. Several grid sizes have been used with the first algorithm and several depth levels has been used with the octree, including the level 13, which uses a grid of 40963 for the leaves.
| Type - level | Creation | Simplif. | Total | Mem (MB) | Points | Triangles |
| UC 2563 | 3.37 s. | 0.70 s. | 4.07 s. | 13.66 | 90,780 | 182,913 |
| UC 20483 | 7.49 s. | 12.80 s. | 19.74 s. | 478.25 | 4,555,618 | 9,128,472 |
| UC 64..20483 | 22.92 s. | 18.25 s. | 41.20 s. | |||
| Octree (12) <1e-5 | 14.43 s. | 6.49 s. | 20.93 s. | 666.42 | 51,228 | 103,619 |
| Octree (12) <1e-6 | 10.27 s. | 305,725 | 614,325 | |||
| UC 40963 | 14.16 s. | 31.74 s. | 46.05 s. | 1,063.35 | 10,287,708 | 20,568,519 |
| Octree (13) <1e-5 | 35.09 s. | 6.75 s. | 41.84 s. | 1,546.47 | 51,235 | 103,630 |
| Octree (13) <1e-6 | 10.32 s. | 307,082 | 617,092 | |||
| Table 3.1: Comparison of the time cost and the memory cost of the different simplification approaches. | ||||||
The benchmark shown in Table 3.1 was performed on a Intel Core2 Quad Q9550 computer running MS Windows 7 64 bits and using the Lucy model with 14,027,872 points and 28,055,742 triangles.
Notice that the memory footprint and the running time is almost the sum of creating each level separately. In fact the creation is a bit faster because some of the work across all levels is done in parallel, such as getting the list of unique keys for each level. The advantage, as mentioned before, is that once the octree is created several meshes can be generated with different levels of detail.
The problem shown in Figure 2.10 of Chapter 2 still remains, although some parts benefit from the octree as it can be seen in the next figure:
Table 3.2 shows the details of the different simplification algorithms and the settings used to generate de images in Figure 3.6. of the centre-left image. Although a very fine decimation grid was used, centre-left picture, the front wing of the car still has some holes. The same applies to the octree output with a very small error tolerance in the bottom-left picture.
The benchmark was performed on a Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits and using the f1 racing car model with 3,005,848 points and 6,011,696 triangles.
| Type - detail | triangles | create + simplify | Memory KB | |
| Top-left | Original model | 6,011,696 | ||
| Top-right | Unif. Clust. 10243 | 1,387,314 | 2.97 s. | 65,750 |
| Centre-left | Unif. Clust. 40963 | 3,463,332 | 6.44 s. | 164,710 |
| Centre-right | Octree (13), 1e-6 | 195,860 | 9.15 s. (6.16 + 2.98) | 335,242 |
| Bottom-left | Octree (13), 1e-7 | 1,328,293 | 0 + 6.39 s. | 335,242 |
| Table 3.2: Comparison of the two simplification approaches used and their cost in time and memory. | ||||
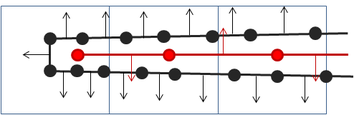
The problem is that the plate of the original mesh just falls inside one single decimation cell, and the algorithm substitutes all points in the cell by a single representative:
|
| Figure 3.7: In blue the cells of the simplification grid, in black the original mesh, with its normals, and in red the resulting simplified mesh, red normals show the orientation problem. |
Depending on which triangle of the original mesh was the first one to generate the simplified version, the normal will be oriented to one side or the other, but it cannot be guaranteed that the resulting normals will be oriented towards the same side, causing the artifacts shown in the above pictures. Furthermore, in simulation processes it is very likely that the attributes of one side may differ very much from the ones of the other side, like a velocity field from two fluids on either side of the plate in opposite directions. A good idea would be to, rather than generating one single vertex per cell, generate several vertices depending on the orientation of the normals at the vertices of the original mesh, like the shape preservation mechanism proposed by Willmot in its article "Rapid Simplification of Multi-Attribute Meshes" [Willmot11].
3.2. Normal based simplification and smoothing
Willmott's shape preservation: using normal direction
The shape preservation technique explained in the article "Rapid Simplification of Multi-Attribute Meshes" by Andrew Willmott [Willmott11], has been implemented. This technique uses the vertex normal information to classify the vertices inside a spatial grid-cell. The classification is done by encoding the normal direction into 3 bits of the cell label id, using only the sign of the components of the normal.
This can be seen as a subdivision of the original spatial cell into 8 sub-cells according to the sign of the normal components as shown in the next figure:
| Figure 3.8: Using the sign (left) of the normals of the cylinder, the corresponding points are distributed into four sub-cells inside the single spatial cell; then each sub-cell calculates its own optimal representative, generating four differentiated points for the final generated square prism (right). | |||
This technique, also called normal subdivision criterion in this work, has been implemented in the original uniform simplification algorithm, which used the two-level cuckoo hash algorithm, and not in the octree version.
Up to now, given a point and a decimation grid, the indices of the cell where this point belongs to were calculated and encoded in a 64-bit cell_id, used then as key in the hash table. Now, to encode the sign of the normal components the last three bits are used, leaving 61-bits to encode the i, j and k indices of the cell. This barely limits the possibilities of our simplification algorithm, as still a decimation grid of 1MB3 cells can be addressed.
Two changes were needed in the algorithm to implement this technique:
1. extend the DecimationGrid data structure so that given a point and a normal an extended cell_id could be generated (61 bits to encode the cell indices and 3 bits for the sign of the normal components);
2. as some input models do not include normal information, this has to be calculated by the algorithm.
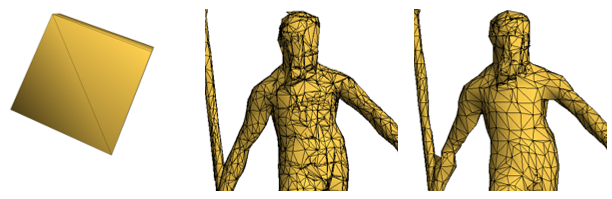
This type of refinement preserves important details, as shown in Figure 3.9 shows, using the Neptune model:
- the image top-left shows the original model with 4,007,872 triangles;
- the image top-centre, a uniform grid 323 created 2,078 triangles and 14 lines in 1.47 s. and using 295 KB of memory;
- the image top right, a uniform grid 323 with normal classification, created 9,342 triangles and 44 lines in 1.96 s. and using 349 KB of memory.
Tests done on Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits.

|
| Figure 3.9: On the left, the original "neptune" model, in the middle simplified using the standard uniform clustering, and on the right, using normals. |
Unfortunately, the new version tends to generate many triangles which could be collapsed without introducing important artifacts. Also, as a spatial cell is subdivided into eight sub-cells, the points are distributed into these sub-cells, leaving the possibility that some sub-cells generate lines instead of triangles.
The nature of the discretization using the sign of normals also creates some artifacts, as shown in Figure 3.10:

| ||
| Figure 3.10: A sphere was simplified to a "cube" using the 23 grid using 12 triangles, using the normals discretization, it becomes a strange object with 31 triangles. | ||
Normal planar filter
Depending on the orientation, the above technique might generate too many triangles in quasi planar surfaces, where the normal orientations just differ by very few degrees. If this fluctuation of the normals just happens near one of the boundaries of discretization, for instance a ground a little bit corrugated with normals of the form (± 0.1, 0.995, 0.0), the algorithm will generate many triangles which could have been simplified away.
| |
| Figure 3.11: Example of a quasi planar terrain, in the right two thirds of the profile. Shown is a profile in the y plane of the "gcanyon" model. |
To overcome this problem, a new filter has been developed and is applied when the optimal representative of the cells are calculated, just after creating the quadric map.
With the above shape preservation technique each spatial cell is subdivided into eight sub-cells, classifying points with normals pointing to the same quadrant. When all points in the cell have normals pointing to the same direction, only one of the sub-cells are used, i.e. filled with information. On the other hand, if, for instance, all points of a sphere fall into the same spatial cell, then all eight sub-cells are filled with information, as the normals of the points are oriented in all directions. Points belonging to an axis-oriented cylinder section, however, will be classified into four sub-cells.
Points from a perfect planar surface will also fill only one sub-cell, but if the surface is not perfect then the points will fill, eventually two, three or four sub-cells. In this case the new filter joins these two, three or four sub-cells into the same spatial cell.
To decide if, for instance, four sub-cells should be joined because they belong to a quasi-planar surface, or should be left separated, because they belong to a cylinder section, our new filter checks the normals stored in the sub-cells.
After creating the quadric map, the information stored in the cell of the decimation grid is the qef matrix Q and the accumulated coordinates of the points grouped in this cell (x, y, z, w), being w the number of points in the sub-cell. For this filter to work, each sub-cell also stores the accumulated normal components. The alternative would be to store in the cell the normals of all vertices grouped in that cell and then check the angle of the cone that contains all these normals. The shape preservation technique already classifies the normals into quadrants and this ensures that accumulating the normals in each sub-cell will not nullify them. Accumulating the normals also is a way of calculating the preponderant orientation of all normals in the quadrant.
Two, three or four sub-cells will be joined if the normals lie within a cone of 60 degrees, i.e. the angle between every two normals is less than 60 degrees. The value for this angle has been found good enough in several tests in this and other fields of usage, like calculating sharp edges of a mesh for display purposes.
The algorithm does not distinguish between spatial cells (classified by point coordinates) and sub-cells (classified by point coordinates and normal sign components). The hash table stores all used sub-cells.
The filter goes through all sub-cells and for each one them locates all its siblings. If there are two, three or four of them the information is joined and the optimal representative is calculated and used in all two, three o four sub-cells. Otherwise, the optimal representative is calculated as always, i.e. inverting the qef matrix to calculate the optimal representative or, if it is singular or the calculated point lies outside the cell, then the average of the accumulated points is used.
As already demonstrated by Garland [Garland97] and Schaefer [Schaefer03], two QEF matrices can be added to obtain the accumulated quadric error function matrix.
A gather mechanism is used in the algorithm to avoid potential collisions, and only the current cell if modified to store the optimal representative. To avoid repeated calculations or possible conflicts, the cell also uses a status flag to store the state of the cell: UNPROCESSED, PROCESSED_BUT_NOT_JOINED and PROCESSED_AND_JOINED.
The final algorithm to find the optimal representative for a certain cell is shown below.
Applying this filter the results obtained show a significant improvement in the simplified mesh, Figure 3.12. After applying the filter in the Neptune model, the previous simplified mesh with 9,342 triangles and 44 lines was reduced to 5,898 triangles and 25 lines. For comparison:
- uniform grid 323 created 2,078 triangles and 14 lines in 1.47 s. and using 295 KB of memory;
- uniform grid 323 with normal subdivision created 9,342 triangles and 44 lines in 1.96 s. and using 349 KB of memory.
- uniform grid 323 with normal planar filter created 5,898 triangles and 25 lines, 2.10 s., 429 KB
Tests done on Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits.
Results
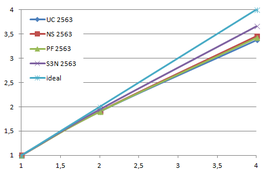
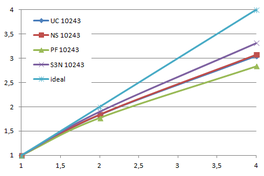
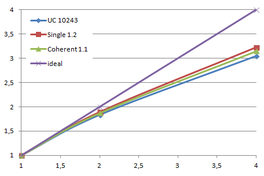
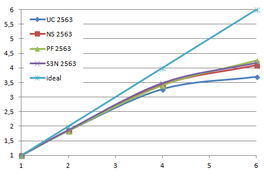
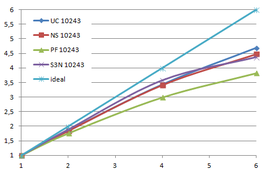
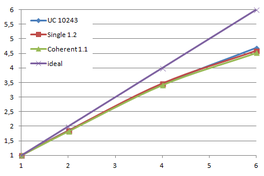
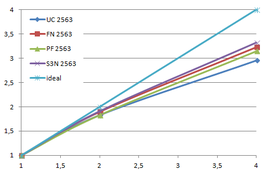
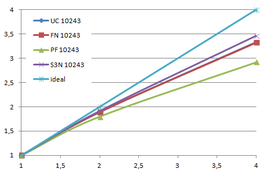
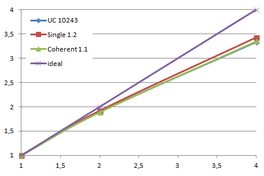
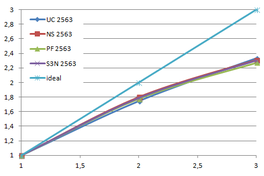
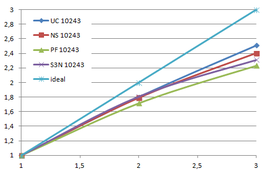
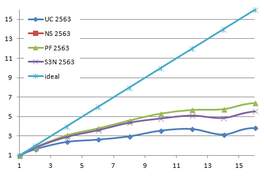
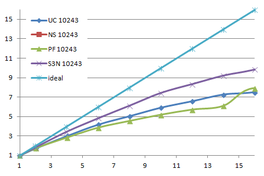
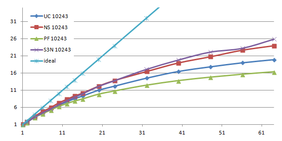
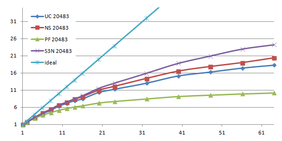
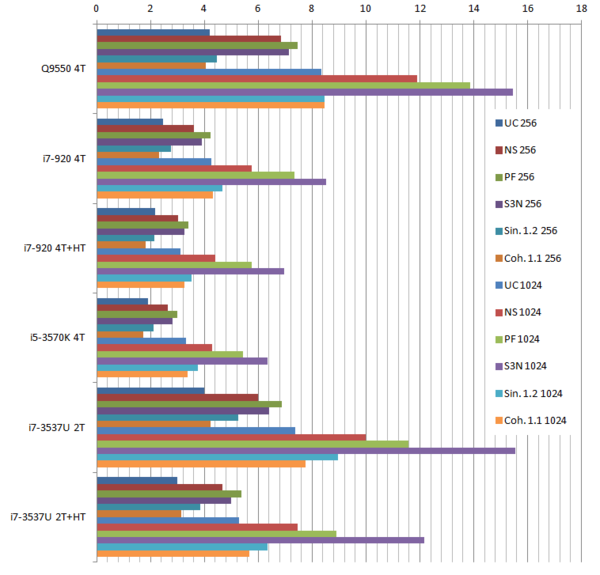
Using the "Lucy" model (14,027,872 points and 28,055,742 triangles) in the same development platform (Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits) the obtained times and memory cost for different degrees of simplification using the three algorithms (UC: uniform clustering, NS: normals subdivision criterion, PF: normal planar filter) are shown in the next table:
| Type - level | T simplif. | T interp. | T total | Mem (MB) | points | Triangles |
| UC 2563 | 3.66 s. | 0.47 s. | 4:14 s. | 8.46 | 90,780 | 182,902 |
| NS 2563 | 4.28 s. | 0.51 s. | 4.79 s. | 13.15 | 141,082 | 312,696 |
| PF 2563 | 4.79 s. | 0.63 s. | 5.43 s. | 16.16 | 93,503 | 188,756 |
| UC 10243 | 7.24 s. | 0.95 s. | 8.19 s. | 122.78 | 1,317,615 | 2,642,388 |
| NS 10243 | 8.58 s. | 1.03 s. | 9.61 s. | 142.25 | 1,526,656 | 3,103,481 |
| PF 10243 | 9.47 s. | 1.76 s. | 11.23 s. | 174.89 | 1,317,901 | 2,643,980 |
| Table 3.3: Comparison of the time cost and the memory cost of the different simplification approaches (UC: uniform clustering, NS: normal subdivision, PF: planar filter). | ||||||
Tsimplif. refers to the time to create, find optimal representatives and simplify the input mesh. Tinterp. refers to the time needed to interpolate the attributes, i.e. clearing the cells, sending the attributes of the original mesh to the same cells where their respective points would be grouped, and calculate the average value for the simplified mesh. This averaging is the first approach to handling attributes on the vertices of the original mesh and will be explained in the next section. Ttotal refers to the sum of both times.
For the normal subdivision and the normal planar filter algorithms the cost of calculating the normals of the original mesh should be added, this increases their times in 2.2 seconds.
The increase in memory requirements of the normal subdivision hash table is due to the fact that more cells are needed, as all cell of the traditional uniform clustering are subdivided into several sub-cells according to the normals orientation.
The increase in memory usage of the planar filter approach, despite that it generates less vertices, is because it needs to store not only all sub-cells as the normal subdivision algorithm but also each sub-cell stores the accumulated normals of the grouped vertices. So the cell size is increased from 14 floats to 18 floats.
The process of the sub-cells in planar filter is also more complex in comparison to the normal subdivision approach; this last one is the same as the normal uniform clustering. In this new scheme, for each sub-cell its status needs to be checked; if is a joined sub-cell then the information of the siblings is gathered and if one of them has already generated the result, get it, if not, it should calculate it.
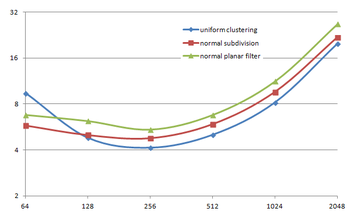
Several degrees of simplification have been performed with the three algorithms on the same model and the same platform and are summarized in following figures:
| Time (s) |
 Grid size Grid size
|
| Memory(KB) |
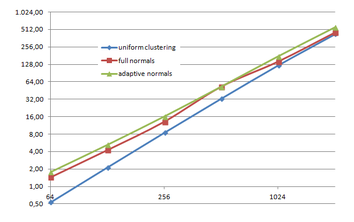 Grid size Grid size
|
| Figure 3.13: The graphs show the time and memory cost of several simplification degrees, scale is logarithmic. |
When this new scheme is applied to the f1 racing car model, an improvement in quality of the simplified mesh can be noticed. Even in very coarse meshes, the front and rear wings, and the thin plate blow the pilot's cabin do not present the artifacts shown in Figure 3.6.

|

|

|

|

|
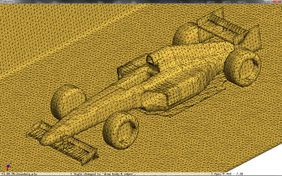
|
| Figure 3.14: Comparison against the original uniform decimation grid (top), of the subdivision of cells using the normals sign (centre), and the normal planar filter (bottom). | |
Table 3.4 lists the mesh information and cost of the algorithms on the same platform (Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits)
| Type - detail | points | triangles | Time | Memory |
| Original model | 3,005,848 | 6,011,696 | ||
| Uniform clustering 2563 | 83,739 | 168,452 | 1.11 s. | 7,999 KB |
| Normal subdivision | 92,742 | 202,714 | 2.09 s. | 8,857 KB |
| Normal planar filter | 87,483 | 180,664 | 2.19 s. | 10,889 KB |
| Table 3.4: Comparison of the resources of three different algorithms used to generate the images in Figure 3.14. | ||||
3.3. Incorporating attributes in Quadric Error Metrics
When the above implementation was incorporated in GiD [GiD11], the scalars defined on the vertices of the original mesh were averaged on each cell, as shown in Figure 2.11. The drawback is that features such as discontinuities present in the values inside the cell may disappear. The same applies for minimum or maximum values, they are smoothed out.
Another problem is that the nature of the uniform simplification grid is also reflected in the scalar field creating a "staircase" effect in smooth curvatures, and smoothing discontinuities as the ones shown in Figure 3.15.
As explained in section 2.2, a way to include the attributes in the simplification process is to extend the QEF matrix by considering that the vertices of the input mesh are defined in including their coordinates (x, y, z) and their attributes (a1, a2, …, an-2).
Using the three n-dimensional points of the triangle two orthonormal vectors can be calculated, e1 and e2, which lie in the plane and define a local frame with origin in one of them:
|
|
Using these orthonormal vectors we can calculate the different parts of our quadric matrix:
|
|
To simplify a mesh using only the geometrical information a 4x4 matrix was used to represent the quadric error function which then was inverted to calculate the optimal representative of a cell, with their group of original vertices.
In this work the number of attributes which will be used to calculate the optimal representatives in the simplification process, together with the geometrical information, will be limited to one scalar and the three components of a vector, as these types of attributes are the ones most used in the simulation area. Afterwards, given a time-step of the simulation analysis, the resulting implementation can easily be extended to handle all attributes present on the vertices in this single time-step, so that the simplified mesh maintains the features of the geometry and all attributes. Usually the simulation engineer visualizes results of a single time-step or compares them with the ones from another time-step, so that the cost of creating another simplified mesh with the new attributes when the time-step is changed can be assumed.
Considering the proposed attributes following table shows the dimension of the QEF matrix and the information that should be stored in the cell:
| Simplification criteria | vertex | Q | # unique coefficients | accumulation vector size | |
| geometry only | 4 x 4 | 10 | 4 | ||
| geometry + scalar | 5 x 5 | 15 | 5 | ||
| geometry + vector | 7 x 7 | 28 | 8 | ||
| geometry + normals | 7 x 7 | 28 | 8 | ||
| Table 3.5: Each cell of the simplification grid stores the QEF information and an accumulation vector (accumulates the n coordinates of original points which are grouped into the cell and its number: ; all this will be used to calculate the optimal representative. | |||||
Normal information of the original mesh can also be considered a vector field, and can also be incorporated in the qef matrix . However this work will not handle geometry, normals and attributes in the same qef matrix. Two separated options have been implemented in the application: extended qef with geometry and attributes that defined a vector, and extended qef with geometry and the normal information.
Implementation details
The simplification process consists of four steps:
1. create the hash data structure;
2. create the quadric map: each triangle creates the QEF matrix and each vertex accumulates this information and its coordinates in the appropriate cell of the decimation grid;
3. find the optimal representative for each cell: inverting the qef matrix or using the average of the accumulated coordinates;
4. generate the simplified mesh: using the optimal representatives, generating new simplified triangles or discarding others.
Incorporating the scalar information into the qef matrix in the developed algorithm meant:
- to modify the quadric map creation algorithm (step 2) and extend it to handle the attributes;
- to expand the cell information to store the enlarged qef matrix and to accumulate the attributes of the vertices grouped in the cell, in the same way as is done with the coordinates;
- to calculate the optimal representative: to determine if the qef matrix is singular or not, and if not singular, calculating the inverse; or, eventually, averaging the accumulated values.
This implies that all operations which were done using 3- and 4-dimensional vectors and matrices, have been extended to support up to 7-dimensional vectors and matrices.
Neither the hash data structure nor the simplification scheme needed to be drastically changed.
To calculate the inverse of the 5x5, 6x6 and 7x7 matrices, first a direct approach was used. The code to do the inverse of these matrices was obtained using the computer algebra system Maple 14 [Maple12]. After some tests the direct inversion of 7x7 matrices seemed to take very long, so an alternative method was implemented to compare with. The Gauss-Jordan elimination algorithm from Numerical Recipes book was implemented [Press07].
Next table shows the time differences measured using the "Lucy" model (14,027,872 points and 28,055,742 triangles) in the same development platform (Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits). A unique simplification grid of 10243 is shown which reduces the original model to 1,317,615 points and 2,642,388 triangles. To test the inversion of the 5x5 matrices an artificial scalar, module of the point coordinates, was used and to test the inversion of the 7x7 matrices, the nodal normals were used. The table shows the cost of computing the optimal representative with the extended QEF matrix using the direct inversion approach and the Gauss-Jordan elimination method.
| Simplification | Q | inversion | Time | Memory |
| UC 10243 | geometry | 8.29 s. | 125,726 KB | |
| UC 10243 | geometry + scalar | Direct | 9.68 s. | 168,997 KB |
| UC 10243 | geometry + scalar | Gauss-Jordan | 9.52 s. | same |
| UC 10243 | geometry + vector | Direct | 47.14 s. | 284,384 KB |
| UC 10243 | geometry + vector | Gauss-Jordan | 15.39 s. | same |
| Table 3.6: Cost of calculating the optimal representative with attributes, using two different inversion methods, against the previous simplification which uses only the geometrical information. | ||||
For the 7x7 matrices the direct inversion is around 3 times slower than the Gauss-Jordan elimination. The direct approach is for general matrices, perhaps it can be specialized for the type of matrices the algorithm uses. But this specialization and the testing other methods, like the Cholesky decomposition, is left as future work.
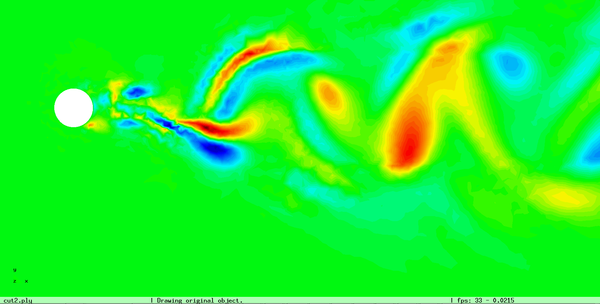
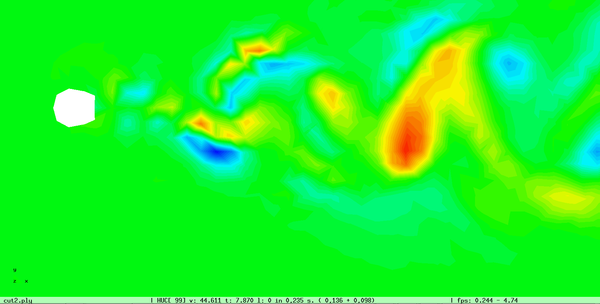
From the following figures it can be observed that the incorporation of the attributes into the simplification process helps to preserve the features present in these attributes, like discontinuities, maximum and minimum values, and to reduce the artifacts introduced by the uniform clustering.
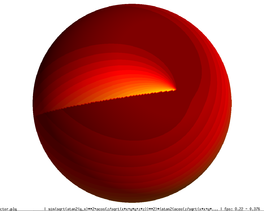
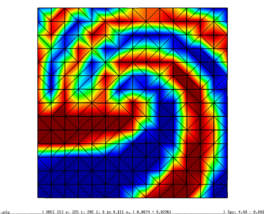
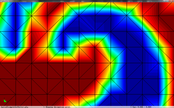
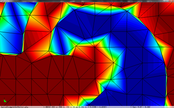
Figure 3.16 shows how the extended qef preserves the discontinuities in the scalar field. The top row shows a close-up of the discontinuity in the spiral example. The left image shows the original model, the centre one the simplified one with only geometrical information. Notice that the discontinuity is moved a bit upwards and the reticular pattern of the simplification grid can be perceived. On the other hand, the left image the scalar information has been "transferred" to the simplified mesh, and the calculated cell's representatives are placed on the discontinuity depicting faithfully this feature.
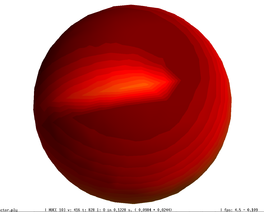
The bottom row illustrates that the discontinuity in the original sphere (left), which was smoothed away (centre) with the original simplification algorithm, shows again (right) with the incorporation of the scalar field information into the quadric error functions.
Incorporating the vector field into the qef also projects the information of these attributes into the simplified mesh, as the next figure shows:
If this improvement is applied on the model shown in Figure 2.11, the minimum and maximum values of the velocity modulus are better represented.
The next figure shows a cut plane of this model, and how the qef matrix with coordinates and the z-velocity component improves the quality of the visualization:
3.4. Conclusions
Although the octree-multi-grid scheme does a good job in concentrating triangles in the areas of the original model with more detail and saves triangles on areas with smooth curvatures or planar ones, it does not balance the memory and time cost it comes with. Compared with the shape preservation mechanism in conjunction with the normal smoothing filter, the later does a better job in preserving interesting details.
Instead of using separated hash tables for the levels of the octree, a single hash table may improve the performance of the construction process. The memory requirement is also an important factor. Other hash schemes should be looked for, with a smaller space factor than the 1.4·N of the two-level-cuckoo-hash. Another point to try is to avoid storing the qef information of the internal nodes of the octree, and store only this at the leaves. When a simplified mesh should be created, given a certain error tolerance, then the qef information of the leaves can be accumulated on the fly, and if needed stored in the final mesh, as it is only needed once per simplified mesh retrieval.
Another possibility is to combine the octree approach with the shape preservation mechanism, in conjunction with the normal planar filter, so that the savings in triangles of the first compensates for the "explosion" of triangles of the second. This is left for future work.
The discretization of the cells into sub-cells according to the normals orientation improves significantly the quality of the final simplified mesh by preserving important details which are useful for the simulation engineer, such as the two sides of a wall that usually have different scalar attributes which should be kept separated. This improvement has been incorporated also in the simplification algorithm used in GiD [GiD11].
The incorporation of the attributes in the resolution of the optimal cell representative is also very important for the simulation engineer, as the examples showed that the features and important characteristic of the attributes are preserved and reflected in the geometry of the simplified model.
To preserve extreme values inside on cell, as the ones in Figure 3.16, a modified version of shape preservation mechanism can be applied. This mechanism uses the normal orientation to subdivide the spatial cell into eight sub-cells according to the sign of the normal's components. In the same way the scalar range of values can be subdivided into two or more parts and then group the values of a cell accordingly into two or more sub-cells. This subdivision can be done in two ways:
- performing the subdivision separated from the one done using the normal criteria: normal(x, y, z) + scalar splits into 8 + 2 sub-cells and normal(x, y, z) + vector(vx, vy, vz) into 8 + 8 sub-cells, or
- extending the geometrical normal subdivision criteria to a normal in Rn incorporating the scalar attributes: normal(x, y, z) splits cell into 8 sub-cells, normal(x, y, z, Scalar) splits it into 16 sub-cells, normal(x, y, z, vx, vy, vz) into 64 sub-cells.
This is left as future work.
4. Increasing occupancy
In the previous chapter we have seen that detail preservation techniques improve the quality of the simplified mesh at the expense of increasing per-cell data, making space efficiency even more critical.
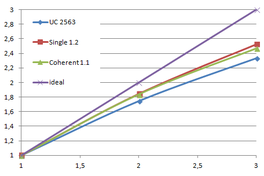
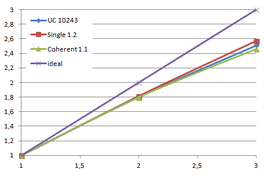
We already discussed the integration of a two-level cuckoo hash approach with vertex clustering simplification. We now deal with two new hash schemes and explore their suitability in our simplification algorithm: the single-level cuckoo hash, presented in Alcantar's dissertation "Efficient hash tables on the GPU" [Alcantara11] and the coherent parallel hash, presented by Garcia, Lefebvre, Hornus and Lasram, in the article "Coherent parallel hashing" [Garcia11].
The dissertation of Alcantara also included more experiments with the two-level cuckoo hash regarding occupancy levels, which were not included in his article [Alcantara09].
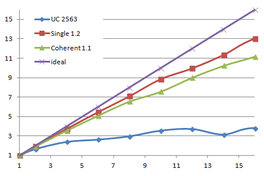
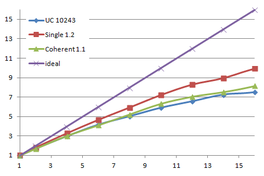
The first section of this chapter experiments with the bucket occupancy of the two-level cuckoo hash applied to the mesh simplification process of this work, trying to lower the space factor from the original 1.4·N.
Afterwards, the parallel implementation of the single-level cuckoo hash and the coherent parallel hash are explained. And finally, some results are presented and conclusions drawn.
4.1. Two-level cuckoo hash
The implementation of the two level cuckoo hash uses buckets with 573 entries for a maximum of 512 elements, but for an average occupancy of 409 elements. This represents a space factor of 1.4·N. The previous work [Pasenau11-2] already experimented increasing this average occupancy, but increasing this limit further than 419 elements, implied too many restarts, increasing the time to build the cuckoo hash table.
As proposed by Alcantara in his dissertation [Alcantara11], the bucket capacity has been increased for a maximum of 1024 and 2048 elements, while increasing the average occupancy, and so reducing the space factor, as can be seen in following table:
| Average occupancy | Maximum occupancy | Size of sub-tables | Bucket size | Space factor | Load factor |
| 409 | 512 | 191 | 573 | 1.401·N | 71.4 % |
| 870 | 1,024 | 383 | 1,149 | 1.321·N | 75.7 % |
| 1,843 | 2,048 | 761 | 2,283 | 1.239·N | 80.7 % |
| Table 4.1: As the bucket size is increased, the average occupancy has also been increased | |||||
The Lucy model has been tested with these bucket sizes to store the cells of the different simplification grids of the uniform clustering algorithm. Table 4.2 shows the times obtained on the development platform (Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits):
| Grid size | T 512 | T 1024 | % 1024/512 | T 2048 | % 2048/512 |
| 1283 | 4.32 s. | 5.51 s. | 127.6 % | 7.86 s. | 182.0 % |
| 2563 | 3.80 s. | 4.20 s. | 110.6 % | 4.68 s. | 123.2 % |
| 5123 | 4.62 s. | 4.80 s. | 104.1 % | 4.77 s. | 103.4 % |
| 10243 | 7.54 s. | 7.66 s. | 101.6 % | 7.51 s. | 99.6 % |
| 20483 | 18.51 s. | 18.60 s. | 100.5 % | 17.95 s. | 97.0 % |
| Table 4.2: Time spent simplifying the "Lucy" model using different bucket sizes an occupancies. | |||||
The implemented algorithm uses OpenMP locks at bucket level, so only one thread is allowed to update a bucket at a time. This explains the increase in time of the coarser levels, as the same number of threads are competing to access few but bigger buckets. This can be solved by reducing the granularity of the locks by using a lock for each sub-table of the bucket, for instance.
The memory savings are shown in this table:
| Grid size | Mem. 512 | Mem. 1024 | % 1024/512 | Mem. 2048 | % 2048/512 |
| 1283 | 2,184 KB | 2,118 KB | 96.9 % | 2,033 KB | 93.1 % |
| 2563 | 8,663 KB | 8,251 KB | 95.3 % | 7,844 KB | 90.6 % |
| 5123 | 33,520 KB | 31,763 KB | 94.8 % | 30,001 KB | 89.5 % |
| 10243 | 125,726 KB | 119,111 KB | 94.7 % | 112,325 KB | 89.3 % |
| 20483 | 434,659 KB | 411,745 KB | 94.7 % | 388,348 KB | 89.4 % |
| Table 4.3: Memory footprint of the hash table using different bucket sizes an occupancies. | |||||
As the hash table increases in size, the algorithm is more memory bound, so the less memory it uses, i.e. the less dispersed the memory access are, the faster it is. Finer levels with bigger buckets benefit from the reduced footprint as can be seen in the above tables, were the 20483 level runs a bit faster with the 2048-buckets than with 512-buckets.
4.2. Single-level cuckoo hash
Concept
Following the two level cuckoo hash scheme, the items are first grouped into buckets and then, three hash functions are used to access the elements inside the bucket. Each bucket uses different set of hash functions which are generated using the stored randomly generated seed and xor-ing it with different constants.
On the other hand, as explained in section 2.4, the single level cuckoo hash scheme uses four hash functions across the whole hash table, and for those elements which could not be placed, a fifth hash function is used to place them on a very small stash table. Depending on the space factor, instead of using four cuckoo hash functions, five or even six functions are needed.
Another difference with respect to the two-level cuckoo hash approach is that the incoming item is directly placed in the table in the first try, evicting the possible occupant. In the two-level cuckoo approach a first round is performed trying to place the item using any of the three hash functions. On the second round is when the items in the table were evicted eventually.
On the performed experiments, the algorithm developed for this work usually used four cuckoo hash functions. The algorithm used five functions for space factors below 1.15·N and six for space factors below 1.1·N.
Creation
To detect empty locations, first the table is filled with an EMPTY_KEY. In the implementation the empty value used is (key_type)-1 .
When an incoming item should be placed, the first hash function is used to calculate its destination. Then the location content is exchanged with the incoming item. If the exchanged content is EMPTY_KEY then the algorithm finishes and looks for another incoming item to place. If the exchanged content is an item, the hash function used to place this evicted item is fetched by calculating all four possible destinations. Then the next hash is used to place the evicted item into a new location. Again, the item is exchanged with the destination contents, and if it was EMPY_KEY, then the algorithm finishes. Otherwise a new location for the newly evicted item is calculated, and so on until the maximum number of evictions is reached (MAX_EVICTIONS). When this number is reached, the evicted item is then placed in a stash table.
The maximum number of evictions has been set to 7·log(N), as proposed in Alcantara's dissertation.
The following listing shows with more detail the algorithm:

|
The atomicExchange() retrieves the value of a memory position and then stores the new value, both operations performed atomically at once.
We target only CPU implementations and the shared memory parallelization scheme we used is OpenMP, which has no atomicExchange() operation [OpenMP11, OpenMP13]:
#pragma omp atomic capture
{v = x; x = expr; } // not supported in OpenMP 3.1, 4.0
Instead we used the lock mechanism; the following line
old_key = '''atomicExchange'''( &hash_table[ idx_to_insert].key(), key_to_insert);
changed to:
'''omp_set_lock'''( &lst_locks[ idx_to_insert]); // get lock for location idx_to_insert
old_key = hash_table[ idx_to_insert].key();
hash_table[ idx_to_insert].key() = key_to_insert;
'''omp_unset_lock'''( &lst_locks[ idx_to_insert]); // release lock for location idx_to_insert
The same has been done for the atomicExchange() in the stash table placement section.
With this modification, this implementation of the hash table needs extra memory to store the locks. To avoid using the memory that this algorithm saves for the table of locks, one lock is used to block the access to several consecutive locations.
After doing some tests, the best compromise between memory requirements and time spent in thread competition, is using one lock for every 16 locations. As mentioned in [Pasenau11-2] the size of OpenMP locks is different between MS Visual Studio 2008 and the GNU's gcc implementation. The size of Microsoft's lock is 8 bytes in a 64 bits platform, against the only 1 byte of GNU's lock.
Retrieving
Retrieving an item given its key in the two level cuckoo hash table implies first to address the bucket where this item is presumably located, then calculate the three possible locations and check their contents to see if one of the three candidates matches the key to retrieve.
To retrieve an item from the single level cuckoo hash table, four locations have to be calculated and if the item is not present in any of them, the stash table should be accessed too. The algorithm details are as follows:

|
Results
Although with the two level cuckoo hash scheme, the cuckoo hash functions have to be generated every time, only two, three or four memory accesses are necessary to store or retrieve an item from the table. All of these accesses are spatially located in one bucket range.
With the single level cuckoo hash scheme, in the best case scenario only one position has to be accessed, but four or eventually five should be checked in the worst case scenario (one more counting the use_stash flag). But all of these accesses are distributed across the whole table which hinders the performance. Table 4.4 shows that when the space factor is reduced, the simplification time increases. The simplification time includes: creation of hash, creation of quadric map, calculate optimal representatives and generation of the simplified mesh
| Grid 10243 | Space factor | T simp. | % SL / TL | Memory | % SL / TL | Average evic. |
| Two level cuckoo | 1.4 | 7.10 s. | 100.0 % | 125,726 KB | 100.0 % | |
| Single level cuckoo | 1.4 | 7.39 s. | 104.1 % | 126,494 KB | 100.6 % | 0.75 |
| Single level cuckoo | 1.3 | 7.39 s. | 104.2 % | 118,194 KB | 94.0 % | 0.93 |
| Single level cuckoo | 1.25 | 7.66 s. | 107.9 % | 114,044 KB | 90.7 % | 1.64 |
| Single level cuckoo | 1.15 | 7.52 s. | 106.1 % | 105,774 KB | 84.1 % | 1.43 |
| Single level cuckoo | 1.1 | 7.70 s. | 108.5 % | 101,594 KB | 80.8 % | 1.67 |
| Table 4.4: Comparison of the single level cuckoo hash scheme using different space factors. | ||||||
The times and the memory footprint were obtained simplifying the Lucy model on the development platform (Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits) using a grid of 10243 cells. The increase in memory between the two hash schemes with the same space factor is due to the memory used to store the locks.
The average number of evictions also increases according to the smaller space factor. It is worth to note that for a space factor of 1.25 the average number of evicted elements is higher than for more compact or spare tables. This disparity is maintained after several runs, despite that they used the same number of functions.
It should be noted that several tries with the Lucy model using the last single level cuckoo hash table, with a space factor of 1.1 and five cuckoo hash functions, showed that some elements, less than five, were placed in the stash table.
The following graph also shows the times and memory consumption for hash tables with space factor of 1.14, which use five cuckoo hash functions, and 1.09, which use six.
Along the x-axis the space factor is represented and along the y-axis, the percentage of time and memory consumption is represented with respect to the two level cuckoo hash table, which with a space factor of 1.4 has 100% of time and memory consumption.
The statistics listed in table 4.5 were compiled using the single level cuckoo hash table to store the cells of the 10243 simplification grid, with more than 50 models and demonstrates that the more compact the hash table is, the more evictions happen in the creation process:
| Space factor | Average evictions | Average max # evictions | MAX_EVICTIONS | # models with stash | Maximum # elements in stash | |
| 1.4 | 0.75 | 30.71 | 74 - 102 | 1 | 1 | |
| 1.3 | 0.93 | 39.55 | 74 - 102 | 1 | 1 | |
| 1.25 | 1.04 | 47.14 | 74 - 102 | 2 | 2 | |
| 1.2 | 1.19 | 58.62 | 74 - 102 | 1 | 1 | |
| 1.15 | 1.44 | 78.82 | 74 - 102 | 12 | 8 | |
| 1.1 | 1.65 | 87.40 | 74 - 102 | 43 | 12 | |
| Table 4.5: Statistics on evictions occurred in the 57 models tested. Max evictions is the average of the maximum number of evictions of all models. MAX_EVICTIONS is the maximum number of allowed evictions before placing the item in the stash table; the shown value is the range defined by the 57 models. As explained in the text MAX_EVICTIONS = 7·log(N) , being N the number of items to place in table which remains constant for the whole table as the same decimation grid is used. | ||||||
The third column shows the average of the number of maximum evictions for all models with the table of the corresponding space factor. This table also shows the curious behavior of the table when a space factor of 1.25 is used, showing that more models need to store more items in the stash table than in a space factor just a bit greater or smaller than 1.25 is used. The models are the Lucy statue with 14,027,872 points and 28,055,742 triangles, and the great canyon map with 8,394,753 points and 16,777,216 triangles.
4.3. Coherent parallel hash
Concept
To maintain spatial coherence Garcia et al. [Garcia11], propose to use just offset functions that places neighbouring items together in the hash table, instead of randomly distribute elements across the whole table.
As explained in section 2.4, Garcia et al. use a series of hash functions which add a different random offset to the key, so that the same key is mapped to different locations of the table. The first function is just the modulus of the table size. Together with the key, the algorithm also stores the age of the key, which tells which one of the hash function was used to store the key. This age is used to evict younger-stored items with older-to-insert items, so that the age, i.e. the effort of inserting a key, is distributed among all the keys, and so very old keys are avoided.
For each location of the hash table, the maximum age of this same location in stored in a separate table, the maximum age table. The maximum age of a certain location indicates the age of the keys with this first hash location, i.e. the number of probes done to all the keys whose first hash location was this same certain location. This is useful not only to limit the probes to look for an existing key, but to discard quickly non existing keys (early key rejection, Figure 2.8).
Garcia et al. state that the maximum age in their examples was below 16, and therefore they used four bits of the key to store the age.
Keys of some of the tested models achieved a maximum age higher than 16, in fact up to 22, depending on the space factor used. More comments about this issue can be found in the Results section, just after the next two sections which deal with implementation details.
As the keys used in the implemented simplification algorithm are 64-bits wide, the implementation of the coherent parallel algorithm for simplification used 8 bits to store the age of the key, leaving 56 bits to store the cell_id from the i, j, k indices of the cell in the decimation grid. If the normal cell subdivision criterion is used within the decimation grid as explained in section 3.2, then 64 - 8 - 3 = 53 bits are left to encode the cell_id, enough to address a grid of 128 KB3 cells.
Creation
First, all locations of the table are initialized to 0. This way, when a key is inserted using the first hash function, as the key's age is 1, the key can be inserted evicting the younger and empty cell.
The incoming key uses the first hash function to calculate its location. The age of the incoming key is compared against the age of the stored one. If the incoming key is younger than the stored one, the next hash function is used and the age of the key incremented until a location is found whose stored key is younger than the incoming one. Then the stored item is evicted and the incoming item is stored. Also, the first location (h0(key)) of the incoming key in the maximum age table is update with the new, and older, age.
If the age of the evicted key is 0, then the location was empty and the algorithm finishes. Otherwise, the key's age of the evicted item points to the hash function used to store the evicted item. Then the next hash function is used to place this evicted item. And so on until the evicted item can be placed in an empty location or until the MAXIMUM_AGE is reached, when then the creation process is restarted with new hash functions.
The algorithm uses 8 bits from the key to store the age, and in the same way, the maximum age table (max_age_table) uses unsigned char to store the maximum age for a certain location.
The following listing shows with more detail the algorithm:

|
The atomicMax() compares the incoming item with the stored in the location and if it is greater, the new item is stored in the location; in any case the contents of the location is returned. All these actions are performed atomically.
As atomicMax() operation is not present in the OpenMP standard [OpenMP11, OpenMP13], this operation will be emulated using the lock mechanism. The line
old_key = '''atomicMax'''( &hash_table[ idx_to_insert].key(), key_to_insert); is transformed to: '''omp_set_lock'''( &lst_locks[ idx_to_insert]); // get lock for location idx_to_insert old_key = hash_table[ idx_to_insert].key(); '''if''' ( key_to_insert > old_key) '''then''' hash_table[ idx_to_insert].key() = key_to_insert;
With this modification, this implementation of the hash table needs extra memory to store the locks. To avoid using the memory that this algorithm saves to hold the locks table, one lock is used to block the access to several consecutive locations.
After doing some tests, the best compromise between memory requirements and time spent in thread competition, is using one lock for every 16 locations. As mentioned in [Pasenau11-2] the size of OpenMP locks is different between MS Visual Studio 2008 and the GNU's gcc implementation. The size of Microsoft's lock is 8 bytes in a 64 bits platform, against the only 1 byte of GNU's lock.
Retrieving
To retrieve an item, the algorithm is quite simple: given a key, use the coherent hash functions to probe their generated locations.
But it is not necessary to check all possible locations generated by all the hash functions. For a certain location, the max_age_table stores the maximum age for all keys which using the first hash function would be placed in this very same location. To retrieve an item, given its key only max_age_table[ h0(key)] locations are to be checked, i.e. so many hash functions are to be evaluated.
Using this information, the retrieving algorithm still remains quite simple:

|
Results
Garcia et al. [Garcia11] use 4 bits to store the age together with the key, as all their tested models had a maximum age below 16. However, some of the tested models in the context of this work, showed a maximum age above 16, reaching the age of 22 for some of them. The next table summarizes the maximum achieved age and the average age for several space factors for 56 tested models using a decimation grid of 2563:
| Space factor | Average age | Max age | models with age >= 16 | |
| 1.4 | 1.82 | 17 | MiRotorXZ_284k | |
| 1.3 | 1.95 | 12 | ||
| 1.25 | 2.14 | 22 | Crater, MiRotorXZ_284k | |
| 1.2 | 2.22 | 19 | MiRotorXZ_284k | |
| 1.15 | 2.35 | 11 | ||
| 1.1 | 2.71 | 20 | Gear_583k, MiRotorXZ_284k | |
| 1.05 | 3.16 | 13 | ||
| Table 4.6: Maximum age statistics for the coherent parallel hash table. | ||||
The table also shows that the more compact the table is, the more effort is needed to insert a key. This effort is distributed among all the inserted items.
The nature of some models would suggest a storage pattern, which at first seems to be bad for a hash table. The crater model is quite planar and generates all cell_id of a certain slice of the decimation grid, other models, like the 'Great Canyon' or the 'Puget Sound' maps also tend to this type of pattern but they behave well with the coherent parallel hash, that is the maximum age of these two last models varies between 7 and 11 in the different runs performed. Or even the manuscript model, with a maximum age between 5 and 9.
The creation of the hash table was harder with some models. Figure 4.2 shows the peculiarities of the 3 models having a maximum age greater than 15, for some space factors:
|
|
| Figure 4.2: The three models which generates maximum ages of 16 or above: top left, 'gear_583k', top right, 'MiRotorXZ_284k', and on the left, 'crater'. | 
|
One of the benefits pointed out by Garcia et al. is that the coherent hash functions preserve the spatial coherence of the input data resulting in higher insertion and query rates. The statistic of table 4.7 confirms that despite the decreasing space factor, which brings an increasing effort in inserting keys, the simplification time does not increase that much:
| Grid 10243 | Space f. | T simp. | % SL / TL | Memory | % SL / TL | Average age | Max. age |
| Two level cuckoo | 1.4 | 7.12 s. | 100.0 % | 125,726 KB | 100.0 % | ||
| Coh. paral. hash | 1.4 | 6.75 s. | 94.8 % | 128,289 KB | 102.4 % | 1.89 | 9 |
| Coh. paral. hash | 1.3 | 6.83 s. | 96.0 % | 119,861 KB | 95.3 % | 2.11 | 9 |
| Coh. paral. hash | 1.25 | 7.35 s. | 103.4 % | 115,646 KB | 92.0 % | 3.24 | 14 |
| Coh. paral. hash | 1.2 | 7.01 s. | 98.6 % | 111,433 KB | 88.6 % | 2.36 | 9 |
| Coh. paral. hash | 1.15 | 7.19 s. | 101.0 % | 107,218 KB | 85.3 % | 2.62 | 11 |
| Coh. paral. hash | 1.1 | 7.39 s. | 103.8 % | 103,004 KB | 81.9 % | 2.94 | 11 |
| Coh. paral. hash | 1.05 | 7.72 s. | 108.6 % | 98,789 KB | 78.6 % | 3.56 | 12 |
| Table 4.7: Comparison of the coherent parallel hash using different space factors. | |||||||
The times and memory consumptions were obtained simplifying the Lucy model on the development platform (Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits) using a grid of 10243 cells. The increase in memory between the two hash schemes with the same space factor is due to the memory used to store the locks and the maximum age table.
The average age increases according to a smaller space factor, which represents the number of probe locations for an incoming item. As with the single level cuckoo times in table 4.4, using a space factor of 1.25 causes a higher creation effort than using a factor of 1.3 or 1.2. Some items being placed in a table with this space factor (1.25) require 14 probe locations, against 9 for just higher or lower space factor. This disparity is maintained after several runs.
This hash scheme also allowed the hash table to reach higher load factors, i.e. lower space factors. The simplification algorithm were able to build a coherent parallel hash table with a space factor of 1.05·N , which corresponds to a load factor of more than 95 %, with the 54 tested models. Some test reached a space factor of 1.01·N or even 1.0001·N (next prime number greater than N), although the creation time doubles the needed to create a table with space factor of 1.4·N.
The following graph shows the times and memory consumption for hash tables. Along the x-axis the space factor is represented and along the y-axis, the percentage of time and memory consumption is represented, with respect to the two level cuckoo hash table, which with a space factor of 1.4 has 100% of time and memory consumption.
It can be seen how the algorithm benefits from the maintained spatial coherence; for the same load factor, coherent parallel hashing is faster than the two level cuckoo hash scheme. And for the same time cost as the two level cuckoo hash, the coherent parallel hash scheme can reduce the load factor from 1.4·N to less than 1.2·N, which represents a memory savings of more than 13 %.
4.4. Conclusions
To compare both algorithms, the graphs from Figure 4.1 and Figure 4.3 have been merged into a new one:
This graph shows that the coherent parallel hash (COH) outperforms the single level cuckoo in time and space factor, despite using just a bit more of memory, about 1.3 % more.
The same comparison has been performed simplifying the Lucy model with a 2563 decimation grid, instead of the 10243 used in the above experiments. Table 4.8 shows times and memory measured on the development platform platform (Intel Core2 Quad Q9550 computer with MS Windows 7 64 bits):
| Single level cuckoo | Coherent parallel hash | ||||||
| Grid 2563 | Space f. | T simp. | % SL / TL | Memory | T simp. | % SL / TL | Memory |
| 1.4 | 3.94 s. | 106.2 % | 8,722 KB | 3.39 s. | 91.0 % | 8,840 KB | |
| 1.3 | 3.96 s. | 106.8 % | 8,151 KB | 3.42 s. | 91.7 % | 8,257 KB | |
| 1.25 | 3.97 s. | 107.0 % | 7,864 KB | 3.44 s. | 92.2 % | 7,969 KB | |
| 1.2 | 3.96 s. | 106.7 % | 7,578 KB | 3.55 s. | 95.1 % | 7,678 KB | |
| 1.15 | 3.97 s. | 107.1 % | 7,292 KB | 3.56 s. | 95.5 % | 7,388 KB | |
| 1.14 | 4.01 s. | 108.1 % | 7,236 KB | ||||
| 1.1 | 4.04 s. | 108.9 % | 7,006 KB | 3.64 s. | 97.5 % | 7,097 KB | |
| 1.09 | 4.05 s. | 109.1 % | 6,949 KB | ||||
| 1.05 | 3.77 s. | 101.1 % | 6,807 KB | ||||
| Two level cuckoo | 1.4 | 3.72 s. | 100.0 % | 8,663 KB | |||
| Table 4.8: Time and memory comparison between the three hash schemes. | |||||||
The graph in Figure 4.5 shows visually that the time difference between the single level cuckoo hash and the coherent parallel hash has increased noticeably:
 load factor load factor
|
| Figure 4.5: Graph showing times and memory of the three hash schemes using the 2563 decimation grid on the Lucy model. |
The time difference, which almost doubles the one from the previous experiment, can be explained looking at the memory footprint. The 10243 decimation grid uses between 100MB and 125MB depending on the hash scheme and space factor used. But the 2563 decimation grid used less memory, between 7MB and 9MB. The tests run on the Intel Core2 Quad Q9550 as CPU which has a L2 cache of 2x6MB. The whole simplification hash table fits in the CPU's cache. Clearly the maintained spatial coherence improves the usage of the CPU's cache, as table accesses are more predictable than the ones generated from the single- and two- level cuckoo hashes.
The simplification algorithm benefits from the spatial coherence maintained by coherent parallel hash proposed by Garcia et al., but supporting older ages.
5. Implementation and results
This chapter describes the implemented algorithms, their performance, and their use. Some tests have been repeated in more recent and powerful platforms. To test the algorithms more thoughtfully, the "Lucy" statue model has been refined from the original 14,027,872 points and 28,055,742 triangles to a mesh of 56,111,513 points and 112,222,968 triangles, by splitting the triangles into four new ones.
5.1. gMeshSim application and library
Application
The gMeshSim application developed in [Pasenau11-2] has been extended to support nodal attributes, the proposed hash schemes, and the algorithms to find optimal cell representatives using the normal subdivision criterion, normal planar filter and extended QEF's.
|
| Figure 5.1: Scalar support in the gMeshSim application: scalar selection menu in order to draw it and be eventually used in the simplification process. |
The program implements all the algorithms presented in this work and are available to the user at https://web.cimne.upc.edu/users/miguel/ . The program reads the attributes defined in the PLY file of the model. These attributes can be used to draw a rainbow colour map on the original and simplified models. They can also be included in the extended QEF simplification algorithms.
Some of the algorithms incorporate the attributes in the extended QEF matrix to calculate the optimal representatives as explained in section 3.3. The generated simplified mesh will also contain the calculated optimal representative for the attributes used in the QEFs. The other attributes are averaged on a per-cell basis using the created hash table.
The simplification algorithms, the ones that do not use any attribute information in the simplification process, after the geometry is simplified, average the attributes also on a per-cell basis using the created hash tables.
As the PLY format only supports scalar attributes, the following convention has been adopted to define vector attributes which will be used in the simplification algorithm that includes the vector information into the QEF matrix. The program uses as vector the first three attributes which begin with these prefixes:
| vx, vy, vz |
| red, green, blue |
| nx, ny, nz |
| r, g, b |
| x, y, z |
| Table 5.1: List of prefixes used to identify groups of three attributes as vector in the geometry + vector guided simplification process. |
With <right mouse button menu> à Model the simplification options can be found:
- the Simplify ( Octree) uses the octree structure explained in section 3.1 to simplify the model after the user enter the desired error tolerance,
- under Simplify ( Hash UC lib) the other simplification methods can be found. After entering the number of cells along one side of the decimation grid is entered the simplification method should be selected and, eventually after entering the space factor, the original model will be simplified.
The list of abbreviations and corresponding implemented algorithm is listed in the next table:
| Abbreviation | Hash scheme used | Method used to find optimal representative | Information used |
| HASH UC | Two level cuckoo | QEF inversion | Coordinates |
| HASH UC ACC | Two level cuckoo | Averaging of cell accumulation | Coordinates |
| HASH UC NORMAL | Two level cuckoo | Normal cell subdivision, QEF inversion | Coordinates, normals |
| HASH UC ADAPT NORMAL | Two level cuckoo | Normal cell subdivision, normal planar filter, QEF inversion | Coordinates, normals |
| HASH UC SCALAR | Two level cuckoo | Extended QEF inversion | Coordinates, selected scalar |
| HASH UC SCALAR3 NORMAL | Two level cuckoo | Extended QEF inversion | Coordinates, normals as vector attributes |
| HASH UC SCALAR3 VECTOR | Two level cuckoo | Extended QEF inversion | Coordinates, identified vector (table 5.1) |
| HASH UC SINGLE | Single level cuckoo (space factor is asked) | QEF inversion | Coordinates |
| HASH UC COHERENT | Coherent parallel hash (space factor is asked) | QEF inversion | Coordinates |
| Table 5.2: List of the implemented methods and corresponding abbreviations used in the program. | |||
For those simplification methods which use the normal information, the application calculates the normals at the vertices of the original mesh.
The application runs on MS Windows x64 and on Linux x64 platforms. It has been developed in C++ using OpenGL and the fltk widgets library (http://www.fltk.org).
Also a command line interface has been implemented in order to test the implemented algorithms against the library of test models.
Library
The simplification algorithms have been implemented as a C++ library behind a C façade, so that it can be integrated easily in any application.
For those simplification methods requiring normal information, the library calculates the normals at the vertices of the original mesh. When performing the simplification, the maximum number of attributes which can be cell-averaged at once is six, as no more attributes can be stored in the cell information data structure. If a mesh has more than six nodal attributes defined, then several iterations have to be performed.
The library can be used either with a single call to simplify a mesh with six or less nodal attributes, or through a handle in a "simplification session". This handle can be used first to simplify the geometry and then to simplify the attributes in several iterations or at a later time.
One time simplification can be done by calling:
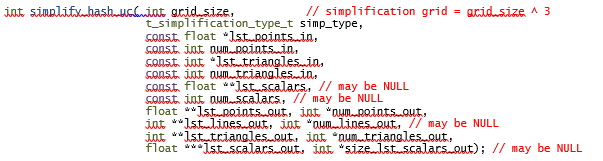
|
The library header does not define any point, vector or triangle types. Points and vectors are three floats and triangles are three integers.
If no lines are desired in the simplified mesh, then NULL pointers should be passed in the lst_lines_out and num_lines_out parameters.
For more complex meshes, lengthy sessions, or when the attributes should cell-averaged on-demand, the handler approach can be used with following procedures:
5.2. Usage in GiD
GiD is a pre- and post-processor program for simulations available at [http http]://www.gidhome.com . The application allows the user to create or import complex geometric models, defined using NURBS, Coon or planar surfaces, apply conditions, such as punctual or distributed loads or wall flow conditions, assign materials properties and define several simulation parameters. Then these geometric models are discretized by creating a mesh of geometric elements like triangles or tetrahedra, and the simulation is launched. When the simulation is finished, GiD reads the results and visualizes them over the original mesh.
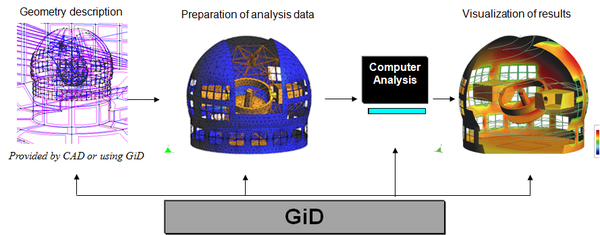
|
| Figure 5.2: Simulation process in GiD. The preparation of the data is called pre-process and the later visualization of the results is called post-process. |
As simulations become larger by making use of HPC clusters the amount of data being visualized is also increasing. Few analysis steps of a f1 racing car in a virtual wind tunnel using a mesh of more than 100 million tetrahedra, and 6 million triangles, already needs around 15 GB of storage.
Interacting with models that big is becoming an issue, both when the visualization is done remotely or with modest graphics hardware.
The simplification library has been incorporated in GiD in two scenarios:
- the user switches the visualization between the original model and the simplified one, drawing the selected result over the visualized model;
- when the user rotates, zooms in, out or moves the model around the screen, GiD performs these actions using a simplified version of the model and when the action finished, GiD renders the original model back, this is known inside GiD as fast rotation mode.
In both scenarios the library is used in "session mode". When the user selects the simplified visualization, the simplified mesh is created from the original model and each time the users selects a result to visualize the original result is averaged on a per-cell basis using the already created hash table to obtain the values for the simplified mesh.
In the second scenario, when the user initiates the action, the original model is simplified if it is not already done, and the actual visualized attributes are interpolated for the simplified mesh.
Nowadays, the simplification algorithm accessible to the final user is the explained in section 3.2, the uniform clustering simplification algorithm using the normal orientation criterion to subdivide the spatial cells of the deformation grid and using the normal planar filter. The two level cuckoo hash is used and the attributes are averaged on a per-cell basis and on user's demand.
The user can switch between the original and the simplified view and back by clicking on an icon of the top button bar, as shown in Figures 5.4 and 5.5.
The only simplification parameter adjustable by the user is the size of the decimation grid and the number of elements that triggers the simplification process:
|
| Figure 5.3: Simplification parameters in post-process in GiD, just in the bottom part of the left panel of the window. |
The model used to illustrate the simplified view option in Figures 5.4 and 5.5, is the f1 racing car model. The test was done running GiD on the master node of CIMNE's cluster using a VNC server. The VNC client run on the development platform.
Table 5.3 shows the increase in responsiveness of GiD using the f1 racing car on a remote GiD through a VNC client:
| # triangles | FPS geometry | FPS contour fill | ||
| Original model | 6,011,696 | 0.426 | 0.253 | |
| Simplified view | 178,648 | 7.095 | 2.845 | |
| Table 5.3: Rendering speed comparison between original and simplified models. The simplification process was done using a decimation grid of 2563 and it took less than 7.5 seconds on a Scientific Linux 6.1 node with 8 cores of the 2 Intel(R) Xeon(R) CPU E5410 @ 2.33GHz. | ||||
|
|
| Figure 5.4: GiD rendering the original model in the top picture, and the 2 % simplified version in the bottom picture. |
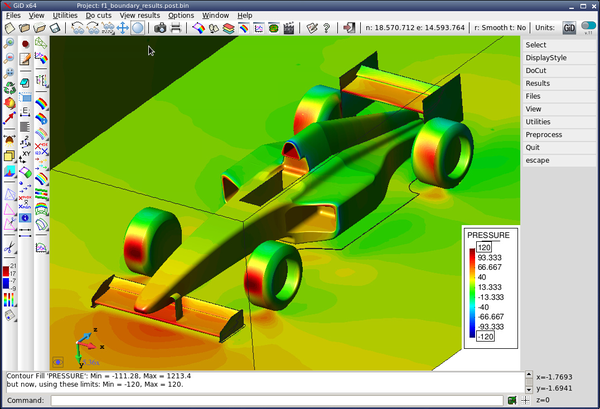
|
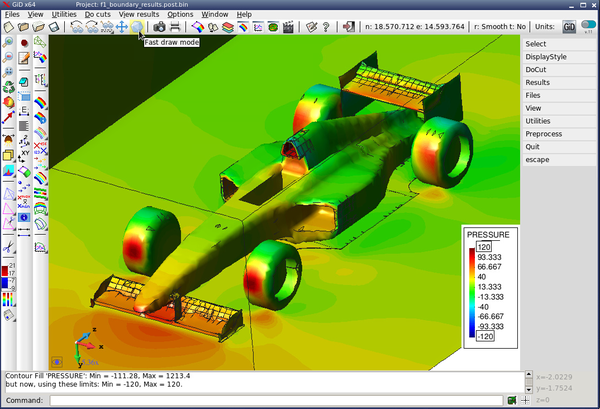
|
| Figure 5.5: GiD drawing the pressure contour fill over the original model in the top picture, and over the 2 % simplified version in the bottom picture. |
5.3. Scalability
Several platforms have been used to evaluate the scalability of the algorithms and to compare how well it performs on newer hardware, as the development platform is dated five years back. Here is a list of the test platforms:
| Platform | Development | Platform 2 | Platform 3 | Platform 4 | Platform 5 |
| CPU | Intel Core2 Quad Q9550 | Intel i7-920 | Intel i5-3570K | Intel i7-3537U (mobile) | 4 x AMD Opteron 6272 |
| # cores | 4 | 4 + HT | 4 | 2 | 16 |
| Frequency | 2.83 GHz | 2.67 GHz | 3.40 GHz | 2.00 GHz | 2.10 GHz |
| L2 cache | 2 x 6 MB | 4 x 256 KB | 4 x 256 KB | 2 x 256 KB | 8 x 2 MB |
| L3 cache | 8 MB | 6 MB | 4 MB | 2 x 8 MB | |
| Operating System | MS Windows 7 64 bits | Ubuntu 12.04.2 64 bits | Ubuntu 13.04 64 bits | Ubuntu 12.04.3 64 bits | Scientific Linux 6.3 |
| Compiles | MS Visual Studio 2008 | gcc 4.6.3 | gcc 4.7.3 | gcc 4.6.3 | gcc 4.4.5 |
| Table 5.4: The different platforms used to test the scalability of the simplification algorithms. | |||||
The scalability tests have been done using the Lucy model, with 14 million points and 28 million triangles, and two decimation grids: 2563 and 10243. For the last platform, a refined version of the Lucy model has been created by splitting every original triangle into four, resulting in a model of 56 millions points and 112 million triangles. Table 5.5 shows the sizes of the simplified models generated using the traditional uniform clustering algorithm, second column, using the normal criterion explained in section 3.2 to subdivide each spatial cell into eight sub-cells according to the normal orientation ( third column) and after applying the normal planar filter:
| Method | Uniform Clustering | Normal subdivision | Planar filter |
| Simplification grid | 2563 | 2563 | 2563 |
| Vertices | 90,780 | 141,082 | 93,503 |
| Triangles | 182,902 | 312,696 | 188,756 |
| Simplification grid | 10243 | 10243 | 10243 |
| Vertices | 1,317,615 | 1,526,656 | 1,317,901 |
| Triangles | 2,642,388 | 3,103,481 | 2,642,980 |
| Table 5.5: Sizes of the simplified models of the Lucy statue with 14,027,872 vertices and 28,055,742 triangles. | |||
| Method | Uniform Clustering | Normal subdivision | Planar filter |
| Simplification grid | 2563 | 2563 | 2563 |
| Vertices | 93,392 | 153,669 | 97,450 |
| Triangles | 188,182 | 364,905 | 197,833 |
| Simplification grid | 10243 | 10243 | 10243 |
| Vertices | 1,408,318 | 1,727,715 | 1,409,233 |
| Triangles | 2,825,306 | 3,621,946 | 2,827,320 |
| Simplification grid | 20483 | 20483 | 20483 |
| Vertices | 5,268,101 | 5,899,896 | 5,268,525 |
| Triangles | 10,569,871 | 11,967,141 | 10,570,761 |
| Table 5.6: Sizes of the simplified models of the Lucy statue with 56,111,513 vertices and 112,222,968 triangles. | |||
The algorithms tested on the different platforms are:
| Abbreviation | Description | |
| UC | Uniform clustering (QEF) with two level cuckoo hash | |
| NS | Cell subdivision using normal orientation | |
| PF | Cell subdivision using normal orientation and normal planar filter | |
| S3N | Normal vector used as vector attribute in QEF matrix to find cell's optimal representatives | |
| Single 1.2 | Uniform clustering with single level cuckoo hash and a space factor of 1.2 | |
| Coherent 1.1 | Uniform clustering with coherent parallel hash and a space factor of 1.1 | |
| Table 5.7: List of algorithms tested and abbreviations used in graphs. | ||
Development platform: graphs showing the scalability of the different algorithms and resolutions
The graphs in Figure 5.6 show the scalability of the algorithms, i.e. on the x-axis the number of cores used by the algorithms and on the y-axis the effectiveness in use of this resource.
The S3N algorithm does more work at cell level and this benefits the scalability of the algorithm, although the wall time spent is twice of the UC. Also the single level cuckoo hash scales a bit better than the other two algorithms because more hash functions need to be evaluated.
Platform 2 (i7): graphs showing the scalability of the different algorithms and resolutions.
The Intel i7 CPU has four physical cores, and eight logical cores ( Hyper-threading). These extra four artificial cores have been represented as two additional cores to the four physical ones, just for graphical purposes and to evaluate if the algorithms can take advantage of this resource.
Like in the graphs of Figure 5.6 of the development platform, the S3N algorithm does more work at cell level and therefore the algorithm shows good scalability if the 4 hyper-threading cores are not included. This extra work of the S3N algorithm requires physical resources. On the other hand, the Uniform clustering benefits clearly of the hyper-threading mechanism as more thread can be processed when some of them have to wait for memory accesses. All algorithms benefit from the hyper-threading mechanism, reaching a speed-up of almost 5. The only exceptions are the PF algorithm and the UC for small decimation grids.
The bottom left picture of Figure 5.7 shows the effect on the L3 cache in the algorithms. The hash size of the UC algorithm, which is 8,662 KB, exceeds the 8 MB of the L3 cache size, but the sizes of the 'single 1.2' and 'coherent 1.1', which are 7,526 KB and 7,050 KB respectively, fits in it.
Platform 3 (i5): graphs showing the scalability of the different algorithms and resolutions.
This Intel i5 CPU is one of the latest CPUs on the market and following graphs show the algorithm performance in this cpu.
In this platform also as the S3N algorithm does more work at the cell level, it shows a greater scalability.
Although the L3 cache of this processor is 6MB, the bottom left picture of Figure 5.8 shows that the larger size of the hash table of the UC algorithm ( 8,662 KB) hinders its performance with respect to the 'single 1.2' and 'coherent 1.1' algorithms, with table sizes of 7,526 KB and 7,050 KB respectively.
Platform 4 (i7 mobile): this is a special platform as it is a laptop using a mobile version of intel's i7 processor that has only 2 physical cores and 2 logical ones ( Hyper-threading).
Again, these extra two artificial cores have been represented as one additional cores to the two physical ones, just for graphical purposes and to evaluate if the algorithms can take advantage of this resource.
The hyper-threading feature is well exploited to get a speed-up higher than 2. But the trend of the good scalability of the S3N algorithm seems to be broken with this mobile platform. In fact the platform seems to favour the UC algorithm with less work on a cell-basis.
The uniform clustering clearly benefits from the hyper-threading mechanism as more threads can be processed when some of them have to wait for memory accesses. The bottom left picture of Figure 5.9 confirms that the greater hash table size of the UC algorithm hurts its performance when compared to the smaller tables of the Single and Coherent algorithms.
Platform 5 (Opteron 6272 cluster): this is a very special platform, a 'hybrid' shared memory supercomputer acquired by the Insituto Universitario de Invertigación, Biocomputación y Física de Sistemas Complejos, at the Universidad de Zaragoza and Zaragoza Scientific Center for Advanced modeling (ZCAM) with FEDER funds. This scientific equipment is called Caesaraugusta [Bifi12].
The cluster is a distributed memory system based on AMD64 processors at the Insituto Universitario de Invertigación, Biocomputación y Física de Sistemas Complejos, at the Universidad de Zaragoza. This cluster is composed of 3.072 processors distributed in 48 computing nodes. Each node integrates 4 Opteron 6272 processors, with a total of 64 cores and 256 GB of shared memory. One of the nodes has been used in this benchmark.
The AMD Opteron 6272 processor is based on the Bulldozer architecture [AMD12, Tom10]. The processor provides 16 cores which in fact are 8 modules with a single FPU, L2 shared cache and L1 instruction cache unit and two integer units, with their own L1 data cache. Figure 5.10 shows the diagram of Bulldozer block of an 8-core processor. The 6272 integrates two of these blocks.
|
| Figure 5.10: Block diagram of the Bulldozer architecture of an 8-core processor. |
Two types of graphs are shown. First, Figure 5.11 shows how well performs the algorithm for small workloads, using the 2563 and 10243 decimation grid on the Lucy model. Then Figure 5.12 shows the simplification algorithm using the Lucy refined model with 112 million elements and up to 64 processors.
Looking at the bottom left image of Figure 5.11 the two-level cuckoo hash used in the uniform clustering algorithm with the 2563 decimation grid behaves very strange. In fact it performs very badly, and this behaviour is also reflected ( top left image) when the same hash scheme is used with the normal subdivision criterion and when the extended qef includes the normals as attributes. This case should be examined in detail, the problem may lie in the memory allocation or cache trashing.
In the same bottom left image of Figure 5.11 shows the good scalability of the single level cuckoo hash, and the coherent parallel hash. The single level cuckoo hash scales better than the coherent may be due to the higher time spent when only one core is used. When using one core, the single level cuckoo hash needs almost 24 seconds to simplify the Lucy model with the 2563 decimation grid, and the coherent parallel hash needs only 15 seconds. When all 16 cores are used, the first hash scheme needed 1.7 seconds and the second just a bit less, 1.3 seconds.
The strange behaviour of the two level cuckoo hash with the smaller simplification grid did not occur when the larger grid was used, as the graphs of the right column of Figure 5.11 show.
When using all 64 processors with the above examples, very small work is left for the processors to do. Although the quickest algorithm, the coherent parallel hash, needed only 0,7 seconds and 2,5 seconds to simplify the Lucy model using the 2563 and 10243 simplification grid respectively, the achieved speed-up were only 21x and 9.8x respectively.
The Lucy model was refined to create a 112 million triangle mesh and simplification grids of 10243 and 20483 were used in the tests done to obtain the graphs in Figure 5.12.
Following table shows the times for one and the 64 processors with the 20483 grid and speed-up:
| Uniform clustering | Normal subdivision | Normal planar filter | Scalar 3 with normals | Single 1.2 | Coherent 1.1 | |
| 1 | 99.8 s. | 160.2 s. | 186.2 s. | 220.7 s. | 154.2 s. | 122.7 s. |
| 64 | 5.4 s. | 7.8 s. | 18.2 s. | 9.1 s. | 6.1 s. | 5.7 s. |
| Speeed-up | 18.3 | 20.4 | 10.2 | 24.2 | 25.3 | 21.4 |
| Table 5.8: Times of the different algorithms on the Caesaraugusta cluster running with 1 and 64 cores. | ||||||
The good performance of the single level cuckoo hash versus the coherent parallel hash can be explained by the refinement done with the Lucy model. The refinement splits the original triangles into four and the id's of the new nodes start after 14,027,872.
The first triangle of the original model is defined by the nodes 1, 2 and 3 and is split into four triangles, with connectivity: T1: (1, 14027873, 14027875), T2: (2, 14027874, 14027873), T3: (3, 14027875, 14027874), T4: (14027873, 14027874, 14027875). The spatial locality of the model is broken in two ways: consecutive vertices in the list of vertices will generate dispersed cell_id, thus accessing the decimation grid in a dispersed way, and when the list of triangles is parsed to generate the qef information to be accumulated in the decimation grid, the information is gathered across the whole vertices table.
This can be solved by using a vertex renumbering algorithm on the refined mesh.
Absolute numbers: following graphs shows how quick the algorithms perform using all of the cores in each one of the platforms. The times, in seconds, includes the simplification of the mesh and the cell-averaging of the attributes.
As can be seen the implemented algorithms clearly benefit from the improvements of the new architectures. Almost all algorithms get a speed-up of 3x when 4 cores are used.
This graph also shows that the simplification algorithms are faster in the 6-month old mobile platform than the 5-year old development platform. Here the improvements in the memory architecture play a very important role, as its bandwidth has more than doubled (measured using the stream benchmark 13,326.7 MB/s @ platform 4 versus 4,897.7 MB/s @ development platform).
6. Conclusions and future work
6.1. Conclusions
A tool has been developed that allows users to interact with large simulation results on remote visualization platforms and on platforms with modest graphics hardware. The developed library both includes state-of-the-art hash schemes to store the information needed to simplify this kind of meshes, and state-of-the-art detail preserving techniques. Moreover, some scientific contributions have been done in those fields. The library is able to simplify a 28 million triangle mesh with its attributes in around 4 seconds on a five year old platform, and in less than 2 seconds using today's processors.
The previous application [Pasenau11-2] has been extended to allow the testing and development of these new schemes. Several test models have been used to obtain a confident level of robustness of the implemented algorithms.
Most part of the library has been included in the pre- and post-processing tool GiD [GiD11], developed at CIMNE, and has been available to the final users since GiD version 11.1.0d, launched in July 2012. Several users already use this tool to interact remotely and get a first impression of the simulation results from CIMNE's own cluster over the network. In fact it is more used than the visualization node, which uses VirtualGL to accelerate 3D rendering on a VNC server. This tool is also being used to interact with models on platforms with modest graphic capabilities.
One of the goals of the FP7's VELaSSCo project, starting in January 2014, is to accelerate the visualization and interaction of huge and distributed simulation data from remote HPC's on local desktop computers. A way to tackle this problem is to simplify the data in-situ so that the bandwidth requirements between the HPC and the visualization platform are reduced.
6.2. Contributions
An adaptive simplification algorithm has been developed based on DeCoro at el. probabilistic octree [DeCoro07] approach. The implemented solution uses the multi-grid scheme to represent the different levels of the octree but stores all occupied nodes of the tree using Alcantara's two-level cuckoo hash [Alcantara09], instead of only storing some of them like the original approach. This generates more accurate cell representatives when few vertices of the original mesh are grouped in the leaves of the tree. For small input meshes the probabilistic octree may store only one vertex at the leaves.
Willmot's shape preservation mechanism [Willmot11] uses the normal criteria to subdivide the spatial cells of the decimation grid into eventually eight sub-cells according to the sign of the components of the grouped normals. After using this criteria, and while the optimal representative of the cell is being calculated, a new normal filter is being applied which joins the split sub-cells whose normals are 'close enough', i.e. their normals are inside a cone of a certain angle. This filter corrects some artifacts that appear when, for instance, normals at the vertices of a plane have noise that triggers the cell subdivision. It also reduces the amount of triangles generated for surfaces with smooth curvature.
Alcantara's single level cuckoo hash scheme [Alcantara11] and the coherent parallel hash scheme from Garcia et al. [Garcia11] have been extended to support 64-bit keys and to store the information of the spatial cells used in the decimation grid. The hash scheme has been extended to support ages of 32, as some of the tested models generated keys with ages greater than 16. Using this hash scheme, that uses 5 bits to encode the age of the key, together with the shape preservation mechanism explained in section 3.2, that uses 3 bits to encode the sign of the components of the normals, leaves only 24 bits free if a 32 bit key is used. These 24 bits can only encode the i, j and k integer indices of a cell in a 2563 decimation grid. But sometimes a bigger decimation grid is needed, for instance on very extensive maps or when the user requests a finer resolution of the simplified mesh.
Therefore the hash schemes have has been extended to support 64-bits keys. With such big keys, information about the attributes can also be encoded using some bits, as hinted in the next section.
6.3. Future work
An immediate task is to implement the shape preservation criteria, together with the smooth normals filter, using the coherent parallel hash algorithm, so that the benefits of the memory savings and faster simplification of the latest compensate the higher memory requirements and processing cost of the former. Also support for the extended QEF, as proposed in section 3.3, will be added to the coherent hash scheme. Both options will be made available to the GiD user.
Also the feature-preserving mechanism of incorporating attributes in the simplification process will also be extended to support more attributes and incorporated in GiD. Some other feature detection mechanisms will be studied and eventually incorporated in the simplification process so that they can be preserved. One of the possible mechanisms is the detection of vortices explained by Jiang et al. [Jiang05].
Another very interesting feature, as explained in detail in section 3.4, is to use a scalar criteria to subdivide the spatial cell of the decimation grid, like the normal criteria of Willmot's shape preservation mechanism does.
Quadric-error simplification algorithms can be applied to surface meshes, but also to volumetric meshes as explained by Garland and Xhou in "Quadric-Based Simplification in Any Dimension" [Garland04]. Instead of working with square normal distances, the authors propose to work with distances in the tangent space with a more generalized quadric error metric. This method makes it easier to implement boundary preservation by just adding a penalty factor at the boundary, instead of introducing an artificial plane as in [Garland98].
The volumetric simplification is also one of the aspects included in the FP7's VELaSSCo project starting next year.
Bibliography
[Alcantara09] Dan A. Alcantara, Andrei Sharf, Fatemeh Abbasinejad, Shubhabrata Sengupta, Michael Mitzenmacher, John D. Owens and Nina Amenta, "Real-Time Parallel Hashing on the GPU", ACM Transactions on Graphics - Proceedings of ACM SIGGRAPH Asia 2009
[Alcantara11] Dan A. Alcantara (2011) "Efficient Hash Tables on the GPU" (Doctoral dissertation), Retrieved from ProQuest Dissertations and Theses. (Accession Order No. AAT 3482095) (http://idav.ucdavis.edu/~dfalcant/research.php)
[AMD12] "The world’s first 16-core x86 processor, delivering a rich mix of performance, scalability and efficiency for today’s highly threaded computing environments", http://www.amd.com/es/Documents/50721C_6000_Series_product_brief.pdf retrieved 2013-09-06
[Bifi12] Memento / Caesaraugusta part of the scientific equipment, Insituto Universitario de Investigación Biocomputación y Física de Sistemas Complejos, Universidad de Zaragoza, http://bifi.es/en/infrastructures/scientific-equipment/memento-caesaraugusta
[Boubekeur08] Tamy Boubekeur , "Meshes, Simplification, Refinement and Multiresolution", Computer Graphics 2 course at TU Berlin, http://www.eecs.tu-berlin.de/cg-archiv/menue/teaching/ss2008/computer_graphics_2/ (August 2013).
[Celis86] Celis, P. 1986, "Robin Hood Hashing" PhD thesis, University of Waterloo, Ontario, Canada.
[DeCoro07] Christopher DeCoro and Natalya Tatarchuk, "Real-time Mesh Simplification Using the GPU", Proceedings of the 2007 symposium on Interactive 3D graphics and games, ACM New York, NY, USA, 2007.
[Devroye04] Devroye, L., Morin, P.,and Viola, A. 2004, "On worst-case robin hood hashing" SIAM Journal on Computing 33, 923–936.
[Dietzfelbinger10] M. Dietzfelbinger, A. Goerdt, M. Mitzenmacher, A. Montanari, R. Pagh, and M. Rink, "Tight thresholds for cuckoo hashing via XORSAT," in 37th Inter-national Colloquium on Automata, Languages and Programming, Jul. 2010, pp. 213-225.
[Dietzfelbinger11] M. Dietzfelbinger, M. Mitzenmacher, and M. Rink, "Cuckoo hashing with pages," in European Symposium on Algorithms, 2011, in submission.
[Fredman84] Michael L. Fredman, János Komlós and Endre Szemerédi , "Storing a spare table with O( 1) worst case access time", Journal of the ACM 31, 3 ( July), 538-544, 1984.
[Garcia11] Ismael García, Sylvian Lefebvre, Samuel Hornus, Anass Lastam, "Coherent Parallel Hashing", ACM Transactions on Graphics ( SIGGRAPH ASIA proceedings), Article 161 (December 2011).
[Garland97] Michael Garland and Paul S. Heckbert, "Surface simplification using quadric error metrics", ACM Siggraph Conference, 209-216, 1997.
[Garland98] Michael Garland and Paul S. Heckbert, "Simplifying Surfaces with Color and Texture using Quadric Error Metrics", Ninth IEEE Visualization 1998 (VIS '98) proceedings, p. 263-269, 1998.
[Garland04] Michael Garland and Yuan Zhou, "Quadric-Based Simplification in Any Dimension", Technical Report no. UIUCDCS-R-2004-2450, June 2004
[GiD11] GiD - the personal pre and postprocessor, CIMNE, http://www.gidhome.com
[Jiang05] Jiang, M., R. Machiraju, and D. Thompson, "Detection and Visualization of Vortices," The Visualization Handbook, pp. 295-309, C. Johnson and C. Hansen, eds, Academic Press, Jan 2005
[Maple12] Maple computer algebra system, version 14, Mapplesoft, http://www.maplesoft.com
[OpenMP11] OpenMP Architecture Review Board, "OpenMP Application Program Interface, Version 3.1, July 2011"
[OpenMP13] OpenMP Architecture Review Board, "OpenMP Application Program Interface, Version 4.0, July 2013"
[Pasenau11] Miguel A. Pasenau, P.Dadvand, R. Rossi, Jordi Cotela, Abel Coll and E. Oñate, "Scalable System for Large Unstructured Mesh Simulation", 23rd International Conference on Parallel Computational Fluid Dynamics 2011, Barcelona Supercomputing Center, 2011, p. 1-5.
[Pasenau11-2] Miguel A. Pasenau, "Simplificación de mallas de triángulos", Final degree project 2011, (http://hdl.handle.net/2099.1/12487)
[Peterson57] PETERSON, W. W. 1957, "Addressing for random-access storage", IBM Journal of Research and Development 1, 2, 130–146.
[Press07] Willian H.Press, Saul A. Teukolsky, Willian T. Vetterling, Brian P. Flannery, "2.1 Gauss-Jordan elimination", Numerical Recipes The Art of Scientific Computing Third edition, Ed. Cambridge University Press, New York: Cambridge University Press, 2007, p. 41-46, Print
[Schaefer03] Scott Schaefer and Joe Warren, "Adaptive Vertex Clustering Using Octrees", Proceedings of SIAM Geometric Design and Computation 2003, SIAM, New York, NY, USA, vol. 2, p. 491-500, 2003.
[Soudah11] Soudah, E, J.Pennecot, J, Suit, Bordone M., E.Oñate. (2011). Medical ‐ GiD: From medical images to simulations, MRI Flow Analysis. In Tavares, Joao & Jorge, R. M. Natal (Eds.) Computational Vision and Medical Image Processing,(pp. 145-160). Porto, Portugal: Springer
[Standford11] "The Stanford 3D Scanning Repository", http://graphics.stanford.edu/data/3Dscanrep
[Tom10] "More on Bulldozer", AMD’s Bulldozer And Bobcat Architectures Pave The Way, [http http]://www.tomshardware.com/reviews/bulldozer-bobcat-hot-chips,2724-2.html retrieved 2013-09-06
[Wikipedia13] Bulldozer (micro architecture), Wikipedia, retrieved 2013-09-06, http://en.wikipedia.org/wiki/Bulldozer_%28processor%29
[Willmot11] Andrew Willmott, "Rapid Simplification of Multi-Attribute Meshes" , Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics, August 2011, Pages 151-158, ACM New York, NY, USA.
[Yilmaz11] Erdal Yilmaz and Shahrouz Aliabadi, "Mesh Multiplication Technique With Surface Correction", Parallel CFD 2011 congress, Barcelona, Catalonia, Spain, 2011.
Annex
This section will present some of the most relevant models among the more than 100 used in this work.
Following table show the characteristics of the included models:
| PLY models | # of vertices | # of triangles | Description |
| lucy.ply | 14,027,872 | 28,055,742 | Lucy angel statue |
| lucy_refined.ply | 56,111,513 | 112,222,968 | The Lucy model refined by splitting each triangle into 4. |
| f1_00_95_boundary.ply f1_boundary_results.ply | 3;005,848 | 6,011,696 | F1 racing car model with results: Pressure and Velocity ( x, y, z and module) |
| SpiralExample3DIntVector.ply | 118,434 | 236,864 | Sphere with several manufactured attributes |
| SpiralExampleIntVector.ply | 112,652 | 224,046 | Quadrilateral surface with several manufactured attributes |
| 803_neptune_manifold.ply | 2,003,932 | 4,007,872 | Model with stretched features showed in section 3.2 |
| rotor_turb_4m.ply | 2,239,880 | 4,479,780 | Model with thin blades |
| xyzrgb_statette-withcolor.ply | 4,999,996 | 10,000,000 | Thai statuette with elephants and five attributes ( red, green, blue, alpha and quality) |
| bunny_standford.ply | 35,947 | 69,451 | Standford's bunny model |
| teapot.ply | 530 | 1.024 | OpenGL's teapot model |
| Table A.1: List of models with their description. | |||
Some pictures of the above models are shown just below.
Document information
Published on 01/01/2014
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?