Abstract
This paper presents the parametric optimization on surface quality characteristics (Ra, Rz and Rt) in hard turning of EN31 steel using multilayer coated carbide insert (TiN/TiCN/Al2O3) and also finds correlations. The experiments have been conducted based on Taguchi’s L9 orthogonal array. Multiple linear regression analysis has been utilized to find the correlations. The integrated multi-response optimization approach using CQL concept in WPCA coupled with Taguchi technique has been implemented. Based on the S/N ratio, the optimal process parameters for surface roughness i.e. Ra and Rz are the depth of cut at level 3 (0.5 mm), the cutting speed at level 3 (140 m/min), and the feed at level 1 (0.04 mm/rev). The optimal process parameters for Rt are found to be the depth of cut at level 3 (0.5 mm), the cutting speed at level 2 (100 m/min), and the feed at level 1 (0.04 mm/rev). Feed and depth of cut are found to be the significant cutting parameters affecting the responses at 95% confidence limit from ANOVA study. The first order model presented high correlation coefficient between the experimental and predicted values. The optimal parametric combination for multi-response (Ra, Rz and Rt) becomes d3–v3–f1 and is greatly improved.
Keywords
Hard machining; Multi-response optimization; Multiple linear regression; Weighted principal component analysis; Taguchi method
1. Introduction
Due to the development of newer engineering materials and targets to obtain higher productivity with good surface quality, the research in the area of cutting tool materials is continuing. The essential requirements or desirable properties for cutting tool materials include high hardness, high hot-hardness, high mechanical strength, stiffness and transverse rupture strength (TRS), high fracture toughness, chemical stability, high fatigue resistance, high heat resistance, high thermal shock resistance, adequate lubricity, resistance to adhesion and diffusion respectively. The thermal conductivity property of the tool material should be low at the surface to resist incoming of heat and high at the core to quickly dissipate the heat entered. High performance in all of these attributes simultaneously is generally not possible. The variation in the requirement of thermal conductivity has caught the attention of researchers for development of coated carbide tools. This has brought a revolution in metal cutting industry over last 30 years and developed bilayer and multilayer coated carbide inserts.
Nowadays, hardened steels about 60 HRC are successfully machined by both mixed ceramic and CBN tools and slowly replace traditional grinding operations. The main advantages of hard turning include reduction of manufacturing cycles and costs, decrease of setup time, reduction of number of necessary machine tools, achievement of comparable surface finish, elimination of part distortion caused by heat treatment, elimination of environmentally harmful coolant, low capital investment cost and low energy consumption [1]. Despite the high potential of hard machining with respect to time, cost and environment, industrial application of this technology is still limited. This is due to the uncertainties related to the surface integrity, part accuracy and economical feasibility. Considering these challenges, research in field of hard turning will definitely be worthwhile.
2. Literature review and objectives
2.1. Performance of coated carbide, ceramic and CBN insert in hard machining
Rech [2] studied various uncoated and coated carbide inserts such as PVD TiN, TiAlN and TiAlN + MoS2 and its tribological performance during machining. The TiN and (Ti,Al)N + MoS2 coatings were observed to be best for enhancement of tribological characteristics compared to uncoated carbide tools i.e. reduction of the tool-chip contact area, reduction of secondary shear zone thickness and of the interface temperature during the machining of 27MnCr5 steels. Lim et al. [3] revealed that coating on cutting tool surface provides higher crater wear resistance at high cutting speed and feed. Reduction of tool wear has been observed for TiN coated HSS tool than uncoated tool in turning hot rolled medium carbon steel. Gökkaya and Nalbant [4] studied various coated and uncoated carbide insert in dry turning AISI 1015 steel. The result revealed that lower surface roughness was obtained using CVD multilayer coated tool outermost with TiN compared to uncoated, coated with AlTiN and coated with TiAlN using the PVD technique. Wang [5] observed that marginal reduction of cutting force occurred during turning mild steel with the use of multilayer hard surface coatings CVD (TiC + Al2O3 + TiN) compared to uncoated carbide insert. Grzesik and Zalisz [6] observed that abrasion, fracture, plastic flow, material transfer and tribochemical effects involved in dry hard machining of AISI 5140 steel (60 HRC) using mixed ceramic insert. Singh and Rao [7] found that feed rate is the significant factor for surface roughness followed by nose radius and cutting velocity during finish hard turning of AISI 52100 steel using mixed ceramic inserts (Al2O3 + TiCN). Yusof et al. [8] compared the machining performance of wiper coated ceramic tool (TiN coating with mixed Al2O3/TiCN substrate) and conventional ceramic for D2 steel (54–55 HRC). Wiper tool provides slightly shorter tool life but with good finer surface finish compared to conventional tool. Paiva et al. [9] performed hard turning of AISI 52100 steel using TiN coated mixed ceramic tool (Al2O3 + TiC). Parametric conditions such as cutting speed of approximately 238 m/min, feed rate of 0.08 mm/rev and depth of cut of 0.32 mm provide maximum material removal rate with good surface quality during machining. Gaitonde et al. [10] experimentally observed that TiN coated wiper ceramic insert (Al2O3 + TiC) performed better in context to surface roughness and tool wear, while the conventional ceramic insert was beneficial in decreasing the machining force, power and specific cutting force during hard turning of D2 steel (59–61 HRC). Zhang et al. [11] investigated the surface integrity of hardened bearing steel (62–63 HRC) using CBN insert and superior surface integrity was generated. For surface roughness, feed rate was found to be the most influencing impact in machining. Özel et al. [12] studied on hard turning of AISI H13 hot work tool steel (55 HRC) using CBN inserts. For surface roughness, workpiece hardness, cutting edge geometry, feed rate and cutting speed were found to be statistically significant. Particularly, honed edge geometry and lower workpiece surface hardness yield better surface roughness, lower tangential and radial forces during machining. Jacobson [13] studied the surface integrity aspects during hard turning of M50 steels (61 HRC) using ceramic and CBN insert. Effective rake angle and tool nose radius influence on residual stress. Higher negative rake angle and smaller nose radius create a more compressive residual stress profile. The hot pressed ceramic produced a better surface than the whisker ceramic. Yallese et al. [14] investigated on hard turning of X200Cr12 steel (60 HRC) using ceramic and CBN insert and 180 m/min cutting speed was found to be limiting factor for both inserts. CBN tool induced lower surface roughness than ceramic insert under limiting criteria of wear. The recommended optimal cutting speed was observed to be 120 m/min implementing CBN tool and 60 m/min cutting speed for ceramic insert respectively. Sahoo and Sahoo [15] studied some comparative performance of uncoated and outer multilayer TiN and ZrCN coated carbide insert during hard machining of AISI 4340 steel and also economically justified.
2.2. Optimization and modeling aspects in machining
Noordin et al. [16] performed turning operation of AISI 1045 steel (187 BHN) using multilayer coated carbide insert (TiCN/Al2O3/TiN) of two types i.e. CNMG120408-FN and TNMG120408-FN through Central composite design (CCD) and response surface methodology (RSM). Most significant factor for surface roughness and the tangential force is observed to be feed during analysis. Risbood et al. [17] studied during turning operation using TiN coated tools and revealed that neural network model sufficiently predicts the surface finish with reasonable degree of accuracy. Suresh et al. [18] performed turning operation of mild steel workpiece using TiN coated carbide inserts and developed surface roughness prediction model through RSM. Experimental findings revealed that surface roughness decreases with an increase of cutting speed and increased as feed increases. Surface roughness increases as the depth of cut and nose radius increases. Using genetic algorithm (GA) technique, optimal machining condition was obtained. Davim [19] studied machining operation using carbide insert on surface roughness using Taguchi method and found a correlation with multiple linear regression analysis. Study concluded that cutting speed and interaction between cutting speed/feed had the higher impact on surface roughness followed by feed. Depth of cut did not show significance on surface roughness. Dabnun et al. [20] conducted dry machining of glass ceramic using uncoated carbide insert through factorial DOE and response surface methodology and developed surface roughness model. For surface roughness, feed rate was observed to be most dominant factor followed by cutting speed and depth of cut. Nian et al. [21] performed multi-response optimization during turning using normalized Taguchi loss function. For multi-responses such as tool life, cutting force, and surface finish, the most significant cutting parameters were feed rate and cutting speed. Datta et al. [22] performed submerged arc welding using full factorial design and developed RSM model. Multi-response optimization has been done using Gray-based Taguchi method and was improved through this methodology. Haq et al. [23] utilized gray based orthogonal array method to optimize multi-responses in drilling Al/SiC metal matrix composite that were greatly improved. Lin [24] optimized multi-responses i.e. tool life, cutting force, and surface roughness during turning using gray relational analysis coupled with Taguchi method that are greatly improved. Tzeng et al. [25] optimized process parameters in turning of high carbon high chromium tool steel (25 HRC) with TiN coated carbide insert through Gray relational analysis. From the study, depth of cut was found to be the most significance parameter on the roughness average and the cutting speed was the most dominant parameter on the roughness maximum and the roundness. Sahoo and Sahoo [26] performed hard turning of 4340 steel (HRC 47 ± 1) using multilayer coated carbide insert and developed mathematical model and multi-response parametric optimization through response surface methodology and gray-based Taguchi method. Sahoo and Sahoo [27] investigated experimental and optimization study in turning of D2 steel using TiN coated carbide insert through Taguchi technique and response surface methodology for development of model. Sahoo et al. [28] studied dry turning of AISI 1040 steel using coated carbide insert through Taguchi’s design of experiment and developed model using regression analysis. Multi-optimization of process parameter has been done through gray relational analysis and model adequacy has been checked and found to be statistically significant.
From the literature review, multilayer coated carbide inserts outperform over uncoated carbide inserts in the range of lower hardness of workpiece. The cost of these inserts is quite less compared to PCBN and ceramic. However their implementation to machine hardened steel under dry environment in the range of HRC 50–60 is lacking. Very little investigations have been carried out to judge the performances. Design of experiment and statistical methods have commonly been used for analysis, prediction and optimization in machining. The Taguchi approach is found to be popular for solving optimization problems in metal machining for single objective function. In shop floor, surface qualities are considered to be the most important parameters for judging machinability. Hence seeking a multiresponse optimization technique to predict a set of optimum process parameters to obtain better surface finish simultaneously will be worthwhile. It is observed from literature that the use of multi-response optimization approach like principal component analysis has rarely been adopted in hard turning applications.
Hence, the present work has been focused to study the performance of multilayer coated carbide tools in hard machining under different parametric ranges. Furthermore, optimization of process parameter for multiple surface quality characteristics (Ra, Rz and Rt) is essential for successful implementation of hard turning instead of cylindrical grinding. Thus, the objective of paper was to optimize the process parameter individually and simultaneously for surface quality characteristics such as Ra, Rz and Rt in hard turning of EN 31 steel (55 HRC) using multilayer coated carbide inserts (TiN/TiCN/Al2O3) under dry environment through Taguchi and weighted principal component analysis (WPCA). Correlations have been developed using multiple linear regression analysis.
3. Experimental procedures
The workpiece material taken was EN 31 steel in the form of round bar of 40 mm diameter and 120 mm long hardened to 55 HRC. The test specimen is especially used as bearing material. The conventional high rigid lathe (HMT, NH 22) of 2040 maximum spindle speed and 11 kW power was used for experimentation under dry cutting environment (Fig. 1). The multilayer coated carbide insert (TiN/TiCN/Al2O3) of ISO geometry CNMG 120408 was used and mounted with a ISO designation PCLNR 2525M12 tool holder. The insert with tool holder has the nose radius of 0.8 mm and major cutting edge angle or approach angle of 95° with back rake angle of −6°. The surface roughness parameters (Ra, Rz and Rt in microns) were measured by surface roughness tester (Taylor Hobson, Surtronic 25) where sampling length and assessment were taken as 0.8 mm and 4 mm respectively. Ra is called the arithmetic surface roughness average; Rz and Rt are the maximum peak-to-valley height within sampling length and assessment length respectively. The measurements have been taken at four different locations of the workpiece and average values are recorded. The workpiece specimens were cleaned first to remove the rust layer to achieve the required diameter.
|
|
|
Figure 1. Lathe (HMT, NH22).
|
4. Determination of optimal process parameters for individual performance characteristics
In this section, optimal process parameters for individual performance characteristics i.e. Ra, Rz and Rt are obtained. The experimental results are assessed using signal-to-noise ratio (S/N) and analysis of variance (ANOVA). The optimal parameters are judged based on the results of mean S/N ratio table of each parameter and significant influence of parameters on responses by ANOVA analysis. Further, the optimal parameters are verified by confirmation run.
4.1. Orthogonal array experimental design
For the experiment, three process parameters with three levels are selected which are shown in Table 1. For the full factorial design, it requires twenty-seven experimental runs which consume lots of time and cost. To avoid this, Taguchi proposed a special designed orthogonal array called L9 where nine experiments could be conducted. The experimental layout for the three cutting parameters using the L9 orthogonal array is shown in Table 2.
| Parameters | Notation | Unit | Levels of parameters | ||
|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |||
| Depth of cut | d | mm | 0.1 | 0.3 | 0.5 |
| Cutting speed | v | m/min | 60 | 100 | 140 |
| Feed | f | mm/rev | 0.04 | 0.08 | 0.12 |
| Run no. | Factor d | Factor v | Factor f |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 |
| 3 | 1 | 3 | 3 |
| 4 | 2 | 1 | 2 |
| 5 | 2 | 2 | 3 |
| 6 | 2 | 3 | 1 |
| 7 | 3 | 1 | 3 |
| 8 | 3 | 2 | 1 |
| 9 | 3 | 3 | 2 |
4.2. Analysis of signal-to-noise ratio
There are three categories for evaluating signal-to-noise ratios (S/N). They are the lower-the-better, the Higher-the-better and the nominal-the-better. For the performance characteristics of surface roughness, lower-the-better is taken for obtaining optimal machining performances. A lower-the-better criterion (in dB) is used for surface roughness as follows [29]:
|
|
(1) |
where y is the value of surface roughness for the ith test in that trial.
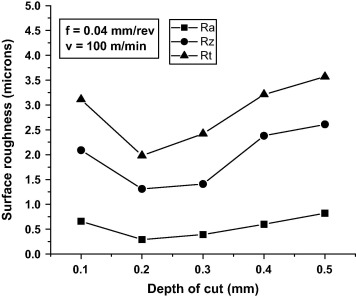
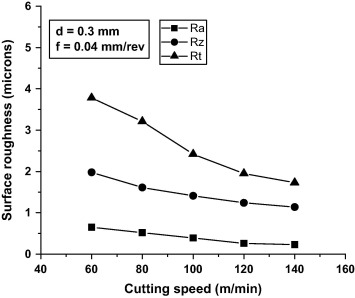
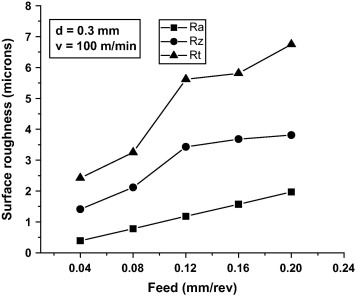
Table 3 shows the experimental results and corresponding S/N ratios of surface roughness for Ra, Rz and Rt calculated through Eq. (1). Next step is to calculate the mean S/N ratio at different levels of process parameters. For example, the mean S/N ratio for the depth of cut at levels 1, 2 and 3 can be calculated by averaging the S/N ratios for the experiments 1–3, 4–6, and 7–9 respectively and so on for other parameters such as cutting speed and feed. Table 4, Table 5 and Table 6 represent the mean S/N ratio for each level of the cutting parameters called mean S/N response table for surface roughness parameters such as Ra, Rz and Rt. Signal represents the desirable values and noise represents the undesirable values. Therefore, highest S/N ratio gives the optimal parametric combination for the responses. Thus, from mean S/N response table, the optimal process parameters for surface roughness i.e. Ra and Rz are the depth of cut at level 3 (0.5 mm), the cutting speed at level 3 (140 m/min), and the feed at level 1 (0.04 mm/rev) respectively. Similarly the optimal process parameters for Rt are found to be the depth of cut at level 3 (0.5 mm), the cutting speed at level 2 (100 m/min), and the feed at level 1 (0.04 mm/rev) respectively. Figure 2, Figure 3 and Figure 4 show the effect of process parameters such as depth of cut, cutting speed and feed on surface roughness parameters such as Ra, Rz and Rt respectively. Surface roughness parameters decrease with increase in depth of cut up to 0.2 mm and then increase with rise of depth of cut. Substantial decrease of surface roughness is noticed with rise of cutting speeds and may be due to drop of cutting forces in hard machining which brings the stability of machining system. Furthermore, surface roughness increases with increase of feed because radial force is prominent in hard machining which thus enhances vibrations and dynamic stability in the cutting zone and thus degrades the surface quality of the machined surface.
| Run | Process parameters and levels | Experimental results | Signal-to-noise ratios | ||||||
|---|---|---|---|---|---|---|---|---|---|
| d | v | f | Ra | Rz | Rt | Ra | Rz | Rt | |
| 1 | 0.1 | 60 | 0.04 | 0.73 | 3.04 | 4.54 | 2.7335 | −9.6575 | −13.1411 |
| 2 | 0.1 | 100 | 0.08 | 0.95 | 3.22 | 5.65 | 0.4455 | −10.1571 | −15.041 |
| 3 | 0.1 | 140 | 0.12 | 1.19 | 3.56 | 6.85 | −1.5109 | −11.029 | −16.7138 |
| 4 | 0.3 | 60 | 0.08 | 0.68 | 2.14 | 3.12 | 3.3498 | −6.6083 | −9.8831 |
| 5 | 0.3 | 100 | 0.12 | 0.81 | 2.75 | 3.95 | 1.8303 | −8.7867 | −11.9319 |
| 6 | 0.3 | 140 | 0.04 | 0.35 | 1.43 | 2.65 | 9.1186 | −3.1067 | −8.4649 |
| 7 | 0.5 | 60 | 0.12 | 0.85 | 2.55 | 3.12 | 1.4116 | −8.1308 | −9.8831 |
| 8 | 0.5 | 100 | 0.04 | 0.22 | 1.23 | 1.9 | 13.1515 | −1.7981 | −5.5751 |
| 9 | 0.5 | 140 | 0.08 | 0.31 | 1.46 | 2.72 | 10.1728 | −3.2871 | −8.6914 |
| Symbol | Process parameters | Mean S/N ratio | Rank | |||
|---|---|---|---|---|---|---|
| Level-1 | Level-2 | Level-3 | Max–Min | |||
| d | Depth of cut | 0.556 | 4.7663 | 8.2453 | 7.6893 | 2 |
| v | Cutting speed | 2.4983 | 5.1425 | 5.9268 | 3.4285 | 3 |
| f | Feed | 8.3346 | 4.656 | 0.577 | 7.7576 | 1 |
| Total mean S/N ratio = 4.5225 | ||||||
| Symbol | Process parameters | Mean S/N ratio | Rank | |||
|---|---|---|---|---|---|---|
| Level-1 | Level-2 | Level-3 | Max–Min | |||
| d | Depth of cut | −10.281 | −6.167 | −4.405 | 5.876 | 1 |
| v | Cutting speed | −8.132 | −6.914 | −5.808 | 2.325 | 3 |
| f | Feed | −4.854 | −6.684 | −9.315 | 4.461 | 2 |
| Total mean S/N ratio = −6.6129 | ||||||
| Symbol | Process parameters | Mean S/N ratio | Rank | |||
|---|---|---|---|---|---|---|
| Level-1 | Level-2 | Level-3 | Max–Min | |||
| d | Depth of cut | −14.965 | −10.093 | −8.05 | 6.915 | 1 |
| v | Cutting speed | −10.969 | −10.849 | −11.29 | 0.441 | 3 |
| f | Feed | −9.06 | −11.205 | −12.843 | 3.783 | 2 |
| Total mean S/N ratio = −11.0362 | ||||||
|
|
|
Figure 2. Effect of depth of cut on surface roughness parameters (Ra, Rz and Rt).
|
|
|
|
Figure 3. Effect of cutting speed on surface roughness parameters (Ra, Rz and Rt).
|
|
|
|
Figure 4. Effect of feed on surface roughness parameters (Ra, Rz and Rt).
|
4.3. Analysis of variance
Analysis of variance is used to provide the information about significance of process parameters affecting the responses. ANOVA is calculated at 95% confidence limit. Table 7, Table 8 and Table 9 show the results of ANOVA for all surface quality characteristics i.e. Ra, Rz and Rt. From the results, it can be concluded that the feed and depth of cut are the significant cutting parameters affecting the responses as their P-value (Probability of significance) is less than 0.05. Cutting speed has been found to be the insignificant parameter for all surface roughness characteristics (Ra, Rz and Rt).
| Source | DF | SS | MS | F | P | Remarks |
|---|---|---|---|---|---|---|
| d | 2 | 88.955 | 44.477 | 26.4 | 0.036 | Significant |
| v | 2 | 19.361 | 9.681 | 5.75 | 0.148 | Insignificant |
| f | 2 | 90.35 | 45.175 | 26.81 | 0.036 | Significant |
| Error | 2 | 3.37 | 1.685 | |||
| Total | 8 | 202.036 | ||||
| Source | DF | SS | MS | F | P | Remarks |
|---|---|---|---|---|---|---|
| d | 2 | 54.555 | 27.278 | 53.24 | 0.018 | Significant |
| v | 2 | 8.112 | 4.056 | 7.92 | 0.112 | Insignificant |
| f | 2 | 30.177 | 15.088 | 29.45 | 0.033 | Significant |
| Error | 2 | 1.025 | 0.512 | |||
| Total | 8 | 93.869 | ||||
| Source | DF | SS | MS | F | P | Remarks |
|---|---|---|---|---|---|---|
| d | 2 | 75.735 | 37.868 | 163.93 | 0.006 | Significant |
| v | 2 | 0.312 | 0.156 | 0.67 | 0.597 | Insignificant |
| f | 2 | 21.59 | 10.795 | 46.73 | 0.021 | Significant |
| Error | 2 | 0.462 | 0.231 | |||
| Total | 8 | 98.099 | ||||
4.4. Confirmation tests
The next step is to conduct confirmation test to predict and verify the improvements of performance characteristics using the optimal level of process parameters. Table 10 and Table 11 show the results of confirmation experiment. The predicted S/N ratio, , using the optimal level of the process parameters can be calculated as [30] follows:
|
|
(2) |
where is the total mean of the S/N ratio, is the mean S/N ratio at the optimal level, and o is the number of the main design parameters that significantly affect the performance characteristics.
| Initial process parameters | Optimal process parameters | ||
|---|---|---|---|
| Prediction | Experiment | ||
| Level | d2–v2–f2 | d3–v3–f1 | d3–v3–f1 |
| Ra | 0.75 | 0.28 | |
| Rz | 2.51 | 1.36 | |
| S/N Ratio (dB) for Ra | 2.4987 | 13.4617 | 11.0568 |
| S/N Ratio (dB) for Rz | −7.9934 | −1.8412 | −2.6707 |
| Improvement of S/N Ratio for Ra = 8.5581Improvement of S/N Ratio for Rz = 5.3227 | |||
| Initial process parameters | Optimal process parameters | ||
|---|---|---|---|
| Prediction | Experiment | ||
| Level | d2–v2–f2 | d3–v2–f1 | d3–v2–f1 |
| Rt | 3.61 | 1.9 | |
| S/N ratio (dB) for Rt | −11.1501 | −5.8866 | −5.575 |
| Improvement of S/N Ratio for Rt = 5.5751 | |||
Good agreement between the predicted machining performance and actual machining performance is shown. The improvement of S/N ratio from initial process parameters to optimal process parameters is 8.5581 for Ra and 5.3227 for Rz respectively. Similarly, the improvement of S/N ratio from initial process parameters to optimal process parameters is 5.5751 for Rt. Based on the result of the confirmation test, the surface roughness (Ra) is decreased 2.68 times, Rz is decreased 1.85 times and Rt is decreased 1.9 times respectively in hard turning of EN31 steel using multilayer coated carbide insert under dry cutting environment.
5. Correlations
The correlations between the process parameters (depth of cut, cutting speed and feed) and the measured Ra, Rz and Rt were obtained by multiple linear regression analysis. The equations obtained were as follows:
|
|
|
|
(3) |
|
|
|
|
(4) |
|
|
|
|
(5) |
The first order model presented high correlation coefficient (R2 = 0.952, 0.932 and 0.918) explaining 95.2%, 93.2% and 91.8% of the variability in the Ra, Rz and Rt respectively. Higher R2 (coefficient of correlation) indicates the goodness of fit for the model to the actual data and high statistical significance of the model [31]. R2 adjusted statistic analysis has been included in the model because greater R2 value may not indicate the accuracy of model. The R2 and adjusted R2 values are very close and do not differ so much. The R2 adj values for Ra, Rz and Rt are 92.3%, 89.2% and 86.9% respectively which indicates 92.3%, 89.2% and 86.9% of variability are explained by the model after considering the significant factors. It concludes that unnecessary terms are not included in the model. It indicates good correlations between the experimental and predicted values of surface quality characteristics.
6. Multi-response optimization using weighted PCA
Multi-response parametric optimization for three surface quality characteristics i.e. Ra, Rz and Rt has been done using weighted principal component analysis (WPCA) coupled with Taguchi method. The study applied WPCA to eliminate response correlation and to evaluate independent or uncorrelated quality indices called principal components which were aggregated by WPCA to compute overall quality index denoted as Multi-Response Performance Index (MPI). A combined quality loss (CQL) was then estimated which was optimized (minimized) finally. The study combined WPCA and Taguchi method for predicting optimal setting. Optimal result was verified through confirmatory test [32].
The experimental data are normalized first (Table 12) considering lower-the-better criteria i.e. Xi∗(k) = [min Xi (k)/Xi (k)] where Xi∗(k) is the normalized data of the kth element in the ith sequence. Then, the correlations between the responses are checked. Table 13 represents Pearson’s correlation coefficient between the responses. All responses are correlated to each other due to non-zero value of correlation coefficients. Principal component analysis (Eigen value, Eigen vector, accountability proportion and cumulative accountability proportion) is applied in order to eliminate the response correlation and shown in Table 14.
| Sl. No | Normalized data for surface roughness characteristics | ||
|---|---|---|---|
| Ra | Rz | Rt | |
| Ideal | 1 | 1 | 1 |
| 1 | 0.3013 | 0.4046 | 0.4185 |
| 2 | 0.2315 | 0.3819 | 0.3362 |
| 3 | 0.1848 | 0.3455 | 0.2773 |
| 4 | 0.3235 | 0.5747 | 0.6089 |
| 5 | 0.2716 | 0.4472 | 0.481 |
| 6 | 0.6285 | 0.8601 | 0.7169 |
| 7 | 0.2588 | 0.4823 | 0.6089 |
| 8 | 1 | 1 | 1 |
| 9 | 0.7096 | 0.8424 | 0.6985 |
| Sl. No | Correlation between responses | Pearson correlation coefficient | Comment |
|---|---|---|---|
| 1 | Ra and Rz | 0.966 | Both are correlated |
| 2 | Ra and Rt | 0.906 | Both are correlated |
| 3 | Rz and Rt | 0.932 | Both are correlated |
| Ψ1 | Ψ2 | Ψ3 | |
|---|---|---|---|
| Eigen value | 2.8695 | 0.0999 | 0.0306 |
| Eigen vector | −0.578 | 0.553 | 0.601 |
| −0.583 | 0.235 | −0.778 | |
| −0.571 | −0.8 | 0.186 | |
| AP (accountability proportion) | 0.957 | 0.033 | 0.01 |
| CAP (cumulative accountability proportion) | 0.957 | 0.99 | 1.000 |
Then correlated responses are converted to uncorrelated quality indices called individual principal component (Z1, Z2 and Z3) and shown in Table 15.
| Sl. No | Individual principal components | ||
|---|---|---|---|
| Z1 | Z2 | Z3 | |
| Ideal | −1.732 | −0.012 | 0.009 |
| 1 | −0.6489 | −0.0731 | −0.0558 |
| 2 | −0.5484 | −0.0511 | −0.0954 |
| 3 | −0.4665 | −0.0384 | −0.1061 |
| 4 | −0.8697 | −0.1731 | −0.1394 |
| 5 | −0.6923 | −0.1295 | −0.0952 |
| 6 | −1.274 | −0.0238 | −0.158 |
| 7 | −0.7784 | −0.2306 | −0.1064 |
| 8 | −1.732 | −0.012 | 0.009 |
| 9 | −1.3001 | 0.0315 | −0.0989 |
Accountability proportion of individual principal components has been treated as individual priority weights. Next, Multi-Response Performance Index (MPI) is calculated using the following equation:
|
|
(6) |
It is observed that the MPI values are negative. The concept of CQL has been introduced which is the absolute deviation of MPI from its ideal value and modulus of its yields positive value. The modulus of deviation facilitates computing signal to noise (S/N) ratio and is shown in Table 16. This CQL is treated as the single response objective function to minimize it. Thus a multi-response optimization problem is converted into a single response optimization problem which can be solved by Taguchi method. Next, the mean response S/N ratio of CQL is calculated for each level of parameters using traditional Taguchi method and shown in Table 17. Optimal parametric combination is derived from Table 17 taking higher value of mean S/N ratio of CQL. Thus the predicted optimal parametric combination becomes d3–v3–f1 i.e. depth of cut (0.5 mm), cutting speed (140 m/min) and feed (0.04 mm/rev) respectively. The three surface roughness characteristics i.e. Ra, Rz and Rt at optimal level are found to be 0.28 μm, 1.36 μm and 1.81 μm respectively.
| Sl. No | MPI | CQL | S/N ratio of CQL |
|---|---|---|---|
| Ideal | −1.6587 | 0 | – |
| 1 | −0.6239 | 1.0339 | −0.2895 |
| 2 | −0.5274 | 1.1304 | −1.0646 |
| 3 | −0.4487 | 1.2091 | −1.6492 |
| 4 | −0.8394 | 0.8184 | 1.7406 |
| 5 | −0.6677 | 0.9901 | 0.0864 |
| 6 | −1.2215 | 0.4363 | 7.2042 |
| 7 | −0.7536 | 0.9042 | 0.8747 |
| 8 | −1.6578 | 0 | – |
| 9 | −1.2441 | 0.4137 | 7.6662 |
| Symbol | Process parameters | Mean S/N ratio | Rank | |||
|---|---|---|---|---|---|---|
| Level-1 | Level-2 | Level-3 | Max–Min | |||
| d | Depth of cut | −1.0012 | 3.0105 | 4.2705 | 5.2717 | 1 |
| v | Cutting speed | 0.7753 | −0.4891 | 4.4071 | −0.2294 | 2 |
| f | Feed | 3.4574 | 2.7808 | −0.2294 | 3.6867 | 3 |
Finally, optimal results are verified by some confirmation run. From confirmation experiment (Table 18), it shows the improvement of quality characteristics. Also the improvement of S/N ratio of CQL is found to be 15.6817 dB which shows the feasibility of the weighted principal component analysis. Therefore, it can be explained that high value of depth of cut and cutting speed and low value of feed lower the surface roughness in hard turning of EN31 steel using multilayer coated carbide insert under dry environment.
| Initial process parameters | Optimal process parameters | |
|---|---|---|
| Experiment | ||
| Level | d2–v2–f2 | d3–v3–f1 |
| Ra | 0.75 | 0.28 |
| Rz | 2.51 | 1.36 |
| Rt | 3.61 | 1.81 |
| S/N ratio of CQL | 0.6415 | 16.3232 |
| Improvement of S/N ratio of CQL = 15.6817 dB | ||
7. Conclusions
Application of the Taguchi parameter design and weighted principal component in the individual and simultaneous optimization of responses in hard turning of EN 31 bearing steel using multilayer coated carbide insert has been studied. The following conclusions are made of the present study:
- Feed and depth of cut are found to be the significant cutting parameters affecting the responses at 95% confidence limit. Cutting speed has been found to be the insignificant parameter for all surface roughness characteristics (Ra, Rz and Rt).
- Surface roughness increases with increase of feed rate and depth of cut. Decreasing trends of surface roughness are noticed with increase of cutting speed. The measured arithmetic surface roughness average (Ra) is quite less than 1.6 microns indicating comparable cylindrical grinding operation for finishing the hardened components.
- Based on the S/N analyses, the optimal process parameters for surface roughness i.e. Ra and Rz are the depth of cut at level 3 (0.5 mm), the cutting speed at level 3 (140 m/min), and the feed at level 1 (0.04 mm/rev). Similarly, the optimal process parameters for Rt are found to be depth of cut at level 3 (0.5 mm), cutting speed at level 2 (100 m/min) and feed at level 1 (0.04 mm/rev) respectively.
- The improvement of S/N ratio from initial process parameters to optimal process parameters is 8.5581 for Ra, 5.3227 for Rz and 5.5751 for Rt respectively.
- Based on the result of the confirmation test, the surface roughness (Ra) is decreased 2.68 times, Rz is decreased 1.85 times and Rt is decreased 1.9 times respectively in hard turning of EN31 steel using multilayer coated carbide insert under dry environment.
- The first order model presented high correlation coefficient (R2 = 0.952, 0.932 and 0.918) explaining 95.2%, 93.2% and 91.8% of the variability in the Ra, Rz and Rt respectively and indicates good correlations between the experimental and predicted values of surface quality characteristics.
- Concept of CQL has been utilized to the objective function. This facilitates the computation of S/N ratio using Taguchi as its value remains always positive. The optimal parametric combination for multi-response (Ra, Rz and Rt) becomes d3–v3–f1 i.e. depth of cut: 0.5 mm, cutting speed: 140 m/min and feed: 0.04 mm/rev and is greatly improved.
- The integrated optimization approach using WPCA coupled with Taguchi technique is found to be efficient and suitable in connection with correlated multi-response optimization in hard machining.
References
- [1] H. Tönshoff, C. Arendt, R.B. Amor; Cutting of hardened steel; Ann. CIRP Keynote Pap., 49 (2) (2000), pp. 547–565
- [2] J. Rech; Influence of cutting tool coatings on the tribological phenomena at the tool-chip interface in orthogonal dry turning; Surf. Coat. Technol., 200 (2006), pp. 5132–5139
- [3] C.Y.H. Lim, S.C. Lim, K.S. Lee; The performance of TiN-coated high speed steel tool inserts in turning; Tribo. Int., 32 (1999), pp. 393–398
- [4] H. Gökkaya, M. Nalbant; The effects of cutting tool coating on the surface roughness of AISI 1015 Steel depending on cutting parameters; Turkish J. Eng. Environ. Sci., 30 (2006), pp. 307–316
- [5] J. Wang; The effect of multi-layer surface coatings of carbide inserts on the cutting forces in turning operations; J. Mater. Process. Technol., 97 (2000), pp. 114–119
- [6] W. Grzesik, Z. Zalisz; Wear phenomenon in the hard steel machining using ceramic tools; Tribol. Int., 41 (2008), pp. 802–812
- [7] D. Singh, P.V. Rao; A surface roughness prediction model for hard turning process; Int. J. Adv. Manuf. Technol., 32 (2007), pp. 1115–1124
- [8] N.M. Yusof, A.M. Zainal, H.D. Kurniawan; Hard turning of cold work tool steel using wiper ceramic tool; Jurnal Mekanikal, 25 (2008), pp. 92–105
- [9] A.P. Paiva, J.R. Ferreira, P.P. Balestrassi; A multivariate hybrid approach applied to AISI 52100 hardened steel turning optimization; J. Mater. Process. Technol., 189 (2007), pp. 26–35
- [10] V.N. Gaitonde, S.R. Karnik, L. Figueira, J.P. Davim; Machinability investigations in hard turning of AISI D2 cold work tool steel with conventional and wiper ceramic inserts; Int. J. Ref. Met. Hard Mater., 27 (2009), pp. 754–763
- [11] C.XP. Zhang, R. Liu, Z. Yao; Experimental study and evaluation methodology on hard surface integrity; Int. J. Adv. Manuf. Technol., 34 (1–2) (2006), pp. 141–148
- [12] T. Özel, T. Hsu, E. Zeren; Effects of cutting edge geometry, workpiece hardness, feed rate and cutting speed on surface roughness and forces in finish turning of hardened AISI H13 steel; Int. J. Adv. Manuf. Technol., 25 (2005), pp. 262–269
- [13] M. Jacobson; Surface integrity of hard-turned M50 steel; Proc. IMechE, Part B: J. Eng. Manuf., 216 (2002), pp. 47–54
- [14] M.A. Yallese, J-F. Rigal, K. Chaoui, L. Boulanouar; The effects of cutting conditions on mixed ceramic and cubic boron nitride tool wear and on surface roughness during machining of X200Cr12 steel (60 HRC); Proc. IMechE, Part B: J. Eng. Manuf., 219 (2005), pp. 35–55
- [15] A.K. Sahoo, B. Sahoo; Experimental investigations on machinability aspects in finish hard turning of AISI 4340 steel using uncoated and multilayer coated carbide inserts; Measurement, 45 (2012), pp. 2153–2165
- [16] M.Y. Noordin, V.C. Venkatesh, S. Sharif, S. Elting, A. Abdullah; Application of response surface methodology in describing the performance of coated carbide tools when turning AISI 1045 steel; J. Mater. Process. Technol., 145 (2004), pp. 46–58
- [17] K.A. Risbood, U.S. Dixit, A.D. Sahasrabudhe; Prediction of surface roughness and dimensional deviation by measuring cutting forces and vibrations in turning process; J. Mater. Process. Technol., 132 (2003), pp. 203–214
- [18] P.V.S. Suresh, P.V. Rao, S.G. Deshmukh; A genetic algorithmic approach for optimization of surface roughness prediction model; Int. J. Mach. Tools Manuf., 42 (2002), pp. 675–680
- [19] J.P. Davim; A note on the determination of optimal cutting conditions for surface finish obtained in turning using Design of Experiment; J. Mater. Process. Technol., 116 (2001), pp. 305–308
- [20] M.A. Dabnun, M.S.J. Hashmi, M.A. El-Baradie; Surface roughness prediction model by design of experiments for turning machinable glass–ceramic (Macor); J. Mater. Process. Technol., 164–165 (2005), pp. 1289–1293
- [21] C.Y. Nian, W.H. Yang, Y.S. Tarng; Optimization of turning operations with multiple performance characteristics; J. Mater. Process. Technol., 95 (1999), pp. 90–96
- [22] Datta, A. Bandyopadhyay, P.K. Pal; Modeling and optimization of features of bead geometry including percentage dilution in submerged arc welding using mixture of fresh flux and fused slag; Int. J. Adv. Manuf. Technol., 36 (2008), pp. 1080–1090
- [23] A.N. Haq, P. Marimuthu, R. Jeyapaul; Multi response optimization of machining parameters of drilling Al/SiC metal matrix composite using grey relational analysis in the Taguchi method; Int. J. Adv. Manuf. Technol., 37 (2008), pp. 250–255
- [24] C.L. Lin; Use of the Taguchi Method and Grey Relational Analysis to optimize turning operations with multiple performance characteristics; Mater. Manuf. Process., 19 (2) (2004), pp. 209–220
- [25] C.J. Tzenga, Y.-H. Linb, Y.-K. Yanga, M.-C. Jeng; Optimization of turning operations with multiple performance characteristics using the Taguchi method and Grey relational analysis; J. Mater. Process. Technol., 209 (2009), pp. 2753–2759
- [26] A.K. Sahoo, B. Sahoo; Performance studies of multilayer hard surface coatings (TiN/TiCN/Al2O3/TiN) of indexable carbide inserts in hard machining: Part-II (RSM, grey relational and techno economical approach); Measurement, 46 (2013), pp. 2868–2884
- [27] A.K. Sahoo, B. Sahoo; Surface roughness model and parametric optimization in finish turning using coated carbide insert: response surface methodology and Taguchi approach; Int. J. Ind. Eng. Comput., 2 (2011), pp. 819–830
- [28] A.K. Sahoo, A.N. Baral, A.K. Rout, B.C. Routra; Multi-objective optimization and predictive modeling of surface roughness and material removal rate in turning using grey relational and regression analysis; Proc. Eng., 38 (2012), pp. 1606–1627
- [29] A.K. Sahoo, S. Pradhan; Modeling and optimization of Al/SiCp MMC machining using Taguchi approach; Measurement, 46 (2013), pp. 3064–3072
- [30] M. Nalbant, H. Gokkaya, G. Sur; Application of Taguchi method in the optimization of cutting parameters for surface roughness in turning; Mater. Des., 28 (2007), pp. 1379–1385
- [31] A.K. Sahoo, S. Pradhan, A.K. Rout; Development and machinability assessment in turning Al/SiCp-metal matrix composite with multilayer coated carbide insert using Taguchi and statistical techniques; Arch. Civ. Mech. Eng., 13 (2013), pp. 27–35
- [32] B.C. Routara, S.D. Mohanty, S. Datta, A. Bandyopadhyay, S.S. Mahapatra; Combined quality loss (CQL) concept in WPCA-based Taguchi philosophy for optimization of multiple surface quality characteristics of UNS C34000 brass in cylindrical grinding; Int. J. Adv. Manuf. Technol., 51 (2010), pp. 135–143
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?