1. Introducción

Los incendios en estructuras civiles constituyen un problema ampliamente reconocido en la ingeniería, donde la estabilidad frente al fuego se evalúa mediante criterios de resistencia que combinan funciones de carga (R), integridad (E) e aislamiento térmico (I) [1] según el Eurocódigo EN 1991-1-2 para acero y hormigón [2] y el Documento Básico SI del Código Técnico de la Edificación (DB-SI), sección SI-6 [3]. Ejemplos recientes ilustran la rapidez y severidad de estos fenómenos: el incendio del complejo residencial de Campanar en Valencia el 22 de febrero de 2024, un fuego de fachada que colapsó una envolvente ventilada con núcleo de polietileno [4]; el siniestro de la Cooperativa Abacus en Igualada en 2010, un fuego de cubierta iniciado en instalaciones fotovoltaicas [5]; y el incendio de la Torre Windsor en Madrid el 12 de febrero de 2005, un fuego de compartimento interior que se propagó vertical y horizontalmente por huecos sin compartimentación efectiva [6]; entre muchos otros (de esquina, de almacén, etc.). Para caracterizar la dinámica del fuego y su interacción con el entorno se emplean herramientas CFD como el programa Fire Dynamics Simulator (FDS) [7, 8] del Instituto Nacional de Estándares y Tecnología (NIST) y el modelo por zonas CFAST [9], aunque sus esquemas térmicos simplificados suelen requerir acoplamientos con programas de cálculo FEM para una simulación termo-estructural más fiel.

En el ámbito marítimo, la normativa SOLAS [10] y el Código FTP [11] establecen ensayos de integridad y aislamiento para compartimentación (clases A-60, B-15, C, etc.) y permiten diseños alternativos con materiales compuestos siempre que demuestren un comportamiento “equivalente al acero” en ensayos de fuego, aunque las Directrices MSC.1/Circ.1574 alertan sobre la carencia de criterios específicos para estructuras de FRP durante y tras un incendio [12]. El incendio del ferry Ro-Ro Sorrento el 28 de abril de 2015 se originó en la bodega de vehículos por un fuego de hidrocarburos que se propagó rápidamente a través de los espacios libres entre bastidores [13]. En contraste, el Felicity Ace sufrió un incendio en una cubierta de vehículos el 16 de febrero de 2022 [14]; en este caso, la presencia de automóviles eléctricos con baterías de iones de litio (fuego de metales, clase D), complicó las operaciones de extinción y prolongó significativamente la duración del fuego. De igual manera se emplean simulaciones de la dinámica del fuego (FDS) o de modelos de zona, pero sin incorporar la respuesta mecánica de la estructura, confiando en ensayos FTP y verificaciones experimentales para el diseño completo. Estas limitaciones sugieren que los enfoques basados en criterios de fluencia o pandeo podrían resultar insuficientes frente a los retos termo-mecánicos de los compuestos.

Este trabajo recopila y referencia metodologías previas para demostrar cómo los fenómenos de fluencia combinados con el pandeo quedan generalmente infraestimados en las fases de diseño de estructuras compuestas frente al fuego.

2. Fundamentos y trabajo previo

El objetivo de esta sección es la caracterización del comportamiento experimental de los compuestos mediante modelos numéricos. El modelo computacional que integra los diferentes modelos fundamentales es el descrito en el trabajo previo [15, 16, 17], el cual es verificado en la sección 3.

2.1. Flexibilidad inherente de los materiales compuestos

Los materiales compuestos muestran una flexibilidad superior a la del acero bajo cargas equivalentes, debido a su menor módulo en direcciones no fibras y a su mayor relación entre resistencia a fluencia y deformación límite. Si definimos el ratio crítico (equivalente al módulo de elasticidad):

(1)

y lo normalizamos respecto al acero ( ${\textstyle {R}_{acero}=1}$ ), obtenemos los siguientes valores indicativos para distintos materiales:

Material	${\textstyle {\sigma }_{y}}$ (MPa)	${\textstyle {\epsilon }_{y}}$ (%)	R (GPa)	$R/{R}_{acero}$
Acero estructural	250	0,20	125	1,00
Aluminio 6061	150	0,30	50	0,40
Hormigón armado (f=40 MPa)	40	0,01	4	0,03
Mampostería cerámica	5	0,10	5	0,04
FRP vidrio-epoxi	500	1,50	33	0,26
FRP carbono-epoxi	1 500	1,00	150	1,20
FRP fibra-viniléster	400	2,00	20	0,16

Tabla 1. Valores de referencia comúnmente aceptados para diferentes materiales.

La Tabla 1 muestra que, salvo en compuestos de fibra de carbono, la rigidez efectiva de los FRP es menor que la del acero, lo que produce desplazamientos significativos bajo el mismo nivel de carga.

Asimismo, los compuestos son ortótropos, i.e., su rigidez y resistencia en la dirección principal de las fibras ( ${\textstyle {E}_{1}}$ , ${\textstyle {\sigma }_{{y}_{1}}}$ ) difieren notablemente de las propiedades transversales ( ${\textstyle {E}_{2}}$ , ${\textstyle {\sigma }_{{y}_{2}}\ll {\sigma }_{{y}_{1}}}$ ), y a su vez de las de la matriz polimérica considerada isotrópica ( ${\textstyle {E}_{m},\,{\sigma }_{{y}_{m}}\ll {\sigma }_{{y}_{3}}}$ ). En diseño de protecciones pasivas frente al fuego, la orientación de fibras suele optimizarse para maximizar la rigidez y resistencia en la dirección de las solicitaciones predominantes, pero la elevada deformabilidad transversal puede inducir grandes desplazamientos y rotaciones entre zonas frías y calientes, acrecentando la necesidad de capturar la no linealidad geométrica en el transcurso del escenario de fuego.

Una forma eficaz y sencilla de capturar la no linealidad geométrica es la teoría corrotacional de Felippa y Haugen [18], que descompone el movimiento en rotaciones rígidas y deformaciones locales, actualizando la orientación de los elementos sin alterar el modelo constitutivo del material (véase [17]).

2.2. Degradación de los materiales compuestos

Los materiales compuestos muestran degradación progresiva de rigidez y resistencia bajo cargas térmicas y mecánicas sin deformación permanente, lo que los hace mejor representados por teorías de daño. Los modelos de daño isotrópico—basados en la formulación termodinámica irreversible de Simo y Ju [19]—introducen variables internas de daño que degradan la matriz constitutiva del material, capturando la pérdida de integridad antes de la falla final.

La teoría Regla de mezclas Serie-Paralelo (SPROM) [20] combina de forma implícita los límites de Voigt (serie) [21] y Reuss (paralelo) [22] para derivar las propiedades ortótropas del laminado a partir de las propiedades de fibra y matriz. Al incorporar un modelo de daño isotrópico en cada componente, SPROM permite obtener un comportamiento ortótropo no lineal completo del compuesto, sin limitarse al régimen elástico (véase [16]).

2.3. Excentricidad inducida por el fuego

En escenarios de fuego compartimentado, la cara expuesta al calor sufre una dilatación térmica que tiende a tensar dicha superficie, mientras que la cara opuesta trabaja a compresión, creando una excentricidad térmica que modifica la curvatura inicial de la estructura. Este efecto se agrava en compuestos por la reducción del módulo de Young y del límite elástico con el aumento de la temperatura, con el consiguiente aumento de la deformabilidad y que acelera la degradación inelástica. Así como por la pirolisis de la resina, proceso de degradación, que disminuye progresivamente la rigidez y altera el comportamiento termo-mecánico [23].

Todos estos efectos dependen de la temperatura a la que están sometidas las secciones. La temperatura puede obtenerse mediante curvas estándar de fuego (ISO 834 [24, 25], hidrocarburos) o mediante simulaciones de dinámica del fuego con FDS o CFAST, cuya salida térmica sirve de entrada a los modelos mecánicos para actualizar las propiedades mencionadas anteriormente (véase [16, 15]).

2.4. Pandeo termo-inelástico

La combinación de la no linealidad geométrica propia de las inestabilidades de pandeo, la no linealidad constitutiva derivada del daño inelástico en los compuestos y la dependencia térmica de ambos fenómenos da lugar al concepto de pandeo termo-inelástico.

Este modelo computacional integrado, que captura grandes desplazamientos rotacionales, degradación de rigidez y variación de propiedades mecánicas con la temperatura, permite predecir con mayor fidelidad el colapso de estructuras de FRP expuestas al fuego (véase [17]).

3. Análisis numérico y experimental

A continuación, se presentan diferentes casos de verificación numérica y validación experimental del modelo computacional que justifican los aspectos discutidos previamente para pandeo termo-inelástico. Algunos de los casos descritos en esta sección son fruto del trabajo previo [15, 16, 17]. Nótese que todos los casos descritos pueden encontrarse con mayor lujo de detalle en [26].

3.1. Unidimensional

Verificación y validación de pandeo en bigas fabricadas con materiales compuestos expuestas a un gradiente de temperaturas de la cara caliente a la cara fría.

3.1.1. Numérico

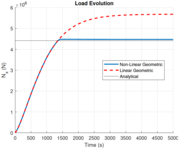
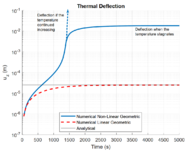
Para validar que la teoría de Felippa y Haugen [18] permite reproducir el fenómeno de pandeo se muestra la Figura 1 en donde se reproduce la biga de Euler mediante la compresión prescrita de los desplazamientos de uno de los extremos de la biga. Se comprueba que la carga del modelo no-lineal geométrico usando la teoría corrotacional se estanca en llegar a la carga crítica y en cambio la deflexión en el punto medio tiende a infinito, reproduciendo un caso claro de pandeo.

Figura 1. (Izquierda) Evolución de la carga respecto el tiempo. (Derecha) Evolución de la deflexión respecto el tiempo.

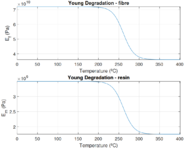
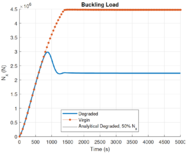
A este mismo problema de la biga de Euler se le puede incorporar el efecto de degradación del módulo de Young con respecto la temperatura. Esta degradación será de un 50% tal y como se muestra en la Figura 2, donde también se aprecia que la carga teórica de pandeo se reduce en igual magnitud para el caso virgen ( ${\textstyle {T}_{amb}<20{^{\circ }}C}$ ) y el degradado ( ${\textstyle {T}_{amb}>350{^{\circ }}C}$ ).

Figura 2. (Izquierda) Degradación del valor del módulo de Young en un 50% para fibra y matriz. (Derecha) Evolución de la carga de pandeo.

3.1.2. Feih et al.

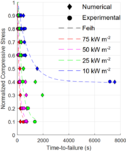
La validación experimental del modelo numérico en una dimensión se lleva a cabo mediante el experimento de Feih et al. [27], en este se describe una viga de material compuesto la cual se expone en una de sus caras a un flujo de calor determinado y la otra se aísla térmicamente. A su vez, esta biga es comprimida hasta llegar al fallo.

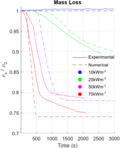
En este experimento se muestran las calibraciones numéricas de los materiales para la pirolisis, la variación de la temperatura en el espesor y la tensión nominal de compresión (véase la Figura 3).

Figura 3. (Izquierda) Evolución de la pirolisis. (Medio) Evolución de la temperatura en la cara fría, intermedia y caliente (0mm, 4.5mm y 9mm). (Derecha) Evolución de la carga y tiempo de fallo.

Se aprecia que para las propiedades del compuesto descrito en [27], la evolución de la fracción másica (pirolisis) se ajusta relativamente bien; las temperaturas predichas se ajustan con detalle a las registradas por los termopares; y que la evolución de la carga respecto al tiempo es también muy similar, exceptuando el caso de 25 kW/m² y en menor medida el de 50 kW/m².

3.2. Bidimensional

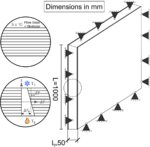
El modelo computacional bajo análisis se desarrolló específicamente para elementos tipo lámina. La diferencia substancial entre pandeo de viga y lámina basados en materiales compuestos radica en la orientación de las fibras y la temperatura a la cual se produce el pandeo para diferentes relaciones de aspecto. I.e., este caso aborda el concepto de pandeo ortótropo.

Figura 4. (Izquierda) Problema bajo consideración. (Derecha) Temperatura a la cual se produce el pandeo con respecto a la orientación de la fibra.

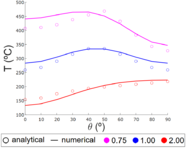
Se trata de una lámina simplemente apoyada en su perímetro. El compuesto se trata de un material ortótropo compuesto de fibra de vidrio y vinilester, todas las capas se orientan igual. Tal y como muestra la Figura 4, la temperatura a la cual pandea la lámina y la orientación de las capas se ajusta bastante con el modelo analítico derivado en [28].

3.3. Tridimensional

Aquí se aportan dos validaciones experimentales. La primera se enmarca dentro del proyecto FIBRESHIP [29] y la segunda respecto al proyecto BESST [30]. Ambas campañas se adecuan al código FTP.

3.3.1. Fibreship

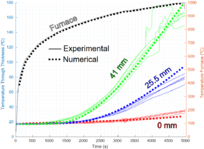
Esta validación se describe en más detalle en [16]. Esta campaña no desarrolla un fallo por pandeo, la lámina simplemente pierde carga resistiva debido a una asimetría. La Figura 5 demuestra que el modelo numérico es capaz de reproducir la evolución térmica basada en el modelo de Henderson [31].

Figura 5. (Izquierda) Campaña experimental FIBRESHIP. (Derecha) Registro de los termopares versus la simulación.

3.3.2. BESST

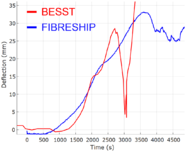
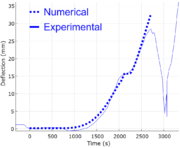
Esta validación sí que reproduce un fenómeno de pandeo termo-inelástico en 3D. En la Figura 6 se puede observar un claro colapso por pandeo y como el modelo numérico evoluciona similarmente al caso experimental hasta el colapso por pandeo del panel (2500s).

Figura 6. (Izquierda) Diferencia del tipo de deflexión en presencia de pandeo y no. (Derecha) Comparativa con el modelo numérico.

4. Marco regulador y criterios de diseño para materiales compuestos

La normativa actual para el diseño de estructuras expuestas al fuego se centra en criterios de barrera y compartimentación (tiempo de resistencia y propagación) sin considerar explícitamente el comportamiento térmico y mecánico interrelacionado de los compuestos. Los estándares SOLAS (capítulo II-2) junto con el Código FTP regulan la integridad e aislamiento de materiales “equivalentes al acero” en buques [10], mientras que el Eurocódigo EN 1991-1-2 [2] define los procedimientos de análisis de acciones térmicas en edificios civiles.

4.1. Criterios de degradación térmica

Sin embargo, estos marcos aprueban la aplicación de curvas de temperatura estándar o ensayos de horno sin atender a fenómenos como la pirolisis o la variación de las propiedades mecánicas con la temperatura, y extrapolan criterios de fluencia y pandeo ideados para materiales metálicos, lo que resulta inadecuado para materiales heterogéneos y ortótropos como los FRP. La pirolisis, proceso de descomposición que libera gases y reduce drásticamente la rigidez, es un efecto propio de la temperatura que debe tenerse en cuenta en los criterios para materiales compuestos.

A su vez, el análisis se fundamenta en el régimen elástico, obviando que el límite elástico varía con la temperatura.

4.2. Criterios de fluencia

Los criterios de fluencia en metalurgia se basan en ensayos uniaxiales y a menudo se generalizan mediante el criterio Tsai–Wu para composites, que combina tensiones en un índice cuadrático [32]. Sin embargo, su aplicación en diseño de estructuras expone dos limitaciones: primera, no incorpora la dependencia térmica de las constantes del criterio, y segunda, no considera la interacción con grandes desplazamientos, lo que dificulta su extrapolación con modelos no lineales geométricos para su integración efectiva.

4.3. Criterios de pandeo inducido por fuego

El ratio de esbeltez empleado en Eurocódigo y normas marítimas (SOLAS/FTP) para predecir pandeo local o global adolece de validez cuando la sección se calienta, pues la reducción de rigidez y el incremento de deformabilidad elevan el índice de esbeltez efectivo y reducen la carga crítica. Además, las limitaciones prácticas en buques y artefactos navales dificultan sobredimensionar espesores o emplear aislamientos intumescentes —que a menudo liberan humos tóxicos—, forzando soluciones tradicionales de compartimentación y tiempos de evacuación basados en ensayos más que en análisis integrados.

5. Conclusiones

Primero, el marco teórico de este estudio presenta limitaciones que se enumeran a continuación: no considera el fenómeno de auto-ignición de la matriz polimérica, carece de modelos poro-térmicos que describan la transferencia simultánea de masa y calor en el espesor, ignora la conductividad térmica en el plano y omite efectos de escala, delaminación, todos esenciales para una predicción más fiel de la respuesta de los compuestos bajo fuego.

Se ha desarrollado un marco teórico que aborda los mecanismos clave de flexibilidad, degradación térmica, excentricidad y pandeo termo-inelástico de materiales compuestos en comparación con los tradicionales. Estos fundamentos han sido validados mediante análisis numéricos en distintos niveles de complejidad —unidimensional, bidimensional y tridimensional— y corroborados con ensayos experimentales de forma satisfactoria.

Las normativas SOLAS/FTP y Eurocódigo fundamentan sus criterios en la compartimentación para evitar la propagación del fuego y en asegurar tiempos de evacuación adecuados mediante ensayos de resistencia. Sin embargo, trabajos previos [17] demostraron que un diseño conforme a estas reglas puede resultar insuficiente al no incorporar simultáneamente la no linealidad constitutiva y geométrica (pandeo termo-inelástico) en el análisis.

No considerar de forma acoplada los efectos térmicos, mecánicos y geométricos puede conducir a infraestimar las protecciones y dimensiones necesarias para salvaguardar la vida humana. En estructuras de materiales compuestos, la baja inercia térmica ofrece un mayor margen de evacuación, lo cual es una ventaja en el diseño de escenarios de fuego, pero el escenario post-incendio suele culminar en un colapso total, a diferencia de los materiales tradicionales que conservan parte de su capacidad portante. Este estudio pone de manifiesto que mejor predicción integral puede limitar este colapso post-incendio al considerar el pandeo termo-inelástico.

6. Referencias

[1]	D. Duthinh, "Structural Design for Fire: A Survey of Building Codes and Standards," Gaithersburg, MD, 2014.
[2]	"EN 1991-1-2:2024," AENOR, 2024.
[3]	"Documento Básico SI, Seguridad en caso de incendio," Ministerio de Vivienda y Agenda Urbana, 2025.
[4]	F. M. Peacock, "REPORT ON THE FIRE WHICH OCCURRED AT A HIGH-RISE BUILDING IN VALENCIA, SPAIN, ON 22 FEBRUARY 2024 (Incendio de Valencia de 2024)".
[5]	"Un incendi crema parcialment el centre logístic d'Abacus a Vilanova del Camí," Manresa, 2023.
[6]	. J. Calavera Ruíz, . E. González-Valle, . J. Díaz-Lozano, . J. L. Cano Muñoz, . J. Fernández-Gómez, . J. M. Izquierdo and . J. Ley Urzaiz, "The fire at the Windsor Building in Madrid. Investigation of the fire behaviour of the residual resistant capacity of the structure after fire," 2005.
[7]	K. Mcgrattan, S. Hostikka, R. Mcdermott, J. Floyd, C. Weinschenk and K. Overholt, "NIST Special Publication 1018 Sixth Edition Fire Dynamics Simulator Technical Reference Guide Volume 1: Mathematical Model".
[8]	K. McGrattan, "Fire Dynamics Simulator (versión 6) Technical Reference Guide, NISTSP1018," 2013.
[9]	R. D. Peacock, G. P. Forney and P. A. Reneke, CFAST - Consolidated Model of Fire Growth and Smoke Transport (Version 7) Volume 3: Software Development and Model Evaluation Guide.
[10]	Dirección General de la Marina Mercante, "SOLAS Ed. consolidada 2020 - Enmendado por la resolución MSC.436(99) y anteriores," 2020.
[11]	International Maritime Organization., "FTP Code : International code for application of fire test procedures, 2010," International Maritime Organization, 2012.
[12]	"Interim Guidelines For Use Of Fibre Reinforced Plastic (Frp) Elements Within Ship Structures: Fire Safety Issues," IMO, 2017.
[13]	"Fire on Board Ro-Ro Pax SORRENTO," 2015.
[14]	"REPORT ON THE INVESTIGATION OF FIRE ON m.v. “FELICITY ACE”," 2022.
[15]	R. Pacheco-Blazquez, D. Di Capua, J. García-Espinosa, O. Casals, T. Hakkarainen, A. Tissari and A. Korkealaakso, "A new computational method for the assessment of the passive fire protection applied to a composite containership," Engineering Structures, vol. 286, p. 116051, 7 2023.
[16]	R. Pacheco-Blazquez, D. Di Capua, J. García-Espinosa, O. Casals and T. Hakkarainen, "Thermo-mechanical analysis of laminated composites shells exposed to fire," Engineering Structures, vol. 253, 2022.
[17]	R. Pacheco-Blazquez, D. Di Capua, J. Garcia-Espinosa and O. Casals, "Methodology and application to assess thermo-mechanical buckling in composite marine structures," Ocean Engineering, vol. 267, p. 113002, 1 2023.
[18]	C. A. Felippa and B. Haugen, "A unified formulation of small-strain corotational finite elements: I. Theory," Computer Methods in Applied Mechanics and Engineering, vol. 194, no. 21-24 SPEC. ISS., pp. 2285-2335, 6 2005.
[19]	J. C. Simo and J. W. Ju, "Strain- and stress-based continuum damage models-I. Formulation," International Journal of Solids and Structures, vol. 23, no. 7, pp. 821-840, 1987.
[20]	F. Rastellini, S. Oller, O. Salomón and E. Oñate, "Composite materials non-linear modelling for long fibre-reinforced laminates," Computers & Structures, vol. 86, no. 9, pp. 879-896, 5 2008.
[21]	W. Voigt, "Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper," Annalen der Physik, vol. 274, no. 12, pp. 573-587, 1889.
[22]	A. Reuss, "Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle .," ZAMM ‐ Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, vol. 9, no. 1, pp. 49-58, 1929.
[23]	A. P. Mouritz and A. G. Gibson, Fire Properties of Polymer Composite Materials, vol. 143, Dordrecht: Springer Netherlands, 2006.
[24]	ISO834:1, "ISO - ISO 834-11:2014 - Fire resistance tests — Elements of building construction — Part 11: Specific requirements for the assessment of fire protection to structural steel elements," 2014.
[25]	ISO834:2, "ISO - ISO 834-2:2019 - Fire-resistance tests — Elements of building construction — Part 2: Requirements and recommendations for measuring furnace exposure on test samples," 2019.
[26]	R. Pacheco-Blazquez, "Constitutive model for fibre-reinforced composite materials exposed to high temperature," Universitat Politècnica de Catalunya, 2022.
[27]	S. Feih, A. P. Mouritz, Z. Mathys and A. G. Gibson, "Tensile strength modeling of glass fiber-polymer composites in fire," Sage PublicationsSage UK: London, England, 2007.
[28]	M. Al-Waily, "INTERNATIONAL JOURNAL OF ENERGY AND ENVIRONMENT Analytical and numerical thermal buckling analysis investigation of unidirectional and woven reinforcement composite plate structural," Online, 2015.
[29]	"Engineering, production and life‐cycle management for the complete construction of large‐length FIBRE‐based SHIPs," [Online]. Available: https://cordis.europa.eu/project/id/723360. [Accessed 12 05 2025].
[30]	F. Evegren, M. Rahm and T. Hertzberg, "Fire Tests of FRP Composite Ship Structures," 2007.
[31]	J. B. Henderson and T. E. Wiecek, "A Mathematical Model to Predict the Thermal Response of Decomposing, Expanding Polymer Composites," 1987. [Online].
[32]	S. Tsai and E. Wu, "General Theory of Strength for Anisotropic Materials," 1971. [Online].